Usefulness of Mendelian Randomization in Observational Epidemiology
Abstract
:1. Introduction
2. Mendelian Randomization in Observation Epidemiology
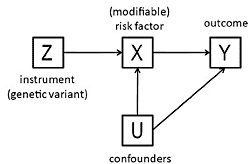
3. The Method of Instrumental Variables
- The beta coefficient is a consistent estimate of the causal effect of X on Y.
- The beta coefficient is actually underestimating the true causal effect of X on Y because of measurement error.
- The beta coefficient is overestimating the true causal effect of X on Y because of the presence of a confounder which is positively related to both X and Y.
- The non-zero beta coefficient is entirely due to the presence of a confounder which is related to both X and Y: in fact there is no causal effect of X on Y.
- The beta coefficient is non-zero because of a causal effect of Y on X, not of X on Y (i.e., reverse causation).
4. Simulations and Example
5. Review of Observational Studies Using Mendelian Randomization
6. Some Limitations of Mendelian Randomization
7. Conclusions
Acknowledgments
Reference and Notes
- Vandenbroucke, JP. When are observational studies as credible as randomised trials? Lancet 2004, 363, 1728–1731. [Google Scholar]
- Stampfer, MJ; Colditz, GA. Estrogen replacement therapy and coronary heart disease: a quantitative assessment of the epidemiologic evidence. Prev. Med 1991, 20, 47–63. [Google Scholar]
- Rossouw, JE; Anderson, GL; Prentice, RL; LaCroix, AZ; Kooperberg, C; Stefanick, ML; Jackson, RD; Beresford, SA; Howard, BV; Johnson, KC; Kotchen, JM; Ockene, J. Risks and benefits of estrogen plus progestin in healthy postmenopausal women: principal results from the Women’s Health Initiative randomized controlled trial. JAMA 2002, 288, 321–333. [Google Scholar]
- Rimm, EB; Stampfer, MJ; Ascherio, A; Giovannucci, E; Colditz, GA; Willett, WC. Vitamin E consumption and the risk of coronary heart disease in men. N. Engl. J. Med 1993, 328, 1450–1456. [Google Scholar]
- Osganian, SK; Stampfer, MJ; Rimm, E; Spiegelman, D; Hu, FB; Manson, JE; Willett, WC. Vitamin C and risk of coronary heart disease in women. J. Am. Coll. Cardiol 2003, 42, 246–252. [Google Scholar]
- MRC/BHF Heart Protection Study of antioxidant vitamin supplementation in 20,536 high-risk individuals: a randomised placebo-controlled trial. Lancet 2002, 360, 23–33.
- Ebrahim, S; Davey, SG. Mendelian randomization: can genetic epidemiology help redress the failures of observational epidemiology? Hum. Genet 2008, 123, 15–33. [Google Scholar]
- Davey, SG; Ebrahim, S. Mendelian randomization’: can genetic epidemiology contribute to understanding environmental determinants of disease? Int. J. Epidemiol 2003, 32, 1–22. [Google Scholar]
- Lewis, SJ; Smith, GD. Alcohol, ALDH2, and esophageal cancer: a meta-analysis which illustrates the potentials and limitations of a Mendelian randomization approach. Cancer Epidemiol. Biomarkers Prev 2005, 14, 1967–1971. [Google Scholar]
- Boccia, S; Hashibe, M; Galli, P; De, FE; Asakage, T; Hashimoto, T; Hiraki, A; Katoh, T; Nomura, T; Yokoyama, A; van Duijn, CM; Ricciardi, G; Boffetta, P. Aldehyde dehydrogenase 2 and head and neck cancer: a meta-analysis implementing a Mendelian randomization approach. Cancer Epidemiol. Biomarkers Prev 2009, 18, 248–254. [Google Scholar]
- Katan, MB. Apolipoprotein E isoforms, serum cholesterol, and cancer. Lancet 1986, 1, 507–508. [Google Scholar]
- Davey, SG; Leary, S; Ness, A; Lawlor, DA. Challenges and novel approaches in the epidemiological study of early life influences on later disease. Adv. Exp. Med. Biol 2009, 646, 1–14. [Google Scholar]
- Lawlor, DA; Harbord, RM; Sterne, JA; Timpson, N; Davey, SG. Mendelian randomization: using genes as instruments for making causal inferences in epidemiology. Stat. Med 2008, 27, 1133–1163. [Google Scholar]
- Thomas, DC; Conti, DV. Commentary: the concept of ‘Mendelian Randomization’. Int. J. Epidemiol 2004, 33, 21–25. [Google Scholar]
- Wehby, GL; Ohsfeldt, RL; Murray, JC. ‘Mendelian randomization’ equals instrumental variable analysis with genetic instruments. Stat. Med 2008, 27, 2745–2749. [Google Scholar]
- Greenland, S; Pearl, J; Robins, JM. Causal diagrams for epidemiologic research. Epidemiology 1999, 10, 37–48. [Google Scholar]
- Nelson, CR; Startz, R. The distribution of the instrumental variables estimator and its t-ratio when the instrument is a poor one. J. Busin 1990, 63, S125–S140. [Google Scholar]
- Stock, JH; Wright, JH; Yogo, M. A survey of weak instruments and weak identification in generalized method of moments. J. Econ. Statist 2002, 4, 518–529. [Google Scholar]
- Firmann, M; Mayor, V; Vidal, PM; Bochud, M; Pecoud, A; Hayoz, D; Paccaud, F; Preisig, M; Song, KS; Yuan, X; Danoff, TM; Stirnadel, HA; Waterworth, D; Mooser, V; Waeber, G; Vollenweider, P. The CoLaus study: a population-based study to investigate the epidemiology and genetic determinants of cardiovascular risk factors and metabolic syndrome. BMC Cardiovasc. Disord 2008, 8, 6. [Google Scholar]
- Perry, JR; Weedon, MN; Langenberg, C; Jackson, AU; Lyssenko, V; Sparso, T; Thorleifsson, G; Grallert, H; Ferrucci, L; Maggio, M; Paolisso, G; Walker, M; Palmer, CN; Payne, F; Young, E; Herder, C; Narisu, N; Morken, MA; Bonnycastle, LL; Owen, KR; Shields, B; Knight, B; Bennett, A; Groves, CJ; Ruokonen, A; Jarvelin, MR; Pearson, E; Pascoe, L; Ferrannini, E; Bornstein, SR; Stringham, HM; Scott, LJ; Kuusisto, J; Nilsson, P; Neptin, M; Gjesing, AP; Pisinger, C; Lauritzen, T; Sandbaek, A; Sampson, M; Zeggini, E; Lindgren, CM; Steinthorsdottir, V; Thorsteinsdottir, U; Hansen, T; Schwarz, P; Illig, T; Laakso, M; Stefansson, K; Morris, AD; Groop, L; Pedersen, O; Boehnke, M; Barroso, I; Wareham, NJ; Hattersley, AT; McCarthy, MI; Frayling, TM. Genetic evidence that raised sex hormone binding globulin (SHBG) levels reduce the risk of type 2 diabetes. Hum. Mol. Genet 2010, 19, 535–544. [Google Scholar]
- Ding, EL; Song, Y; Manson, JE; Hunter, DJ; Lee, CC; Rifai, N; Buring, JE; Gaziano, JM; Liu, S. Sex hormone-binding globulin and risk of type 2 diabetes in women and men. N. Engl. J. Med 2009, 361, 1152–1163. [Google Scholar]
- Perry, JR; Ferrucci, L; Bandinelli, S; Guralnik, J; Semba, RD; Rice, N; Melzer, D; Saxena, R; Scott, LJ; McCarthy, MI; Hattersley, AT; Zeggini, E; Weedon, MN; Frayling, TM. Circulating beta-carotene levels and type 2 diabetes-cause or effect? Diabetologia 2009, 52, 2117–2121. [Google Scholar]
- Herder, C; Klopp, N; Baumert, J; Muller, M; Khuseyinova, N; Meisinger, C; Martin, S; Illig, T; Koenig, W; Thorand, B. Effect of macrophage migration inhibitory factor (MIF) gene variants and MIF serum concentrations on the risk of type 2 diabetes: results from the MONICA/KORA Augsburg Case-Cohort Study, 1984–2002. Diabetologia 2008, 51, 276–284. [Google Scholar]
- Linsel-Nitschke, P; Gotz, A; Erdmann, J; Braenne, I; Braund, P; Hengstenberg, C; Stark, K; Fischer, M; Schreiber, S; El Mokhtari, NE; Schaefer, A; Schrezenmeir, J; Rubin, D; Hinney, A; Reinehr, T; Roth, C; Ortlepp, J; Hanrath, P; Hall, AS; Mangino, M; Lieb, W; Lamina, C; Heid, IM; Doering, A; Gieger, C; Peters, A; Meitinger, T; Wichmann, HE; Konig, IR; Ziegler, A; Kronenberg, F; Samani, NJ; Schunkert, H. Lifelong reduction of LDL-cholesterol related to a common variant in the LDL-receptor gene decreases the risk of coronary artery disease--a Mendelian Randomisation study. PLoS One 2008, 3, e2986. [Google Scholar]
- Cohen, JC; Boerwinkle, E; Mosley, TH, Jr; Hobbs, HH. Sequence variations in PCSK9, low LDL, and protection against coronary heart disease. N. Engl. J. Med 2006, 354, 1264–1272. [Google Scholar]
- Lawlor, DA; Harbord, RM; Timpson, NJ; Lowe, GD; Rumley, A; Gaunt, TR; Baker, I; Yarnell, JW; Kivimaki, M; Kumari, M; Norman, PE; Jamrozik, K; Hankey, GJ; Almeida, OP; Flicker, L; Warrington, N; Marmot, MG; Ben-Shlomo, Y; Palmer, LJ; Day, IN; Ebrahim, S; Smith, GD. The association of C-reactive protein and CRP genotype with coronary heart disease: findings from five studies with 4,610 cases amongst 18,637 participants. PLoS.One 2008, 3, e3011. [Google Scholar]
- Elliott, P; Chambers, JC; Zhang, W; Clarke, R; Hopewell, JC; Peden, JF; Erdmann, J; Braund, P; Engert, JC; Bennett, D; Coin, L; Ashby, D; Tzoulaki, I; Brown, IJ; Mt-Isa, S; McCarthy, MI; Peltonen, L; Freimer, NB; Farrall, M; Ruokonen, A; Hamsten, A; Lim, N; Froguel, P; Waterworth, DM; Vollenweider, P; Waeber, G; Jarvelin, MR; Mooser, V; Scott, J; Hall, AS; Schunkert, H; Anand, SS; Collins, R; Samani, NJ; Watkins, H; Kooner, JS. Genetic Loci associated with C-reactive protein levels and risk of coronary heart disease. JAMA 2009, 302, 37–48. [Google Scholar]
- Casas, JP; Shah, T; Cooper, J; Hawe, E; McMahon, AD; Gaffney, D; Packard, CJ; O’Reilly, DS; Juhan-Vague, I; Yudkin, JS; Tremoli, E; Margaglione, M; Di, MG; Hamsten, A; Kooistra, T; Stephens, JW; Hurel, SJ; Livingstone, S; Colhoun, HM; Miller, GJ; Bautista, LE; Meade, T; Sattar, N; Humphries, SE; Hingorani, AD. Insight into the nature of the CRP-coronary event association using Mendelian randomization. Int. J. Epidemiol 2006, 35, 922–931. [Google Scholar]
- Kamstrup, PR; Tybjaerg-Hansen, A; Steffensen, R; Nordestgaard, BG. Genetically elevated lipoprotein(a) and increased risk of myocardial infarction. JAMA 2009, 301, 2331–2339. [Google Scholar]
- Keavney, B; Danesh, J; Parish, S; Palmer, A; Clark, S; Youngman, L; Delepine, M; Lathrop, M; Peto, R; Collins, R. Fibrinogen and coronary heart disease: test of causality by ‘Mendelian randomization’. Int. J. Epidemiol 2006, 35, 935–943. [Google Scholar]
- Casas, JP; Bautista, LE; Smeeth, L; Sharma, P; Hingorani, AD. Homocysteine and stroke: evidence on a causal link from mendelian randomisation. Lancet 2005, 365, 224–232. [Google Scholar]
- Davey, SG; Lawlor, DA; Harbord, R; Timpson, N; Rumley, A; Lowe, GD; Day, IN; Ebrahim, S. Association of C-reactive protein with blood pressure and hypertension: life course confounding and mendelian randomization tests of causality. Arterioscler. Thromb. Vasc. Biol 2005, 25, 1051–1056. [Google Scholar]
- Almon, R; Alvarez-Leon, EE; Engfeldt, P; Serra-Majem, L; Magnuson, A; Nilsson, TK. Associations between lactase persistence and the metabolic syndrome in a cross-sectional study in the Canary Islands. Eur J Nutr 2009. [Google Scholar]
- Wu, Y; Li, H; Loos, RJ; Qi, Q; Hu, FB; Liu, Y; Lin, X. RBP4 variants are significantly associated with plasma RBP4 levels and hypertriglyceridemia risk in Chinese Hans. J. Lipid Res 2009, 50, 1479–1486. [Google Scholar]
- Trompet, S; Jukema, JW; Katan, MB; Blauw, GJ; Sattar, N; Buckley, B; Caslake, M; Ford, I; Shepherd, J; Westendorp, RG; de Craen, AJ. Apolipoprotein e genotype, plasma cholesterol, and cancer: a Mendelian randomization study. Am. J. Epidemiol 2009, 170, 1415–1421. [Google Scholar]
- Brennan, P; McKay, J; Moore, L; Zaridze, D; Mukeria, A; Szeszenia-Dabrowska, N; Lissowska, J; Rudnai, P; Fabianova, E; Mates, D; Bencko, V; Foretova, L; Janout, V; Chow, WH; Rothman, N; Chabrier, A; Gaborieau, V; Timpson, N; Hung, RJ; Smith, GD. Obesity and cancer: Mendelian randomization approach utilizing the FTO genotype. Int. J. Epidemiol 2009, 38, 971–975. [Google Scholar]
- Ioannidis, A; Ikonomi, E; Dimou, NL; Douma, L; Bagos, PG. Polymorphisms of the insulin receptor and the insulin receptor substrates genes in polycystic ovary syndrome: A Mendelian randomization meta-analysis. Mol Genet Metab 2009. [Google Scholar]
- Rice, NE; Bandinelli, S; Corsi, AM; Ferrucci, L; Guralnik, JM; Miller, MA; Kumari, M; Murray, A; Frayling, TM; Melzer, D. The paraoxonase (PON1) Q192R polymorphism is not associated with poor health status or depression in the ELSA or INCHIANTI studies. Int. J. Epidemiol 2009, 38, 1374–1379. [Google Scholar]
- Bech, BH; Autrup, H; Nohr, EA; Henriksen, TB; Olsen, J. Stillbirth and slow metabolizers of caffeine: comparison by genotypes. Int. J. Epidemiol 2006, 35, 948–953. [Google Scholar]
- Lim, LS; Tai, ES; Aung, T; Tay, WT; Saw, SM; Seielstad, M; Wong, TY. Relation of age-related cataract with obesity and obesity genes in an Asian population. Am. J. Epidemiol 2009, 169, 1267–1274. [Google Scholar]
- Freathy, RM; Timpson, NJ; Lawlor, DA; Pouta, A; Ben-Shlomo, Y; Ruokonen, A; Ebrahim, S; Shields, B; Zeggini, E; Weedon, MN; Lindgren, CM; Lango, H; Melzer, D; Ferrucci, L; Paolisso, G; Neville, MJ; Karpe, F; Palmer, CN; Morris, AD; Elliott, P; Jarvelin, MR; Smith, GD; McCarthy, MI; Hattersley, AT; Frayling, TM. Common variation in the FTO gene alters diabetes-related metabolic traits to the extent expected given its effect on BMI. Diabetes 2008, 57, 1419–1426. [Google Scholar]
- Welsh, P; Polisecki, E; Robertson, M; Jahn, S; Buckley, BM; de Craen, AJ; Ford, I; Jukema, JW; Macfarlane, PW; Packard, CJ; Stott, DJ; Westendorp, RG; Shepherd, J; Hingorani, AD; Smith, GD; Schaefer, E; Sattar, N. Unraveling the Directional Link between Adiposity and Inflammation: A Bidirectional Mendelian Randomization Approach. J Clin Endocrinol Metab 2009. [Google Scholar]
- Bochud, M; Marquant, F; Marques-Vidal, PM; Vollenweider, P; Beckmann, JS; Mooser, V; Paccaud, F; Rousson, V. Association between C-reactive protein and adiposity in women. J. Clin. Endocrinol. Metab 2009, 94, 3969–3977. [Google Scholar]
- Timpson, NJ; Lawlor, DA; Harbord, RM; Gaunt, TR; Day, IN; Palmer, LJ; Hattersley, AT; Ebrahim, S; Lowe, GD; Rumley, A; Davey, SG. C-reactive protein and its role in metabolic syndrome: mendelian randomisation study. Lancet 2005, 366, 1954–1959. [Google Scholar]
- Timpson, NJ; Harbord, R; Davey, SG; Zacho, J; Tybjaerg-Hansen, A; Nordestgaard, BG. Does greater adiposity increase blood pressure and hypertension risk?: Mendelian randomization using the FTO/MC4R genotype. Hypertension 2009, 54, 84–90. [Google Scholar]
- Timpson, NJ; Sayers, A; Davey-Smith, G; Tobias, JH. How does body fat influence bone mass in childhood? A Mendelian randomization approach. J. Bone Miner. Res 2009, 24, 522–533. [Google Scholar]
- Obermayer-Pietsch, BM; Bonelli, CM; Walter, DE; Kuhn, RJ; Fahrleitner-Pammer, A; Berghold, A; Goessler, W; Stepan, V; Dobnig, H; Leb, G; Renner, W. Genetic predisposition for adult lactose intolerance and relation to diet, bone density, and bone fractures. J. Bone Miner Res 2004, 19, 42–47. [Google Scholar]
- Brunner, EJ; Kivimaki, M; Witte, DR; Lawlor, DA; Davey, SG; Cooper, JA; Miller, M; Lowe, GD; Rumley, A; Casas, JP; Shah, T; Humphries, SE; Hingorani, AD; Marmot, MG; Timpson, NJ; Kumari, M. Inflammation, insulin resistance, and diabetes—Mendelian randomization using CRP haplotypes points upstream. PLoS. Med 2008, 5, e155. [Google Scholar]
- Kivimaki, M; Lawlor, DA; Smith, GD; Kumari, M; Donald, A; Britton, A; Casas, JP; Shah, T; Brunner, E; Timpson, NJ; Halcox, JP; Miller, MA; Humphries, SE; Deanfield, J; Marmot, MG; Hingorani, AD. Does high C-reactive protein concentration increase atherosclerosis? The Whitehall II Study. PLoS.One 2008, 3, e3013. [Google Scholar]
- Kivimaki, M; Lawlor, DA; Eklund, C; Smith, GD; Hurme, M; Lehtimaki, T; Viikari, JS; Raitakari, OT. Mendelian randomization suggests no causal association between C-reactive protein and carotid intima-media thickness in the young Finns study. Arterioscler. Thromb. Vasc. Biol 2007, 27, 978–979. [Google Scholar]
- Kivimaki, M; Smith, GD; Timpson, NJ; Lawlor, DA; Batty, GD; Kahonen, M; Juonala, M; Ronnemaa, T; Viikari, JS; Lehtimaki, T; Raitakari, OT. Lifetime body mass index and later atherosclerosis risk in young adults: examining causal links using Mendelian randomization in the Cardiovascular Risk in Young Finns study. Eur. Heart J 2008, 29, 2552–2560. [Google Scholar]
- Viikari, LA; Huupponen, RK; Viikari, JS; Marniemi, J; Eklund, C; Hurme, M; Lehtimaki, T; Kivimaki, M; Raitakari, OT. Relationship between leptin and C-reactive protein in young Finnish adults. J. Clin. Endocrinol. Metab 2007, 92, 4753–4758. [Google Scholar]
- Sunyer, J; Pistelli, R; Plana, E; Andreani, M; Baldari, F; Kolz, M; Koenig, W; Pekkanen, J; Peters, A; Forastiere, F. Systemic inflammation, genetic susceptibility and lung function. Eur. Respir. J 2008, 32, 92–97. [Google Scholar]
- Frayling, TM; Rafiq, S; Murray, A; Hurst, AJ; Weedon, MN; Henley, W; Bandinelli, S; Corsi, AM; Ferrucci, L; Guralnik, JM; Wallace, RB; Melzer, D. An interleukin-18 polymorphism is associated with reduced serum concentrations and better physical functioning in older people. J. Gerontol. A Biol. Sci. Med. Sci 2007, 62, 73–78. [Google Scholar]
- Bochud, M; Chiolero, A; Elston, RC; Paccaud, F. A cautionary note on the use of Mendelian randomization to infer causation in observational epidemiology. Int. J. Epidemiol 2008, 37, 414–416. [Google Scholar]
- Smith, GD; Ebrahim, S. Mendelian randomization: prospects, potentials, and limitations. Int. J. Epidemiol 2004, 33, 30–42. [Google Scholar]
- Greenland, S. An introduction to instrumental variables for epidemiologists. Int. J. Epidemiol 2000, 29, 722–729. [Google Scholar]
- Didelez, V; Sheehan, N. Mendelian randomization as an instrumental variable approach to causal inference. Stat. Methods Med. Res 2007, 16, 309–330. [Google Scholar]
- Zollner, S; Wen, X; Hanchard, NA; Herbert, MA; Ober, C; Pritchard, JK. Evidence for extensive transmission distortion in the human genome. Am. J. Hum. Genet 2004, 74, 62–72. [Google Scholar]
- Isotalo, PA; Wells, GA; Donnelly, JG. Neonatal and fetal methylenetetrahydrofolate reductase genetic polymorphisms: an examination of C677T and A1298C mutations. Am. J. Hum. Genet 2000, 67, 986–990. [Google Scholar]
- Zetterberg, H; Regland, B; Palmer, M; Ricksten, A; Palmqvist, L; Rymo, L; Arvanitis, DA; Spandidos, DA; Blennow, K. Increased frequency of combined methylenetetrahydrofolate reductase C677T and A1298C mutated alleles in spontaneously aborted embryos. Eur. J. Hum. Genet 2002, 10, 113–118. [Google Scholar]
- Minelli, C; Thompson, JR; Tobin, MD; Abrams, KR. An integrated approach to the meta-analysis of genetic association studies using Mendelian randomization. Am. J. Epidemiol 2004, 160, 445–452. [Google Scholar]
- Thompson, JR; Minelli, C; Abrams, KR; Tobin, MD; Riley, RD. Meta-analysis of genetic studies using Mendelian randomization--a multivariate approach. Stat. Med 2005, 24, 2241–2254. [Google Scholar]
- Thomas, DC; Lawlor, DA; Thompson, JR. Re: Estimation of bias in nongenetic observational studies using “Mendelian triangulation” by Bautista et al. Ann. Epidemiol 2007, 17, 511–513. [Google Scholar]
- Robins, J; Rotnitzky, A. Estimation of treatment effects in randomised trials with non-compliance and a dichotomous outcome using structural mean models. Biometrika 2004, 90, 763–783. [Google Scholar]
- Vansteelandt, S; Goetghebeur, S. Causal inference with generalized structural mean models. J. Royal Statist. Soc. Series B (Statistical Methodology) 2003, 65, 817–835. [Google Scholar]
- Palmer, TM; Thompson, JR; Tobin, MD; Sheehan, NA; Burton, PR. Adjusting for bias and unmeasured confounding in Mendelian randomization studies with binary responses. Int. J. Epidemiol 2008, 37, 1161–1168. [Google Scholar]
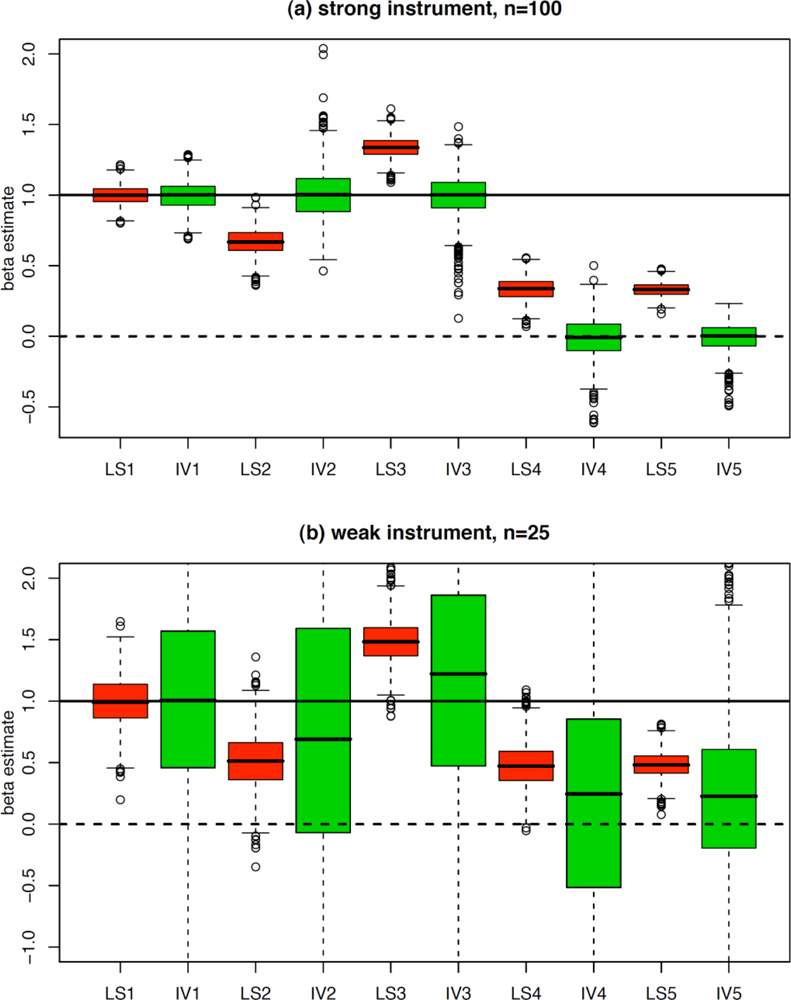

| Model | Step 1 | Step 2 | Step 3 | Step 4 | Step 5 |
|---|---|---|---|---|---|
| 1. Causal effect of X on Y | Z = N(0,1) | X = Z+N(0,1) | Y = X+N(0,1) | ||
| 2. Causal effect of X on Y and measurement errors on X and Y | Z = N(0,1) | Xtrue = Z+N(0,1) | Ytrue = Xtrue+N(0,1) | X = Xtrue+N(0,1) | Y = Ytrue+N(0,1) |
| 3. Causal effect of X on Y and presence of a confounder | Z = N(0,1) | U = N(0,1) | X = Z+U+N(0,1) | Y = X+U+N(0,1) | |
| 4. No causal effect between X and Y and presence of a confounder | Z = N(0,1) | U = N(0,1) | X = Z+U+N(0,1) | Y = U+N(0,1) | |
| 5. Causal effect of Y on X (reverse causation) | Z = N(0,1) | Y = N(0,1) | X = Z+Y+N(0,1) |
| Outcome (Y) | Gene | Variant(s) (Z) | Risk factor (X) | Causality* | Reference |
|---|---|---|---|---|---|
| Cardiovascular epidemiology | |||||
| Type 2 diabetes | SHBG | rs1799941 | SHBG | + | [20] |
| Type 2 diabetes | SHBG | rs6257, rs6259 | SHBG | + | [21] |
| Type 2 diabetes | BCMO1 | rs6564851 | β-carotene | − | [22] |
| Type 2 diabetes | MIF | rs1007888 | MIF | + | [23] |
| - Coronary artery disease | LDLR | rs2228671 | LDL-cholesterol | [24] | |
| Coronary heart disease | PCSK9 | Y142X, C679X | LDL | + | [25] |
| Coronary heart disease | CRP | rs1130864 | CRP | − | [26] |
| Coronary heart disease | CRP | rs7553007 | CRP | − | [27] |
| Myocardial infarction | CRP | rs1130864 | CRP | − | [28] |
| Myocardial infarction | LPA | KIV-2 (CNV) | Lp(a) | + | [29] |
| Myocardial infarction | FGB | −148C/T | fibrinogen | − | [30] |
| -Stroke | MTHFR | C677T | homocysteine | + | [31] |
| Hypertension | CRP | rs1800947, | CRP | − | [32] |
| Metabolic syndrome | LCT | rs4988235 (-13910-C/T) | Milk consumption | + | [33] |
| Hypertriglyceridemia | RBP4 | rs3758538 | RBP4 | − | [34] |
| Cancer epidemiology | |||||
| Cancer | APOE | E2, E3, E4 | cholesterol | − | [35] |
| Head and neck cancer | ALDH2 | rs671 | Alcohol consumption | + | [10] |
| Oesophageal cancer | ALDH2 | rs671 | Alcohol consumption | + | [9] |
| Lung or kidney cancer | FTO | rs9939609 | BMI | + | [36] |
| Other topics | |||||
| Polycystic ovary syndrome | IRS-1 | Gly972Arg | Insulin | + | [37] |
| Depression | PON1 | rs662 | PON1 activity | − | [38] |
| Stillbirth | CYP1A2, NAT2, GSTA1 | slow/fast metabolizers | caffeine | + | [39] |
| Cataract | FTO | rs9939609 | BMI | + | [40] |
| Outcome (Y) | Gene (s) | Variant(s) (Z) | Risk factor (X) | Causality* | Reference |
|---|---|---|---|---|---|
| Metabolic traits (insulin, lipids, etc) | FTO | rs9939609 | BMI | + | [41] |
| BMI | CRP | rs1800947, rs1205 | CRP | − | [42] |
| BMI | CRP, | rs7553007 | CRP | + | [43] |
| LEPR | rs1805096 | ||||
| BMI, blood pressure, triglycerides, HDL, waist-to-hip ratio, HOMA-R | CRP | rs1800947, rs1130864, rs1205 | CRP | − | [44] |
| Blood pressure | MC4R | rs17782313 rs9939609 | BMI | + | [45] |
| FTO | |||||
| Blood pressure | CRP | rs1800947, | CRP | − | [32] |
| Bone mass | MC4R | rs17782313 | adiposity | + | [46] |
| FTO | rs9939609 | ||||
| Bone mass density, bone fractures | LCT | rs4988235 (-13910-C/T) | Calcium intake | + | [47] |
| HbA1c | CRP | rs1130864, rs1205, rs3093077 | CRP | − | [48] |
| Carotid-intima media thickness | CRP | rs1130864, rs1205, rs3093077 | CRP | − | [49] |
| Carotid-intima media thickness | CRP | rs 2794521, rs3091244, rs1800947, rs1130864, rs1205 | CRP | − | [50] |
| Carotid-intima media thickness | FTO | rs9939609 | BMI | + | [51] |
| Serum leptin | CRP | rs 2794521, rs3091244, rs1800947, rs1130864, rs1205 | CRP | − | [52] |
| Lung function | CRP | rs1205, rs1800947 | CRP | + | [53] |
| Physical functioning | IL-18 | rs5744256 | IL-18 | + | [54] |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bochud, M.; Rousson, V. Usefulness of Mendelian Randomization in Observational Epidemiology. Int. J. Environ. Res. Public Health 2010, 7, 711-728. https://doi.org/10.3390/ijerph7030711
Bochud M, Rousson V. Usefulness of Mendelian Randomization in Observational Epidemiology. International Journal of Environmental Research and Public Health. 2010; 7(3):711-728. https://doi.org/10.3390/ijerph7030711
Chicago/Turabian StyleBochud, Murielle, and Valentin Rousson. 2010. "Usefulness of Mendelian Randomization in Observational Epidemiology" International Journal of Environmental Research and Public Health 7, no. 3: 711-728. https://doi.org/10.3390/ijerph7030711
APA StyleBochud, M., & Rousson, V. (2010). Usefulness of Mendelian Randomization in Observational Epidemiology. International Journal of Environmental Research and Public Health, 7(3), 711-728. https://doi.org/10.3390/ijerph7030711