Acoustic Sensor Network for Relative Positioning of Nodes
Abstract
:1. Introduction
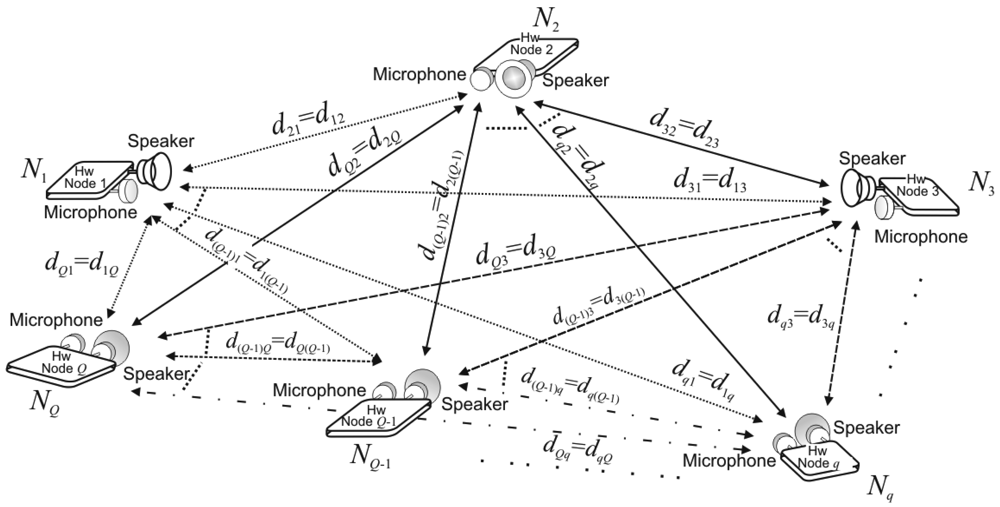
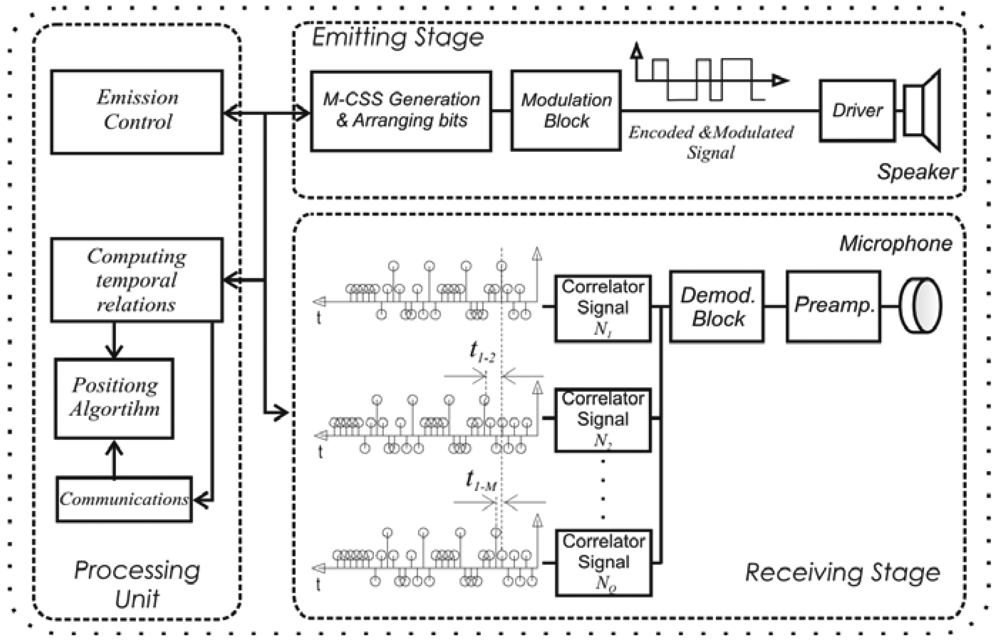
2. System Architecture
2.1. Encoding Scheme to Multi-User Detection
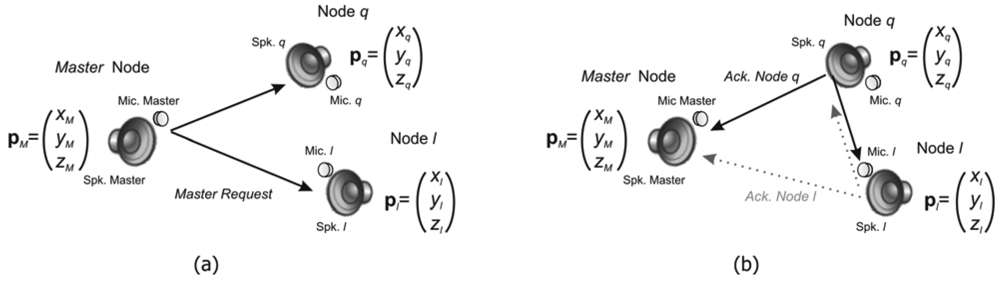
2.2. Principle of Measurements
2.3. Pseudo-Time-of-Flight Equations
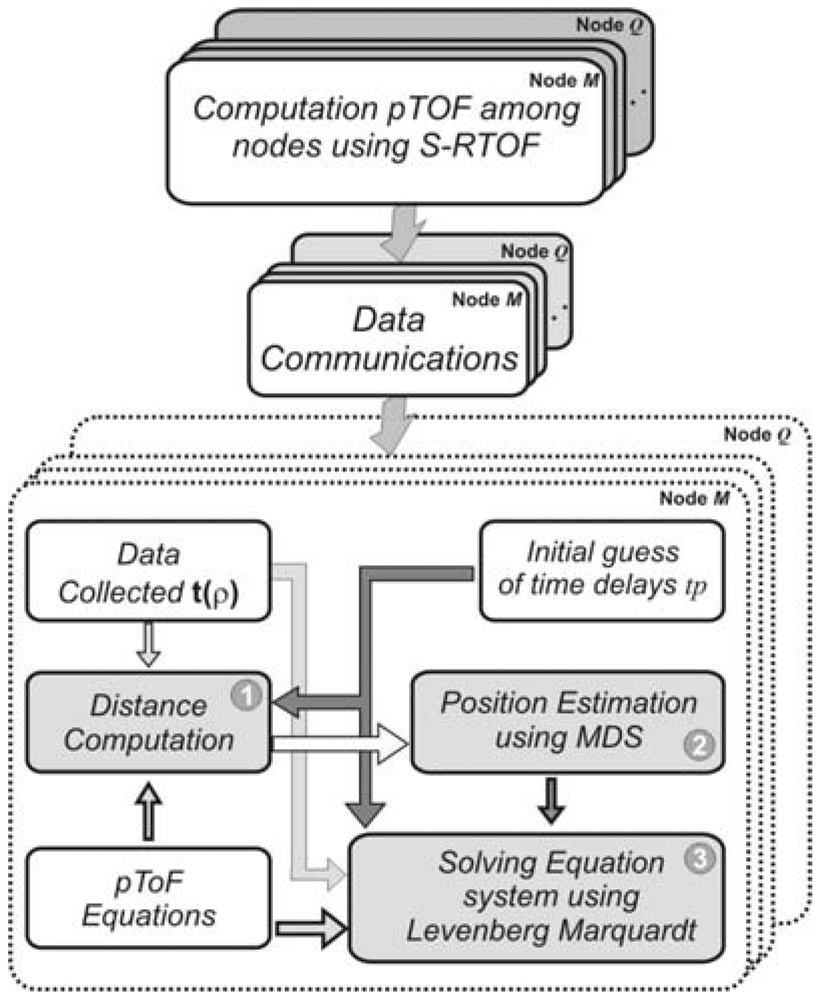
3. Positioning Algorithm
3.1. MDS Position Estimation
Computation of distances between Master and every slave node
Computation of distances between every pair of slave nodes
Computation of node positions
3.2. Refining Results
4. Simulations Results and Performance Analysis
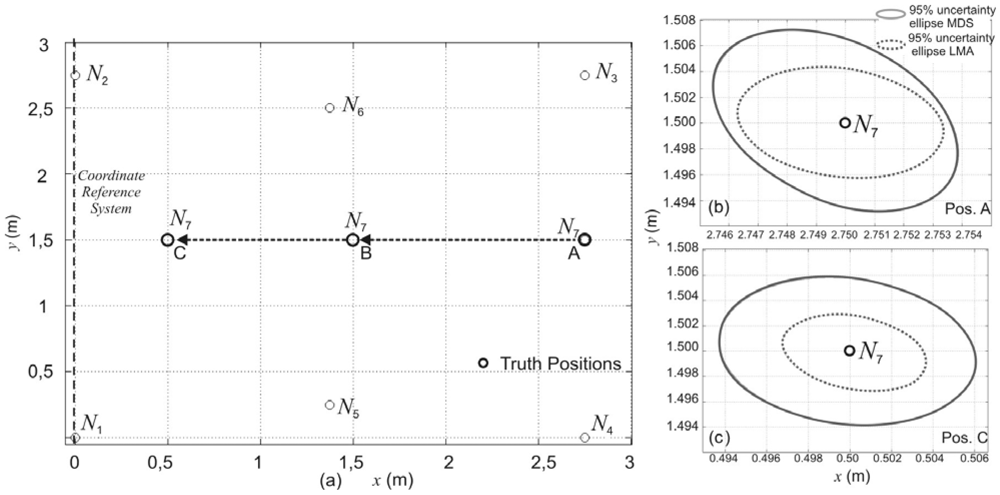
4.1. Node Position Estimation Considering a Gaussian Error in the pTOF Measurements
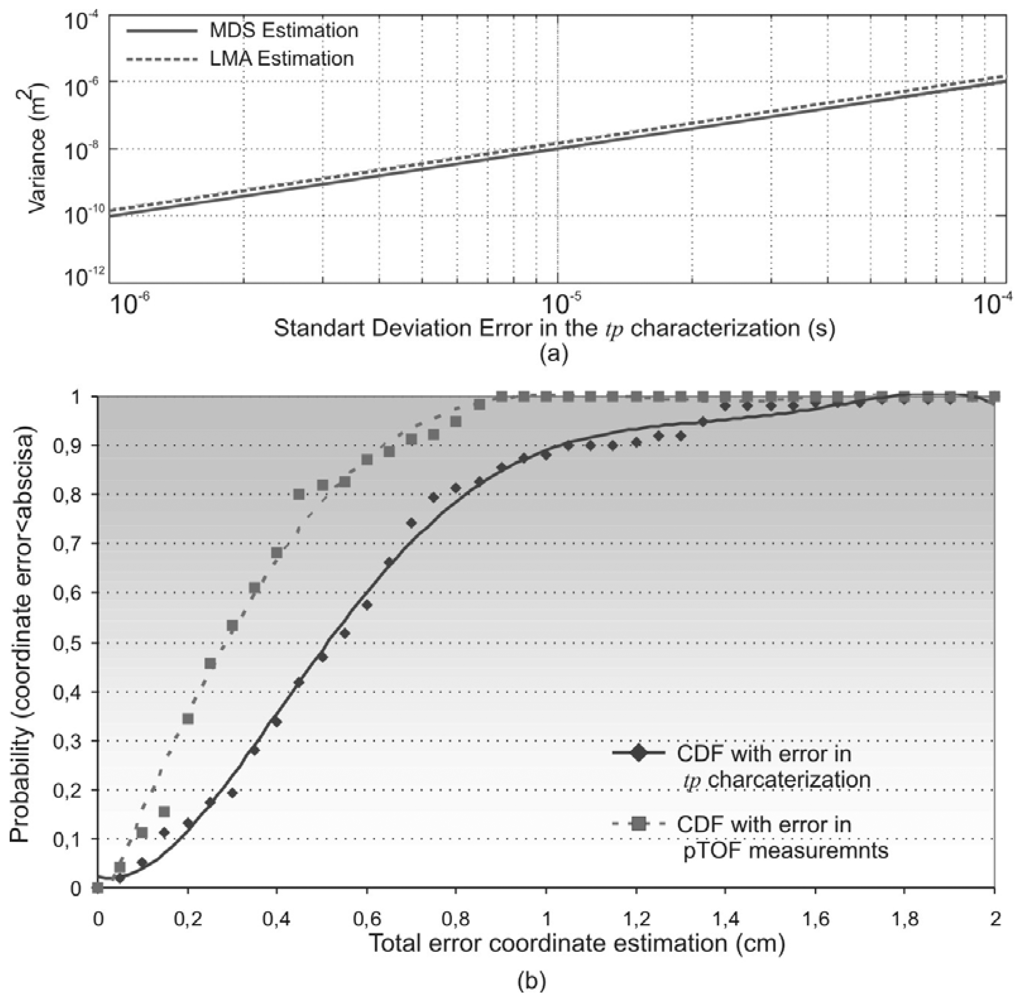
4.2. Node Position Estimation Considering Errors in the Signal Processing Delay Characterization
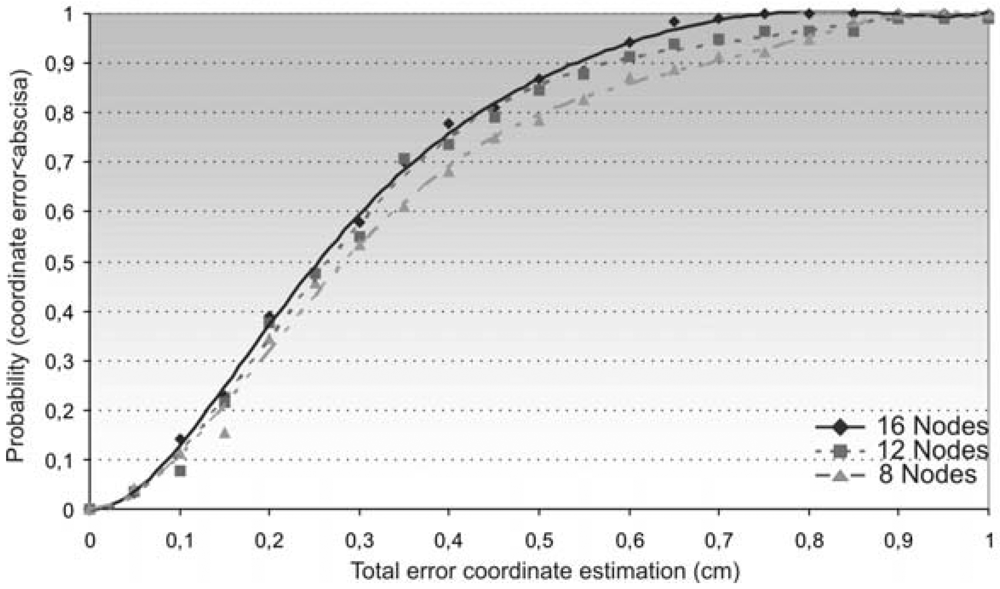
4.3. Node Position Estimation Varying the Topology of Nodes
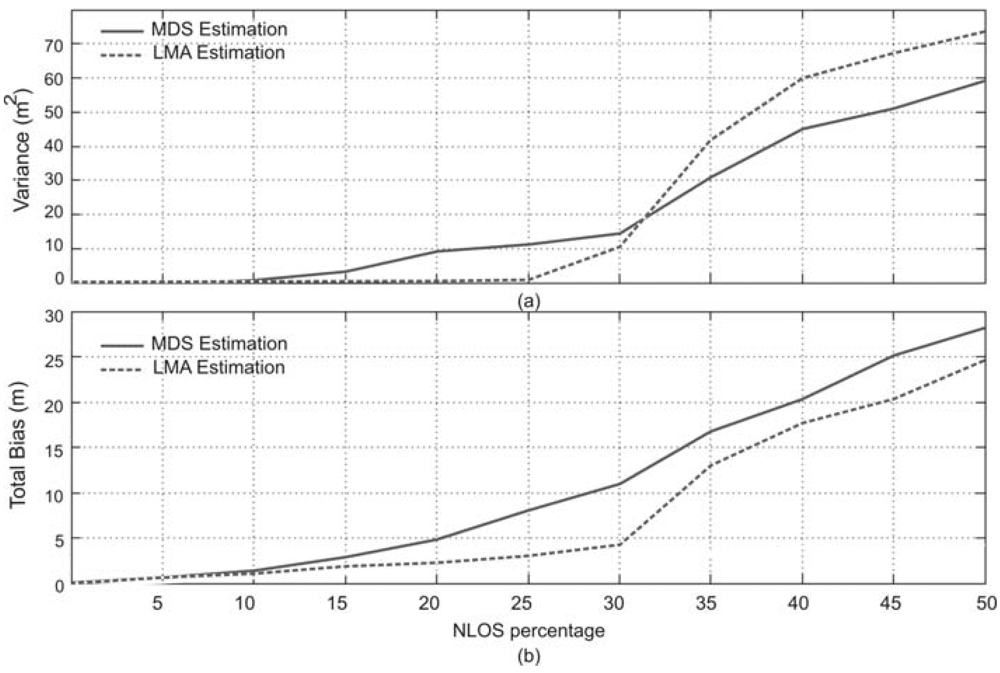
4.4. Effect of Non-Gaussian Errors in Node Position Estimation
5. Conclusions
Acknowledgments
References and Notes
- Hazas, M.; Kray, C.; Gellersen, H.; Agbota, H.; Kortuem, G.; Krohn, A. A relative positioning system for co-located mobile devices. Third International Conference on Mobile Systems, Applications, and Services (MobiSys'05), Seattle, WA, USA, June 6-8, 2005; pp. 177–190.
- Navarro-Serment, L.; Grabowski, R.; Paredis, C.; Kohsla, P. Millibots. IEEE Robot. Automat. 2002, 9, 31–40.
- Higtower, J.; Borriello, G. Location systems for ubiquitous computing. IEEE Comput. 2001, 34, 57–66. [Google Scholar]
- Patwari, N.; Hero, A.; Perkins, M.; Correal, N.; O'dea, R. Relative location estimation in wireless sensor networks. IEEE Trans. Signal Process 2005, 51, 2137–2148. [Google Scholar]
- Krohn, A.; Zimmer, T.; Beigl, M. Enhancing tabletop games with relative positioning technology. In Advances in Pervasive Computing; Oesterreichische Computer Gesellschaft: Wien, Austria, 2004. [Google Scholar]
- Torgerson, W.S. Multidimensional scaling: theory and method. Psychometrika 1952, 17, 401–419. [Google Scholar]
- Shang, Y.; Meng, J.; Shi, H. A new algorithm for relative localization in wireless sensor networks. 18th International Parallel and Distributed Processing Symposium (IPDPS'04), Santa Fe, NM, USA, April 26-30, 2004; p. 24.
- Moses, R.; Krishnamurthy, D.; Patterson, R. A self-localization method for wireless sensor networks. Eurasip J. appl. Signal Process 2003, 4, 348–358. [Google Scholar]
- Raykar, V.; Kozintsev, I.; Lienhart, R. Position calibration of microphones and loudspeakers in distributed computing platforms. IEEE Trans. Speech Audio Proc. 2005, 13, 70–83. [Google Scholar]
- De Marziani, C.; Urena, J.; Hernández, Á.; Mazo, M.; Alvarez, F.; García, J.J.; Villadangos, J.M.; Jimenez, A. Simultaneous Measurement of Times-of-Flight and Communications in Acoustic Sensor Networks. Workshop on Intelligent Signal Processing (WISP'05), Faro, Portugal, September 1-3, 2005; pp. 122–127.
- Wylie-Green, M.P.; Wang, S.S. Robust range estimation in the presence of the non-line-of-sight error. IEEE Vehicular Technology Conference, Rhodes, Greece, May 6-9, 2001; pp. 101–105.
- Chan, Y.; Tsui, W.; So, H.; Ching, P. Time-of-arrival based localization under NLOS conditions. IEEE Trans. Veh. Technol. 2006, 55, 12–24. [Google Scholar]
- Fan, P.; Darnell, M. Sequence design for communications applications; Research Studies Press Ltd.: London, UK, 1996. [Google Scholar]
- ZigBee Alliance. Available online: http://www.zigbee.org (accessed on December 15th, 2007).
- Tseng, C.-C.; Liu, C.L. Complementary set of sequences. IEEE Trans. Inform. Theor. 1972, IT-18, 644–652. [Google Scholar]
- De Marziani, C.; Ureña, J.; Hernandez, A.; Mazo, M.; Alvarez, F.J.; Garcia, J.J.; Donato, P. Modular architecture for efficient generation and correlation of complementary set of sequences. IEEE Trans. Sig. Process 2007, 55, 2323–2337. [Google Scholar]
- De Marziani, C.; Urena, J.; Hernandez, A.; Mazo, M.; Garcia, J.J.; Jimenez, A.; Villadangos, J.M.; Perez, M.C.; Ochoa, A.; Alvarez, F. Inter-symbol interference reduction on macro-sequences generated from complementary set of sequences. IEEE Industrial Electronics, IECON 2006—32nd Annual Conference 2006, Paris, France, November 7-10, 2006; pp. 3367–3372.
- Rydström, M.; Urruela, A.; Ström, E.; Svensson, A. A low complexity algorithm for sensor localization. 11th European Wireless Conference (EW'05), Nicosia, Cyprus, April 10-13, 2005; pp. 714–718.
- McCrady, D.; Doyle, L.; Forstrom, H.; Dempsey, T.; Martorana, M. Mobile ranging using low-accuracy clocks. IEEE Trans. Microwave Theory 2000, 48, 951–957. [Google Scholar]


© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
De Marziani, C.; Ureña, J.; Hernandez, Á.; Mazo, M.; García, J.J.; Jimenez, A.; Pérez Rubio, M.C.; Álvarez, F.; Villadangos, J.M. Acoustic Sensor Network for Relative Positioning of Nodes. Sensors 2009, 9, 8490-8507. https://doi.org/10.3390/s91108490
De Marziani C, Ureña J, Hernandez Á, Mazo M, García JJ, Jimenez A, Pérez Rubio MC, Álvarez F, Villadangos JM. Acoustic Sensor Network for Relative Positioning of Nodes. Sensors. 2009; 9(11):8490-8507. https://doi.org/10.3390/s91108490
Chicago/Turabian StyleDe Marziani, Carlos, Jesus Ureña, Álvaro Hernandez, Manuel Mazo, Juan Jesús García, Ana Jimenez, M. Carmen Pérez Rubio, Fernando Álvarez, and José Manuel Villadangos. 2009. "Acoustic Sensor Network for Relative Positioning of Nodes" Sensors 9, no. 11: 8490-8507. https://doi.org/10.3390/s91108490
APA StyleDe Marziani, C., Ureña, J., Hernandez, Á., Mazo, M., García, J. J., Jimenez, A., Pérez Rubio, M. C., Álvarez, F., & Villadangos, J. M. (2009). Acoustic Sensor Network for Relative Positioning of Nodes. Sensors, 9(11), 8490-8507. https://doi.org/10.3390/s91108490



