1. Introduction
Inherent instability such as in pull-in phenomenon and stiction exists in both microelectromechanical (MEM) and nanoelectromechanical (NEM) actuators. Such instability is due to some kind of surface force, i.e. electrostatic, van der Waals (vdW), Casimir and capillary forces. Although vdW and Casimir forces can be neglected when designing a MEM actuator, they play important roles at nanoscales [
8-
13].
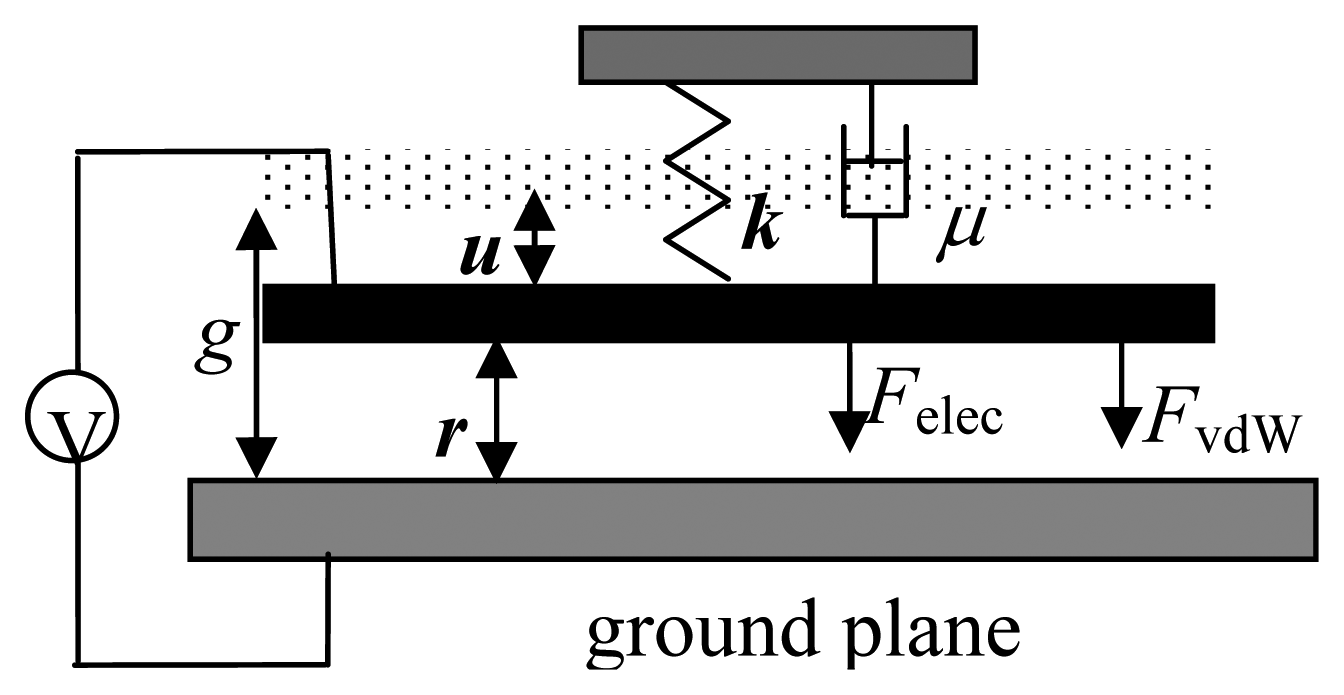
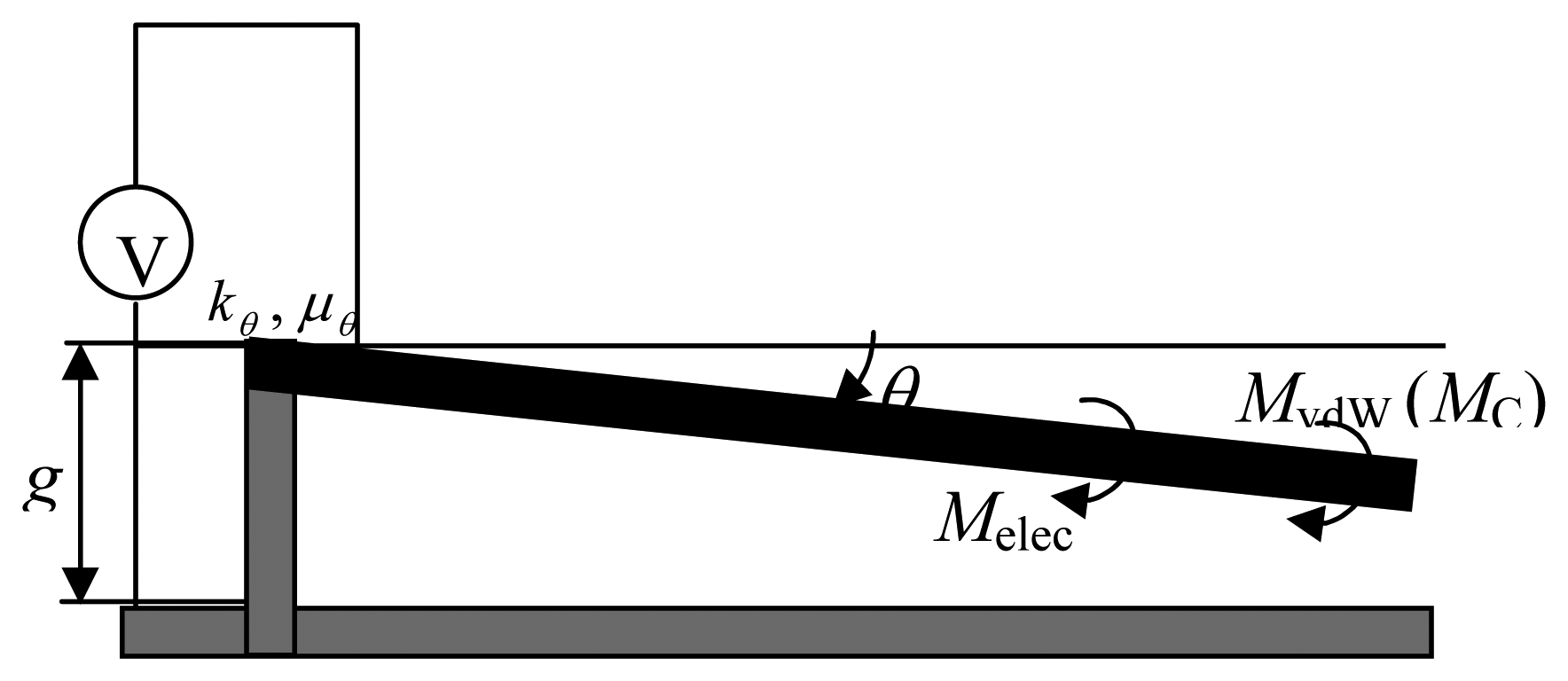
A typical MEM (NEM) parallel-plate (or torsional) actuator is made up of two conducting electrodes, one is typically fixed and the other, which is controlled by an equivalent mechanical spring, is movable (or rotary) [
1-
4]. The corresponding system can be simplified to one degree of freedom (1DOF). The 1DOF is the displacement,
u, of the upper movable beam for the parallel-plate model, and is the torsional angle,
θ, for the torsional model. At a certain voltage, the movable electrode becomes unstable and collapses (or
pulls-in) to the ground plane. The voltage and displacement (or torsional angle) of the actuators under this state are said to be the pull-in voltage and pull-in displacement (or the pull-in angle) for the parallel-plate (or torsional) actuators, respectively. They are briefly described as the pull-in parameters.
Using a one-dimensional (1D) model, the pull-in parameters have been analytically obtained by many researchers when electrostatic [
5-
7], vdW and Casimir forces [
8-
16] are considered. The bifurcation analysis for an electrostatic micro-(nano-) actuator has been addressed in [
9-
17] with the consideration of electrostatic, vdW, and Casimir forces for the parallel-plate and torsional actuators. In [
9,
11,
12], the influences of vdW or Casimir force (torque) on the electrostatic parallel-plate (torsional) actuators was studied. There are two bifurcation points, of which one is a Hopf bifurcation point, and the other is an unstable saddle point. The phase portraits are also drawn, in which periodic orbits are around the Hopf bifurcation point, but the periodic orbit will break into a homoclinic orbit when meeting the unstable saddle point.
In this paper, the influence of damping on the dynamical behavior of the electrostatic parallel-plate and torsional actuators with the vdW or Casimir force (torque) is presented, and the results are compared with those in Refs. [
9,
11,
12]. The damping considered in this paper can be a kind of gas (squeeze film) friction which is assumed, without loss of generality, to be linearly proportional to the velocity.
4. Dynamical behavior
In this section, we just discuss the dynamical behavior of the parallel-plate model with the electrostatic and vdW forces.
To discuss the dynamical behavior of
equation (3), first we transform the second-order ordinary differential equation (ODE)
(3) into the first-order ODE. Then we set
x =
Δ,
y = dΔ/d
τ and obtain:
The stationary solutions of this system can be obtained by setting zero of the right-hand side of
equation (17). From the first
equation of (17), we easily get
y = 0 Substituting
y = 0 into the second
equation of (17), we obtain an equivalent function:
to solve
x. The critical condition of this equation has solved in Section 2.1. Now, in order to see clearly the variation of the equilibrium point
x with the continuous change of parameters
a and
bvdW, we solve
equation (18) numerically for
x as a function of
a and
bvdW. We plot the variation of
x with parameter
a for different parameter
bvdW, the solution is shown in
Figure 7. Because
a =
ε0wLV2/2
kg3 is positive, then the solution is physical meaningful when the solution curves are on the right of
a = 0. So from this figure, we notice that
equation (18) has one or two equilibrium points for
a ≥ 0 just when
, otherwise there is no equilibrium point.
In order to check the stability of the equilibrium points, we need the Jacobian matrix of
equation (17):
We first discuss the stability of the equilibrium points with the given parameters
a = 0 and
. According to
Figure 7, there are two equilibrium points (
x1,0)and (
x2,0) satisfying the inequality
x1<
x*<
x2.
Firstly, we consider the equilibrium point stability of the special state that there is no electrostatic force on the upper movable beam. Then substituting
and
x =
x1 <
x* into
equation (19), we get:
Its corresponding eigenvalues are
Here, we discuss the property of the eigenvalues when the damping coefficient is positive. Because
x1<
x*, then
is absolutely negative. When
, the two eigenvalues λ
1,2 are all real, and they all are absolutely negative. This means the equilibrium point (
x1,0) is a stable node. According to the property of node, this point is an equilibrium point at first. At this position, the elastic force is equal to the vdW force, and the parallel-plate actuator keeps balance state. When we add a small perturbation on the upper movable beam, the perturbation will die out at the stable node. When
, the two eigenvalues λ
1,2 are a pair of complex conjugates, and the real parts of them are absolutely negative. This means the equilibrium point (
x1,0) is a stable focus. According to the property of focus, this point is also an equilibrium point at first. When we add a small perturbation on the upper movable beam, then the trajectory close to the equilibrium position resembles a spiral. Above all, at the point of (
x1,0), the real parts of the eigenvalues are negative, this equilibrium point (
x1,0) is always stable. Subsequently, we take
and
x =
x2 >
x* into
equation (19), solve its eigenvalue equation, we know that it has two real roots, of which one is positive, the other is negative. This means that the equilibrium point (
x2,0) is a saddle point. At equilibrium position, if we add a small perturbation on it, the trajectory of the upper movable beam will leave the equilibrium position because one of the eigenvalues is positive. We then call this equilibrium state unstable.
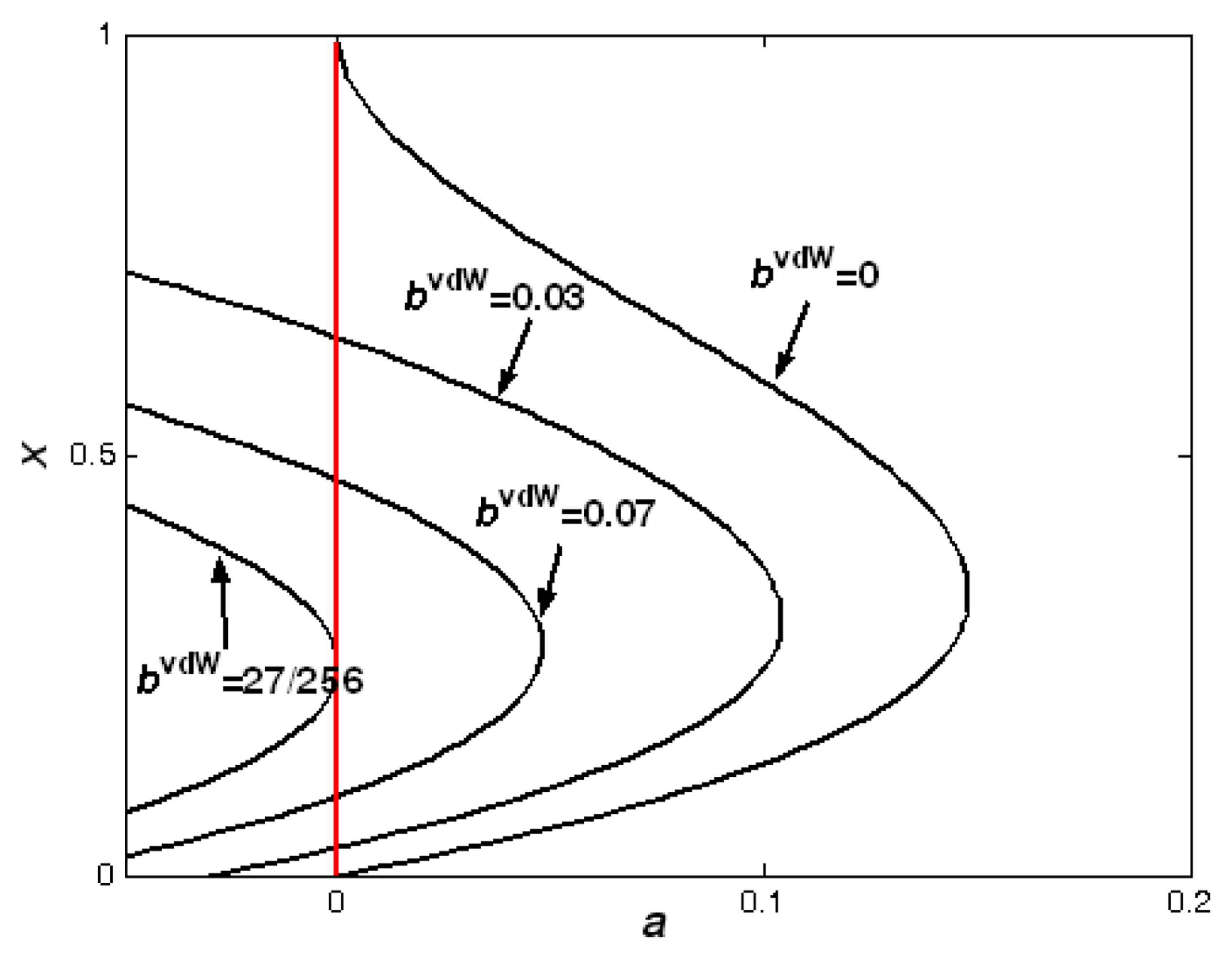
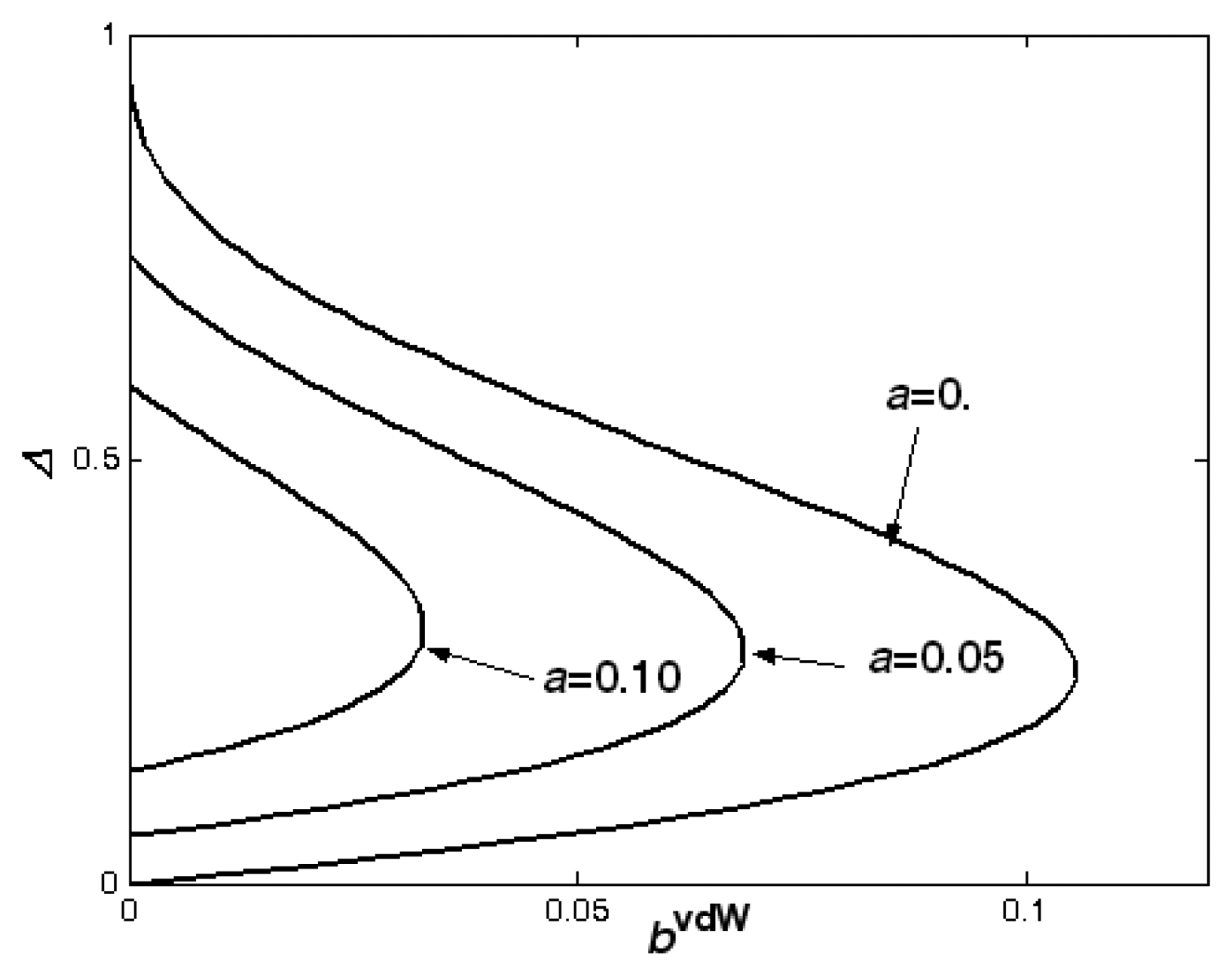
Secondly, applying the same method to discuss the stability of the two solutions with any different given
a and
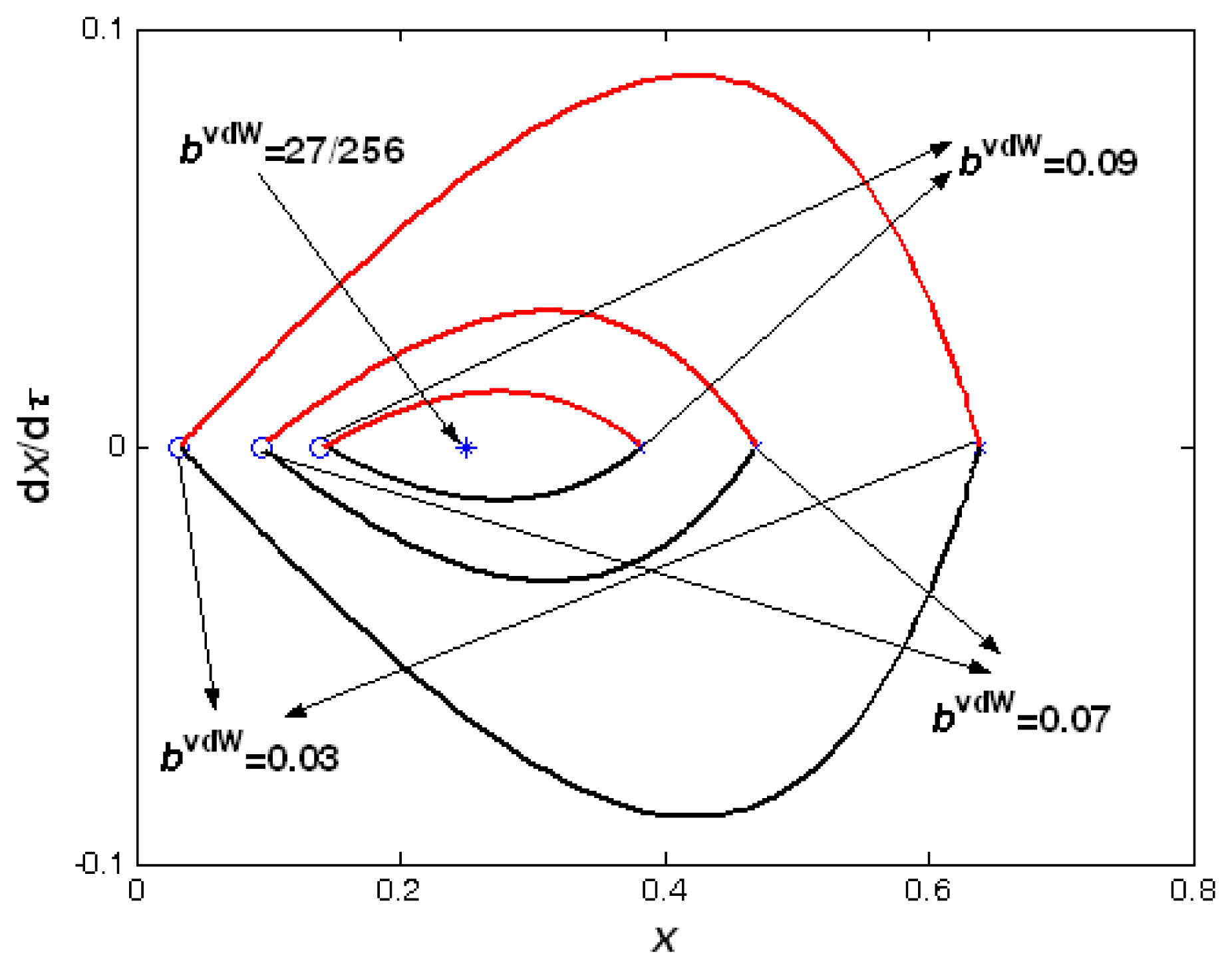
bvdW, we plot the bifurcation diagram as
Figure 8. In
Figure 8, all the points of the lower branch represent the stable points, and all the points of the upper branch are the unstable saddle points, the upper beam is unstable.
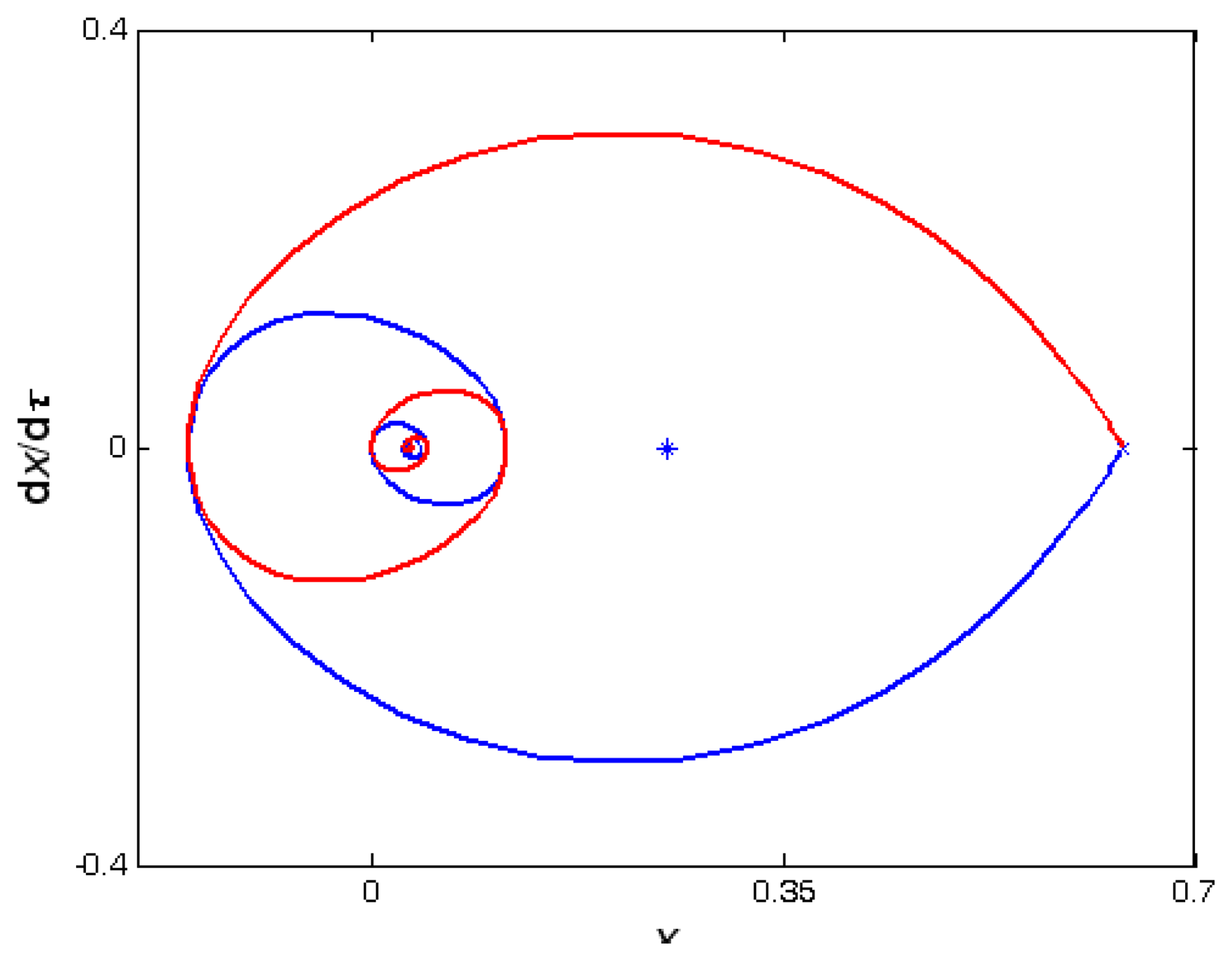
According to the properties of the stable node, stable focus, and saddle point, there exist two heteroclinic orbits which depart from the unstable saddle point and be end at the stable point. In order to see the movement process of the equilibrium points, we draw the phase portraits with
a = 0 by setting parameter
bvdW equal to 0.03, 0.07 and 0.09, respectively. These phase portraits are shown in
Figures 9,
10,
11 and
12. From the discussion in the paragraph above, one knows that the ability of the stable point is different with the variation of damping coefficient
μ̄In
Figure 9, we set
μ̄ = 3. This value of
μ̄ makes sure that
for three different
bvdW. By observing
Figure 9, there are two equilibrium points for three different
bvdW, one is the stable node (marked by “°”), and the other is the unstable saddle point (marked by “×”). There are two heteroclinic orbits between the unstable saddle point and the stable node. We note that the heteroclinic orbit is convergent to the stable node from the unstable saddle point with exponent. In Figures
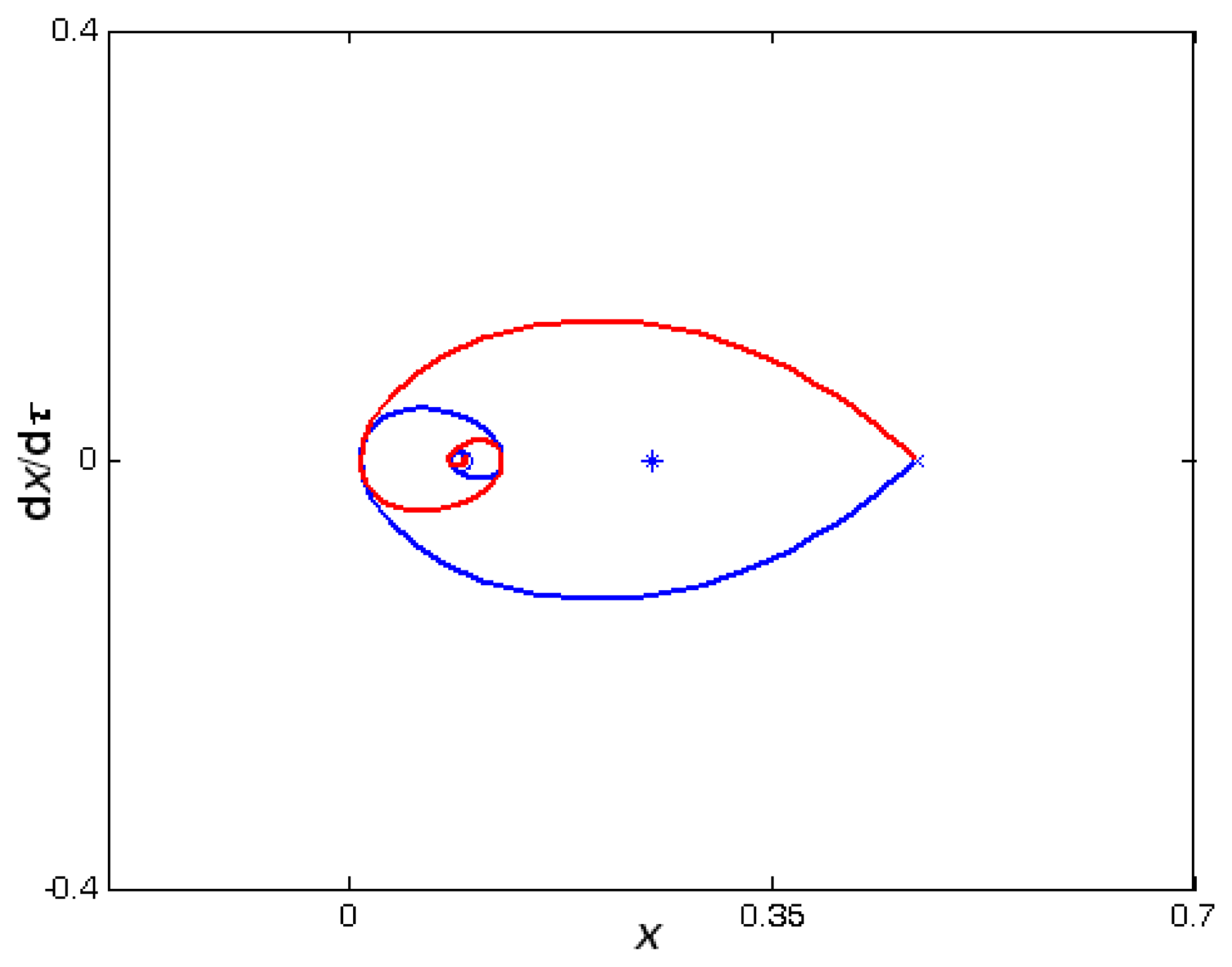
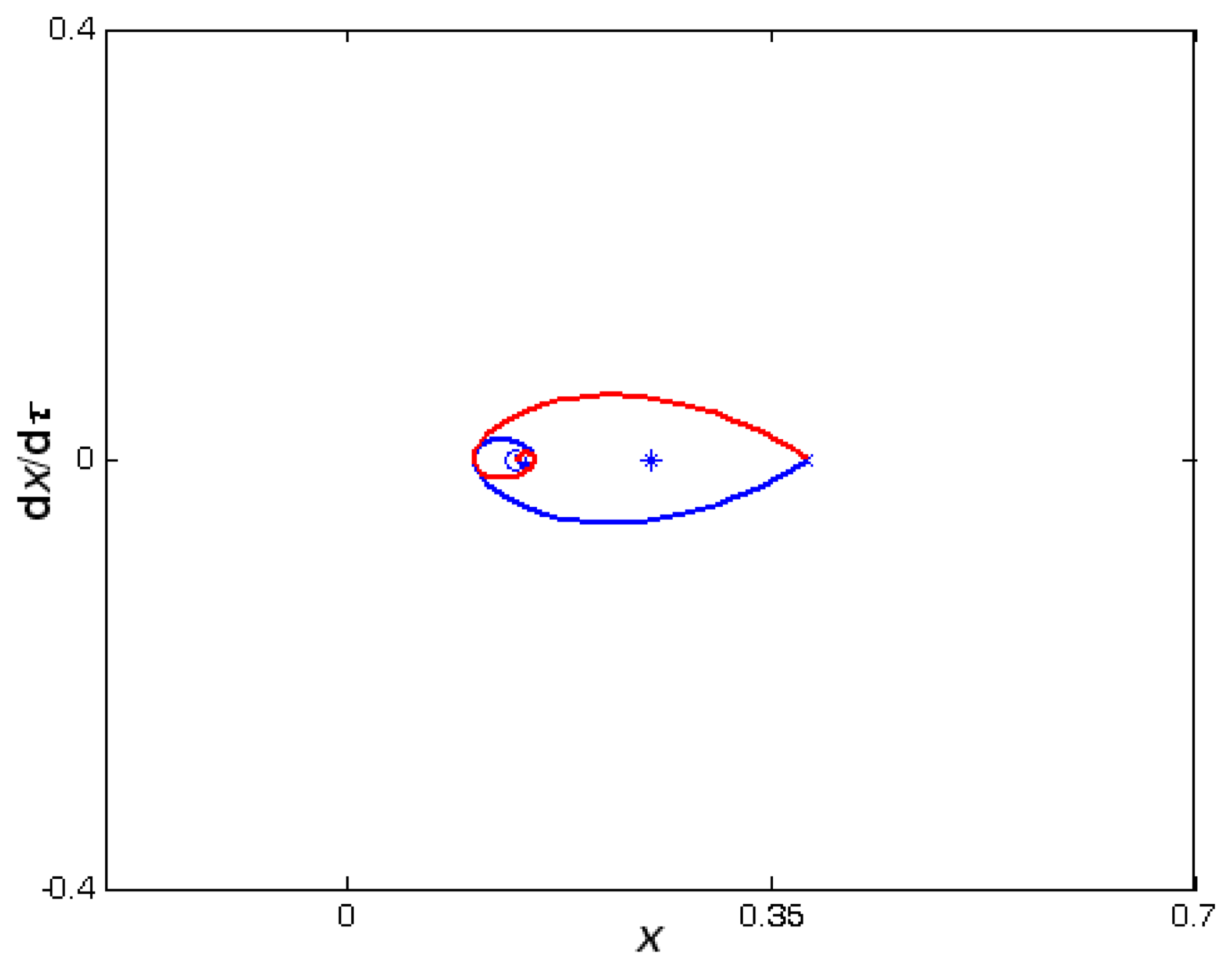
10-
12, we set
μ̄ = 0.5. This value of
μ̄ makes sure that
for three different
bvdW. By observing Figures
10-
12, there are also two equilibrium points for three different
bvdW, one is the stable focus (marked by “°”), and the other is the unstable saddle point (marked by “×”). There are two heteroclinic orbits between the unstable saddle point and the stable node. We note that the heteroclinic orbit is convergent to the stable focus from the unstable saddle point spirally, which is different from the stable node because of the difference of their eigenvalues.
From these four figures, we also note that the stable point which is node or focus, and unstable saddle point move to the point “*” from opposite direction with bvdW is increasing. These two points turn into the pull-in point
with
. At this critical condition, the pull-in phenomenon occurs, the reason of structure invalidation is that the original two equilibrium points merge as one with the changing of parameter bvdW.
According to the eigenvalue
equation (20), at least the real part of one of eigenvalues λ
1, λ
2 is positive when the damping coefficient is negative. At this time, the system is unstable, which should be avoided in engineering applications.
Until now, the dynamical behavior of
equation (3) is thoroughly discussed, that is, the dynamical behavior of the parallel-plate model with the electrostatic and vdW forces. For
equations (4),
(7), and
(8), their dynamic behavior can be discussed similarly to
equation (3).
5. Discussion and Conclusions
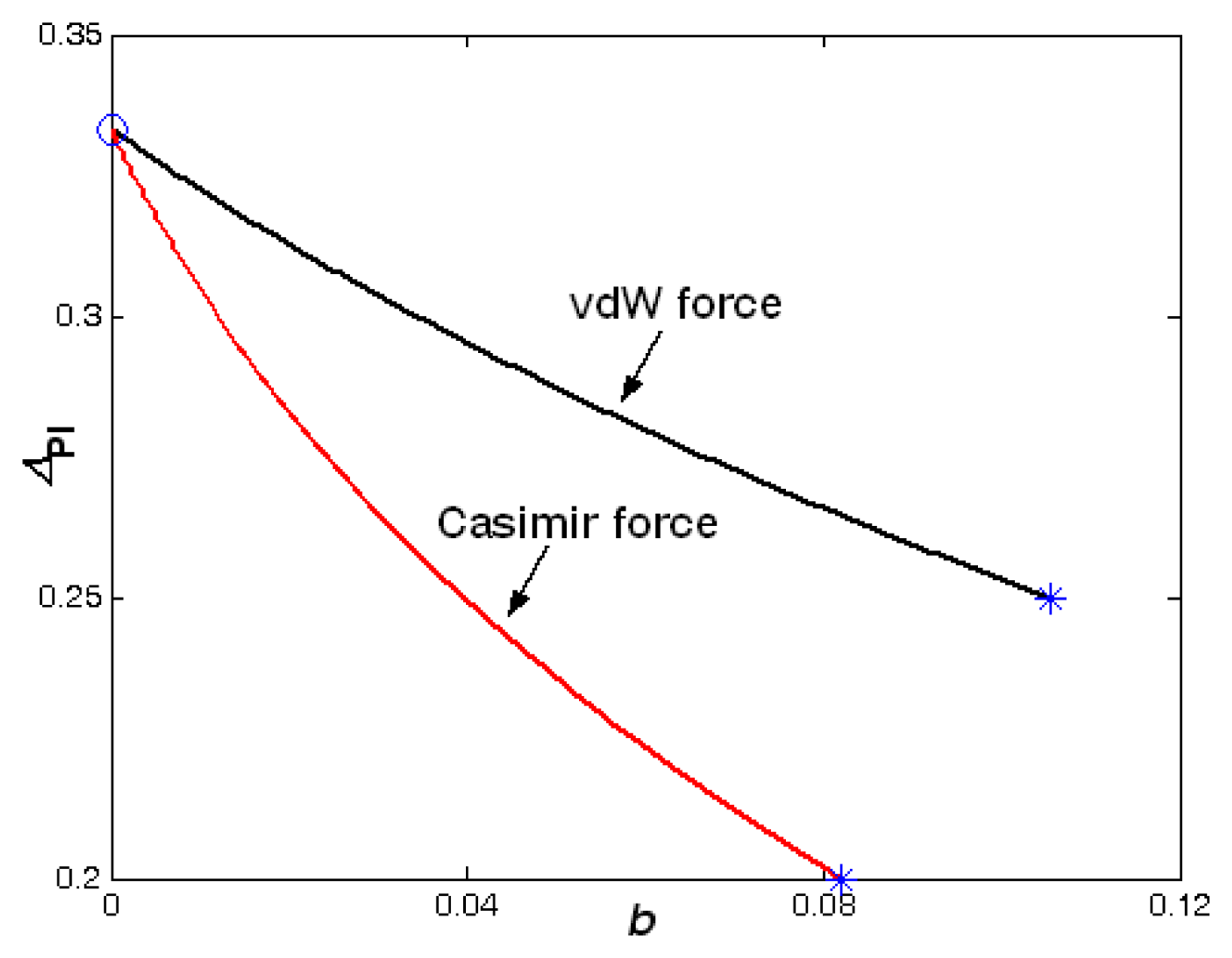
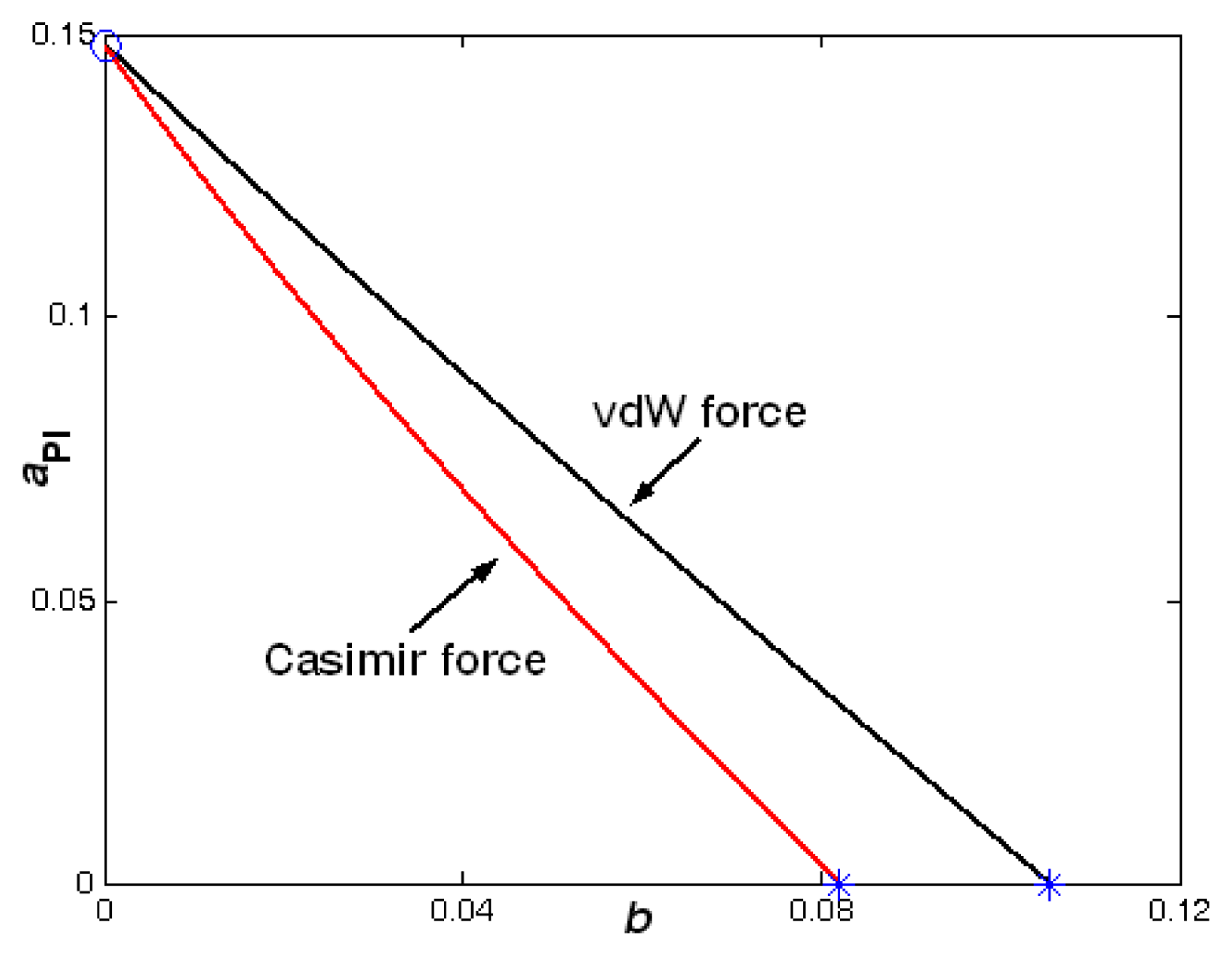
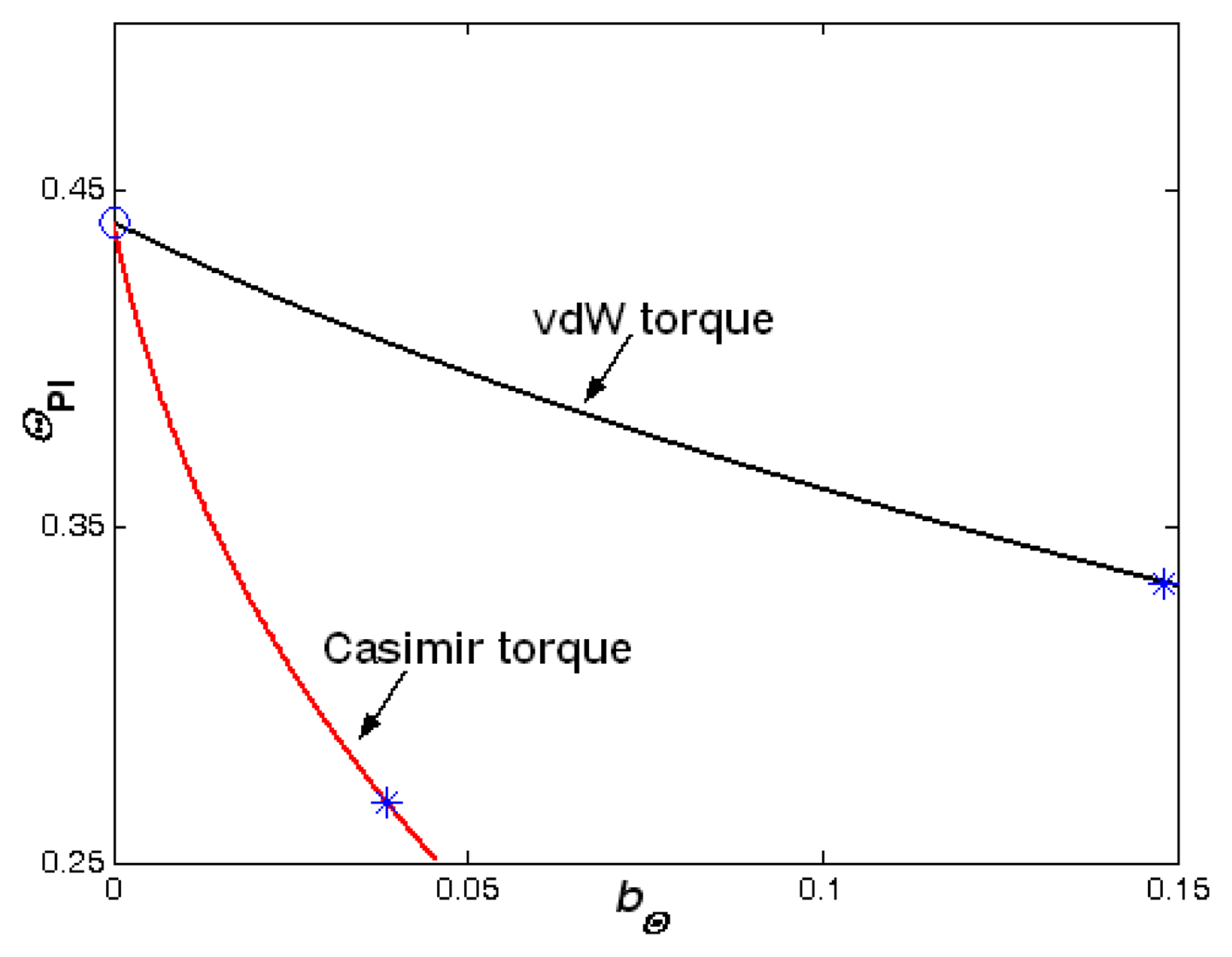
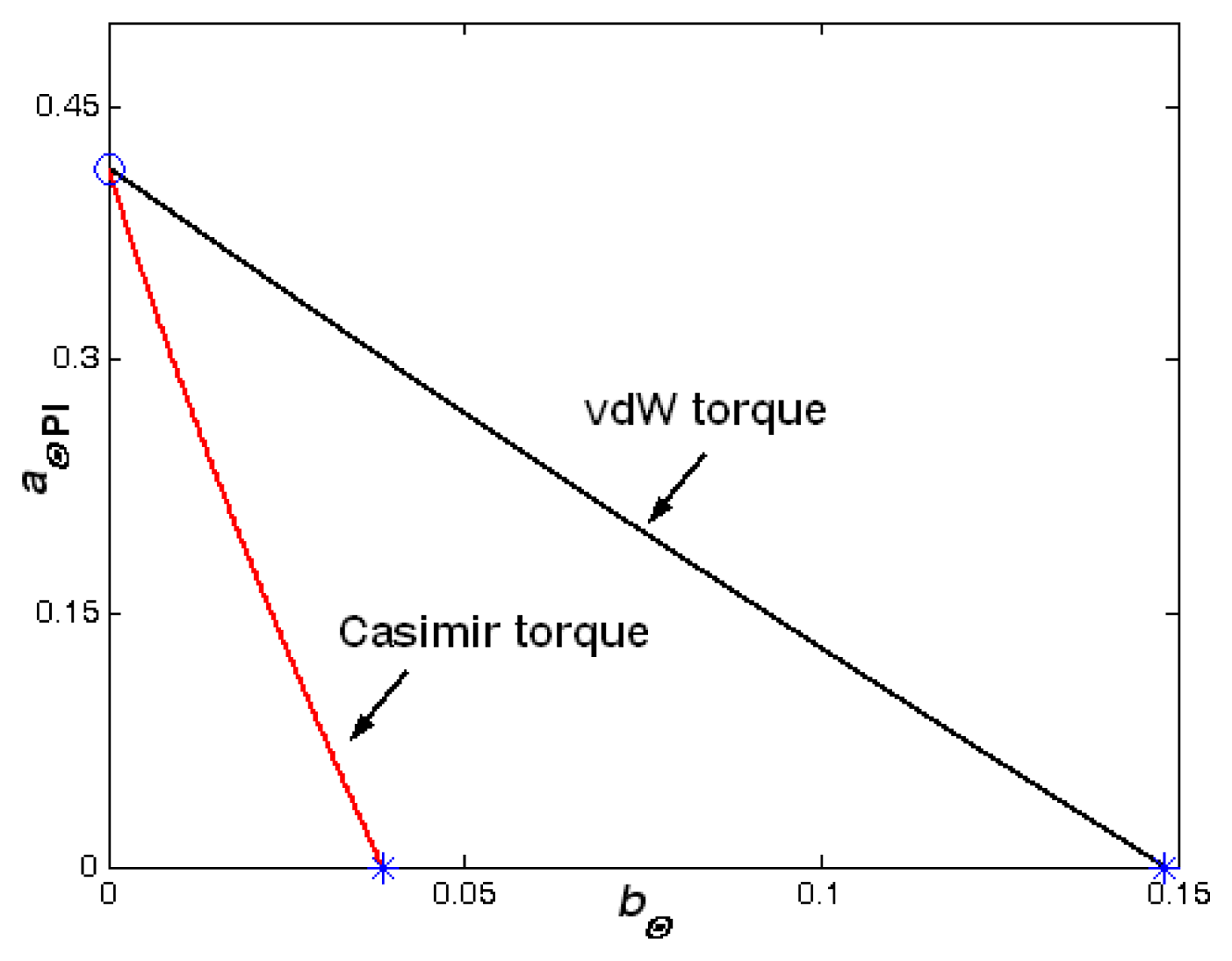
The influence of damping on the dynamical behavior of the electrostatic parallel-plate and torsional actuators with the vdW or Casimir force (torque) is presented. First, we studied the variation of two pull-in parameters with another parameter with different surface forces (torques), we get two special points for each case shown in Figures
3-
6. The first special point plotted by “°” shows that the vdW or Casimir force (torque) is zero on the actuator. The second point plotted by “
*” illustrates the actuator will lose its stability even though there is no applied voltage. With the appearance the vdW or Casimir force (torque), the pull-in parameters are all decreasing. From Figures
3-
6, we also know that the influence of Casimir force (torque) is stronger than that of vdW force (torque) for the same parallel-plate (torsional) actuators with the same geometrical parameters. This result is the same as [
9,
11,
12]. Then we can conclude that the damping does not affect the number of equilibrium points.
Secondly, we studied the stability of equilibrium points. One equilibrium point is an unstable saddle with different damping coefficient, the other is a stable node when damping coefficient is greater than some critical value, and otherwise it is a stable focus. Then there are two heteroclinic orbits passing from the unstable saddle point to the stable node or focus. Compared with the results in [
9,
11,
12], we find that the Hopf bifurcation point is changed into the stable node or focus with different damping coefficient with the appearance of damping, the unstable saddle point is still the same.
As a matter of fact, there are numerous possible sources of dissipation and damping in NEM actuators, which may broadly be classified as either intrinsic or extrinsic. Extrinsic dissipation or damping, such as gas (squeeze film) friction, clamping loss and surface loss, results from interaction of the actuator microstructure with the environment; whereas intrinsic dissipation or damping, such as thermoelastic relaxation, phonon-phonon and phonon-electron interaction, results from properties of the resonating material. The dissipation and damping mechanisms in NEM actuators are quite complicated [
19]. This paper only considered the simplest case of damping in the NEM actuators. To gain a better understanding of the dynamic behavior of nano-resonators, more studies are needed on the dissipation or damping mechanisms and their roles in attenuation of the vibration.