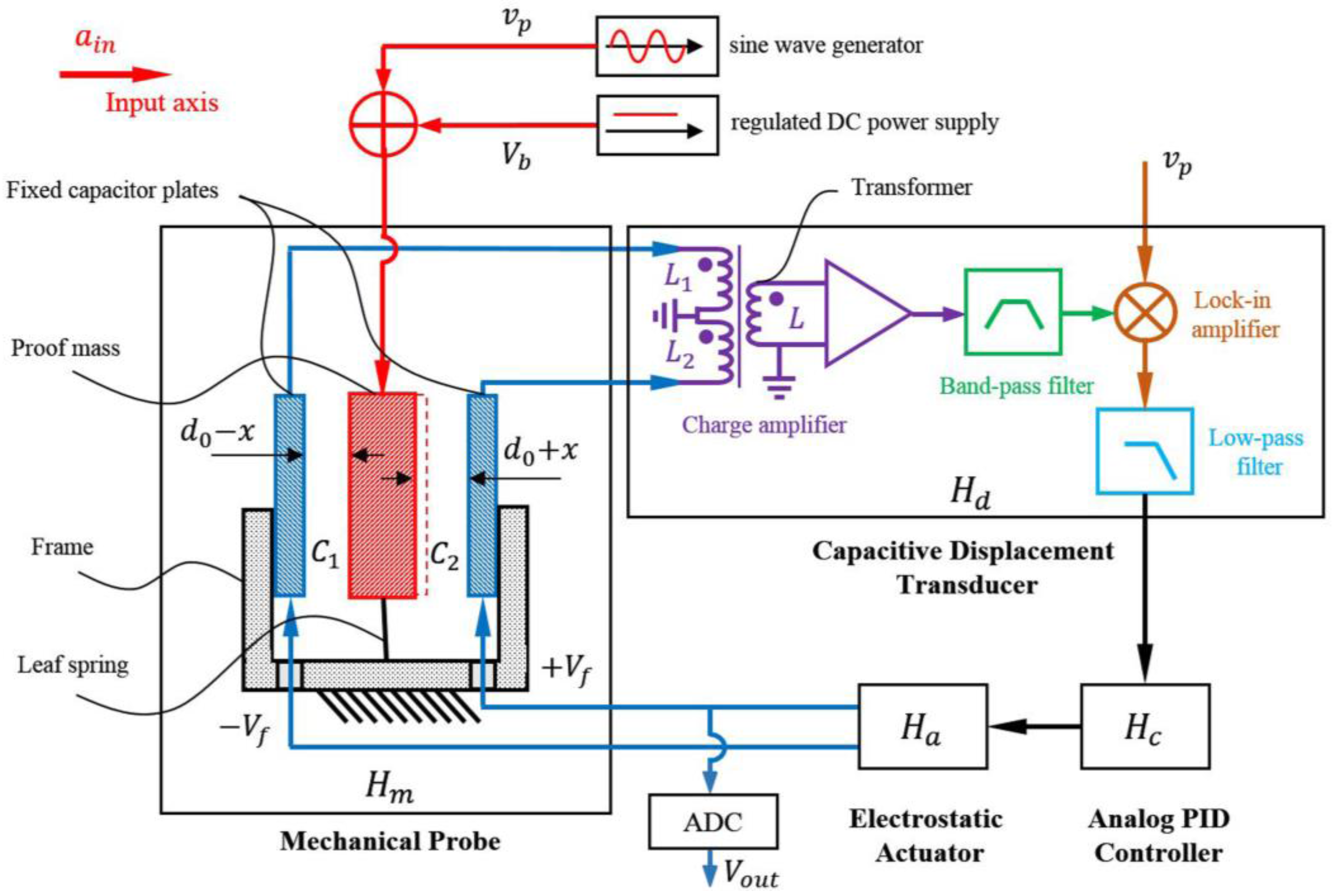
2.1. Working Principle of the Electrostatic Accelerometer
A block diagram of the electrostatic accelerometer system is shown in
Figure 1. The electrostatic accelerometer consists of a mechanical probe, a high precision capacitive displacement transducer, an analog proportional-integral-differential (PID) controller, and a high-performance electrostatic actuator. Here,
,
,
,
represent the transfer functions of these four stages, respectively. The mechanical probe of this electrostatic accelerometer is derived from a typical spring-mass structure. The rectangular proof mass is inversely supported by a set of leaf springs. Two fixed capacitor plates, together with the proof mass, form two gap-varying differential capacitors, which can transfer the external acceleration into a differential output of the capacitors, namely
and
. The capacitive displacement transducer consists of four parts: a charge amplifier, a band-pass filter, a lock-in amplifier, and a low-pass filter [
18,
19]. The driving voltage applied to the proof mass is composed of an AC pumping voltage
and a DC bias voltage
. The analog PID controller and the electrostatic actuator together constitute an electrostatic closed-loop feedback. Taking the output of the low-pass filter as the input of the PID controller, an appropriate voltage is produced by the PID controller and is then sent to the electrostatic actuator for further amplification. Finally, two opposite feedback voltages
are obtained and are then applied to the two fixed capacitor plates to generate two opposite electrostatic forces. The applied
is sampled by a 24-bits Analog to Digital Converter (ADC), which is the output voltage
of the accelerometer.
Once an external acceleration is applied to the input axis direction, there would be a displacement of the proof mass with respect to the frame that is caused by the input acceleration. Because the proof mass is sandwiched between the two capacitor plates that are fixed to the frame, this displacement will introduce variations of the capacitance of the two differential capacitors and . This variation is then sensed by the capacitive displacement transducer. After that, the PID controller obtains the displacement information and leads the electrostatic actuator to generate two opposite electrostatic forces, which eventually drive the proof mass back to its null position.
Since the spring-mass structure has a typical spring-mass-damper system, according to Newton’s second law of motion, the equation of motion of the electrostatic force-rebalanced flexure accelerometer can be expressed as [
18,
19,
20,
21]
where
is the mass of the proof mass,
is the damping coefficient,
is the stiffness coefficient of the spring,
is the input acceleration, and
is the electrostatic feedback force. In the closed-loop mode, the electrostatic force
is equivalent to the input force
acted on the proof mass to keep the proof mass still and always remain at its null position. Therefore, the value of the electrostatic feedback force will be taken as a measure of the input acceleration, and is noted as the output acceleration
of the accelerometer. According to the block diagram, as shown in
Figure 1, the relationship between
and
can be written as
Because the gain
is much bigger than 1 within the working bandwidth of the accelerometer, the output acceleration
. Therefore, the input acceleration
can be easily obtained by collecting the feedback voltage
, which is denoted as the output voltage
of the accelerometer:
where
is the voltage-to-acceleration transfer function of the electrostatic actuator.
As shown in
Figure 1, a DC bias voltage
and an AC pumping voltage
are applied to the proof mass, for linearization of the electrostatic feedback actuator and capacitance sensing, respectively. Furthermore, two opposite feedback voltages
are applied to the two fixed capacitor plates to generate a difference of potential between the proof mass and the fixed plates, in order to restore the proof mass to its null position. Those voltages would contribute to an electrostatic field between the proof mass and the fixed plates, and yield an electrostatic feedback force on the proof mass [
21,
22,
23,
24]:
where
is the root mean square (RMS) value of the pumping voltage
. The first item in Equation (4) is the effective electrostatic feedback force, and hence the output acceleration can be written as
Thus, the voltage-to-acceleration transfer function
can be written as
The reciprocal of is the so-called scale factor of the accelerometer, namely .
The second item in Equation (4) is the so-called back-action force, which pushes the proof mass away from its null position and hence could be considered as an equivalent electrostatic spring with a negative stiffness as [
18,
21]
The spring stiffness of the spring-mass structure in the closed-loop mode is hence reduced to
Equation (8) implies that the effective stiffness of the spring-mass system can be adjusted by changing the electrostatic negative stiffness in the closed-loop mode, in which the stiffer springs are used to achieve the same effect as with softer springs in the open-loop mode.
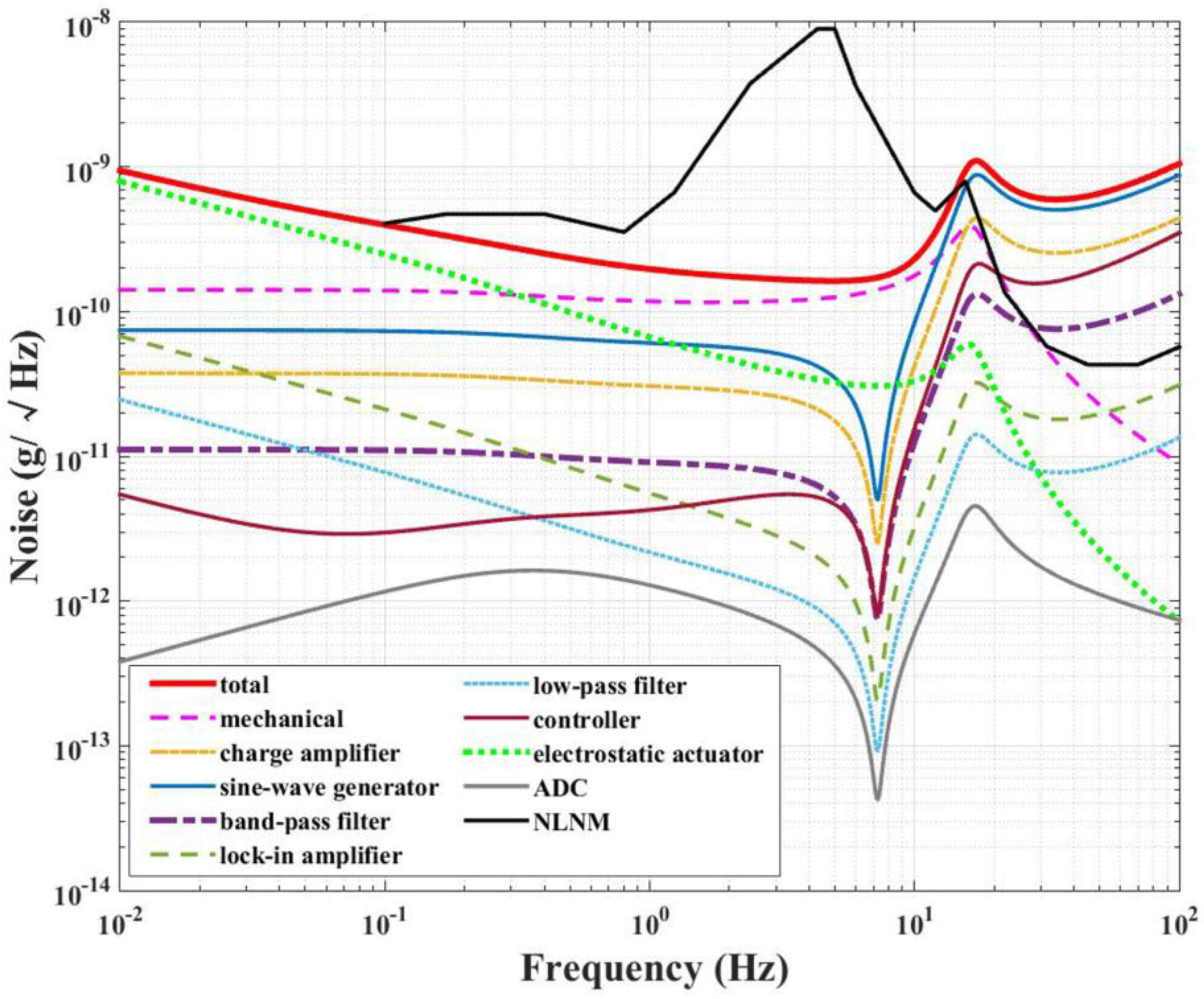
In order to meet the requirements of GGIs on the accelerometer, it is of the utmost importance to achieve ultra-low noise. The overall NEA of an accelerometer can be generally divided into two parts
in which
denotes the mechanical NEA of the spring-mass structure and
is the electronic NEA of the sensing and feedback electronic circuit. As an accelerometer with the self-noise lower than 0.3
is required, the
should be below 0.3
.
2.2. Design and Model Analysis of the Spring-Mass Structure
For a typical spring-mass-damper system, the mechanical NEA of the spring-mass structure in a unit bandwidth at all of the frequencies can be written as [
21]
where
is the Boltzmann constant,
is the temperature in Kelvin unit,
is the resonant angular frequency, and
is the quality factor of the spring-mass structure.
According to Equation (10), the most effective way to reduce
is to use a larger proof mass
. However, this will result in an increase in electrostatic voltage to hold the proof mass at its null position, hence bringing more noise from the electrostatic actuator. Using the softer supporting spring with a smaller stiffness
is another feasible method to reduce
. However, it will make
closer to or even smaller than
, making the spring-mass-damper system unstable in the closed-loop mode. The value
Q depends on airy viscous damping and materials’ internal damping, thus the capsulation and material of the spring-mass structure should also be considered to get a larger quality factor value. In addition, the spring should be tough enough to support the proof mass, thereby a spring-mass structure with higher stiffness at the cross-axis directions is required to suppress the cross couplings with the sensitive input axis in developing GGI [
7,
8]. Consequently, all of those issues should be carefully considered when designing a spring-mass structure.
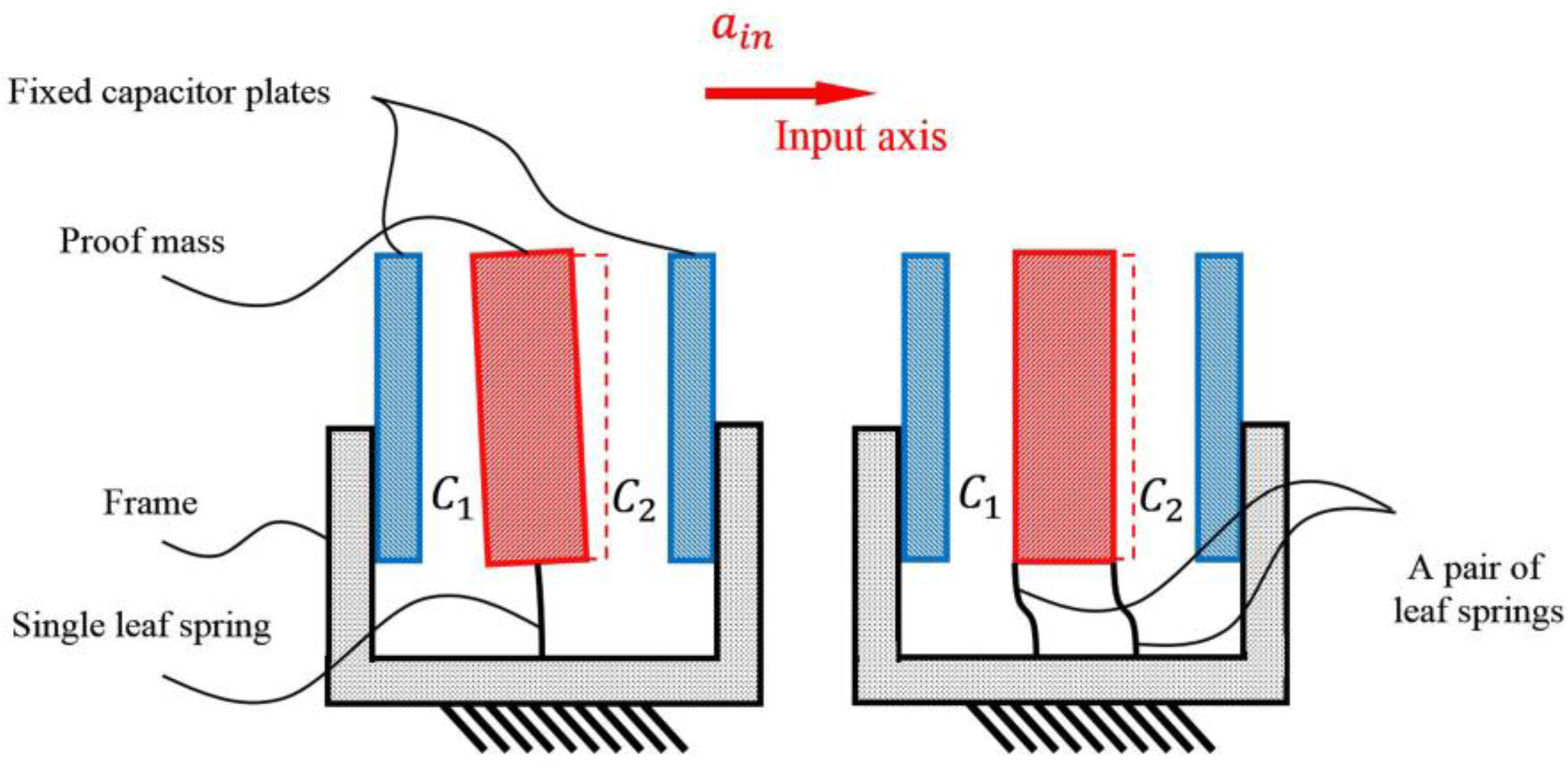
In the process of our design and simulation, we found that if the proof mass is inversely supported by two pairs of parallel leaf springs of the same stiffness, the proof mass, centered between two capacitor plates, will move along a true straight line with no swinging motion, thus both capacitor plates are kept parallel. As compared with the single leaf spring structure, as shown in
Figure 2, the pairing of two parallel springs not only increase the linearity of the mechanical probe, but also significantly suppress the cross coupling between the sensitive axis and the torsional direction. Furthermore, this structure is strong enough to support a proof mass of up to tens of grams, implying that larger proof masses can be used in this design by adding more pairs of parallel leaf springs with proper stiffness. Because the rotation of the proof mass is almost eliminated, this novel design also ensures the spring-mass structure a very high rejection ratio at the cross-axis directions.
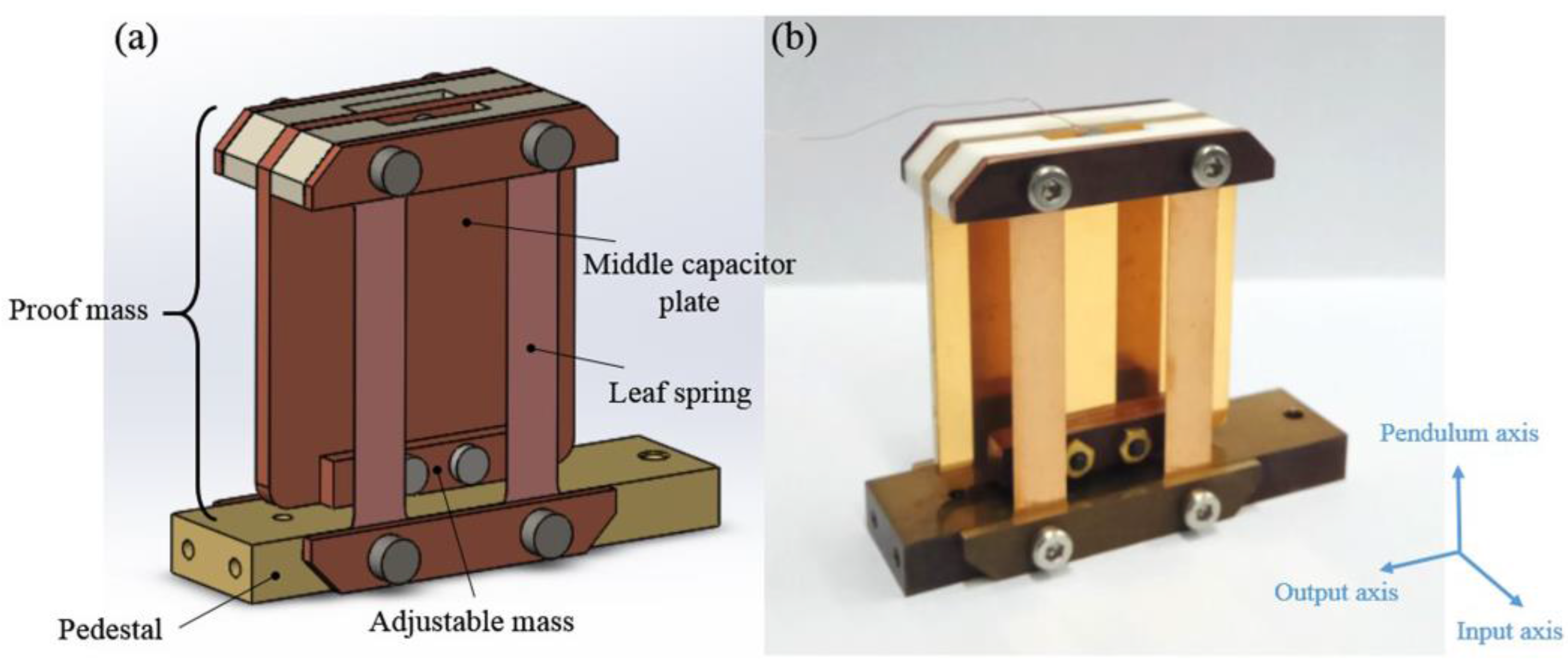
The spring-mass structure has been fabricated, as shown in
Figure 3. The optimized parameters, with the aim to obtain a low noise and a large cross-axis rejection, are listed in
Table 1. The spring-mass structure is fixed to a copper pedestal, and the proof mass with a weight of 27.5 g is inversely supported by two pairs of straight parallel beryllium-bronze leaf springs. An adjustable mass, mounted at the bottom of the proof mass, is used to precisely adjust the centroid of the proof mass. The proof mass is mainly made of the red copper to obtain a heavy mass, and it also acts as a middle capacitor plate coated by a 400 nm gold layer on its surface to prevent oxidization.
The total stiffness of the leaf springs can be written as
where
,
,
, and
represent the width, thickness, length, and Young’s modulus of the leaf springs, respectively.
With the parameters of the proposed spring-mass structure, as shown in
Table 1, the static mechanical mode can be analyzed by using the finite element analysis (FEA). The 22 lowest oscillation modes are listed in
Table 2 in the order of increasing frequency. The modes marked as
,
,
,
,
, and
are corresponding to the six degrees of freedom of the spring-mass structure to characterize the motion along the input, output, pendulous axis, and the rotation around the input axis, output, pendulous axis with the frequencies of 7.163, 444.2, 2592, 1458, 1047, 304.5 Hz, respectively. The modes marked as
,
,
characterize the fundamental, second harmonic, and third harmonic bending modes of the four leaf springs, which are 426, 1192, 2360 Hz, respectively. The mode
describes the first order rotation modes of the four leaf springs around the pendulous axis with the frequency of about 1590 Hz.
According to the FEA results, the proof mass oscillates at a frequency of 7.163 Hz along the input axis at the fundamental vibrational mode
, and the second mode
is the rotation around the pendulous axis with a frequency of 304.5 Hz. The rejection ratio at the cross-axis directions can be estimated by comparing the stiffness, which can be written as
where
,
represent the stiffness and angular frequency of the modes at the cross-axis directions,
,
are the stiffness and angular frequency of the fundamental mode
. Therefore, the minimum rejection ratio at the cross-axis directions is
, which is just the ratio of the effective spring stiffness of the mode at the cross-axis directions to the fundamental vibrational mode
. It is about four to five times higher when compared to the traditional force-balanced flexure accelerometer. As the proof mass is sandwiched by the two capacitor plates symmetrically, the modes
,
,
could not influence the capacitive displacement transducer because there is no variation of the differential capacitors. The rotation mode around the output axis
has a frequency of 1047 Hz, and the rejection ratio is
. Finally, the modes
,
,
,
are just the vibrations of the leaf springs and will not affect the displacement detection either.
According to Equation (10), the mechanical NEA of the spring-mass structure is . If one hopes to obtain a mechanical NEA below 0.3 , the quality factor Q should be greater than 3, which can be easily achieved by mounting the spring-mass structure into a small vacuum cavity. Furthermore, a quality factor of 30 will further reduce mechanical NEA to below 0.1 .
2.3. Noise Analysis of the Sensing and Feedback Circuit
To evaluate the NEA of the circuit
, we present a noise model for the accelerometer, as shown in
Figure 4. The circuit of the accelerometer contains three parts: the capacitive displacement transducer
, the analog PID controller
, and the electrostatic actuator
, respectively. The capacitive displacement transducer, shown in the dashed line box, is similar to that of Josselin V et al., and Hu M et al. [
18,
19]. This design consists of a charge amplifier, a band-pass filter, a lock-in amplifier, and a low-pass filter with transfer functions
,
,
, and
, respectively. The low-frequency variation of the capacitance of the two differential capacitors, which represents the external acceleration to be measured, is carried by a high-frequency sine wave
and is input to the charge amplifier by a differential transformer. Through the signal conditioning of band-pass filter, this differential variation of the capacitance is then demodulated by the lock-in amplifier and finally filtered by the low-pass filter.
According to
Figure 4, there are nine types of noise sources that contribute to the total noise of the accelerometer. As the mechanical noise
has been discussed in
Section 2.2, here we investigate electronic noise, consisting of the other eight types of noise sources, namely the charge amplifier’s voltage noise
, the sine wave generator’s equivalent voltage noise at the output of charge amplifier
, the band-pass filter’s voltage noise
, the lock-in amplifier’s voltage noise
, the low-pass filter’s voltage noise
, the analog PID controller’s voltage noise
, the ADC’s voltage noise
and the electrostatic actuator’s NEA noise
which also contains the noise of the regulated DC power supply. Therefore, the power spectral density (PSD) of the electronic noise
could be deduced as
where
.
To get an accurate noise calculation, each part of the noise from the circuit should be carefully considered. The noise of the sine-wave generator is different from the other seven parts because it is related to the imbalances of the capacitance bridge and transformer bridge, and it will be discussed individually in the first place. The noise contributions from the other seven stages are discussed subsequently by using a method similar to that used in [
18,
19].
The sine-wave generator’s equivalent voltage noise at the output of charge amplifier can be written as
where
is the voltage noise of the sine-wave generator,
is the variation of the capacitance of the differential capacitors, and
is the feedback capacitor of the charge amplifier. In the closed-loop mode, because of the integral effect of the PID controller, the displacement of the proof mass is approximately equal to zero so that there is almost no change in capacitance. Thus, the noise
can be ignored ideally. However, in fact, there are imbalances of the differential capacitors
,
and the inductances of the primary windings
,
, which generate a bias capacitance
This bias capacitance may lead to an increase of the noise
as
. According to the first item of Equation (13), the NEA of the noise from the sine-wave generator can be written as
With the demand
and the typical parameters of
,
and
, the
is desired. Besides, the bias capacitance
also contributes a bias acceleration
, which is
Because is required in the development of GGI, the equivalent bias capacitance is desired. In this work, the imbalance of the capacitance bridge is compensated by selecting a transformer with suitable parameters to make below 0.5 pF.
The noises of the other seven parts of the circuit are originated from several basic noise sources including:
the input voltage noise and input bias current noise of the amplifier,
the thermal voltage noise generated by the resistor,
the thermal noise of the transformer bridge caused by hysteresis loss, eddy current loss, and residual loss of the transformer.
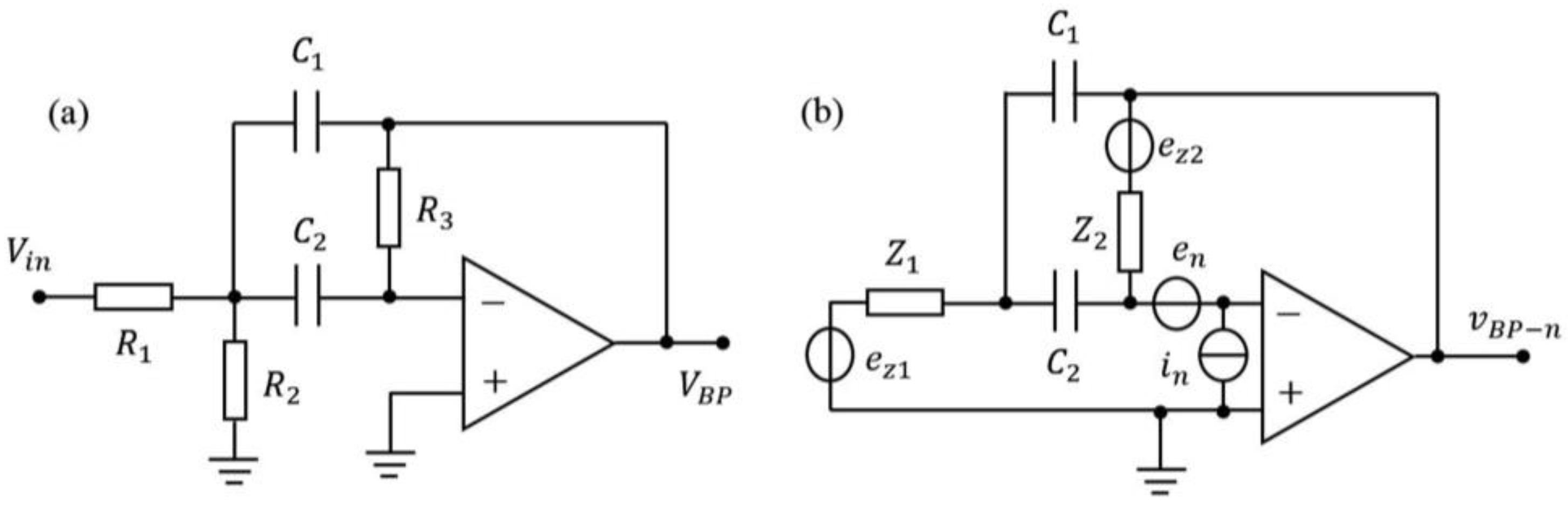
For example, from the noise model of the band-pass filter shown in
Figure 5, the basic noise sources are the input voltage noise
and the input bias current noise
of the amplifier, and the thermal voltage noises
,
generated by the resistors
and
. If the noise components are uncorrelated, the variances are added as
where
,
,
,
are the transfer functions from
,
,
, and
to the output of band-pass filter. The noise caused by the other six parts of the circuit can be discussed in the same way, as introduced by references [
18,
19], and the basic noise sources of each part are different. To get an accurate result of noise analysis, every basic noise sources (
,
,
,
) of the seven parts are evaluated and measured to meet the requirements in the process of making and debugging the sensing and feedback circuit.