Post-Seismic Deformation from the 2009 Mw 6.3 Dachaidan Earthquake in the Northern Qaidam Basin Detected by Small Baseline Subset InSAR Technique
Abstract
:1. Introduction
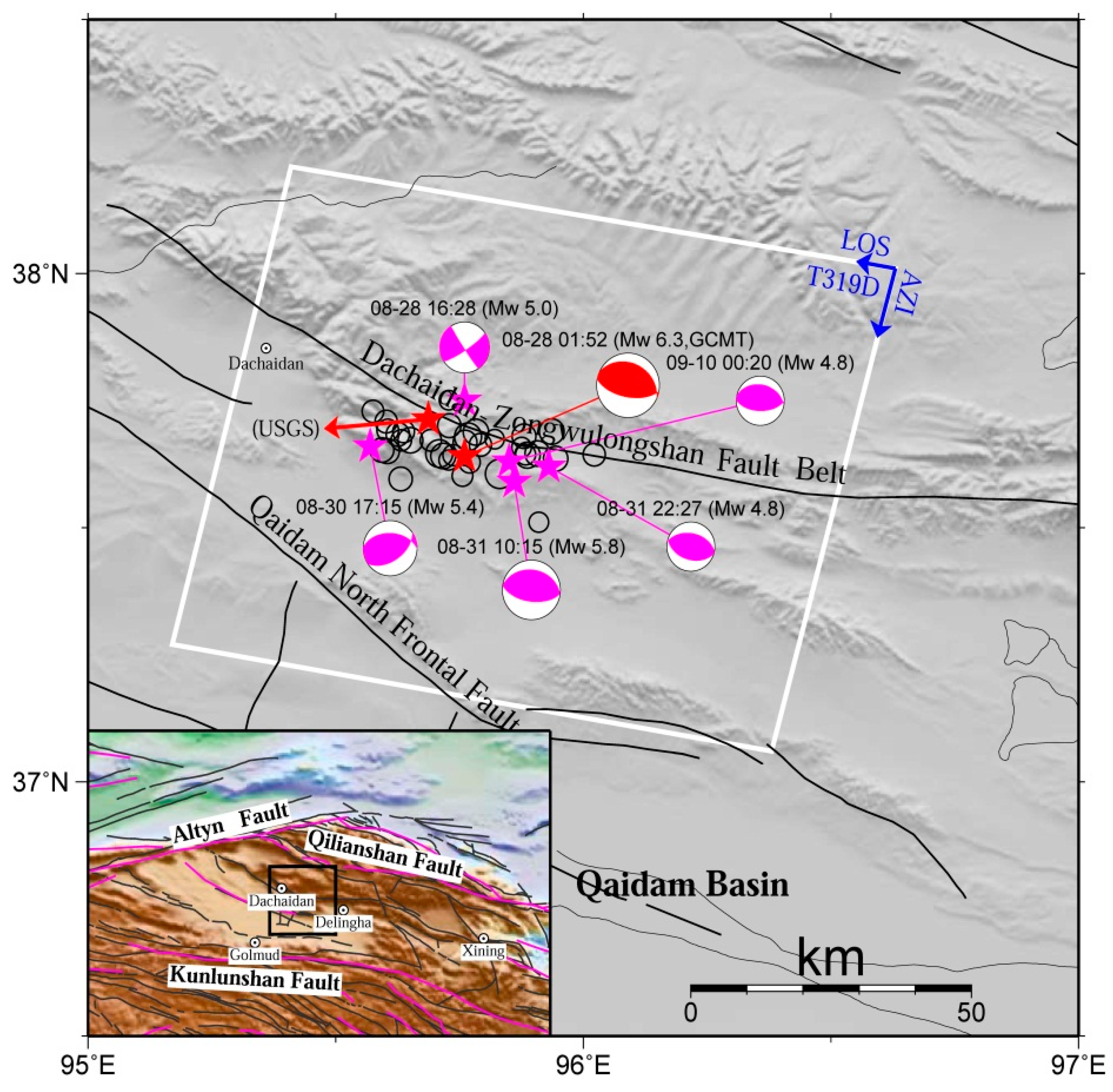
2. Small Baseline Subset InSAR Time Series Method
3. Data Source and Processing
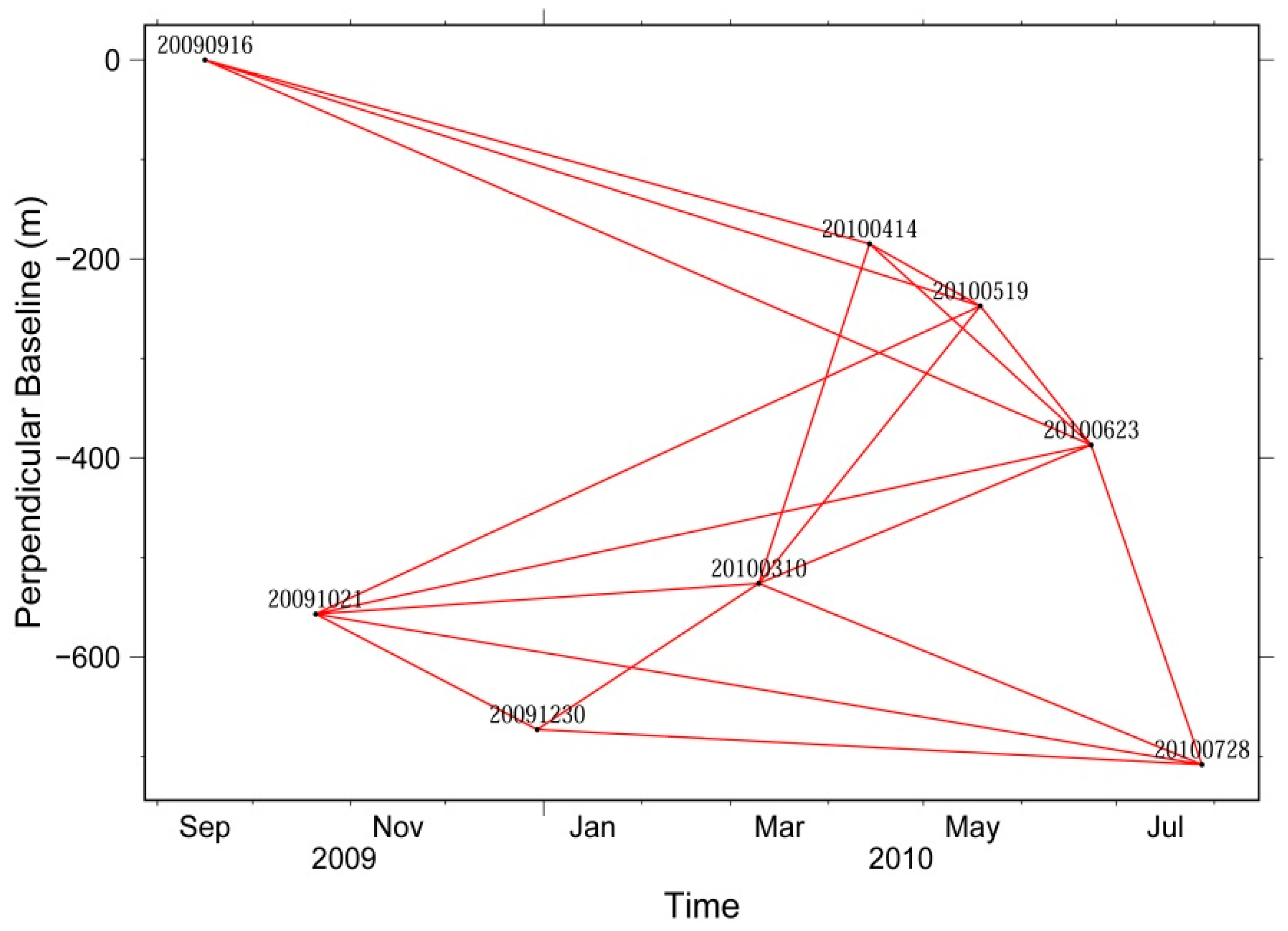
3.1. Data Source
| Date (yyyymmdd) | Track No. | T a (days) | Bperp b (m) | Σ c (cm) | L d (km) | |
|---|---|---|---|---|---|---|
| 1 | 20090916 | 39451 | 19 | 0 | 0.07 | 4.72 |
| 2 | 20091021 | 39952 | 54 | −556.9 | 0.20 | 4.72 |
| 3 | 20091230 | 40954 | 124 | −672.9 | 0.36 | 4.72 |
| 4 | 20100310 | 41956 | 194 | −526.2 | 0.36 | 4.24 |
| 5 | 20100414 | 42457 | 229 | −184.8 | 0.35 | 4.40 |
| 6 | 20100519 | 42958 | 264 | −247.5 | 0.34 | 4.84 |
| 7 | 20100623 | 43459 | 299 | −386.9 | 0.37 | 5.56 |
| 8 | 20100728 | 43960 | 334 | −708.1 | 0.46 | 6.12 |
3.2. Data Processing
4. Results and Discussions
4.1. Temporal Features of Post-Seismic Deformation
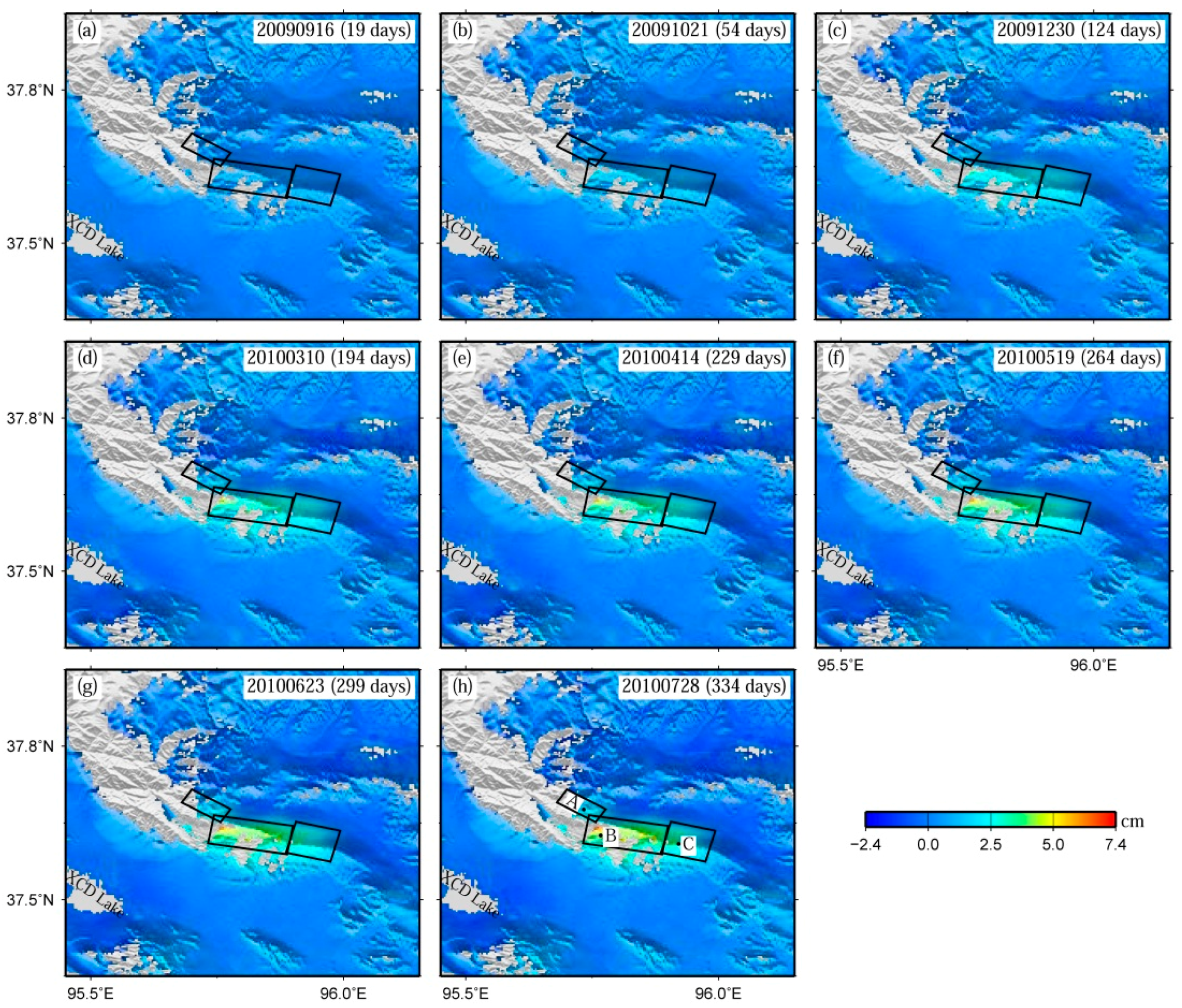
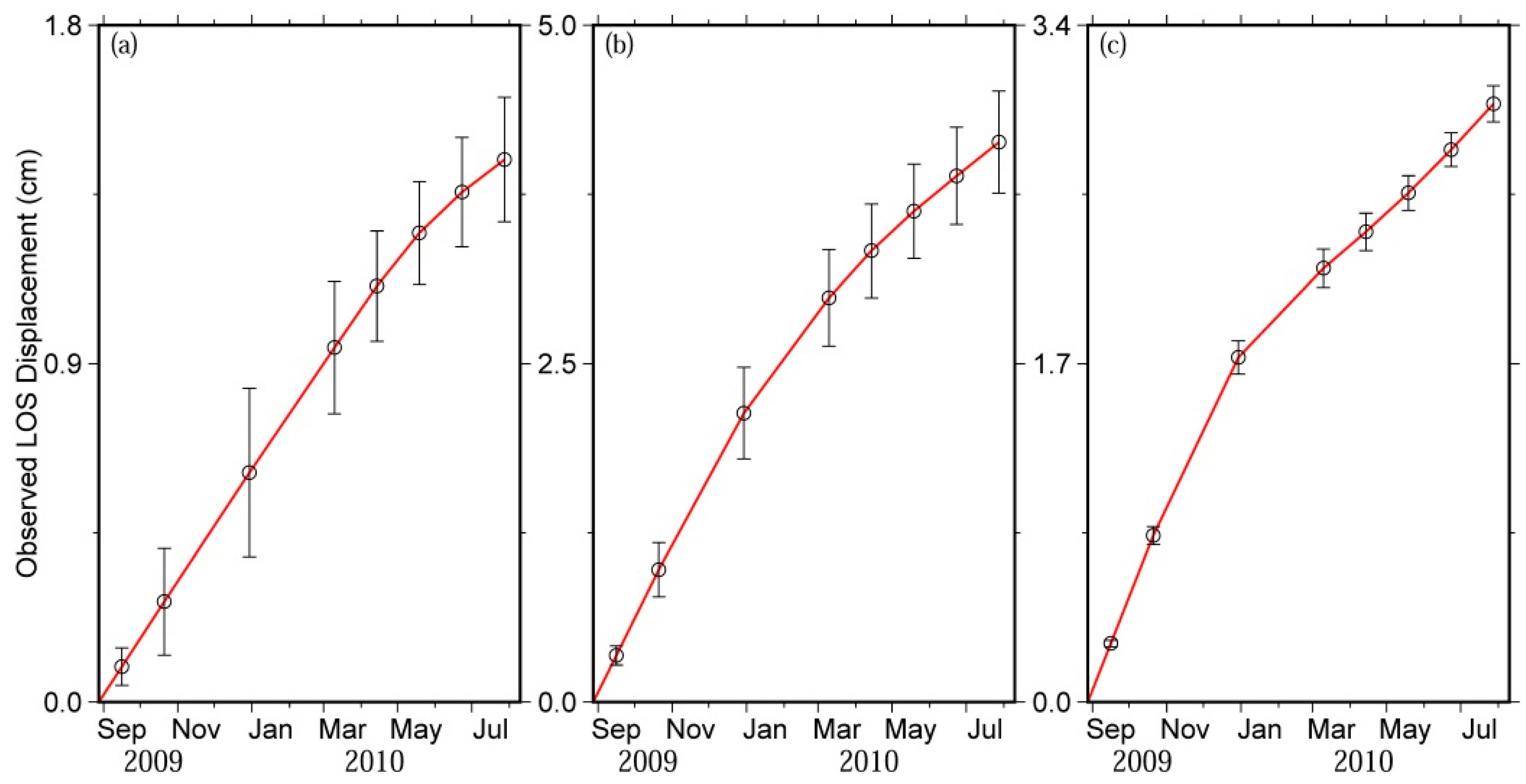
4.2. Spatial Features of Post-Seismic Deformation
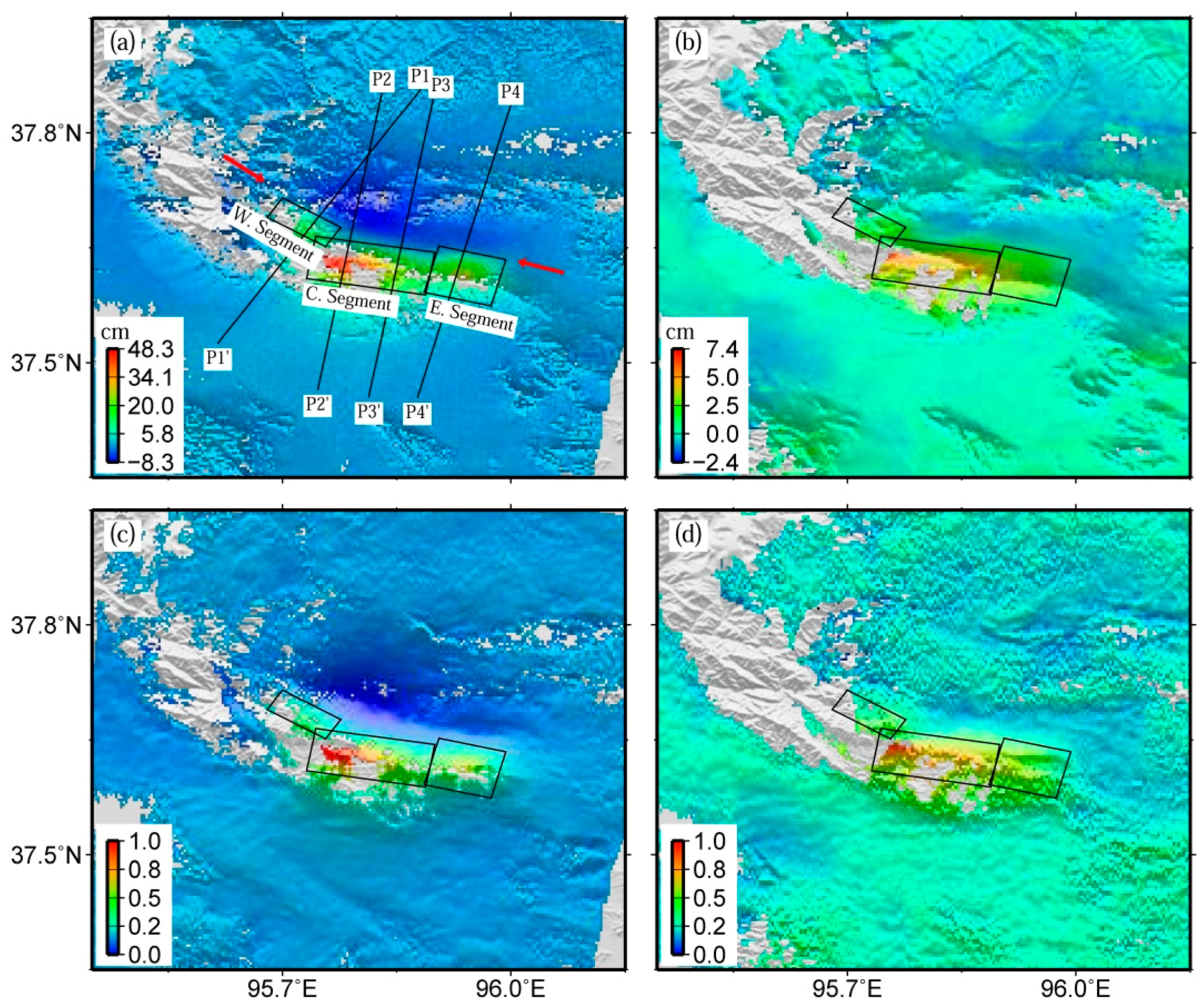
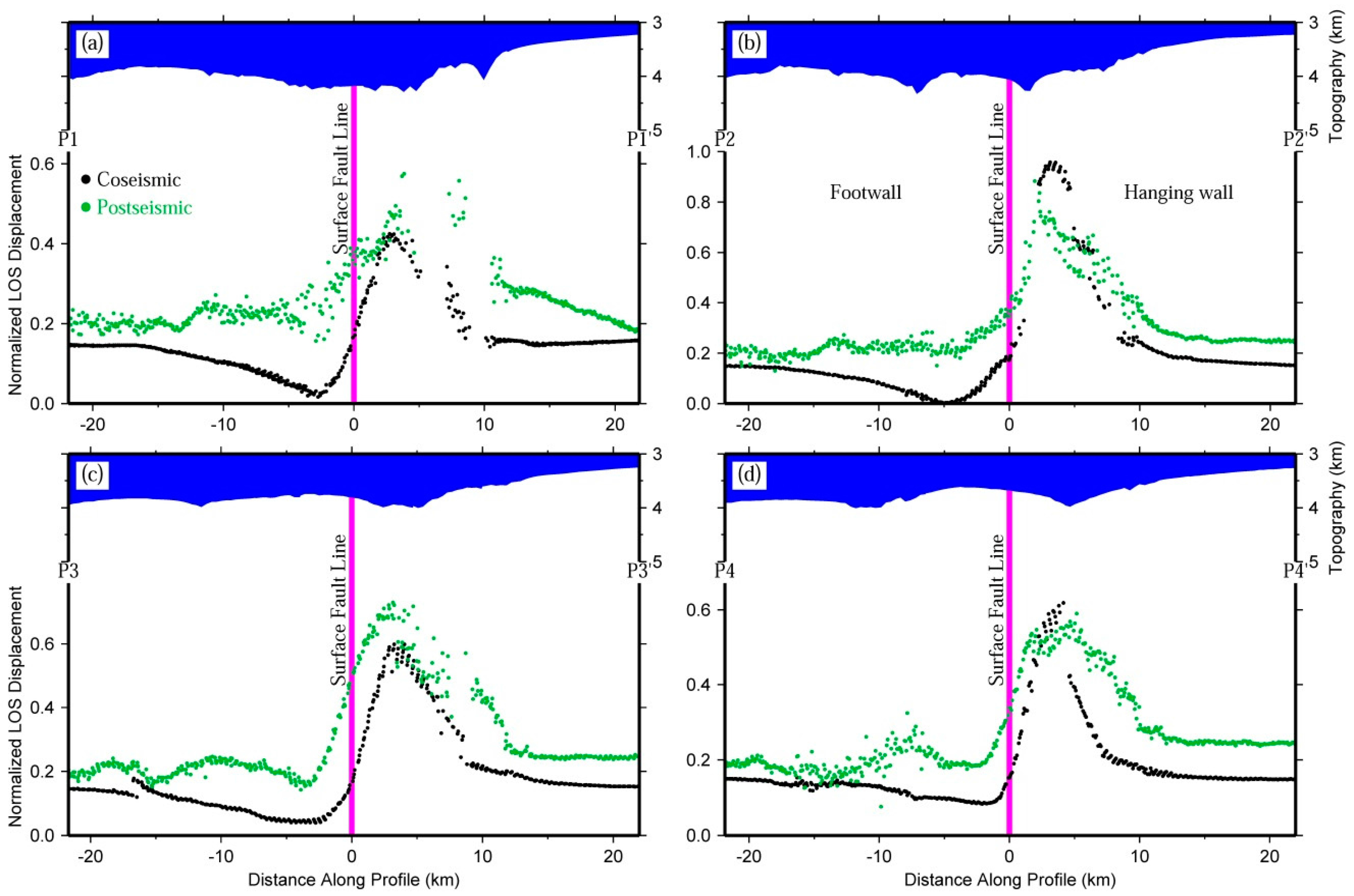
4.3. Correlation between Post-Seismic and Co-Seismic Deformation
4.4. Correlation between Post-Seismic Deformation and Co-Seismic Rupturing Fault
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Elliott, J.; Parsons, B.; Jackson, J.; Shan, X.; Sloan, R.; Walker, R. Depth segmentation of the seismogenic continental crust: The 2008 and 2009 Qaidam earthquakes. Geophys. Res. Lett. 2011, 38, L06305. [Google Scholar] [CrossRef]
- Liu, W.; Wang, P.; Ma, Y.; Chen, Y. Relocation of Dachaidan Ms 6.4 Earthquake Sequence in Qinghai Province in 2009 Using the Double Difference Location Method. Plateau Earthq. Res. 2011, 23, 24–26. [Google Scholar]
- Ma, Y.; Liu, W.; Wang, P.; Yang, X.; Chen, Y. Characteristics and anomaly of earthquake sequence activity of Dachaidan Ms 6.3 and Ms 6.4 in 2008 and 2009. Earthq. Res. China 2012, 28, 188–199. [Google Scholar]
- Chen, G.; Xu, X.; Zhu, A.; Zhang, X.; Yuan, R.; Klinger, Y.; Nocquet, J.M. Seismotectonics of the 2008 and 2009 Qaidam earthquakes and its implication for regional tectonics. Acta Geol. Sin. 2013, 87, 618–628. [Google Scholar]
- Liu, Y.; Xu, C.; Wen, Y.; Fok, H.S. A new perspective on fault geometry and slip distribution of the 2009 Dachaidan Mw 6.3 earthquake from InSAR observations. Sensors 2015, 15, 16786–16803. [Google Scholar] [CrossRef] [PubMed]
- GCMT. Global CMT Catalog Search. Available online: http://www.globalcmt.org/CMTsearch.html (accessed on 29 October 2015).
- USGS. Magnitude 6.2—Northern Qinghai, China. Available online: http://earthquake.usgs.gov/earthquakes/eqinthenews/2009/us2009kwaf/ (accessed on 29 October 2015).
- Zha, X.; Dai, Z. Constraints on the seismogenic faults of the 2003–2004 Delingha earthquakes by InSAR and modeling. J. Asian Earth Sci. 2013, 75, 19–25. [Google Scholar] [CrossRef]
- Deng, Q.; Zhang, P.; Ran, Y.; Yang, X.; Min, W.; Chu, Q. Basic characteristics of active tectonics of China. Sci. China Ser. D 2003, 46, 356–372. [Google Scholar]
- Zhang, P.; Deng, Q.; Zhang, G.; Ma, J.; Gan, W.; Min, W.; Mao, F.; Wang, Q. Active tectonic blocks and strong earthquakes in the continent of China. Sci. China Ser. D 2003, 46, 13–24. [Google Scholar]
- Peltzer, G.; Saucier, F. Present-day kinematics of Asia derived from geologic fault rates. J. Geophys. Res. 1996, 101, 27943–27956. [Google Scholar] [CrossRef]
- Lisowski, M.; Prescott, W.; Savage, J.; Johnston, M. Geodetic estimate of coseismic slip during the 1989 Loma Prieta, California, earthquake. Geophys. Res. Lett. 1990, 17, 1437–1440. [Google Scholar] [CrossRef]
- Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
- Segall, P.; Davis, J.L. GPS applications for geodynamics and earthquake studies. Annu. Rev. Earth Planet. Sci. 1997, 25, 301–336. [Google Scholar] [CrossRef]
- Wright, T.J. Remote monitoring of the earthquake cycle using satellite radar interferometry. Phil. Trans. R. Soc. Lond. A 2002, 360, 2873–2888. [Google Scholar] [CrossRef] [PubMed]
- Funning, G.J.; Parsons, B.; Wright, T.J.; Jackson, J.A.; Fielding, E.J. Surface displacements and source parameters of the 2003 Bam (Iran) earthquake from Envisat advanced synthetic aperture radar imagery. J. Geophys. Res. 2005, 110, B09406. [Google Scholar] [CrossRef]
- Zha, X.; Fu, R.; Dai, Z.; Jing, P.; Ni, S.; Huang, J. Applying InSAR technique to accurately relocate the epicentre for the 1999 Ms = 5.6 Kuqa earthquake in Xinjiang province, China. Geophys. J. Int. 2009, 176, 107–112. [Google Scholar] [CrossRef]
- Tong, X.; Sandwell, D.T.; Fialko, Y. Coseismic slip model of the 2008 Wenchuan earthquake derived from joint inversion of interferometric synthetic aperture radar, GPS, and field data. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Y.; Wen, Y.; Wang, R. Coseismic slip distribution of the 2008 Mw 7.9 Wenchuan earthquake from joint inversion of GPS and InSAR data. Bull. Seismol. Soc. Am. 2010, 100, 2736–2749. [Google Scholar] [CrossRef]
- Qiao, X.; Yang, S.; Du, R.; Ge, L.; Wang, Q. Coseismic slip from the 6 October 2008, Mw 6.3 Damxung earthquake, Tibetan Plateau, constrained by InSAR observations. Pure Appl. Geophys. 2011, 168, 1749–1758. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, C.; Wen, Y.; He, P.; Jiang, G. Fault rupture model of the 2008 Dangxiong (Tibet, China) Mw 6.3 earthquake from Envisat and ALOS data. Adv. Space Res. 2012, 50, 952–962. [Google Scholar] [CrossRef]
- Wen, Y.; Xu, C.; Liu, Y.; Jiang, G.; He, P. Coseismic slip in the 2010 Yushu earthquake (China), constrained by wide-swath and strip-map InSAR. Nat. Hazards Earth Syst. Sci. 2013, 13, 35–44. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, M.; Wang, Y.; Wu, Y.; Che, S.; Shen, Z.K.; Bürgmann, R.; Sun, J.; Yang, Y.; Liao, H. GPS constrained coseismic source and slip distribution of the 2013 Mw 6. 6 Lushan, China, earthquake and its tectonic implications. Geophys. Res. Lett. 2014, 41, 407–413. [Google Scholar] [CrossRef]
- Kaneko, Y.; Hamling, I.; Van Dissen, R.; Motagh, M.; Samsonov, S. InSAR imaging of displacement on flexural-slip faults triggered by the 2013 Mw 6.6 Lake Grassmere earthquake, central New Zealand. Geophys. Res. Lett. 2015, 42, 781–788. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.; Rossi, M.; Adragna, F. Radar interferometric mapping of deformation in the year after the Landers earthquake. Nature 1994, 369, 227–230. [Google Scholar] [CrossRef]
- Savage, J.; Svarc, J. Postseismic deformation associated with the 1992 Mw = 7.3 Landers earthquake, southern California. J. Geophys. Res. 1997, 102, 7565–7577. [Google Scholar] [CrossRef]
- Peltzer, G.; Rosen, P.; Rogez, F.; Hudnut, K. Poroelastic rebound along the Landers 1992 earthquake surface rupture. J. Geophys. Res. 1998, 103, 30131–30145. [Google Scholar] [CrossRef]
- Bürgmann, R.; Ergintav, S.; Segall, P.; Hearn, E.H.; McClusky, S.; Reilinger, R.E.; Woith, H.; Zschau, J. Time-dependent distributed afterslip on and deep below the Izmit earthquake rupture. Bull. Seismol. Soc. Am. 2002, 92, 126–137. [Google Scholar] [CrossRef]
- Hearn, E.H. What can GPS data tell us about the dynamics of post-seismic deformation? Geophys. J. Int. 2003, 155, 753–777. [Google Scholar] [CrossRef]
- Hsu, Y.J.; Simons, M.; Avouac, J.P.; Galetzka, J.; Sieh, K.; Chlieh, M.; Natawidjaja, D.; Prawirodirdjo, L.; Bock, Y. Frictional afterslip following the 2005 Nias-Simeulue earthquake, Sumatra. Science 2006, 312, 1921–1926. [Google Scholar] [CrossRef] [PubMed]
- Ryder, I.; Parsons, B.; Wright, T.J.; Funning, G.J. Post-seismic motion following the 1997 Manyi (Tibet) earthquake: InSAR observations and modelling. Geophys. J. Int. 2007, 169, 1009–1027. [Google Scholar] [CrossRef]
- Ryder, I.; Bürgmann, R.; Sun, J. Tandem afterslip on connected fault planes following the 2008 Nima-Gaize (Tibet) earthquake. J. Geophys. Res. 2010, 115, B03404. [Google Scholar] [CrossRef]
- Fielding, E.J.; Lundgren, P.R.; Bürgmann, R.; Funning, G.J. Shallow fault-zone dilatancy recovery after the 2003 Bam earthquake in Iran. Nature 2009, 458, 64–68. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Li, Z.; Xu, C.; Ryder, I.; Bürgmann, R. Postseismic motion after the 2001 Mw 7.8 Kokoxili earthquake in Tibet observed by InSAR time series. J. Geophys. Res. 2012, 117, B08405. [Google Scholar]
- Bie, L.; Ryder, I.; Nippress, S.E.J.; Bürgmann, R. Coseismic and post-seismic activity associated with the 2008 Mw 6.3 Damxung earthquake, Tibet, constrained by InSAR. Geophys. J. Int. 2014, 196, 788–803. [Google Scholar] [CrossRef]
- Diao, F.; Xiong, X.; Wang, R.; Zheng, Y.; Walter, T.R.; Weng, H.; Li, J. Overlapping post-seismic deformation processes: Afterslip and viscoelastic relaxation following the 2011 Mw 9.0 Tohoku (Japan) earthquake. Geophys. J. Int. 2014, 196, 218–229. [Google Scholar] [CrossRef]
- Feng, W. Modelling Co- and Post-Seismic Displacements Revealed by InSAR, and Their Implications for Fault Behaviour. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2015. [Google Scholar]
- Hu, J.; Li, Z.; Ding, X.; Zhu, J.; Sun, Q. Derivation of 3-d coseismic surface displacement fields for the 2011 Mw 9.0 Tohoku-Oki earthquake from InSAR and GPS measurements. Geophys. J. Int. 2013, 192, 573–585. [Google Scholar] [CrossRef]
- Massonnet, D.; Rabaute, T. Radar interferometry: Limits and potential. IEEE. Trans. Geosci. Remote Sens. 1993, 31, 455–464. [Google Scholar] [CrossRef]
- Kotsis, I.; Kontoes, C.; Paradissis, D.; Karamitsos, S.; Elias, P.; Papoutsis, I. A methodology to validate the InSAR derived displacement field of the 7 September 1999 Athens earthquake using terrestrial surveying. Improvement of the assessed deformation field by interferometric stacking. Sensors 2008, 8, 4119–4134. [Google Scholar] [CrossRef]
- Tahayt, A.; Feigl, K.; Mourabit, T.; Rigo, A.; Reilinger, R.; McClusky, S.; Fadil, A.; Berthier, E.; Dorbath, L.; Serroukh, M. The Al Hoceima (Morocco) earthquake of 24 February 2004, analysis and interpretation of data from Envisat ASAR and SPOT5 validated by ground-based observations. Remote Sens. Environ. 2009, 113, 306–316. [Google Scholar] [CrossRef]
- Zhou, X.; Chang, N.B.; Li, S. Applications of SAR interferometry in earth and environmental science research. Sensors 2009, 9, 1876–1912. [Google Scholar] [CrossRef] [PubMed]
- Rosen, P.A.; Hensley, S.; Peltzer, G.; Simons, M. Updated repeat orbit interferometry package released. Eos Trans. AGU 2004, 85, 47. [Google Scholar] [CrossRef]
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. In Gamma SAR and interferometric processing software. In Proceedings of the ERS-ENVISAT Symposium, Gothenburg, Sweden, 16–20 October 2000; pp. 16–20.
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; Volume 2, p. 301. [Google Scholar]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE. Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Li, Z.; Fielding, E.; Cross, P. Integration of InSAR time series analysis and water vapour correction for mapping postseismic deformation after the 2003 Bam (Iran) earthquake. IEEE. Trans. Geosci. Remote Sens. 2009, 47, 3220–3230. [Google Scholar]
- Yang, C.S.; Zhang, Q.; Zhao, C.Y.; Wang, Q.L.; Ji, L.Y. Monitoring land subsidence and fault deformation using the small baseline subset InSAR technique: A case study in the Datong Basin, China. J. Geodyn. 2014, 75, 34–40. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Goldstein, R.; Zebker, H.; Werner, C. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, C.; Li, Z.; Wen, Y.; Forrest, D. Interseismic slip rate of the Garze-Yushu fault belt in the Tibetan Plateau from C-band InSAR observations between 2003 and 2010. Adv. Space Res. 2011, 48, 2005–2015. [Google Scholar] [CrossRef]
- Biggs, J.; Wright, T.; Lu, Z.; Parsons, B. Multi-interferogram method for measuring interseismic deformation: Denali fault, Alaska. Geophys. J. Int. 2007, 170, 1165–1179. [Google Scholar] [CrossRef]
- Parsons, B.; Wright, T.; Rowe, P.; Andrews, J.; Jackson, J.; Walker, R.; Khatib, M.; Talebian, M.; Bergman, E.; Engdahl, E. The 1994 Sefidabeh (eastern Iran) earthquakes revisited: New evidence from satellite radar interferometry and carbonate dating about the growth of an active fold above a blind thrust fault. Geophys. J. Int. 2006, 164, 202–217. [Google Scholar] [CrossRef]
- Thatcher, W.; Rundle, J.B. A model for the earthquake cycle in underthrust zones. J. Geophys. Res. 1979, 84, 5540–5556. [Google Scholar] [CrossRef]
- Wright, T.J.; Elliott, J.; Wang, H.; Ryder, I. Earthquake cycle deformation and the moho: Implications for the rheology of continental lithosphere. Tectonophysics 2013, 609, 504–523. [Google Scholar] [CrossRef]
- Matsu’ura, M.; Sato, T. A dislocation model for the earthquake cycle at convergent plate boundaries. Geophys. J. Int. 1989, 96, 23–32. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar]
- Hsu, Y.J.; Yu, S.B.; Chen, H.Y. Coseismic and postseismic deformation associated with the 2003 Chengkung, Taiwan, earthquake. Geophys. J. Int. 2009, 176, 420–430. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H. New, improved version of generic mapping tools released. Eos Trans. AGU 1998, 79, 579. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Xu, C.; Wen, Y.; Li, Z. Post-Seismic Deformation from the 2009 Mw 6.3 Dachaidan Earthquake in the Northern Qaidam Basin Detected by Small Baseline Subset InSAR Technique. Sensors 2016, 16, 206. https://doi.org/10.3390/s16020206
Liu Y, Xu C, Wen Y, Li Z. Post-Seismic Deformation from the 2009 Mw 6.3 Dachaidan Earthquake in the Northern Qaidam Basin Detected by Small Baseline Subset InSAR Technique. Sensors. 2016; 16(2):206. https://doi.org/10.3390/s16020206
Chicago/Turabian StyleLiu, Yang, Caijun Xu, Yangmao Wen, and Zhicai Li. 2016. "Post-Seismic Deformation from the 2009 Mw 6.3 Dachaidan Earthquake in the Northern Qaidam Basin Detected by Small Baseline Subset InSAR Technique" Sensors 16, no. 2: 206. https://doi.org/10.3390/s16020206







