Gauge Factor and Stretchability of Silicon-on-Polymer Strain Gauges

Abstract

Strain gauges are widely applied to measure mechanical deformation of structures and specimens. While metallic foil gauges usually have a gauge factor slightly over 2, single crystalline silicon demonstrates intrinsic gauge factors as high as 200. Although silicon is an intrinsically stiff and brittle material, flexible and even stretchable strain gauges have been achieved by integrating thin silicon strips on soft and deformable polymer substrates. To achieve a fundamental understanding of the large variance in gauge factor and stretchability of reported flexible/stretchable silicon-on-polymer strain gauges, finite element and analytically models are established to reveal the effects of the length of the silicon strip, and the thickness and modulus of the polymer substrate. Analytical results for two limiting cases, i.e., infinitely thick substrate and infinitely long strip, have found good agreement with FEM results. We have discovered that strains in silicon resistor can vary by orders of magnitude with different substrate materials whereas strip length or substrate thickness only affects the strain level mildly. While the average strain in silicon reflects the gauge factor, the maximum strain in silicon governs the stretchability of the system. The tradeoff between gauge factor and stretchability of silicon-on-polymer strain gauges has been proposed and discussed.

1. Introduction

Strain gauges are widely used across all engineering fields to measure mechanical deformation of a solid object. The most common type of strain gauges consists of a patterned metal foil on a stiff plastic backing sheet glued to the solid object. Deformation in the object leads to deformation in the foil, thereby causing its electrical resistance to change. The fractional change in resistance, ΔR/R₀, is related to the mechanical strain ε by the gauge factor (GF):

$$GF=\frac{\mathrm{\Delta }R/R_0}{\epsilon }$$

(1)

The GF for metallic foils are typically between 2 to 5 [1], due mostly to changes in length and cross-sectional area instead of changes in resistivity of the metal wires [2]. For precision measurements, however, semiconductor gauges are preferred over metal foils. In 1954 Smith first discovered the so-called piezoresistive effects [3], whereby the static resistance of a piece of semiconductor can be changed by a mechanical stress. In fact, it is the resistivity of the semiconductor that varies significantly with deformation, attributing to the strong dependence of the bandgap on inter-atomic spacing [3–5]. For example, the gauge factor of p-type (110) single crystalline silicon can be as high as 200 [3,6,7]. Since then, silicon-based microelectromechanical systems (MEMS) have found widespread use in load cells and pressure sensors [5]. Large piezoresistive coefficients, linear and instantaneous responses, multiplexing capabilities, and mature processing technologies represent attractive aspects of silicon for these applications. Due to the intrinsic stiffness and brittleness, however, semiconductor gauges are widely used as ‘hard’ sensors for small strain measurement on flat surfaces of stiff objects. If the surface of the target object is curvilinear, the gauge will be too stiff to completely conform to the surface. If the target object is too soft, the stiff gauge will significantly constrain the local deformation in the underlying region, resulting in understated strain measurement. If the target object is deforming too much, silicon will easily rupture.

Strain measurement on curvilinear surfaces and/or soft, highly deformable objects calls for flexible or even stretchable strain gauges. Examples of applications include structural health monitoring on curvilinear surfaces [8], multiplexed arrays of strain gauges for three-dimensional shape-mapping [9], gauges integrated on contact lenses for intraocular pressure monitoring [10], gauges mounted on human skin to monitor gait/joint motion [11–13], and gauges wrapped around beating heart to detect ischemia-induced heart stiffening [14]. Candidates of strain sensing materials for flexible/stretchable strain gauges include metals, silicon, piezoresistive elastomers, and even carbon nanotubes and graphene. Although carbon-doped elastomer exhibit intrinsic stretchability and strong piezoresistivity, the resistance of the percolated conductive networks is susceptible to drifting and hysteresis due to the viscoelasticity of rubber materials [15]. Inorganic materials generally offer better stability and repeatability, but their compliance and deformability are very limited. To make a gauge flexible or even stretchable, polymers are used as substrates to support thin wires or strips of strain sensing component. Metal wires exhibit much lower intrinsic gauge factors than silicon. Although flexible strain gauges based on carbon nanotubes [16] or graphene [17] have been reported, none has the maturity and proven effectiveness of silicon. As a result, we will focus on the mechanical responses of flexible and stretchable gauges based on polymer-supported thin silicon strips in this work.

Recent work shows that ultrathin sheets of single crystalline silicon, i.e., silicon nanomembranes, can survive severe bending or stretch when supported by polymer substrates [18]. Depending on the substrate material, flexible strain gauges based on polyimide substrates [9] and tissue-like strain gauges based on elastomer substrates [13,14] have been reported. We notice that even silicon strips with the same thickness, orientation, and doping concentration, when bonded to different types of polymer substrates, the GF and stretchability (the applied strain beyond which silicon ruptures) can vary by orders of magnitude. For example, when polyimide substrates are used, GF obtained from uniaxial tension tests are 43 and the system cannot be stretched beyond 1% [9]. In contrast, when the substrate is elastomer, the measured GF reduced to 0.23 but the system can be stretched beyond 25% without inducing any cracks in silicon [13,14]. Mechanics models accounting for the silicon length and thickness as well as substrate modulus and thickness need to be developed to explain the discrepancies found in different systems and to guide the rationalized design of future flexible/stretchable silicon-on-polymer strain gauges.

In this paper, we describe finite element and analytical modeling of thin silicon strips bonded to polymer substrates of wide ranges of Young's modulus and thickness. Both gauge factor and stretchability can be predicted and effects of material and geometric variables are revealed. The tradeoff between GF and stretchability is proposed for the first time to provide guidance for the choice of substrate material and thickness. This paper is organized as follows: Section 2 describes the basic models adopted in this paper. Section 3 presents the finite element modeling (FEM) results. Section 4 provides analytical results for two limiting cases. Section 5 discusses the tradeoff between GF and stretchability. Concluding remarks are provided in Section 6.

2. Model Setup

Silicon-based stretchable strain gauges are often composed of arrays of strips. The modeling work in this paper will just focus on a unit cell cut out of the periodic array. A schematic of a unit cell and its corresponding 2D plane strain model are depicted in Figure 1A,B. L represents the length of the silicon strip, h and H are the thicknesses of silicon and polymer, respectively. To minimize the number of variables, the size of the unit cell is fixed to be 1.5 L for all the models following a convention of island-on-polymer analysis [19–21]. When a uniform tensile strain, ε_app, is applied to the substrate, the resistance of the silicon strip will change by ΔR, and the effective GF of the strain gauge system is defined as:

$$GF=\frac{\mathrm{\Delta }R/R_0}{{\epsilon }_{\text{app}}}$$

(2)

Although strain distribution in silicon might not be uniform, it has been proven [11] that the fractional change of resistance is proportional to the average longitudinal strain in silicon, i.e.:

$$\mathrm{\Delta }R/R_0={\mathit{\text{GF}}}_{\text{Si}}{\epsilon }_{\text{avg}}$$

(3)

where GF_Si represents the intrinsic gauge factor of silicon. Depending on the crystal orientation as well as the doping type and concentration [22], the GF_Si of p-type (110) silicon can reach as high as 200 [3,6,7]. The overall average strain in silicon, ε_avg, can be calculated by just averaging the strain of the neutral axis over the total length of silicon. This is because the strain of the neutral axis is the average strain across the thickness due to the linear strain distribution in the thickness direction. Using ε_n(x) to denote strain along the neutral axis of silicon as shown in Figure 1B, ε_avg is defined as:

$${\epsilon }_{\text{avg}}=\frac{{\int }_{-L/2}^{L/2}{\epsilon }_{\mathrm{n}}(x)dx}{L}$$

(4)

Plugging Equation (3) into Equation (2) yields:

$$GF={\mathit{\text{GF}}}_{\text{Si}}\frac{{\epsilon }_{\text{avg}}}{{\epsilon }_{\text{app}}}$$

(5)

suggesting that to find out the effective GF of the strain gauge system, we need to calculate the average strain in silicon.

The maximum strain in silicon, ε_max, will be related to the stretchability of the system. We define stretchability as the critical strain applied to the substrate, ${\epsilon }_{\text{app}}^{\text{cr}}$, beyond which silicon will rupture. For brittle silicon, we adopt a failure criterion, ε_max = ε_cr, in which ε_max represents the maximum tensile strain in silicon and ε_cr denotes the intrinsic critical strain-to-rupture of silicon that is to be measured experimentally. The failure criterion can be rewritten in the normalized form ${\epsilon }_{max}/{\epsilon }_{\text{app}}={\epsilon }_{\text{cr}}/{\epsilon }_{\text{app}}^{\text{cr}}$, which can be rearranged to obtain the stretchability:

$${\epsilon }_{\text{app}}^{\text{cr}}=\frac{{\epsilon }_{\text{cr}}}{{\epsilon }_{max}/{\epsilon }_{\text{app}}}$$

(6)

When the polymer substrate is very thin or very soft, there will be slight concave bending in the silicon strip when the substrate is subject to tensile strain (Figure 1C,D). As a result, the maximum strain in silicon always takes place along the bottom of silicon. Using ε_b(x) to denote strain along the bottom of silicon as shown in Figure 1B, then:

$${\epsilon }_{max}=max\{{\epsilon }_{\mathrm{b}}(x)\}$$

(7)

As we have related the device performance indices, GF and stretchability, to ε_avg and ε_max in silicon respectively, in the following we will calculate ε_avg and ε_max to ultimately determine GF and stretchability. Through dimensional analysis, we can get

$$\frac{{\epsilon }_{\text{avg}}}{{\epsilon }_{\text{app}}}=f\left(\frac{{\overline{E}}_{\text{Si}}}{{\overline{E}}_{\mathrm{s}}},\frac{L}{h},\frac{h}{H}\right)$$

(8)

and:

$$\frac{{\epsilon }_{max}}{{\epsilon }_{\text{app}}}=g\left(\frac{{\overline{E}}_{\text{Si}}}{{\overline{E}}_{\mathrm{s}}},\frac{L}{h},\frac{h}{H}\right)$$

(9)

Where Ē = E/(1 − v²) represents the plane strain modulus with v being the Poisson's ratio. Our goal is to find out the functional forms of f and g. Several shear lag models have been built to solve similar problems of stiff thin films on compliant substrates [14,23,24], but they had to make special assumptions of shear stress distribution along the film/substrate interface. In fact, there is no uniform function of interface shear stress distribution that is applicable to wide ranges of Ē_Si/Ē_s, L/h, and H/h, which is the case for stretchable silicon-on-polymer strain gauges. As a result, we will first use FEM to find exact solutions for ε_avg/ε_app and ε_max/ε_app, and then use analytical methods to derive the functional forms of Equations (8) and (9) for extreme cases (e.g., L/H ≫ 1 and L/H ≪ 1) and compare with FEM results.

3. Finite Element Modeling

Over one hundred finite element models are built using commercial software package ABAQUS 6.11 to reveal the effect of the three variables in Equations (8) and (9). The boundary conditions and geometries are chosen to resemble the experimental setups when the sample is subject to uniaxial tension for GF calibration [9,13,14]. Because of symmetry, only the right half of the system shown in Figure 1B is modeled. A symmetric boundary condition is applied along the axis of symmetry, and the right end of the substrate is subject to a uniform horizontal displacement so that ε_app is fixed to be 10% for all models. Nonlinear geometry analysis has to be enabled in ABAQUS because large deformation can be found in the portion of the polymer substrate that is not covered by silicon. Silicon thickness h is set to be 340 nm, the same thickness as the silicon nanomembrane used in most stretchable strain gauges [9,13,14]. Silicon length L varies from 10 μm to 20,000 μm and substrate thickness H varies from 30 μm to 3,000 μm, all are representative experimental parameters. The substrate length is set to be always 1.5 L for this unit cell. Perfect bonding is assumed between silicon and the substrate. Silicon and substrate are meshed using linear beam and plane-strain elements respectively. We model (110) silicon as a linear elastic material and polymer substrates as Neo-Hookean materials. Although the stress-strain curves for linear elastic and Neo-Hookean materials are not quite differentiable for strains up to 10%, we found the Neo-Hookean constitutive law is very helpful to achieve convergent solutions when nonlinear geometry analysis is enabled in ABAQUS. Effective materials properties in terms of Young's modulus and Poisson's ratio are listed in

Table 1. Elastic properties of materials used in FEM.

Part	Element Type	Material	Young's Modulus (E)	Poisson's Ratio (v)
silicon	beam	(110) Silicon [25]	169 GPa	0.27
		Ecoflex [26]	60 kPa	0.49
substrate	plane strain	10:1 PDMS [27]	2 MPa	0.49
		Polyimide [28]	2.5 GPa	0.34

.

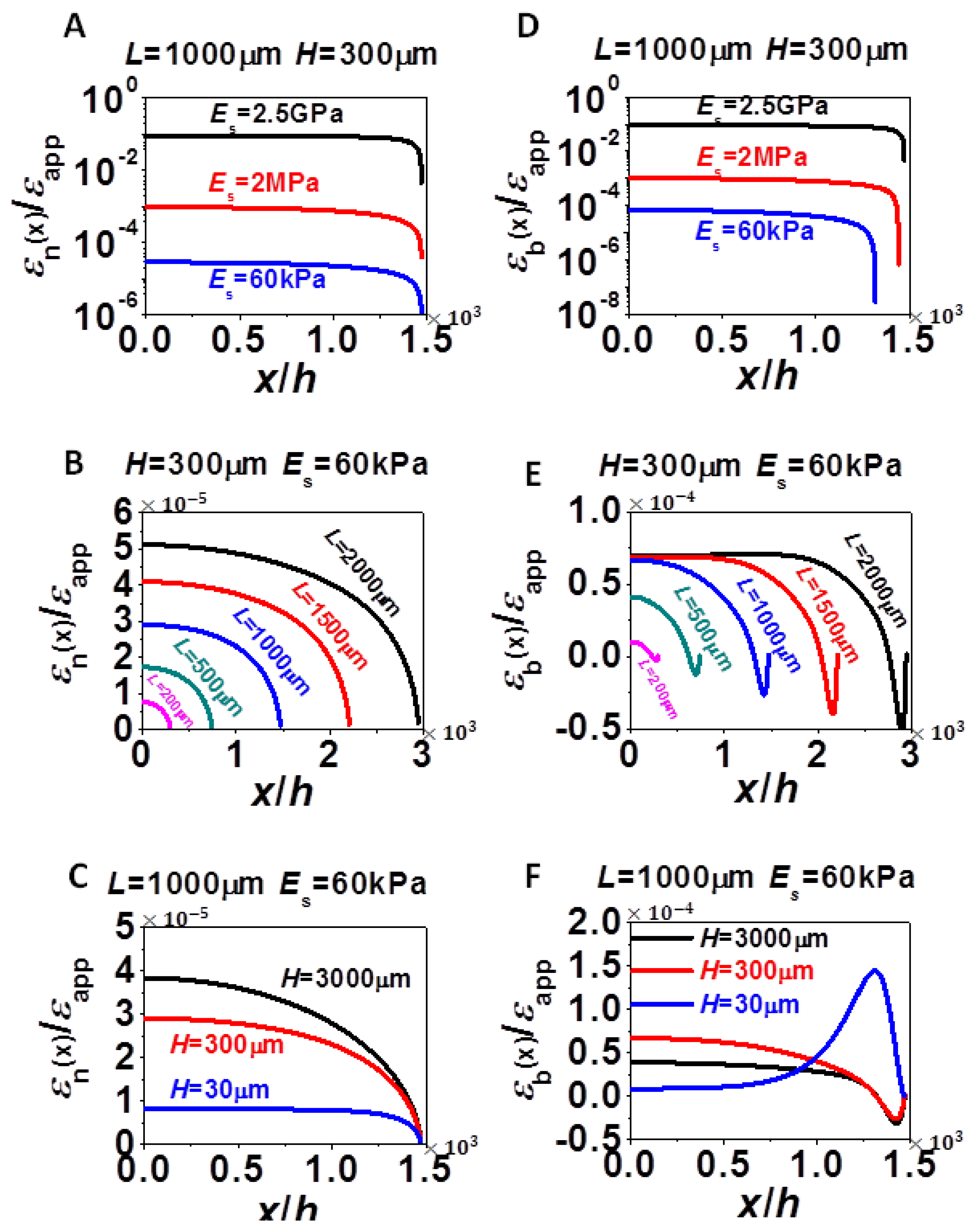
Representative contour plots of longitudinal strain in the substrate and in silicon are given in Figure 1C–E. They are from models with parameters L = 1,000 μm, E_s = 60 kPa and H varying from 30 μm to 3,000 μm. When the substrate is stretched by 10%, strain in silicon is as small as 10⁻⁷ to 10⁻⁴, depending on substrate thickness. It is because silicon is six orders of magnitude stiffer than Ecoflex substrate (E_s = 60 kPa) so that it is highly resistant to elongation, whereas the portion of the substrate not covered by silicon has to accommodate the applied strain by tensile strains up to 25%. Due to huge elastic mismatch between silicon and Ecoflex, horizontally applied tensile strain on a thin substrate will cause bending deformation in the silicon strip, especially near the end (Figure 1C,D). Therefore when the substrate is thin, the strain along the neutral axis of silicon, ε_n, is always smaller than the strain along the bottom of silicon, ε_b. Although ε_n is monotonic with x, ε_b might not be so due to localized bending near the end of the strip. When the substrate is thick enough (Figure 1E), it can be considered semi-infinite and hence can suppress the bending, resulting in identical ε_n and ε_b. Figure 1C–E only list FEM results for E_s = 60 kPa, as the substrate becomes stiffer, the bending will be less significant.

3.1. Strain Distribution in Silicon

Figure 2 offers the distribution of ε_n and ε_b along x for different E_s, L, and H.Figure 2A-C plot ε_n and Figure 2D-E plot ε_b. In all the plots, x = 0 represents the center of silicon and x = L/2 represents the right edge of silicon, as defined in Figure 1B. A generic feature of every strain distribution curve in Figure 2 is that strains always vanish at the traction free edge. Because of the traction free edge, the internal normal force of silicon at position x, i.e., E_Sihε_n(x), has to balance the integration of interfacial shear stress from position x to the edge of silicon, L/2. As shown in Figure 2A-C, ε_n gradually builds up towards the center of silicon because interfacial shear force also builds up as we move away from the edge. The rate of strain growth decreases as x approaches the center of silicon because the interfacial shear stress decays from the edge to the center of silicon. If L is large enough, a plateau of maximum tensile strain could be reached toward the center of silicon. The distribution of ε_b shares some similarity with ε_n, as shown in Figure 2D-E. However, ε_b is not always monotonic with x. When the substrate is soft, e.g., E_s = 60 kPa, edge bending can cause large variations in ε_b, as shown in Figure 2E,F.

To study one effect at a time, we first vary E_s with L = 1,000 μm and H = 300 μm fixed. The distribution of ε_n and ε_b for different E_s (60 kPa, 2 MPa, and 2.5 GPa) are plotted in Figure 2A,D, with vertical axis in logarithmic scales. A key observation is that both ε_n and ε_b increase as substrate modulus increases. It is simply because the stiffer substrate can apply higher shear stress to silicon, meaning that silicon can be stretched more by stiffer substrate. When substrate is very stiff, i.e., when E_s = 2.5 GPa, there is little difference between ε_n and ε_b curves because the assembly will stay almost flat. But when E_s = 60 kPa, ε_b are larger than ε_n due to slight global concave bending.

To study the effect of L, we fix H = 300 μm and E_s = 60 kPa. The distribution of ε_n and ε_b for different L (200, 500, 1,000, 1,500, and 2,000 μm) are plotted in Figure 2B,E. The plateau values of both ε_n and ε_b increase as L increases because the longer L provides the longer distance for interfacial shear force (and hence the normal strain) to build up. Although ε_n monotonically decreases with increasing x, ε_b curves in Figure 2D always have some abnormal behaviors near the edge of silicon, as the result of highly localized curvature near the edge of silicon, as evident in Figure 1C-E.

To study the effect of H, we fix L = 1,000 μm and E_s = 60 kPa and vary H from 30 μm to 3,000 μm in Figure 2C,F. Since thicker substrates provide stronger constraint to silicon, the plateau value of ε_n is higher when H is larger. The variation of ε_b is more complicated than ε_n because when substrate is soft (e.g., E_s = 60 kPa in this case), bending strain could become very significant. Depending on substrate thickness, bending strain distribution also varies a lot. When H = 3,000 μm, there is very small bending curvature in the majority part of silicon (Figure 1E) and hence the plateau values of the black curves in Figure 2C,F are very similar. At the edge of silicon, localized concave bending induces compressive strain at the bottom of silicon because the neutral axis of the assembly is located somewhere within the substrate, hence a dip presents in the black curve of Figure 2F. When H = 300 μm, neutral axis locates within silicon, hence slight global concave bending (Figure 1D) will induce tensile strain along the bottom of silicon, resulting in elevated red curve in Figure 2F. Toward the edge of silicon, the neutral axis will gradually shift into the substrate and hence a dip also presents. When H = 30 μm, bending occurs almost exclusively at the edge (Figure 1C), hence the plateau values of the blue curves in Figure 2C,F are very similar. However, toward the edge of silicon, there is highly localized concave bending. Since neutral axis is within silicon, the bottom of silicon is subject to large tensile strain, resulting in a big bump in the blue curve of Figure 2F. As a conclusion, Figure 2 has demonstrated that unlike ε_n(x), ε_b(x) is not a monotonic function and the effect of H on it is not monotonic either. To find the maximum tensile strain, ε_max, in silicon, we need to find the maximum positive values of each ε_b(x) curve, which does not necessarily occur at the center of silicon.

3.2. Average Strain and Maximum Strain

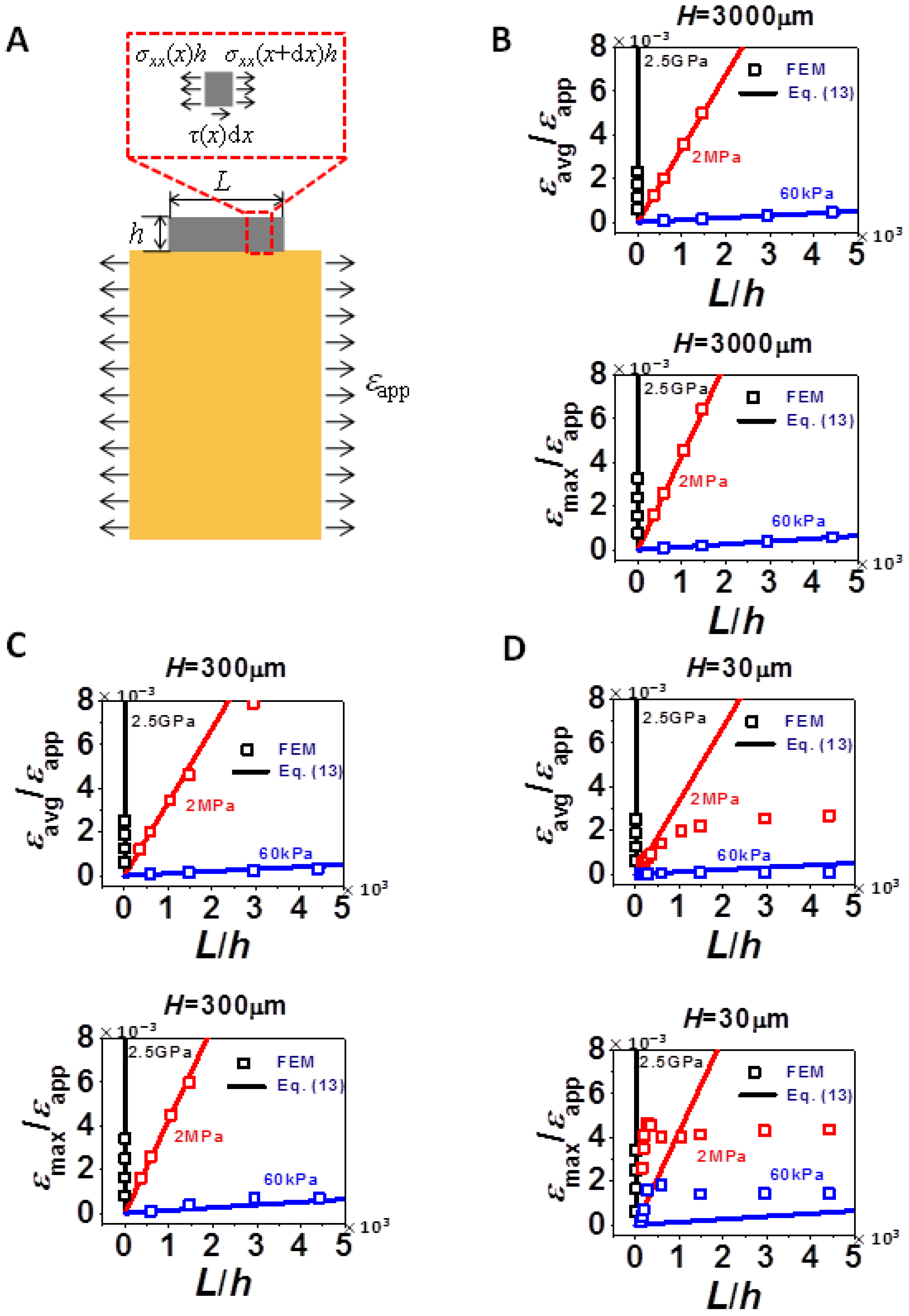
With the insights from strain distribution in Figure 2, Figures 3 and 4 investigate the effect of the three variables L, H, and E_s, on the average strain (ε_avg) and the maximum strain (ε_max) in silicon. Average strains are calculated from averaging the values of ε_n (Equation (4)) and maximum strains are determined through finding the maximum positive values of ε_b (Equation (7)). Figure 3 plots normalized ε_avg as a function of L/h. The same set of data is presented in two different ways: each plot in Figure 3A-C has a fixed E_s and varying H whereas each plot of Figure 3D-F has a fixed H and varying E_s. All plots in Figure 3 show that ε_avg increases with increased film size (L), substrate thickness (H) and substrate modulus (E_s), all of which imply the stronger constraint the substrate is able to apply to silicon, the higher ε_avg. Due to experimental limitations on L and H, changing E_s would be the most effective way to tune ε_avg, by orders of magnitude. According to Figure 3A-C, it is interesting to notice that when L is very small, especially compared to H, there exists a linear relation between ε_avg and L. According to Figure 3D-F, it is also easy to discover that when L is large enough, ε_avg will always reach a plateau, i.e., ε_avg becomes independent of L, and the smaller the H, the faster the plateau can be reached. We will thereby consider the limiting cases of L/H ≪ 1 and L/H ≫ 1 and try to derive analytical solutions for ε_avg in Section 4.

Figure 4 plots the normalized ε_max as a function of L/H for various H and E_s in a format similar to Figure 3. Each plot in Figure 4A-C has a fixed E_s and varying H whereas each plot of Figure 4D-F has a fixed H and varying E_s.

The difference between ε_max and ε_avg is that ε_max has extra bending contribution. Therefore, similar to ε_avg, ε_max always increases with increased L and E_s, and with increased H in most cases. However, when the substrate is very compliant and when L is small, Figure 4A shows that ε_max could be higher in thinner substrate due to localized bending effect we discussed for Figure 2F. As E_s increases to 2.5 GPa, as shown in Figure 4C, bending effect is almost negligible and hence ε_max and ε_avg become undistinguishable, i.e., Figures 3C and 4C look identical. Similar conclusions can be applied to thick substrate (H = 3,000 μm) when comparing Figures 3F and 4F. For the two limiting cases, L/H ≪ 1 and L/H ≫ 1, we also observed similar features as in Figure 3, i.e., linear when L/H ≪ 1 and plateau when L/H ≫ 1. Hence analytical solutions of ε_max will be derived in Section 4 as well.

4. Analytical Modeling

In this section, we are going to develop analytical models for two limiting cases: L/H ≪ 1 and L/H ≫ 1, and the analytical solutions will be compared with the FEM results.

4.1. When L/H ≪ 1

When L/H ≪ 1, h/H ≪ 1 is also true since experimentally L > h is always valid. In this case, H is no longer a relevant variable in the system and the substrate can be considered infinitely thick. Hence ε_avg and ε_max only depend on Ē_s/Ē_Si and L/h, and Equation (8) degenerates to:

$$\frac{\epsilon }{{\epsilon }_{\text{app}}}=f\left(\frac{{\overline{E}}_{\mathrm{s}}}{{\overline{E}}_{\text{Si}}},\frac{L}{h}\right)$$

(10)

To determine the f function, a shear lag model is adopted as shown in Figure 5A. The free body diagram (FBD) of a thin slice of silicon would give the following equilibrium equation:

$$h\frac{d\sigma }{dx}=\tau (x)$$

(11)

where τ(x) represents the shear stress distribution along the silicon/substrate interface. Since τ(x) is unknown and we don't want to make an arbitrary assumption for it, it is simply acknowledged that τ(x) is proportional to the Young's modulus of the substrate, Ē_s. Applying Hooke's law in silicon, σ = Ē_Siε, and integrating once on both sides, Equation (11) reduces to:

$$\epsilon \sim \frac{{\overline{E}}_{\mathrm{s}}}{{\overline{E}}_{\text{Si}}}\frac{L}{h}$$

(12)

And Equation (10) becomes:

$$\frac{\epsilon }{{\epsilon }_{\text{app}}}=\alpha \frac{{\overline{E}}_{\mathrm{s}}}{{\overline{E}}_{\text{Si}}}\frac{L}{h}$$

(13)

where α is a proportional coefficient to be found out through fitting FEM results of small L's. α is a generic coefficient which once fitted, should be applicable to all combinations of L, H, and E_s, provided L/H ≪ 1. We choose to fit the data of strain gauges with H = 3,000 μm, E_s = 2.5 GPa and very small L. The two black curves in Figure 5B are the fitted curves and α is found to be 0.219 for ε_max/ε_app and 0.279 for ε_max/ε_app. We then plot Equation (13) against FEM results of all the other combinations of E_s and H, as long as L's are small. The results are shown in Figure 5B-D. Each figure contains the comparison of Equation (13) and FEM results for ε_avg/ε_app in the upper frame and ε_max/ε_app in the lower frame. It is evident that Equation (13) is able to capture very wide ranges of E_s when H is beyond 300 μm, for both ε_avg/ε_app and ε_max/ε_app. When H = 30 μm as shown in Figure 5D, Equation (13) is able to capture ε_avg/ε_app over a wide range of E_s but is only able to capture ε_max/ε_app when E_s = 2.5 GPa, due to the abnormal ε_max induced by large local bending.

In conclusion, when L/H ≪ 1, average and maximum strains in silicon scale linearly with Ē_s and L. Since Ē_s can be easily changed by orders of magnitude as shown in Table 1, strains in silicon could also be tuned cross wide ranges.

4.2. When L/H ≫ 1

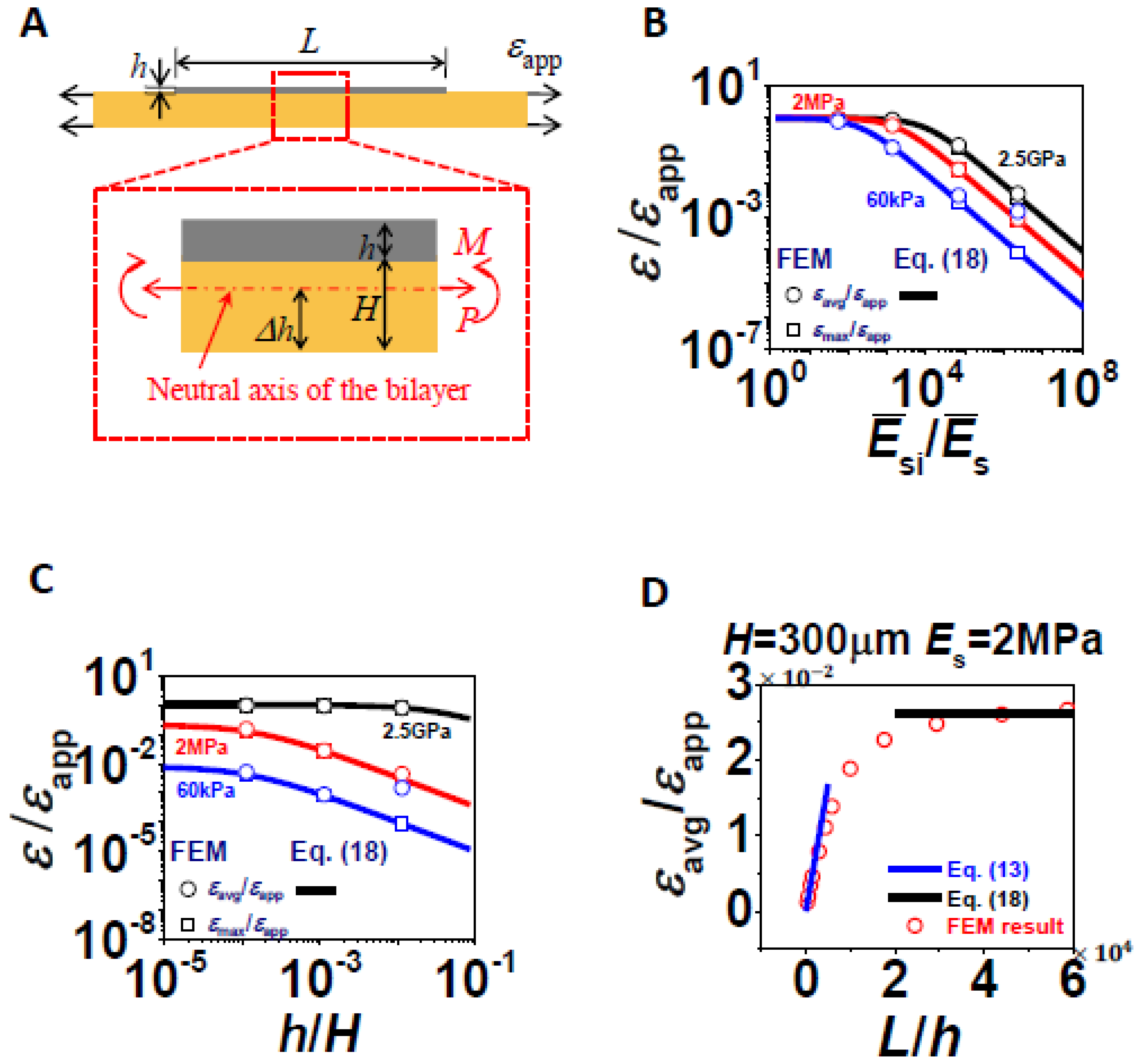
When L/H ≫ 1, assuming L/H ≫ 1 is always valid, relevant variables reduce to Ē_Si/Ē_s and h/H. To derive analytical solution for this case, we make two cross-sectional cuts within the length of silicon and the FBD is shown in Figure 6A. The neutral axis of this bilayer is given by [29]:

$$\Delta =\frac{1+2\Sigma \eta +\Sigma {\eta }^2}{2\eta (1+\Sigma \eta )}$$

(14)

where Σ = Ē_Si/Ē_s, η = h/H.

Boundary conditions are decomposed to P and M, which are both acting at the neutral axis. Assuming the following relation between P and ε_app:

$${\epsilon }_{\text{app}}=\beta \frac{p}{{\overline{E}}_{\mathrm{s}}H}+(1-\beta )\frac{P}{{\overline{E}}_{\text{Si}}h+{\overline{E}}_{\mathrm{s}}H}$$

(15)

where β is a parameter capturing the relative contribution from uncovered substrate and (1−β) captures the relative contribution from the covered substrate of the silicon-substrate bilayer structure. In this paper, since substrate length is fixed to be 1.5 L, then ideally β = 1/3. But for substrate with finite thickness, β is assumed to have linear relationship with H/h such that:

$$\beta =\frac{a}{\eta }+b$$

(16)

where a and b are constants to be fitted.

Following this practice, the simplest form of average strain in silicon can be written as:

$${\epsilon }_{\text{avg}}=\frac{P}{{\overline{E}}_{\text{Si}}h+{\overline{E}}_{\mathrm{s}}H}$$

(17)

Combining Equations (15)–(17) gives:

$$\frac{{\epsilon }_{\text{avg}}}{{\epsilon }_{\text{app}}}=\frac{1}{1+a\Sigma +b\Sigma \eta }$$

(18)

Through curve fitting of FEM results, a and b can be obtained as a = 5.46 × 10⁻⁵ and b = 0.428. Equation (18) turned out to be an universal expression to capture ε_avg/ε_app and ε_max/ε_app, over wide ranges of Σ and η provided L ≫ H. For very big Σ and η, i.e., very compliant and thin substrate, Equation (18) cannot capture ε_max/ε_app very well due to localized bending effects.

Figure 6B,C plots Equation (18) (as curves) against FEM results (as markers) in log log scale. Some important conclusions can be drawn and rationalized from the two plots. First, when the substrate is as stiff as silicon, or when the substrate is infinitely thick, ε/ε_app approaches 1. When the substrate becomes extremely soft or extremely thin, ε/ε_app can be reduced by orders of magnitude, and should eventually die out. Figure 6C also tells that the effect of h/H is insignificant when the substrate is very stiff but gradually becomes more effective as the substrate modulus reduces.

With the two semi-analytical solutions given by Equations (13) and (18), it is useful to plot them for a representative combination of (Σ, η) in a L/H plot as shown in Figure 6(D). It is clear that Equations (13) and (18) can successfully bond the FEM results, except the transition zone.

5. Tradeoff between Gauge Factor and Stretchability

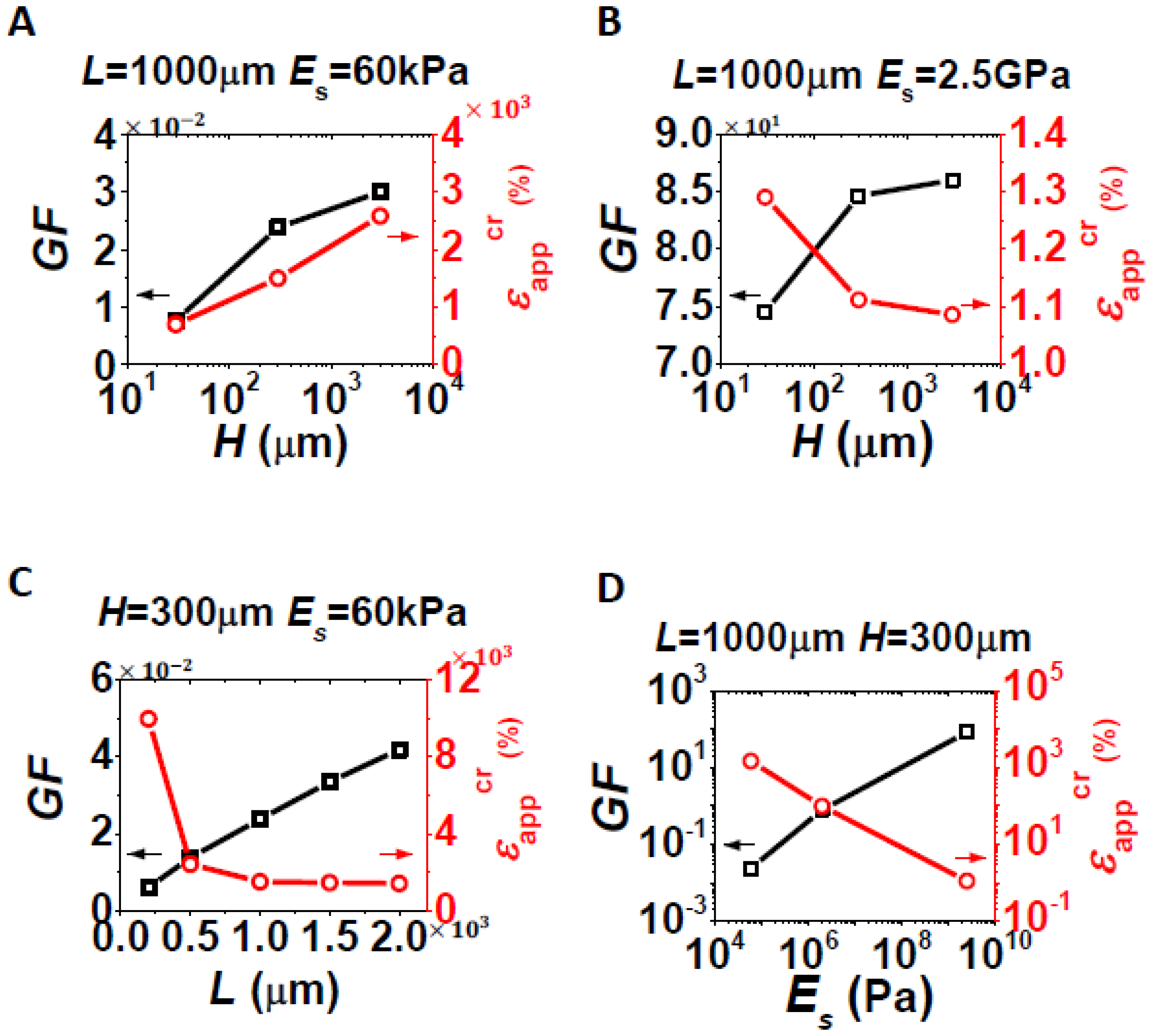
After finding out ε_avg/ε_app and ε_max/ε_app, the final step is to use Equations (5) and (6) to determine the gauge factor, GF, and the stretchability, ${\epsilon }_{\text{app}}^{\text{cr}}$, of a particular strain gauge. For the purpose of illustration, we have to assume some reasonable numbers for the intrinsic properties for silicon, including GF_Si = 100 [9] and ε_cr = 1%. Some representative results are shown in Figure 7, with GF in black and ${\epsilon }_{\text{app}}^{\text{cr}}$ in red in each plot. First, effects of H are studied for fixed L, and E_s, as shown in Figure 7A,B. Comparing the two plots, GF always increases as H increases, but the variation of ${\epsilon }_{\text{app}}^{\text{cr}}$ with H depends on E_s. When the substrate is really soft and silicon is short, as the case for Figure 7A, the assembly is easy to bend especially when H is small. The local bending induced strain contributes significantly to ε_max which is inversely proportional to ${\epsilon }_{\text{app}}^{\text{cr}}$ according to Equation (6). As a result, thinner substrate induces higher maximum strain and hence lower stretchability. When the substrate is stiff, e.g., E_s = 2.5 GPa as shown in Figure 7B, there is almost no bending in the assembly and hence the thicker substrate induces higher maximum strain (Figure 4C). It is interpreted as a tradeoff between stretchability and GF. As constraints from the substrate become stronger, i.e., as L, H, or E_s increases, the larger strain in silicon suggests the higher GF but the lower stretchability, which has been confirmed by Figure 7C,D. Effects of L are studied for fixed H and E_s, as shown in Figure 7C. For longer strip, the GF is larger but the stretchability is lower. This is always the case for other H and E_s combinations. Similar effects are observed for E_s, as shown in Figure 7D, except that the scales of both GF and ${\epsilon }_{\text{app}}^{\text{cr}}$ are in log scale, suggesting a big tuning range. For example, when E_s = 60 kPa, the critical applied strain to rupture silicon $({\epsilon }_{\text{app}}^{\text{cr}})$ can be as high as 10,000% in theory, which implies that the stretchability of the strain gauge is only limited by the stretchability of the substrate. But it corresponds to a GF as low as 0.006. Practically, GF should be at least 1 for strain measurement, which implies E_s should be 2 MPa and beyond, which still corresponds to stretchability beyond 100%.

The goal of plots in Figure 7 is to provide guidance for engineers to choose the right strain gauge systems under certain constraints or to predict the performance of a given stretchable strain gauge based on silicon nanomembrane. For example, to measure an object which deforms up to 30%, we will need to choose experimentally appropriate L, H, and E_s to make a strain gauge with a stretchability of 30% and maximized GF. Since the effects of L and H are within one order of magnitude as shown in Figure 7A–C, we could fix them at reasonable numbers and the key is to select the right stiffness for the substrate, using a plot as shown in Figure 7D. A stretchability of 30% corresponds to a E_s = 1.1 × 10⁷ Pa, which in turn predicts the GF to be 3.27.

We have three final remarks on applying the analysis in this paper to real strain gauge samples [9,13,14]. In real samples, brittle silicon strip is usually sandwiched between two layers of insulating polyimide, and the strip is connected to metallic interconnects (usually in serpentine shape) for data acquisition. Laminating insulating polymers on silicon strip is equivalent to an increase of h, which would decrease strain in silicon and hence decrease the system GF. Adding interconnects to silicon is equivalent to an increase of L, which would increase strain in silicon and hence increase the system GF. Therefore the idealized model in Figure 1B may not offer the most accurate quantitative prediction for a practical sample. But we can always run 3D FEM to calculate the strain in silicon taking into account the actual layout of the circuits and the multilayer lamination to predict a pertinent GF and stretchability for that specific strain gauge system.

The coupling between tension and bending is a generic problem associated with mechanical strain gauges. This study has also shed light on this issue. When E_s ≪ E_Si, the neutral axis of the bilayer almost overlaps with the neutral axis of silicon. In this case bending will induce minimum ε_avg in silicon and hence bending effect can be neglected. When E_s is close to E_Si, the neutral axis of the bilayer lies far away from the neutral axis of silicon. In this case the bending will induce large ε_avg in silicon. To minimize the bending induced signal when the substrate is a stiff polymer, one can add an identical polymer layer on top of silicon, forming a sandwiched structure to locate silicon along the neutral axis of the sandwich structure. This structure can be readily analyzed by replacing the old H with the new 2H, leaving everything else unchanged.

Due to the mismatch in coefficients of thermal expansion (CTE) between silicon and polymer, temperature variation will induce stress and hence resistance change in silicon. The best known method to eliminate temperature effect is to use Wheatstone bridge instead of single resistors. The mechanical analysis on a single resistor offered in this paper is readily applicable to each linear arm of the Wheatstone bridge.

6. Conclusions

In conclusion, we performed strain analysis on polymer-bonded thin silicon strips using both FEM and analytical methods. The gauge factor and stretchability of a silicon-on-polymer strain gauge have been predicted as functions of the normalized length of silicon, and the normalized thickness and modulus of the polymer substrate. In general, we found that the longer strip, the thicker or the stiffer substrate will transfer a larger fraction of the applied strain to silicon. Silicon length and substrate thickness has only moderate effects on strain in silicon whereas varying the stiffness of the substrate could change the strain and hence the gauge factor and stretchability by orders of magnitude. A tradeoff between GF and stretchability has been discovered. Since wide ranges of gauge factor and stretchability can be achieved through tuning the substrate modulus, results from this work can be used as guidelines to design appropriate strain gauges or to predict the performance of fabricated strain gauges.