Seismic Target Classification Using a Wavelet Packet Manifold in Unattended Ground Sensors Systems
Abstract
: One of the most challenging problems in target classification is the extraction of a robust feature, which can effectively represent a specific type of targets. The use of seismic signals in unattended ground sensor (UGS) systems makes this problem more complicated, because the seismic target signal is non-stationary, geology-dependent and with high-dimensional feature space. This paper proposes a new feature extraction algorithm, called wavelet packet manifold (WPM), by addressing the neighborhood preserving embedding (NPE) algorithm of manifold learning on the wavelet packet node energy (WPNE) of seismic signals. By combining non-stationary information and low-dimensional manifold information, WPM provides a more robust representation for seismic target classification. By using a K nearest neighbors classifier on the WPM signature, the algorithm of wavelet packet manifold classification (WPMC) is proposed. Experimental results show that the proposed WPMC can not only reduce feature dimensionality, but also improve the classification accuracy up to 95.03%. Moreover, compared with state-of-the-art methods, WPMC is more suitable for UGS in terms of recognition ratio and computational complexity.1. Introduction
Unattended ground sensor (UGS) systems consist of a lot of sensor nodes and are usually employed for battlefield situation awareness through detection of seismic, acoustic and infrared signals emitted by moving targets [1]. Pedestrians, wheeled vehicles, tracked vehicles and helicopters are the seismic targets of focal interest to land-based monitoring systems, nevertheless they are out of the monitoring capability of radars, thus, UGSs are responsible for detecting and recognizing them. Acoustic sensors and seismic sensors are typically used in UGS systems, however, acoustic target recognition will be affected by weather, Doppler effects and environmental noise. Fortunately, seismic signals are less sensitive to these factors [2], therefore, seismic sensors have become a dominant kind of sensor for UGS systems [3].
However, moving targets' seismic signals are non-stationary [3]. In addition, the seismic signal generated by a moving target is characterized by target velocity, target structure, the signal's propagation distance and local underlying geology, etc. [4,5], and is not a simply linear combination of these factors. Therefore, the seismic signal of a moving target is usually considered as a kind of signal with a high-dimensional feature space [4,6,7]. In order to obtain the compact time-frequency feature of each kind of seismic target, it is necessary to reduce correlation contents and fuse the feature set to a minimum but robust one. Thus, a robust seismic feature with the properties of non-stationary and low-dimensional is in urgent demand.
Current feature extraction methods for seismic signals can be classified into three categories, namely, time domain [8,9], frequency domain [4,10,11] and time-frequency domain [3]. On the one hand, time-domain analysis may not be able to recognize targets very accurately because of the interference noise, complicated signal waveforms and variations of the terrain [3]. On the other hand, the accuracy of frequency domain methods may be degraded due to underlying non-stationary in the observed signal [12]. Therefore, recent research has concentrated on time-frequency domain methods (e.g., wavelet transform) thanks to their denoising and localization properties [12].
The conventional seismic target recognition methods usually consist of four steps, just as discussed in [13]. First, the wavelet packet transform (WPT) that overcomes the fixed time-frequency resolution is performed on the original signal. Second, to alleviate the time-variant characteristics of the WPT coefficients, wavelet packet node energy (WPNE) is used as an essential time-frequency feature measure of the target [13]. Although the WPNE provides us with a multi-resolution view of a signal, it still has correlation information. Therefore, the third step is to reduce the dimensionality of the feature space, using some feature selection criteria to discard those feature components which contain little discriminate information, and result in a feature subset having a reduced number of parameters without compromising the classification performance. Finally, the reduced dimensional feature vector is then used as an input to a classifier. In reference [13], even if the feature selection has been already employed to discard redundant information, a complex neural network classifier is still indispensable. In [3], principal component analysis (PCA) is employed to reduce the dimensionality of seismic feature space. Unfortunately, PCA is only suitable for signals whose feature space is globally linear, while seismic features are only locally linear, therefore, the performance obtained in [3] is unsatisfying. Recently, manifold learning has emerged in feature extraction for its capability of effectively identifying low-dimensional structure hidden in high-dimensional data [14–19]. The technique can be realized through several algorithms, including Laplacian Eigenmap [20], locally linear embedding (LLE) [21], and ISOMAP [22], etc. These methods yield impressive results on some benchmark artificial data sets, besides some real applications, however, their nonlinear properties make them computationally expensive [23]. Moreover, they can't deal directly with the out-of-sample problem [24,25], which states that only the low dimensional embedding map of training samples can be computed by these traditional manifold learning methods, but the samples out of the training set (i.e., testing samples) cannot be calculated directly, analytically or even cannot be calculated at all [23,26], due to the shortage of a definite mapping matrix. Fortunately, the neighborhood preserving embedding (NPE) algorithm [23] of manifold learning, with a definite mapping matrix, was put forward. Thanks to its specific mapping matrix and excellent merits in dimensionality reduction, NPE may be adequate for seismic pattern recognition.
In this paper, wavelet packet manifold classification (WPMC) is developed for seismic target recognition. Specifically, the WPMC is produced by the three following steps: first, wavelet packet transforms are performed on seismic signals and then WPNE is obtained. Second, a novel feature, wavelet packet manifold (WPM), is obtained by applying the NPE algorithm on WPNE. Third, classification is performed using a K nearest neighbors (KNN) classifier. Since through the combination of manifold learning and wavelet packet transform, distinctive features are obtained, then the classifier is less important and easily implemented. Experiments show the WPMC method not only can reduce the feature dimensionality, but also achieve a satisfying recognition rate. Due to its great advantages in recognition rate and computation consumption, WPMC may be widely used in UGS.
This paper is organized into five sections, including the present one. Section 2 introduces the WPM model. Section 3 illustrates how the WPM feature of seismic targets is more insensitive to environmental variations than other traditional methods and thus suitable for pattern recognition. Section 4 explains how classification is conducted on seismic targets. Finally, conclusions and discussion are provided in Section 5.
2. WPM Principle
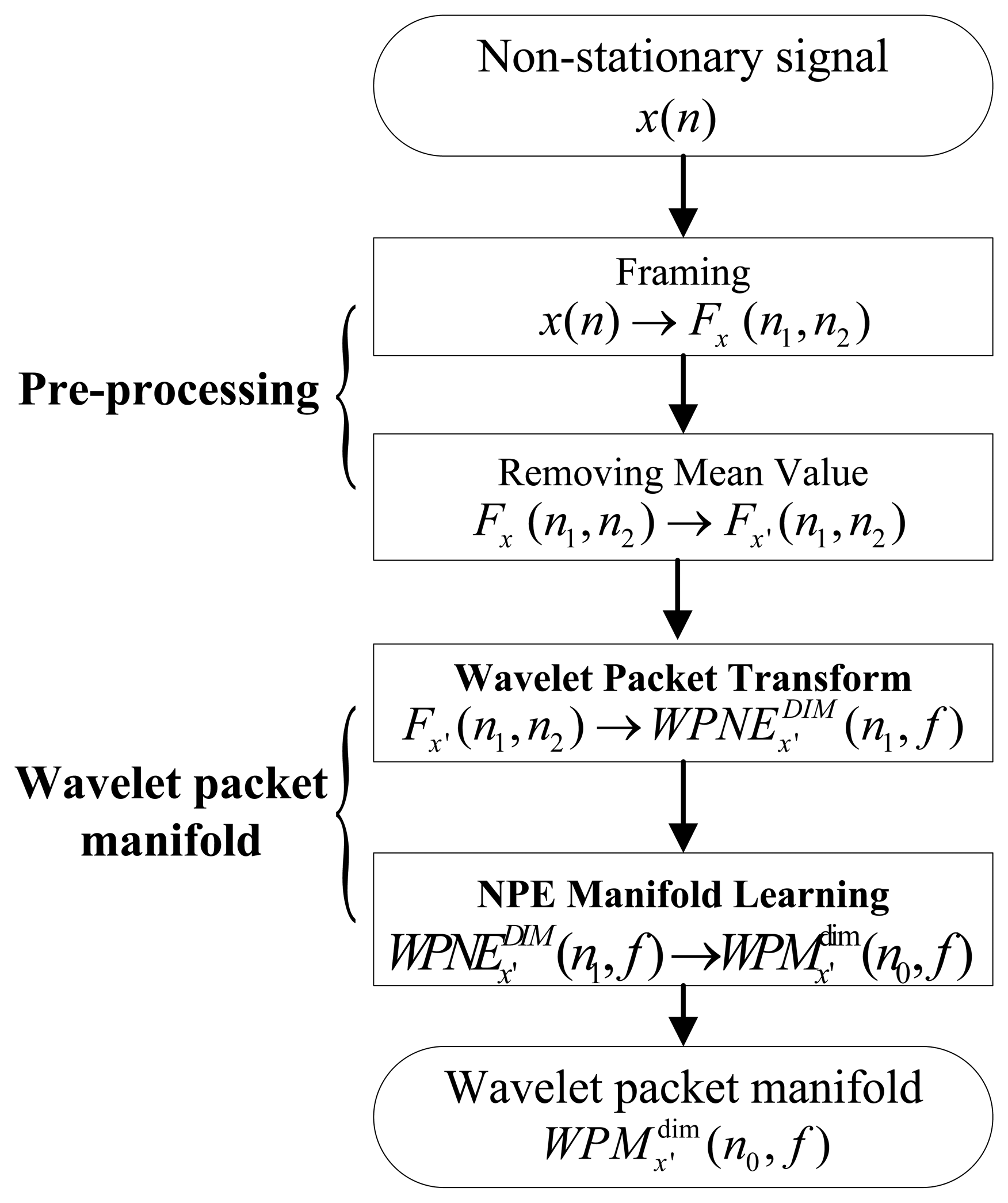
It is known that wavelet packet transforms (WPT) are commonly used to reveal the non-stationary characteristics of a seismic target [3,12]. In addition, the NPE algorithm of manifold learning can reveal the low-dimensional structure hidden in high-dimensional data [23]. Therefore, this paper intends to construct a robust feature which is non-stationary and low-dimensional, called WPM, by applying the NPE algorithm to WPNE. To achieve this aim, two techniques comprising WPT and the NPE algorithm of manifold learning are integrated, as indicated in Figure 1. Given an analyzed signal x(n), the WPM principles are described in the following subsections.
2.1. Wavelet Packet Transform
The wavelet transform (WT) possesses good localization performance both in the time and frequency domains [27]. The wavelet packet transform (WPT) is a direct expansion of the conventional discrete wavelet transform (DWT) [28]. In the WPT, both the approximation space and detail space are decomposed to get new lower resolution approximation spaces plus detail spaces. Let Φ(t) and ψ(t) be the scaling function and the corresponding mother wavelet function in the conventional DWT respectively, and , . Using two-scale equations [13], we construct the wavelet packet basis as follows:
The decomposition coefficients of the jth level can be obtained from the (j − 1)th level, finally we can get the coefficients of all levels through sequential analogy. After j levels decompositions are accomplished, the frequency ranges of all sub-bands at the jth level are:
2.2. NPE Manifold Learning
In NPE, searching low-dimensional embedding of high-dimensional space works as follows: given a set of points X = (x1, x2, …, xm) in RDIM, find a mapping matrix A that transforms these m points to a set of points Y = (y1, y2, …, ym) in Rdim (dim ≪ DIM), such that yi “represents” xi, where yi = ATxi. The computation of matrix A is divided into three parts.
2.2.1. Constructing an Adjacency Graph
Let G denote an adjacency graph with m nodes. The ith node of graph corresponds to the vector xi. In NPE algorithm, K nearest neighbors (KNN) method is adopted to construct G.
2.2.2. Computing the Weights
In this step, we need to compute the weights on the edges of G. Let W denotes the weight matrix with Wij having the weight of the edge from node i to node j, and 0 if there is no such edge. The weights on the edges can be measured by minimizing the following objective function:
2.2.3. Computing the Projections
In order to compute the projections, we need to solve the following generalized eigenvector problem:
Let the column vectors a0,…, ad−1 be the solutions of Equation (9), ordered according to their eigenvalues, λ0≤…≤λd−1 Thus, the embedding is as follows:
2.3. Wavelet Packet Manifold
To apply the NPE algorithm on wavelet packet features, first the of a seismic signal is calculated, then the mapping matrix A of NPE algorithm is obtained by substituting for matrix X (see Section 2.2), finally is achieved by means of multiplying by A:
Here, the sizes of and matrix A are NF × 2j, NF × d respectively, therefore the dimensionality of is dim = d × 2j. The low dimensional manifold of a new sample can be computed quickly, through multiplying matrix A by the sample's .
When wavelet packet transform is executed on the seismic signal, each row of matrix contains the non-stationary information of a specific frequency band. By reducing the row dimensionality of matrix , the non-stationary information and low-dimensional information of a given frequency band is concentrated on the corresponding row of . Therefore, the whole matrix of can illustrate the non-stationary and low-dimensional information of target. Consequently, WPM may provide a robust representation for seismic targets.
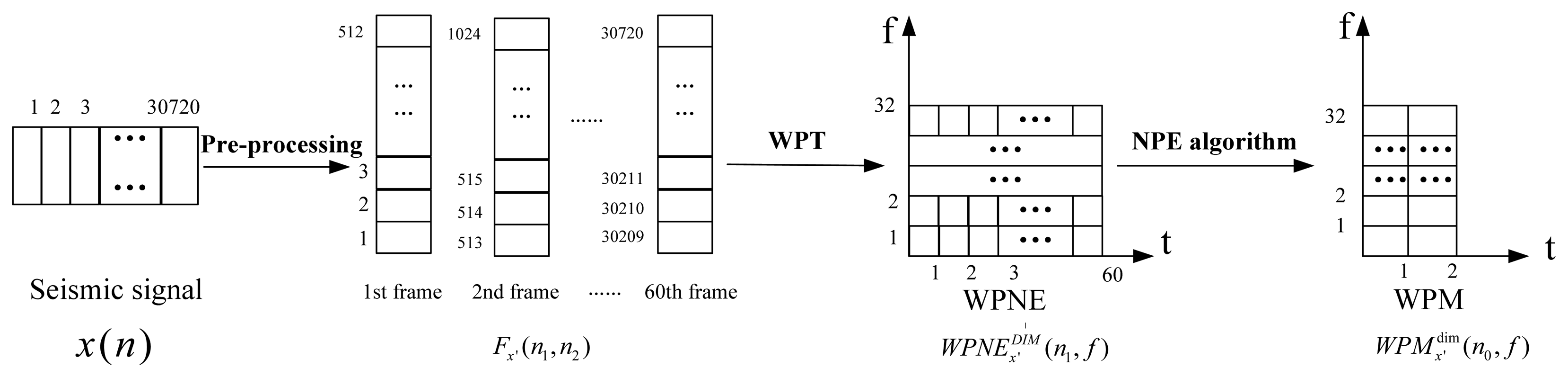
The change of feature dimensionality can be illustrated by an example. If there are 30,720 sampled points and the length of each frame is 512, then the sampled points could be divided into 60 frames. Making five levels wavelet packet transforms on each frame, WPNE, size of 60 × 32, is obtained. Finally, when the NPE algorithm is applied on the WPNE with the parameter d chosen as 2, the WPM feature is achieved with the size of 2 × 32, as shown in Figure 2. Through dimensionality reduction, the dimensionality of the target feature is reduced from 60 × 32 to 2 × 32.
3. WPM Signature Analysis
WPM with the properties of non-stationary and low-dimensional is analyzed in Section 2, so the main task of Section 3 is to show that WPM is a robust representation for seismic targets. As is known to us, the features of seismic target are strongly influenced by two environmental factors which are environmental noise and environmental underlying geology [5]. Therefore, the aim of this section is to verify that WPM of seismic targets is more insensitive to the variations of environment than other traditional time-frequency features by an experimental approach.
3.1. Feature Evaluation
In the evaluation, two parameters including between-class scatter and within-class scatter are employed to quantitatively describe the feature capability in pattern classification. Mathematically, for a given feature set {f1,……,fQ}, where Q is the number of feature samples, the two parameters are defined as follows [30]:
3.2. Feature Performance
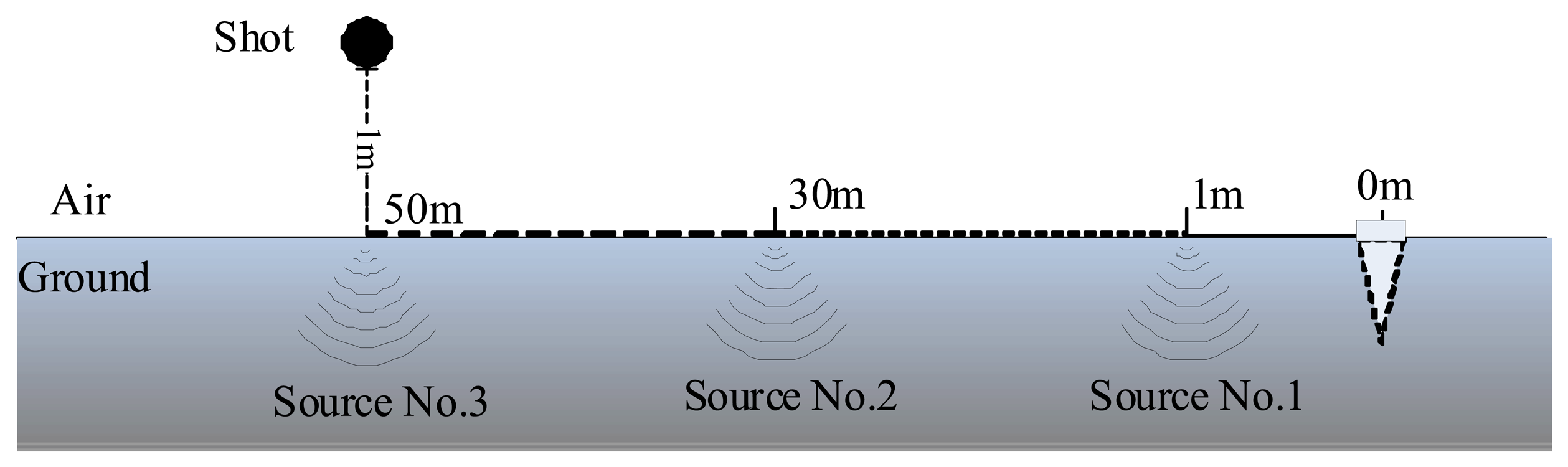
To simplify the exposition, a seismic signal generated by a shot is regarded as the target model. In experiment, the shot falling freely from a height of 1.5 meters hits the ground and induces a seismic signal. The freely falling body motion of the shot is repeated at the same height but three different positions located 1, 10, 30 meters away from the seismic sensor, respectively. The heights of the freely falling body motions are the same, so the strengths of the shots stimulate on the ground are identical. The signal sources produced at three positions are denoted as Source No. 1, Source No. 2 and Source No. 3, separately. HSJ-L1 10-1250, a vertical geophone made by OYO GEOSPACE (Houston, TX, USA), is employed to measure the seismic waves [31], with 1,024 Hz sample frequency. These are no other targets existing in the experimental field when the experiment is executed, so the seismic target is considered as a shot when a bump happens, yet the seismic target is regarded as background noise when no operations are taken. The experimental situation is displayed in Figure 3.
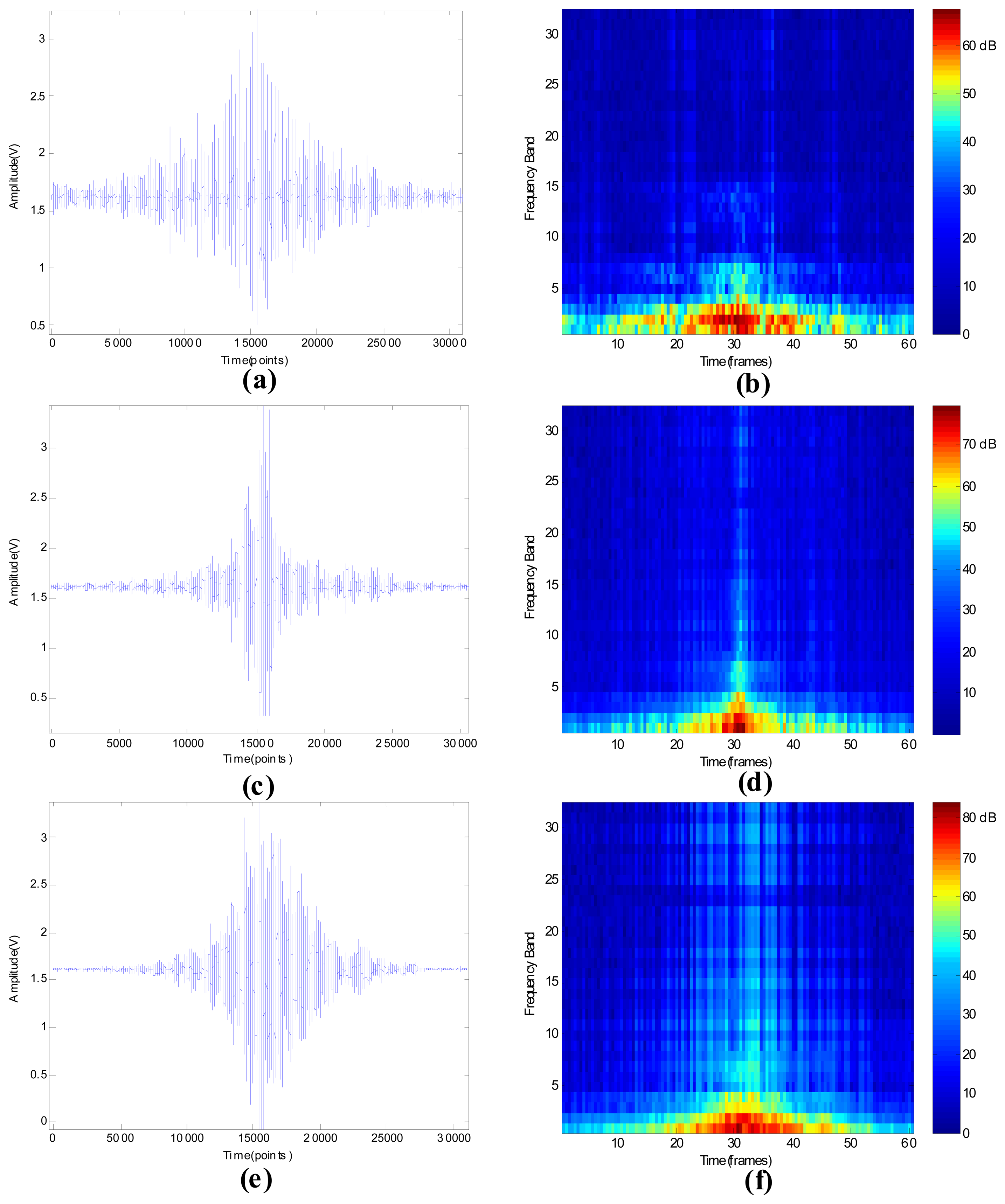
The seismic signal (SS), wavelet packet node energy (WPNE) and wavelet packet manifold (WPM) determined in a certain demonstrative experiment which is conducted in a gravel road are shown in Figure 4, where the length of frame is 512 sample points and 128 overlapping points exist in the adjacent frames.
As shown in Figure 4(a,c,e), sharp impulses can only be observed when the shot is hitting the ground, because the sampled seismic signal is induced by background noise when a bump doesn't happen. Examination of Figure 4(a,c,e) shows the gradual degradation of the impulses as the propagation distance increases from 1 meter to 30 meters and the transition of impulses from sharpness to flatness, which means the signal-noise-ratio (SNR) decreases heavily as the propagation distance increases, because the farther signal propagates, the worse the signal degrades. As displayed in Figure 4(a,b), in the moment that impulses occur, the WPNE is obvious different from other times'. According to Figure 4(b,d,f), the WPNEs of impulses become more and more indistinct as the propagation distance increases. Seismic signals are generated in three different positions with different signal-noise-ratios and with different underlying geology conditions, while their signatures, including the waveform in time-domain and WPNEs in time-frequency domain, change considerably when the position of the target varies. In order to combine the non-stationary information and low-dimensional information, the NPE algorithm is applied on WPNE to construct WPM and the dimensionality of WPM is reduced to 3 × 1 (the dimensionality of WPM is first reduced to 32 × 1, subsequently it is reduced to 3 × 1) to clearly display the results as described in Figure 4(i). Fortunately, regardless of the differences of geology condition and environmental noise, the WPMs of the signals generated at the three positions gather at one point, what's more, they are different from noises.
In order to further verify that the robustness of WPM algorithm is better than other traditional time-frequency methods, the above demonstrative experiment was conducted 300 times on three different geologies, specifically the experiment of shot hitting the ground is repeated 100 times in each geology. The Sr of different features which were obtained in the three geologies are detailed in Table 1.
In Table 1, TFM denotes another manifold feature which is calculated by addressing manifold learning on a signal's STFT distribution [14]. According to the above results, the Sr of WPM is the smallest, no matter in which geology condition. Therefore, we can draw a conclusion that WPM, with the properties of non-stationary and low-dimensionality, can capture the pattern difference of seismic targets and be more robust than others, so WPM can be regarded as a kind of feature for target classification.
4. Classification Experiment
4.1. Experimental Description
The underlying geology condition of the experimental field isn't very homogenous, since the field is transformed from a building wasteland and lots of building rubbish remains underground. A seismic sensor is vertically buried 10 centimeters into the ground where 10 meters away from the road. The category of the employed seismic sensor is as discussed in Section 3.2. The experimental situation is shown in Figure 5. In this paper, four categories of seismic targets, including pedestrians, tracked vehicles, wheeled vehicles and helicopters, are involved in our classification, and part of their specifications are listed in Table 2. When the experiment is conducted, the targets move on at a constant velocity, while different targets have different velocities, just as Table 3 shows. Specifically, the helicopter flies at the height of 300 meters above the road and the reason why a helicopter can induce the ground seismic signal can be seen in [2].
4.2. Data Sets
Data sets, including training sets and test sets, are sampled in the test field. Each kind of target has 100 samples in the training set and other 50 samples in the testing set. In the experiment, the sampling rate is 1,024 Hz and frame length is 1,024 sample points. There is an overlap of 512 points existing between the adjacent frames. If 5 levels wavelet packet transform is executed on the signal frame, 32 (25 = 32) sub-bands are obtained in the 5th level and the bandwidth of each sub-band is equal to 16 (512/25 = 16) Hz. We make a recognition operation every 60 frames, namely, the size of WPNEs that used in every classification operation is 1,920 (32 × 60 = 1,920).
The obtained seismic signals and WPNEs of seismic targets are depicted in Figure 6. Compared with other ground targets, the envelope of the pedestrian's time-domain signal is the longest and the sparsest because its velocity is the slowest and its impact on ground is the weakest. Among the ground seismic targets, the velocity of the wheeled vehicle is the fastest, so the span of its envelope is the shortest. The velocity of the tracked vehicle is between the former two, but its envelope density is maximal, since its weight is the largest and its stimulation on the ground is the strongest. According to Figure 6(b), only the WPNEs of the first seven frequency bands, corresponding to the signal of 0∼112 Hz, changes significantly when this target is passing through the seismic sensor zone. This phenomenon reveals that the principal frequency component of a pedestrian concentrates around 0∼112 Hz, and it matches well to the conclusion of [32]. The wheeled vehicle, tracked vehicle and helicopter have some differences with the pedestrian, their feature frequencies are higher than pedestrian and as high as 512 (16 × 32 = 512) Hz. Therefore, their WPNEs of all 32 frequency bands will vary obviously when these targets move across the sensor, as shown in Figure 6(b,d,h). The images of Figure 6(b,d,f,h), size of 32 × 60, indicate that the dimensionality of WPNEs is 1,920 (32 × 60 = 1,920). This dimensionality is still too large to classify. Therefore, the manifold of WPNE, WPM, is extracted using the NPE algorithm.
4.3. WPM Parameters
The extraction of WPM involves several parameters, such as frame length, decomposition level of wavelet packets, the nearest neighbors' number k and output dimensionality d of NPE. A nonlinear optimization technique, particle swarm optimization (PSO), is employed to investigate the effect of these parameters on the Sr of WPM. Specifically, the frame length of 256, 512, 1,024, 2,048, 4,096, the decomposition level of 2∼10, the nearest neighbor's number k of 1∼50 and output dimensionality d of 1∼30 are searched by PSO. The optimal parameters obtained by PSO are listed in Table 4.
4.4. Designment of Classifier
The merits of WPM, low-dimensionality and small-scale, determine it is an excellent type of feature for classification. On the basis of WPM, the K-nearest neighbors classifier, which is based on statistical theory and easily implemented, can achieve accurate recognition.
In the KNN classifier, supposing c categories exist in the training set, they are C1, C2, …, Cc, respectively. Each category has Ni samples, i = 1, 2, …, c. Euclidean distance that between test sample X and each training sample is as follows:
If a class satisfies Equation (21):
4.5. Classification Performance
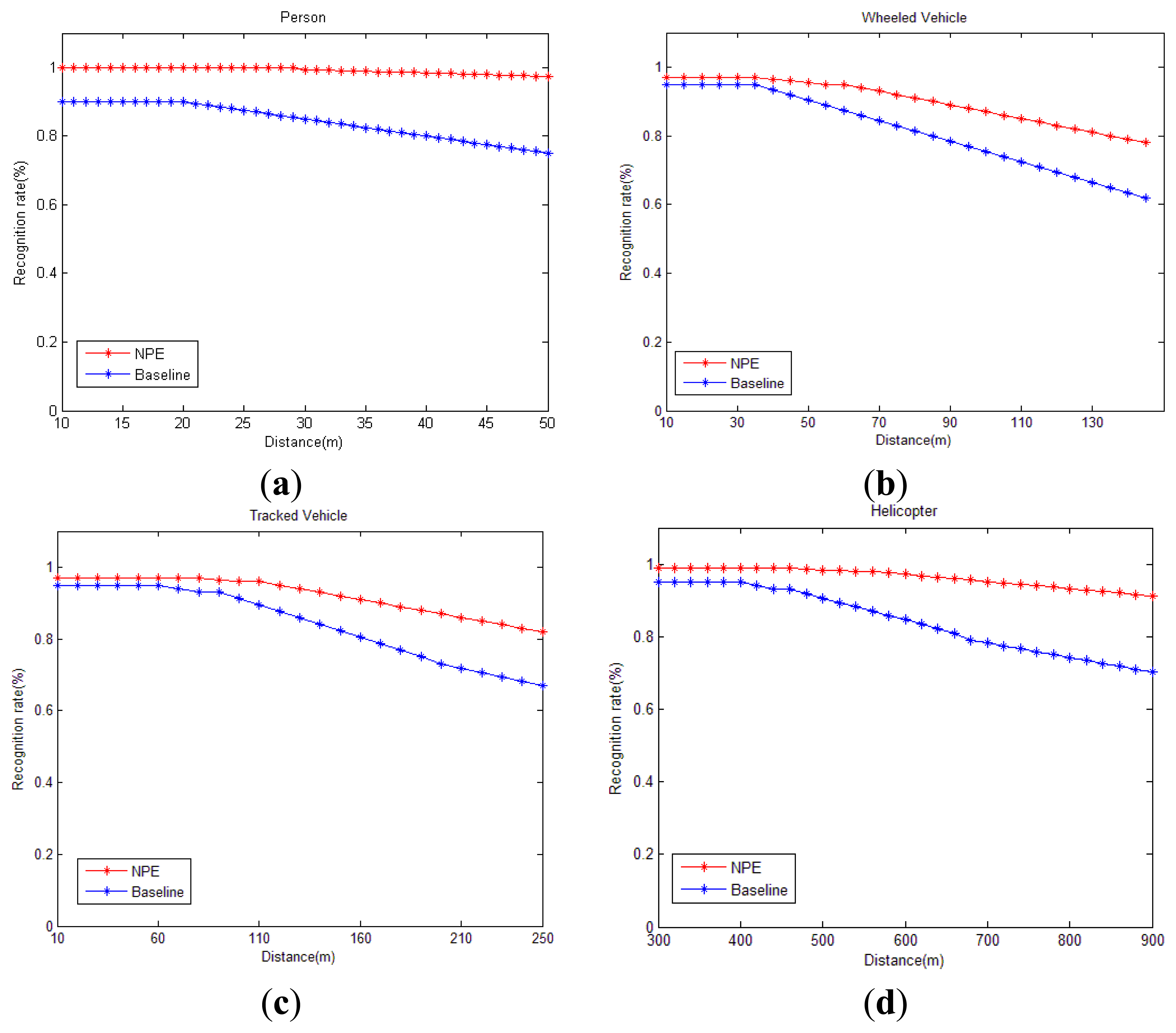
Real-time classification results vary with environment, as shown in Figure 7. The horizontal axis of Figure 7 represents the target position which is denoted by the slant distance between the target and sensor. Naturally, different positions have different signal-noise ratios and different underlying geology conditions. The baseline curve displays the classification results of a method that directly uses WPNE with size of 32 × 60. The NPE curve represents the target recognition rate using WPM whose parameters are as shown in Table 4. In Figure 7, all recognition rates will go down when the distance increases. Fortunately, the NPE curve decreases more slowly than the baseline one. Experimental results denote that the WPM feature is more robust and suitable for moving target classification. Table 5 details the average result of Figure 7. As to the recognition of the four targets, the average classification rate of the NPE approach is 11.53% higher than baseline.
4.6. Complexity Analysis
As to a UGS system, the resources of its sensor nodes is very limited. Their complexity of any algorithms developed for the UGS application should be as simple as possible. For the purposes of comparison, we use state-of-the-art methods SDF [12,33] and the algorithm described in reference [32] (called algorithm Algo) which are methods for recognizing seismic targets, and implement them independently. The SDF-based feature extraction algorithm mitigates the noise by using wavelet analysis, captures the essential signatures of the original signals in the time-frequency domain, and generates robust low-dimensional feature vectors for pattern classification. Specifically, five symbols are used in SDF and db6 is adapted as wavelet basis by all three algorithms. All of the methods are executed on the Matlab 2011a environment of an industrial computer (dual core, 2.9 GHz-frequency and 2 GB memory) to process the data sets detailed in Section 4.2. The results are shown in Table 6.
According to [12,32] and the above Table 6, on the one hand, the proposed WPMC can process the situation of four targets' classification while the other two algorithms can only do so for only three targets. On the other hand, WPMC achieves higher classification accuracy with lower computation consumption. The results confirm the excellent performance of the proposed WPM feature for seismic targets' classification.
5. Conclusion and Discussion
This paper has presented a new WPM signature by combining the wavelet packet node energy and NPE algorithm of manifold learning for a better representation of moving seismic targets. The proposed WPM can not only describe target features in low-dimensional space, but also improve the recognition rate of seismic targets. Furthermore, the advantage of WPM makes it possible that even some simple classifiers, such as KNN, would be good enough for seismic targets classification. The WPM-based classification method enables seismic sensor nodes to carry out precise classification, it does not require the target to be at a certain range from the sensor nodes or a very homogenous underlying geology conditions. Thanks to the excellent merits of WPM in low-dimensionality and feature robustness, the WPMC is very suitable for UGS. Nevertheless, the WPMC is also limited in single target classification due to the complex feature space of mixed targets. In addition, whether the accuracy of classification algorithm will depend on the speed being constant during the classification periods need to be further investigated. These are studies that the authors will focus on in the future.
Acknowledgments
The authors would like to thank Xueyuan Zhang for providing advice on experiments, as well as the associate editor and anonymous reviewers for their valuable comments and suggestions to improve this paper. This work was supported by Research Fund 9140C18020211ZK34.
Conflict of Interest
The author declares no conflict of interest.
References
- William, P.E.; Hoffman, M.W. Classification of military ground vehicles using time domain harmonics' amplitudes. IEEE Trans. Instrum. Measur. 2011, 60, 3720–3731. [Google Scholar]
- Sleefe, G.E.; Ladd, M.D.; McDonald, M.S.; Elbring, G.J. Acoustic and Seismic Modalities for Unattended Ground Sensors. Proceedings of the Unattended Ground Sensor Technologies and Applications, Orlando, FL, USA, 8–9 March 1999.
- Tian, Y.; Qi, H.; Wang, X. Target Detection and Classification Using Seismic Signal Processing in Unattended Ground Sensor Systems. Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing, Orland, FL, USA, 3–5 May 2002.
- Altmann, J. Acoustic and seismic signals of heavy military vehicles for co-operative verification. J. Sound Vib. 2004, 273, 713–740. [Google Scholar]
- Zhou, Q.; Tong, G.; Xie, D.; Li, B.; Yuan, X. A seismic-based feature extraction algorithm for robust ground target classification. IEEE Signal Process. Lett. 2012, 19, 639–642. [Google Scholar]
- Liu, X.F.; Zheng, X.D.; Xu, G.C.; Wang, L.; Yang, H. Locally linear embedding-based seismic attribute extraction and applications. Appl. Geophys. 2010, 7, 365–375. [Google Scholar]
- Altmann, J.; Linev, S. Acoustic-seismic detection and classification of military vehicles—developing tools for disarmament and peace-keeping. Appl. Acoust. 2002, 63, 1085–1107. [Google Scholar]
- Succi, G.; Clapp, D.; Gampert, R.; Prado, G. Footstep detection and tracking. Unattended Ground Sensor Technol. Appl. III. 2001, 4393, 22–29. [Google Scholar]
- Liang, Z.; Wei, J.; Zhao, Y.; Liu, H.; Li, B.; Zheng, C. The statistical meaning of kurtosis and its new application to identification of persons based on seismic signals. Sensors 2008, 8, 5106–5119. [Google Scholar]
- Gramann, R.A.; Bennett, M.B.; O′Brien, T.D. Vehicle and Personnel Detection Using Seismic Sensors. Proceedings of the SPIE Conference on Sensors, C3I, Information, and Training Technologies for Law Enforcement, Boston, MA, USA, 7 January 1998.
- Lacombe, J.; Peck, L.; Anderson, T.; Fish, D. Seismic detection algorithm and sensor deployment recommendations for perimeter security. Proc. SPIE. 2006, 6231, 623109. [Google Scholar]
- Jin, X.; Sarkar, S.; Ray, A.; Gupta, S.; Damarla, T. Target detection and classification using seismic and PIR sensors. IEEE Sensors J. 2012, 12, 1709–1718. [Google Scholar]
- Yen, G.G.; Lin, K.C. Wavelet packet feature extraction for vibration monitoring. IEEE Trans. Ind. Electron. 2000, 47, 650–667. [Google Scholar]
- He, Q.B.; Liu, Y.B. Time-frequency manifold as a signature for machine health diagnosis. IEEE Trans. Instrum. Measur. 2012, 61, 1218–1230. [Google Scholar]
- He, Q.; Liu, Y.B.; Long, Q.; Wang, J. Time-Frequency Manifold for Gear Fault Signature Analysis. Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Binjiang, China, 10–12 May 2011.
- Wang, Y.; Yang, J.N.; Liu, H. Acoustic targets feature extraction method based on manifold learning. Electron. Lett. 2012, 48, 139–140. [Google Scholar]
- Liu, H.; Yang, J.A. A novel approach to research on feature extraction of acoustic targets based on manifold learning. Acta Phys. Sin. 2012, 60, 074302. [Google Scholar]
- He, Q. Vibration signal classification by wavelet packet energy flow manifold learning. J. Sound Vib. 2013, 332, 1881–1894. [Google Scholar]
- Li, X.; Shu, L. Kernel based nonlinear dimensionality reduction and classification for genomic microarray. Sensors 2008, 8, 4186–4200. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar]
- Tenenbaum, J.B.; Silva, V.D.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar]
- He, X.; Cai, D.; Yan, S.; Zhang, H. Neighborhood Preserving Embedding. Proceedings of the Tenth IEEE International Conference on Computer Vision, Beijing, China, 17–21 October 2005.
- Bengio, Y.; Paiement, J.F.; Vincent, P.; Delalleau, O.; Le Roux, N.; Ouimet, M. Out-of-sample extensions for lle, isomap, mds, eigenmaps, and spectral clustering. Adv. Neur. Inf. Process. Syst. 2004, 16, 177–184. [Google Scholar]
- Zhao, X.; Zhang, S. Facial expression recognition based on local binary patterns and kernel discriminant isomap. Sensors 2011, 11, 9573–9588. [Google Scholar]
- Pang, Y.; Zhang, L.; Liu, Z.; Yu, N.; Li, H. Neighborhood preserving projections (NPP): A novel linear dimension reduction method. Adv. Intell. Comput. 2005, 3644, 117–125. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial Mathematics: Philadelphia, PA, USA, 1992; Volume 61. [Google Scholar]
- Cody, M.A. The wavelet packet transform, extending the wavelet transform. Dr. Dobb's J. 1994, 19, 44–46. [Google Scholar]
- Averbuch, A.; Hulata, E.; Zheludev, V.; Kozlov, I. A wavelet packet algorithm for classification and detection of moving vehicles. Multidimens. Syst. Signal Process. 2001, 12, 9–31. [Google Scholar]
- He, Q.; Kong, F.; Yan, R. Subspace-based gearbox condition monitoring by kernel principal component analysis. Mech. Syst. Signal Process. 2007, 21, 1755–1772. [Google Scholar]
- Lan, J.; Nahavandi, S.; Lan, T.; Yin, Y. Recognition of moving ground targets by measuring and processing seismic signal. Measurement 2005, 37, 189–199. [Google Scholar]
- Cao, H. Research on Collaborative Classification of Ground Targets in Sensor Networks for Battlefield Surveillance. Ph.D. Thesis, Shanghai Institute of Microsystem and Information Technology, China Academy of Science, Shanghai, China, 6 June 2009. [Google Scholar]
- Jin, X.; Gupta, S.; Ray, A.; Damarla, T. Symbolic Dynamic Filtering of Seismic Sensors for Target Detection and Classification. Proceedings of the IEEE American Control Conference (ACC), San Francisco, CA, USA, 29 June 2011.


| STFT | WPNE | WPM | TFM [14] | |
|---|---|---|---|---|
| Grass | 32 | 21 | 3 | 19 |
| Gravel | 30.1 | 22 | 2 | 14 |
| Hard Soil | 25.2 | 18.9 | 1.5 | 16.4 |
| Feature | Wheeled Vehicle | Tracked Vehicle | Low-Altitude Helicopter | |||
|---|---|---|---|---|---|---|
| Car | Truck | SUV | Van | |||
| Weight (kg) | 1,425 | 6,800 | 1,635 | 1,713 | 40,200 | 3,850 |
| Number of Cylinders | 4 | 6 | 4 | 5 | 10 | 8 |
| Engine Capacity | 78 | 170 | 110 | 140 | 3,240 | 1,468 |
| Ground Seismic Source | Low-Altitude Acoustic-Seismic Source | |||
|---|---|---|---|---|
| Target Category | Pedestrian | Wheeled Vehicle | Tracked Vehicle | Helicopter |
| Velocity (km/h) | 6 | 50 | 40 | 120 |
| Frame Length | Decomposition Level | k | d |
|---|---|---|---|
| 1,024 | 5 | 20 | 1 |
| Pedestrian | Wheeled | Tracked | Helicopter | Avg. | |
|---|---|---|---|---|---|
| Baseline | 84.33% | 81.45% | 84.04% | 84.17% | 83.50% |
| NPE | 99.13% | 92.57% | 92.14% | 96.35% | 95.03% |
| WPMC | SDF | Algo | |
|---|---|---|---|
| Algorithm Flow | 5 levels wavelet packet transform + NPE algorithm + KNN classifier | wavelet transform + symbolization + SVM | 7 levels wavelet packet transform + fuzzy neural classifier |
| Target Categories | 4 | 3 | 3 |
| Classification rate | 95.03% | 90.0% | 85.3% |
| Running time | 98 s | 120 s | 170.2 s |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Huang, J.; Zhou, Q.; Zhang, X.; Song, E.; Li, B.; Yuan, X. Seismic Target Classification Using a Wavelet Packet Manifold in Unattended Ground Sensors Systems. Sensors 2013, 13, 8534-8550. https://doi.org/10.3390/s130708534
Huang J, Zhou Q, Zhang X, Song E, Li B, Yuan X. Seismic Target Classification Using a Wavelet Packet Manifold in Unattended Ground Sensors Systems. Sensors. 2013; 13(7):8534-8550. https://doi.org/10.3390/s130708534
Chicago/Turabian StyleHuang, Jingchang, Qianwei Zhou, Xin Zhang, Enliang Song, Baoqing Li, and Xiaobing Yuan. 2013. "Seismic Target Classification Using a Wavelet Packet Manifold in Unattended Ground Sensors Systems" Sensors 13, no. 7: 8534-8550. https://doi.org/10.3390/s130708534




