Remote Driven and Read MEMS Sensors for Harsh Environments
Abstract
: The utilization of high accuracy sensors in harsh environments has been limited by the temperature constraints of the control electronics that must be co-located with the sensor. Several methods of remote interrogation for resonant sensors are presented in this paper which would allow these sensors to be extended to harsh environments. This work in particular demonstrates for the first time the ability to acoustically drive a silicon comb drive resonator into resonance and electromagnetically couple to the resonator to read its frequency. The performance of this system was studied as a function of standoff distance demonstrating the ability to excite and read the device from 22 cm when limited to drive powers of 30 mW. A feedback architecture was implemented that allowed the resonator to be driven into resonance from broadband noise and a standoff distance of 15 cm was demonstrated. It is emphasized that no junction-based electronic device was required to be co-located with the resonator, opening the door for the use of silicon-based, high accuracy MEMS devices in high temperature wireless applications.1. Introduction
There is a need for high accuracy, repeatable and reproducible sensors that can operate in harsh or constrained environments. In these situations, temperature limitations, physical access or other factors rule out the possibility of using batteries or other “active” energy harvesting techniques to power the sensors and new sensor architectures and interrogating techniques must be developed.
Remote interrogation of sensors is accomplished in productized sensors today in one of three ways. In the first method, a battery is used at the sensor node which enables the use of a local microprocessor for signal conditioning and communications uplink. There are challenges incorporating this technology in applications where size, weight, power, cost and lifetime at elevated temperature of the sensor are important. In a second method, energy is harvested to locally power the sensor node [1–4]. This class of sensors can accomplish battery-free operation, but will require either a rectifying technology (i.e., semiconductor junction) [5] or other robust energy harvesting technique to allow the sensor node to function. This will introduce temperature limitations in the applications that the sensor can be used in.
A third method is to eliminate the need for a direct energy harvesting technology. An example of this method is surface acoustic wave (SAW) technology [6,7] and more recently, lamb wave resonators in AlN [8]. Gratings written into these devices can serve as RF time delays so that energy is temporarily stored and then reflected back to the interrogator. This enables time discrimination against diffuse backscatter. Furthermore, the delay can be made sensitive to temperature, pressure and strain. Another example of this class of sensor is a simple resonant circuit such as an LC resonator [9–12] at intermediate frequencies or transmission line resonator at high frequencies. Proper geometrical design can make either the inductor or capacitor (or both) sensitive to the variable of interest and changes in the resonant frequency (or sensor impedance) can be read out using interrogators similar to “grid-dip” meters or RF reflectometers familiar in radio technology. Yet, there are few examples where this approach has yielded robust results with high accuracy in harsh environments.
In order to address this challenge, high Q silicon-based MEMS micromechanical resonators are considered [13–16]. These devices are considered “world-class” when applied, for example, to the pressure sensing market and have been in mass production since the early 1990s. They maintain the inherent mechanical robustness of silicon while leveraging wafer-scale processing for high volume and low cost. Another very important benefit of these devices is that they convert the measured variable into a frequency output [17,18]. With proper design, the fact that the oscillation frequency of the MEMS resonator becomes proportional to the measurand of interest can be a distinct advantage. In particular, the output of the device can now be considered digital (i.e., a frequency output that can be “counted”) so that as long as the signal can be detected, temperature induced amplitude variations do not affect the accuracy of the sensor. In current productized formats, these devices are used in an electrically interrogated, closed-loop topology thereby limiting their application in harsh environments due to their use of piezoresistors to detect the resonant oscillations of the device.
A combination of a high Q resonator with the ability to remotely readout the sensor without local, active electronics could allow these devices to be used up to temperatures at which silicon creep becomes an issue (typically > 350 °C and < 500 °C). However, it is necessary to develop a mechanism to deliver energy to the mechanical structure at the right frequency to drive the oscillations, and then a second mechanism is required to read out that frequency. Key factors considered were to try to minimize power consumption and complexity of the interrogator, while maximizing the standoff distance or “read range”.
One method to excite and read a MEMS resonator remotely would be through optically modulated signal and reading a Fabry Perot cavity formed by the resonator and the vacuum cavity around the sensor. The resonator oscillates due to the heat absorbed by heavily doped silicon at the wavelength of the modulation signal. This technique was demonstrated in the context of high accuracy pressure measurements needed to monitor a geothermal well [19,20]. An optimized resonator for this application was packaged as part of a fiber optical cable and deployed in a geothermal well at over 1200 m below ground seeing temperatures in excess of 200 °C [21]. In this approach, the interrogator was located at the top of the well.
One drawback of the optical approach is the size and integration of the sensor into an optical cable along with the size and complexity of the interrogator. Alternatively, we have demonstrated that excitation energy can be delivered wirelessly to the resonator (in this case a comb drive) through induction such that it oscillates at its resonant frequency. This frequency was then wirelessly, inductively read through a separate LC resonator formed from a different set of comb fingers at a separate frequency [22].
In contrast, this work demonstrates a new method where the comb drive is driven into resonance wirelessly through the use of acoustics and read wirelessly through inductive coupling. The method described here demonstrates more than a 2× improvement in standoff distance over the prior work and a closed loop feedback system allowing the resonator to be driven from broadband noise.
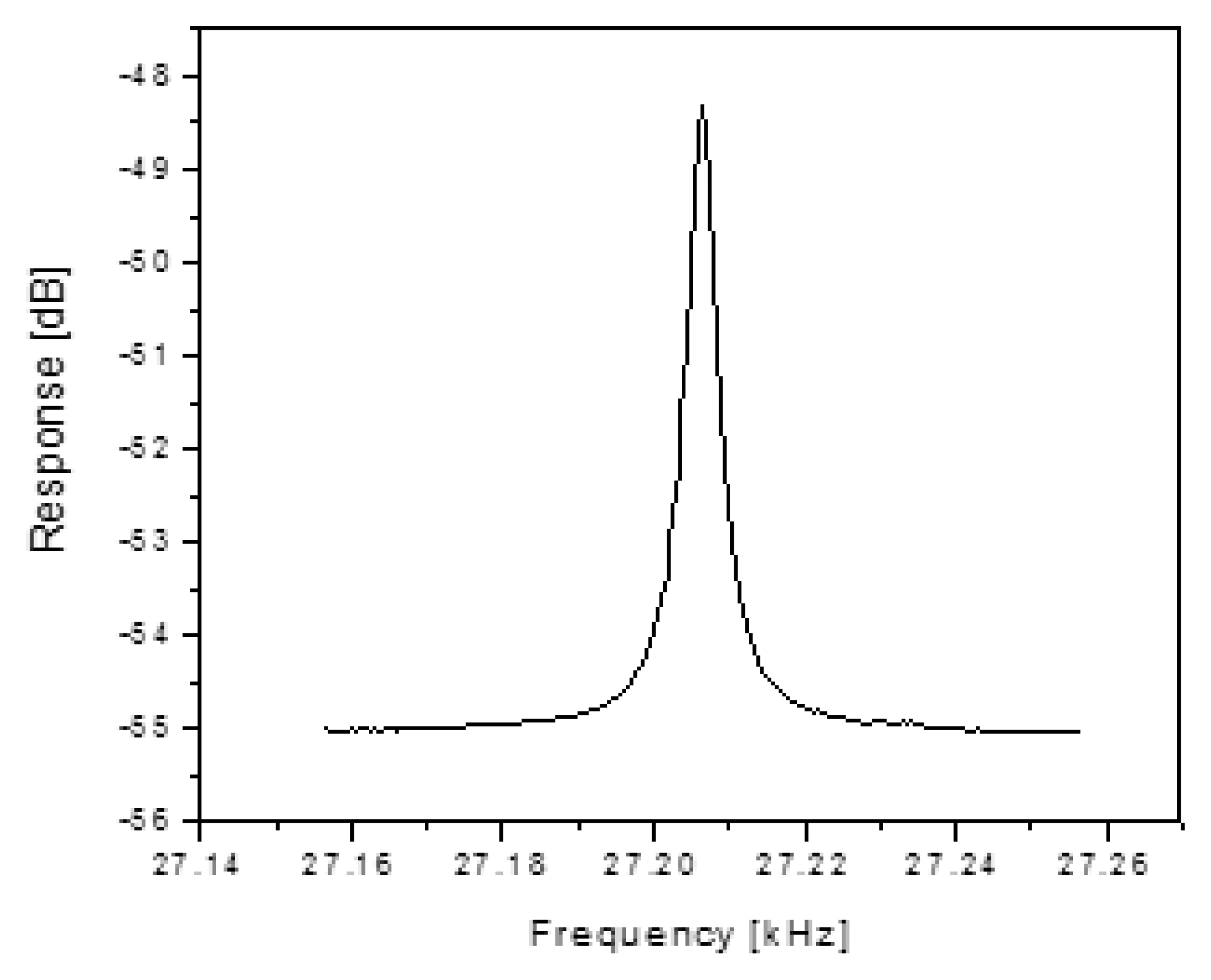
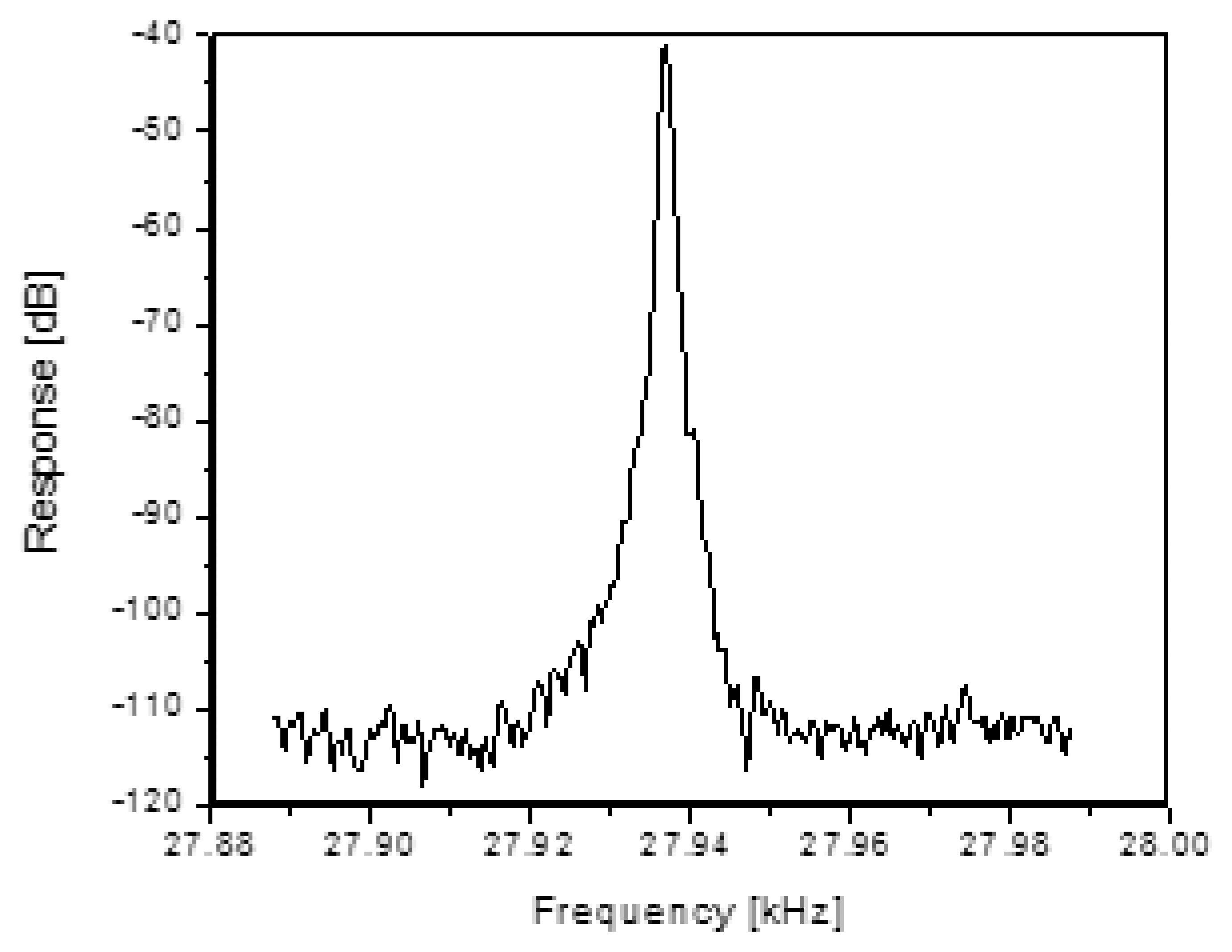
Silicon comb drive resonators used for this work were based on existing GE production devices with a dual set of comb teeth with a gap size of 5 μm and an overall length of 500 μm. Details of the device are similar to that in [14,23]. Wafer bonding is used to isolate these devices in vacuum such that they have a characteristic mechanical resonant frequency of approximately 30 kHz and a Q of upwards of 6500. The top wafer of the structure has a diaphragm that is physically connected to the comb drive in such a way that the deflection of the diaphragm modulates the resonant frequency of the comb drive. Measurement of the resonant frequency and Q for these comb drives was made using a network analyzer to sweep the frequency and measure the output. Figure 1 shows the frequency response of a typical resonator. This characterization is important in order to gage the performance of the wireless methods with respect to required drive power, detected signal levels, signal distortion, resonant frequency and loop gain (or loss).
2. Acoustic Drive
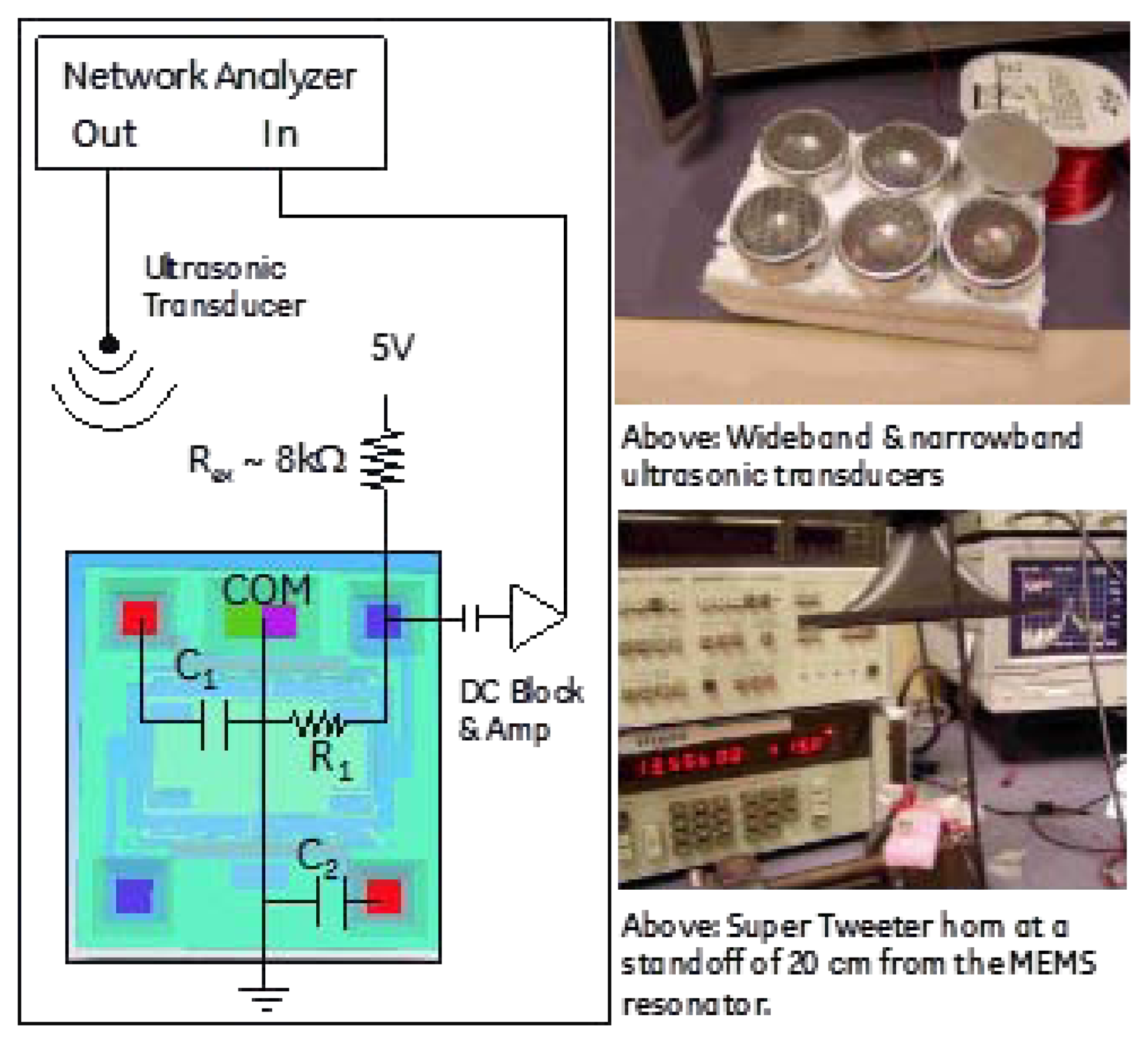
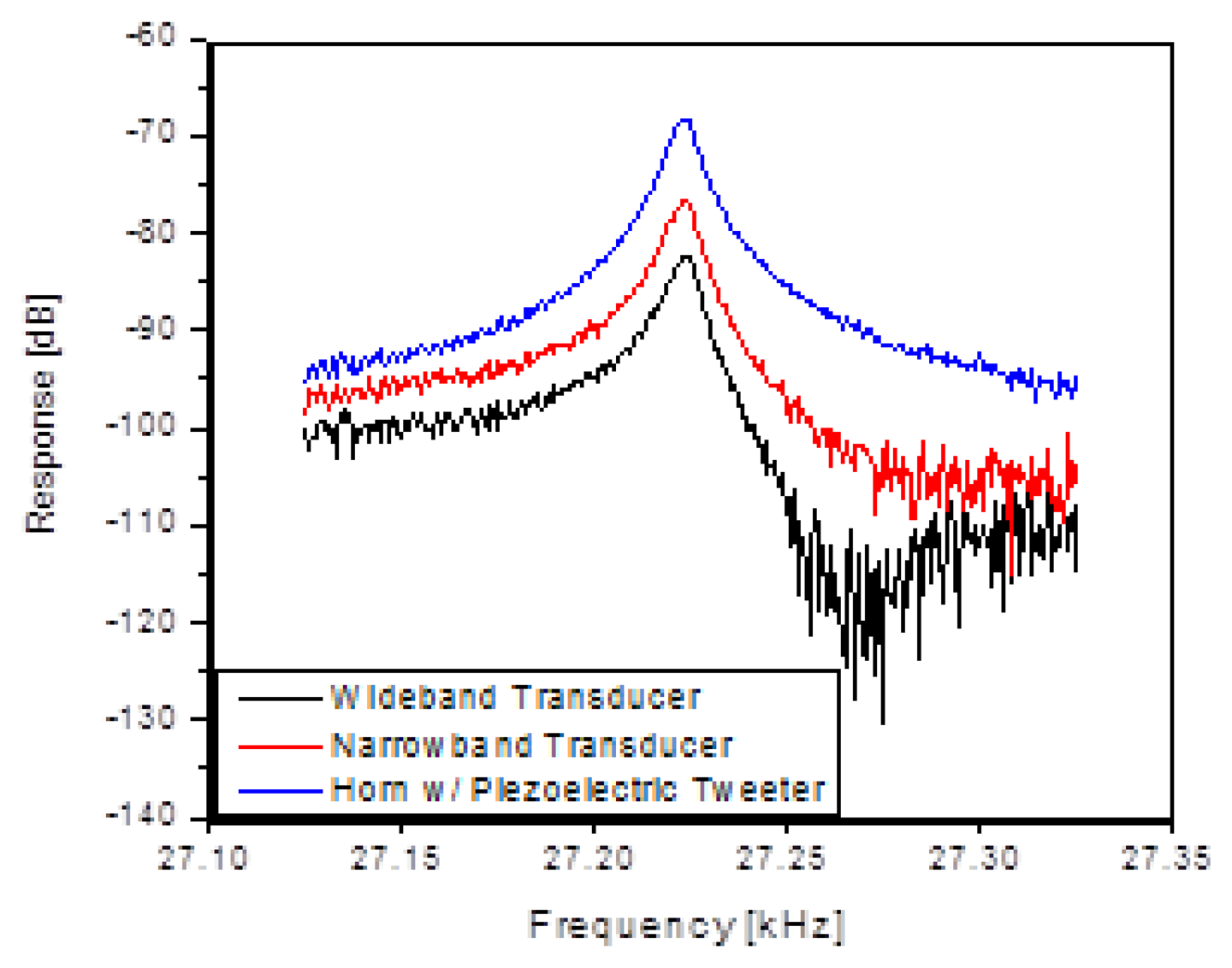
The first architecture considered was acoustically driving the silicon comb drive into resonance and measuring the frequency response using the piezoresistors located as part of the comb drive. In this case, the electrical aspects of the MEMS device were not important for the drive-side response. Figure 2 shows the experimental setup and transducers used to measure the efficiency of acoustic drive. Several ultrasonic driving techniques were tried with success, and in the end a low cost COTS quasi-resonant ultrasonic transducer (TR89/B, Type 31, Massa Products Corporation, Hingham, MA, USA) produced the most reliable results. With impedance matching, it is possible to turn this into a very narrowband transducer. However, it was used un-matched to allow for varying resonant frequencies in the device and driven directly from a 50 Ω source. Figure 3 shows response of the MEMS resonator as a function of the acoustic transducer type.
The Massa device is specified for a transmitting sensitivity of 25 dB compared to 1 μbar/V at 1 foot. When the acoustic impedance, Za, is known, the sound pressure, p, can be related to the sound intensity, I, in power per unit area as:
As demonstrated in Figure 4, the expected 6 dB/octave dependence on acoustic power was verified, as was the dependence on acoustic drive level (data is shown later in Figure 10). Finally, within a range of about ±10 cm, there was not a significant dependence on lateral mismatch between acoustic transducer and the sensor. Overall, the success of the acoustic driving was somewhat surprising because the only way to mechanically couple into the resonator is via the diaphragm. The mechanical resonance frequency of the diaphragm (nominally 100 kHz) is an important factor, but something that was not examined in detail. As a final comment, it is likely that more advanced acoustic design techniques (such as phased array transducers) could be used to optimize the excitation distance, power delivery and impedance matching to the die. These techniques are common in ultrasound technology but were not employed here.
3. Inductive Read
Inspired by the capacitive electrical equivalent of the comb drive, a readout method based on induction was developed. This capacitance can be resonated with an inductance to form an LC “tank” circuit. Energizing this tank circuit with an external drive coil at its electrical resonance frequency:
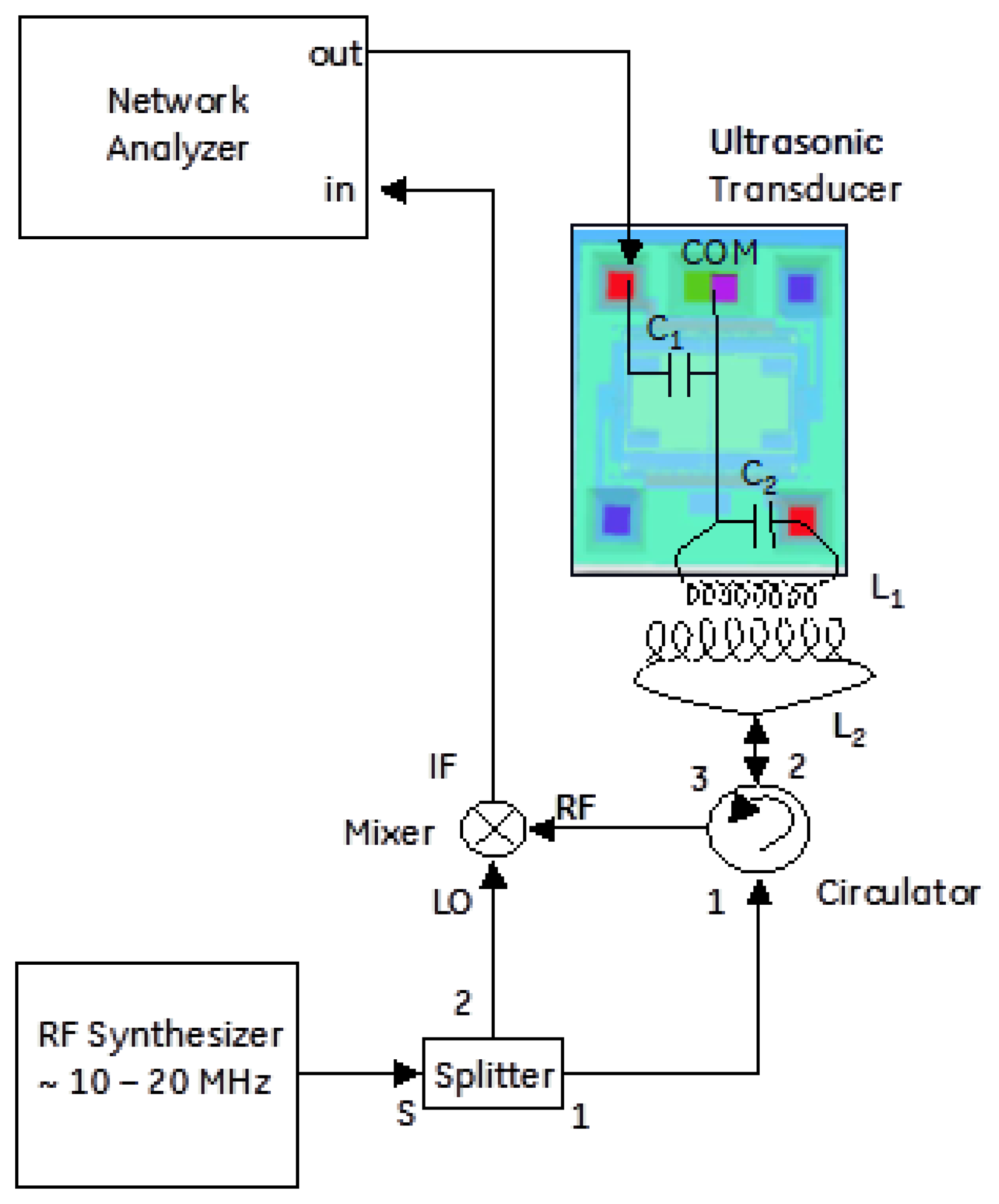
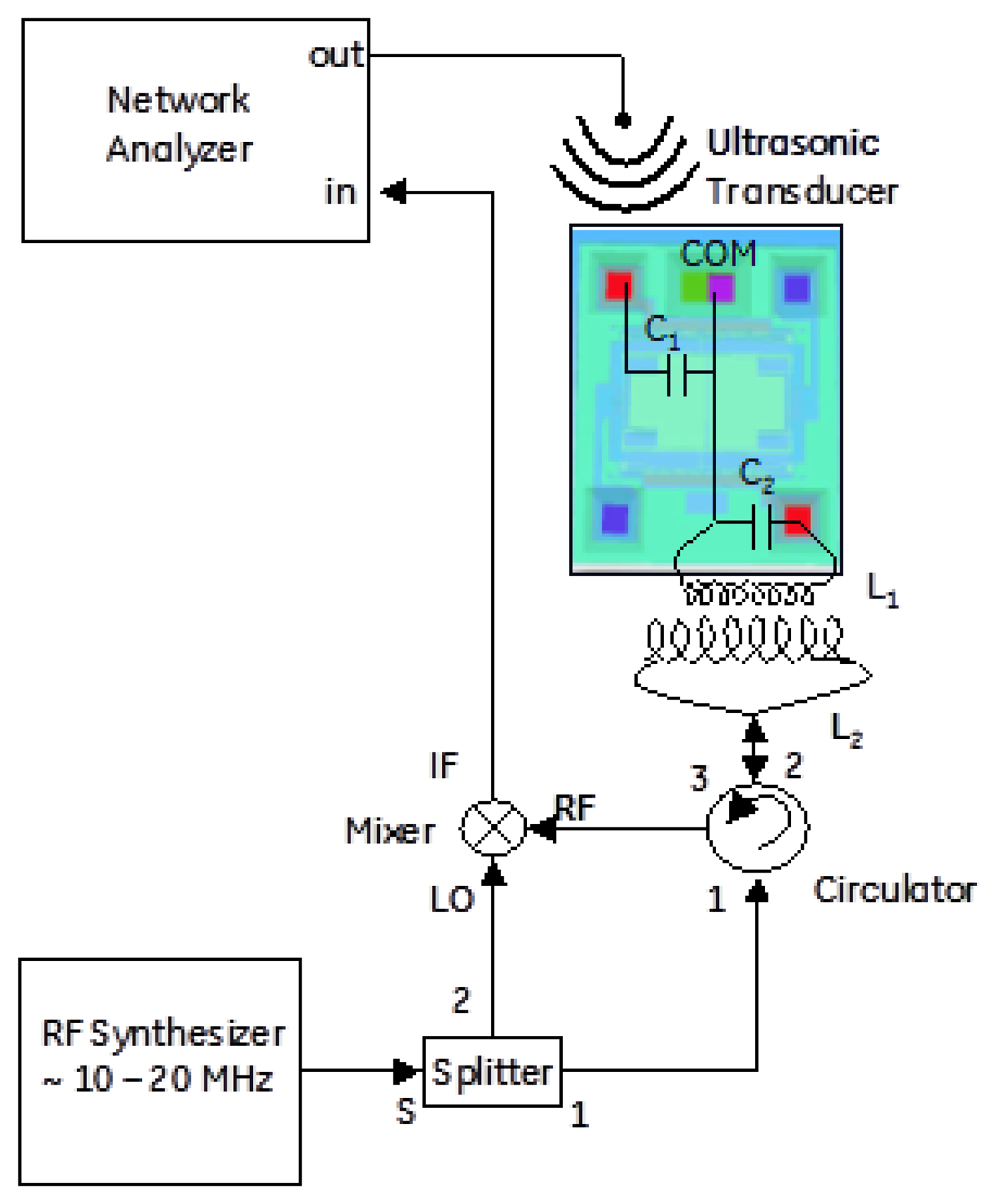
Figure 5 shows the packaged die where a 5-loop coil of wire resonated the die capacitance at 14.2 MHz. A second 5-loop coil of wire, stood off from the die-coupled loop by ∼1 cm, was driven by an RF synthesizer. The synthesizer output was also coupled to a diode that served to down-convert the re-radiated signal. While not the same device as shown in Figure 1, the comb drive response was shown experimentally to have a similar Q and resonant frequency driven electrically as when driven acoustically.
In order to optimize the configuration to maximize the read range and minimize the required power, a more detailed understanding of the inductive link was required, enabling a more careful design of the coils, geometry and receiver electronics. The magnetic field, B, at distance r from an N-turn coil loop of radius a carrying a current I is given by:
If the drive current is an AC signal at the drive frequency, ωd, this field will induce a voltage in a second receive coil. Assuming the receive coil of Nr turns of area Ar is oriented at an angle α to the transmit coil, and is part of an LC tank circuit with an electrical quality factor Qd, the induced voltage is given by:
The goal is to maximize this voltage in order to maximize the force on the comb drive capacitor. The first key constraint is that the LC resonant frequency should be close to “standardized” frequency allocations, of which the relevant ones are at 127 kHz and 13.56 MHz. Given die capacitances of about 60 pF for the silicon comb drive, frequencies between 10 MHz and 20 MHz were targeted. A simple expression for the inductance L (in mH) of an Nr–turn coil loop of radius ar (in cm) and length l (in cm) is given by:
To maximize V(r) under the constraint of a fixed resonant frequency, Nr and Ar must be maximized. In practice, a 6-turn coil of 2.5 cm radius and 0.25 cm length was chosen to provide an inductance of 3.6 mH, which resonated the 58 pF of the capacitor of the comb drive at ∼11 MHz. The expected electrical quality factor, Qd, of the tank can be determined from the parasitic resistance, R, from:
With parasitic resistances of about 16.5 Ω, the expected Qd ∼15 is a little larger than the measured Qd ∼12 using simple RF reflection and transmission measurements. This would be an important factor to optimize in an advanced design. Of course, the quality factor cannot get too high or it will be hard to re-radiate the 30 kHz resonant oscillations within the bandwidth of the LC tank.
The design of the read coil is another important factor in efficient delivery of power to the die. A reasonable strategy is to match the driving coil to the impedance of the driving system, which is typically 50 Ω. The magnetic field falls off as 1/r3 outside of the radius of the drive coil, so a large drive coil is desirable to maximize the read range. For this work a single-turn square coil, ∼15 cm on edge, was chosen and it was matched to a 50 Ω drive with a simple capacitive network.
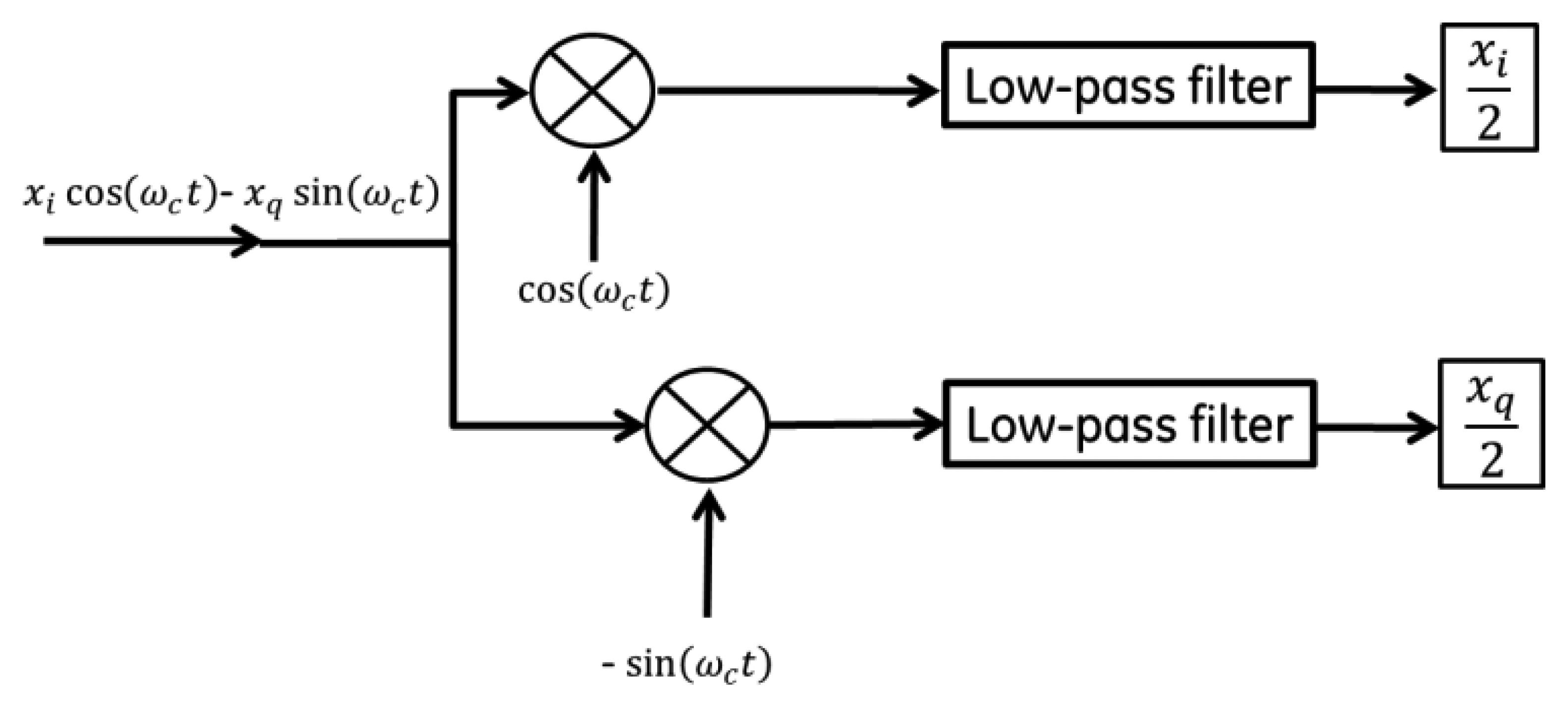
In order to readout the signal, homodyne detection between the back-reflected signal and the original RF driving signal is performed. A very simple schematic of this setup is shown in Figure 6. In practice, the phase between the local oscillator and RF back-reflection determines the quality of the detected signal. Most measurements suggested the modulation was dominated by FM, with small residual of AM, but this would have to be studied more systematically. One step beyond the architecture of Figure 6 is the more general In-phase/Quadrature (I/Q) demodulator topology illustrated in Figure 7, where the relative phase between local oscillator and reflected signal is accounted for [25]. This would allow full recovery of amplitude and phase for a general form of modulation. This receiver architecture will also allow for time varying displacement between the “reader” coil and the “sensor” coil as would be found, for example in a handheld interrogation approach. Signal processing of the I and Q legs allows the receiver to track the maximum signal amplitude, assuming the variations in relative phase are “slow” relative to the signal bandwidth. Using this configuration, the dependence of the received signal on the relative phase between the local oscillator and the back reflection from the antenna can be eliminated.
4. Acoustic Drive and Inductive Read
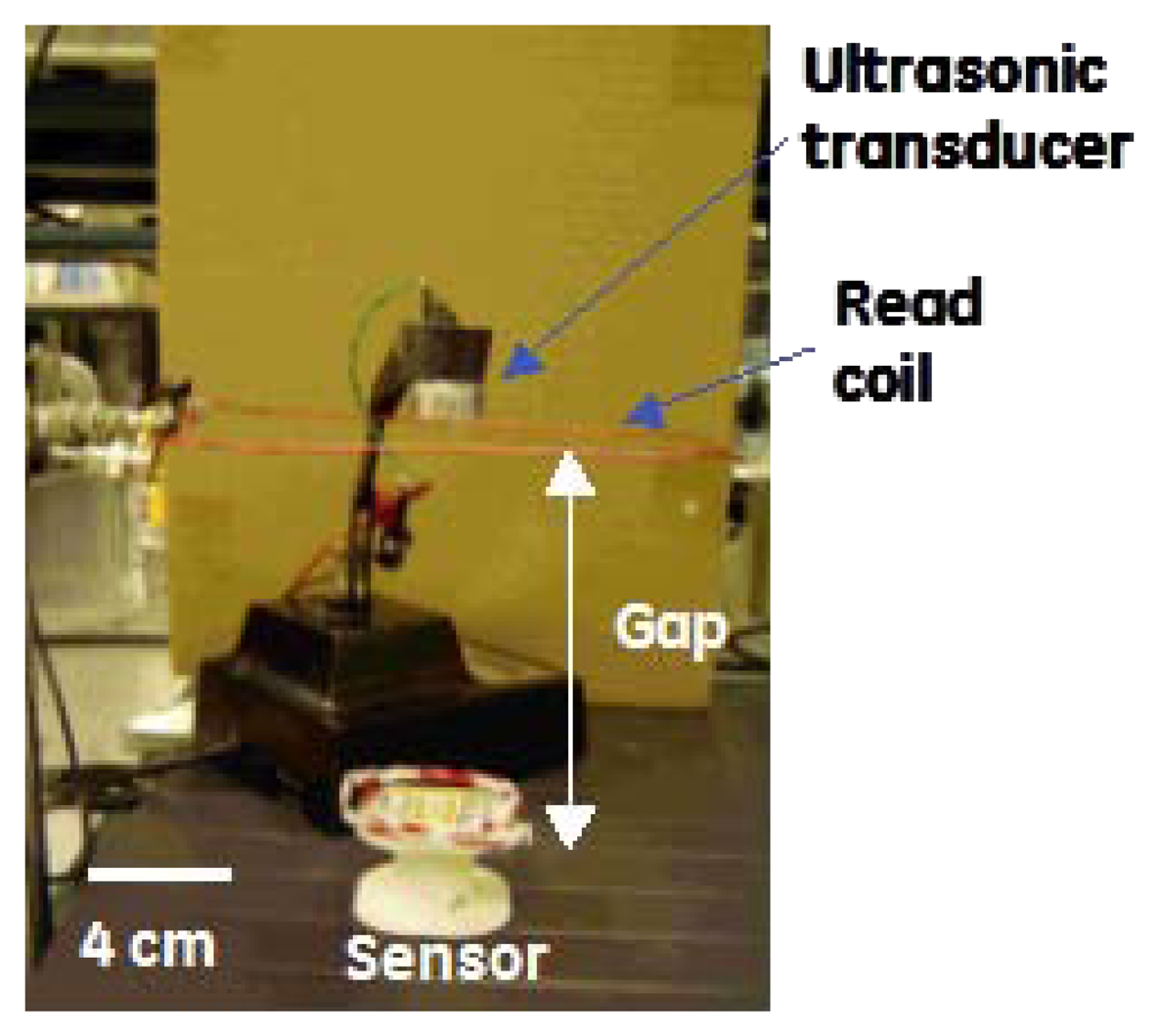
Acoustic drive and inductive read were combined into a single architecture for remote standoff detection of the resonant frequency of the MEMS device. A schematic and picture of the wireless architecture is shown in Figures 8 and 9. The acoustic transducer and driving coil can be seen co-located near the middle of the picture and the sensor is shown at the bottom.
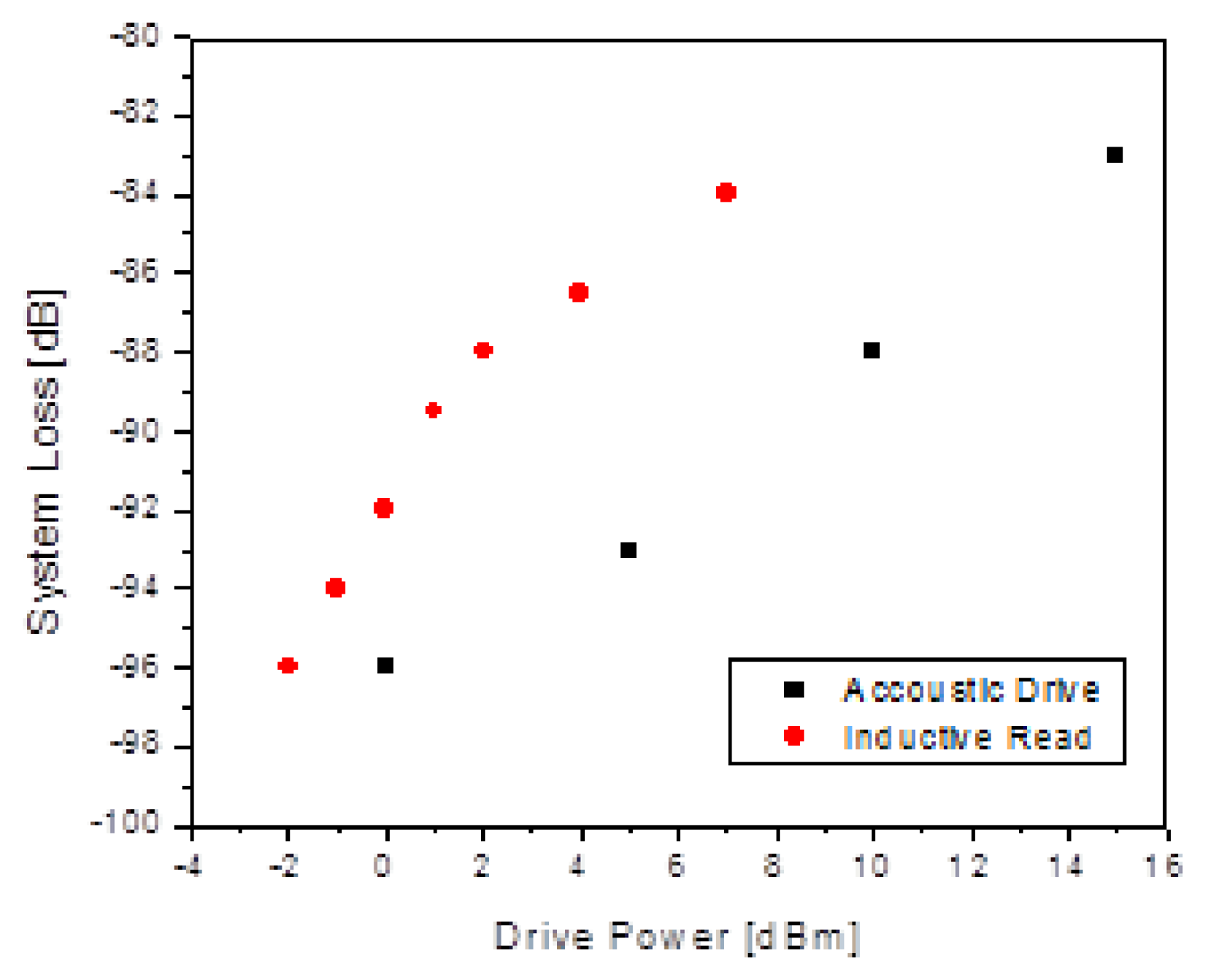
First measurements focused on the relationship of the received signal to various operating parameters as seen in Figure 10. The dependence on the acoustic drive power was in line with the expected dependence due to the “direct drive” nature of the acoustic excitation. This can be seen using Equation (1), with Pdrive as the drive power level and p as the sound pressure level. This pressure produces a corresponding driving force, F, on the inertial mass resulting in amplitude, xo, of the inertial mass, with an associated motional power, Pmech, as shown in:
However, for the inductive readout, the situation is a bit more complicated. According to Equation (3), the unmodulated RF read power, Pread, produces a force, F, on the read capacitor proportional to this power. The amplitude of motion is proportional to F, implying a doubling of the sensitivity of the motional energy to the inductive read power level compared to the acoustic case:
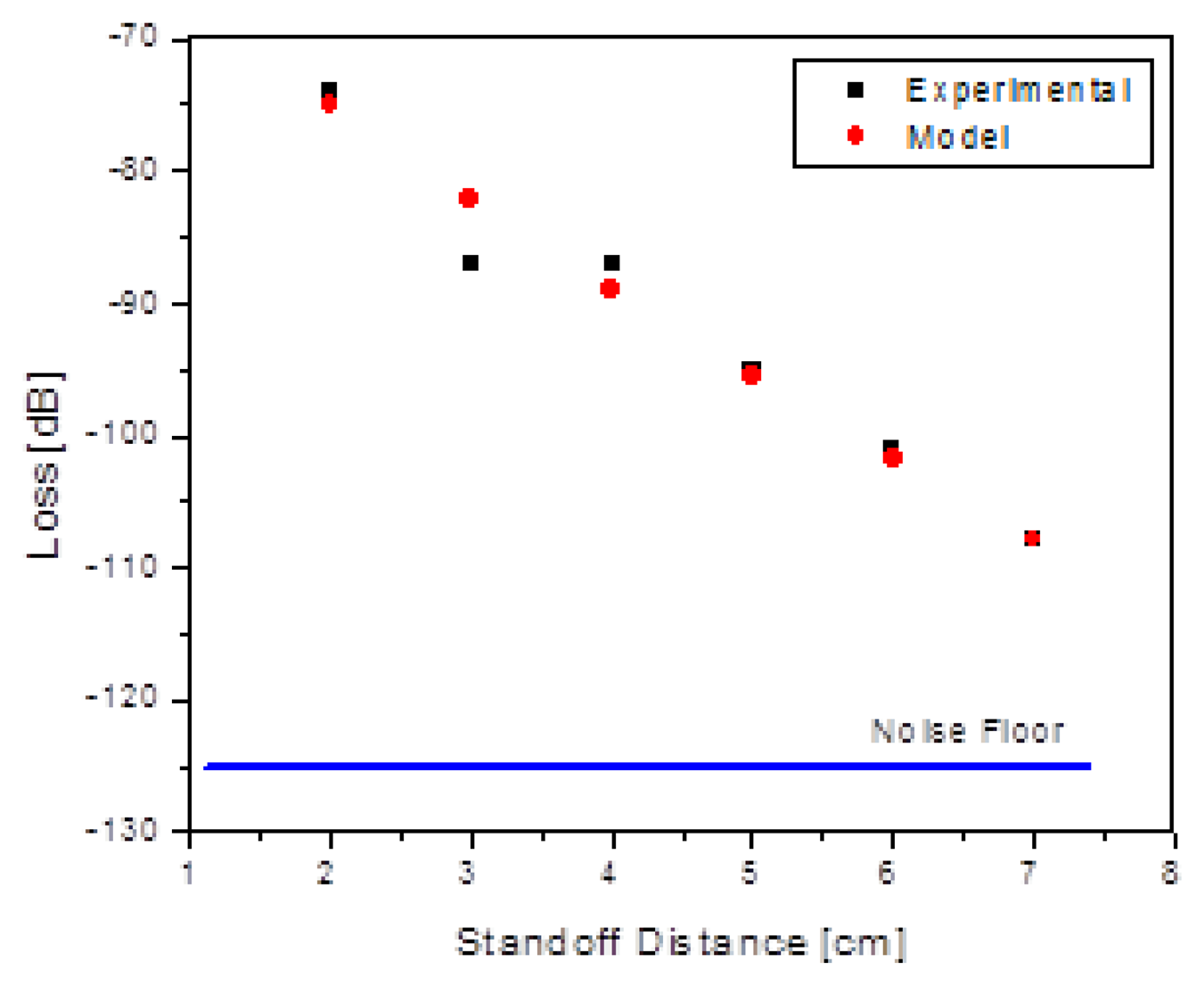
A second important dependence was the variation of the received signal level with standoff distance, r. Based on the technical discussion above, a simple model for this dependence would look functionally like the following:
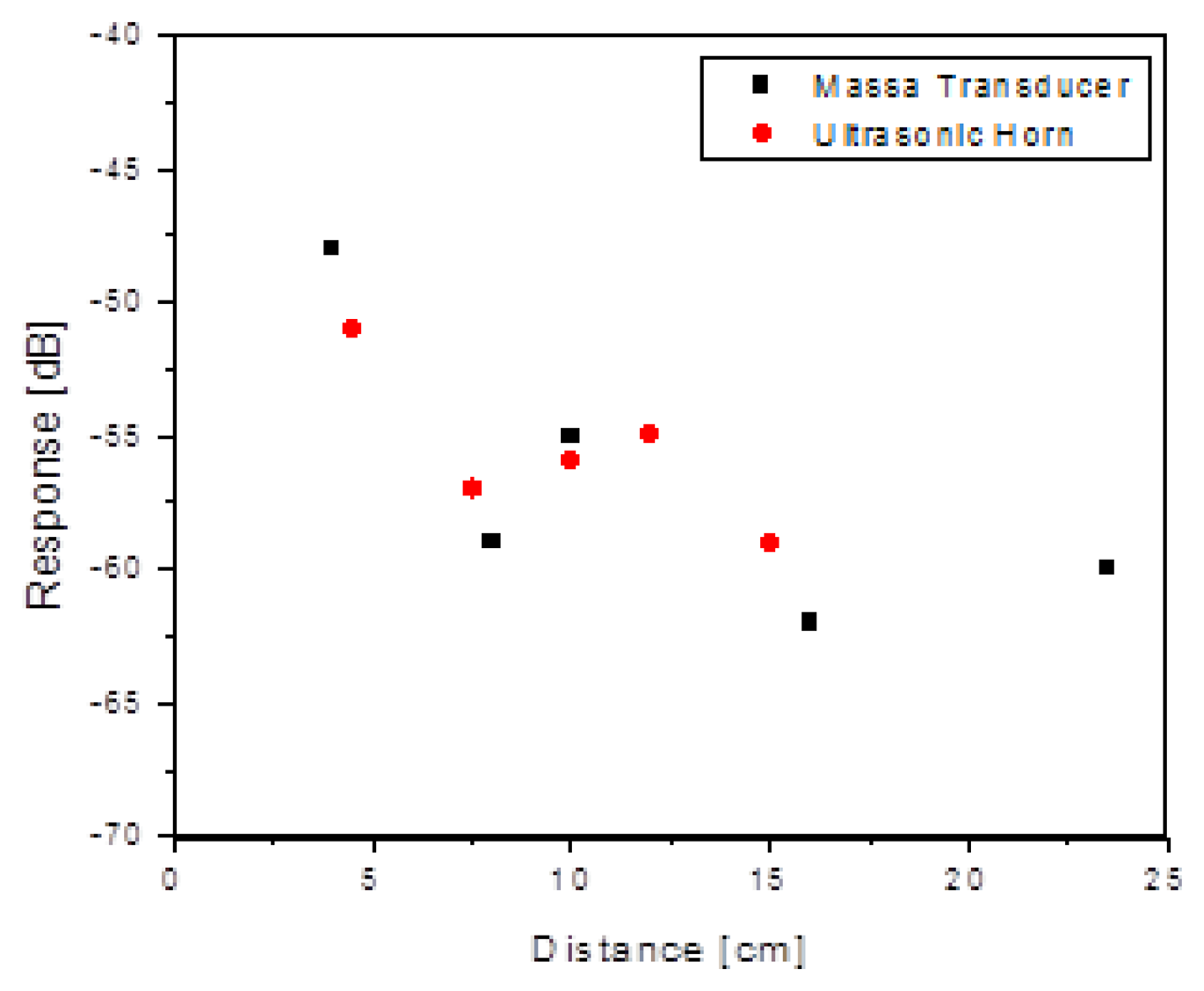
The first factor in Equation (11) accounts for the fact that the voltage induced in the sensor coil in the forward direction of the inductive “link” is proportional to the magnetic field, so the power delivered to the die is proportional to the square of the magnetic field. Hence, for a 2-way link, the dependence of received signal should go as the fourth power of the B field. The second factor in Equation (11) is the square-law dependence on the acoustic drive distance. Measurements of the dependence of the received signal on standoff distance were made, and overlaid with this simple physical model. Figure 11 shows good agreement of the data with the functional form.
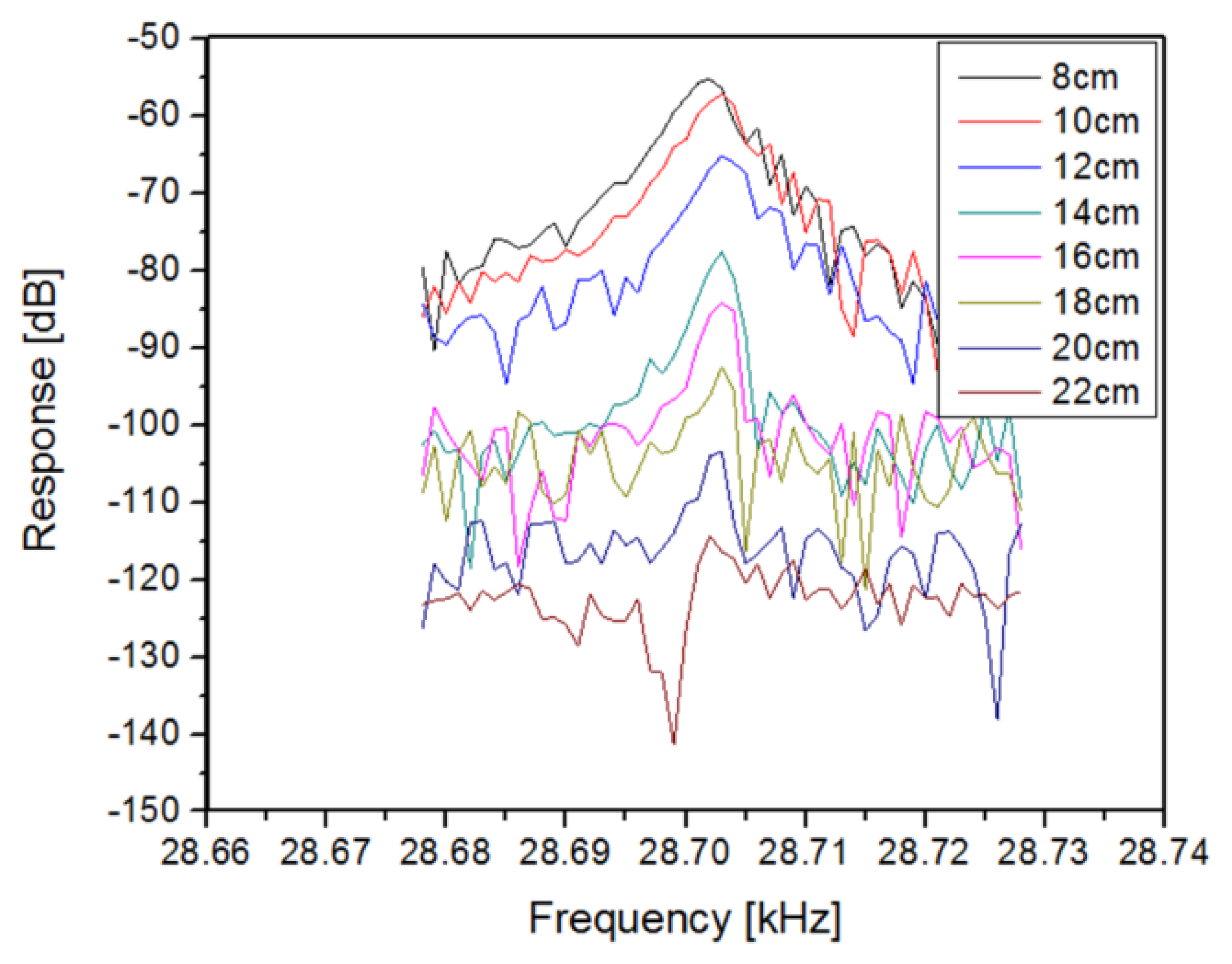
With this understanding in place, the dependence of the received signal as a function of standoff distance was measured, with a maximum standoff of 22 cm achieved (Figure 12). Note that the drive levels are not constant for this data, but were set so that they did not exceed “practical” values of +15 dBm (∼30 mW). The intent was simply to find the largest standoff distance and the acoustic and inductive drive levels under this constraint. It would clearly be possible to achieve greater distances using higher drive levels for the acoustic and inductive links.
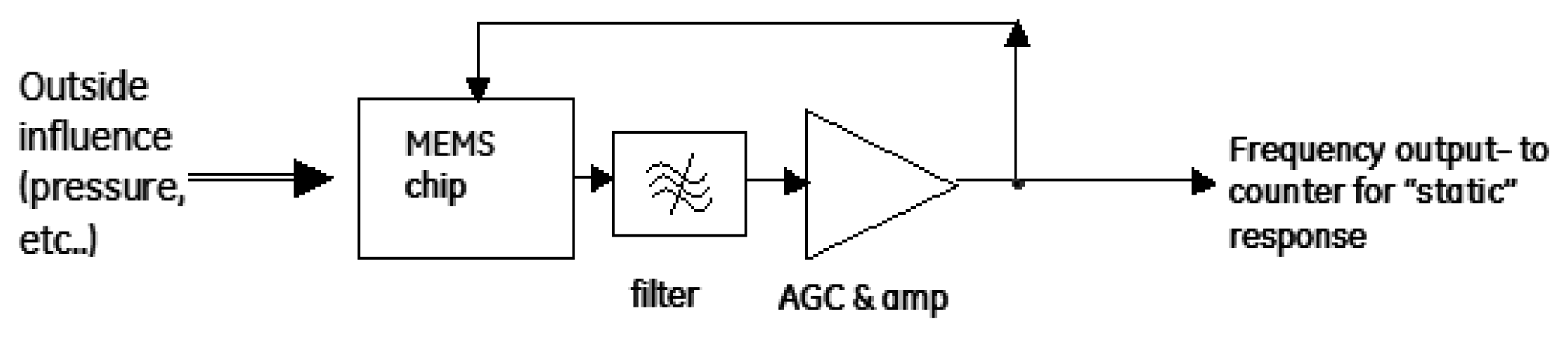
One practical issue with this data is that a very expensive network analyzer was used to sweep the acoustic frequency in order to detect resonance. For low cost applications, it would be desirable to have the device “autodetect” its own resonance frequency [26]. This is typically achieved by taking the output of the detector and then applying gain and feeding it back to the drive signal as seen in Figure 13.
With enough gain, and minimal phase shift, the system can be made to oscillate on its own, from broadband noise, due to the high Q of the micromechanical resonator. A sketch of the setup used to force the system to oscillate by applying feedback with the appropriate amount of gain as shown in Figure 14. This setup eliminates the need for any expensive frequency sweeping (e.g., network analyzer) or a sophisticated method for finding the resonance frequency. After implementing this approach, the system oscillated up to a standoff distance of 15 cm, limited only by the available gain in the variable amplifier setup. Figure 15 shows an example of the sensor response when in the feedback loop shown in Figure 14. The required ∼100 dB of gain was achieved by cascading stages, and a simple multi-op-amp based design could be used in practice.
5. Conclusions
Using an acoustic drive and inductive readout, a micromechanical resonator was driven into resonance and wirelessly interrogated on its own from broadband noise, without the need for any junction-based electronic device (such as a diode) local to the sensor. This demonstration opens the door for the use of silicon-based high accuracy MEMS devices in high temperature wireless applications. The standoff dependence of both acoustic driving and inductive readout was determined separately and as part of the system as a whole. Oscillation from broadband noise was shown up to 15 cm away and complete wireless system with laboratory electronics up to 20 cm. Drive and readout architectures were shown that are suitable for handheld, portable applications. Further work is necessary to understand both the temperature dependence of the resonator system and the potential effects of intermediary materials between the sensor and its interrogating electronics.
Acknowledgments
The authors would like to thank Ted Furlong, Steve Walls, Peter Kinnell, Roger Jones and Joe Krisciunas for their support of this work. This paper is dedicated to the memory of Rod Brown who was instrumental in supporting this research program.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gould, D.; Sklorz, A.; Meiners, M.; Lang, W.; Benecke, W. Passive Wireless Temperature Sensing Using RF Technology for an Automotive Application. Proceedings of Sixth IASTED Conference on Wireless and Optical Communications, Banff, AB, Canada, 3–5 July 2006.
- Karthaus, U.; Fischer, M. Fully integrated passive UHF RFID transponder IC with 16.7 um minimum RF input power. IEEE J. Solid-State Circuits 2003, 38, 1602–1608. [Google Scholar]
- DeHennis, A.; Wise, K. A wireless microsystem for the remote sensing of pressure, temperature, and relative humidity. J. Microelectromech. Syst. 2005, 14, 12–22. [Google Scholar]
- Suster, M.; Ko, W.; Young, D. An optically powered wireless telemetry module for high temperature MEMS sensing and communication. J. Microelectromech. Syst. 2003, 13, 536–541. [Google Scholar]
- Takeuchi, S.; Shimoyama, I. Selective drive of electrostatic actuators using remote inductive powering. Sens. Actuators A 2002, 95, 269–273. [Google Scholar]
- Schimetta, G.; Dollinger, F.; Scholl, G.; Weigel, R. Wireless Pressure and Temperature Measurement using a SAW Hybrid Sensor. Proceedings of 2000 IEEE Ultrasonics Symposium, San Juan, PR, USA, 22–25 October 2000; pp. 445–448.
- Kalinin, V. Passive Wireless Strain and Temperature Sensors Based on SAW Technology. Proceedings of 2004 IEEE Radio and Wireless Conference, Atlanta, GA, USA, 19–22 September 2004; pp. 187–190.
- Yen, T.-T.; Lin, C.M.; Zhao, X.; Senesky, D.G.; Hopcroft, M.A.; Pisano, A.P. Characterization of Aluminum Nitride Lamb Wave Resonators Operating at 600 °C For Harsh Environment RF Applications. Proceedings of the IEEE International Conference on Microelectromechanical Systems, Wanchai, Hong Kong, 24–28 January 2010; pp. 731–734.
- Takahata, K.; Gianchandani, Y. A micromachined capacitive pressure sensor using a cavity-less structure with bulk metal/elastomer layers and its wireless telemetry applications. Sensors 2008, 8, 2317–2330. [Google Scholar]
- Akar, O.; Tay, A.; Najafi, K. A wireless batch sealed absolute capacitive pressure sensor. Sens. Actuators A 2000, 95, 29–38. [Google Scholar]
- Fonseca, M.; English, J.; von Arx, M.; Allen, M. Wireless micromachined ceramic pressure sensor for high temperature applications. J. Microelectromech. Syst. 2002, 11, 337–343. [Google Scholar]
- Radosavljevic, G.; Zivanov, L.; Smetana, W.; Maric, A.; Unger, M.; Nad, L. A wireless embedded resonant pressure sensor fabricated in the standard LTCC technology. IEEE Sens. 2009, 9, 1956–1962. [Google Scholar]
- Welham, C.; Gardner, J.; Greenwood, J. A laterally driven micromachined resonant pressure sensor. Sens. Actuators A 1996, 52, 86–91. [Google Scholar]
- Welham, C.; Greenwood, J.; Bertioli, M. A high accuracy resonant pressure sensor by fusion bonding and trench etching. Sens. Actuators A 1999, 76, 298–304. [Google Scholar]
- Greenwood, J.; Wray, T. High accuracy pressure measurement with a silicon resonant sensor. Sens. Actuators A 1993, 37–38, 82–85. [Google Scholar]
- Greenwood, J.; Satchell, D. Miniature silicon resonant pressure sensor. IEE Proc. D Control Theory Appl. 1988, 135, 369–372. [Google Scholar]
- Bartels, O. The Passive Tyre-Pressure Transponder: Specifics of the Implementation. Available online: http://www.iqmobil.de (accessed on 20 September 2010).
- Bartels, O. Apparatus for Wire-Free Transmission from Moving Parts. U.S. Patent 6,378,360 30 April 2002. [Google Scholar]
- Challener, W.; Knobloch, A.; Ajgoankar, M.; Chamarthy, P.; Xia, H. Subsystem Design and Validation for Optical Sensors for Monitoring Enhanced Geothermal Systems. Proceedings of Thirty-Sixth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, 31 January–2 February 2011.
- Palit, S.; Challener, W.; Lopez, J.; Mandal, S.; Xia, H. A Multi-Modality Fiber Optic Sensing Cable for Monitoring Enhanced Geothermal Systems. Proceedings of Thirty-Seventh Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 30 January–1 February 2012.
- Challener, W.; Palit, S.; Craddock, R.; Knobloch, A. MOEMS Pressure Sensors for Geothermal Well Monitoring. Proceedings of SPIE Photonics West, San Francisco, CA, USA, 2–7 February 2013. [CrossRef]
- Vernooy, D.; Knobloch, A.; Ahmad, F.; Sexton, D. Remote Excitation and Readout of a High Q Silicon Resonator. Proceedings of 2010 IEEE Sensors, Kona, HI, USA, 1–4 November 2010; pp. 1108–1112.
- Greenwood, J. Sensor. U.S. Patent 6,584,864 1 July 2003. [Google Scholar]
- Koskenvuori, M.; Tittonen, I. Towards micromechanical radio: Overtone excitations of a microresonator through non-linearities of the second and third order. J. Microelectromech. Syst. 2008, 17, 363–369. [Google Scholar]
- Krauss, H.; Bostian, C.; Raab, F. Solid State Radio Engineering; John Wiley & Sons: New York, NY, USA, 1980; pp. 310–312. [Google Scholar]
- Nguyen, C.; Howe, R. An integrated CMOS micromechanical resonator high Q oscillator. IEEE J. Solid-State Circuits 1999, 38, 440–454. [Google Scholar]


© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Knobloch, A.J.; Ahmad, F.R.; Sexton, D.W.; Vernooy, D.W. Remote Driven and Read MEMS Sensors for Harsh Environments. Sensors 2013, 13, 14175-14188. https://doi.org/10.3390/s131014175
Knobloch AJ, Ahmad FR, Sexton DW, Vernooy DW. Remote Driven and Read MEMS Sensors for Harsh Environments. Sensors. 2013; 13(10):14175-14188. https://doi.org/10.3390/s131014175
Chicago/Turabian StyleKnobloch, Aaron J., Faisal R. Ahmad, Dan W. Sexton, and David W. Vernooy. 2013. "Remote Driven and Read MEMS Sensors for Harsh Environments" Sensors 13, no. 10: 14175-14188. https://doi.org/10.3390/s131014175



