2. Hollow Glass Waveguides
In hollow core glass waveguides (HGWs) light can propagate through an air core by multiple reflections on the metallic inner wall [
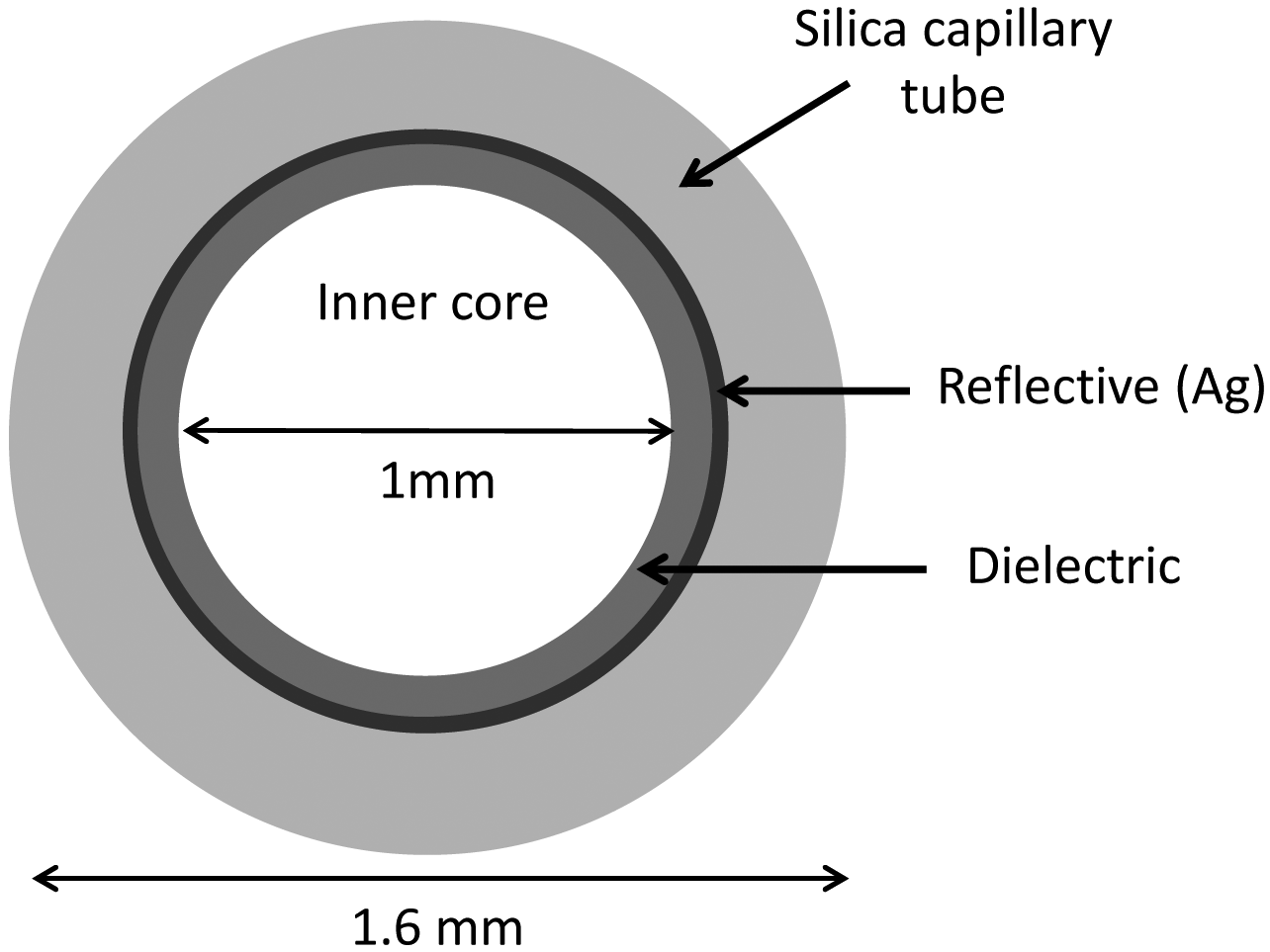
6]. The schematic of a typical hollow guide fiber is shown in
Figure 1. The main advantages are high power threshold, low insertion loss, low nonlinearity, and no end-reflection [
7]. Furthermore, hollow waveguides show low beam divergence and losses are proportional to
a−3, where
a is the bore radius. Drawbacks are the high bending losses, which are proportional to R
−1, where R is the bending radius [
8]. Considering the cylindrical geometry of an hollow waveguide, the optical modes are transverse electric (TE
lm) or transverse magnetic (TM
lm). There are also hybrid or mixed modes designated by HE
lm and EH
lm. These hybrid fiber modes have a small component of the electric field along the fiber or optic axis and correspond to skew rays (a ray that does not cross the fiber axis; rather it travels in a corkscrew or helical path down the fiber). In order to reduce the overall waveguide transmission losses due to the absorption of radiation in the metallic layer, the waveguide core is additionally coated with dielectric films [
9]. Actually, the losses at IR frequencies are greatly reduced by adding dielectric thin films to metallic or metallic coated waveguides. The thickness of the dielectric film chosen to minimize losses depends on the wavelength and on the refractive index of the dielectric material employed [
10]. A schematic sketch of the proposed waveguide concept is reported in
Figure 1.
In a hollow waveguide the total transmission losses depend on the nature and number of the propagating modes and increase dramatically for the higher order modes [
6]. Therefore, it is often desirable to excite through the waveguide only the lowest-order mode and when a Gaussian beam is focused on-axis into a hollow waveguide, only the hybrid HE
1,m modes are excited.
Characterization of mode dispersion characteristics and propagation losses is conventionally done by employing time domain spectroscopy or bulky gas lasers. However, to address the mode stability and to evaluate the bending loss, the characterization system is required to distinguish between waveguide modes.
In the present work we report on experimental studies aiming at coupling the low loss optical modes of hollow waveguides having a metal and dielectric internal coating with high efficiency mid-IR quantum cascade lasers (QCLs), therefore prospecting a novel integrated optical system suitable for high sensitivity and high resolution spectroscopy experiments.
3. Experiments and Results
HWGs having lengths in the range 2–14 cm and bore diameter of 1 mm have been used to guide the optical beam of two external cavity edge-emitting mid-IR QCLs [
11]. Three different dielectric coating were deposited over the internal silver layer with thickness of 1 μm: (i) AgI (0.6 μm); (ii) polystyrene (Ps, 7.7 μm); (iii) a double dielectric layer of AgI/Ps (0.6/7.7 μm). The fabrication of Ag/AgI-coated HGWs begins with a silica tubing, which has polymer (UV acrylate) coating on the outside surface. A liquid-phase chemistry technique [
7] is used to deposit the Ag and the dielectric films inside the glass tubing. The first step involves depositing a silver film using standard Ag plating technology. Immediately after the silver is deposited, an iodine solution is pumped through the tubing and, through a subtraction process, a layer of AgI is formed. By controlling the concentration of the iodine solution and reaction time, an AgI film of the correct optical thickness can be deposited. To prepare silver/polystyrene (Ps)-coated hollow glass waveguides, an Ag film is first deposited within a glass substrate tube by combining a solution containing AgNO
3 and NH
4OH with a reducing solution containing dextrose and Na
2EDTA [
12]. The Ag film grows at a rate of approximately 1 μm/h, and Ag films were normally about 1 μm thick. The Ps films were deposited over the Ag coatings by using a liquid-flow coating process in which a Ps/toluene solution is drawn through the HGW at a constant coating velocity.
In all cases the coating is expected to reduce the mode dispersion and the attenuation of the optical modes with lower losses. Indeed, adding a thin film on the inner surface of silver wall changes the boundary conditions and can in principle reverse the dominant mode order. As a consequence, the thickness for the non-absorbing coating can enhance or suppress specific modes, if the inner coating thickness is larger than the critical value [
9]:
where n is the refractive index of the dielectric film and λ is the wavelength of propagating light in the waveguide. For what concern the thickness of PS, using
Equation (1), we estimate a critical value of the layer thickness of d
PS = 0.53 μm (λ
a = 5.7 μm) and d
PS = 1.1 μm (λ
b = 10.5 μm). The PC layer thickness has been set to 7.7 μm, much higher than the critical value for both wavelengths. We select this layer thickness since poor quality interference patterns in the near IR have been observed for thinner PC layers, meaning that the films are not uniform and so lower reflectance and thus larger losses are expected.
Two commercial mid-IR QCL sources based on an external cavity configuration were used for our experiments. The selected emission wavelengths are λa = 5.27 μm and λb = 10.5 μm (Daylight Solutions Inc., San Diego, CA, USA, model #21052-MHF and #21106-MHF, respectively). The average optical powers measured using a pyroelectric detector were 93 mW (λa) and 65 mW (λb). We tested metallic/dielectric waveguides for both wavelengths, considering that at the employed laser wavelengths, the dielectric film thickness deposited in the inner waveguide core are larger than the critical coating thickness for AgI and Ps.
The intensity profile of the propagating optical mode has been collected by means of a pyroelectric detector having a sensitive area of 1 mm × 1 mm, mounted on a compact motorized XY stage. The 2D multi-point image of the beam profile was obtained by recording the total transmitted power in the range 1–5.1 cm away from the waveguide output in the far field configuration for each scanning position, with a spatial resolution of about 0.2 μm for both XY scanning directions.
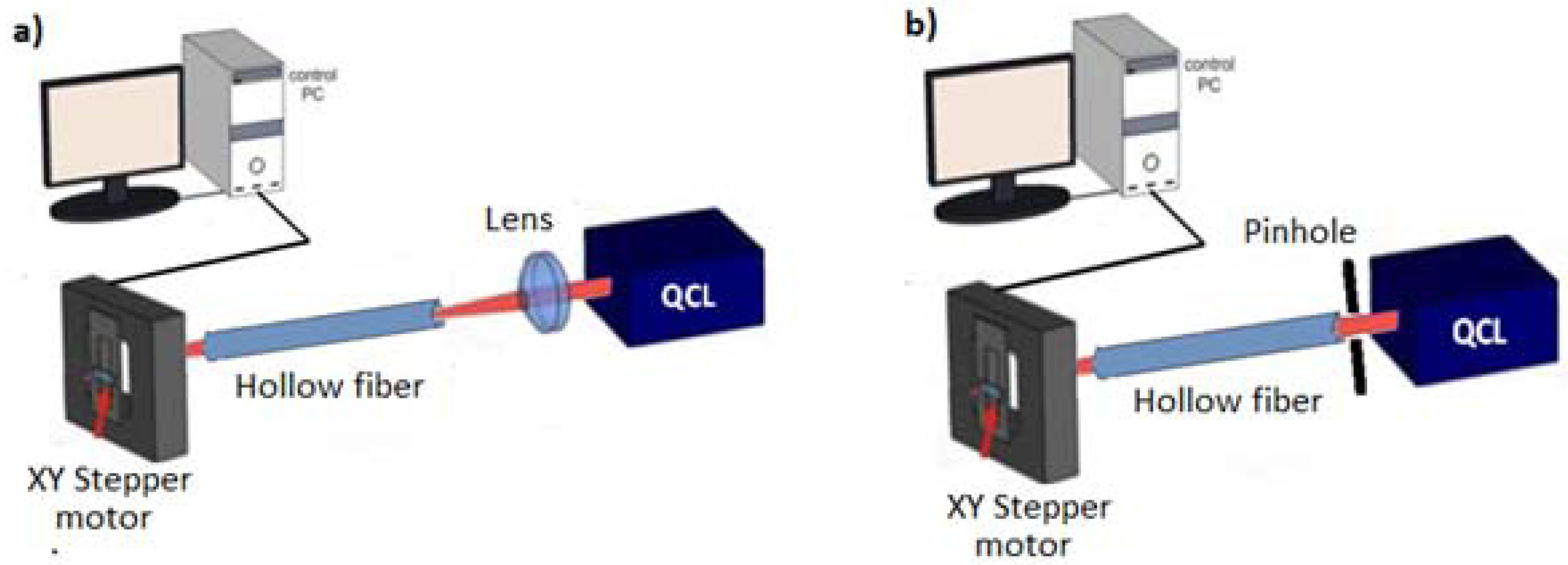
A first set of experiments were carried out coupling the QCL and the hollow waveguide by using a ZnSe lens to focus the collimated beam into a ∼100 μm spot at the waveguide entrance [
13–
15], as schematically shown in
Figure 2(a).
The focusing lens allows to obtain an input spot size smaller than the waveguide bore diameter in order to reduce the amount of energy blocked by the waveguide walls, thus reducing the light absorption heating, which is a critical point for high-power applications.
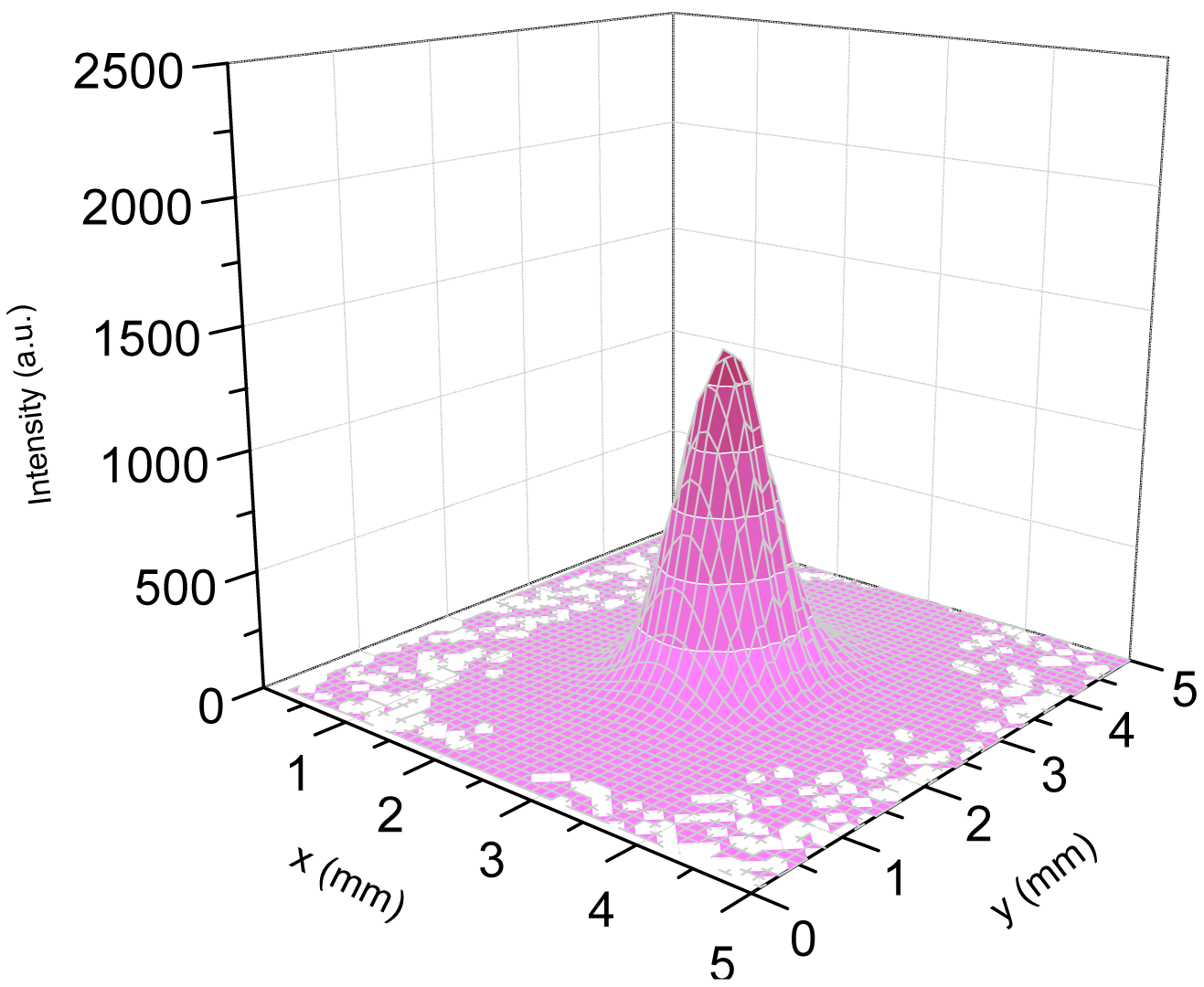
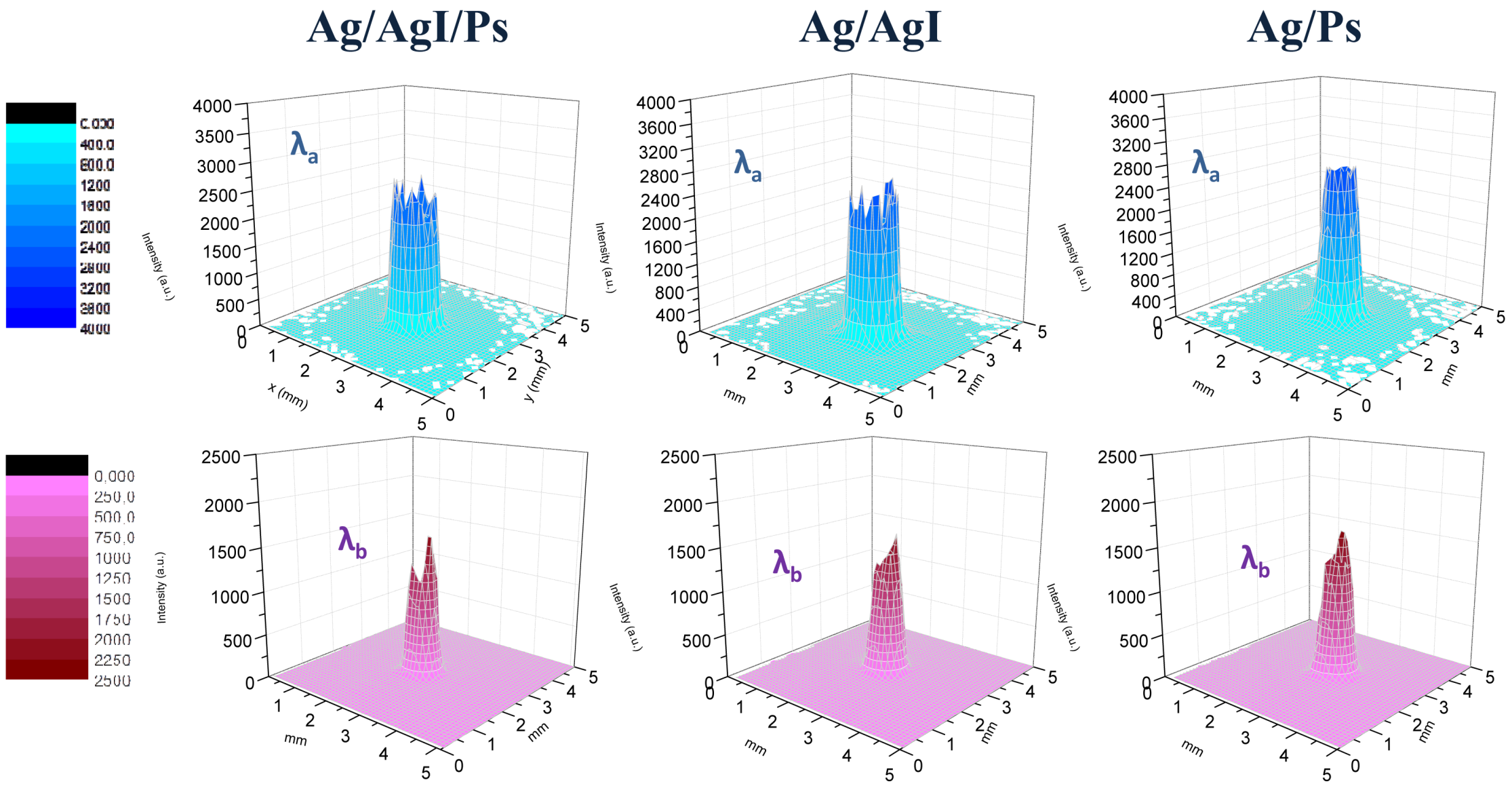
Figure 3 shows a representative far field 3D spatial intensity distribution measured for the λ
b QCL source The QCL current was set at 900 mA. The intensity distribution profile exhibits a Gaussian-like beam shape, as expected for a standard edge emitting QCL.
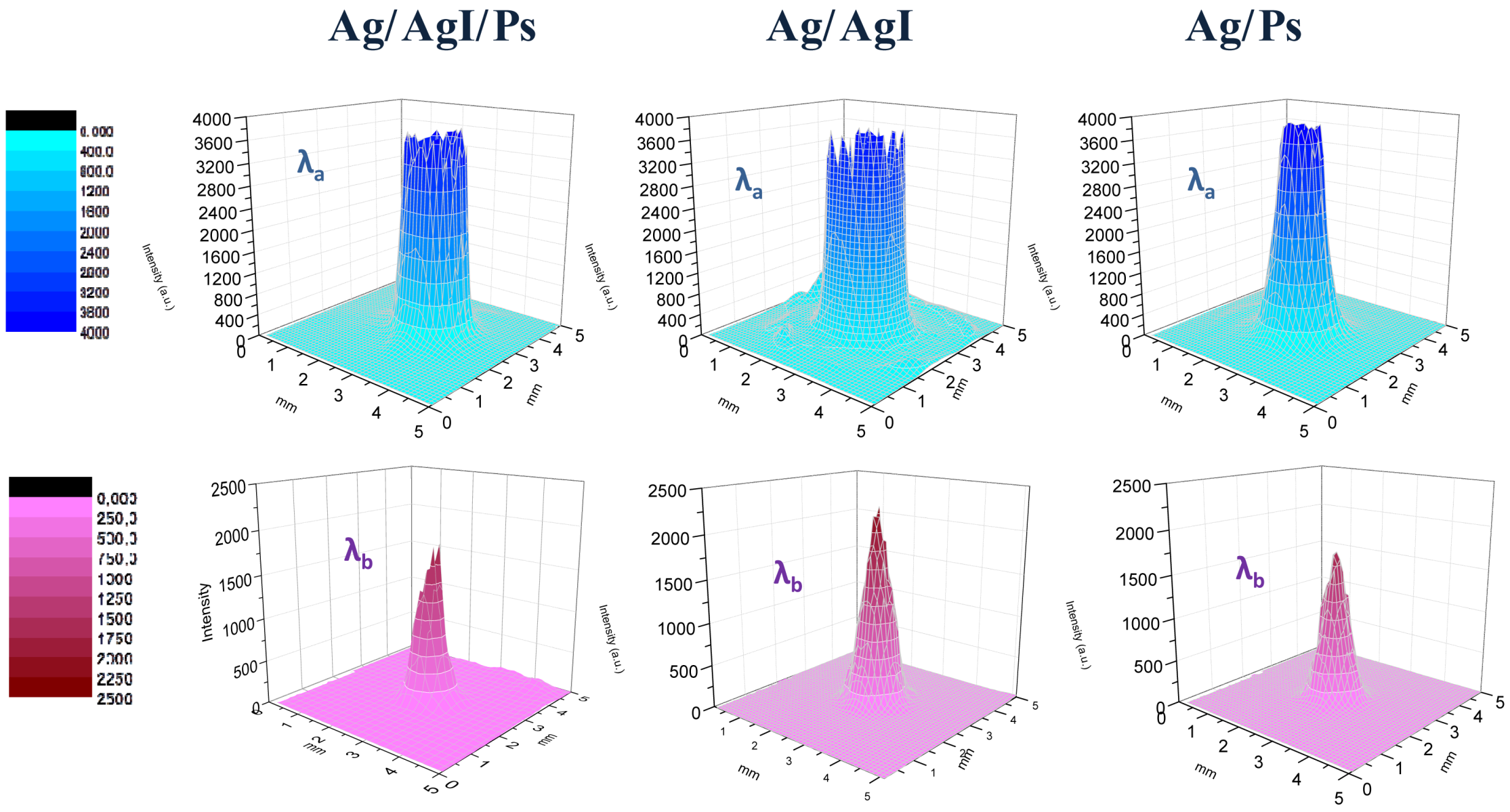
Figure 4 shows the far-field spatial intensity distribution of the two employed QCLs at the exit of a 12 cm long waveguide for different internal dielectric coating configuration measured 2 cm away from the waveguide output.
In a different experimental scheme, the QCL sources were placed directly in close contact with the fiber input with no intermediate optics, in so-called back-to-back configuration, as schematically shown in
Figure 2(b). A steel circular pinhole with the same diameter of the hollow core was placed in contact with the waveguide exit to prevent detection of scattered light not propagating through the waveguide.
Figure 5 shows the far-field spatial intensity distribution of the two wavelengths at the exit of a 12 cm long waveguide in back-to-back configuration measured 2 cm away from the waveguide output. The electric field intensity distribution shows that the beam shape is perfectly matched to the hybrid HE
11 mode since the electric field associated to the optics field at the boundary is reduced along the entire contour of the waveguide wall, meaning that the deposited inner dielectric coating thickness suppresses effectively the higher losses TE-like modes. Note that the theoretical beam profile for HE
11 mode in the waveguide can be approximated by the zero order Bessel function
.
Despite the condition a ≫ λ is satisfied, we observed a single mode profile at the waveguide output in all investigated cases. However, it must be considered that in hollow waveguides the propagating losses for the higher order modes increase as the mode parameter squared u
lm[
6]:
Thus the losses for the higher-order modes become so high that they are damped out and only the lowest-order modes can propagate.
Our results demonstrate that the HE
11 mode losses in an optimally designed waveguide become lower than those for TE
01 mode [
16], even for dielectric coatings with a moderate absorption coefficient. It is worth noting that the output beam profile of hollow waveguides depends not only on the bore diameter or the propagating wavelength, but also on the quality and launch conditions (with or without the focal lens) of the input beam, as theoretically expected [
6]. We found that the beam divergence is larger when the ZnSe lens is used to focalize the laser beam at the waveguide entrance, especially for the wavelength λ
a, because additional optical modes are propagating through the straight waveguide.
4. Propagation Losses and Coupling Efficiency
Propagating losses in hollow waveguides are highly dependent on the launch conditions,
i.e., the ratio
ω/
a, where
ω is the beam waist at the waveguide entrance [
8]. The power coupling efficiency of the incident beam to excite each low-loss HE
1m waveguide mode depends critically on the beam waist to bore radius ratio. Theoretically up to ∼100% of power coupling efficiency of an incident Gaussian beam to the lowest-loss HE
11 mode can be obtained. At small f-numbers more power is coupled to the higher-order modes. Instead at large f-numbers the beam can be clipped by waveguide walls. Since the HE
11 mode has the lowest theoretical loss, it is necessary to optimize the launch conditions in order to couple most of the input beam into this mode. This is possible by changing the value of the ratio
ω/
a (
i.e., varying the focusing lens position with respect to the waveguide entrance) and maximizing the output power in order to couple most of the light in the HE
11 mode. Our experiments have been performed under these conditions.
The propagation losses and the coupling efficiency can be determined by making two measurements. First we measured the optical power I0 at the waveguide entrance, then the light is coupled into the fiber and the optical power IS at the output-end of the fiber is measured. Absolute values of the losses of the excited mode of the straight waveguide were determined by using the following equation:
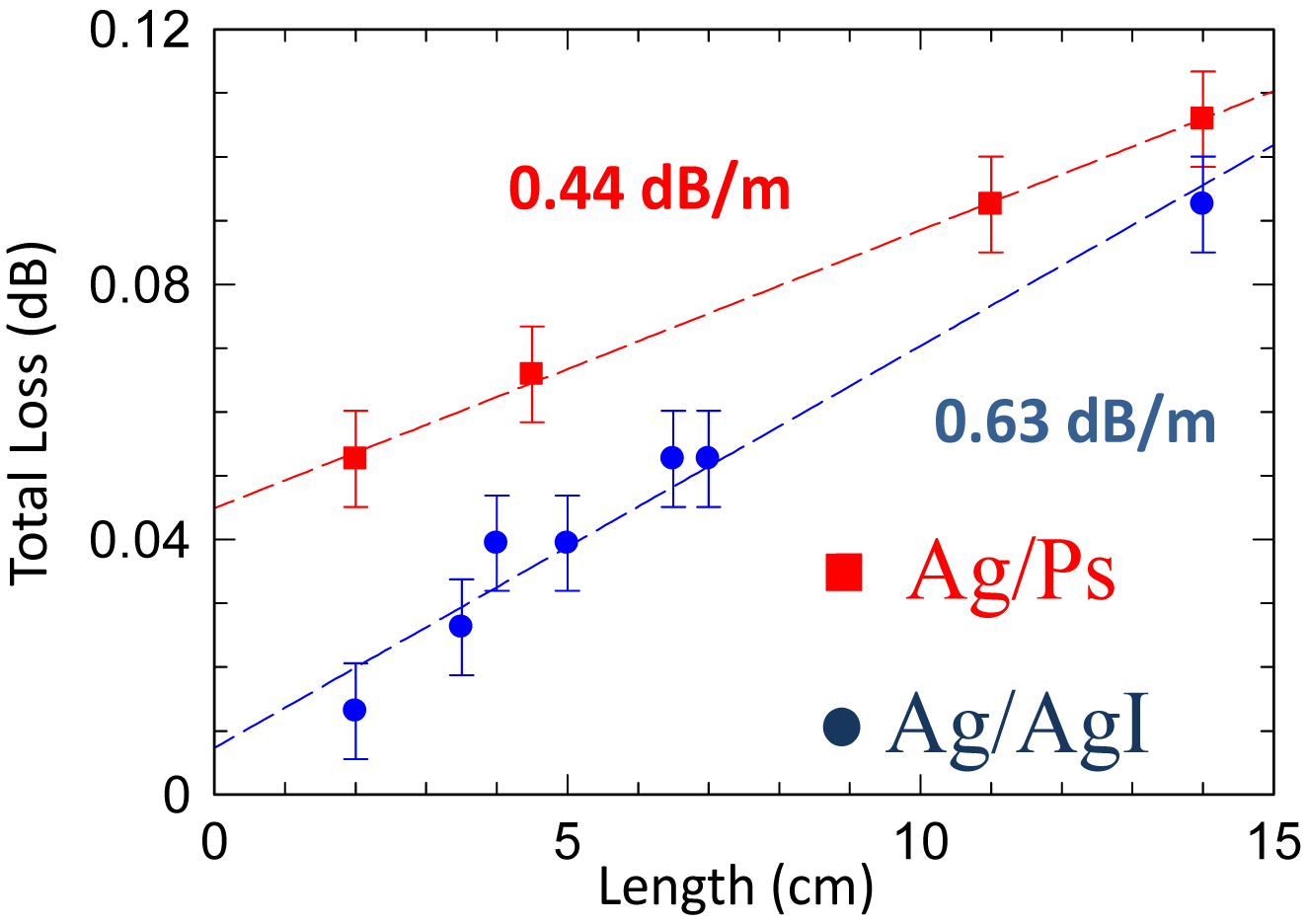
The graph in
Figure 6 shows the values measured by coupling hollow waveguides of different lengths (in the range 2–14 cm) with laser light at λ
a wavelength in back-to-back configuration.
The transmission losses increase linearly with the waveguide length. From the slope of the linear fit to the data we measured transmission losses of 0.63 dB/m for Ag/AgI coatings and 0.44 dB/m for Ag/Ps coatings. These values are nearly one order of magnitude lower that optical power attenuation measured using single-mode hollow core photonic crystal fibers made of silica glass [
17].
The coupling efficiency values between the QCL source and the waveguide is extracted from the intercept at zero length of the linear fits to the data. Coupling efficiencies as high as 99.8 ± 0.2% for the AgI dielectric film and 99.0 ± 0.1% for Ps coating have been obtained. The small variation between the coupling efficiencies is due to slight differences in the launch conditions,
i.e., the ratio
ω/
a. The theoretical coupling efficiency is 99.6% [
8].
5. Output Divergence Angle
The output divergence angle characterizes the diffraction of light leaving the waveguide. The output-beam divergence of a HGW depends critically on three factors: (i) the nature of the optical mode propagating through the guide; (ii) the wavelength and the polarization of the incoming beam; (iii) the bore diameter.
In principle the output beam divergence can give an indication of the number of high-order mode propagating in the hollow waveguide. The HE
1m modes will couple to free-space modes with a beam divergence
θm given by:
where
u1m is a parameter which depends on the order number (
m) of the HE
1m mode. The values for
u1m rapidly increase for the higher-order modes [
7,
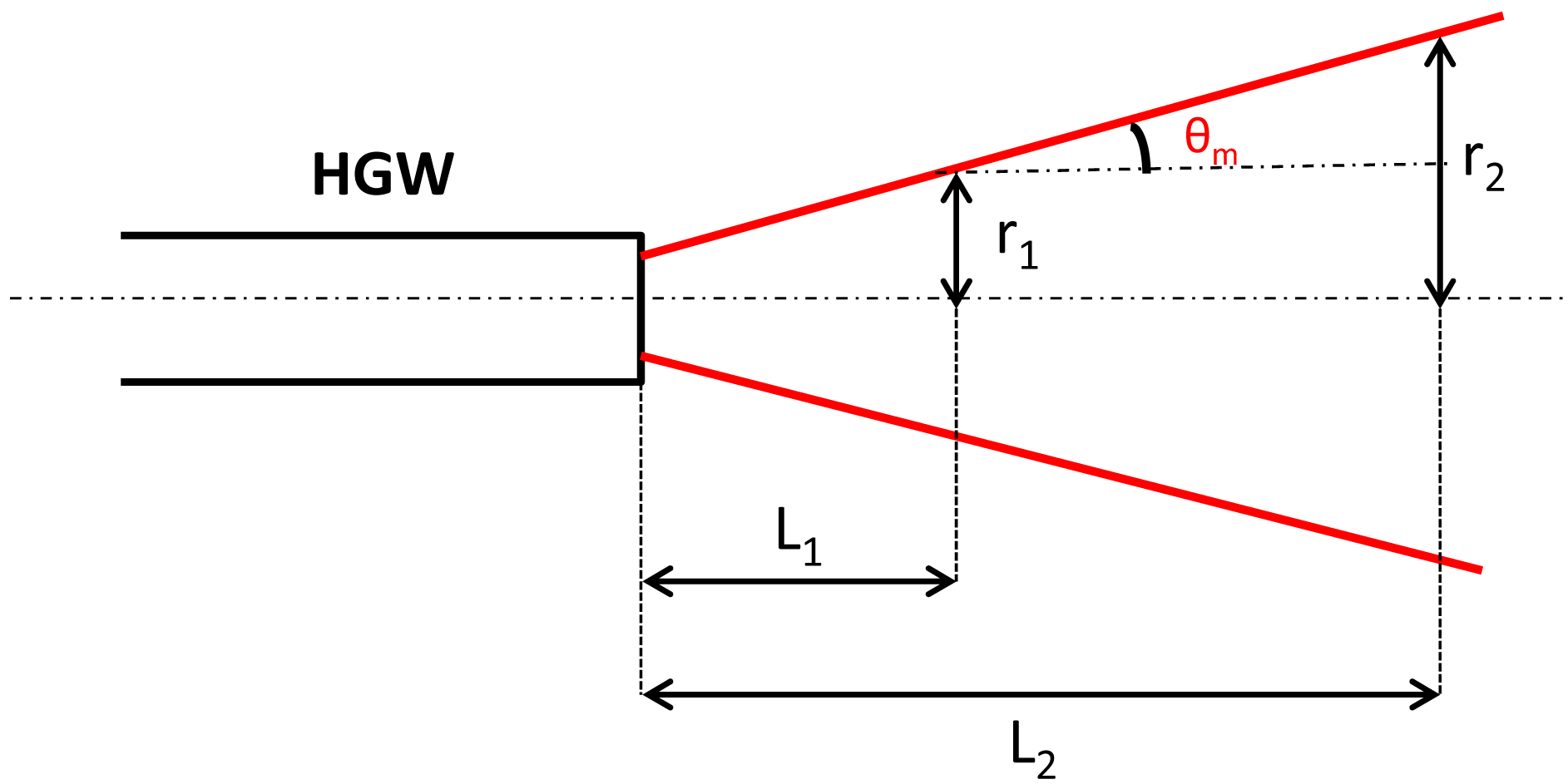
9]. The schematic of the output divergence measurements is shown in
Figure 7.
The output divergence angle
θm has been calculated from:
where r1 and r2 are the radial distances at which the light intensity drops to 1/e2 of its maximum central value, measured respectively at L1 = 1 cm and L2 = 5.1 cm distance from the fiber output as measured from the far-field scans.
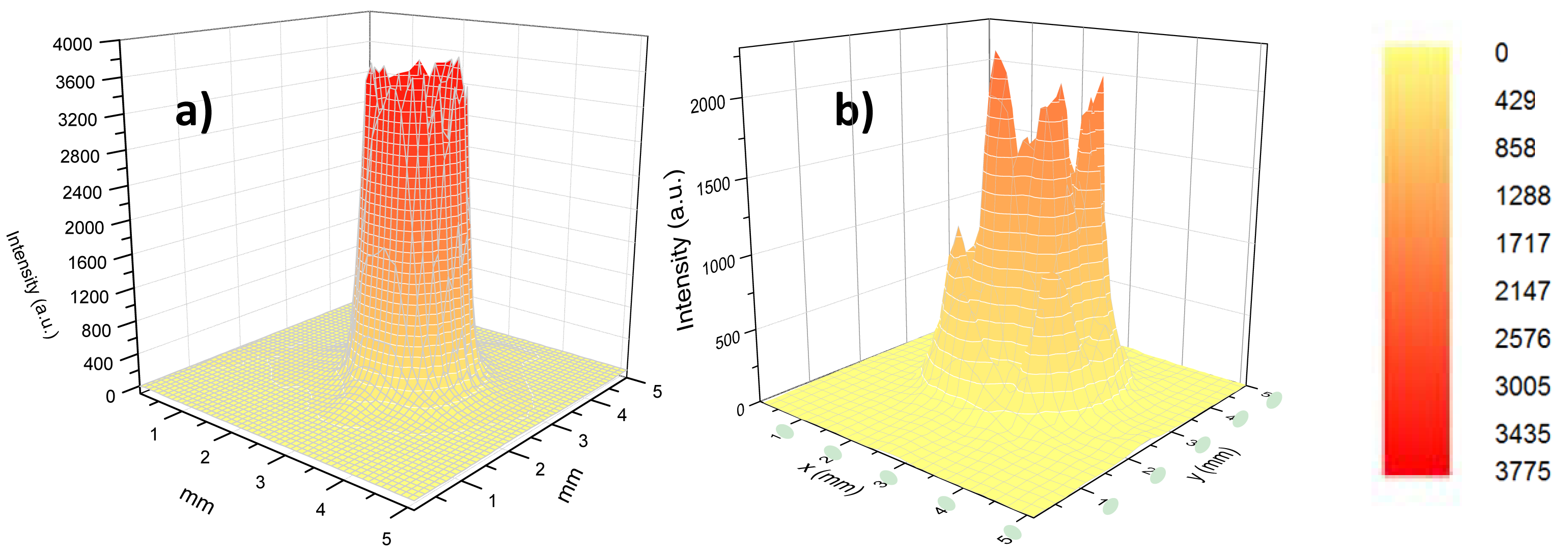
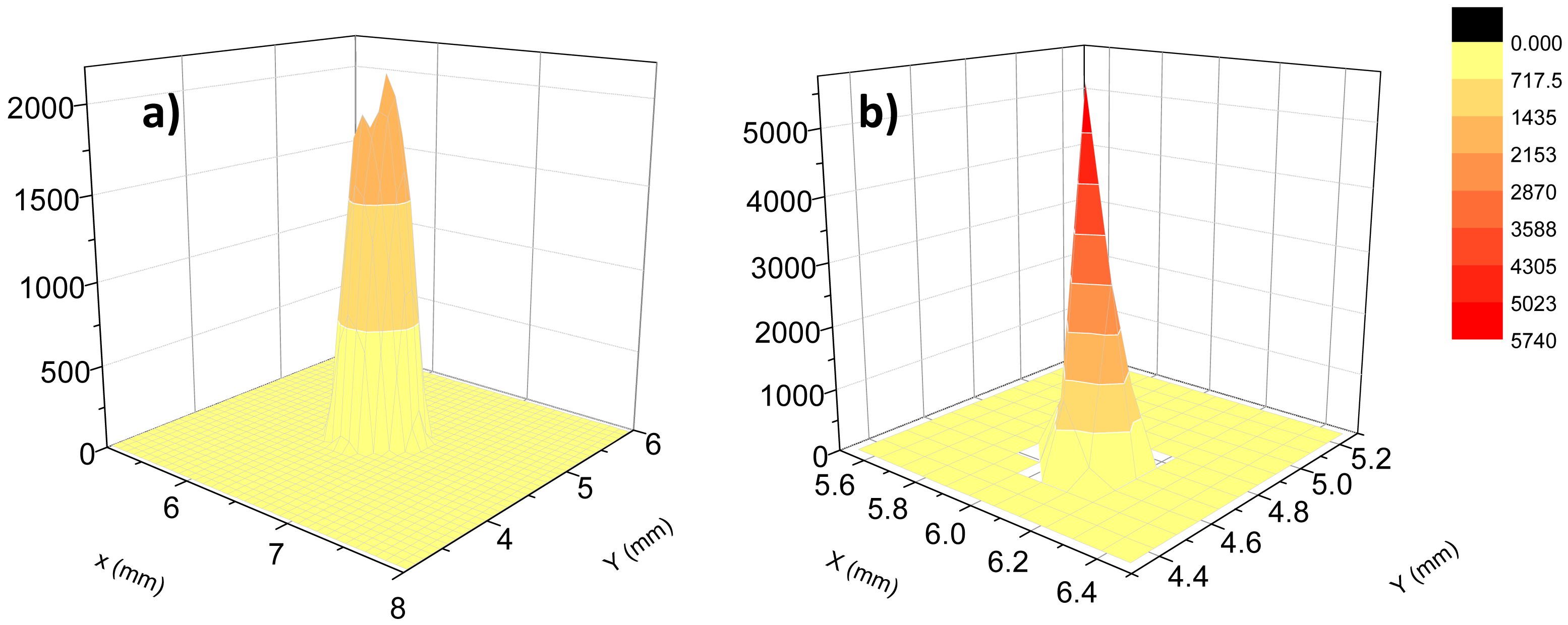
Figure 8 shows the 3D-far field scans measured for a 12 cm long HWG with AgI dielectric internal coating and at λ
a propagating wavelength. From these data we extracted
r1 = 0.5 mm and
r2 = 0.75 mm and estimated a divergence of
θm = 4.92 mrad. By using
Equation (4), we estimated a mode parameter
u1m = 2.94, in good agreement with the expected theoretical value for the first propagating mode
u11 = 2.405.
Much larger values are expected for higher order mode [
6], as shown in
Table 1 further confirming single-mode propagation of the laser beam in the hollow waveguide and good mode coupling between the laser-input optical mode and the waveguide lowest-loss HE
11 mode.
6. Single-Mode HWG for Optical Sensing Applications
A particularly attractive application for IR-fiber optics is optical sensing. In general, silica-based optical fibers are used in a large number of sensor applications such as: chemical and radiometric sensing, fiber optic gyros, etc. Fewer applications for IR-fibers have been demonstrated. The main reasons are the higher losses and the difficulty to achieve single mode propagation fibers, which are typically required in spectroscopic sensors.
For examples, in quartz enhanced photoacoustic (QEPAS) sensing, it is critical to avoid laser illumination of the acoustic detection module (ADM), since the radiation blocked by the Quartz tuning fork (QTF) and associated micro-resonator tubes creates an undesirable background when absorbed by the ADM structural elements. This background is usually several times larger than the thermal noise level of QEPAS and carries a shifting fringe-like interference pattern, which limits the detection sensitivity [
18–
20]. Thus, it is important to employ a mid-infrared QEPAS excitation beam of high quality and stability and if employing a fiber coupling system, single mode beam delivery is strictly required. Recently, we designed and assembled a QEPAS system fiber coupled with a single mode QCL and exploited its high performance for the detection of SF
6 gas traces in the ppt range. Single mode laser delivery has been obtained using a hollow fiber with inner Ag–AgI coatings and an internal bore size of 300 μm, having a loss of 1 dB/m. Additional collimating optics have been designed to be attached to the output of the fiber and provide a focusing distance of 40 mm. In
Figure 9 is shown the 3D laser beam profile measured using a pyroelectric camera (mod. Spiricon Pyrocam IIIC, AhrensburgGermany) at the output of the fiber (
Figure 9(a)) and at the focusing plane of the collimator (
Figure 9(b)). From
Figure 8(b) we can estimate a focused beam waist diameter of ∼170 μm, well below the gap between the QTF prongs (∼300 μm). As a results, in the QEPAS experiments almost all (99.4%) of the laser beam coming out the collimator were transmitted through the ADM module without touching it, thus reducing the background pattern and allowing to reach detection sensitivity in the part-per-trillion (ppt) concentration range. A record normalized noise equivalent absorption coefficient for QEPAS of 2.7 × 10
−10 cm
−1·W/Hz
½ was achieved [
20].