Review on the Modeling of Electrostatic MEMS
Abstract
:1. Introduction
2. Development of Related Studies on Electro-Mechanics for MEMS Devices
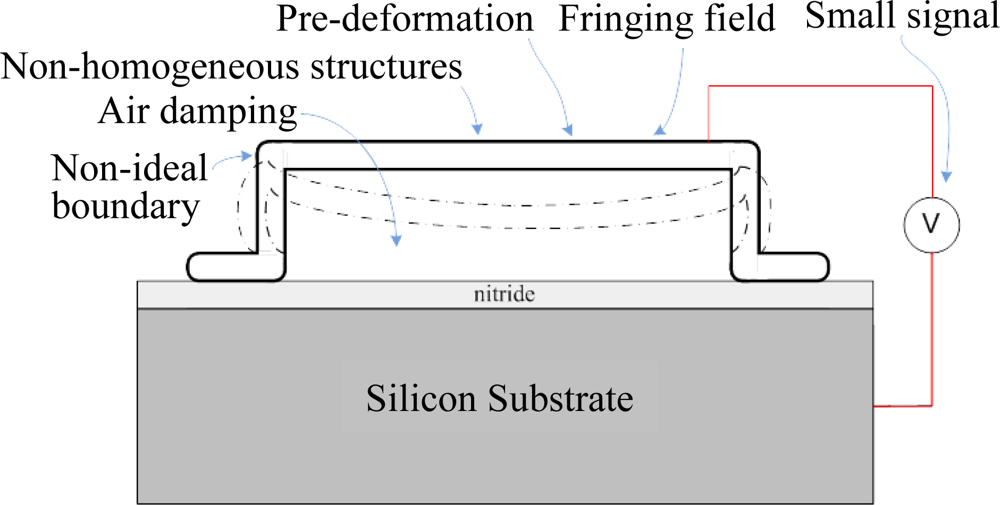
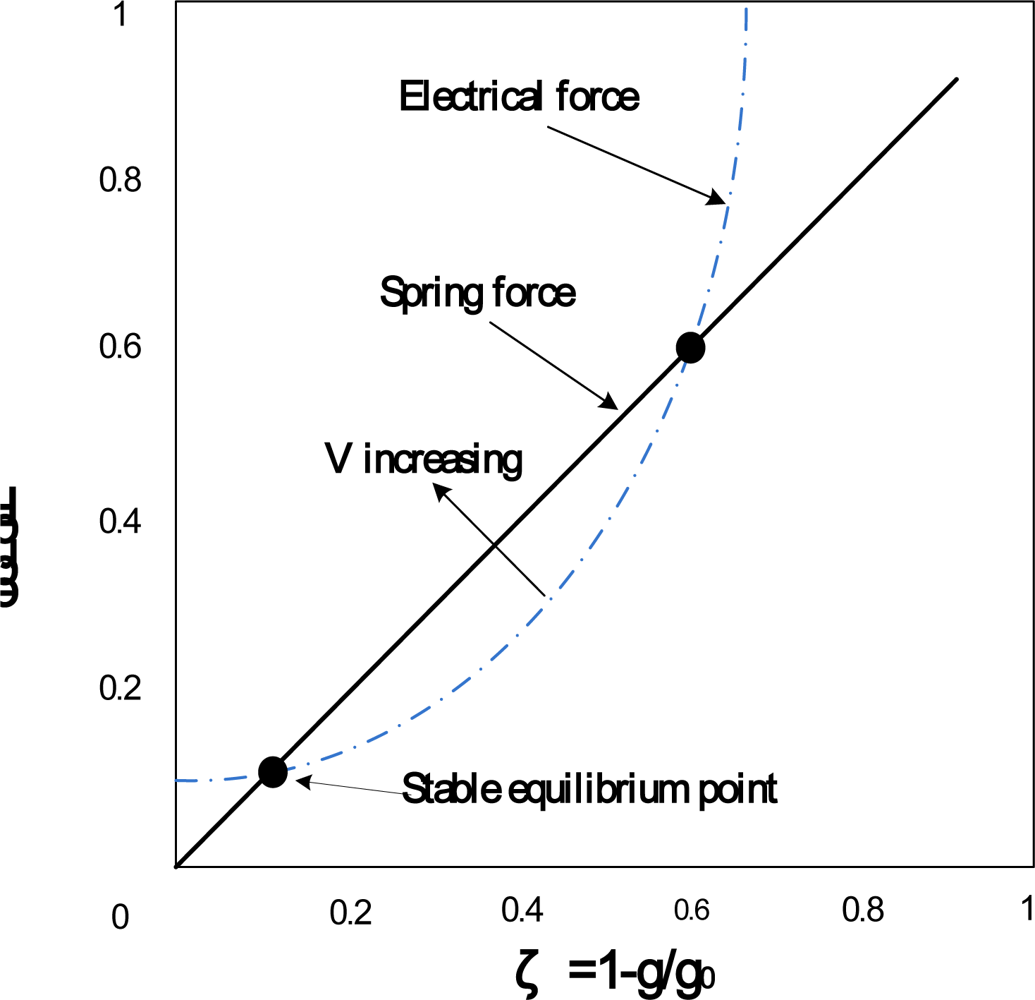
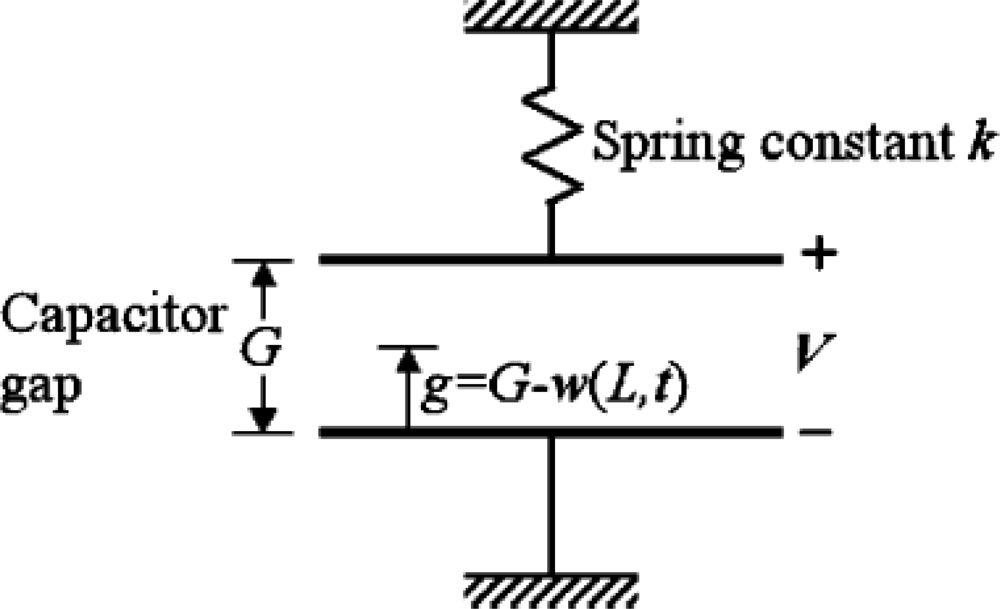
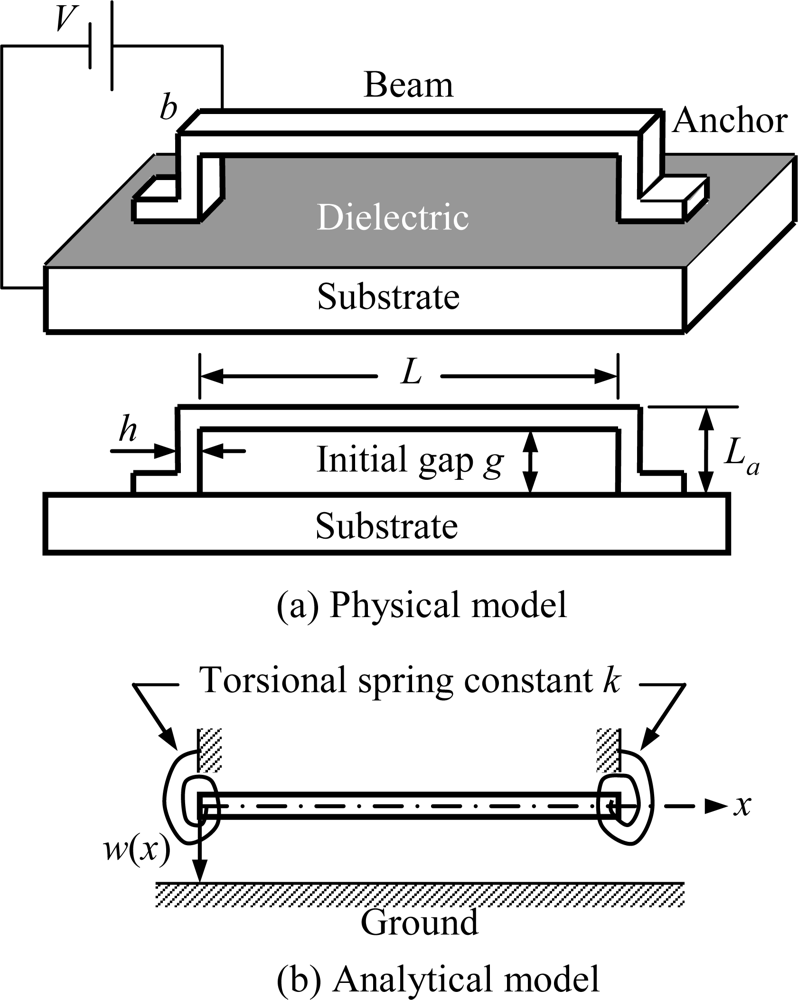
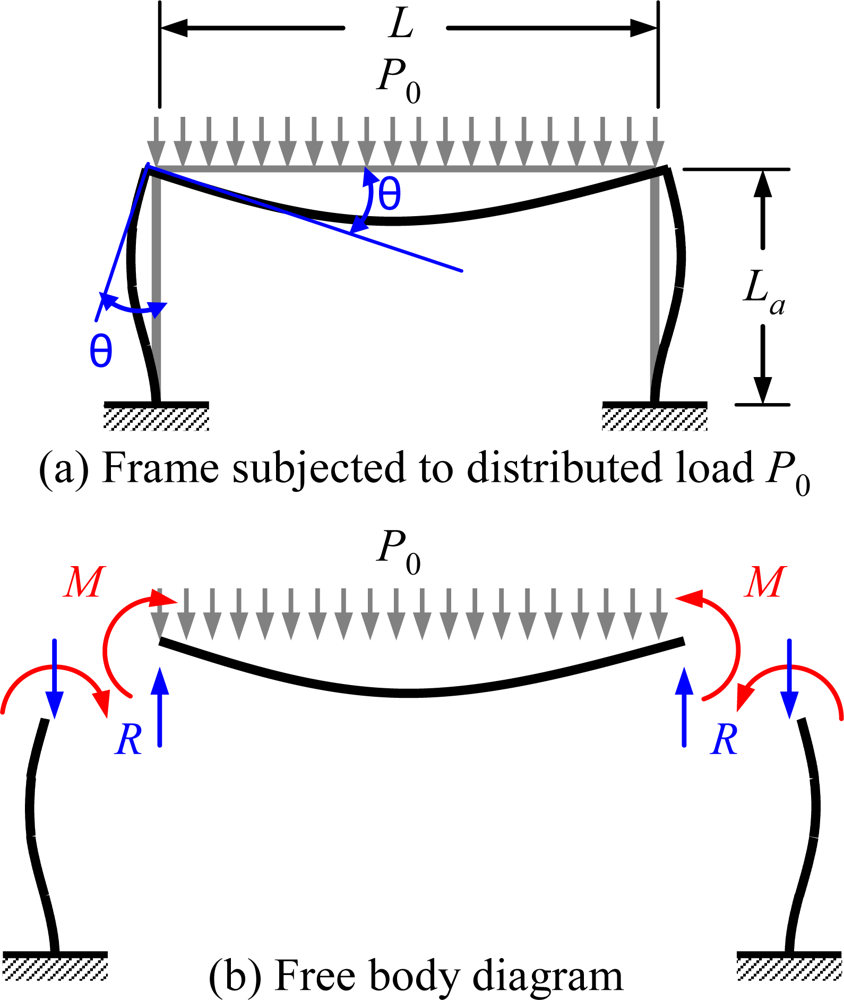
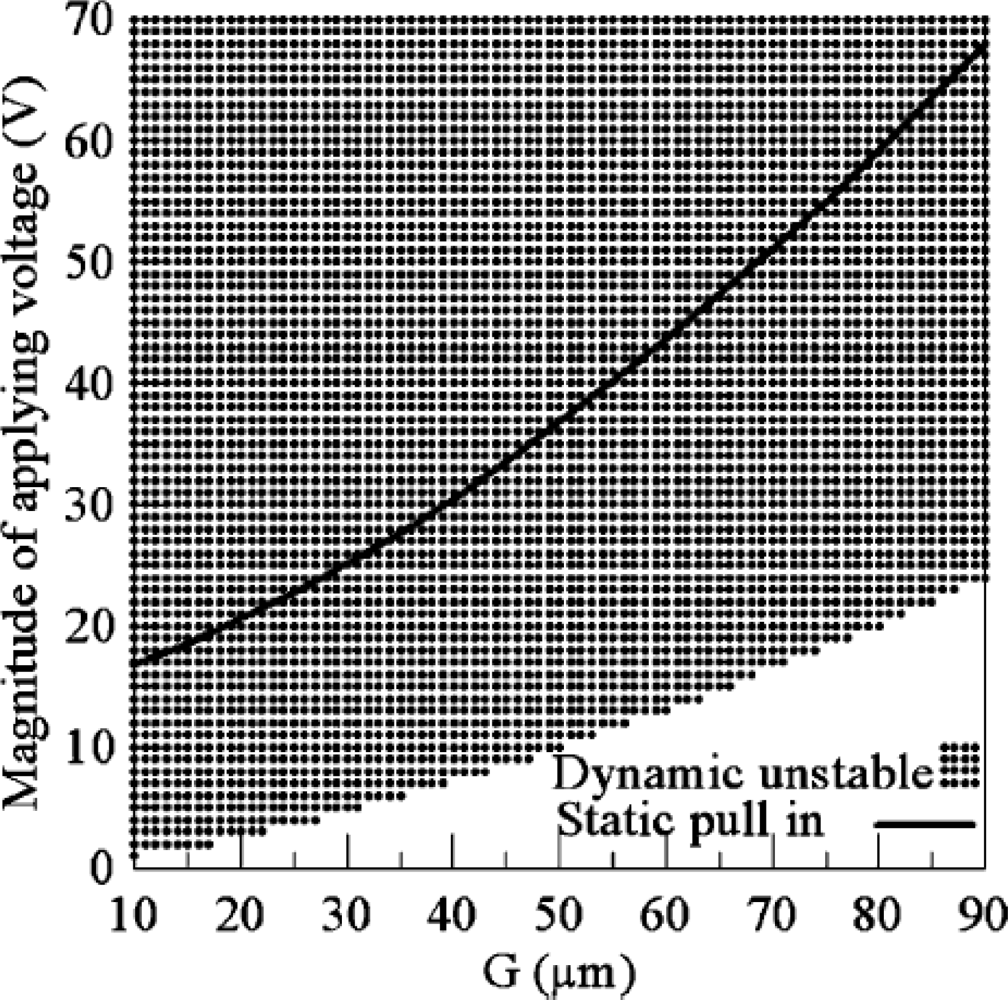
2.1. Physical Model of Quasi-Static Pull-in Voltage
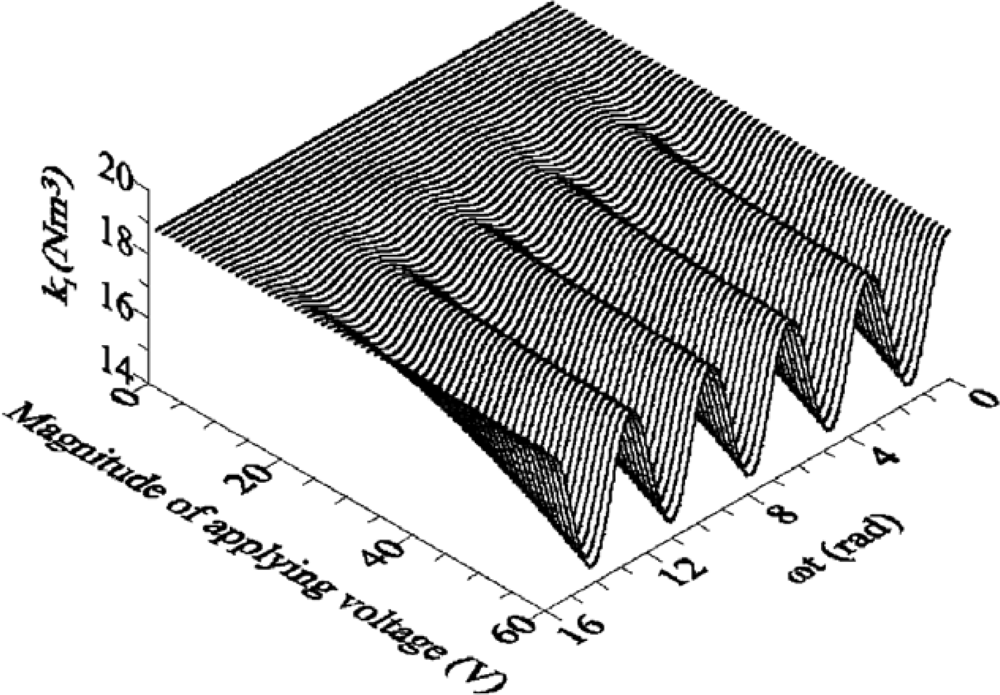
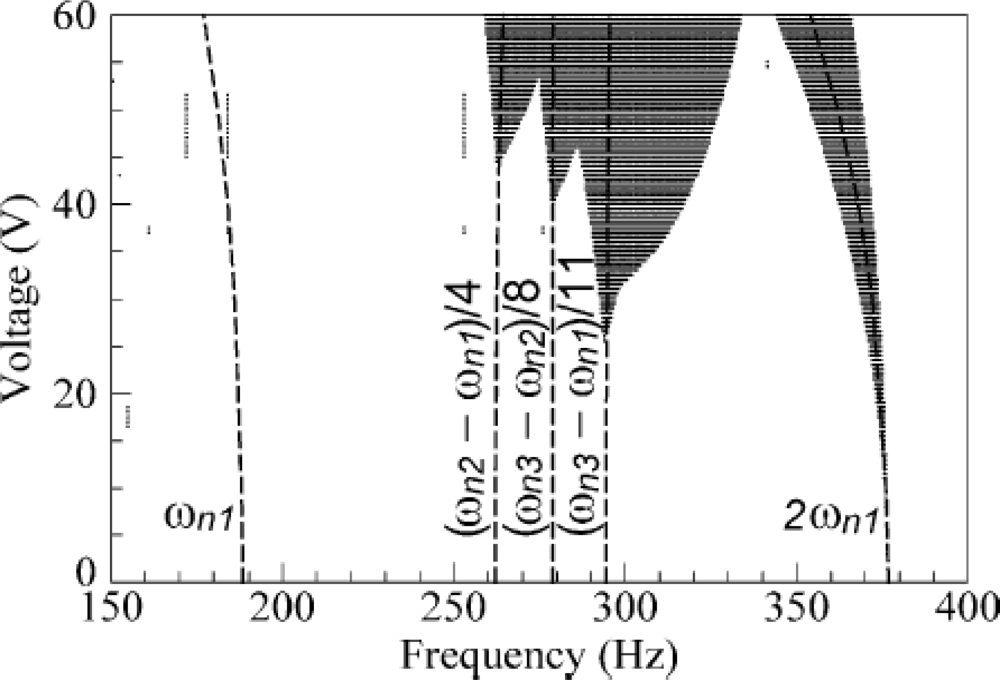
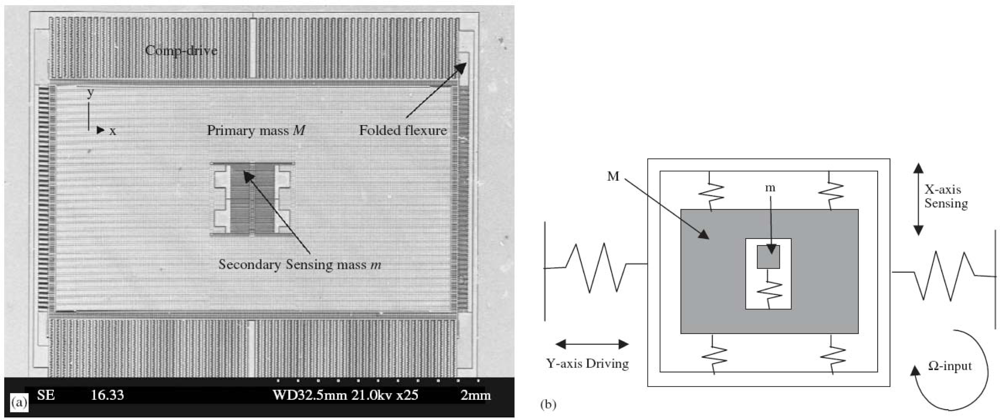
2.2. Microstructure Dynamic Response Analysis
2.3. Air Damping Effect
2.4. Numerical/CAD Methods
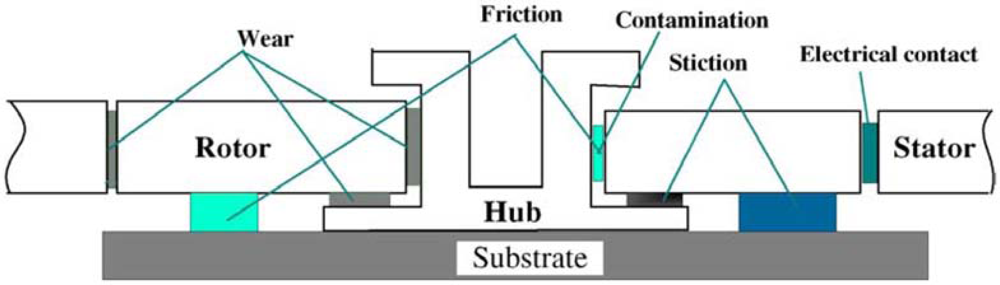
2.5. Breakdown Mechanism Analysis of Microstructures
3. Extracting the Mechanical Properties Utilizing Electromechanical Behavior of the Microstructures
4. Conclusions
Acknowledgments
References
- Akar, O.; Akin, T.; Najafi, K. A wireless batch sealed absolute capacitive pressure sensor. Sensor Actuator A-Phys 2001, 95, 29–38. [Google Scholar]
- Schonhardt, S.; Korvink, J.G.; Mohr, J.; Hollenbach, U.; Wallrabe, U. Optimization of an electromagnetic comb drive actuator. Sensor Actuator A-Phys 2009, 154, 212–217. [Google Scholar]
- Jang, L.S.; Kan, W.H.; Chen, M.K.; Chou, Y.M. Parameter extraction from BVD electrical model of PZT actuator of micropumps using time-domain measurement technique. Microfluid. Nanofluid 2009, 7, 559–568. [Google Scholar]
- Kamisuki, S.; Fujii, M.; Takekoshi, T.; Tezuka, C.; Atobe, M. A high resolution, electrostatically-driven commercial inkjet head. Proceedings of the IEEE Thirteenth Annual International Conference on MEMS, Miyazaki, Japan, 23–27 January 2000; pp. 793–798.
- Nguyen, C.T.C.; Katehi, L.P.B.; Rebeiz, G.M. Micromachined devices for wireless communications. Proc. IEEE 1998, 86, 1756–1768. [Google Scholar]
- Tilmans, H.A.C.; Legtenberg, R.; Schurer, H.; Ijntema, D.J.; Elwenspoek, M.; Fluitman, J.H.J. (Electro-) mechanical characteristics of electrostatically driven vacuum encapsulated polysilicon resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1994, 41, 4–6. [Google Scholar]
- Krylov, S. The pull-in behavior of electrostatically actuated bistable microstructures. J. Micromech. Microeng 2008, 18, 055026. [Google Scholar]
- Osterberg, P.M.; Senturia, S.D. M-TEST: A test chip for MEMS material property measurement using electrostatically actuated test structures. J. Microelectromech. Syst 1997, 6, 107–118. [Google Scholar]
- Castaner, L.M.; Senturia, S.D. Speed-energy optimization of electrostatic actuators based on pull-in. J. Microelectromech. Syst 1999, 8, 290–298. [Google Scholar]
- Castaner, L.; Rodriguez, A.; Pons, J.; Senturia, S.D. Pull-in time-energy product of electrostatic actuators: Comparison of experiments with simulation. Sensor Actuator A-Phys 2000, 83, 263–269. [Google Scholar]
- Fargas-Marques, A. Resonant pull-in condition in parallel-plate electrostatic actuators. J. Microelectromech. Syst 2007, 16, 1044. [Google Scholar]
- Krylov, S.; Seretensky, S.; Schreiber, D. Pull-in behavior and multistability of a curved microbeam actuated by a distributed electrostatic force. Proceedings of MEMS 2008: The 21st IEEE International Conference on Micro Electro Mechanical System, Tucson, AZ, USA, 13–17 January 2008; pp. 499–502.
- Krylov, S. Higher order correction of electrostatic pressure and its influence on the pull-in behavior of microstructures. J. Micromech. Microeng 2006, 16, 1382. [Google Scholar]
- Krylov, S.; Maimon, R. Pull-in dynamics of an elastic beam actuated by continuously distributed electrostatic force. J. Vibr. Acoust. Trans. ASME 2004, 126, 332–342. [Google Scholar]
- Zou, Q.; Li, Z.; Liu, L. New methods for measuring mechanical properties of thin films in micromachining: beam pull-in voltage method and long beam deflection (LBD) method. Sensor Actuator A-Phys 1995, 48, 137–143. [Google Scholar]
- Degani, O.; Socher, E.; Lipson, A.; Leitner, T.; Setter, D.J.; Kaldor, S.; Nemirovsky, Y. Pull-in study of an electrostatic torsion microactuator. J. Microelectromech. Syst 1998, 7, 373–379. [Google Scholar]
- Degani, O.; Nemirovsky, Y. Design considerations of rectangular electrostatic torsion actuators based on new analytical pull-in expressions. J. Microelectromech. Syst 2002, 11, 20–26. [Google Scholar]
- Nadal-Guardia, R.; Dehe, A.; Aigner, R.; Castaner, L.M. Current drive methods to extend the range of travel of electrostatic microactuators beyond the voltage pull-in point. J. Microelectromech. Syst 2002, 11, 255–263. [Google Scholar]
- Pamidighantam, S.; Puers, R.; Baert, K.; Tilmans, H.A.C. Pull-in voltage analysis of electrostatically actuated beam structures with fixed-fixed and fixed-free end conditions. J. Micromech. Microeng 2002, 12, 458–464. [Google Scholar]
- Wei, L.C.; Mohammad, A.B.; Kassim, N.M. Analytical modeling for determination of pull-in voltage for an electrostatic actuated MEMS cantilever beam. Proceedings of IEEE International Conference on Consumer Electronics, Sydney, Australia, June 2002; pp. 233–238.
- Xiao, Z.; Peng, W.; Wu, X.; Farmer, K.R. Pull-in study for round double-gimbaled electrostatic torsion actuators. J. Micromech. Microeng 2002, 12, 77–81. [Google Scholar]
- O’Mahony, C.; Hill, M.; Duane, R.; Mathewson, A. Analysis of electromechanical boundary effects on the pull-in of micromachined fixed-fixed beams. J. Micromech. Microeng 2003, 13, S75–S80. [Google Scholar]
- Cheng, J.; Zhe, J.; Wu, X. Analytical and finite element model pull-in study of rigid and deformable electrostatic microactuators. J. Micromech. Microeng 2004, 14, 57–68. [Google Scholar]
- Chowdhury, S.; Ahmadi, M.; Miller, W.C. A closed-form model for the pull-in voltage of electrostatically actuated cantilever beams. J. Micromech. Microeng 2005, 15, 756–763. [Google Scholar]
- Chao, P.C.P.; Chiu, C.W.; Tsai, C.Y. A novel method to predict the pull-in voltage in a closed form for micro-plates actuated by a distributed electrostatic force. J. Micromech. Microeng 2006, 16, 986–998. [Google Scholar]
- Chowdhury, S.; Ahmadi, M.; Miller, W.C. Pull-in voltage study of electrostatically actuated fixed-fixed beams using a VLSI on-chip interconnect capacitance model. J. Microelectromech. Syst 2006, 15, 639–651. [Google Scholar]
- Elata, D.; Bamberger, H. On the dynamic pull-in of electrostatic actuators with multiple degrees of freedom and multiple voltage sources. J. Microelectromech. Syst 2006, 15, 131–140. [Google Scholar]
- Gorthi, S.; Mohanty, A.; Chatterjee, A. Cantilever beam electrostatic MEMS actuators beyond pull-in. J. Micromech. Microeng 2006, 16, 1800–1810. [Google Scholar]
- Hu, Y.C. Closed form solutions for the pull-in voltage of micro curled beams subjected to electrostatic loads. J. Micromech. Microeng 2006, 16, 648–655. [Google Scholar]
- Hu, Y.C.; Lin, D.T.W.; Lee, G.D. In A closed form solution for the pull-in voltage of the micro bridge with initial stress subjected to electrostatic loads. Proceedings of 1st IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Zhuhai, China, 18–21 January 2006; pp. 757–761.
- Stefano, L.; Giuseppe, R. Control of pull-in dynamics in a nonlinear thermoelastic electrically actuated microbeam. J. Micromech. Microeng 2006, 16, 390. [Google Scholar]
- Zhang, Y.; Zhao, Y.P. Numerical and analytical study on the pull-in instability of micro-structure under electrostatic loading. Sensor Actuator A-Phys 2006, 127, 366–380. [Google Scholar]
- Gusso, A.; Delben, G.J. Influence of the Casimir force on the pull-in parameters of silicon based electrostatic torsional actuators. Sensor Actuator A-Phys 2007, 135, 792–800. [Google Scholar]
- Hu, Y.C.; Chang, P.Z.; Chuang, W.C. An approximate analytical solution to the pull-in voltage of a micro bridge with an elastic boundary. J. Micromech. Microeng 2007, 17, 1870–1876. [Google Scholar]
- Hu, Y.C.; Lee, G.D. A closed form solution for the pull-in voltage of the micro bridge. Tamkang. J. Sci. Eng 2007, 10, 147–150. [Google Scholar]
- Nayfeh, A.H. Dynamic pull-in phenomenon in MEMS resonators. Nonlinear Dyn 2007, 48, 153. [Google Scholar]
- Alsaleem, F.A.; Younis, M.I.; Ouakad, H.M. On the nonlinear resonances and dynamic pull-in of electrostatically actuated resonators. J. Micromech. Microeng 2009, 19, 045013. [Google Scholar]
- Zhang, W.M.; Meng, G.; Li, H.G. Electrostatic micromotor and its reliability. Microelectron. Reliab 2005, 45, 1230–1242. [Google Scholar]
- Quevy, E.; Bigotte, P.; Collard, D.; Buchaillot, L. Large stroke actuation of continuous membrane for adaptive optics by 3D self-assembled microplates. Sensor Actuator A-Phys 2002, 95, 183–195. [Google Scholar]
- Chan, E.K.; Dutton, R.W. Electrostatic micromechanical actuator with extended range of travel. J. Microelectromech. Syst 2000, 9, 321–328. [Google Scholar]
- Hung, E.S.; Senturia, S.D. Extending the travel range of analog-tuned electrostatic actuators. J. Microelectromech. Syst 1999, 8, 497–505. [Google Scholar]
- Legtenberg, R.; Gilbert, J.; Senturia, S.D.; Elwenspoek, M. Electrostatic curved electrode actuators. J. Microelectromech. Syst 1997, 6, 257–265. [Google Scholar]
- Ye, W.J.; Mukherjee, S. Optimal shape design of three-dimensional MEMS with applications to electrostatic comb drives. Int. J. Numer. Methods Eng 1999, 45, 175–194. [Google Scholar]
- Ye, W.J.; Mukherjee, S.; MacDonald, N.C. Optimal shape design of an electrostatic comb drive in microelectromechanical systems. J. Microelectromech. Syst 1998, 7, 16–26. [Google Scholar]
- Kuang, J.H.; Chen, C.J. The nonlinear electrostatic behavior for shaped electrode actuators. Int. J. Mech. Sci 2005, 47, 1172–1190. [Google Scholar]
- Rhoads, J.; Shaw, S.W.; Turner, K.L. Nonlinear Dynamics and Its Applications in Micro- and Nano-Resonators. Proceedings of DSCC 2008: The 2008 ASME Dynamic Systems and Control Conference, Ann Arbor, Michigan, USA, 20–22 October 2008.
- Busta, H.; Amantea, R.; Furst, D.; Chen, J.M.; Turowski, M.; Mueller, C. A MEMS shield structure for controlling pull-in forces and obtaining increased pull-in voltages. J. Micromech. Microeng 2001, 11, 720–725. [Google Scholar]
- Bao, M.H.; Yang, H.; Yin, H.; Shen, S.Q. Effects of electrostatic forces generated by the driving signal on capacitive sensing devices. Sensor Actuator A-Phys 2000, 84, 213–219. [Google Scholar]
- McCarthy, B.; Adams, G.G.; McGruer, N.E.; Potter, D. A dynamic model, including contact bounce, of an electrostatically actuated microswitch. J. Microelectromech. Syst 2002, 11, 276–283. [Google Scholar]
- Lin, R.M.; Wang, W.J. Structural dynamics of microsystems—Current state of research and future directions. Mech. Syst. Sig. Process 2006, 20, 1015–1043. [Google Scholar]
- Mahmoodi, S.N. Modeling, nonlinear dynamics, and identification of a piezoelectrically actuated microcantilever sensor. IEEE/ASME Trans. Mechatron 2008, 13, 58. [Google Scholar]
- Zhang, W.M.; Meng, G. Nonlinear dynamic analysis of electrostatically actuated resonant MEMS sensors under parametric excitation. IEEE Sens. J 2007, 7, 370–380. [Google Scholar]
- Ai, S.B.; Pelesko, J.A. Dynamics of a canonical electrostatic MEMS/NEMS system. J. Dyn. Differ. Equ 2008, 20, 609–641. [Google Scholar]
- Leus, V.; Elata, D. On the dynamic responses of electrostatic MEMS switches. J. Microelectromech. Syst 2008, 17, 236–243. [Google Scholar]
- Li, L.J.; Uttamchandani, D. Dynamic response modelling and characterization of a vertical electrothermal actuator. J. Micromech. Microeng 2009, 19, 075014. [Google Scholar]
- Fargas, M.A.; Costa, C.R.; Shkel, A.M. Modeling the electrostatic actuation of MEMS: State of the art 2005; IOC-DT-P-2005-18; Institute of Industrial and Control Engineering: Barcelona, Spain, 2005. [Google Scholar]
- Batra, R.C.; Porfiri, M.; Spinello, D. Review of modeling electrostatically actuated microelectromechanical systems. Smart Mater. Struct 2007, 16, R23–R31. [Google Scholar]
- Bao, M.; Yang, H. Squeeze film air damping in MEMS. Sensor Actuator A-Phys 2007, 136, 3–27. [Google Scholar]
- Veijola, T. Equivalent-circuit model of the squeezed gas film in a silicon accelerometer. Sensor Actuator A-Phys 1995, 48, 239. [Google Scholar]
- Wang, X.; Liu, Y.; Wang, M.; Chen, X. Study on the squeezed air-damping on MEMS parallel plates. China Mech. Eng 2005, 16, 1276–1278. [Google Scholar]
- Wang, X.; Wang, M.; Liu, Y. The Analysis of Squeezed Air-Damping on the Planar MEMS Structures; American Society of Mechanical Engineers: New York, NY, USA, 2005; pp. 811–812. [Google Scholar]
- Feng, C.; Zhao, Y.; Liu, D. Air damping in micro-beam resonators. J. Univ. Sci. Technol. Beijing 2007, 29, 841–844. [Google Scholar]
- Blech, J.J. On isothermal squeeze films. J. Lubr. Technol. (Trans. ASME) 1983, 105, 615–620. [Google Scholar]
- Lee, J.W.; Tung, R.; Raman, A.; Sumali, H.; Sullivan, J.P. Squeeze-film damping of flexible microcantilevers at low ambient pressures: Theory and experiment. J. Micromech. Microeng 2009, 19, 105029. [Google Scholar]
- Mol, L.; Rocha, L.A.; Cretu, E.; Wolffenbuttel, R.F. Squeezed film damping measurements on a parallel-plate MEMS in the free molecule regime. J. Micromech. Microeng 2009, 19, 074021. [Google Scholar]
- Suijlen, M.A.J.; Koning, J.J.; van Gils, M.A.J.; Beijerinck, H.C.W. Squeeze film damping in the free molecular flow regime with full thermal accommodation. Sensor Actuator A-Phys 2009, 156, 171–179. [Google Scholar]
- Luo, A.C.J.; Wang, F.-Y. Nonlinear dynamics of a micro-electro-mechanical system with time-varying capacitors. J. Vib. Acoust 2004, 126, 77–83. [Google Scholar]
- Liu, S.; Davidson, A.; Lin, Q. Simulation studies on nonlinear dynamics and chaos in a MEMS cantilever control system. J. Micromech. Microeng 2004, 14, 1064–1073. [Google Scholar]
- Li, G.; Aluru, N.R. Linear, nonlinear and mixed-regime analysis of electrostatic MEMS. Sensor Actuator A-Phys 2001, 91, 278–291. [Google Scholar]
- Zhang, W.M.; Meng, G. Nonlinear dynamical system of micro-cantilever under combined parametric and forcing excitations in MEMS. Sensor Actuator A-Phys 2005, 119, 291–299. [Google Scholar]
- Adams, S.G.; Bertsch, F.M.; Shaw, K.A.; MacDonald, N.C. Independent tuning of linear and nonlinear stiffness coefficients [actuators]. J. Microelectromech. Syst 1998, 7, 172–180. [Google Scholar]
- Zhang, W.H.; Baskaran, R.; Tumer, K.L. Effect of cubic nonlinearity on auto-parametrically amplified resonant MEMS mass sensor. Sensor Actuator A-Phys 2002, 102, 139–150. [Google Scholar]
- Lee, S.; Kim, J.; Moon, W.; Choi, J.; Park, I.; Bae, D. A multibody-based dynamic simulation method for electrostatic actuators. Nonlinear Dyn 2008, 54, 53–68. [Google Scholar]
- Aluru, N.R.; White, J. Efficient numerical technique for electromechanical simulation of complicated microelectromechanical structures. Sensor Actuator A-Phys 1997, 58, 1–11. [Google Scholar]
- Younis, M.I.; Abdel-Rahman, E.M.; Nayfeh, A. A reduced-order model for electrically actuated microbeam-based MEMS. J. Microelectromech. Syst 2003, 12, 672–680. [Google Scholar]
- Lee, Y.C.; McCarthy, B.; Diao, J.; Zhang, Z.; Harsh, K.F. Computer-aided design for microelectromechanical systems (MEMS). Int. J. Mater. Prod. Technol 2003, 18, 356–380. [Google Scholar]
- Senturia, S.D.; Harris, R.M.; Johnson, B.P.; Kim, S.; Nabors, K.; Shulman, M.A.; White, J.K. A computer-aided design system for microelectromechanical systems (MEMCAD). J. Microelectromech. Syst 1992, 1, 3–13. [Google Scholar]
- De, S.K.; Aluru, N.R. Full-Lagrangian schemes for dynamic analysis of electrostatic MEMS. J. Microelectromech. Syst 2004, 13, 737–758. [Google Scholar]
- Li, G.Y.; Wang, L. Influence of bonding parameters on electrostatic force in anodic wafer bonding. Thin Solid Films 2004, 462–463, 334–338. [Google Scholar]
- Hu, Y.C.; Chang, C.M.; Huang, S.C. Some design considerations on the electrostatically actuated microstructures. Sensor Actuator A-Phys 2004, 112, 155–161. [Google Scholar]
- Chowdhury, S.; Ahmadi, M.; Miller, W.C. Proceedings of 2003 International Conference on MEMS, NANO and Smart Systems, Banff, Alberta, Canada, 20–23 July 2003; pp. 297–302.
- Younis, M.I. A study of the nonlinear response of a resonant microbeam to an electric actuation. Nonlinear Dyn 2003, 31, 91. [Google Scholar]
- Spearing, S.M. Materials issues in microelectromechanical systems (MEMS). Acta. Mater 2000, 48, 179–196. [Google Scholar]
- Zhang, W.M.; Meng, G. Contact dynamics between the rotor and bearing hub in an electrostatic micromotor. Microsyst. Technol 2005, 11, 438–443. [Google Scholar]
- Srikar, V.T.; Spearing, S.M. Materials selection for microfabricated electrostatic actuators. Sensor Actuator A-Phys 2003, 102, 279–285. [Google Scholar]
- Zhang, W.M.; Meng, G. Stability, bifurcation and chaos of a high-speed rub-impact rotor system in MEMS. Sensor Actuator A-Phys 2006, 127, 163–178. [Google Scholar]
- Ghisi, A.; Fachin, F.; Mariani, S.; Zerbini, S. Multi-scale analysis of polysilicon MEMS sensors subject to accidental drops: Effect of packaging. Microelectron. Reliab 2009, 49, 340–349. [Google Scholar]
- Ghisi, A.; Kalicinski, S.; Mariani, S.; De Wolf, I.; Corigliano, A. Polysilicon MEMS accelerometers exposed to shocks: Numerical-experimental investigation. J. Micromech. Microeng 2009, 19, 035023. [Google Scholar]
- Mariani, S.; Ghisi, A.; Corigliano, A.; Zerbini, S. Multi-scale analysis of MEMS sensors subject to drop impacts. Sensers 2007, 7, 1817–1833. [Google Scholar]
- Mariani, S.; Ghisi, A.; Corigliano, A.; Zerbini, S. Modeling impact-induced failure of polysilicon MEMS: A multi-scale approach. Sensors 2009, 9, 556–567. [Google Scholar]
- Mariani, S.; Ghisi, A.; Fachin, F.; Cacchione, F.; Corigliano, A.; Zerbini, S. A three-scale FE approach to reliability analysis of MEMS sensors subject to impacts. Meccanica 2008, 43, 469–483. [Google Scholar]
- Mariani, S.; Perego, U. Extended finite element method for quasi-brittle fracture. Int. J. Numer. Meth. Eng 2003, 58, 103–126. [Google Scholar]
- Senturia, S.D. Microsystem Design; Kluwer Academic Publishers: Boston, MA, USA, 2001. [Google Scholar]
- Osterberg, P.; Yie, H.; Cai, X.; White, J.; Senturia, S. Self-consistent simulation and modeling of electrostatically deformed diaphragms. Proceedings of MEMS’94, Oiso, Japan, January 1994; pp. 28–32.
- Lishchynska, M.; Cordero, N.; Slattery, O.; O’Mahony, C. Modelling electrostatic behaviour of microcantilevers incorporating residual stress gradient and non-ideal anchors. J. Micromech. Microeng 2005, 15, S10–S14. [Google Scholar]
- Hu, Y.C.; Wei, C.S. An analytical model considering the fringing fields for calculating the pull-in voltage of micro curled cantilever beams. J. Micromech. Microeng 2007, 17, 61–67. [Google Scholar]
- Chuang, W.C.; Hu, Y.C.; Lee, C.Y.; Shih, W.P.; Chang, P.Z. Electromechanical behavior of the curled cantilever beam. J. Micro/Nanolithogr. MEMS MOEMS 2009, 8, 033020–033028. [Google Scholar]
- Nayfeh, A.H. Reduced-order models for MEMS applications. Nonlinear Dyn 2005, 41, 211. [Google Scholar]
- Clark, J.V.; Zhou, N.; Pister, K.S.J. Modified Nodal Analysis for MEMS with Multi-Energy Domains; Computational Publications: Cambridge, MA, USA, 2000; pp. 723–726. [Google Scholar]
- Wen, F.; Li, W.; Rong, H. Creation of the macromodel of equivalent circuit and IP library for clamped-clamped beam microsensor. Res. Prog. Solid State Electr 2004, 24, 68–72. [Google Scholar]
- Zhang, J.; Li, W.H. Method of system-level dynamic simulation for a MEMS cantilever based on the mechanical description. Chinese J. Sens. Actuators 2006, 19, 1376–1380. [Google Scholar]
- Yao, J.J.; MacDonald, N.C. A micromachined, single-crystal silicon, tunable resonator. J. Micromech. Microeng 1995, 5, 257. [Google Scholar]
- Veijola, T.; Mattila, T.; Jaakkola, O.; Kiihamaki, J.; Lamminmaki, T.; Oja, A.; Ruokonen, K.; Seppa, H.; Seppala, P.; Tittonen, I. Large-displacement modelling and simulation of micromechanical electrostatically driven resonators using the harmonic balance method. IEEE MTT-S Int. Microwave Symp. Dig 2000, 1, 99–102. [Google Scholar]
- Gerlachmeyer, U.E. Micromachined capacitive accelerometer. Sensor Actuator A-Phys 1991, 27, 555–558. [Google Scholar]
- Bergqvist, J.; Gobet, J. Capacitive microphone with a surface micromachined backplate using electroplating technology. J. Microelectromech. Syst 1994, 3, 69–75. [Google Scholar]
- Andrews, M.; Harris, I.; Turner, G. A comparison of squeeze-film theory with measurements on a microstructure. Sensor Actuator A-Phys 1993, 36, 79–87. [Google Scholar]
- Darling, R.B.; Hivick, C.; Xu, J.Y. Compact analytical modeling of squeeze film damping with arbitrary venting conditions using a Green’s function approach. Sensor Actuator A-Phys 1998, 70, 32–41. [Google Scholar]
- Schaaf, S.A.; Chambr Paul, L. Flow of Rarefied Gases; Princeton University Press: Princeton, NJ, USA, 1961. [Google Scholar]
- Li, B.Q.; Wu, H.Y.; Zhu, C.C.; Liu, J.H. The theoretical analysis on damping characteristics of resonant microbeam in vacuum. Sensor Actuator A-Phys 1999, 77, 191–194. [Google Scholar]
- Yang, Y.J.; Kamon, M.; Rabinovich, V.L.; Ghaddar, C.; Deshpande, M.; Greiner, K.; Gilbert, J.R. Modeling Gas Damping and Spring Phenomena in MEMS with Frequency Dependent Macro-Models; Institute of Electrical and Electronics Engineers Inc: Interlaken, Switzerland, 2001; pp. 365–368. [Google Scholar]
- Gao, R.; Wang, X.; Wang, M.; Yu, M.; Xie, M. Nonlinear dynamics of lateral micro-resonator including viscous air damping. Chinese J. Mech. Eng 2007, 20, 75–78. [Google Scholar]
- Zhu, Y.M.; Jia, J.Y.; Fan, K.Q. Study on the air damp of the plate movement in the MEMS devices. J. Univ. Electr. Sci. Technol. China 2007, 36, 965–968. [Google Scholar]
- Hung, E.S.; Yang, Y.J.; Senturia, S.D. Low-order models for fast dynamical simulation of MEMS microstructures. Proceedings of the IEEE International Conference on Solid State Sensors and Actuators, Chicago, IL, USA, 16–19 June 1997; pp. 1101–1104.
- Stewart, J.T. Finite element modeling of resonant microelectromechanical structures for sensing applications. Proceedings of Micromachined Devices and Components, Austin, TX, USA, 23–24 October 1995; pp. 643–646.
- Swart, N.R.; Bart, S.F.; Zaman, M.H.; Mariappan, M.; Gilbert, J.R.; Murphy, D. AutoMM: Automatic generation of dynamic macromodels for MEMS devices. Proceedings IEEE MEMS Workshop, Heidelberg, Germany, 25–29 January 1998; pp. 178–183.
- Mukherjee, T. Emerging simulation approaches for micromachined devices. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst 2000, 19, 1572. [Google Scholar]
- Zhang, W.M.; Meng, G.; Chen, D. Stability, nonlinearity and reliability of electrostatically actuated MEMS devices. Sensors 2007, 7, 760–796. [Google Scholar]
- van Spengen, W.M.; Puers, R.; De Wolf, I. A physical model to predict stiction in MEMS. J. Micromech. Microeng 2002, 12, 702–713. [Google Scholar]
- Lee, S.; Ramadoss, R.; Buck, M.; Bright, V.M.; Gupta, K.C.; Lee, Y.C. Reliability testing of flexible printed circuit-based RF MEMS capacitive switches. Microelectron. Reliab 2004, 44, 245–250. [Google Scholar]
- Wibbeler, J.; Pfeifer, G.; Hietschold, M. Parasitic charging of dielectric surfaces in capacitive microelectromechanical systems (MEMS). Sensor Actuator A-Phys 1998, 71, 74–80. [Google Scholar]
- Knudson, A.R.; Buchner, S.; McDonald, P.; Stapor, W.J.; Campbell, A.B.; Grabowski, K.S.; Knies, D.L.; Lewis, S.; Zhao, Y. The effects of radiation on MEMS accelerometers. IEEE Trans. Nucl. Sci 1996, 43, 3122–3126. [Google Scholar]
- Gabriel, K.J.; Behi, F.; Mahadevan, R.; Mehregany, M. In situ friction and wear measurements in integrated polysilicon mechanisms. Sensor Actuator A-Phys 1990, 21, 184–188. [Google Scholar]
- Tanner, D.M.; Miller, W.M.; Peterson, K.A.; Dugger, M.T.; Eaton, W.P.; Irwin, L.W.; Senft, D.C.; Smith, N.F.; Tangyunyong, P.; Miller, S.L. Frequency dependence of the lifetime of a surface micromachined microengine driving a load. Microelectron. Reliab 1999, 39, 401–414. [Google Scholar]
- Kahn, H.; Tayebi, N.; Ballarini, R.; Mullen, R.L.; Heuer, A.H. Fracture toughness of polysilicon MEMS devices. Sensor Actuator A-Phys 2000, 82, 274–280. [Google Scholar]
- Komvopoulos, K. Surface engineering and microtribology for microelectromechanical systems. Wear 1996, 200, 305–327. [Google Scholar]
- Bart, S.F.; Mehregany, M.; Tavrow, L.S.; Lang, J.H.; Senturia, S.D. Electric micromotor dynamics. IEEE Trans. Electron Devices 1992, 39, 566–575. [Google Scholar]
- Tai, Y.C.; Muller, R.S. Frictional study of IC-processed micromotors. Sensor Actuator A-Phys 1990, 21, 180–183. [Google Scholar]
- Ren, S.L.; Yang, S.R.; Wang, J.Q.; Liu, W.M.; Zhao, Y.P. Preparation and tribological studies of stearic acid self-assembled monolayers on polymer-coated silicon surface. Chem. Mater 2004, 16, 428–434. [Google Scholar]
- Hu, Y.C.; Huang, P.Y. Wafer-level microelectromechanical system structural material test by electrical signal before pull-in. Appl. Phys. Lett 2007, 90, 121908. [Google Scholar]
- Hu, Y.C.; Shih, W.P.; Lee, G.D. A method for mechanical characterization of capacitive devices at wafer level via detecting the pull-in voltages of two test bridges with different lengths. J. Micromech. Microeng 2007, 17, 1099–1106. [Google Scholar]
- Hu, Y.C.; Shih, W.P.; Lee, G.D. A method for mechanical characterization of capacitive devices at wafer level via detecting the pull-in voltages of two test bridges with different lengths. J. Micromech. Microeng 2007, 17, 1099–1106. [Google Scholar]
- Gorman, D.J. Free Vibration Analysis of Beams and Shafts; John Wiley & Sons: Hoboken, NJ, USA, 1975. [Google Scholar]

© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chuang, W.-C.; Lee, H.-L.; Chang, P.-Z.; Hu, Y.-C. Review on the Modeling of Electrostatic MEMS. Sensors 2010, 10, 6149-6171. https://doi.org/10.3390/s100606149
Chuang W-C, Lee H-L, Chang P-Z, Hu Y-C. Review on the Modeling of Electrostatic MEMS. Sensors. 2010; 10(6):6149-6171. https://doi.org/10.3390/s100606149
Chicago/Turabian StyleChuang, Wan-Chun, Hsin-Li Lee, Pei-Zen Chang, and Yuh-Chung Hu. 2010. "Review on the Modeling of Electrostatic MEMS" Sensors 10, no. 6: 6149-6171. https://doi.org/10.3390/s100606149
APA StyleChuang, W.-C., Lee, H.-L., Chang, P.-Z., & Hu, Y.-C. (2010). Review on the Modeling of Electrostatic MEMS. Sensors, 10(6), 6149-6171. https://doi.org/10.3390/s100606149




