Correlation of Dual Colour Single Particle Trajectories for Improved Detection and Analysis of Interactions in Living Cells
Abstract
:1. Introduction
2. Theory
2.2. Correlation Threshold
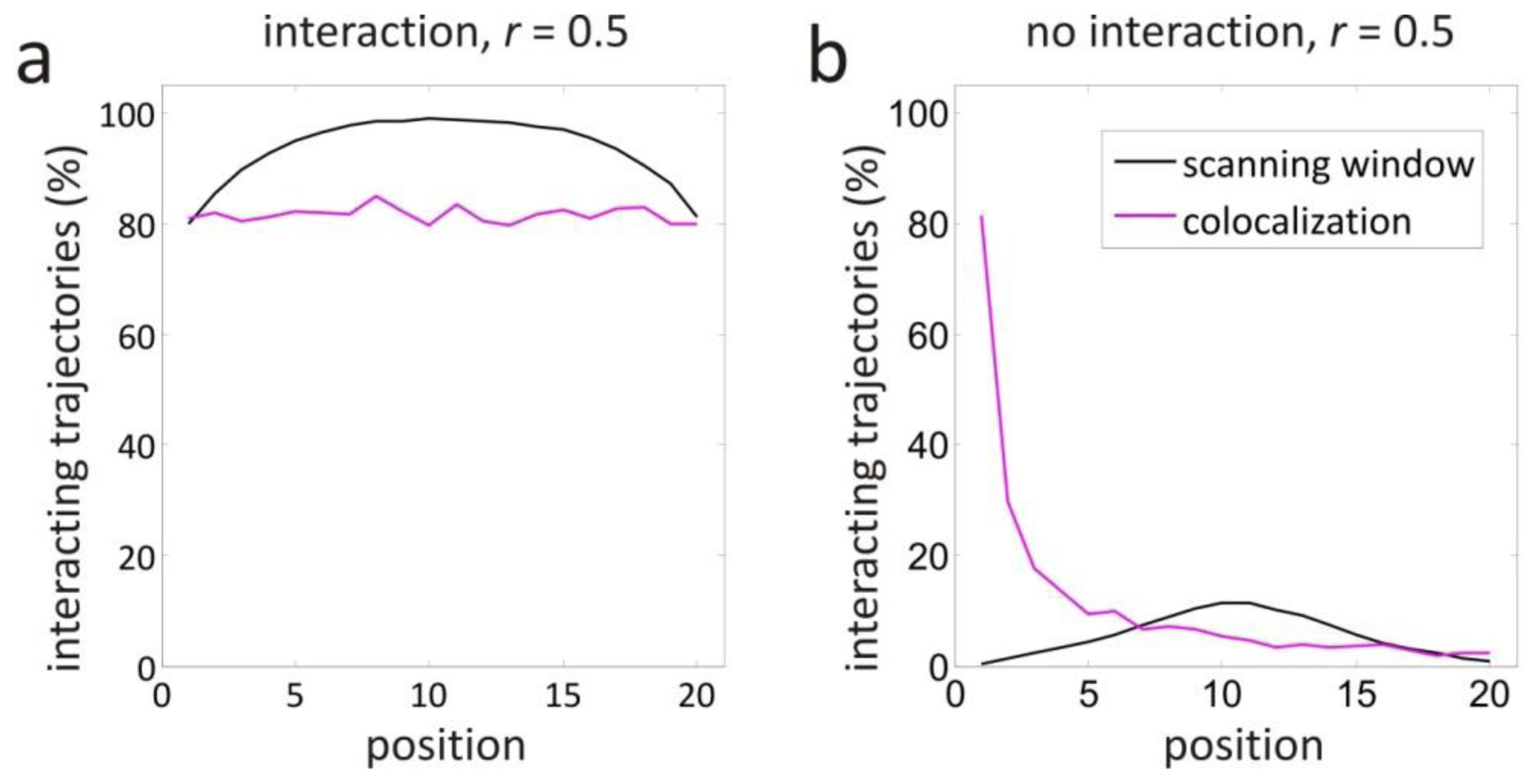
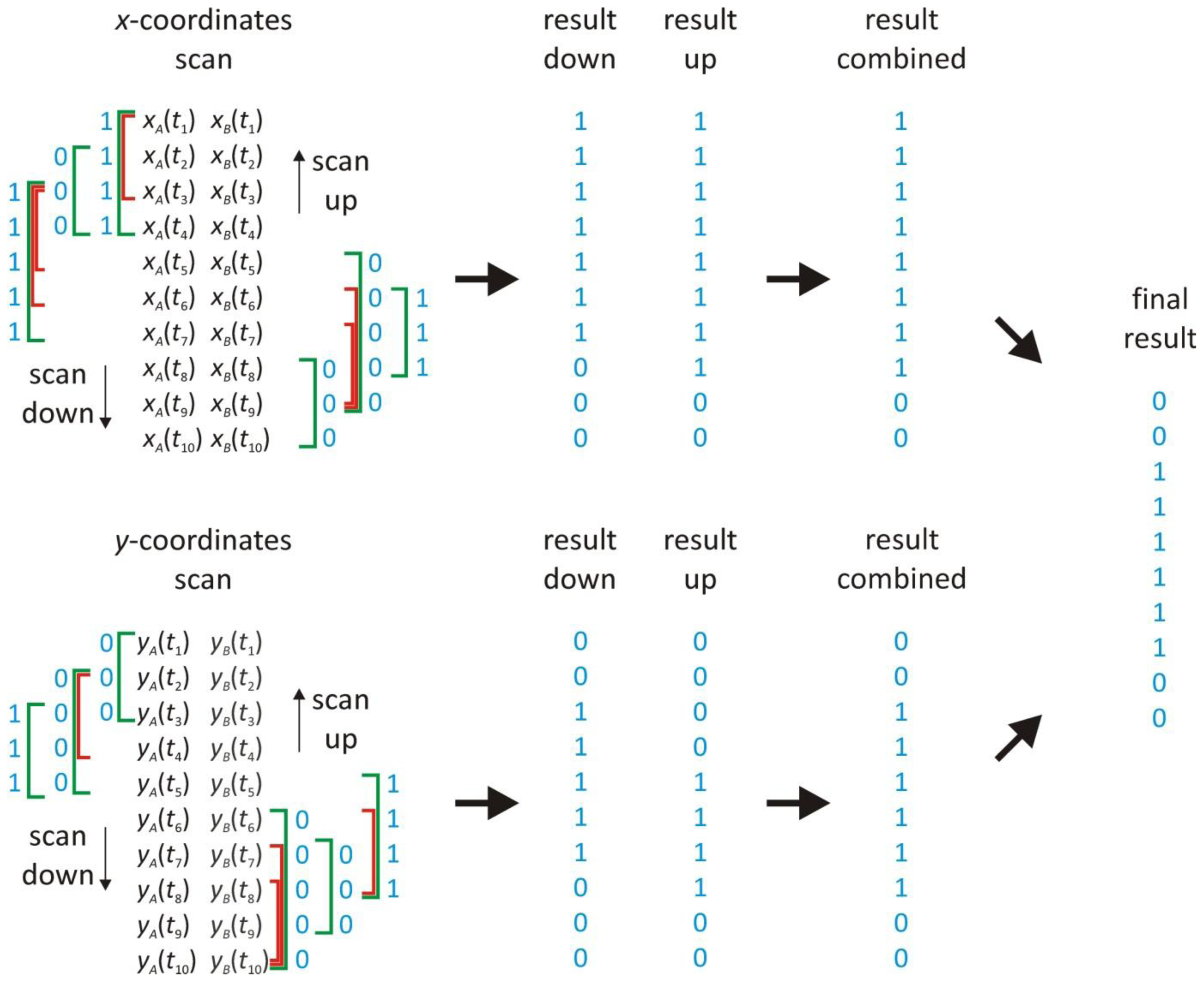
2.3. Scanning Window Concept
2.4. Numerical Determination of ρmin and P
2.5. Scanning Window Method
3. Results
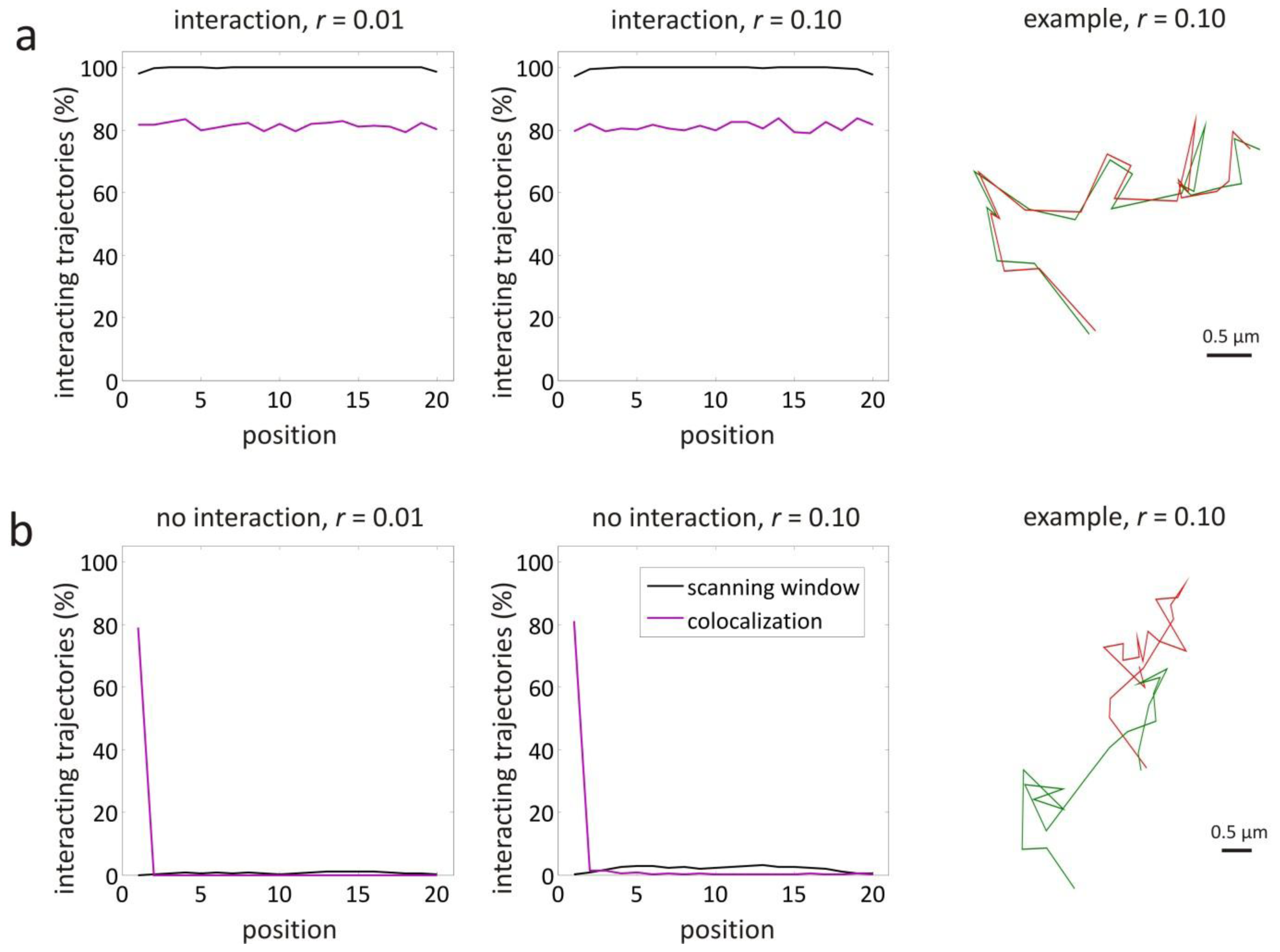
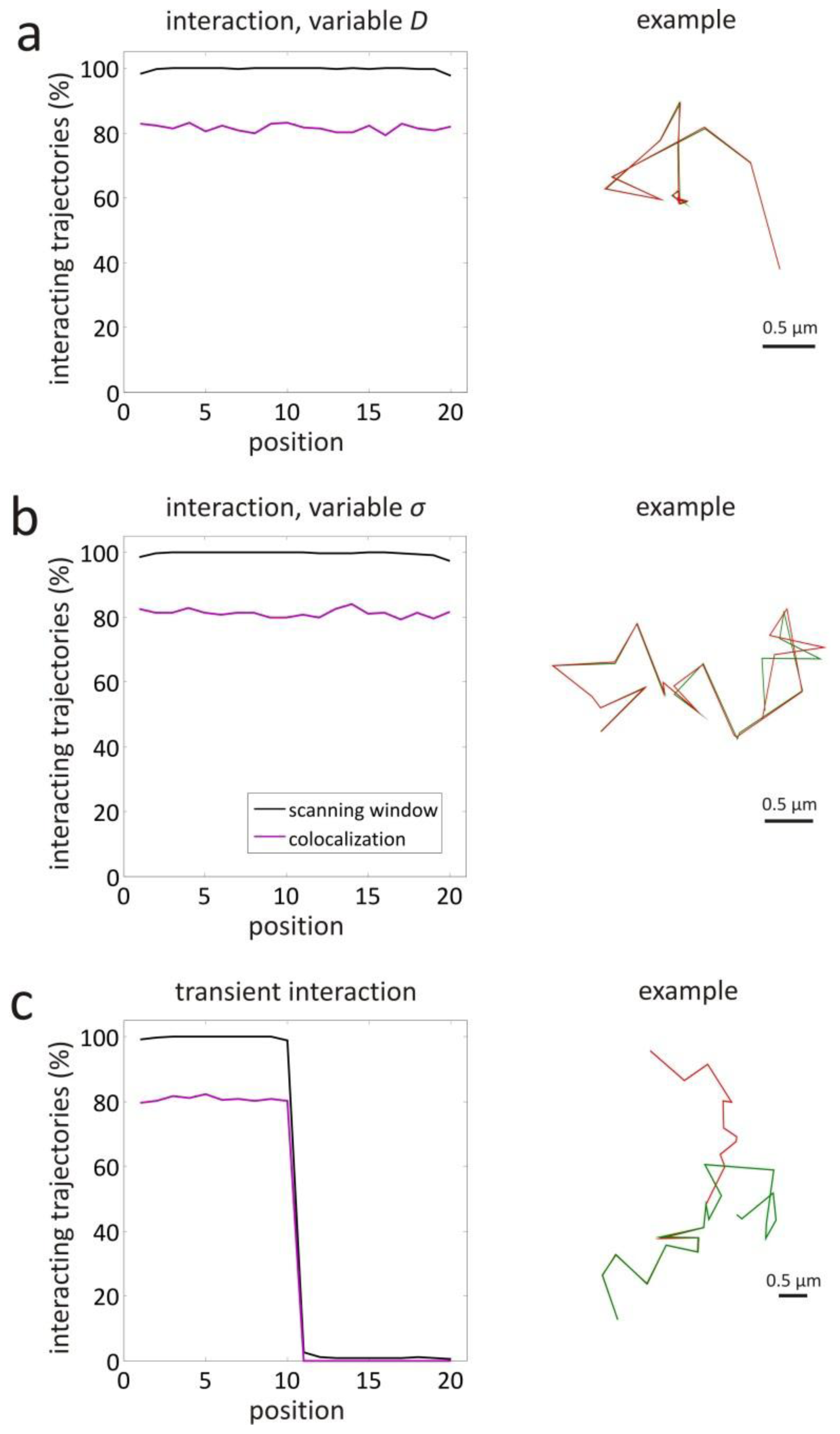
3.1. Validation by Simulations
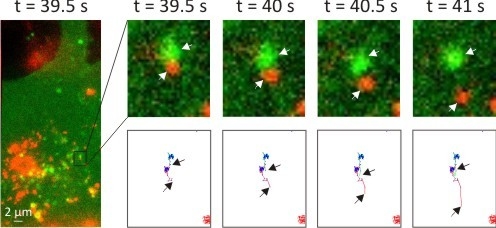
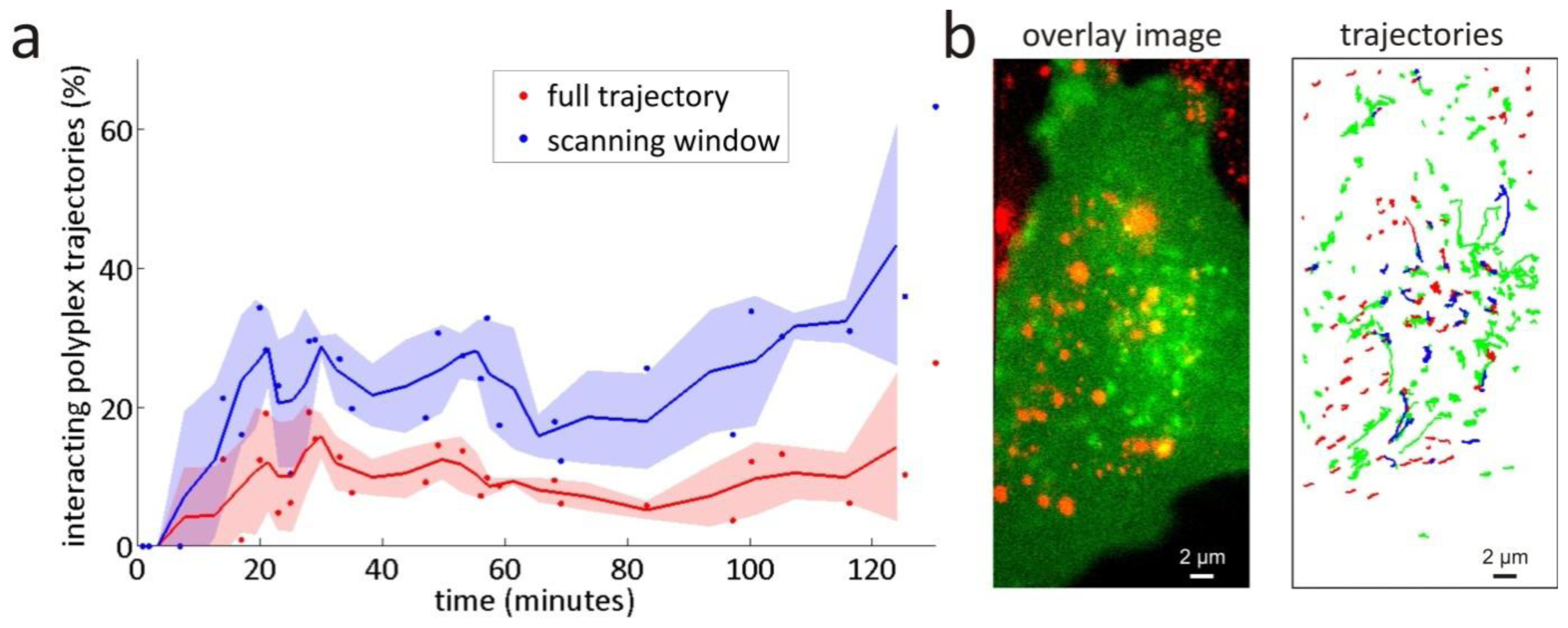
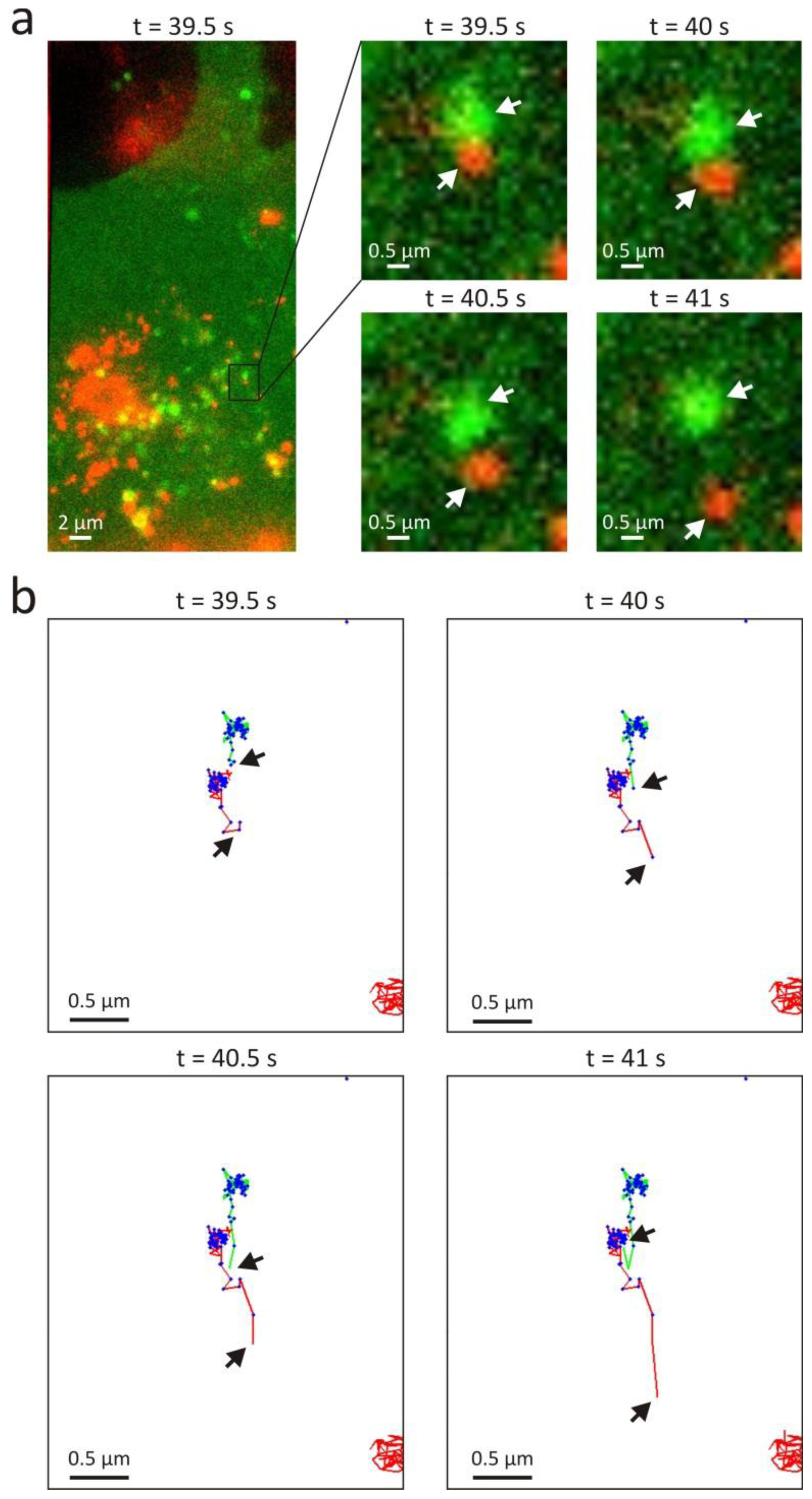
3.2. Intracellular Trafficking of Nanomedicines
4. Discussion
5. Materials and Methods
5.1. Validations Simulations
5.2. Live-Cell Sample Preparation
5.3. Experimental Set-Up
5.4. SPT Experiments and Analysis
6. Conclusions
Acknowledgments
Appendix
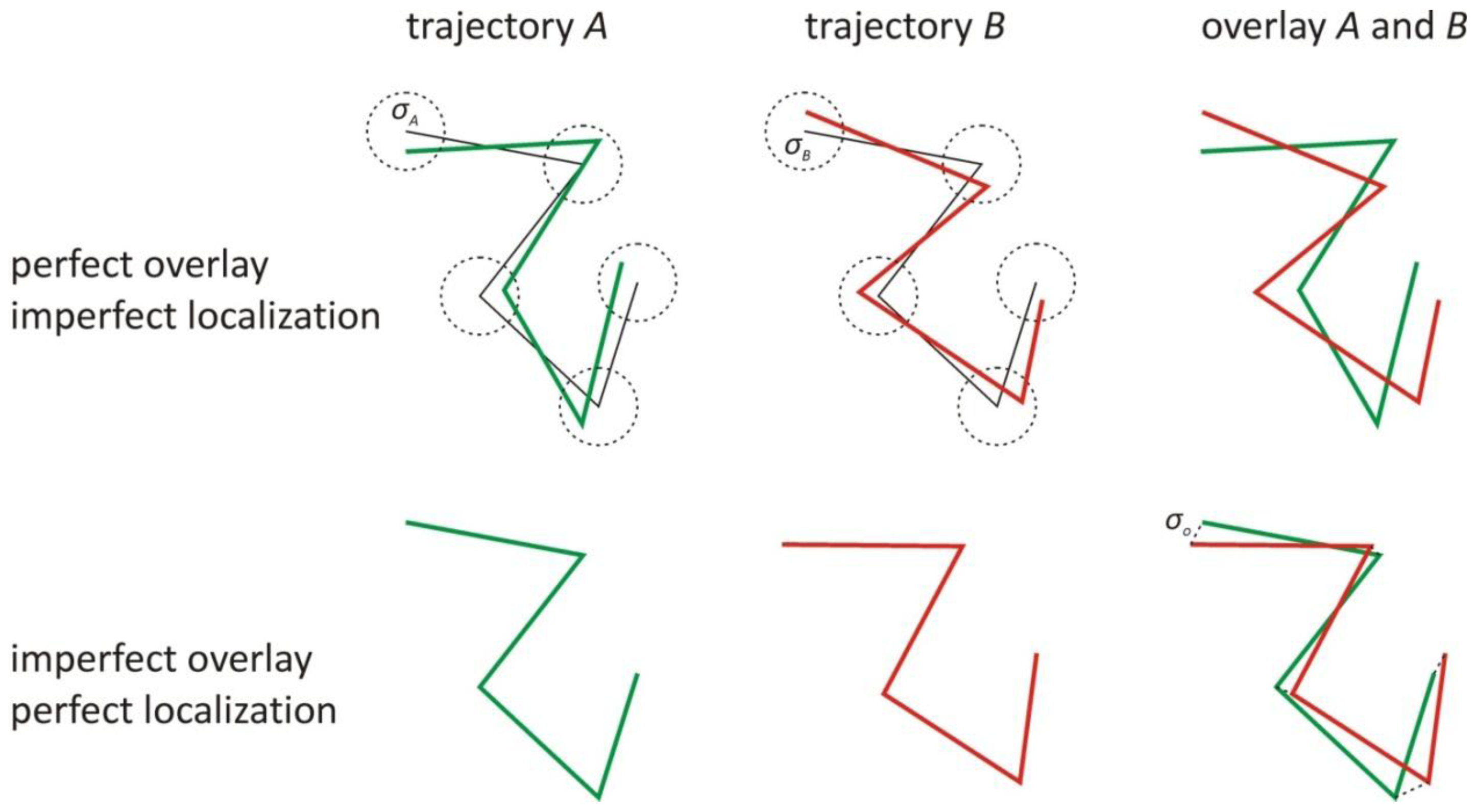
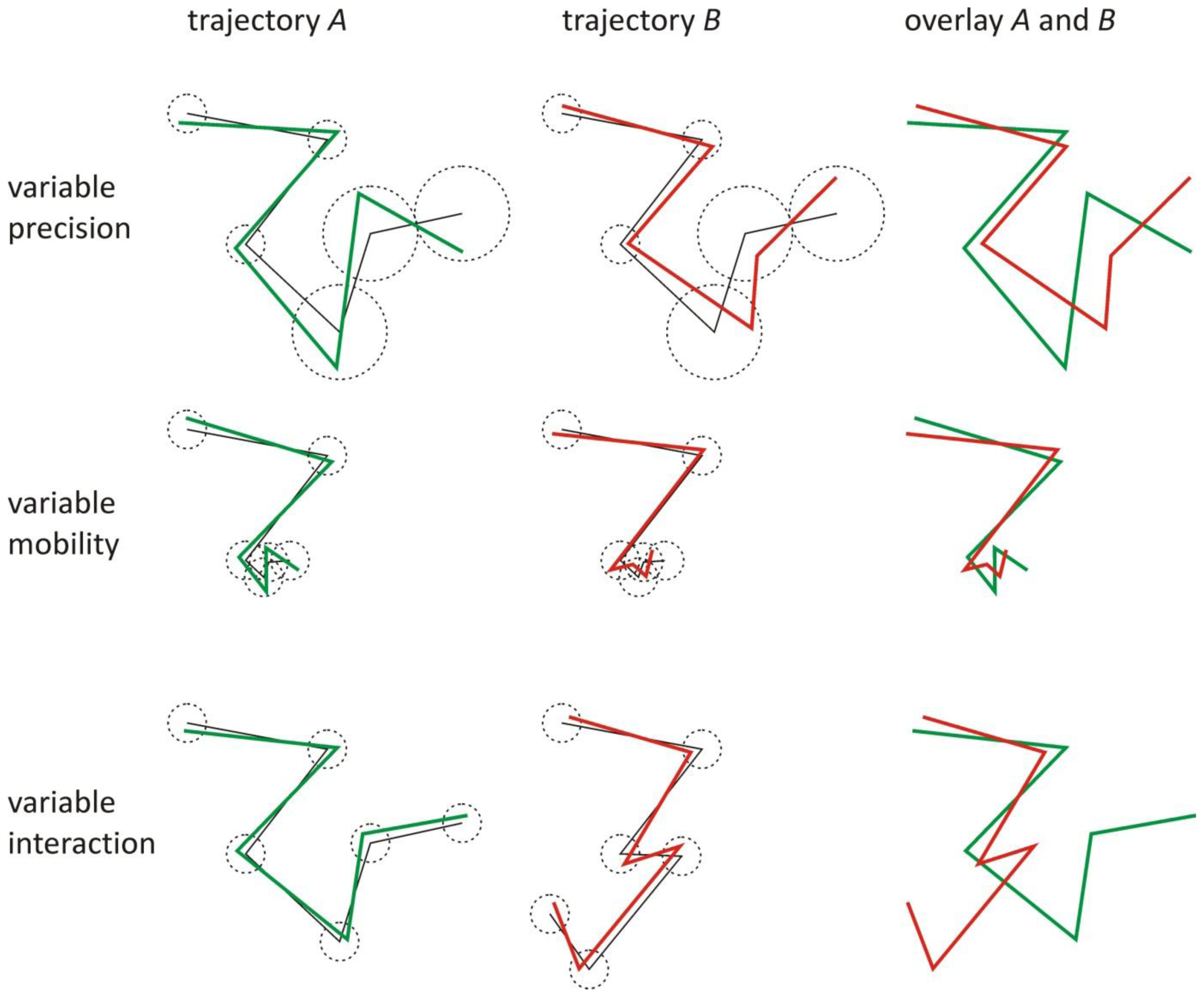
1. The Effect of the Localization and Overlay Precision on the Correlation
2. Correlation between Trajectories of Interacting Objects
3. The Influence of a High Localization Error
4. Negative Control Experiment

Conflict of Interest
References
- Remaut, K.; Sanders, N.N.; de Geest, B.G.; Braeckmans, K.; Demeester, J.; de Smedt, S.C. Nucleic acid delivery: Where material sciences and bio-sciences meet. Mater. Sci. Eng. R-Rep 2007, 58, 117–161. [Google Scholar]
- Bolte, S.; Cordelieres, F.P. A guided tour into subcellular colocalization analysis in light microscopy. J. Microsc 2006, 224, 213–232. [Google Scholar]
- Comeau, J.W.D.; Costantino, S.; Wiseman, P.W. A guide to accurate fluorescence microscopy colocalization measurements. Biophys. J 2006, 91, 4611–4622. [Google Scholar]
- Dunn, K.W.; Kamocka, M.M.; McDonald, J.H. A practical guide to evaluating colocalization in biological microscopy. Am. J. Physiol. Cell Physiol 2011, 300, C723–C742. [Google Scholar]
- Zinchuk, V.; Zinchuk, O.; Okada, T. Quantitative colocalization analysis of multicolor confocal immunofluorescence microscopy images: Pushing pixels to explore biological phenomena. Acta Histochem. Cytochem 2007, 40, 101–111. [Google Scholar]
- Adler, J.; Pagakis, S.N.; Parmryd, I. Replicate-based noise corrected correlation for accurate measurements of colocalization. J. Microsc 2008, 230, 121–133. [Google Scholar]
- Costes, S.V.; Daelemans, D.; Cho, E.H.; Dobbin, Z.; Pavlakis, G.; Lockett, S. Automatic and quantitative measurement of protein-protein colocalization in live cells. Biophys. J 2004, 86, 3993–4003. [Google Scholar]
- Demandolx, D.; Davoust, J. Multicolour analysis and local image correlation in confocal microscopy. J. Microsc 1997, 185, 21–36. [Google Scholar]
- Fletcher, P.A.; Scriven, D.R.L.; Schulson, M.N.; Moore, E.D.W. Multi-image colocalization and its statistical significance. Biophys. J 2010, 99, 1996–2005. [Google Scholar]
- Li, Q.; Lau, A.; Morris, T.J.; Guo, L.; Fordyce, C.B.; Stanley, E.F. A syntaxin 1, G alpha(o), and N-type calcium channel complex at a presynaptic nerve terminal: Analysis by quantitative immunocolocalization. J. Neurosci 2004, 24, 4070–4081. [Google Scholar]
- Manders, E.M.M.; Verbeek, F.J.; Aten, J.A. Measurement of colocalization of objects in dual-color confocal images. J. Microsc 1993, 169, 375–382. [Google Scholar]
- Jares-Erijman, E.A.; Jovin, T.M. FRET imaging. Nat. Biotechnol 2003, 21, 1387–1395. [Google Scholar]
- Agrawal, A.; Deo, R.; Wang, G.D.; Wang, M.D.; Nie, S.M. Nanometer-scale mapping and single-molecule detection with color-coded nanoparticle probes. Proc. Natl. Acad. Sci. USA 2008, 105, 3298–3303. [Google Scholar]
- Lacoste, T.D.; Michalet, X.; Pinaud, F.; Chemla, D.S.; Alivisatos, A.P.; Weiss, S. Ultrahigh-resolution multicolor colocalization of single fluorescent probes. Proc. Natl. Acad. Sci. USA 2000, 97, 9461–9466. [Google Scholar]
- Malkusch, S.; Endesfelder, U.; Mondry, J.; Gelleri, M.; Verveer, P.J.; Heilemann, M. Coordinate-based colocalization analysis of single-molecule localization microscopy data. Histochem. Cell Biol 2012, 137, 1–10. [Google Scholar]
- Morrison, I.E.G.; Karakikes, I.; Barber, R.E.; Fernandez, N.; Cherry, R.J. Detecting and quantifying colocalization of cell surface molecules by single particle fluorescence imaging. Biophys. J 2003, 85, 4110–4121. [Google Scholar]
- Pertsinidis, A.; Zhang, Y.X.; Chu, S. Subnanometre single-molecule localization, registration and distance measurements. Nature 2010, 466, 647–651. [Google Scholar]
- Trabesinger, W.; Hecht, B.; Wild, U.P.; Schutz, G.J.; Schindler, H.; Schmidt, T. Statistical analysis of single-molecule colocalization assays. Anal. Chem 2001, 73, 1100–1105. [Google Scholar]
- Lachmanovich, E.; Shvartsman, D.E.; Malka, Y.; Botvin, C.; Henis, Y.I.; Weiss, A.M. Co-localization analysis of complex formation among membrane proteins by computerized fluorescence microscopy: Application to immunofluorescence co-patching studies. J. Microsc 2003, 212, 122–131. [Google Scholar]
- Ober, R.J.; Ram, S.; Ward, E.S. Localization accuracy in single-molecule microscopy. Biophys. J 2004, 86, 1185–1200. [Google Scholar]
- Thompson, R.E.; Larson, D.R.; Webb, W.W. Precise nanometer localization analysis for individual fluorescent probes. Biophys. J 2002, 82, 2775–2783. [Google Scholar]
- Brown, C.M.; Petersen, N.O. An image correlation analysis of the distribution of clathrin associated adaptor protein (AP-2) at the plasma membrane. J. Cell. Sci 1998, 111, 271–281. [Google Scholar]
- Wiseman, P.W.; Squier, J.A.; Ellisman, M.H.; Wilson, K.R. Two-photon image correlation spectroscopy and image cross-correlation spectroscopy. J. Microsc 2000, 200, 14–25. [Google Scholar]
- Churchman, L.S.; Okten, Z.; Rock, R.S.; Dawson, J.F.; Spudich, J.A. Single molecule high-resolution colocalization of Cy3 and Cy5 attached to macromolecules measures intramolecular distances through time. Proc. Natl. Acad. Sci. USA 2005, 102, 1419–1423. [Google Scholar]
- Dunne, P.D.; Fernandes, R.A.; McColl, J.; Yoon, J.W.; James, J.R.; Davis, S.J.; Klenerman, D. DySCo: Quantitating associations of membrane proteins using two-color single-molecule tracking. Biophys. J 2009, 97, L5–L7. [Google Scholar]
- Koyama-Honda, I.; Ritchie, K.; Fujiwara, T.; Iino, R.; Murakoshi, H.; Kasai, R.S.; Kusumi, A. Fluorescence imaging for monitoring the colocalization of two single molecules in living cells. Biophys. J 2005, 88, 2126–2136. [Google Scholar]
- Dupont, A.; Stirnnagel, K.; Lindemann, D.; Lamb, D.C. Tracking image correlation: Combining single-particle tracking and image correlation. Biophys. J 2013, 104, 2373–2382. [Google Scholar]
- Vercauteren, D.; Deschout, H.; Remaut, K.; Engbersen, J.F.J.; Jones, A.T.; Demeester, J.; de Smedt, S.C.; Braeckmans, K. Dynamic colocalization microscopy to characterize intracellular trafficking of nanomedicines. ACS Nano 2011, 5, 7874–7884. [Google Scholar]
- Peeters, L.; Sanders, N.N.; Jones, A.; Demeester, J.; de Smedt, S.C. Post-pegylated lipoplexes are promising vehicles for gene delivery in RPE cells. J. Control Release 2007, 121, 208–217. [Google Scholar]
- Bausinger, R.; von Gersdorff, K.; Braeckmans, K.; Ogris, M.; Wagner, E.; Brauchle, C.; Zumbusch, A. The transport of nanosized gene carriers unraveled by live-cell imaging. Angew. Chem. Int. Ed 2006, 45, 1568–1572. [Google Scholar]
- De Bruin, K.; Ruthardt, N.; von Gersdorff, K.; Bausinger, R.; Wagner, E.; Ogris, M.; Brauchle, C. Cellular dynamics of EGF receptor-targeted synthetic viruses. Mol. Ther 2007, 15, 1297–1305. [Google Scholar]
- Helmuth, J.A.; Burckhardt, C.J.; Koumoutsakos, P.; Greber, U.F.; Sbalzarini, I.F. A novel supervised trajectory segmentation algorithm identifies distinct types of human adenovirus motion in host cells. J. Struct. Biol 2007, 159, 347–358. [Google Scholar]
- Braeckmans, K.; Vercauteren, D.; Demeester, J.; de Smedt, S.C. Single Particle Tracking. In Nanoscopy and Multidimensional Optical Fluorescence Microscopy; Diaspro, A., Ed.; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2010. [Google Scholar]
- Deschout, H.; Neyts, K.; Braeckmans, K. The influence of movement on the localization precision of sub-resolution particles in fluorescence microscopy. J. Biophotonics 2012, 5, 97–109. [Google Scholar]
- Janesick, J.R. Scientific Charge-Coupled Devices; SPIE Press: Bellingham, WA, USA; p. 2001.
- Savin, T.; Doyle, P.S. Static and dynamic errors in particle tracking microrheology. Biophys. J 2005, 88, 623–638. [Google Scholar]
- Saxton, M.J.; Jacobson, K. Single-particle tracking: Applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct 1997, 26, 373–399. [Google Scholar]
| Simulated values of the probability P | ||||||
|---|---|---|---|---|---|---|
| w = 3 | w = 4 | w = 5 | w = 6 | … | w = 200 | |
| r= 0.01 | 0.97177 | 0.99992 | 1 | 1 | 1 | |
| r= 0.02 | 0.90433 | 0.99872 | 1 | 1 | 1 | |
| r= 0.03 | 0.82096 | 0.99532 | 0.99980 | 1 | 1 | |
| r= 0.04 | 0.73582 | 0.99020 | 0.99950 | 1 | 1 | |
| r= 0.05 | 0.65341 | 0.98112 | 0.99815 | 0.99982 | 1 | |
| ⋮ | ||||||
| r= 1.00 | 0.04623 | 0.07992 | 0.12200 | 0.19284 | 1 | |
| Simulated values of the correlation threshold ρmin | ||||||
|---|---|---|---|---|---|---|
| w = 3 | w = 4 | w = 5 | w = 6 | … | w = 200 | |
| r= 0.01 | 0.99693 | 0.95043 | 0.97095 | 0.99242 | 0.99998 | |
| r= 0.02 | 0.99692 | 0.95013 | 0.88554 | 0.89819 | 0.9999 | |
| r= 0.03 | 0.99692 | 0.95003 | 0.88114 | 0.91113 | 0.99972 | |
| r= 0.04 | 0.99692 | 0.95004 | 0.88418 | 0.87069 | 0.99965 | |
| r= 0.05 | 0.99692 | 0.95001 | 0.87854 | 0.81552 | 0.99925 | |
| ⋮ | ||||||
| r= 1.00 | 0.99693 | 0.95002 | 0.87836 | 0.81141 | 0.77525 | |
| Trajectory parameters used for the validation simulations | |||||
|---|---|---|---|---|---|
| Situation | Position | Interaction | D (μm2/s) | S (μm) | σ (nm) |
| interaction, r = 0.01 | 1–20 | yes | 1 | 0.447 | 4.47 |
| interaction, r = 0.10 | 1–20 | yes | 1 | 0.447 | 44.7 |
| no interaction, r = 0.01 | 1–20 | no | 1 | 0.447 | 4.47 |
| no interaction, r = 0.10 | 1–20 | no | 1 | 0.447 | 44.7 |
| interaction, variable D | 1–10 | yes | 1 | 0.447 | 4.47 |
| 11–20 | yes | 0.01 | 0.0447 | 4.47 | |
| interaction, variable σ | 1–10 | yes | 1 | 0.447 | 4.47 |
| 11–20 | yes | 1 | 0.447 | 44.7 | |
| variable interaction | 1–10 | yes | 1 | 0.447 | 4.47 |
| 11–20 | no | 1 | 0.447 | 4.47 | |
Supplementary Files
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Deschout, H.; Martens, T.; Vercauteren, D.; Remaut, K.; Demeester, J.; De Smedt, S.C.; Neyts, K.; Braeckmans, K. Correlation of Dual Colour Single Particle Trajectories for Improved Detection and Analysis of Interactions in Living Cells. Int. J. Mol. Sci. 2013, 14, 16485-16514. https://doi.org/10.3390/ijms140816485
Deschout H, Martens T, Vercauteren D, Remaut K, Demeester J, De Smedt SC, Neyts K, Braeckmans K. Correlation of Dual Colour Single Particle Trajectories for Improved Detection and Analysis of Interactions in Living Cells. International Journal of Molecular Sciences. 2013; 14(8):16485-16514. https://doi.org/10.3390/ijms140816485
Chicago/Turabian StyleDeschout, Hendrik, Thomas Martens, Dries Vercauteren, Katrien Remaut, Jo Demeester, Stefaan C. De Smedt, Kristiaan Neyts, and Kevin Braeckmans. 2013. "Correlation of Dual Colour Single Particle Trajectories for Improved Detection and Analysis of Interactions in Living Cells" International Journal of Molecular Sciences 14, no. 8: 16485-16514. https://doi.org/10.3390/ijms140816485