- Article
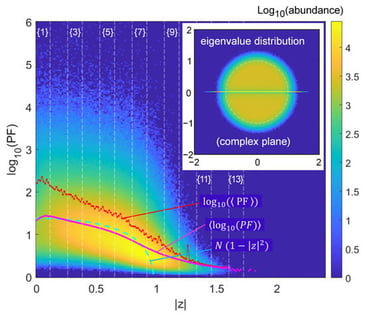
We explore how easy it is to enforce the advent of exceptional points starting from random matrices of non-Hermitian nature. We use the Petermann factor, whose mathematical version is called “overlap”, for guidance, as well as simple pseudo-spectral tools. We attempt to proceed in the most agnostic way, by adding random perturbation and checking basic metrics such as the sum of all vectors’ Petermann factors, equivalently the sum of diagonal overlaps. Issues such as the location of high Petermann factors vs. the modulus of eigenvalue are addressed. We contrast the fate of exploratory approaches in the Ginibre set (real matrices) and complex matrices, noting the special role of exceptional points on the real axis for the Ginibre matrices, completely absent in complex matrices.
29 January 2026