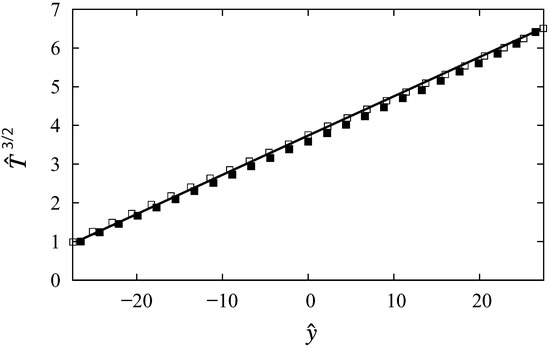
We analyze the transport properties of a low density ensemble of identical macroscopic particles immersed in an active fluid. The particles are modeled as inelastic hard spheres (granular gas). The non-homogeneous active fluid is modeled by means of a non-uniform stochastic thermostat. The theoretical results are validated with a numerical solution of the corresponding the kinetic equation (direct simulation Monte Carlo method). We show a steady flow in the system that is accurately described by Navier-Stokes (NS) hydrodynamics, even for high inelasticity. Surprisingly, we find that the deviations from NS hydrodynamics for this flow are stronger as the inelasticity decreases. The active fluid action is modeled here with a non-uniform fluctuating volume force. This is a relevant result given that hydrodynamics of particles in complex environments, such as biological crowded environments, is still a question under intense debate. Full article

We give a short survey on the concept of contact Hamiltonian dynamics and its use in several areas of physics, namely reversible and irreversible thermodynamics, statistical physics and classical mechanics. Some relevant examples are provided along the way. We conclude by giving insights into possible future directions. Full article

We consider the sets of quasi-regular points in the countable symbolic space. We measure the sizes of the sets by Billingsley-Hausdorff dimension defined by Gibbs measures. It is shown that the dimensions of those sets, always bounded from below by the convergence exponent of the Gibbs measure, are given by a variational principle, which generalizes Li and Ma’s result and Bowen’s result. Full article

The Fractal Dimension (FD) of an image defines the roughness using a real number which is highly associated with the human perception of surface roughness. It has been applied successfully for many computer vision applications such as texture analysis, segmentation and classification. Several techniques can be found in literature to estimate FD. One such technique is Differential Box Counting (DBC). Its performance is influenced by many parameters. In particular, the box height is directly related to the gray-level variations over image grid, which badly affects the performance of DBC. In this work, a new method for estimating box height is proposed without changing the other parameters of DBC. The proposed box height has been determined empirically and depends only on the image size. All the experiments have been performed on simulated Fractal Brownian Motion (FBM) Database and Brodatz Database. It has been proved experimentally that the proposed box height allow to improve the performance of DBC, Shifting DBC, Improved DBC and Improved Triangle DBC, which are closer to actual FD values of the simulated FBM images. Full article

Lagged Poincaré plots have been successful in characterizing abnormal cardiac function. However, the current research practices do not favour any specific lag of Poincaré plots, thus complicating the comparison of results of different researchers in their analysis of heart rate of healthy subjects and patients. We researched the informative nature of lagged Poincaré plots in different states of the autonomic nervous system. It was tested in three models: different age groups, groups with different balance of autonomous regulation, and in hypertensive patients. Correlation analysis shows that for lag l = 6, SD1/SD2 has weak (r = 0.33) correlation with linear parameters of heart rate variability (HRV). For l more than 6 it displays even less correlation with linear parameters, but the changes in SD1/SD2 become statistically insignificant. Secondly, surrogate data tests show that the real SD1/SD2 is statistically different from its surrogate value and the conclusion could be made that the heart rhythm has nonlinear properties. Thirdly, the three models showed that for different functional states of the autonomic nervous system (ANS), SD1/SD2 ratio varied only for lags l = 5 and 6. All of this allow to us to give cautious recommendation to use SD1/SD2 with lags 5 and 6 as a nonlinear characteristic of HRV. The received data could be used as the basis for continuing the research in standardisation of nonlinear analytic methods. Full article

Recently, a new algorithm named dynamic group optimization (DGO) has been proposed, which lends itself strongly to exploration and exploitation. Although DGO has demonstrated its efficacy in comparison to other classical optimization algorithms, DGO has two computational drawbacks. The first one is related to the two mutation operators of DGO, where they may decrease the diversity of the population, limiting the search ability. The second one is the homogeneity of the updated population information which is selected only from the companions in the same group. It may result in premature convergence and deteriorate the mutation operators. In order to deal with these two problems in this paper, a new hybridized algorithm is proposed, which combines the dynamic group optimization algorithm with the cross entropy method. The cross entropy method takes advantage of sampling the problem space by generating candidate solutions using the distribution, then it updates the distribution based on the better candidate solution discovered. The cross entropy operator does not only enlarge the promising search area, but it also guarantees that the new solution is taken from all the surrounding useful information into consideration. The proposed algorithm is tested on 23 up-to-date benchmark functions; the experimental results verify that the proposed algorithm over the other contemporary population-based swarming algorithms is more effective and efficient. Full article

The entropy generation due to heat transfer and fluid friction in mixed convective peristaltic flow of methanol-Al₂O₃ nano fluid is examined. Maxwell’s thermal conductivity model is used in analysis. Velocity and temperature profiles are utilized in the computation of the entropy generation number. The effects of involved physical parameters on velocity, temperature, entropy generation number, and Bejan number are discussed and explained graphically. Full article

Accurately determining dependency structure is critical to understanding a complex system’s organization. We recently showed that the transfer entropy fails in a key aspect of this—measuring information flow—due to its conflation of dyadic and polyadic relationships. We extend this observation to demonstrate that Shannon information measures (entropy and mutual information, in their conditional and multivariate forms) can fail to accurately ascertain multivariate dependencies due to their conflation of qualitatively different relations among variables. This has broad implications, particularly when employing information to express the organization and mechanisms embedded in complex systems, including the burgeoning efforts to combine complex network theory with information theory. Here, we do not suggest that any aspect of information theory is wrong. Rather, the vast majority of its informational measures are simply inadequate for determining the meaningful relationships among variables within joint probability distributions. We close by demonstrating that such distributions exist across an arbitrary set of variables. Full article

Bertschinger, Rauh, Olbrich, Jost, and Ay (Entropy, 2014) have proposed a definition of a decomposition of the mutual information $MI(\mathbf{X}:\mathbf{Y},\mathbf{Z})$ into shared, synergistic, and unique information by way of solving a convex optimization problem. In this paper, we discuss the solution of their Convex Program from theoretical and practical points of view. Full article

The model for a broadcast channel with confidential messages (BC-CM) plays an important role in the physical layer security of modern communication systems. In recent years, it has been shown that a noiseless feedback channel from the legitimate receiver to the transmitter increases the secrecy capacity region of the BC-CM. However, at present, the feedback coding scheme for the BC-CM only focuses on producing secret keys via noiseless feedback, and other usages of the feedback need to be further explored. In this paper, we propose a new feedback coding scheme for the BC-CM. The noiseless feedback in this new scheme is not only used to produce secret keys for the legitimate receiver and the transmitter but is also used to generate update information that allows both receivers (the legitimate receiver and the wiretapper) to improve their channel outputs. From a binary example, we show that this full utilization of noiseless feedback helps to increase the secrecy level of the previous feedback scheme for the BC-CM. Full article

The problem of measuring the disparity of a particular probability density function from a normal one has been addressed in several recent studies. The most used technique to deal with the problem has been exact expressions using information measures over particular distributions. In this paper, we consider a class of asymmetric distributions with a normal kernel, called Generalized Skew-Normal (GSN) distributions. We measure the degrees of disparity of these distributions from the normal distribution by using exact expressions for the GSN negentropy in terms of cumulants. Specifically, we focus on skew-normal and modified skew-normal distributions. Then, we establish the Kullback–Leibler divergences between each GSN distribution and the normal one in terms of their negentropies to develop hypothesis testing for normality. Finally, we apply this result to condition factor time series of anchovies off northern Chile. Full article

Suppose we have a pair of information channels, ${\kappa }_1,{\kappa }_2$ , with a common input. The Blackwell order is a partial order over channels that compares ${\kappa }_1$ and ${\kappa }_2$ by the maximal expected utility an agent can obtain when decisions are based on the channel outputs. Equivalently, ${\kappa }_1$ is said to be Blackwell-inferior to ${\kappa }_2$ if and only if ${\kappa }_1$ can be constructed by garbling the output of ${\kappa }_2$ . A related partial order stipulates that ${\kappa }_2$ is more capable than ${\kappa }_1$ if the mutual information between the input and output is larger for ${\kappa }_2$ than for ${\kappa }_1$ for any distribution over inputs. A Blackwell-inferior channel is necessarily less capable. However, examples are known where ${\kappa }_1$ is less capable than ${\kappa }_2$ but not Blackwell-inferior. We show that this may even happen when ${\kappa }_1$ is constructed by coarse-graining the inputs of ${\kappa }_2$ . Such a coarse-graining is a special kind of “pre-garbling” of the channel inputs. This example directly establishes that the expected value of the shared utility function for the coarse-grained channel is larger than it is for the non-coarse-grained channel. This contradicts the intuition that coarse-graining can only destroy information and lead to inferior channels. We also discuss our results in the context of information decompositions. Full article

This paper presents a modeling approach, followed by entropy calculations of the dynamics of large systems of interacting active particles viewed as living—hence, complex—systems. Active particles are partitioned into functional subsystems, while their state is modeled by a discrete scalar variable, while the state of the overall system is defined by a probability distribution function over the state of the particles. The aim of this paper consists of contributing to a further development of the mathematical kinetic theory of active particles. Full article

The Information Geometry of extended exponential families has received much recent attention in a variety of important applications, notably categorical data analysis, graphical modelling and, more specifically, log-linear modelling. The essential geometry here comes from the closure of an exponential family in a high-dimensional simplex. In parallel, there has been a great deal of interest in the purely Fisher Riemannian structure of (extended) exponential families, most especially in the Markov chain Monte Carlo literature. These parallel developments raise challenges, addressed here, at a variety of levels: both theoretical and practical—relatedly, conceptual and methodological. Centrally to this endeavour, this paper makes explicit the underlying geometry of these two areas via an analysis of the limiting behaviour of the fundamental geodesics of Information Geometry, these being Amari’s (+1) and (0)-geodesics, respectively. Overall, a substantially more complete account of the Information Geometry of extended exponential families is provided than has hitherto been the case. We illustrate the importance and benefits of this novel formulation through applications. Full article