Absorption and Chemisorption of Small Levitated Single Bubbles in Aqueous Solutions
Abstract
:1. Introduction
2. Theory
2.1. Bubble Rising Velocity and Drag Models
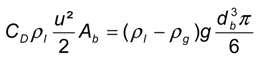
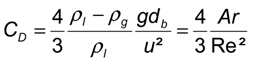
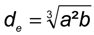
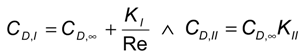
2.2. Mass Transfer of Single Bubbles
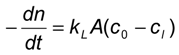
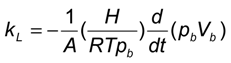
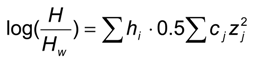
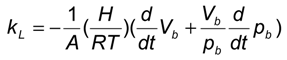
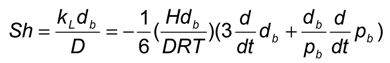
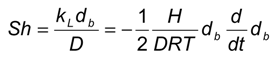
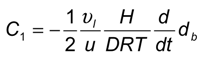
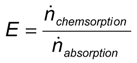
3. Experimental Methods
3.1. Apparatus and Procedure
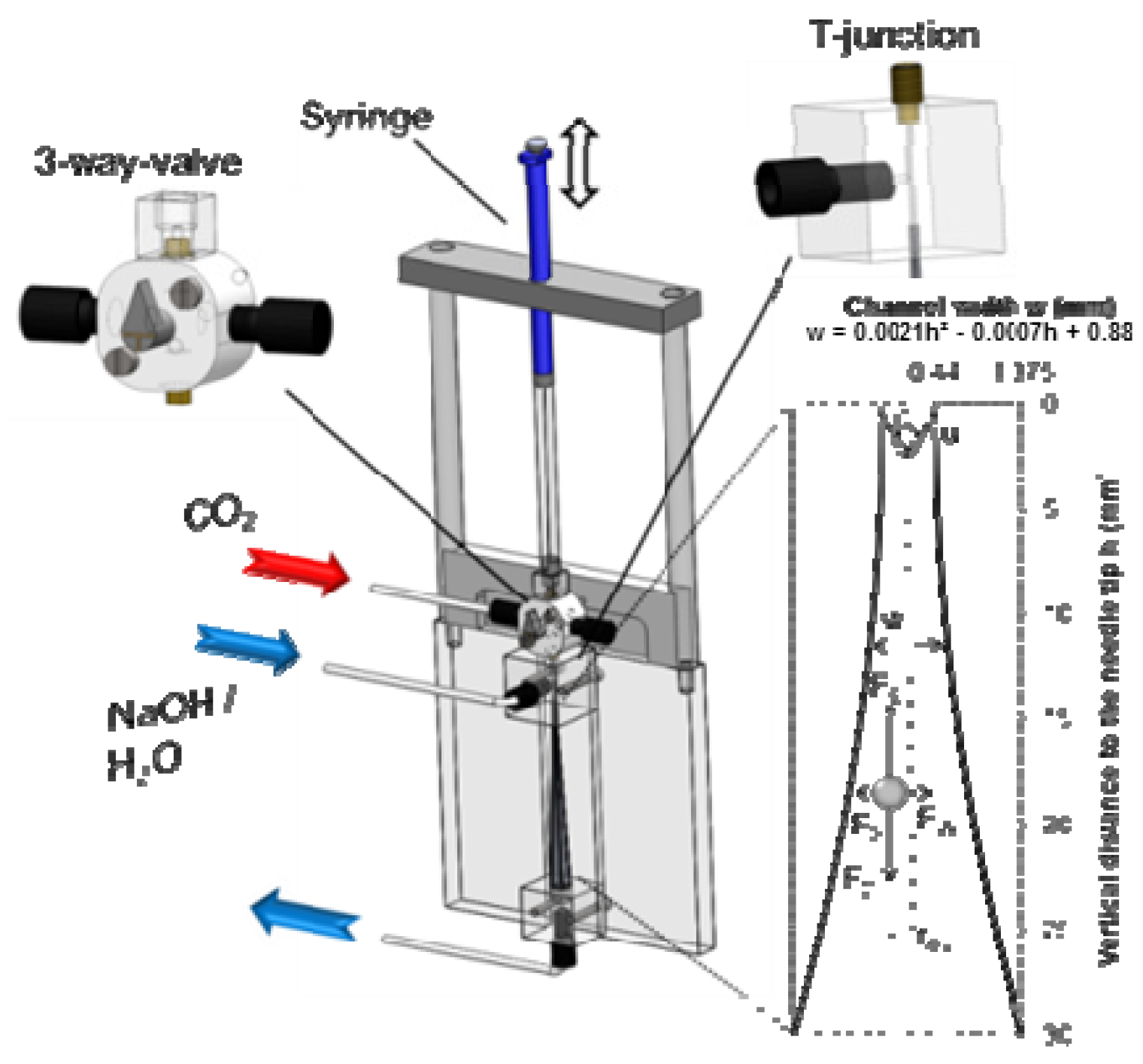
3.2. Bubble Diameter Determination with ImageJ
4. Results and Discussion
4.1. Levitation Position
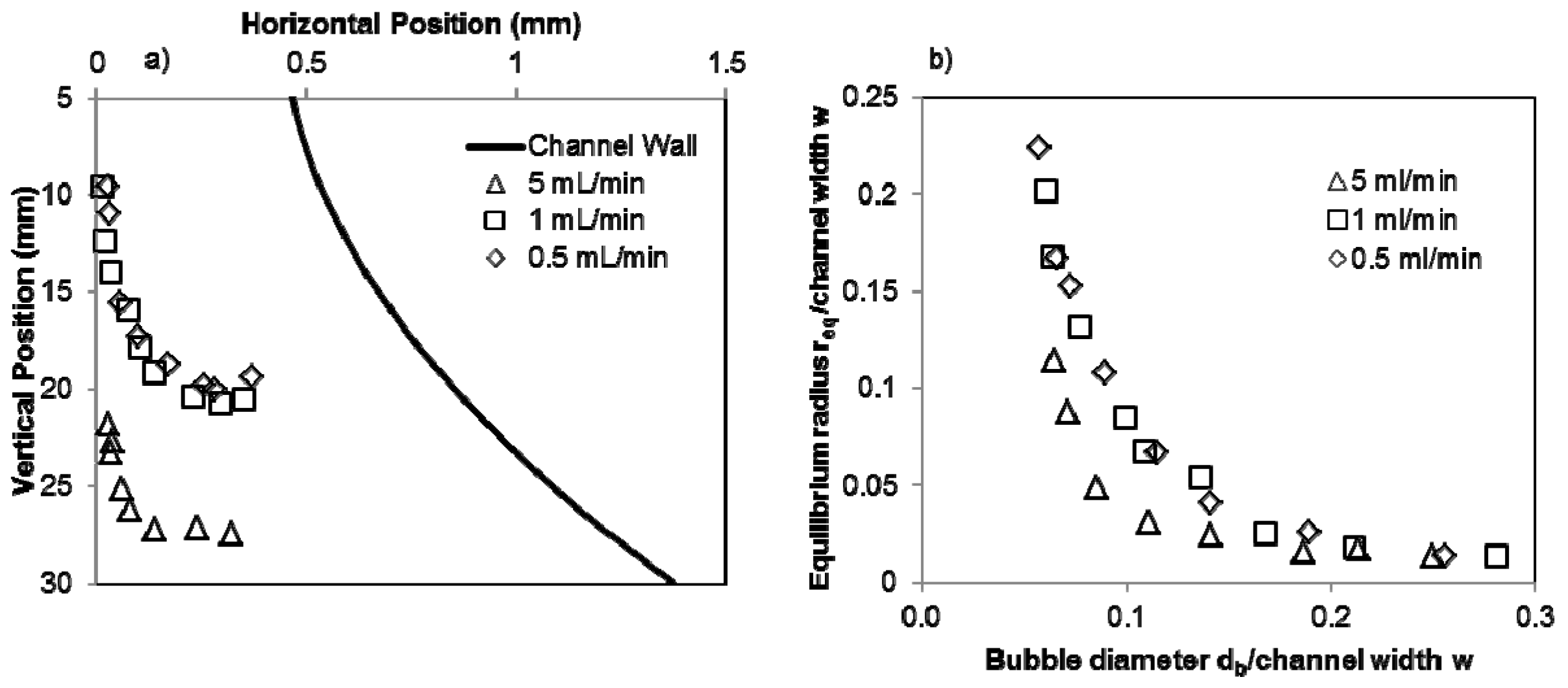
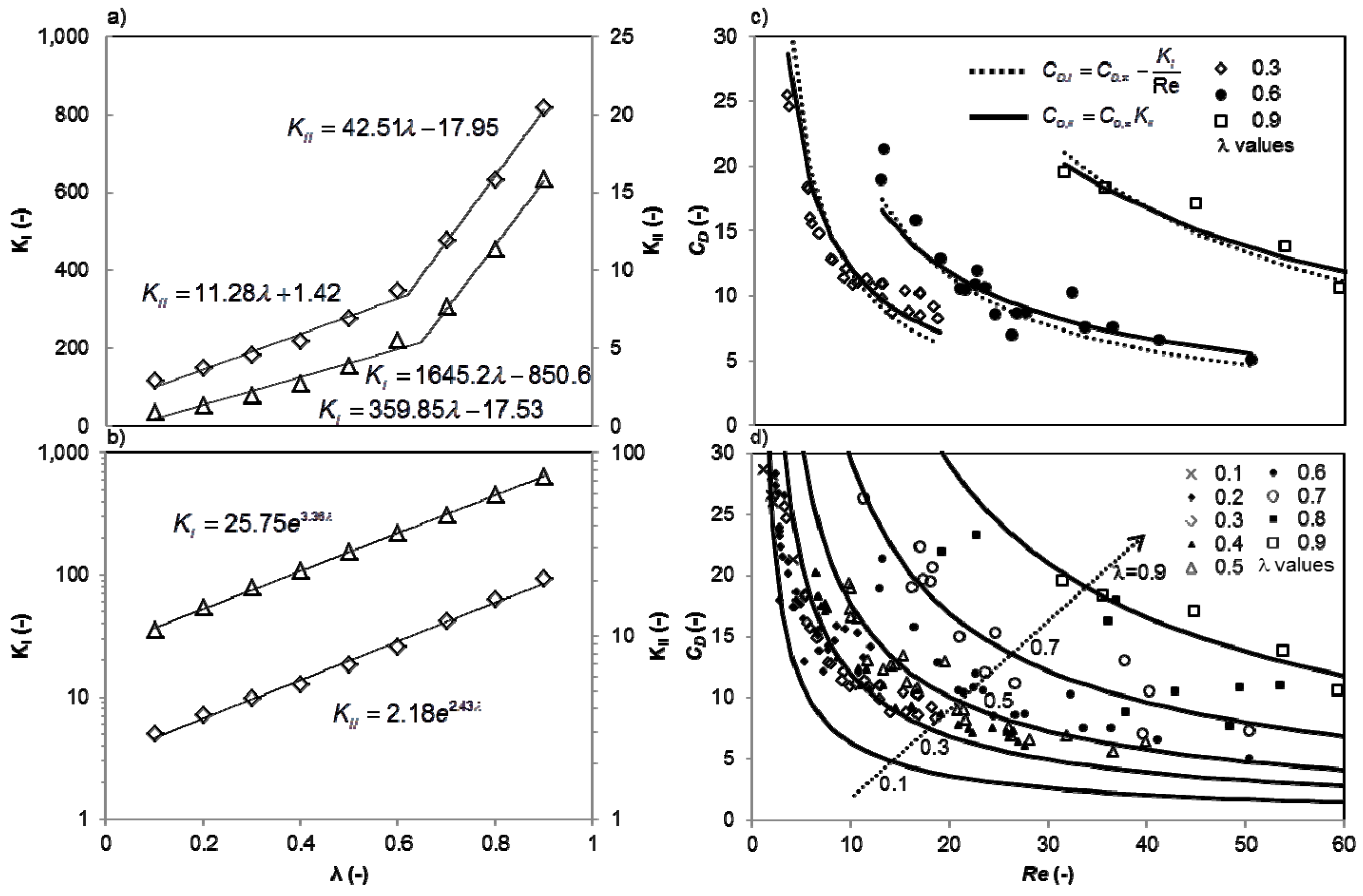
4.2. Modeling Drag Force Coefficient CD
4.3. Absorption of N2 and CO2
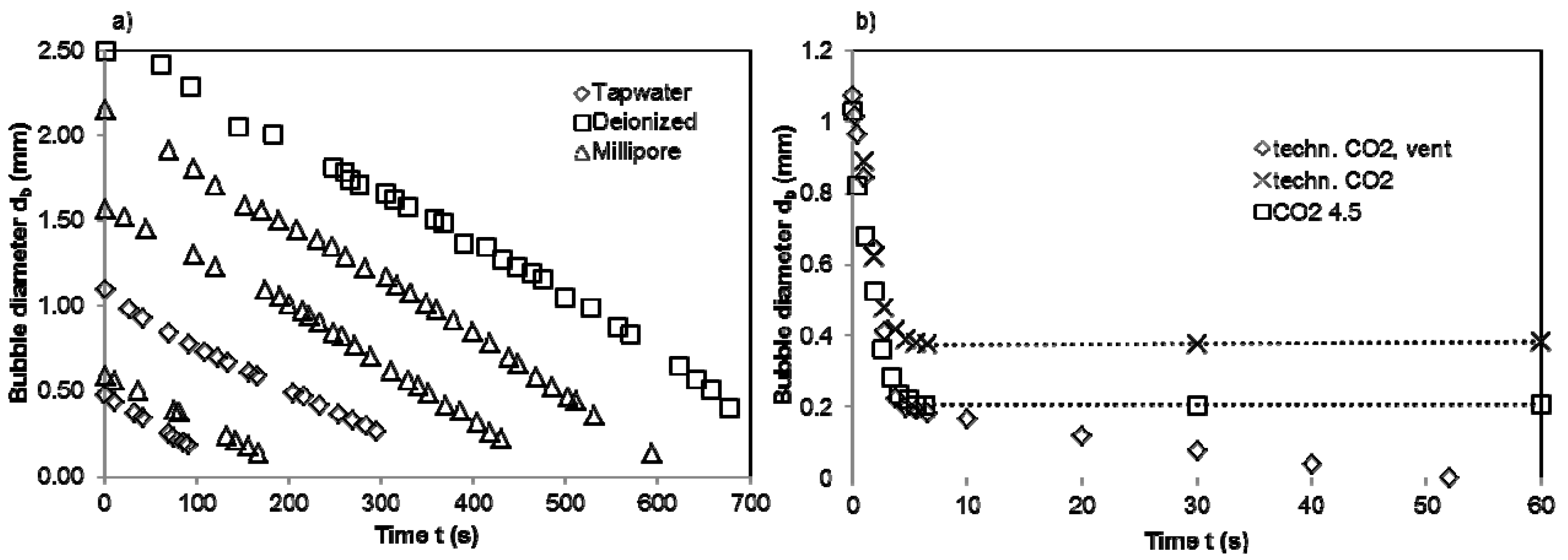
4.4. Chemisorption of CO2
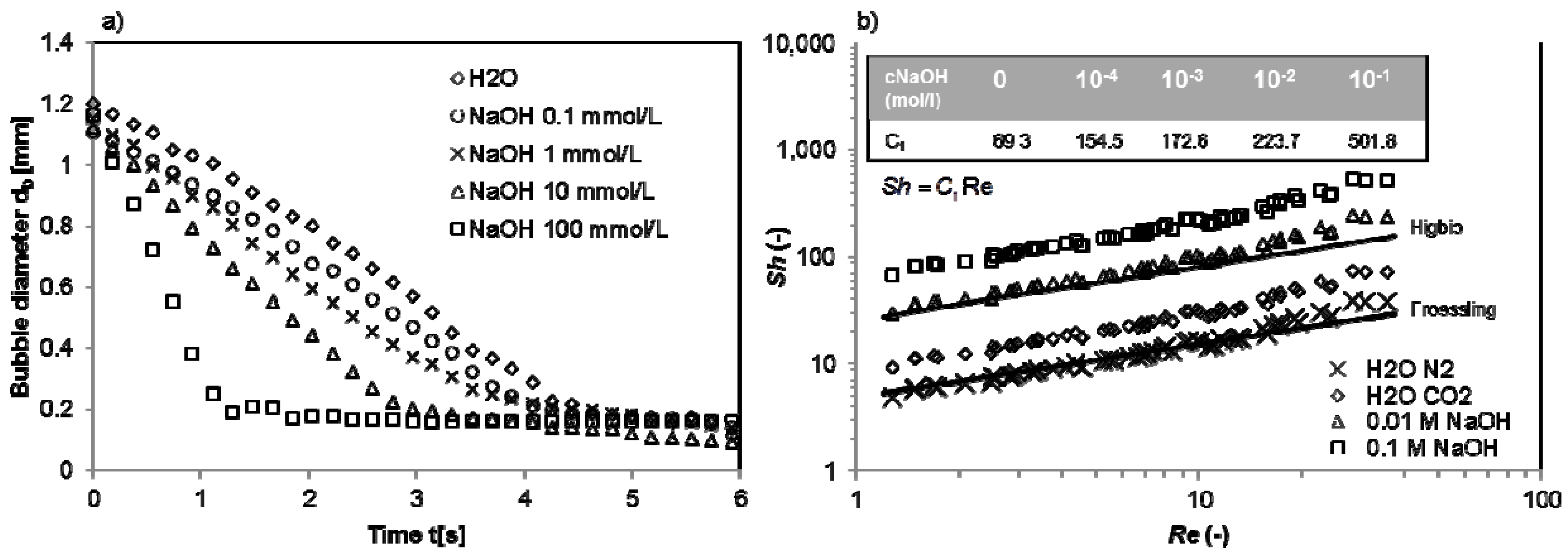
5. Conclusions
Nomenclature
| a | maximum Feret diameter, mm |
| A | surface area, m2 |
| Ar | Archimedes number, − |
| b | minimum Feret diameter, mm |
| c | concentration, mol∙m−3 |
| C1 | constant, − |
| CD | drag force coefficient, − |
| d | diameter, mm |
| D | diffusion coefficient, m2∙s−1 |
| E | enhancement factor, − |
| h | Henry constant model parameter, − |
| h | height, mm |
| H | Henry constant, bar∙m3∙mol−1 |
| k | mass transfer coefficient, m∙s−1 |
| K | drag force model constant, − |
| n | amount of substance, mol |
| p | pressure, barg (gauge) |
| r | radius, mm |
| R | universal gas constant, J∙mol−1∙K−1 |
| Re | Reynolds number, − |
| Sc | Schmidt number, − |
| Sh | Sherwood number, − |
| t | time, s |
| T | temperature, K |
| u | channel flow velocity, m∙s−1 |
| V | volume, m³ |
| z | valence electrons, − |
Greek symbols
| λ | ratio of bubble diameter to channel width, − |
| ρ | density, kg∙m−3 |
| σ | surface tension, N∙m−1 |
| ν | kinematic viscosity, m2∙s−1 |
Variable index nomenclature
| atm | atmosphere |
| b | bubble |
| D | drag |
| e | volume equivalent |
| eq | equilibrium |
| g | gas |
| l | liquid |
| L | liquid |
| w | water |
| 0 | gas-liquid interface |
| ∞ | infinite flow field |
Acknowledgments
Conflicts of Interest
References
- Stitt, E.H. Alternative multiphase reactors for fine chemicals—A world beyond stirred tanks? Chem. Eng. J. 2002, 90, 47–60. [Google Scholar]
- Schneider, M.-A.; Maeder, T.; Ryser, P.; Stoessel, F. A microreactor-based system for the study of fast exothermic reactions in liquid phase: Characterization of the system. Chem. Eng. J. 2004, 101, 241–250. [Google Scholar] [CrossRef]
- Stefanidis, G.D.; Vlachos, D.G.; Kaisare, N.S.; Maestri, M. Methane steam reforming at microscales: Operation strategies for variable power output at millisecond contact times. AIChE J. 2009, 55, 180–191. [Google Scholar] [CrossRef]
- Crespo-Quesada, M.; Grasemann, M.; Semagina, N.; Renken, A.; Kiwi-Minsker, L. Kinetics of the solvent-free hydrogenation of 2-methyl-3-butyn-2-ol over a structured Pd-based catalyst. Catal. Today 2009, 147, 247–254. [Google Scholar] [CrossRef]
- Grasemann, M.; Renken, A.; Kashid, M.N.; Kiwi-Minsker, L. A novel compact reactor for three-phase hydrogenations. Chem. Eng. Sci. 2010, 65, 364–371. [Google Scholar] [CrossRef]
- Kockmann, N.; Roberge, D.M. Harsh reaction conditions in continuous-flow microreactors for pharmaceutical production. Chem. Eng. Technol. 2009, 32, 1682–1694. [Google Scholar] [CrossRef]
- Günther, A.; Jensen, K.F. Multiphase microfluidics: From flow characteristics to chemical and materials synthesis. Lab Chip 2006, 6, 1487–1503. [Google Scholar] [CrossRef]
- Doku, G.N.; Verboom, W.; Reinhoudt, D.N.; van den Berg, A. On-microchip multiphase chemistry—A review of microreactor design principles and reagent contacting modes. Tetrahedron 2005, 61, 2733–2742. [Google Scholar] [CrossRef]
- Hessel, V.; Angeli, P.; Gavriilidis, A.; Löwe, H. Gas-liquid and gas-liquid-solid microstructured reactors: Contacting principles and applications. Ind. Eng. Chem. Res. 2005, 44, 9750–9769. [Google Scholar] [CrossRef]
- Kashid, M.N.; Kiwi-Minsker, L. Microstructured reactors for multiphase reactions: State of the art. Ind. Eng. Chem. Res. 2009, 48, 6465–6485. [Google Scholar] [CrossRef]
- Kockmann, N.; Gottsponer, M. Heat transfer limitations of gas-liquid exothermic reactions in microchannels. In Proceedings of the ASME 2010 8th International Conference on Nanochannels, Microchannels, and Minichannels Collocated with 3rd Joint US-European Fluids Engineering Summer Meeting, Montreal, QC, Canada, 1–5 August 2010; Paper No. FEDSM-ICNMM 2010–30389. pp. 193–199.
- Kockmann, N. Sicherheitsaspekte bei der Prozessentwicklung und Kleinmengenproduktion mit Mikroreaktoren. Chemie Ingenieur Technik 2012, 84, 715–726. [Google Scholar] [CrossRef]
- Lochiel, A.C.; Calderbank, P.H. Mass transfer in the continuous phase around axisymmetric bodies of revolution. Chem. Eng. Sci. 1964, 19, 471–484. [Google Scholar] [CrossRef]
- Peebles, F.N.; Garber, H.J. Studies of the motion of gas bubbles in liquids. Chem. Eng. Prog. 1953, 49, 88–97. [Google Scholar]
- Kulkarni, A.A.; Joshi, J.B. Bubble formation and bubble rise velocity in gas-liquid systems: A review. Ind. Eng. Chem. Res. 2005, 44, 5873–5931. [Google Scholar] [CrossRef]
- Duineveld, P.C. The rise velocity and shape of bubbles in pure water at high reynolds number. J. Fluid Mech. 1995, 292, 325–332. [Google Scholar] [CrossRef]
- Garner, F.H.; Hammerton, D. Circulation inside gas bubbles. Chem. Eng. Sci. 1954, 3, 1–11. [Google Scholar] [CrossRef]
- Peters, F.; Biermann, S. Streulichtuntersuchungen an einem kleinen, levitierten Bläschen. In Proceedings of the Fachtagung der Deutschen Gesellschaft für Laser-Anemometrie, Karlsruhe, Germany, 7–9 September 2004.
- Nüllig, M.; Peters, F. Diffusion of small gas bubbles into liquid studied by the rotary chamber technique. Chemie Ingenieur Technik 2013, 85, 1074–1079. [Google Scholar] [CrossRef]
- Vasconcelos, J.M.T.; Orvalho, S.P.; Alves, S.S. Gas-liquid mass transfer to single bubbles: Effect of surface contamination. AIChE J. 2002, 48, 1145–1154. [Google Scholar] [CrossRef]
- Schulze, G.; Schlünder, E.U. Absorption von einzelnen gasblasen in vorbeladenem wasser. Chemie Ingenieur Technik 1985, 57, 233–235. [Google Scholar] [CrossRef]
- Takemura, F.; Yabe, A. Rising speed and dissolution rate of carbon dioxide bubble in slightly contaminated water. J. Fluid Mech. 1999, 378, 319–334. [Google Scholar] [CrossRef]
- Takemura, F.; Matsumoto, Y. Dissolution rate of spherical carbon dioxide bubbles in strong alkaline solutions. Chem. Eng. Sci. 2000, 55, 3907–3917. [Google Scholar] [CrossRef]
- Madhavi, T.; Golder, A.K.; Samanta, A.N.; Ray, S. Studies on bubble dynamics with mass transfer. Chem. Eng. J. 2007, 128, 95–104. [Google Scholar] [CrossRef]
- Matulka, P. Partikelbewegung und Trennung in laminar durchströmten Rohren mit nachfolgender Strömungsaufweitung. Ph.D. Thesis 2013. [Google Scholar]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Wham, R.M.; Basaran, O.A.; Byers, C.H. Wall effects on flow past solid spheres at finite reynolds number. Ind. Eng. Chem. Res. 1996, 35, 864–874. [Google Scholar] [CrossRef]
- Danckwerts, P.V. Gas-Liquid Reactions; McGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Carroll, J.J.; Slupsky, J.D.; Mather, A.E. The solubility of carbon dioxide in water at low pressure. J. Phys. Chem. Ref. Data 1991, 20, 1201–1209. [Google Scholar] [CrossRef]
- Calderbank, P.H.; Lochiel, A.C. Mass transfer coefficients, velocities and shapes of carbon dioxide bubbles in free rise through distilled water. Chem. Eng. Sci. 1964, 19, 485–503. [Google Scholar] [CrossRef]
- Vas Bhat, R.D.; Kuipers, J.A.M.; Versteeg, G.F. Mass transfer with complex chemical reactions in gas-liquid systems: Two-step reversible reactions with unit stoichiometric and kinetic orders. Chem. Eng. J. 2000, 76, 127–152. [Google Scholar] [CrossRef]
- Perry, R. Perry’s Chemical Engineers Handbook, 7th ed.; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Matas, J.-P.; Morris, J.F.; Guazzelli, E. Lateral force on rigid sphere in large-inertia laminar pipe flow. J. Fluid Mech. 2009, 621, 59–67. [Google Scholar] [CrossRef]
- Haberman, W.L.; Sayre, R.M. Motion of rigid and fluid spheres in stationary and moving liquids inside cylindrical tubes. David Taylor Model Basin Report 1958, 1143. [Google Scholar]
- Büchner, E.-W. Experimentelle Untersuchung über Strömungskräfte auf ruhend und bewegten Kugeln in einer ebenen Poiseuille-Strömung. Ph.D. Thesis 1987. [Google Scholar]
- Sakai, M.; Kusakabe, K. Gas absorption during the burst of an individual bubble on the water surface. J. Chem. Eng. Jpn. 2004, 37, 1117–1121. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tollkötter, A.; Kockmann, N. Absorption and Chemisorption of Small Levitated Single Bubbles in Aqueous Solutions. Processes 2014, 2, 200-215. https://doi.org/10.3390/pr2010200
Tollkötter A, Kockmann N. Absorption and Chemisorption of Small Levitated Single Bubbles in Aqueous Solutions. Processes. 2014; 2(1):200-215. https://doi.org/10.3390/pr2010200
Chicago/Turabian StyleTollkötter, Alexander, and Norbert Kockmann. 2014. "Absorption and Chemisorption of Small Levitated Single Bubbles in Aqueous Solutions" Processes 2, no. 1: 200-215. https://doi.org/10.3390/pr2010200
APA StyleTollkötter, A., & Kockmann, N. (2014). Absorption and Chemisorption of Small Levitated Single Bubbles in Aqueous Solutions. Processes, 2(1), 200-215. https://doi.org/10.3390/pr2010200




