Conductivity-Dependent Flow Field-Flow Fractionation of Fulvic and Humic Acid Aggregates
Abstract
:1. Introduction
2. Experimental Section
3. Results and Discussion
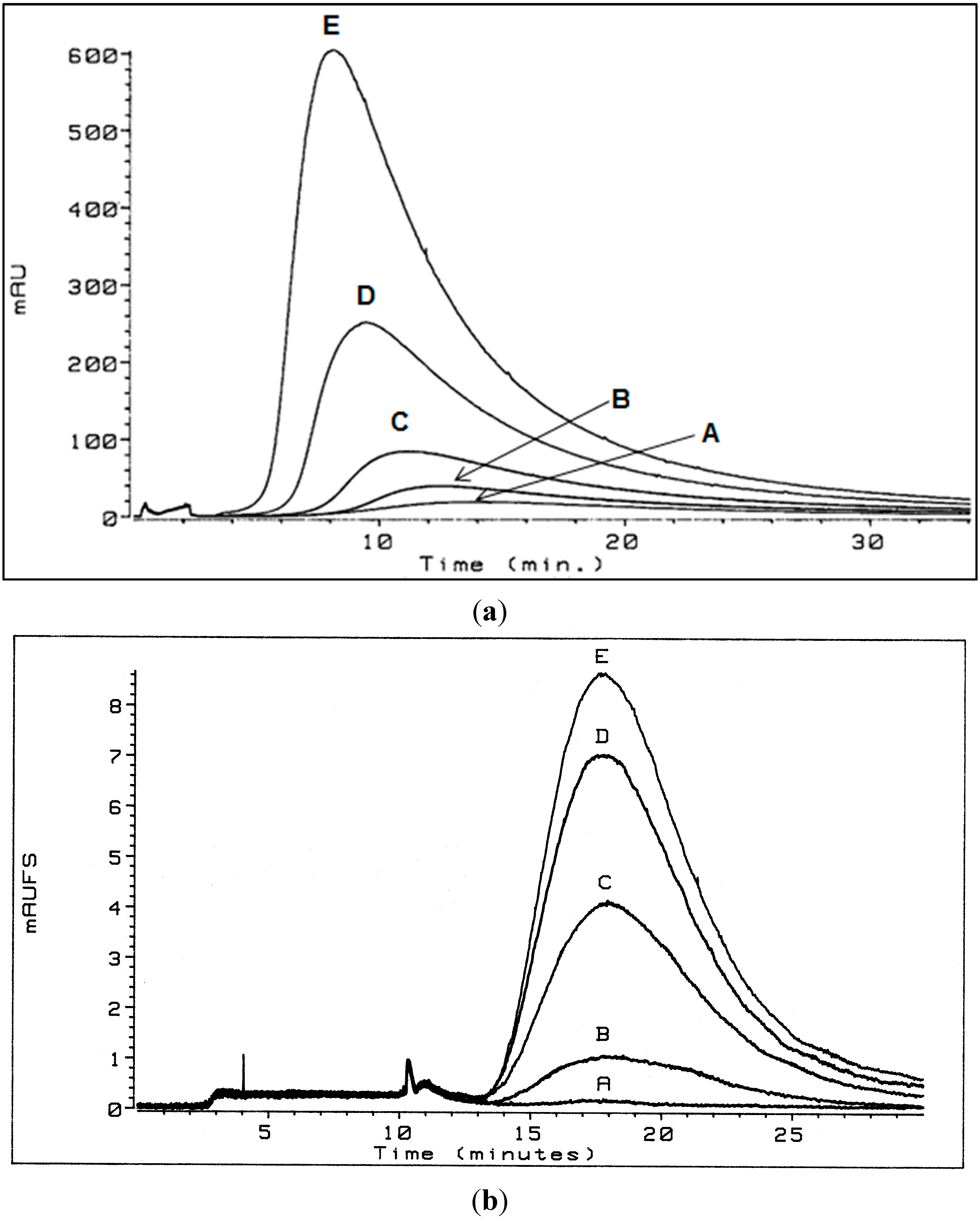
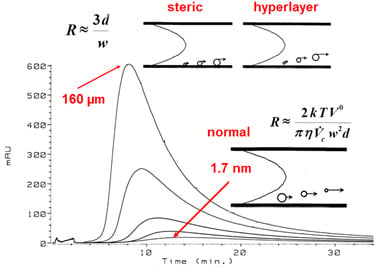
3.1. Flow Field-Flow Fractionation (Flow FFF) of Humic Substances (HSs)
3.1.1. Low Electrolytic Conductivity Solutions
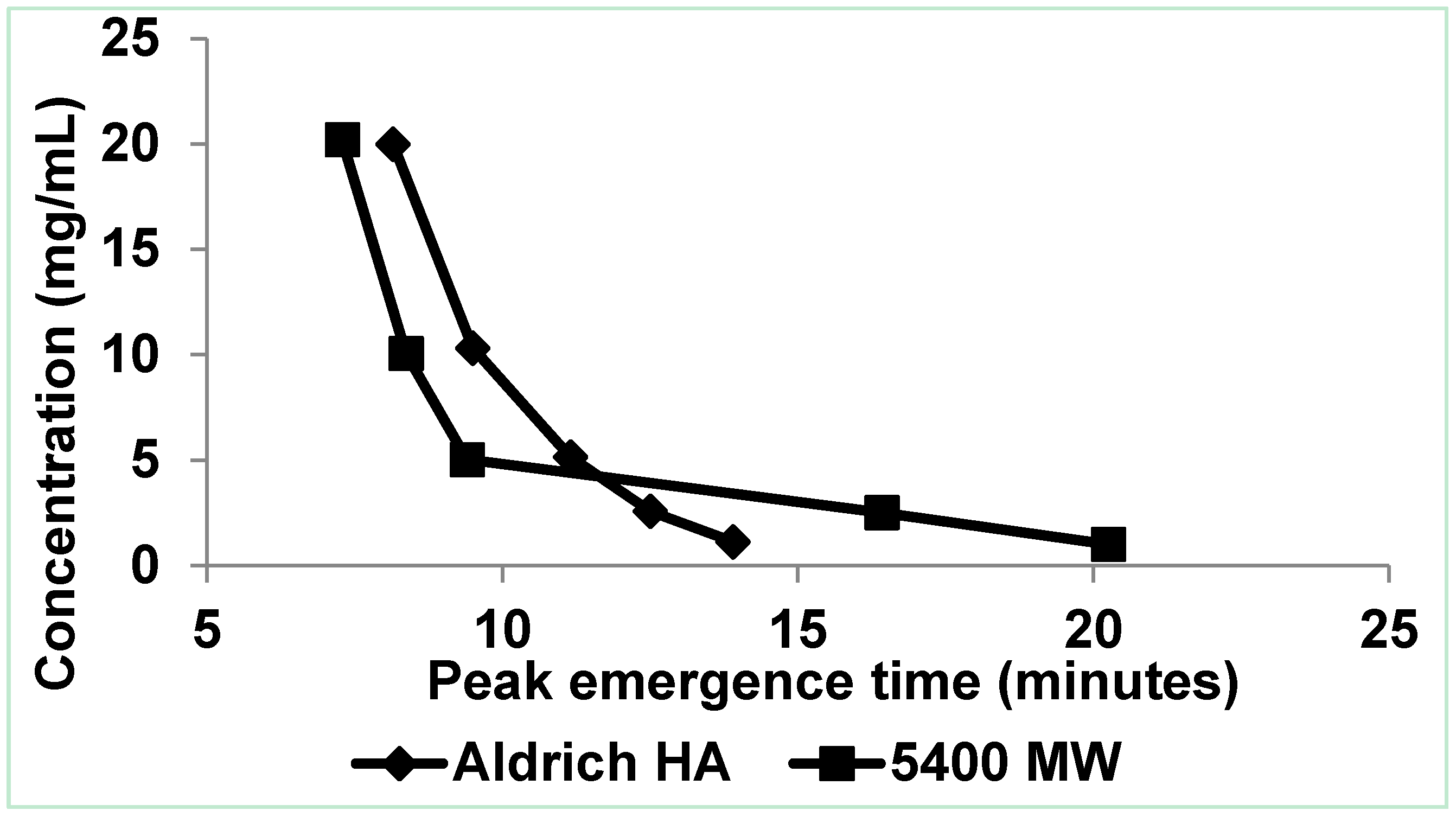

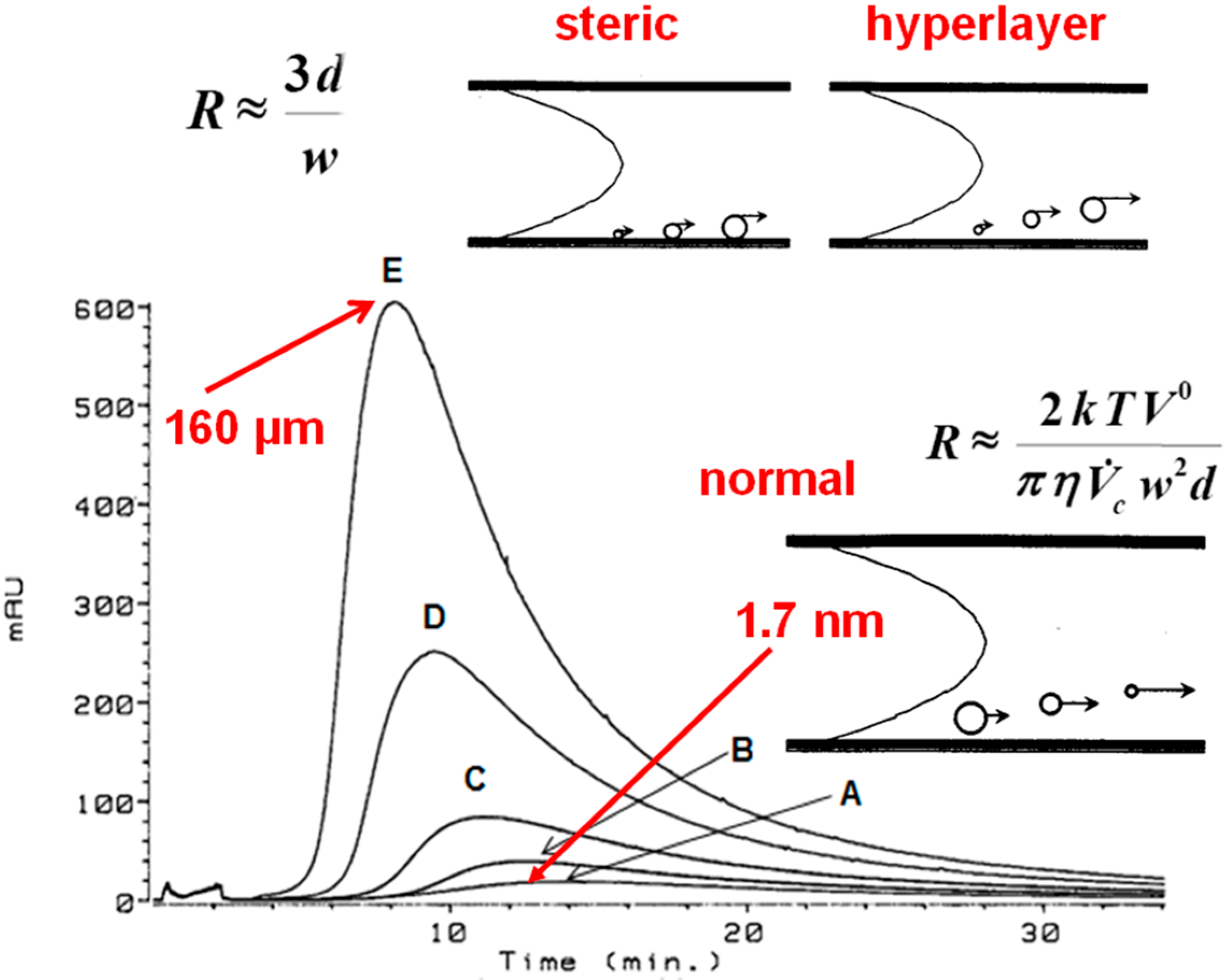
3.1.2. High Electrolytic Conductivity Solutions
| Humic substance | dmin (nm) | dp (nm) | dmax (nm) |
|---|---|---|---|
| Ultraviolet detection | |||
| Aldrich | 0.76 | 2.2 | 7.3 |
| Aldrich extract | 0.73 | 2.3 | 7.8 |
| SRFA | 0.83 | 2.0 | 6.0 |
| Fluorescence detection | |||
| Aldrich | 0.88 | 2.2 | 7.6 |
| Aldrich extract | 0.88 | 2.3 | 7.0 |
| SRFA | 0.93 | 2.1 | 5.8 |
| Humic substance | Dp (m2 s-1 × 1010) |
|---|---|
| Ultraviolet detection | |
| Aldrich | 2.0 |
| Aldrich extract | 1.9 |
| SRFA | 2.2 |
| Fluorescence detection | |
| Aldrich | 1.9 |
| Aldrich extract | 1.9 |
| SRFA | 2.1 |
3.2. Dynamic Light Scattering (DLS) of Humic Substances (HSs)
3.2.1. Low Electrolytic Conductivity Solutions
3.2.2. High Electrolytic Conductivity Solutions
3.3. Integrating the Data
3.3.1. Aggregates >100 μm
3.3.2. Aggregates 6–100 µm
3.3.3. Aggregates 10–100 nm, 100–1000 nm, and 1–6 µm
3.3.4. Aggregates <10 nm
4. Conclusions
Conflicts of Interest
References
- Zularisam, A.; Ismail, A.F.; Salim, M.; Sakinah, M.; Ozaki, H. The effects of natural organic matter (NOM) fractions on fouling characteristics and flux recovery of ultrafiltration membranes. Desalination 2007, 212, 191–208. [Google Scholar] [CrossRef]
- Esfahani, M.R.; Stretz, H.A.; Wells, M.J.M. Abiotic reversible self-assembly of fulvic and humic acid aggregates in low electrolytic conductivity solutions by dynamic light scattering and zeta potential investigation. Sci. Total Environ. 2015, 537, 81–92. [Google Scholar] [CrossRef] [PubMed]
- Dycus, P.J.M.; Healy, K.D.; Stearman, G.K.; Wells, M.J.M. Diffusion coefficients and molecular weight distributions of humic and fulvic acids determined by flow field-flow fractionation. Sep. Sci. Technol. 1995, 30, 1435–1453. [Google Scholar] [CrossRef]
- Schmit, K.H.; Wells, M.J.M. Preferential adsorption of fluorescing fulvic and humic acid components on activated carbon using flow field-flow fractionation analysis. J. Environ. Monit. 2002, 4, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Dycus, P.J.M. Macromolecules: Separation by Flow Field-Flow Fractionation. Master’s Thesis, Tennessee Technological University, Cookeville, TN, USA, 1993. [Google Scholar]
- Benincasa, M.A.; Cartoni, G.; Imperia, N. Effects of ionic strength and electrolyte composition on the aggregation of fractionated humic substances studied by flow field-flow fractionation. J. Sep. Sci. 2002, 25, 405–415. [Google Scholar] [CrossRef]
- Lead, J.R.; Wilkinson, K.J.; Balnois, E.; Cutak, B.J.; Larive, C.K.; Assemi, S.; Beckett, R. Diffusion coefficients and polydispersities of the Suwannee River fulvic acid: Comparison of fluorescence correlation spectroscopy, pulsed-field gradient nuclear magnetic resonance, and flow field-flow fractionation. Environ. Sci. Technol. 2000, 34, 3508–3513. [Google Scholar] [CrossRef]
- Martin, M.; Beckett, R. Size Selectivity in field-flow fractionation: Lift mode of retention with near-wall lift force. J. Phys. Chem. A 2012, 116, 6540–6551. [Google Scholar] [CrossRef] [PubMed]
- Guetzloff, T.F.; Rice, J.A. Does humic acid form a micelle? Sci. Total Environ. 1994, 152, 31–35. [Google Scholar] [CrossRef]
- Smejkalova, D.; Piccolo, A. Aggregation and disaggregation of humic supramolecular assemblies by NMR diffusion ordered spectroscopy (DOSY-NMR). Environ. Sci. Technol. 2007, 42, 699–706. [Google Scholar] [CrossRef]
- Lei, W.; Zhu, Z.; Wang, Z.; Chen, P. Surface activity of humic acids. Ranliao Huaxue Xuebao 1986, 14, 177–181. (In Chinese) [Google Scholar]
- Tarasevich, Y.I.; Dolenko, S.A.; Trifonova, M.Y.; Alekseenko, E.Y. Association and colloid-chemical properties of humic acids in aqueous solutions. Colloid J. 2013, 75, 207–213. [Google Scholar] [CrossRef]
- Assemi, S.; Newcombe, G.; Hepplewhite, C.; Beckett, R. Characterization of natural organic matter fractions separated by ultrafiltration using flow field-flow fractionation. Water Res. 2004, 38, 1467–1476. [Google Scholar] [CrossRef] [PubMed]
- Verdugo, P. Marine microgels. Annu. Rev. Mar. Sci. 2012, 4, 375–400. [Google Scholar] [CrossRef] [PubMed]
- Verdugo, P.; Santschi, P.H. Polymer dynamics of DOC networks and gel formation in seawater. Deep Sea Res. Part II Top. Stud Oceanogr. 2010, 57, 1486–1493. [Google Scholar] [CrossRef]
- Chin, W.-C.; Orellana, M.V.; Verdugo, P. Spontaneous assembly of marine dissolved organic matter into polymer gels. Nature 1998, 391, 568–572. [Google Scholar] [CrossRef]
- Wershaw, R.L.; Hayes, T.M. Solubilization of Anthropogenic Compounds by Humic Substances. In Humic Substances and Chemical Contaminants; Clapp, C.E., Hayes, M.H.B., Senesi, N., Bloom, P.R., Jardine, P.M., Eds.; Soil Science Society of America: Madison, WI, USA, 2001; pp. 165–176. [Google Scholar]
- Beckett, R.; Ranville, J. Natural Organic Matter. In Interface Science in Drinking Water Treatment; Newcombe, G., Dixon, D., Eds.; Elsevier: London, UK, 2006; pp. 299–315. [Google Scholar]
- Wershaw, R.L. Membrane-Micelle Model for Humus in Soils and Sediments and its Relation to Humification; Technical Report for US Geological Survey; U.S. Geological Survey (USGS): Denver, CO, USA, 1994. [Google Scholar]
- Manning, T.J.; Sherrill, M.L.; Bennett, T.; Land, M.; Noble, L. Effect of chemical matrix on humic acid aggregates. Fla. Sci. 2004, 67, 266–280. [Google Scholar]
- Mukerjee, P.; Mysels, K.J. Critical Micelle Concentrations of Aqueous Surfactant Systems; National Bureau of Standards: Washington, D.C., USA, 1971; p. 4. [Google Scholar]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wells, M.J.M. Conductivity-Dependent Flow Field-Flow Fractionation of Fulvic and Humic Acid Aggregates. Chromatography 2015, 2, 580-593. https://doi.org/10.3390/chromatography2030580
Wells MJM. Conductivity-Dependent Flow Field-Flow Fractionation of Fulvic and Humic Acid Aggregates. Chromatography. 2015; 2(3):580-593. https://doi.org/10.3390/chromatography2030580
Chicago/Turabian StyleWells, Martha J. M. 2015. "Conductivity-Dependent Flow Field-Flow Fractionation of Fulvic and Humic Acid Aggregates" Chromatography 2, no. 3: 580-593. https://doi.org/10.3390/chromatography2030580