Adverse-Mode FFF: Multi-Force Ideal Retention Theory
Abstract
:1. Introduction
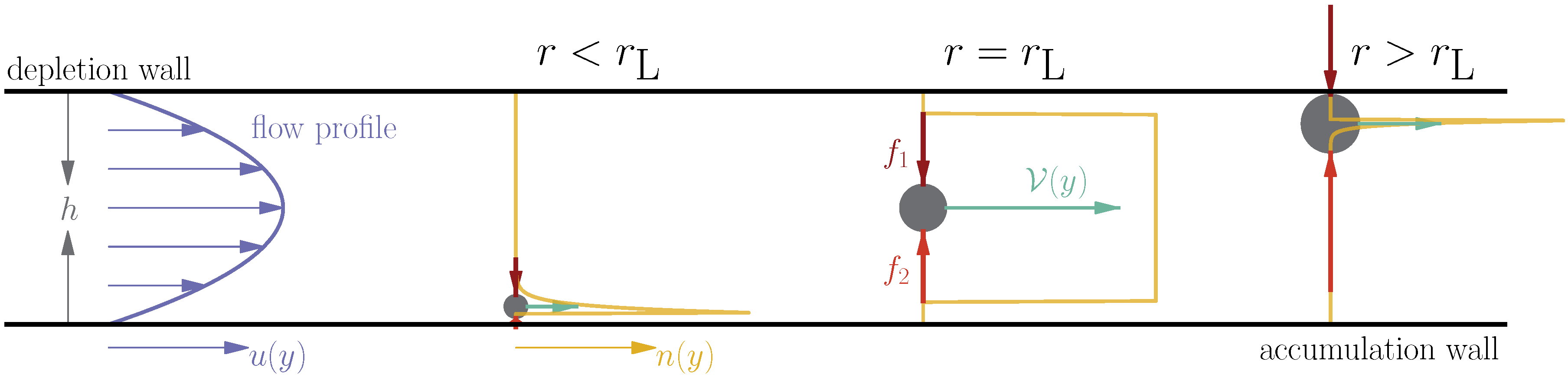
2. Multi-Force Ideal Retention Theory
2.1. Retention Ratio of the Multi-Force Ideal Retention Theory
2.2. Higher Moments of the Multi-Force Ideal Retention Theory
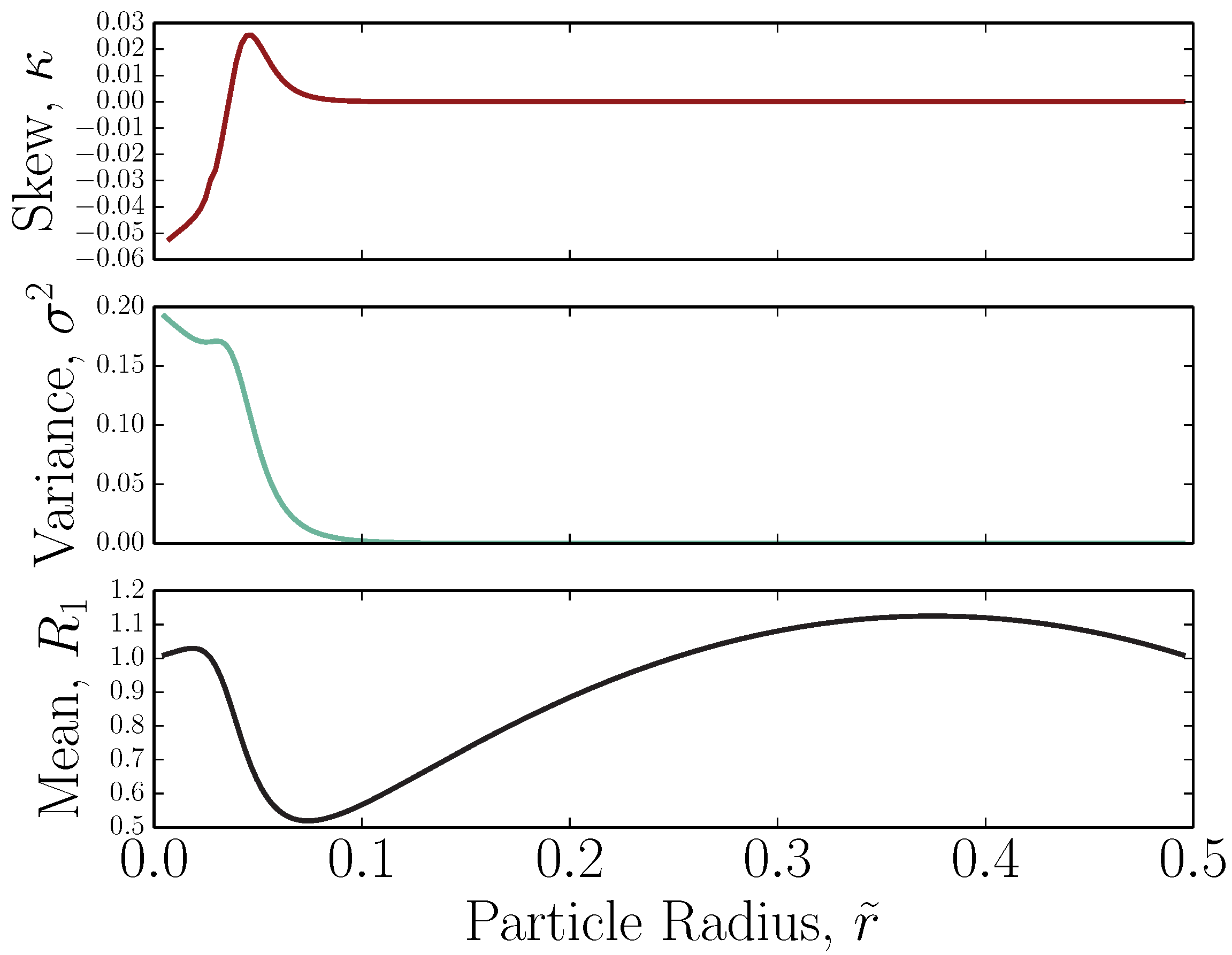
3. Adverse-Mode FFF: Benefit of Two Opposing Forces
3.1. Adverse-Mode: Retention Ratio Peak
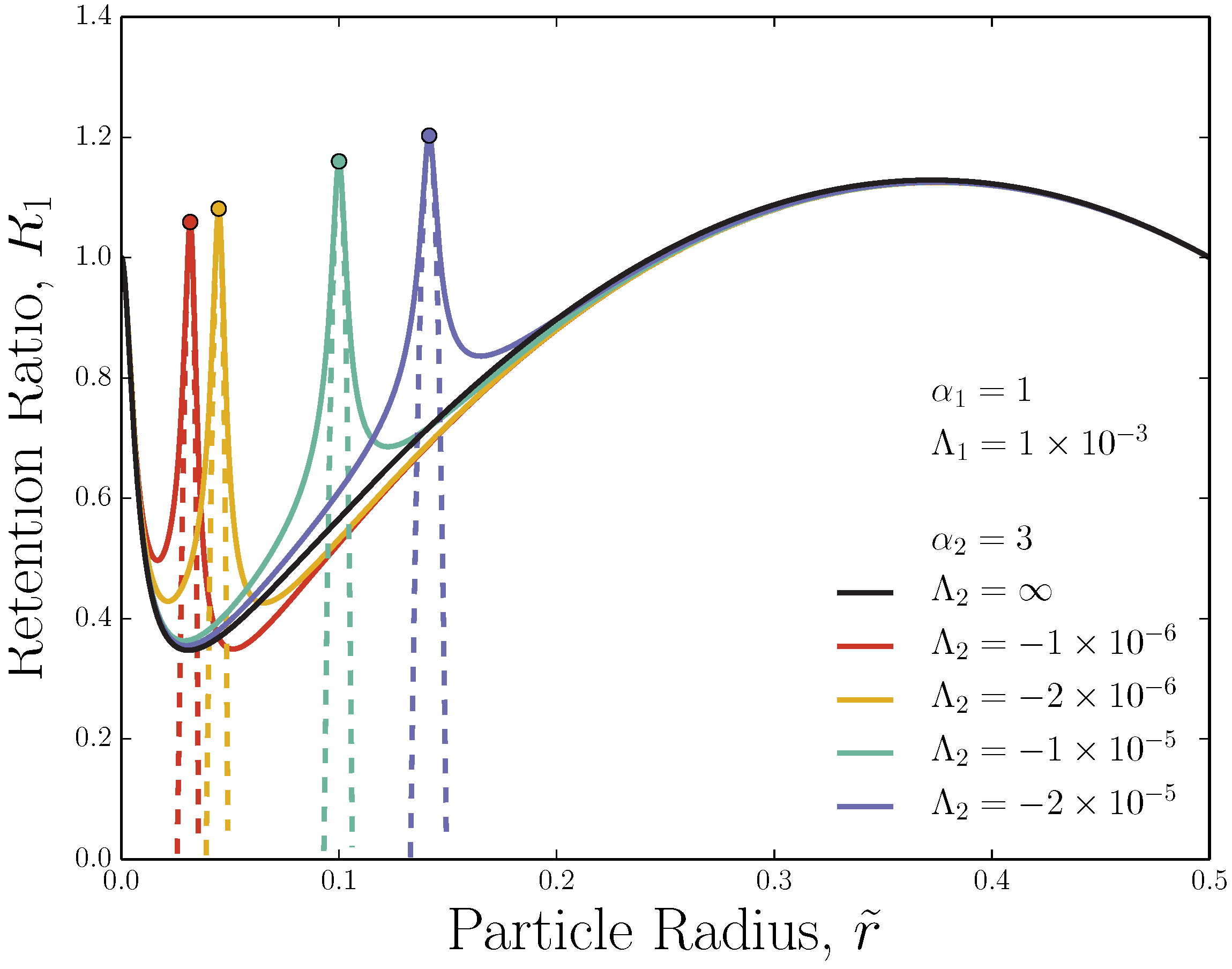
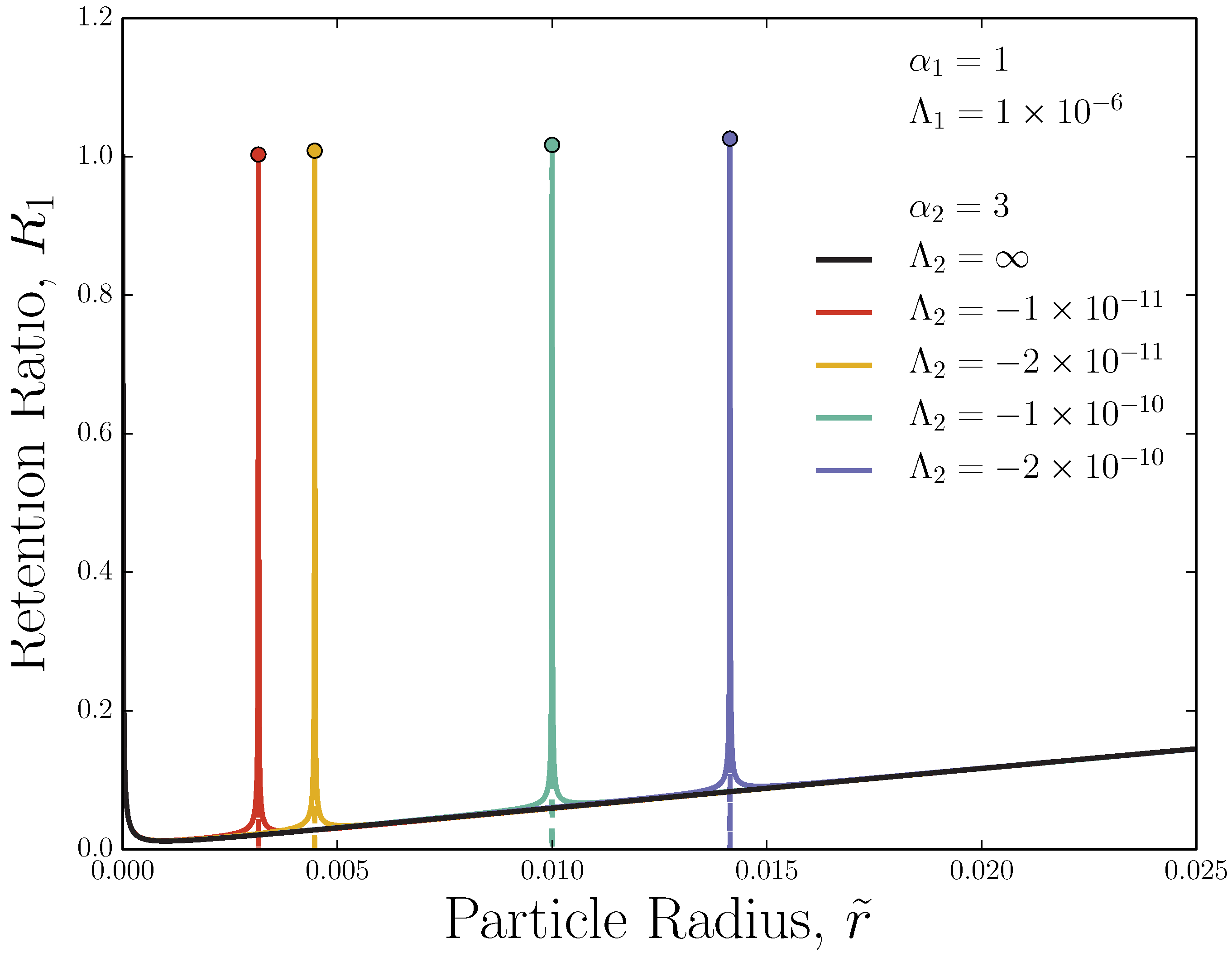
3.2. Adverse-Mode: Retention Ratio Peak Width
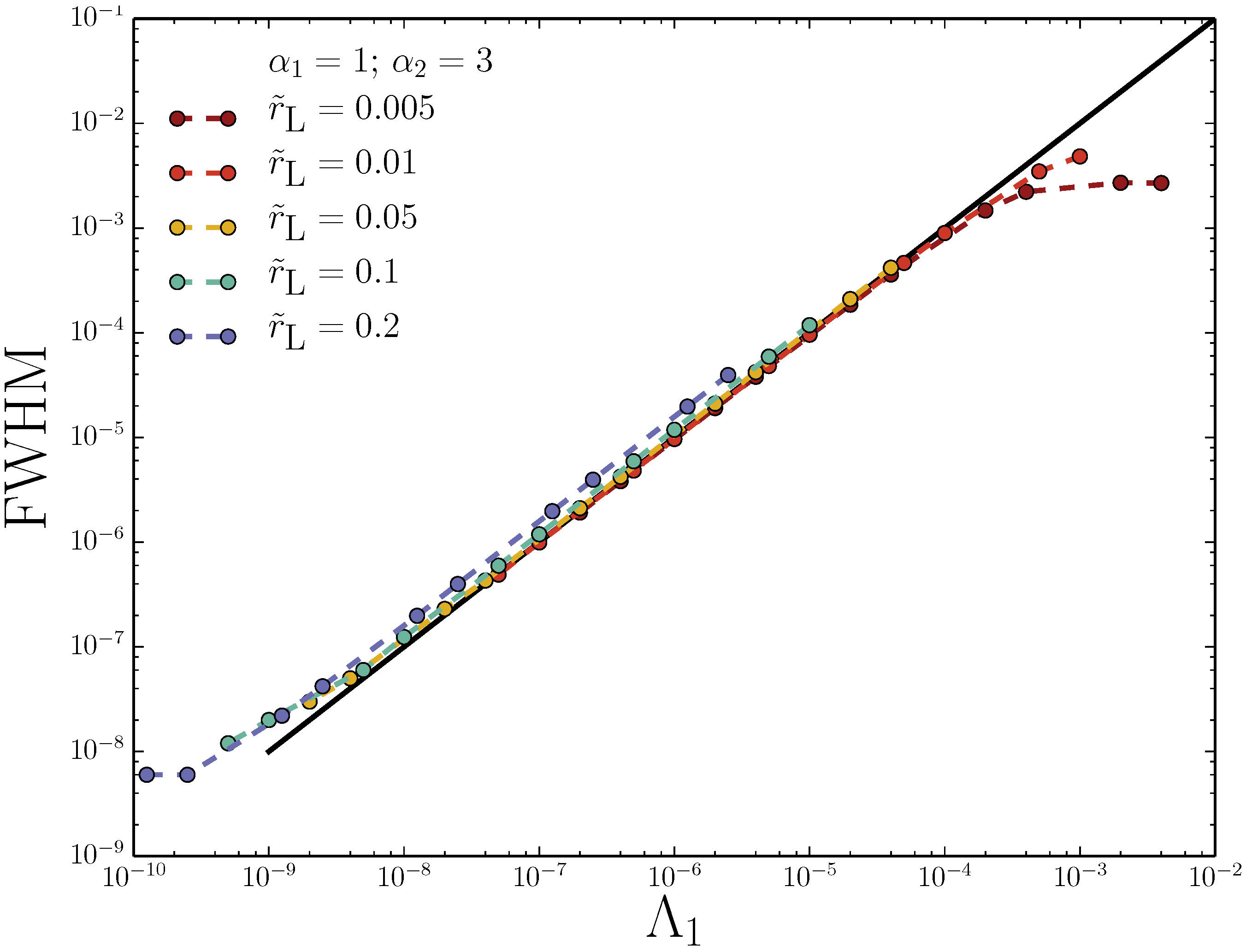
3.3. Adverse-Mode: Ideal Variance Peak
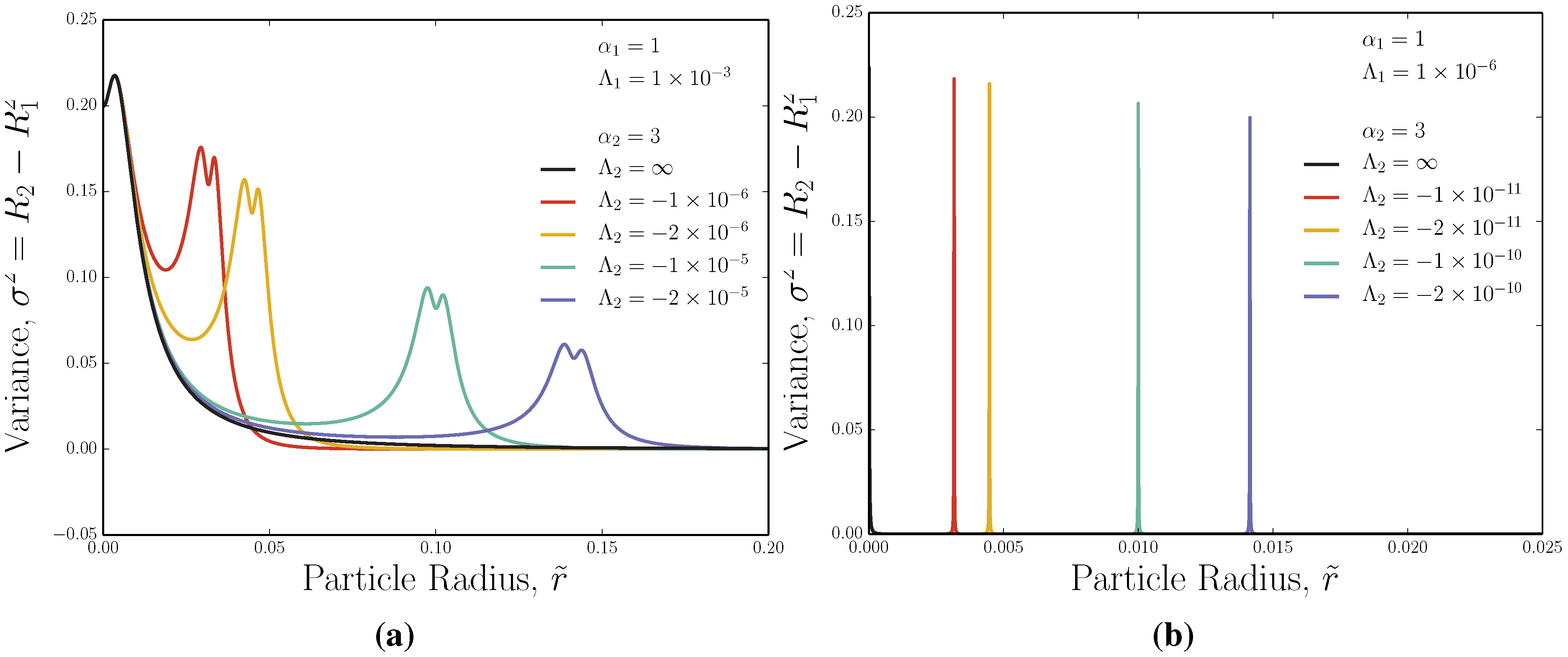
4. Implementation and Feasibility
- The retention ratio peaks can be quite sharp for experimentally-achievable fields and;
- the peak position can be simply predicted.
- Apply an external field with (such as flow-FFF, electrical-FFF or thermal-FFF) to an eluting sample. This field should have a small enough that elution occurs in the steric-mode regime of FFF.
- Apply a field with and (such as centrifugal-FFF) to oppose the first field. must be smaller than for adverse-FFF to be successful.
- Incrementally decrease from an initial large value, shifting to smaller values.
- Identify the abrupt increase in retention ratio (plummet in retention time) when .
- Determine solute size through Equation (25).
- Having found , simultaneously decrease the pair of device retention ratios and to hone the peak and improve the measurement accuracy.
5. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Reschiglian, P.; Zattoni, A.; Roda, B.; Michelini, E.; Roda, A. Field-flow fractionation and biotechnology. Trends Biotechnol. 2005, 23, 475–483. [Google Scholar] [CrossRef] [PubMed]
- Kowalkowski, T.; Buszewski, B.; Cantado, C.; Dondi, F. Field-Flow Fractionation: Theory, Techniques, Applications and the Challenges. Crit. Rev. Anal. Chem. 2006, 36, 129–135. [Google Scholar] [CrossRef]
- Ratanathanawongs Williams, S.; Lee, D. Field-flow fractionation of proteins, polysaccharides, synthetic polymers, and supramolecular assemblies. J. Sep. Sci. 2006, 29, 1720–1732. [Google Scholar] [CrossRef]
- Roda, B.; Zattoni, A.; Reschiglian, P.; Moon, M.; Mirasoli, M.; Michelini, E.; Roda, A. Field-flow fractionation in bioanalysis: A review of recent trends. Anal. Chim. Acta 2009, 635, 132–143. [Google Scholar] [CrossRef] [PubMed]
- Qureshi, R.; Kok, W. Application of flow field-flow fractionation for the characterization of macromolecules of biological interest: A review. Anal. Bioanal. Chem. 2011, 399, 1401–1411. [Google Scholar] [CrossRef] [PubMed]
- Rambaldi, D.; Reschiglian, P.; Zattoni, A. Flow field-flow fractionation: Recent trends in protein analysis. Anal. Bioanal. Chem. 2011, 399, 1439–1447. [Google Scholar] [CrossRef] [PubMed]
- Runyon, J.R.; Ulmius, M.; Nilsson, L. A perspective on the characterization of colloids and macromolecules using asymmetrical flow field-flow fractionation. Colloids Surf. A: Physicochem. Eng. Asp. 2014, 442, 25–33. [Google Scholar] [CrossRef]
- Baalousha, M.; Stolpe, B.; Lead, J. Flow field-flow fractionation for the analysis and characterization of natural colloids and manufactured nanoparticles in environmental systems: A critical review. J. Chromatogr. A 2011, 1218, 4078–4103. [Google Scholar] [CrossRef] [PubMed]
- Stolpe, B.; Guo, L.; Shiller, A.M.; Aiken, G.R. Abundance, size distributions and trace-element binding of organic and iron-rich nanocolloids in Alaskan rivers, as revealed by field-flow fractionation and ICP-MS. Geochim. Cosmochim. Acta 2013, 105, 221–239. [Google Scholar] [CrossRef]
- Koopmans, G.; Hiemstra, T.; Regelink, I.; Molleman, B.; Comans, R. Asymmetric flow field-flow fractionation of manufactured silver nanoparticles spiked into soil solution. J. Chromatogr. A 2015, 1392, 100–109. [Google Scholar] [CrossRef] [PubMed]
- Tanase, M.; Zolla, V.; Clement, C.C.; Borghi, F.; Urbanska, A.M.; Rodriguez-Navarro, J.A.; Roda, B.; Zattoni, A.; Reschiglian, P.; Cuervo, A.M.; et al. Hydrodynamic size-based separation and characterization of protein aggregates from total cell lysates. Nat. Protoc. 2015, 10, 134–148. [Google Scholar] [CrossRef] [PubMed]
- Zattoni, A.; Roda, B.; Borghi, F.; Marassi, V.; Reschiglian, P. Flow field-flow fractionation for the analysis of nanoparticles used in drug delivery. J. Pharm. Biomed. Anal. 2014, 87, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.S.; Lee, J.Y.; Moon, M.H. High Speed Size Sorting of Subcellular Organelles by Flow Field-Flow Fractionation. Anal. Chem. 2015, 87, 6342–6348. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, L. Separation and characterization of food macromolecules using field-flow fractionation: A review. Food Hydrocoll. 2013, 30, 1–11. [Google Scholar] [CrossRef]
- Moquin, A.; Neibert, K.D.; Maysinger, D.; Winnik, F.M. Quantum dot agglomerates in biological media and their characterization by asymmetrical flow field-flow fractionation. Eur. J. Pharm. Biopharm. 2015, 89, 290–299. [Google Scholar] [CrossRef] [PubMed]
- Moore, L.; Williams, P.; Nehl, F.; Abe, K.; Chalmers, J.; Zborowski, M. Feasibility study of red blood cell debulking by magnetic field-flow fractionation with step-programmed flow. Anal. Bioanal. Chem. 2014, 406, 1661–1670. [Google Scholar] [CrossRef] [PubMed]
- Rameshwar, T.; Samal, S.; Lee, S.; Kim, S.; Cho, J.; Kim, I. Determination of the Size of Water-Soluble Nanoparticles and Quantum Dots by Field-Flow Fractionation. J. Nanosci. Nanotechnol. 2006, 6, 2461–2467. [Google Scholar] [CrossRef] [PubMed]
- Stolpe, B.; Hassellöv, M. Changes in size distribution of fresh water nanoscale colloidal matter and associated elements on mixing with seawater. Geochim. Cosmochim. Acta 2007, 71, 3292–3301. [Google Scholar] [CrossRef]
- Von der Kammer, F.; Legros, S.; Hofmann, T.; Larsen, E.; Loeschner, K. Separation and characterization of nanoparticles in complex food and environmental samples by field-flow fractionation. TrAC Trends Anal. Chem. 2011, 30, 425–436. [Google Scholar] [CrossRef]
- Ratanathanawongs Williams, S.; Runyon, J.; Ashames, A. Field-Flow Fractionation: Addressing the Nano Challenge. Anal. Chem. 2011, 83, 634–642. [Google Scholar] [CrossRef] [PubMed]
- Giddings, J.; Myers, M. Steric Field-Flow Fractionation: A New Method for Separating 1 to 100 µm Particles. Sep. Sci. Technol. 1978, 13, 637–645. [Google Scholar] [CrossRef]
- Giddings, J.C.; Williams, P.S. Multifaceted analysis of 0.01 to 100 µm particles by sedimentation field-flow fractionation. Am. Lab. 1993, 95, 88–95. [Google Scholar]
- Berg, H.; Purcell, E.; Stewart, W. A method for separating according to mass a mixture of macromolecules or small particles suspended in a fluid. II. Experiments in a gravitational field. Proc. Natl. Acad. Sci. USA 1967, 58, 1286–1291. [Google Scholar] [CrossRef]
- Lee, S.; Kang, D.; Park, M.; Williams, P. Effect of Carrier Fluid Viscosity on Retention Time and Resolution in Gravitational Field-Flow Fractionation. Anal. Chem. 2011, 83, 3343–3351. [Google Scholar] [CrossRef] [PubMed]
- Berg, H.; Purcell, E. A method for separating according to mass a mixture of macromolecules or small particles suspended in a fluid. III. Experiments in a centrifugal fluid. Proc. Natl. Acad. Sci. USA 1967, 58, 1821–1828. [Google Scholar] [CrossRef]
- Mélin, C.; Perraud, A.; Akil, H.; Jauberteau, M.O.; Cardot, P.; Mathonnet, M.; Battu, S. Cancer Stem Cell Sorting from Colorectal Cancer Cell Lines by Sedimentation Field Flow Fractionation. Anal. Chem. 2012, 84, 1549–1556. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, K.; Kesner, L.; Myers, M.; Giddings, J. Electrical Field-Flow Fractionation of Proteins. Science 1972, 176, 296–298. [Google Scholar] [CrossRef] [PubMed]
- Gigault, J.; Gale, B.; Le Hecho, I.; Lespes, G. Nanoparticle Characterization by Cyclical Electrical Field-Flow Fractionation. Anal. Chem. 2011, 83, 6565–6572. [Google Scholar] [CrossRef] [PubMed]
- Vickrey, T.; Garcia-ramirez, J. Magnetic Field-Flow Fractionation: Theoretical Basis. Sep. Sci. Technol. 1980, 15, 1297–1304. [Google Scholar] [CrossRef]
- Williams, P.; Carpino, F.; Zborowski, M. Characterization of magnetic nanoparticles using programmed quadrupole magnetic field-flow fractionation. Philos. Trans. R. Soc. A 2010, 368, 4419–4437. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Wang, X.; Becker, F.; Gascoyne, P. Introducing dielectrophoresis as a new force field for field-flow fractionation. Biophys. J. 1997, 73, 1118–1129. [Google Scholar] [CrossRef]
- Shim, S.; Gascoyne, P.; Noshari, J.; Stemke Hale, K. Dynamic physical properties of dissociated tumor cells revealed by dielectrophoretic field-flow fractionation. Integr. Biol. 2011, 3, 850–862. [Google Scholar] [CrossRef] [PubMed]
- Semyonov, S.; Maslow, K. Acoustic field-flow fractionation. J. Chromatogr. A 1988, 446, 151–156. [Google Scholar] [CrossRef]
- Budwig, R.; Anderson, M.; Putnam, G.; Manning, C. Ultrasonic particle size fractionation in a moving air stream. Ultrasonics 2010, 50, 26–31. [Google Scholar] [CrossRef] [PubMed]
- Giddings, J. Field-Flow Fractionation. Chem. Eng. News Arch. 1988, 66, 34–45. [Google Scholar] [CrossRef]
- Kononenko, V.; Giddings, J.; Myers, M. On the possibility of photophoretic field-flow fractionation. J. Microcolumn Sep. 1997, 9, 321–327. [Google Scholar] [CrossRef]
- Giddings, J.; Yang, F.; Myers, M. Theoretical and experimental characterization of flow field-flow fractionation. Anal. Chem. 1976, 48, 1126–1132. [Google Scholar] [CrossRef]
- Cumberland, S.; Lead, J. Particle size distributions of silver nanoparticles at environmentally relevant conditions. J. Chromatogr. A 2009, 1216, 9099–9105. [Google Scholar] [CrossRef] [PubMed]
- Wahlund, K.; Giddings, J. Properties of an asymmetrical flow field-flow fractionation channel having one permeable wall. Anal. Chem. 1987, 59, 1332–1339. [Google Scholar] [CrossRef] [PubMed]
- Yohannes, G.; Jussila, M.; Hartonen, K.; Riekkola, M.L. Asymmetrical flow field-flow fractionation technique for separation and characterization of biopolymers and bioparticles. J. Chromatogr. A 2011, 1218, 4104–4116. [Google Scholar] [CrossRef] [PubMed]
- Thompson, G.; Myers, M.; Giddings, J. An Observation of a Field-Flow Fractionation Effect with Polystyrene Samples. Sep. Sci. 1967, 2, 797–800. [Google Scholar] [CrossRef]
- Runyon, J.; Williams, S.R. A theory-based approach to thermal field-flow fractionation of polyacrylates. J. Chromatogr. A 2011, 1218, 7016–7022. [Google Scholar] [CrossRef] [PubMed]
- Cölfen, H.; Antonietti, M. Field-Flow Fractionation Techniques for Polymer and Colloid Analysis. In New Developments in Polymer Analytics I; Schmidt, M., Ed.; Springer: Berlin, Germany; Heidelberg, Germany, 2000; Volume 157, pp. 67–187. [Google Scholar]
- Messaud, F.; Sanderson, R.; Runyon, J.; Otte, T.; Pasch, H.; Williams, S.R. An overview on field-flow fractionation techniques and their applications in the separation and characterization of polymers. Prog. Polym. Sci. 2009, 34, 351–368. [Google Scholar] [CrossRef]
- Fraunhofer, W.; Winter, G. The use of asymmetrical flow field-flow fractionation in pharmaceutics and biopharmaceutics. Eur. J. Pharm. Biopharm. 2004, 58, 369–383. [Google Scholar] [CrossRef] [PubMed]
- Sant, H.; Gale, B. Microscale Field-Flow Fractionation: Theory and Practice. In Microfluidic Technologies for Miniaturized Analysis Systems; Hardt, S., Schönfeld, F., Eds.; Springer: New York, NY, USA, 2007; pp. 471–521. [Google Scholar]
- Wahlund, K.G. Flow field-flow fractionation: Critical overview. J. Chromatogr. A 2013, 1287, 97–112. [Google Scholar] [CrossRef] [PubMed]
- Martin, M.; Beckett, R. Size Selectivity in Field-Flow Fractionation: Lift Mode of Retention with Near-Wall Lift Force. J. Phys. Chem. A 2012, 116, 6540–6551. [Google Scholar] [CrossRef] [PubMed]
- Westermann-Clark, G. Note on Nonisothermal Flow in Field-Flow Fractionation. Sep. Sci. Technol. 1978, 13, 819–822. [Google Scholar] [CrossRef]
- Belgaied, J.; Hoyos, M.; Martin, M. Velocity profiles in thermal field-flow fractionation. J. Chromatogr. A 1994, 678, 85–96. [Google Scholar] [CrossRef]
- Pasol, L.; Martin, M.; Ekiel-Jeżewska, M.; Wajnryb, E.; Bławzdziewicz, J.; Feuillebois, F. Motion of a sphere parallel to plane walls in a Poiseuille flow. Application to field-flow fractionation and hydrodynamic chromatography. Chem. Eng. Sci. 2011, 66, 4078–4089. [Google Scholar] [CrossRef]
- Shendruk, T.; Tahvildari, R.; Catafard, N.; Andrzejewski, L.; Gigault, C.; Todd, A.; Gagne-Dumais, L.; Slater, G.; Godin, M. Field-Flow Fractionation and Hydrodynamic Chromatography on a Microfluidic Chip. Anal. Chem. 2013, 85, 5981–5988. [Google Scholar] [CrossRef] [PubMed]
- Shendruk, T.; Slater, G. Hydrodynamic chromatography and field flow fractionation in finite aspect ratio channels. J. Chromatogr. A 2014, 1339, 219–223. [Google Scholar] [CrossRef] [PubMed]
- Slater, G.; Shendruk, T. Can slip walls improve field-flow fractionation or hydrodynamic chromatography? J. Chromatogr. A 2012, 1256, 206–212. [Google Scholar] [CrossRef] [PubMed]
- Martin, M.; Feuillebois, F. Onset of sample concentration effects on retention in field-flow fractionation. J. Sep. Sci. 2003, 26, 471–479. [Google Scholar] [CrossRef]
- Sant, H.; Gale, B. Characterization of a microscale thermal-electrical field-flow fractionation system. J. Chromatogr. A 2012, 1225, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Johann, C.; Elsenberg, S.; Schuch, H.; Rösch, U. Instrument and Method to Determine the Electrophoretic Mobility of Nanoparticles and Proteins by Combining Electrical and Flow Field-Flow Fractionation. Anal. Chem. 2015, 87, 4292–4298. [Google Scholar] [CrossRef] [PubMed]
- Kato, H.; Nakamura, A. Separation of nano- and micro-sized materials by hyphenated flow and centrifugal field-flow fractionation. Anal. Methods 2014, 6, 3215–3218. [Google Scholar] [CrossRef]
- Shendruk, T.; Slater, G. Operational-modes of field-flow fractionation in microfluidic channels. J. Chromatogr. A 2012, 1233, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Ratier, C.; Hoyos, M. Acoustic Programming in Step-Split-Flow Lateral-Transport Thin Fractionation. Anal. Chem. 2010, 82, 1318–1325. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.B.; Vykoukal, J.; Becker, F.F.; Gascoyne, P.R. Separation of Polystyrene Microbeads Using Dielectrophoretic/Gravitational Field-Flow-Fractionation. Biophys. J. 1998, 74, 2689–2701. [Google Scholar] [CrossRef]
- Yang, J.; Huang, Y.; Wang, X.B.; Becker, F.F.; Gascoyne, P.R.C. Cell Separation on Microfabricated Electrodes Using Dielectrophoretic/Gravitational Field-Flow Fractionation. Anal. Chem. 1999, 71, 911–918. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.B.; Yang, J.; Huang, Y.; Vykoukal, J.; Becker, F.F.; Gascoyne, P.R.C. Cell Separation by Dielectrophoretic Field-flow-fractionation. Anal. Chem. 2000, 72, 832–839. [Google Scholar] [CrossRef] [PubMed]
- Giddings, J. Nonequilibrium Theory of Field-Flow Fractionation. J. Chem. Phys. 1968, 49, 81–85. [Google Scholar] [CrossRef]
- Williams, P. Retention ratio and nonequilibrium bandspreading in asymmetrical flow field-flow fractionation. Anal. Bioanal. Chem. 2015, 407, 4327–4338. [Google Scholar] [CrossRef] [PubMed]
- Mudalige, T.K.; Qu, H.; Sánchez-Pomales, G.; Sisco, P.N.; Linder, S.W. Simple Functionalization Strategies for Enhancing Nanoparticle Separation and Recovery with Asymmetric Flow Field Flow Fractionation. Anal. Chem. 2015, 87, 1764–1772. [Google Scholar] [CrossRef] [PubMed]
- Perez-Rea, D.; Bergenståhl, B.; Nilsson, L. Development and evaluation of methods for starch dissolution using asymmetrical flow field-flow fractionation. Part I: Dissolution of amylopectin. Anal. Bioanal. Chem. 2015, 407, 4315–4326. [Google Scholar] [PubMed]
- Ngaza, N.; Brand, M.; Pasch, H. Multidetector-ThF3 as a Novel Tool for the Investigation of Solution Properties of Amphiphilic Block Copolymers. Macromol. Chem. Phys. 2015, 216, 1355–1364. [Google Scholar] [CrossRef]
- Greyling, G.; Pasch, H. Tacticity Separation of Poly(methyl methacrylate) by Multidetector Thermal Field-Flow Fractionation. Anal. Chem. 2015, 87, 3011–3018. [Google Scholar] [CrossRef] [PubMed]
- Tasci, T.O.; Johnson, W.P.; Fernandez, D.P.; Manangon, E.; Gale, B.K. Biased Cyclical Electrical Field Flow Fractionation for Separation of Sub 50 nm Particles. Anal. Chem. 2013, 85, 11225–11232. [Google Scholar] [CrossRef] [PubMed]
- Tasci, T.O.; Johnson, W.P.; Fernandez, D.P.; Manangon, E.; Gale, B.K. Circuit modification in electrical field flow fractionation systems generating higher resolution separation of nanoparticles. J. Chromatogr. A 2014, 1365, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Kwen, H.D.; Kim, Y.S.; Choi, S.H.; Lee, S. γ-ray synthesis and size characterization of CdS quantum dot (QD) particles using flow and sedimentation field-flow fractionation (FFF). Microchem. J. 2014, 117, 34–39. [Google Scholar] [CrossRef]
- Woo, I.S.; Jung, E.C.; Lee, S. Retention behavior of microparticles in gravitational field-flow fractionation (GrFFF): Effect of ionic strength. Talanta 2015, 132, 945–953. [Google Scholar] [CrossRef] [PubMed]
- Ponyik, C.; Wu, D.; Ratanathanawongs Williams, S. Separation and composition distribution determination of triblock copolymers by thermal field-flow fractionation. Anal. Bioanal. Chem. 2013, 1, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Gale, B.; Sant, H. Nanoparticle analysis using microscale field flow fractionation. In Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series (San Jose, USA); SPIE: Bellingham, WA, USA, 2007; Volume 6465, p. 18. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shendruk, T.N.; Slater, G.W. Adverse-Mode FFF: Multi-Force Ideal Retention Theory. Chromatography 2015, 2, 392-409. https://doi.org/10.3390/chromatography2030392
Shendruk TN, Slater GW. Adverse-Mode FFF: Multi-Force Ideal Retention Theory. Chromatography. 2015; 2(3):392-409. https://doi.org/10.3390/chromatography2030392
Chicago/Turabian StyleShendruk, Tyler N., and Gary W. Slater. 2015. "Adverse-Mode FFF: Multi-Force Ideal Retention Theory" Chromatography 2, no. 3: 392-409. https://doi.org/10.3390/chromatography2030392




