Abstract
The knapsack problem is one of the most widely researched NP-complete combinatorial optimization problems and has numerous practical applications. This paper proposes a quantum-inspired differential evolution algorithm with grey wolf optimizer (QDGWO) to enhance the diversity and convergence performance and improve the performance in high-dimensional cases for 0-1 knapsack problems. The proposed algorithm adopts quantum computing principles such as quantum superposition states and quantum gates. It also uses adaptive mutation operations of differential evolution, crossover operations of differential evolution, and quantum observation to generate new solutions as trial individuals. Selection operations are used to determine the better solutions between the stored individuals and the trial individuals created by mutation and crossover operations. In the event that the trial individuals are worse than the current individuals, the adaptive grey wolf optimizer and quantum rotation gate are used to preserve the diversity of the population as well as speed up the search for the global optimal solution. The experimental results for 0-1 knapsack problems confirm the advantages of QDGWO with the effectiveness and global search capability for knapsack problems, especially for high-dimensional situations.
1. Introduction
The 0-1 knapsack problem (KP01) is a classical combinatorial optimization problem. It has many practical applications, such as project selection, investment decisions, and complexity theory [1,2]. Two classes of approaches were previously proposed to solve the KP01 [3]. The first class of approaches includes exact methods based on mathematical programming and operational research. It is possible to obtain the exact solutions of small-scale KP01 problems by exact methods such as branching and bound algorithm [4] and dynamic programming [5]. However, KP01 problems in various complex situations are NP-hard problems, and it is impractical to obtain optimal solutions using deterministic optimization methods for large-scale problems. The second class contains approximate methods based on metaheuristic algorithms [6]. Metaheuristic algorithms are shown to be effective approaches to solving complex engineering problems in a reasonable time when compared with exact methods [7]. Therefore, the application of metaheuristic algorithms has drawn a great deal of attention in the field of optimization.
In recent years, most of the metaheuristic algorithms, such as the genetic algorithm (GA) [8], ant colony optimization (ACO) [9], particle swarm algorithm (PSO) [10], artificial bee colony (ABC) [11], cuckoo search (CS) [12], firefly algorithm (FA) [13], and improved approaches based on these algorithms [14,15,16,17,18,19], were applied to KP01 problems and achieved outstanding results. However, these metaheuristic algorithms require not only a large amount of memory for storing the population of solutions, but also a long computational time for finding the optimal solutions. In the last few years, novel metaheuristic algorithms were proposed. Wang et al. [20,21] improved the swarm intelligence optimization approach inspired by the herding behavior of krill and came up with the krill herd (KH) algorithm to solve combinatorial optimization problems. Faramarzi et al. [22] presented a metaheuristic called the Marine Predators Algorithm (MPA) with an application in engineering design problems. MPA follows the rules that naturally govern in optimal foraging strategy and encounters a rate policy between predator and prey in marine ecosystems. Inspired by the phototaxis and Lévy flights of moths, Wang et al. [23] developed a new metaheuristic algorithm called the moth search (MS) algorithm. MS was applied to solve discounted 0-1 knapsack problems [24] and set-union knapsack problems [25]. Gao et al. [26] presented a novel selection mechanism augmenting the generic DE algorithm (NSODE) to achieve better optimization results for solving fuzzy job-shop scheduling problems. Abualigah et al. [27] proposed the arithmetic optimization algorithm (AOA) based on the distribution behavior of the main arithmetic operators in mathematics: multiplication, division, subtraction, and addition. Wang et al. [28] proposed a new nature-inspired metaheuristic algorithm called monarch butterfly optimization (MBO) by simulating the migration of monarch butterflies. MBO was applied to solve classic KP01 [29], discounted KP01 [30], and large-scale KP01 [31,32] problems with superior searching accuracy, convergent capability, and stability. In most metaheuristic algorithms, it is difficult to use the information from individuals in previous iterations in the updating process. Wang et al. [33] presented a method for reusing the information available from previous individuals and feeding previous useful information back into the updating process in order to guide later searches.
The emergence of quantum computing [34,35] was derived from the principles of quantum theory such as quantum superposition, quantum entanglement, quantum interference, and quantum collapse. Quantum computing brings new ideas to optimization due to its underlying concepts, along with the ability to process huge numbers of quantum states simultaneously in parallel. The merging of metaheuristic optimization and quantum computing recently became a growing theoretical and practical interest aiming at deriving benefits from quantum computing capabilities to enhance the convergence and speed of metaheuristic algorithms. Several scholars investigated the effect of introducing quantum computing in metaheuristic algorithms to maintain a balance between exploration and exploitation. Han and Kim proposed a genetic quantum algorithm (GQA) [36] and a quantum inspired evolutionary algorithm (QEA) [37] by merging classical evolutionary algorithms with quantum computing concepts such as the quantum bit and the quantum rotation gate. Talbi et al. [38] proposed a new algorithm inspired by genetic algorithms and quantum computing for solving the traveling salesman problem (TSP). Chang et al. [39] proposed a quantum-inspired electromagnetism-like mechanism (QEM) to solve the KP01. Xiong et al. [40] presented an analysis of quantum rotation gates in quantum-inspired evolutionary algorithms. To avoid the problem of premature convergence, mutation operation [41], crossover operation [42], new termination criterion, and new rotation gate [43] were applied to the QEA and subsequently improved.
The differential evolution (DE) algorithm [44], proposed by Storn and Price, was derived from differential vectors of solutions for global optimization. Several simple operations including mutation, crossover, and selection were used in the DE algorithm to explore the search space. Subsequently, several algorithms combining the DE algorithm with quantum computing were designed to increase global search ability. Hota and Pat [45] extended the concept of differential operators with adaptive parameter control to the quantum paradigm and proposed the adaptive quantum-inspired differential evolution (AQDE) algorithm. In addition, quantum interference operation [46] and mutation operation [47] were brought into a quantum-inspired DE algorithm.
Several metaheuristic algorithms combining the QEA and DE were proven to be effective and efficient for solving the KP01. Wang et al. [48] proposed a quantum swarm evolutionary (QSE) algorithm that updated quantum angles automatically with improved PSO. Layeb [49] presented a quantum inspired harmony search algorithm (QIHSA) based on a harmony search algorithm (HSA) and quantum computing. Zouache et al. [50] proposed a merged algorithm called quantum-inspired differential evolution with particle swarm optimization (QDEPSO) to solve the KP01. Gao et al. [51] proposed a quantum-inspired wolf pack algorithm (QWPA) with quantum rotation and quantum collapse to improve the performance of the wolf pack algorithm for the KP01.
The grey wolf optimizer (GWO) proposed by Mirjalili et al. [52] mimics the specific behavior of grey wolves based on leadership hierarchy in nature. Srikanth et al. [53] presented a quantum-inspired binary grey wolf optimizer (QIBGWO) to solve the problem of unit commitment scheduling.
Population diversity is crucial in evolutionary algorithms to enable global exploration and to avoid poor performance due to premature convergence [54]. However, it is hard for classical algorithms to enhance diversity and convergence performance because their population quickly converges to a specific region of the solution space. In addition, these algorithms require a large amount of memory as well as long computational time to find the optimal solution for high-dimensional situations. To avoid these difficulties, we propose a new algorithm, called quantum-inspired differential evolution algorithm with grey wolf optimizer (QDGWO). The proposed algorithm combines the features of the QEA, DE, and GWO to solve the 0-1 knapsack problem. To preserve diversity throughout the evolution, the new algorithm adopts the concepts of quantum representation and the integration of the quantum operators such as quantum measurement and quantum rotation. The adaptive operations of the DE (mutation, crossover, selection) and GWO can increase the adaptation and diversification in updating individuals. The experimental results demonstrate the competitive performance of the proposed algorithm.
2. Related Work
2.1. Knapsack Problem
The 0-1 knapsack problem is a well-known combinatorial optimal problem that has been studied in areas such as project selection, resource distribution, and the network interdiction problem. The KP01 was demonstrated to be NP-complete [55,56]. It can be described as follows:
Given a set W of m items, W = (x1, x2, x3, …, xm). wi is the weight item xi, and pi is the profit of xi. C is the weight capacity of the knapsack. The objective is to find the subset Xoptimal from set of m items that maximizes the total profit, while keeping the total weight of the selected items from exceeding C.
The 0-1 knapsack problem can be defined as:
where xi can take either the value 1 (as selected) or the value 0 (as not selected, also called rejected).
2.2. Grey Wolf Optimizer (GWO)
The GWO algorithm [52] is inspired by the leadership hierarchy and hunting mechanism of grey wolves. To model the social order of grey wolves in the GWO, the best solution is considered the alpha (α) wolf, and the second and third best solutions are beta (β) and delta (δ) wolves, respectively. The rest of the feasible solutions are considered as omega (ω) wolves. In the GWO, α, β, and δ wolves lead the hunting, and the ω wolves go after these leading wolves when searching for the global optimal solution (target) as the prey, as shown in Figure 1.
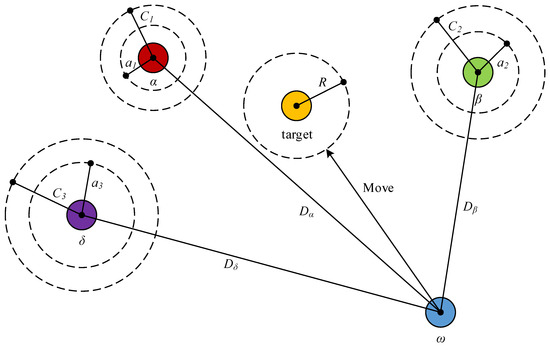
Figure 1.
Position updating mechanism of GWO.
Grey wolves have the ability to recognize the location of prey and encircle them during the hunt. In order to simulate the hunting behavior of grey wolves mathematically, it is supposed that the α, β, and δ wolves have better knowledge about the potential location of prey. Therefore, the GWO saves the first three best solutions arrived at so far and forces the other ω wolves to update their positions according to the position of the best search agents.
During optimization, the GWO algorithm allows its search agents to update their position based on the location of the alpha, beta, and delta wolves with the distance vector between itself and the three best wolves when attacking the prey. Finally, the position and fitness of the alpha wolf are regarded as the global optimal solution in searching for the optimization when a termination criterion is satisfied.
3. Quantum-Inspired Differential Evolution with Adaptive Grey Wolf Optimizer
The proposed QDGWO algorithm is presented for the knapsack problems. First, the proposed algorithm adopts the quantum computing principles such as quantum representation and quantum measurement operation. Quantum representation allows the representation of the superposition of all potential states in one quantum individual. Second, adaptive mutation operations (used in the DE), crossover operations (used in the DE), and quantum observation are combined to generate new solutions as trial individuals in the solution space. Finally, the selection operator chooses the better solutions between the stored individuals and the trial individuals generated by the mutation and crossover operations of the DE. In the event that the trial individuals are worse than the current individuals, the QDGWO integrates the adaptive GWO and quantum rotation gate to preserve the diversity of the population of solutions as well as accelerate the search for the global optimum. The framework of the QDGWO algorithm is shown in Figure 2.
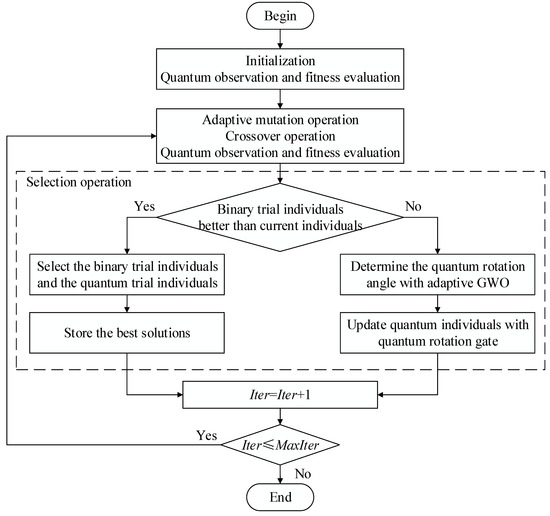
Figure 2.
Framework of QDGWO.
3.1. Binary Representation
The choice of the representation for individuals, also known as individual coding, is a crucial issue in evolutionary algorithms. The proposed QDGWO algorithm adopts the binary coding, which is the most appropriate way to indicate the selection or rejection of items. Each individual X is represented as a binary vector with length m (m is the item size): X = (x1, x2, …, xm), where m is the number of items.
The following example shows the binary
representation for item selection: x1 and x3 from the item set W are selected: W = {x1, x2, x3, x4} → X = (1 0 1 0).
The binary population is made up of the binary individuals at the tth generation, where n is the size of population.
3.2. Quantum Representation
The representation of the AQDE [45] is used in the proposed algorithm, where each quantum individual q corresponds to a phase vector qθ, which is a string of phase angles θi (1 ≤ i ≤ m), which can be given by
where m is the length of the quantum bit (qubit) individual.
Each quantum individual q is a string of qubits:
The probability amplitudes of a quantum bit are expressed as a pair of numbers (cos(θi), sin(θi)). |sin(θi)|2 represents the probability of selecting item xi, and |cos(θi)|2 represents the probability of rejecting item xi.
The quantum population is made up of the quantum individuals at the tth generation, where n is the size of the population.
3.3. Initialization
The general principle of superposition of quantum mechanics assumes that the original state must be considered as the result of a superposition of two or more other states in an infinite number of ways [57]. Therefore, the initial quantum individual is regarded as a superposition of all possible states. For 0-1 knapsack problems, each state represents a combination of selecting or rejecting items, and the initial quantum individual is required to generate every possible combination. For this, each vector qθi is initialized by:
where rij = random{1,3,5,7}, which means rij is an odd integer generated randomly in the set while . This means that for initial individuals, |cos(θij)|2 = |sin(θij)|2 = 1/2, so that the probabilities of selecting item xi and rejecting item xi are equal.
The initial quantum individual which corresponds to can be given by:
where m is the length of the qubit quantum individual.
is the initial quantum population, where n is the size of the population.
3.4. Quantum Observation and Fitness Evaluation
Based on the quantum superposition principle, a quantum state is a superposition of all possibly stationary states. The quantum superposition state will collapse to a stationary state by quantum observation. In the proposed QDGWO algorithm, the quantum superposition states are represented by quantum individuals, and the stationary states are represented through binary individuals. Before evaluating the fitness of individuals, quantum observation and reparation for quantum individuals q are required to receive binary individuals X, as shown in Algorithm 1.
After quantum observation, the fitness of binary individual X is evaluated as:
| Algorithm 1 Quantum Observation and Reparation |
| Input: quantum individuals q |
| Output: binary individuals X |
| //Initialize the bits of individual X to 0. |
| // Initialize the total weights of the individuals to 0. |
| while () do |
| //Generate the random integer . |
| if (xi = 0) then |
| if(r > |cos(θi)|2) then |
| //Select item xi and include the weight wi of item xi in the total weight wtotal. |
| end if |
| end if |
| end while |
| //The total weight wtotal has exceeded the capacity C when the loop is ended, so item xi needs to be extracted from the selected items for reparation. |
3.5. Adaptive Mutation Operation with Dynamic Iteration Factor
The mutation operation is one of the main operations in differential evolution. In the QDGWO, DE/best/2, proposed by Price and Storn [44], is used to select parent vectors. In this strategy, the mutation vector is generated by the vector qθα corresponding to the current best binary individual Xα and the difference between two different target vectors qθr1 and qθr2 which are randomly selected. This difference is weighted by the differentiation control factor F.
The quantum mutation vector at the tth generation can be generated by:
where .
To improve the performance of differential operations in different phases, we propose an adaptive strategy to determine the differentiation control factor F with the iteration of evolution:
where F0 is the initial differentiation control factor, and F1 is the adaptive f differentiation control factor. tmax is the maximum iteration number of the algorithm.
With this adaptive strategy, in the early stage of the iteration, the smaller t will be proposed with a larger Ft, which is beneficial for attaining good diversity of individuals for global searching. Ft will be smaller and smaller during the iteration. In the late stages, Ft is close to F0, which aids in local searching for the global optimal solution.
The quantum mutation individual corresponding to the quantum mutant vector can be obtained by:
where m is the length of the qubit quantum individual.
The quantum mutation population is made up of the quantum mutation individuals at the tth generation, where n is the size of the population.
3.6. Crossover Operation
The crossover operation is another main operation in differential evolution. The trial vector is generated by crossover between the mutant vector and the target vector with a binomial crossover strategy [44].
The quantum trial vector at the tth generation can be generated by:
where is the probability of the crossover operation which is randomly generated at tth iteration. In addition, is an integer to ensure that obtains at least one vector from .
The quantum trial individual corresponding to the quantum trial vector can be obtained by:
where m is the length of the qubit quantum individual.
The quantum trial population is made up of the quantum trial individuals at the tth generation, where n is the size of the population.
3.7. Selection Operation
After the crossover operation, the trial quantum individuals will be transformed into binary individuals by observation and reparation, as discussed in Section 3.4. The population of trial quantum individuals is transformed into a population of trial binary individuals .
The selection operation generates the individuals of next iteration between the current individuals and the trial binary individuals , as follows:
The quantum individuals of the next iteration are generated by:
where is a quantum rotation gate (QRG) with an adaptive GWO. is presented in Section 3.8.
3.8. Quantum Rotation Gate with Adaptive GWO
The quantum rotation gate is used to update the values of the qubits in a quantum individual as follows [36]:
The quantum individuals of the next iteration after quantum rotation are presented as:
where is the rotation angle of the QRG, and s(αi βi) is the direction signal of the rotation angle.
The polar plot of the QRG for qubits is illustrated in Figure 3, and the quantum rotation angle parameters used in [36] are shown in Table 1.
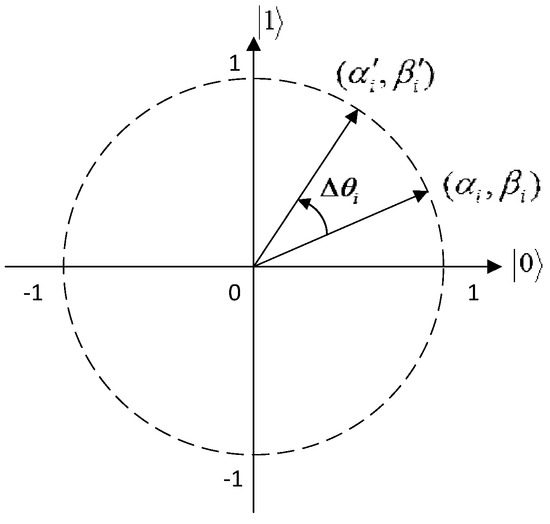
Figure 3.
Polar plot of quantum rotation gate for qubit.

Table 1.
Lookup table of rotation angle.
Generally speaking, the core concept of the quantum rotation gate is to motivate the probability amplitudes of each qubit in quantum individuals to converge to the corresponding bits of the current best solution in the population. Realistically, the lookup table is a convergence strategy. In this strategy, the fitness f(x) of the binary solution x after quantum observation is compared with the fitness f(b) of the current best solution b. The quantum rotation gate will update the probability amplitude (αi, βi) toward the direction that favors the emergence of the better solution between x and b. For example, if xi = 0 and bi = 1, and f(xi) > f(bi), then xi is the current best solution. This means that the state is the optimal state for the ith qubit of a quantum individual, and that the QRG will update (αi, βi) to increase the probability of the state to make the probability amplitude evolve toward the direction benefiting the appearance of xi = 0. If (αi, βi) is located in the first quadrant as shown in Figure 2, the quantum rotation is in a clockwise direction, which favors xi = 0.
Normally, quantum rotation can bring the quantum chromosomes closer to the current optimal chromosomes and generate the exploitation near the current optimal solution to find better solutions. As with other metaheuristic algorithms, individuals of the population converge more closely to the best solution after quantum rotation. The QRG makes the population evolve continuously and speeds up the convergence of the algorithm.
The magnitude of determines the granularity of the search and should be chosen appropriately. A too-small value of the rotation angle will affect the convergence speed and may even lead to a stagnant state. However, if the value is too large, the solutions may diverge or converge prematurely to a local optimal solution [37].
The traditional QRG requires predefined rotation angles, and the value and direction of should be designed for specific application problems. Because the values of quantum rotation angles are dependent on the problems, the verification of angle selection becomes important, although tedious, work when traditional QRGs are used for optimization problems. If the quantum rotation angles can be obtained adaptively without relying on predefined data, the efficiency of the QRG will be greatly improved, while the types of applications with the QRG can be easily increased. This is exactly what metaheuristic algorithms are good at. Of the large number of metaheuristics, the GWO is a novel swarm optimization algorithm motivated by the social behavior of grey wolves. Because the GWO has the advantages of simple principles, fast searching speed, high seeking accuracy, and easy implementation, it can be easily combined with practical engineering problems [58]. Therefore, the GWO has high theoretical research value and application value, and becomes suitable for generating quantum rotation angles.
In addition, the traditional QRG motivates the probability amplitudes of each qubit in quantum individuals to converge to the corresponding bits of the current best solution in the population. If the current best solution is not the global optimal solution, the direction of quantum rotation may be far from the global optimal solution, and the algorithm may be trapped in local optimal stagnation. Since the GWO records multiple best individuals, it is useful for the QRG to jump out of local optimum with the GWO.
In the proposed QDGWO algorithm, the rotation angle of the QRG is determined with an adaptive GWO. This is described as follows: In the original GWO algorithm, the positions of other ω wolves are updated by the distance vector between themselves and the three best wolves, while for the α, β, and δ wolves, they can hunt the prey more freely. The hunting zone for α, β, and δ wolves will become smaller during the iteration. In the adaptive GWO, these features of the GWO will be inherited and developed.
For a quantum rotation gate with an adaptive GWO (), is calculated using the position of α, β, and δ wolves as follows:
where ; n is the size of the population; m is the number of items; is the rotation angle magnitude; is the jth component in the binary individual of the ith wolf during tth iteration; and , and are determined by comparing the fitness of the current binary individual with α, β, and δ wolves as follows:
where N(0,1) is the Gaussian distribution, , .
For the ω wolves, they hunt the prey based on their own positions vs. the positions of the three best wolves. It is obvious that for the ith wolf in the ω wolves group, . Therefore, the rotation angle of the ith wolf can be calculated with the binary individuals of α, β, δ, and the ith wolf.
For α, β, and δ wolves, they have the duty of searching for the optimal solution from their old positions. With increasing t, , and will be much smaller in the late stages of the iteration than what they are in the early stages of the iteration, which helps the ω wolves converge toward an estimated position of prey calculated by α, β, and δ wolves. This strategy is helpful for jumping out of local optimal stagnation, especially in the final stage of iterations.
The speed of convergence and quality of the solution are greatly affected by the magnitude of the rotation angle , which is given by:
where is linearly decreasing from to during the iteration.
In the end, can be generated by:
where is the direction signal of the rotation angle as follows:
With the adaptive strategy of and , the searching granularity of the QDGWO changes from coarse to fine. A different searching granularity in the iteration will facilitate the process for search agents to reach the global optimal solution.
3.9. Procedure of QDGWO Algorithm
Based on the description above, the procedure of the QDGWO and its main steps can be summarized as shown in Algorithm 2.
| Algorithm 2 QDGWO |
| // Initializes the iteration |
| Initialize Q(0) by Equations (5) and (6) |
| while (t < MaxIter) do |
| Observe to get X(t) from q(t)//Quantum observation |
| Evaluate fitness of X(t) by Equation (7) |
| Apply mutation on qM(t) by Equations (8) and (11)//Adaptive mutation |
| Obtain qC(t) by crossover by Equations (12) and (13)//Crossover |
| Observe to get XC(t) from qC(t)//Quantum observation |
| Evaluate fitness of XC(t) |
| if the trial binary individuals XC(t) is better than X(t) then |
| Update X(t+1) and q(t+1) by Equations (14) and (15)//Selection |
| else |
| Update q(t + 1) using QRG with adaptive GWO by Equations (16)–(24) |
| end if |
| end while |
3.10. Example of QDGWO Algorithm to Solve KP01
In the following, a KP01 problem is described as an example to be solved by the QDGWO algorithm.
Given a set of ten items, W = (x1, x2, x3, …, x10), and wi is the weight of the ith item xi; pi is the value of xi; and C is the weight capacity of the knapsack. Suppose that wi = i, and pi = wi+5, and .
Then, this 0-1 knapsack problem can be defined as:
where wi = i, and pi = wi + 5 = i + 5.
In this example, the population size was set to 20, and the maximum number of iterations was set to 200. The other parameters are presented in Table 2. The evolution process of , an individual of the quantum population, is shown below.

Table 2.
Parameters of algorithms in experiments.
The initial quantum population was initialized by Equations (5) and (6). The vector qθ1 was initialized by , and the quantum individual was initialized by .
After quantum observation, the binary individual was generated as , and the fitness of was evaluated as .
The mutation vector was generated by Equations (8)–(11), where t = 0; ; and (rand(0,1) was randomly generated as 0.68).
The vector qθα corresponding to the current best binary individual Xα and two different random target vectors qθr1 and qθr2 are shown as:
The quantum mutation vector was generated by:
The quantum trial vector at the tth generation was generated by Equations (12) and (13):
where CR was randomly generated as 0.35, and rnbr_i = 3.
After quantum observation, the trial binary individual was generated as , and the fitness was evaluated as . Because , qt+1 should be updated by the QRG with an adaptive GWO.
The positions and profits of the current three best wolves were shown as:
Additionally, ; ; ; .
Then, the quantum individual of the next iteration was generated by Equations (16)–(24) as:
The individuals of the next iteration continued to evolve until the maximum number of iterations was reached. After the iterations, the best profit of this KP01 problem was 57, and one of the best solutions was (0,1,1,1,1,1,1,0,0,0).
4. Experimental Results
To assess the performance of the proposed QDGWO algorithm, two groups of datasets are used for solving the KP01.
All experiments were conducted with Matlab 2016b, running on an Intel Core i7-4790 CPU @ 3.60 GHz, and Windows 7 Ultimate Edition.
In the first experiment described in [37], there were 50, 250, 500, 1000, 1500, 2000, 2500, and 3000 dimension sets of data by Equation (26) to test the performance of the QDGWO in high-dimension situations.
Given a set of m items, W = (x1, x2, x3, …, xm).
where wi is the weight of the ith item xi; pi is the value of xi; C is the weight capacity of the knapsack; and m is the number of items.
In the first experiment, m ranged from 50 to 3000, and the maximum number of iterations in all cases was set to 1000.
To verify the effectiveness and efficiency of the QDGWO, the results of the proposed algorithm were compared with three algorithms: QEA [37], AQDE [45], and QSE [48]. The parameters of algorithms used in the experiments are presented in Table 2, where the population size is 20. The best profits, the average profits, the worst profits, and the standard deviations of 30 independent runs are shown in Table 3 and Figure 4, Figure 5, Figure 6 and Figure 7. The Wilcoxon signed-rank test [59] is performed for the results of the competing algorithms in Table 3 with a significance level α = 0.05, where +, −, and = indicate that this algorithm is superior, inferior, or equal to the QDGWO, respectively.

Table 3.
Experimental results for 0-1 knapsack problems (Experiment 1).
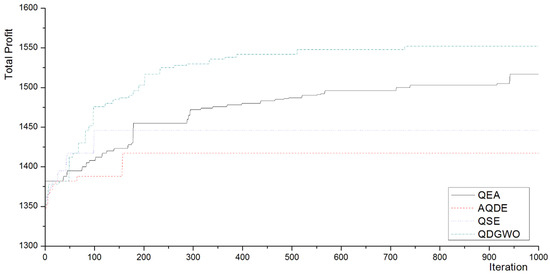
Figure 4.
Best profits for the 0-1 knapsack problems (250 items in Experiment 1).
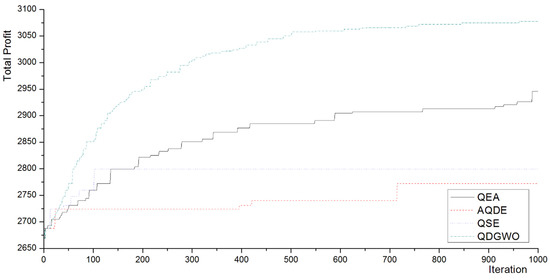
Figure 5.
Best profits for the 0-1 knapsack problems (500 items in Experiment 1).
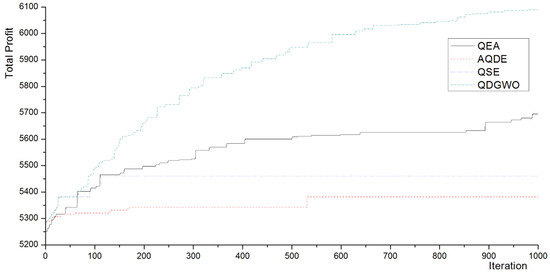
Figure 6.
Best profits for the 0-1 knapsack problems (1000 items in Experiment 1).
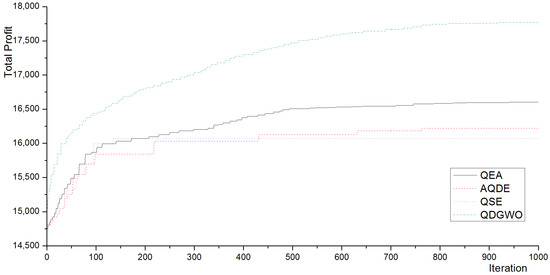
Figure 7.
Best profits for the 0-1 knapsack problems (3000 items in Experiment 1).
To illustrate the importance of the role of the crossover operation of the DE in exploring the global optimum, comparative tests between the QDGWO with and without the crossover operation were performed. Moreover, we compared the binomial crossover operator of the DE with the exponential crossover operator of the DE. The best profits, the average profits, the worst profits, and the standard deviations of 30 independent runs are presented in Table 4. The Wilcoxon signed-rank test [59] is performed for the results in Table 4 with a significance level α = 0.05, where +, −, and = indicate that this strategy is superior, inferior, or equal to the QDGWO with a binomial crossover of the DE, respectively.

Table 4.
Experimental results of QDGWO algorithm without crossover of DE, with binomial crossover of DE, and with exponential crossover of DE.
In the second experiment described in [49], there were 50, 200, 500, 1000, 1500, and 2000 dimension sets of data by Equation (27) to test the performance of the QDGWO in high-dimension situations.
Given a set of m items, W = (x1, x2, x3, …, xm).
where wi is the weight of the ith item xi; pi is the value of xi; C is the weight capacity of the knapsack; and m is the number of items.
In the second experiment, m ranged from 50 to 2000, and the maximum number of iterations in all cases was set to 1000.
To present the performance of the proposed algorithm in the global optimization, we compared the QDGWO algorithm with the QIHSA [49] for knapsack problems. The optimization results of the success rate (SR%) and the best profit are shown in Table 5. The Wilcoxon signed-rank test [59] is performed for the results of the QIHSA in Table 5 with a significance level α = 0.05, where +, −, and = indicate that this algorithm is superior, inferior, or equal to the QDGWO, respectively.

Table 5.
Experimental results of QDGWO and QIHSA for 0-1 knapsack problems (Experiment 2).
The obtained results demonstrate the competitive performance of the proposed QDGWO algorithm. According to the results, the proposed algorithm is more efficient for the high-dimensional 0-1 knapsack problems, as shown in Table 4 and Figure 3, Figure 4 and Figure 5. Compared with the QEA [25], AQDE [33], QSE [36], and QIHSA [37], the QDGWO was the most effective and efficient algorithm in the experiments. The advantages of the QDGWO became more obvious when the number of items was large, especially in high dimensional cases of the knapsack problems.
The proposed algorithm obtains both rapid exploration and high exploitation in searching solutions. The QDGWO converges quickly to the global optimal solution. For example, the algorithm approaches the global optimum at about the 500th iteration in the case of 500 items (see Figure 4). However, the algorithm continues searching near the global optimal solution, i.e., the exploitation. To illustrate this, in the case of 500 items (see Figure 4), the QDGWO continues seeking further optimization after approaching the optimal solution and obtains better solutions in the exploitation until the end of the iterations.
Based on the results shown in Table 3, it can be concluded that the crossover operation plays a significant role in searching the solution space efficiently. However, the performance of the QDGWO is not very sensitive to which kind of crossover operator is used in the algorithm. From the experiment results, the binomial crossover operator of the DE yields slightly better optimal solutions than the exponential crossover operator of the DE in all cases. The results can be interpreted to show that quantum updating with the quantum rotation gate remains the most decisive and crucial operation in exploring the search space even if the crossover operation is required to improve the solutions.
Finally, compared with the other four methods, the experimental results show the advantages of the collaborative optimization with operations of adaptive mutation, crossover, and quantum rotation gate with the adaptive GWO in investigating the search space.
5. Conclusions
A quantum-inspired differential evolution algorithm with grey wolf optimizer (QDGWO) was proposed to solve the 0-1 knapsack problems. The proposed algorithm combined the superposition principles of quantum computing, differential evolution operations, and the hunting behaviors of grey wolves. The QDGWO used the principles of quantum computing such as quantum superposition states and quantum gates. Furthermore, it contained mutation, crossover, and selection operations of the DE. To maintain a better balance between the exploration and exploitation of searching for the global optimal solution, the proposed algorithm adapted a quantum rotation gate with the adaptive GWO to update the population of solutions. The results of tests performed for resolving the knapsack problems demonstrate that the QDGWO was able to enhance diversity and convergence performance for solving 0-1 knapsack problems. In addition, the QDGWO was effective and efficient in finding the optimal solutions for high-dimensional situations.
Although the QDGWO displays excellent performance in solving 0-1 knapsack problems, there are several directions of improvement for the proposed algorithm. First, to improve the effectiveness of the QDGWO, initial solutions of the quantum population can be generated with metaheuristic methods. In addition, the proposed approaches can be applied to solve other combinatorial optimization problems. Moreover, it is worth studying how to use the concepts of quantum computing in other novel metaheuristic approaches such as the MPA [22] and AOA [27], as well as multi-objective optimization algorithms.
Author Contributions
Conceptualization, Y.W. and W.W.; methodology, Y.W.; software, Y.W.; validation, Y.W.; formal analysis, Y.W.; investigation, Y.W.; resources, Y.W.; data curation, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W. and W.W.; visualization, Y.W.; supervision, W.W.; funding acquisition, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 61873240).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the anonymous reviewers for their constructive comments and suggestions. This work was supported in part by the National Natural Science Foundation of China (No. 61873240).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kellerer, H.; Pferschy, U.; Pisinger, D. Knapsack Problems; Springer: Berlin/Heidelburg, Germany, 2004. [Google Scholar]
- Wang, X.; He, Y. Evolutionary algorithms for knapsack problems. J. Softw. 2017, 28, 1–16. [Google Scholar]
- Jourdan, L.; Basseur, M.; Talbi, E.G. Hybridizing exact methods and metaheuristics: A taxonomy. Eur. J. Oper. Res. 2009, 199, 620–629. [Google Scholar] [CrossRef]
- Shih, W. A branch and bound method for the multiconstraint zero-one knapsack problem. J. Oper. Res. Soc. 1979, 30, 369–378. [Google Scholar] [CrossRef]
- Toth, P. Dynamic programming algorithms for the zero-one knapsack problem. Computing 1980, 25, 29–45. [Google Scholar] [CrossRef]
- Zou, D.; Gao, L.; Li, S.; Wu, J. Solving 0-1 knapsack problem by a novel global harmony search algorithm. Appl. Soft Comput. 2011, 11, 1556–1564. [Google Scholar] [CrossRef]
- Fogel, D.B. Introduction to evolutionary computation. In Evolutionary Computation 1; Taylor & Francis Group: New York, NY, USA, 2000. [Google Scholar]
- Chen, G.-L.; Wang, X.-F.; Zhuang, Z.-Q.; Wang, D.-S. Genetic Algorithm and Its Applications; The People’s Posts and Telecommunications Press: Beijing, China, 2003. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Yang, X.-S.; Xin, S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspired Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Feng, Y.-H.; Wang, G.-G.; Wang, L. Solving randomized time-varying knapsack problems by a novel global firefly algorithm. Eng. Comput. 2018, 34, 621–635. [Google Scholar] [CrossRef]
- Cao, J.; Yin, B.; Lu, X.; Kang, Y.; Chen, X. A modified artificial bee colony approach for the 0-1 knapsack problem. Appl. Intell. 2017, 48, 1582–1595. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, Y.; Luo, Q. Hybrid symbiotic organisms search algorithm for solving 0-1 knapsack problem. Int. J. Bio-Inspired Comput. 2018, 12, 23–53. [Google Scholar] [CrossRef]
- Feng, Y.-H.; Jia, K.; He, Y.-C. An improved hybrid encoding cuckoo search algorithm for 0-1 knapsack problems. Comput. Intell. Neurosci. 2014, 2014, 970456. [Google Scholar] [CrossRef]
- Zhou, Y.-Q.; Chen, X.; Zhou, G. An improved monkey algorithm for a 0-1 knapsack problem. Appl. Soft Comput. 2016, 38, 817–830. [Google Scholar] [CrossRef]
- Sun, J.; Miao, Z.; Gong, D.-W.; Zeng, X.-J.; Li, J.-Q.; Wang, G.-G. Interval multi-objective optimization with memetic algorithms. IEEE Trans. Cybern. 2020, 50, 3444–3457. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.-H.; Gandomi, A.H.; Hao, G.-S.; Wang, H.-Q. Chaotic krill herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Wang, G.-G.; Bai, D.; Gong, W.; Ren, T.; Liu, X.; Yan, X. Particle-swarm krill herd algorithm. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; pp. 1073–1080. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine predators algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Wang, G.-G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2016, 10, 151–164. [Google Scholar] [CrossRef]
- Feng, Y.-H.; Wang, G.-G. Binary moth search algorithm for discounted {0-1} knapsack problem. IEEE Access 2018, 6, 10708–10719. [Google Scholar] [CrossRef]
- Feng, Y.-H.; Yi, J.-H.; Wang, G.-G. Enhanced moth search algorithm for the set-union knapsack problems. IEEE Access 2019, 7, 173774–173785. [Google Scholar] [CrossRef]
- Gao, D.; Wang, G.-G.; Pedrycz, W. Solving fuzzy job-shop scheduling problem using DE algorithm improved by a selection mechanism. IEEE Trans. Fuzzy Syst. 2020, 28, 3265–3275. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014. [Google Scholar] [CrossRef]
- Feng, Y.-H.; Wang, G.-G.; Deb, S.; Lu, M.; Zhao, X.-J. Solving 0-1 knapsack problem by a novel binary monarch butterfly optimization. Neural Comput. Appl. 2017, 28, 1619–1634. [Google Scholar] [CrossRef]
- Feng, Y.-H.; Wang, G.-G.; Li, W.-B.; Li, N. Multi-strategy monarch butterfly optimization algorithm for discounted {0-1} knapsack problem. Neural Comput. Appl. 2018, 30, 3019–3036. [Google Scholar] [CrossRef]
- Feng, Y.-H.; Wang, G.-G.; Dong, J.-Y.; Wang, L. Opposition-based learning monarch butterfly optimization with Gaussian perturbation for large-scale 0-1 knapsack problem. Comput. Electr. Eng. 2018, 67, 454–468. [Google Scholar] [CrossRef]
- Feng, Y.-H.; Yu, X.; Wang, G.-G. A novel monarch butterfly optimization with global position updating operator for large-scale 0-1 knapsack problems. Mathematics 2019, 7, 1056. [Google Scholar] [CrossRef]
- Wang, G.-G.; Tan, Y. Improving metaheuristic algorithms with information feedback models. IEEE Trans. Cybern. 2019, 49, 542–555. [Google Scholar] [CrossRef]
- Benioff, P. The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. J. Stat. Phys. 1980, 22, 563–591. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1999, 21, 467–488. [Google Scholar] [CrossRef]
- Han, K.-H.; Kim, J.-H. Genetic quantum algorithm and its application to combinatorial optimization problems. In Proceedings of the International Congress on Evolutionary Computation (CEC2000), San Diego, CA, USA, 16–19 July 2000; Volume 2, pp. 1354–1360. [Google Scholar]
- Han, K.-H.; Kim, J.-H. Quantum-inspired evolutionary algorithm for a class of combinatorial optimization. IEEE Trans. Evol. Comput. 2002, 6, 580–593. [Google Scholar] [CrossRef]
- Talbi, H.; Draa, A.; Batouche, M. A new quantum-inspired genetic algorithm for solving the travelling salesman problem. In Proceedings of the 2004 IEEE International Conference on Industrial Technology, 2004, IEEE ICIT’04, Hammamet, Tunisia, 8–10 December 2004; Volume 3, pp. 1192–1197. [Google Scholar]
- Chang, C.-C.; Chen, C.-Y.; Fan, C.-W.; Chao, H.-C.; Chou, Y.-H. Quantum-inspired electromagnetism-like mechanism for solving 0/1 knapsack problem. In Proceedings of the 2010 2nd International Conference on Information Technology Convergence and Services, Cebu, Philippines, 11–13 August 2010; pp. 1–6. [Google Scholar]
- Xiong, H.; Wu, Z.; Fan, H.; Li, G.; Jiang, G. Quantum rotation gate in quantum-inspired evolutionary algorithm: A review, analysis and comparison study. Swarm Evol. Comput. 2018, 42, 43–57. [Google Scholar] [CrossRef]
- Zhou, W.; Zhou, C.; Liu, G.; Lv, H.; Liang, Y. An improved quantum-inspired evolutionary algorithm for clustering gene expression data. In Computational Methods; Springer: Dordrecht, The Netherlands, 2006; pp. 1351–1356. [Google Scholar]
- Xiao, J.; Yan, Y.; Lin, Y.; Yuan, L.; Zhang, J. A quantum-inspired genetic algorithm for data clustering. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 1513–1519. [Google Scholar]
- Han, K.-H.; Kim, J.-H. Quantum-inspired evolutionary algorithms with a new termination criterion, HεGate, and two-phase scheme. IEEE Trans. Evol. Comput. 2004, 8, 156–169. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Hota, A.R.; Pat, A. An adaptive quantum-inspired differential evolution algorithm for 0-1 knapsack problem. In Proceedings of the 2010 Second World Congress on Nature and Biologically Inspired Computing (NaBIC), Kitakyushu, Japan, 15–17 December 2010; pp. 703–708. [Google Scholar]
- Draa, A.; Meshoul, S.; Talbi, H.; Batouche, M. A quantum-inspired differential evolution algorithm for solving the N-queens problem. Neural Netw. 2011, 1, 21–27. [Google Scholar]
- Su, H.; Yang, Y. Quantum-inspired differential evolution for binary optimization. In Proceedings of the 2008 Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008; Volume 1, pp. 341–346. [Google Scholar]
- Wang, Y.; Feng, X.-Y.; Huang, Y.-X.; Pu, D.-B.; Zhou, W.-G.; Liang, Y.-C.; Zhou, C.-G. A novel quantum swarm evolutionary algorithm and its applications. Neurocomputing 2007, 70, 633–640. [Google Scholar] [CrossRef]
- Layeb, A. A hybrid quantum inspired harmony search algorithm for 0-1 optimization problems. J. Comput. Appl. Math. 2013, 253, 14–25. [Google Scholar] [CrossRef]
- Zouache, D.; Moussaoui, A. Quantum-inspired differential evolution with particle swarm optimization for knapsack problem. J. Inf. Sci. Eng. 2015, 31, 1757–1773. [Google Scholar]
- Gao, Y.; Zhang, F.; Zhao, Y.; Li, C. Quantum-inspired wolf pack algorithm to solve the 0-1 knapsack problem. Math. Probl. Eng. 2018, 2018, 5327056. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Srikanth, K.; Panwar, L.K.; Panigrahi, B.K.; Herrera-Viedma, E.; Sangaiah, A.K.; Wang, G.-G. Meta-heuristic framework: Quantum inspired binary grey wolf optimizer for unit commitment problem. Comput. Electr. Eng. 2018, 70, 243–260. [Google Scholar] [CrossRef]
- Sudholt, D. The benefits of population diversity in evolutionary algorithms: A survey of rigorous runtime analyses. In Theory of Evolutionary Computation; Springer: Cham, Switzerland, 2020; pp. 359–404. [Google Scholar]
- Pisinger, D. Where are the hard knapsack problems? Comput. Oper. Res. 2005, 32, 2271–2284. [Google Scholar] [CrossRef]
- Vasquez, M.; Yannick, V. Improved results on the 0-1 multidimensional knapsack problem. Eur. J. Oper. Res. 2005, 165, 70–81. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Principles of Quantum Mechanics, 4th ed.; Oxford University Press: New York, NY, USA, 1981; p. 12. [Google Scholar]
- Wang, J.S.; Li, S.X. An improved grey wolf optimizer based on differential evolution and elimination mechanism. Sci. Rep. 2019, 9, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Woolson, R.F. Wilcoxon signed-rank test. In Wiley Encyclopedia of Clinical Trials, 1–3; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).