Abstract
Traditional evolution algorithms tend to start the search from scratch. However, real-world problems seldom exist in isolation and humans effectively manage and execute multiple tasks at the same time. Inspired by this concept, the paradigm of multi-task evolutionary computation (MTEC) has recently emerged as an effective means of facilitating implicit or explicit knowledge transfer across optimization tasks, thereby potentially accelerating convergence and improving the quality of solutions for multi-task optimization problems. An increasing number of works have thus been proposed since 2016. The authors collect the abundant specialized literature related to this novel optimization paradigm that was published in the past five years. The quantity of papers, the nationality of authors, and the important professional publications are analyzed by a statistical method. As a survey on state-of-the-art of research on this topic, this review article covers basic concepts, theoretical foundation, basic implementation approaches of MTEC, related extension issues of MTEC, and typical application fields in science and engineering. In particular, several approaches of chromosome encoding and decoding, intro-population reproduction, inter-population reproduction, and evaluation and selection are reviewed when developing an effective MTEC algorithm. A number of open challenges to date, along with promising directions that can be undertaken to help move it forward in the future, are also discussed according to the current state. The principal purpose is to provide a comprehensive review and examination of MTEC for researchers in this community, as well as promote more practitioners working in the related fields to be involved in this fascinating territory.
1. Introduction
Due to its extensive application in science and engineering fields, global optimization is a topic of great interest nowadays. Without a loss of generality, it implies the minimization of a specific objective function or fitness function [1]. Effective and common approaches for optimization problems can be mainly divided into deterministic and heuristic methods. Deterministic methods (such as linear programming and nonlinear programming) can find a global or an approximately global optimum using mathematical formulas. Generally speaking, they take advantage of the analytical properties of the optimization problem to generate a sequence of solutions that converge to a global optimum [2]. On the other hand, heuristic methods use random processes, and thus cannot guarantee the quality of the obtained solutions. Comparatively speaking, to find an acceptable solution, the deterministic approach needs fewer objective function evaluations than the stochastic approach. However, stochastic approaches have been found to be more flexible and efficient than deterministic approaches, especially for complex “black box” problems [3].
Evolutionary algorithms (EAs) are a kind of population-based stochastic optimization methods involving the Darwinian principles of “Natural selection and survival of the fittest” [4,5,6,7,8]. The algorithm starts with a population of randomly generated individuals. Then, new offspring are produced iteratively by undergoing evolutionary operators such as crossover and mutation, and fitter offspring will survive to the next generation. The production and selection procedure terminates when a predefined condition is satisfied. Due to their simple implementation and strong search capability, in the last few decades, EAs have been successfully applied to solve a wide range of real-world optimization problems in areas such as defense and cybersecurity, biometrics and bioinformatics, finance and economics, sport, and games [9,10].
Despite their great successes in science and engineering, existing EAs still contain some drawbacks. One major point is that traditional EAs typically start to solve a problem from scratch, assuming a zero prior knowledge state, and focus on solving one problem at a time [11,12]. However, it is well known that real-world problems seldom exist in isolation and are usually mixed with each other. The knowledge extracted from past learning experiences can be constructively applied to solve more complex or new encountered tasks.
Traditional machine learning algorithms only work well under a common assumption that the distributions of the training and test data are the same [13]. Nevertheless, the domains, tasks, and distributions may be very different in many real-world applications. In such cases, transfer learning or multitask learning between multiple source tasks and a target task would be desirable. In contrast to tabula rasa learning, transfer learning in the field of machine learning can leverage on a pool of available data from various source tasks to improve the learning efficacy of a related target task. The fundamental motivation for transfer learning in machine learning community was discussed in a NIPS (Conference and Workshop on Neural Information Processing Systems) 1995 post-conference workshop on “Learning to Learn: Knowledge Consolidation and Transfer in Inductive Systems” [14]. Since 1995, it has attracted substantial scholar attention, and achieved significant success [13,15,16,17]. Although the notion of knowledge transfer or transfer learning has been prominent in machine learning, it is relatively scarce, and has received far less attention in the evolutionary computation community. Frankly speaking, a detailed description of transfer learning in machine learning is beyond the scope of this review article, which is limited in transfer learning or multi-task learning in evolutionary computation.
As a novel paradigm, transfer optimization can facilitate the automatic knowledge transfer across optimization problems [11,12]. Following from the formalization, the conceptual realizations of this paradigm are classified into three distinct categories, namely sequential transfer optimization, multi-task optimization (MTO), the main focus of this article, and multiform optimization. Note that the concept of multi-task optimization is also described using other terms such as multifactorial optimization (MFO) [18], multitasking optimization (MTO) [19], multi-task learning (MTL) [20], multitask optimization (MTO) [11], multitasking [12], evolutionary multitasking (EMT) [21], evolutionary multi-tasking (EMT) [22], and multifactorial operation optimization (MFOO) [23].
The basic concept of multi-task optimization was originally introduced by Prof. Ong [24]. In contrast to the traditional EAs which optimize only one task in a single run, the main idea of MTO is to solve multiple self-contained optimization tasks simultaneously. Due to its strong search capability and parallelism nature, it has attracted great research attention since it was proposed in 2015. Nevertheless, to the best of our knowledge, there is no effort being conducted on the comprehensive survey, especially in future trends and challenges, about MTO. Thus, the intention of this article is to present an attempt to fill this gap.
Up to now, no research monograph on this topic has been published, except a book chapter written by Gupta et al. [25]. The review of the literature in this paper consists of 140 articles from refereed journals and conference proceedings. These papers listed in the bibliography are drawn from the past five years. Note that dissertations [26,27,28,29] have generally not been included, although the tendency is to be inclusive when dealing with borderline cases. One of the major concerns here is that these results and key contributions with rarely novel ideas in dissertations are usually the collection of previous results published in journals or conferences.
The remaining of this review is organized as follows. The basic definition and some confusing concepts of MTO are introduced in Section 2. In this section, we also conduct a statistical analysis of the literature. In Section 3, the mathematical analysis of conventional multi-task evolutionary computation (MTEC) is provided which theoretically explains why some existing MTECs perform better than traditional methods. Then, Section 4 describes some basic implementation approaches for MTEC, such as chromosome encoding and decoding scheme, intro-population reproduction, inter-population reproduction, balance between intra-population reproduction and inter-population reproduction, and evaluation and selection strategy. Further, related extension issues of MTEC are summarized in Section 5. In Section 6, a review of the applications of MTEC in science and engineering is conducted. Finally, the trends and challenges for further research of this exciting field are discussed in Section 7. Finally, Section 8 is devoted to main conclusions.
2. Basic Concept of Multi-Task Optimization and Multi-Task Evolutionary Computation
2.1. Definition of Multi-Task Optimization
Generally, the goal of multi-task optimization is to find the optimal solutions for multiple tasks in a single run. Without a loss of generality, suppose there are K minimization tasks to be optimized simultaneously. Specifically, denote Ti as the ith minimization task to be solved. Then, the definition of a MTO problem can be mathematically represented as follows [18]:
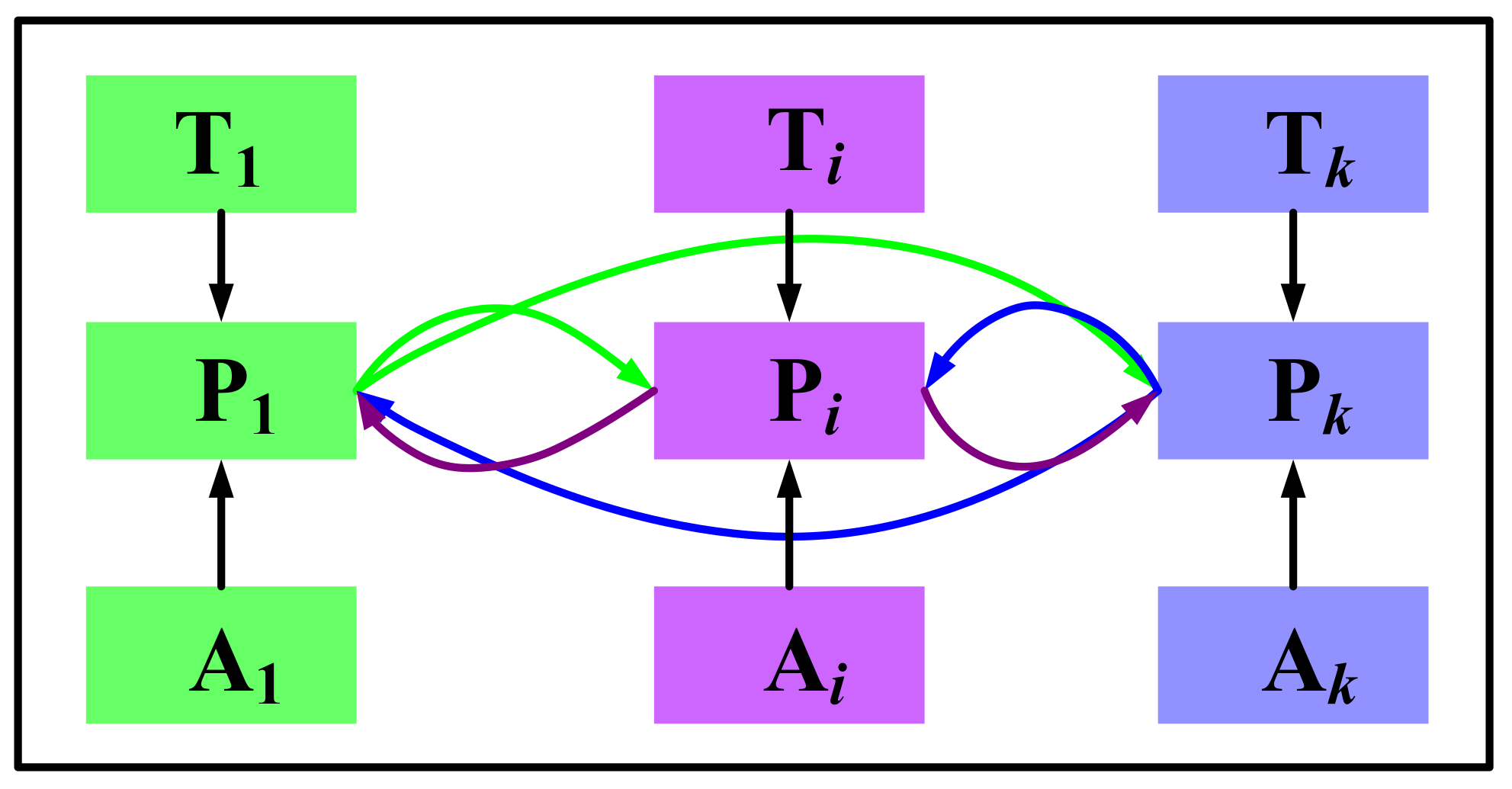
where is a feasible solution of the ith task Ti. Note that Ti itself could be single-objective optimization or multi-objective optimization problem. A general schematic of multi-task optimization is depicted in Figure 1.
Figure 1.
An illustration of a multi-task optimization problem [30].
To evaluate the individuals in MTO, several properties associated with every individual are defined as follows [18]:
Definition 1 (Factorial Cost):
The factorial cost of individualpion taskTjis the objective valuefjof potential solutionpi, which is denoted as.
Definition 2 (Factorial Rank):
The factorial rank of pi on Tj is the rank index of pi in the sorted objective value list in an ascending order, which is denoted as.
Definition 3 (Skill Factor):
The skill factor is defined by the index of the task assigned to an individual. The skill factor of pi is given by.
Definition 4 (Scalar Fitness):
The scalar fitness of pi is the inverse of , which is given by .
Herein, the skill factor is regarded as the cultural trait which can be inherited from its parents in MTO. The scalar fitness is used as the unified performance criterion in a multi-task framework.
2.2. Confusing Concepts of MTO
As an emerging paradigm in evolutionary computation community, multi-task optimization is easy to confuse with other optimization concepts outlined and distinguished in this section.
2.2.1. Multi-Objective Optimization (MOO)
In a real-world scenario, a decision maker in the general case has to simultaneously account for multiple disparate or even contradictory criteria while selecting a particular plan of action. Mathematically, a multi-objective optimization problem can be formulated as follows:
where x is the decision variable vector. Typically, no single optimal solution can minimize all the objectives simultaneously due to the confliction between each pair of objectives. Thus, the main purpose of an MOO problem is to obtain an optimal solution set, called a Pareto solution set, with splendid convergence and diversity.
In the literature, multi-objective evolutionary algorithms (MOEAs) that are commonly used today can be classified into three categories [31]: (a) dominance-based MOEAs, such as NSGA-II [32], (b) indicator-based MOEAs, such as HypE [33], and (c) decomposition-based MOEAs, such as MOEA/D [34].
Although MOO and MTO problems both involve the optimization of multiple objective functions, they are two distinct optimization paradigms. MOO focuses on efficiently resolving conflicts among competing objective functions in one task. As a result, solving a MOO problem typically yields a Pareto solution set that provides the best trade-offs among all objective functions. Differently, MTO aims to leverage the implicit parallelism of a population-based search to seek out the optimal solutions for two or more tasks simultaneously. Therefore, the output of a MTO problem contains two or more optimal solutions corresponding to each task.
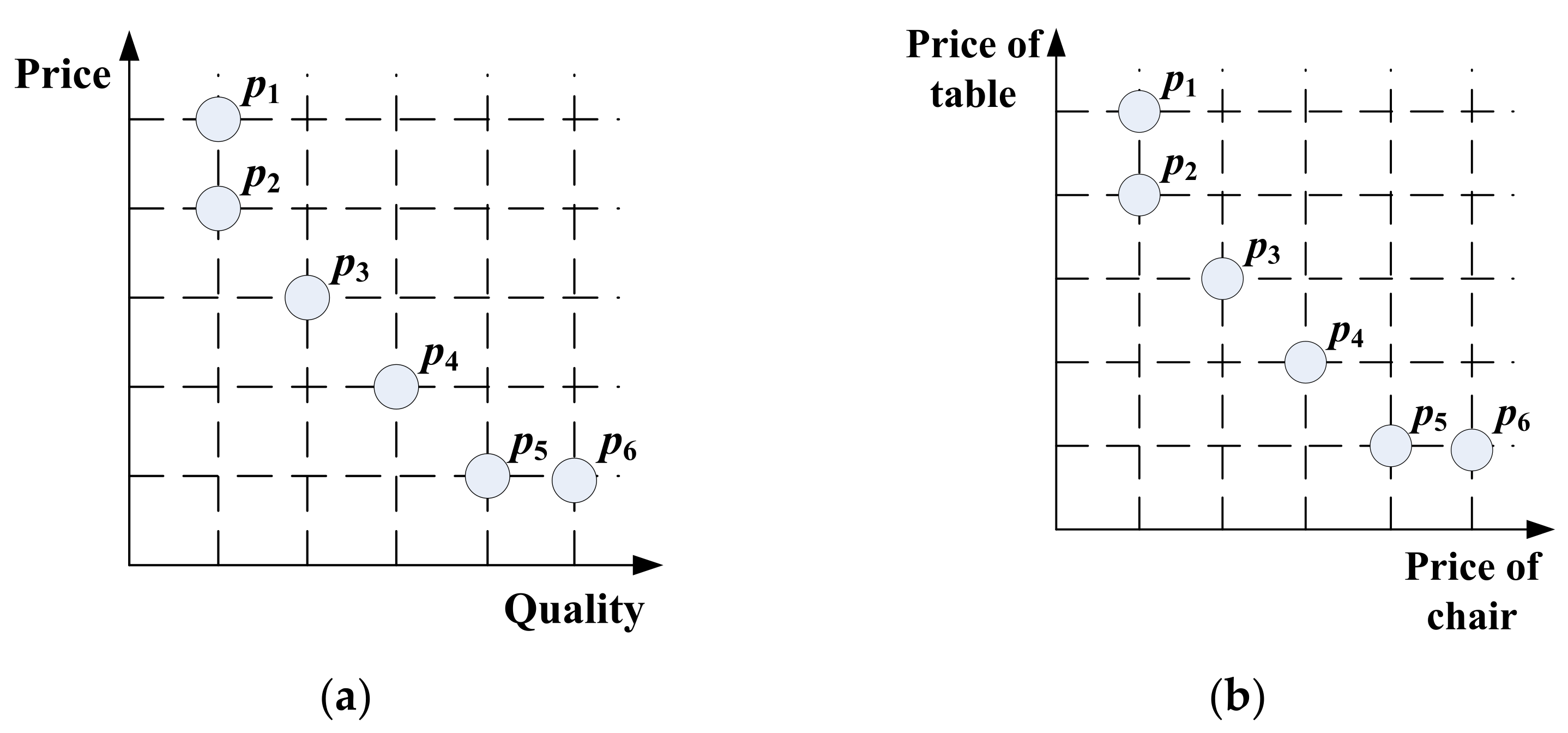
In order to further exhibit the distinction between MOO and MTO, we refer to their population distributions in Figure 2. In real life, you can imagine a scenario where you plan to buy a cheap and fine table in a furniture store. Actually, this problem that you face is a multi-objective optimization problem. Based on the definition of Pareto optimal solution, individuals {p2, p3, p4, p5} are incomparable to each other and are better than the individuals {p1, p6} in Figure 2a. As a result, the output of this MOO problem is the Pareto optimal solution set {p2, p3, p4, p5}, and then you can buy any table from this set based on personal preference.
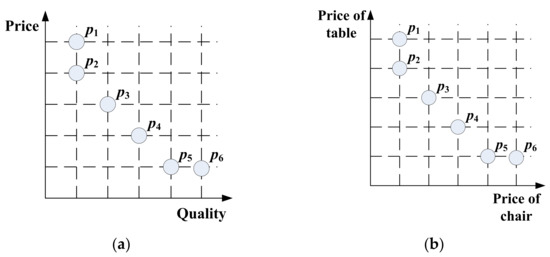
Figure 2.
Population distribution for multi-objective optimization (MOO) and multi-task optimization (MTO) problems. (a) Multi-objective optimization problem finding a cheap and fine table. (b) Multi-task optimization problem finding a cheap table and a cheap chair concurrently.
In contrast, you may possibly plan to buy a cheapest table and a cheapest chair at once, which is a typical multi-task optimization problem. In Figure 2b, individuals {p1, p2} are the cheapest chairs, and individuals {p5, p6} are the cheapest tables in this furniture store. Thus, the output of this MTO problem is two optimal solution sets: {p1, p2} and {p5, p6}, and then you can buy randomly ONE table from the set {p5, p6} and ONE chair from the set {p1, p2}.
2.2.2. Sequential Transfer Optimization
The search process of many existing EAs typically begins from scratch, assuming a zero prior knowledge state. However, there is a great deal of knowledge from past exercises that can be exploited the similar search spaces in order to improve the algorithm performance. For instance, an engineering team designing a turbine for an aircraft engine would use, as a reference, past designs that have been successful and modify them accordingly to suit the current application [20].
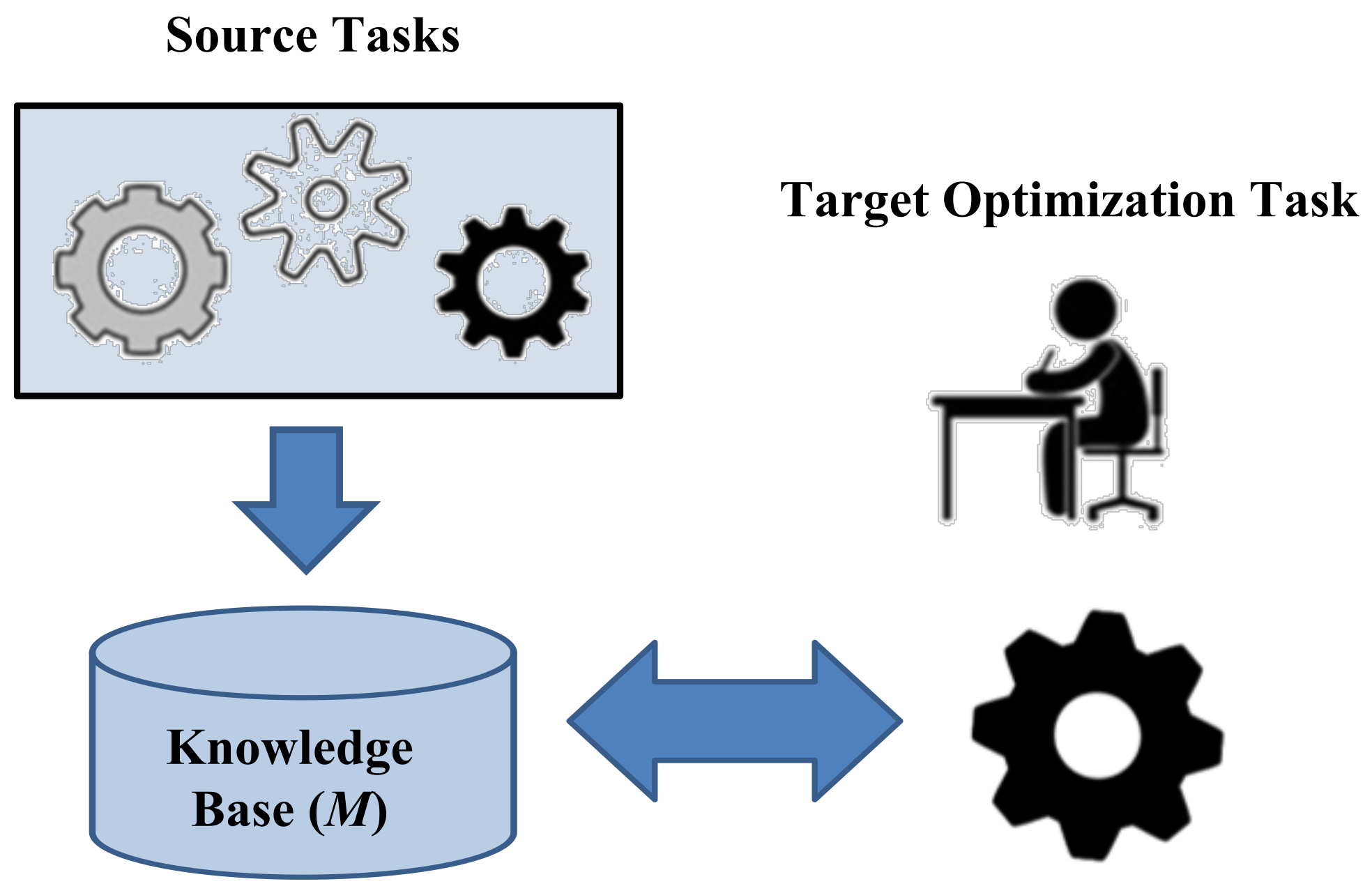
Mathematically, we make the strict assumption that while tackling task TK, the tasks T1, T2, …, TK−1 have already been addressed previously with the extracted information available in the knowledge base M [12]. Herein, TK is said to act as the target optimization task, while T1, T2, …, TK−1 are said to be source tasks. As illustrated in Figure 3, the objective of sequential transfer optimization is to improve the learning of the predictive function of a target task using knowledge from any source task.
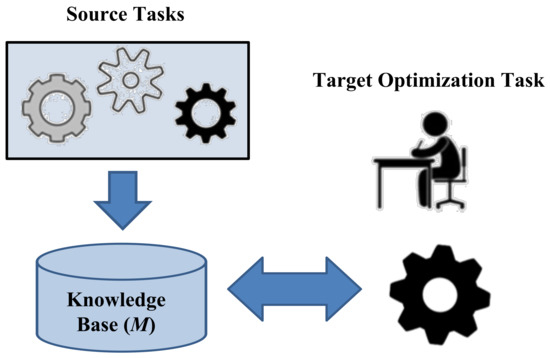
Figure 3.
An illustration of a sequential transfer optimization problem [12].
2.2.3. Multi-Form Optimization
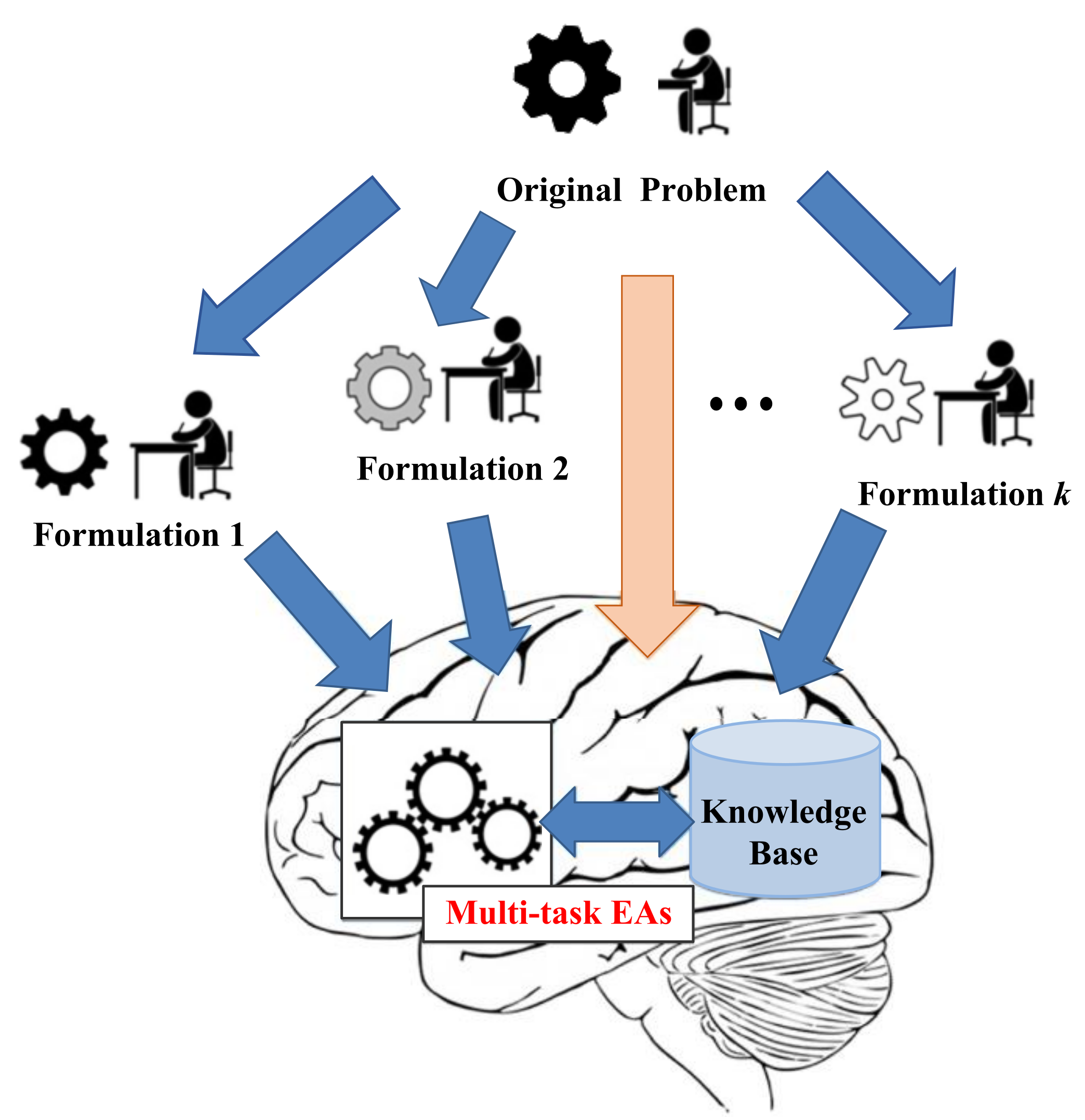
Different from multi-task optimization dealing with distinct self-contained tasks simultaneously, multi-form optimization is a novel concept for exploiting multiple alternate formulations of a single target task [12]. As illustrated in Figure 4, instead of treating each formulation independently, the basic idea of multi-form optimization is to combine different formulations into a single multi-task optimization algorithm [20].
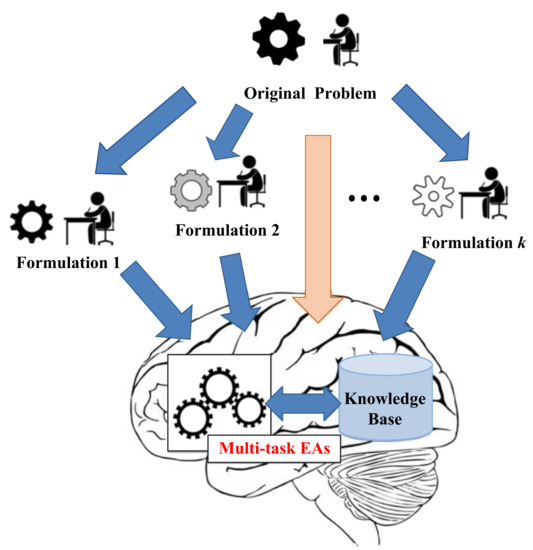
Figure 4.
An illustration of multi-form optimization problem [30].
The challenge of multi-form optimization lies in the fact that it may often be difficult to ascertain which formulation is most suited for a particular problem at hand, given the known limits on computational resources. Alternate formulations induce different search behaviors, some of which may be more effective than others for a particular problem instance [30].
2.3. Multifactorial Evolutionary Algorithm
As a pioneering implementation of multi-task optimization, the multifactorial evolutionary algorithm (MFEA), inspired by the multifactorial inheritance [35,36], has gained increasing research interests due to its effectivity [18]. Algorithm 1 gives a description of the entire process of the canonical MFEA.
| Algorithm 1 Basic Structure of the Canonical MFEA | |
| 1 | Randomly sample N∙K individuals to form initial population P(0); |
| 2 | for each task Tk do |
| 3 | for every individual pi in P(0) do |
| 4 | Evaluate pi for task Tk; |
| 5 | end for |
| 6 | end for |
| 7 | Calculate skill factor r over population P(0); |
| 8 | Calculate scalar fitness according to skill factor r; |
| 9 | t = 1; |
| 10 | while stopping conditions are not satisfied do |
| 11 | while offspring generated for each task < N do |
| 12 | Sample two individuals (xi and xj) randomly from P(t); |
| 13 | if then |
| 14 | [xa, xb] ← intra-task crossover between xi and xj; |
| 15 | Assign offspring xa and xb with skill factor (); |
| 16 | else if rand < rmp then |
| 17 | [xa, xb] ← inter-task crossover between xi and xj; |
| 18 | Assign each offspring with skill factor or randomly; |
| 19 | end if |
| 20 | [xa] ← mutation of xi; |
| 21 | Assign offspring xa with skill factor ; |
| 22 | [xb] ← mutation of xj; |
| 23 | Assign offspring xb with skill factor ; |
| 24 | Evaluate [xa, xb] for their assigned task only; |
| 25 | end while |
| 26 | Calculate skill factor r over population P(t); |
| 27 | Calculate scalar fitness according to skill factor r; |
| 28 | Select survivors to next generation; |
| 29 | t = t+1; |
| 30 | end while |
At the initialization phase, MFEA randomly generates a single population with N∙K individuals in a unified search space (line 1). The individuals in the population then have a skill factor (see Definition 3 in Section 2.1), indicating the most suitable task in terms of ranking values on different tasks, and a scalar fitness (see Definition 4 in Section 2.1), determining by the reciprocal of the ranking value with respect to the most suitable task (lines 2–8).
There are two key features of MFEA, called assortative mating and selective imitation, which distinguish it from traditional EAs. The assortative mating mechanism allows not only the standard intra-task crossover between parents from the same task (lines 13–15) but also the inter-task crossover between distinct optimization instances (lines 16–18). The intensity of knowledge transfer is controlled by a user-defined parameter labeled as random mating probability (rmp). Since mutation is essential in genetic algorithms, MFEA with mutation applied on all newly generated candidates may achieve better performance (lines 20–23). As each newly generated individual has been assigned skill factor, the evaluation for the individual is taken only on the task corresponded to such skill factor (line 24). After evaluation, the whole population obtain new ranking values and thus new skill factor and scalar fitness (lines 26–27), which is then used to select survivors for the next generation (line 28). Selective imitation is derived from the memetic concept of vertical cultural transmission, which aims to reduce the computational burden by evaluating an individual for their assigned task only.
2.4. Literature Review and Analysis
After retrieving several important full-text databases, abstract databases, and Google Scholar, 69 articles published in peer-review journals and 71 papers published in conference proceedings were collected and reviewed for this paper. The quantity of papers published each year is contained in Table 1.

Table 1.
The quantity of papers published each year in the past five years. The number in parentheses represents the quantity of papers published first online.
As the first paper in this field, [24] is a keynote presentation abstract published in 2016 by Springer, while the International Conference on Computational Intelligence, Cyber Security and Computational Models was held in Coimbatore, India in December 2015. Interestingly, the first journal paper [37] was received on 1 December, 2015, and published online on 26 February, 2016, while it was published in the first volume of Complex & Intelligent Systems in 2015. For simplicity, two papers both count towards 2016, as shown in Table 1.
From Table 1, we noticed that the quantity increased for the past five years and exploded in the past two years. It had already reached 39 and 57 in 2019 and 2020, respectively, more than two thirds of the total. The results demonstrate the high research intensity and productivity in MTO, becoming a hot research topic in the evolutionary computation community.
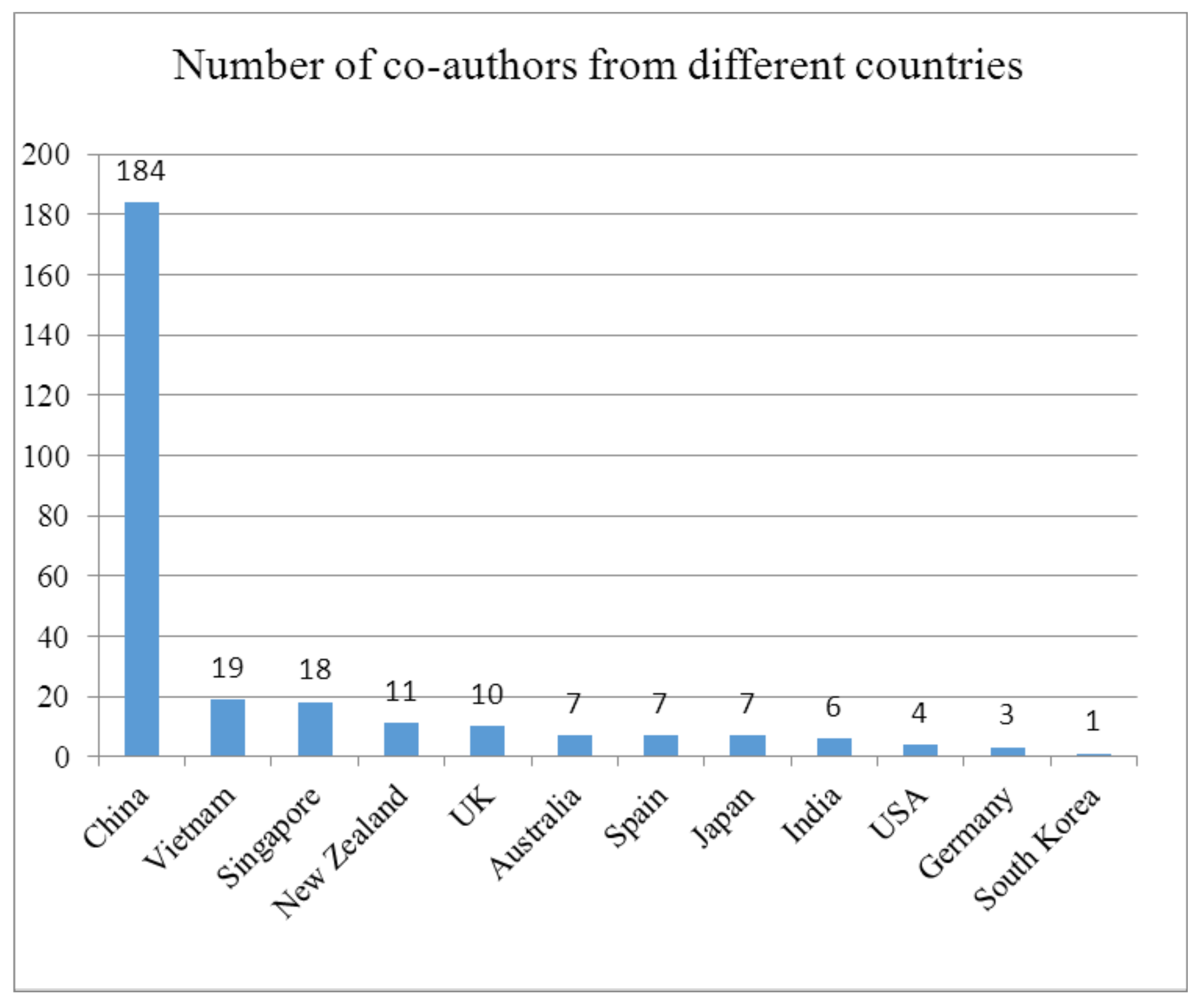
These articles involve 277 co-authors from 12 countries, including China (184), Vietnam (19), Singapore (18), New Zealand (11), and the UK (10), as shown in Figure 5. The most prolific contributing authors in this field are summarized in Table 2. From here we see clearly that China and Singapore have demonstrated great research power in this field, and some famous research teams have emerged from China and Singapore. It is worth noting that these prominent scholars have some kind of academic connection (research scientist, Ph.D candidate, co-investigator, etc.) with the pioneer of MTO, Prof. Ong. In addition, each paper was written by 4.21 co-authors on average.
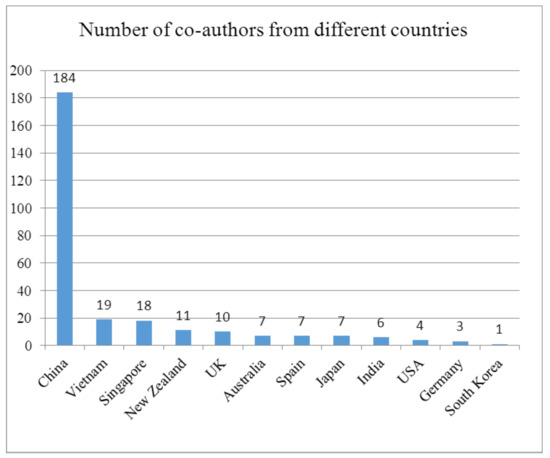
Figure 5.
Number of co-authors from different countries.

Table 2.
The most prolific contributing authors devoted to MTO and MTEC.
These articles were published in 34 journals and 24 international conferences. The preferential journals involve IEEE Transactions on Cybernetics (12), IEEE Transactions on Evolutionary Computation (12), IEEE Access (4), and Information Sciences (3), while the preferential conferences involve IEEE Congress on Evolutionary Computation (IEEE CEC) (33), Genetic and Evolutionary Computation Conference (GECCO) (8), and IEEE Symposium Series on Computational Intelligence (IEEE SSCI) (6). It is evident that the publication distribution shows a high concentration. The authors tend to publish these research results in the top journals and conferences in the evolution computation community, in order to promote their academic reputations. Open Access journals (like IEEE Access), meanwhile, are new options for scholars trying to seize the initiative first and achieve high visibility.
As of January 31, 2021, the most cited papers are [11,12,18,21,38,39], in descending order, and the other papers were cited less 70 times. Although [18] by Gupta et al. is not the first paper published in a journal or submitted to a journal, it has been widely recognized by the evolution computation community. The possible reason for this is that it provided the algorithmic background, biological foundation, basic concepts, algorithm framework, simulation experiments, and excessive experimental results of MFEA. As a result, this paper has been cited 233 times so far and considered the most classic paper in MTO and MTEC.
3. Theoretical Analyses of Multi-Task Evolutionary Computation
Experimentally, many success stories have surfaced in multi-task optimization scenarios in recent years, and demonstrated the superiority of multi-task evolutionary computation over traditional methods. A natural question is whether MTEC always improves convergence performance.
Follows directly from Holland’s schema [40], under fitness proportionate selection, single-point crossover, and no mutation, the expected number of individuals in a population containing given a schema at generation is deduced in [30]. This demonstrates that, compared to conventional methods, the potential ability for MTEC to utilize knowledge transferred from other tasks in the multi-task environment to accelerate convergence towards high quality schema. Further, it was proved that the MFEA with parent-centric evolutionary operators and (μ, λ) selection can asymptotically converge to the global optimum of each constitutive task, regardless of the choice of rmp [41]. On the other hand, the reduction in the convergence rate of MFEA depends on the chosen rmp and single-task optimization may lead to faster convergence feature in the worst case.
Referring to [41], Tang et al. further proved that, by aligning two subspaces, the inter-task knowledge transfer method proposed in [42] can implicitly minimize the KL-divergence between two different subpopulations. In this way, we can implement the low-drift inter-task knowledge transfer.
In [43], adaptive model-based transfer (AMT) was proposed and analyzed theoretically. The theoretical result indicates that, by combining all available (source + target) probabilistic models, the gap between the underlying distributions of parent population and offspring population is reduced. In fact, with increasing number of source models, we can in principle make the gap arbitrarily small. Therefore, the proposed AMT framework facilitates the global convergence characteristic.
Yi et al. [44] discovered mathematically that the proposed interval dominance method has a strict transitive relation to the original method when and can be applied when comparing the dominance relationship between interval values.
The principal finding of [45] is that, for vehicle routing problems (VRPs), the positive knowledge transfer across tasks is strictly related to the intersection degree among the best solutions. More concretely, Osaba et al. have shown that intersection degrees greater than 11% are enough for ensuring a minimum positive activity.
Recently, Lian et al. [46] provided a novel theoretical analysis and evidence of the effectiveness of MTEC. It was proved that the upper bound of expected running time for the proposed simple (4 + 2) MFEA algorithm on the Jumpk function can be improved to O (n2 + 2k) while the best upper bound for single-task optimization on the same problem is O (nk−1). This theoretical result indicates that MTEC is probably a promising approach to deal with some distinct problems in the field of evolutionary computation. The proposed MFEA algorithm is further analyzed on several benchmark pseudo-Boolean functions [47]. Theoretical analysis results show that, by properly setting the parameter rmp for the group of problems with similar tasks, the upper bound of expected runtime of (4 + 2) MFEA on the harder task can be improved to be the same as on the easier one, while for the group of problems with dissimilar tasks, the expected upper bound of (4 + 2) MFEA on each task are the same as that of solving them independently. This study theoretically explains why some existing MFEAs perform better than traditional EAs.
4. Basic Implementation Approaches of Multi-Task Evolutionary Computation
Gupta and Ong [48] provided a clearer picture of the relationship between implicit genetic transfer and population diversification. The experimental results highlighted that genetic transfer is a more appropriate metaphor for explaining the success of MTEC. Da et al. [49] further considered the incorporation of gene-culture interaction to be a pivotal aspect of effective MTEC algorithms. In [50], the inheritance probability (IP) of the selective imitation was firstly defined and then the influence on MTEC algorithm was studied experimentally. To alleviate the influence of IP on the algorithm performance, an adaptive inheritance mechanism (AIM) was thus introduced to automatically adjust the IP value for different tasks at different evolutionary stages.
Solving the multi-task optimization problem in a natural way is the multipopulation evolution strategy, in which each subpopulation evolves and exploits separate search spaces independently in order to solve the corresponding task. As an example, in Figure 6, a multi-population evolution model is depicted to solve two tasks [51]. According to the multi-population evolution model of MTEC, various implementation approaches of each element proposed so far are described in detail in the following subsection.
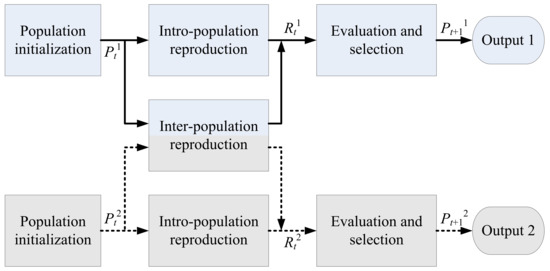
Figure 6.
Multi-population evolution model for a simple case comprising two tasks [51].
4.1. Chromosome Encoding and Decoding Scheme
For effective EAs including MTEC, the unified individual representation scheme coupled with the decoding process is perhaps the most important ingredient, which directly affects the problem-solving process.
Canonical MFEA employed the unified representation scheme in a unified search space [18]. In particular, every variable of individual is simply encoded by a random key between 0 and 1 [52]. For the case of continuous optimization, decoding can be achieved in a straightforward manner by linearly mapping each random key from the genotype space to the design space of the appropriate optimization task [18,38]. For instance, consider a task Tj in which the ith variable is bounded in the range [Li, Ui]. If the ith random-key of a chromosome y takes value yi ∈ [0, 1], then the decoding procedure is given by
In contrast, for the case of discrete optimization (such as knapsack problem (KP), quadratic assignment problem (QAP), and capacitated vehicle routing problem (CVRP)), the chromosome decoding scheme is usually problem dependent.
However, there are two obvious limitations of using a random key representation when dealing with permutation-based combinatorial optimization problems (PCOPs) [53]. Firstly, the decoding can be inefficient, since the transformation from the random key representation to the permutation is required for each fitness evaluation of EAs. Secondly, the decoding process can be highly prone to losses, since only information on relative order is derived. Therefore, Yuan et al. [53] introduced an exquisite and effective variant, called permutation based unified representation, to better adapt to PCOPs. To encode multiple VRPs, the permutation-based representation [54,55] was also adopted [56,57]. With it, a chromosome is encoded as a giant tour represented by a sequence in which each dimension is a customer id. In addition, the extended split approach [54,55] was introduced to translate a permutation-based chromosome into a feasible routing solution.
Chandra et al. [58] employed direct encoding strategy for weight representation, where all the weights are encoded in a consecutive order. Therefore, different tasks results in varied length real-parameter chromosomes in the MTEC algorithm.
The solutions offered by genetic programming (GP) are typically represented by an expression tree [59]. In the multifactorial GP (MFGP) paradigm, a novel scalable chromosome encoding scheme, gene expression representation with automatically defined functions [60], was utilized to effectively represent multiple solutions simultaneously [61]. In particular, this encoding scheme using a fixed length of strings contains one main function and multiple automatically defined functions (ADFs). The main function gives the final output, while the ADFs represent subfunctions of the main function. The corresponding decoding scheme was also proposed in [61].
Binh et al. [62] proposed an individual encoding and decoding method in unified search space for solving clustered shortest-path tree (CluSPT) problem. The number of clusters of individuals is equal to the maximum number of clusters of all tasks and the number of vertices of cluster i is the maximum number of vertexes of cluster i of all tasks. Note that such individual encoding and decoding approaches can also apply to the minimum routing cost clustered tree (CluMRCT) problem [63].
Thanh et al. [64,65] introduced the Cayley Code encoding mechanism to solve clustered tree problems. Cayley Code was chosen to be the solution representation for two reasons. The first advantage is that it can encode a solution into spanning tree easier than other methods. The other one is that it takes full advantage of existing evolutionary operators such as one-point crossover and swap-change mutation. In addition, three typical coding types in the Cayley Code families were also analyzed when performed on both single-task and multi-task optimization problems.
The Edge-sets structure has been proved to be efficient in finding spanning trees in graphs [66]. In [67], it was used to construct optimal data aggregation trees in wireless sensor networks. Each gene represents an edge, each taking a value of 0 or 1, corresponding to whether the edge is present in the spanning tree. In [68], solution presented by edge-sets representation was also built for the CluSPT problem. An individual has three properties: an ES property (edges connecting all clusters), IE property (vertices in each cluster connecting it to other vertices of different clusters), and LR property (roots of all clusters). In order to transform a chromosome in unified search space into solutions for each task, the decoding scheme contains two separate parts. For the first task, a solution for the CluSPT problem is constructed from an individual in a unified search space by using its key properties, while the decoding method for the second task is the HBRGA algorithm proposed in [69]. However, this method cannot guarantee that the sub-graphs in clusters are also spanning trees, leading to create invalid solutions. Recently, Binh and Thanh [70] introduced another method for generating random solutions which can only produce valid solutions.
Nowadays, connectivity among communication devices in networks has been playing a significant role and multi-domain networks have been designed to help resolving scalability issues. Recently, Binh et al. [71] introduced MFEA with a new solution representation. With it, a chromosome consists of two parts in a unified search space: the first part encodes the priority of the corresponding nodes while the second part encodes the index of edges in the solution. In addition, the corresponding decoding scheme was also proposed in [71].
Constructing optimal data aggregation trees in wireless sensor networks is an NP-hard problem for larger instances. A new MFEA was proposed to solve multiple minimum energy cost aggregation tree (MECAT) problems simultaneously [67]. The authors also presented am encoding and decoding strategy, a crossover operator, and a mutation operator enabling multifactorial evolution between instances.
For solving multiple optimization tasks of fuzzy system, the encoding and decoding scheme was proposed in [72]. Each individual comprises multiple chromosomes corresponding to every fuzzy variables of the fuzzy system. Each chromosome is a series of gene sequences, and per gene has one-to-one correspondence with a membership function parameter of the fuzzy variable. When a decoding procedure is carrying out, according to the task space to be decoded, in the order that the output variable is decoded first and the input variables are decoded later, taking first few parameters of the required length from each chromosome and arranging them in ascending order, then splicing them to obtain the decoded individual.
For solving the community detection problem and active module identification problem simultaneously, a unified genetic representation and problem-specific decoding scheme was proposed [73]. An individual is encoded as an integer vector, to which each integer representing the label of community to which corresponding node is assigned.
For semantic Web service composition, a permutation-based representation was proposed [74]. A permutation is a sequence of all the services in the repository, and each service appears exactly once in the sequence. Using a forward graph building technique [75], a DAG-based solution can easily be decoded from the above permutation-based solution.
Membership function plays an important role in mining fuzzy associations. Wang and Liaw [76] proposed a structure-based representation MFEA for mining fuzzy associations. The optimization of each membership function is treated as a single task, and the proposed method can optimize all tasks in one run. More importantly, the structure based representation [77] can avoid the illegality by the transformation procedure and also reduce the number of arrangements of membership functions.
Very recently, in an evolutionary multitasking graph-based hyper-heuristic (EMHH), the chromosome of an individual is represented as a sequence of heuristics, with each bit representing a low-level heuristic [78].
4.2. Intro-Population Reproduction
As a core search operator, intro-population reproduction can significantly affect the performance of MTEC, as shown in Figure 6. The most widely utilized one is probably genetic mechanisms, namely crossover and mutation. Specifically, several typical genetic strategies include simulated binary crossover [18,79], ordered crossover (OX) [57,80], one-point crossover [59,61], DE crossover [61], guided differential evolutionary crossover [81], partially mapped crossover (PMX) and two-point crossover (TPX) [71], Gaussian mutation [18], uniform mutation [61], swap mutation (SW) [57,80], polynomial mutation [53,79], DE mutation [61], mutation using the Powell search method [81], swap-change mutation [64], and one-point mutation [71]. The other EAs, differential evolution (DE) [82,83,84,85,86,87], particle swarm optimization (PSO) [85,86,87,88,89,90,91,92,93,94], artificial bee colony (ABC) [95], fireworks algorithm (FWA) [96], self-organized migrating algorithm (SOMA) [97], brain storm optimization (BSO) [98,99], Bat Algorithm (BA) [100], and genetic programming (GP) [61], are also utilized as fundamental algorithm for MTEC paradigms.
In addition, inspired by cooperative co-evolution genetic algorithm (CCGA), an evolutionary multi-task algorithm was proposed for the high-dimensional global optimization problem [101]. In this, a MTO problem is decomposed into multiple lower-dimensional sub-problems. In [22], the novel hyper-rectangle search strategy was designed based on the main idea of opposition-based learning. It contains two modes, which enhance the exploration ability in the unified search space and improve the exploitation ability in the sub-space of each task, respectively.
4.3. Inter-Population Reproduction
The major function of inter-population reproduction is knowledge transfer between different subpopulations, which may help to accelerate the search process and find global solutions [51]. Therefore, when, what, and how to transfer are the key issues in MTEC. An excellent MTEC algorithm should be able to deal with the three problems properly [102].
4.3.1. When to Transfer
As depicted in Figure 6, inter-population reproduction can happen at any stage of the optimization process in a multi-task scenario. Generally, the offspring are generated via genetic transfer (crossover and mutation) across tasks for each generation in [18].
In fact, knowledge transfer across tasks can also occur with a fixed generation interval along the evolution search. The interval of inter-population reproduction was set to 10 generations in EMT (evolutionary multitasking) [21], and the generation interval was fixed at 20 generations in SGDE [102]. Experimental results based on the island model revealed that better results are observed from small transfer intervals than from large transfer intervals [103].
Due to the essential differences among the landscapes of the optimization tasks, Wen and Ting [104] suggested stopping the information transfer when the parting way is detected. In MT-CPSO, if a particle within a particular population did not improve its personal best position over prescribed consecutive generations, knowledge acquired from the other task was transferred across to assist the search in more promising regions [53]. Obviously, the greater the value of the prescribed iterations is, the smaller the probability of inter-population reproduction is. Similarly, in SOMAMIF, the current optimal fitness of each population was firstly judged, and the knowledge transfer demand across tasks was triggered when the evolution process of a task stagnated for successive generations [97].
4.3.2. What to Transfer
In MFEA and its variants, each solution in every task will be selected as a transferred solution based on the same probability. The light-weight knowledge transfer strategy was proposed by Zheng et al. [105]. To be more specific, the best solutions found so far on transfer other tasks to the given task and randomly replace some individuals during the optimization process.
However, some transferred solutions, even the best solutions found so far, do not help to optimize the other tasks, thereby leading to the low efficiency of achieving the positive transfer. In evolutionary multi-task via explicit autoencoding, transferred solutions are selected from the nondominated solutions in each task [21], while the performance of this method may primarily rely on the high degree of underlying intertask similarities [41]. Recently, Lin et al. [19] proposed a new strategy for selecting valuable solutions for positive transfer. In the proposed approach, a transferred solution achieves positive transfer if it is nondominated in its target task. Then, in the original search space of this positive-transfer solution, its several closest (based on the Euclidean distance) solutions will turn into the transferred solutions, since these solutions are more likely to achieve positive transfer.
In the existing DE-based on MTEC, the knowledge is transferred only by randomly selecting the solutions from different tasks to generate offspring without regarding the search property of DE. In fact, the successful difference vectors from the past generations can not only retain the important landscape information of the optimization problem, but also preserve the population diversity during the evolutionary process. Motivated by this consideration, Cai et al. [87] proposed a difference vector sharing mechanism for DE-based MTEC, aiming at capturing, sharing, and utilizing the knowledge of the promising difference vectors found in the evolutionary process.
More recently, Lin et al. [106] have utilized incremental Naive Bayes classifiers to select valuable solutions to be transferred during multi-task search, thus leading to the promising convergence of tasks. Furthermore, under the existing mapping strategies, tasks may be trapped in local Pareto Fronts with the guide of knowledge transfer. Thus, with the aim of improving overall convergence behavior, a randomized mapping among tasks is added that enhances the exploration capacity of transferred solutions.
Zhou et al. [107] investigated what information, except to the selective individuals, should be transferred in an MFEA framework. In particular, the difference between the individual solution and the estimated optimal solution, called the individual gradient (IG), was introduced as the additional knowledge to be transferred. The proposed approach was applied to mobile agent path planning (MAPP) [107] and the autonomous underwater vehicles (AUV) 3D path planning problem [108].
Based on a novel idea of multiproblem surrogates (MPS), an adaptive knowledge reuse framework was proposed for surrogate-assisted multi-objective optimization of computationally expensive problems [109]. The MPS provides the capability of acquiring and spontaneously transferring learned models gained from distinct but possibly related problem-solving experiences. The proposed framework consists of four primary steps: initialization, aggregation, multi-problem surrogate, and evolutionary optimization. The authors further present one possible instantiation, which utilizes a Tchebycheff aggregation approach, Gaussian process surrogate models with linear meta-regression, and an expected improvement measure to quantify the merit of evaluating a new point.
4.3.3. How to Knowledge Transfer Implicitly
As the most natural way, knowledge transfer across tasks is realized implicitly when two individuals possessing different skill factors are selected for generating the offspring via crossover. The implicit MTEC usually employs a single population with unified solution representation to solve multiple optimization tasks.
Compared with single-population SBX crossover, two parents come from two different subpopulations (Pk and Pr). Take MFEA as an example, knowledge transfer is done by inter-population SBX crossover as below [18]:
For MT-CPSO (multitasking coevolutionary particle swarm optimization), the inter-population reproduction is provided as follows [88,92,93]:
where and are the position of the i-th particle and its corresponding updated particle in subpopulation Pk, respectively, is the current global best position in subpopulation Pr, and rand is a random number between 0 and 1.
To explore the generality of MFEA with different search mechanisms, Feng et al. [85] investigated two MTEC approaches by using PSO and DE as the search engine, respectively. While the other genetic operators are kept the same as the original MFEA, the velocity is updated for MFPSO (multifactorial particle swarm optimization) using the following equation [85]:
For MFDE (multifactorial differential evolution), the mutation operator with genetic materials transfer is defined as following [85]:
For AMFPSO (adaptive multifactorial particle swarm optimization), the velocity is updated using the following equation [94]:
where and are the velocity of the i-th particle and its corresponding updated particle in subpopulation Pk, respectively, and are the position of the i-th particle and its best found-so-far particle in subpopulation Pk, respectively, is the current global best position in subpopulation Pk, r1 and r2 are random and mutually exclusive integers, c1, c2, c3, and are four parameters to adapt to problems, and rand is a random number within 0 and 1.
Recently, Song et al. [90] proposed a multitasking multi-swarm optimization (MTMSO) algorithm, in which knowledge transfer across tasks was realized via arithmetic crossover on the personal best of each particle among different tasks for every generation.
For MPEF-SHADE (multi-population evolution framework—success-history based adaptive DE), the mutation operator with genetic materials transfer is defined as following [82,83]:
where and are the i-th individual and the corresponding updated individual in subpopulation Pk, respectively, is the current best individual in subpopulation Pr, Fi is the scaling factor, and r1 and r2 are random and mutually exclusive integers.
The transfer spark was proposed to exchange information between different tasks in MTO-FWA [96]. The core idea is to bind a firework and its generated explosion sparks and guiding sparks into a task module to solve a specific problem. Based on this, assume the ith firework for the optimization task k is denoted as and the transfer spark generated by under the guiding of is represented as . Therefore, and can be obtained by Equations (11) and (12), respectively
where Mk and Mj denote the total number of the individuals that the skill factor is k and j, respectively.
In order to enhance knowledge transfer among different tasks, Yin et al. [110] integrated a new cross-task knowledge transfer as following, which used a search direction from another task
where and are the elite individuals of task k and r, respectively. The elite individual of the task is used to speed up the population convergence and the difference vector from another task can enhance the search diversity.
In EMT-RE framework for large-scale optimization, the knowledge transfer across tasks was conducted implicitly through the chromosomal crossover with two solutions possessing different skill factors [111]. If the current task is exactly the original task, the mutant chromosome is simply generated from intermediate vector ui by:
where is a randomly chosen individual from the current task, and Fi is the differential weight for controlling the amplitude of difference. If not, ui will be mapped into the embedded space of the current task by the pseudo inverse of random embedding matrix pinv(Ap):
where pinv(A) is approximated by .
Under the existing mapping strategies, tasks may be trapped in local Pareto Fronts with the guide of the knowledge transfer. Thus, with the aim of improving overall convergence behavior, a randomized mapping among tasks was added as follows, that enhances the exploration capacity of transferred solutions [106].
where , , and , which controls the probability of exploring the search space.
4.3.4. How to Knowledge Transfer Explicitly
In contrast to the existing implicit MTEC, the explicit MTEC algorithm employs an independent population for each optimization task and conducts knowledge transfer across tasks in an explicit manner. There are several advantages of explicit MTEC [112]. First, since each task has separate population for evolution, task-specific solution encoding schemes are employed for different tasks. Next, by only designing an explicit knowledge transfer operator, the explicit MTEC paradigm can be easily developed by employing different existing evolutionary solvers with various search capabilities for each optimization task. As different search mechanisms possess various search biases, the employment of problem-specific search operators in explicit MTEC could lead to a significantly improved algorithm performance. Further, rather than probabilistically selecting solutions for mating across tasks in the implicit MTEC, more flexible solution selection schemes, such as elite selection, can be performed before transfer in the explicit EMT for reducing negative knowledge transfer effects. However, compared with the accomplishments made in the implicit MTEC algorithms, only a few attempts have been conducted for developing the explicit MTEC approaches.
As a pioneering work, Bali et al. [113] put forward an MFEA variant with a linearized domain adaptation strategy, named LDA-MFEA, for transforming the search space of a simple task into its constitutive complex task which possesses a similar search space. The goal is to alleviate the negative transfer and to improve the quality of the generated offspring.
Feng et al. [21,114] developed an explicit MTEC algorithm to learn optimal linear mappings between different multiobjective tasks using a denoising autoencoder. In this method, different evolutionary mechanisms with different biases are cooperatively applied to solve various tasks simultaneously and the learned mappings serve as a bridge between tasks so that adaptive knowledge transfers can be conducted. By configuring the input and output layers to represent two task domains, the hidden representation provides a possibility for conducting knowledge transfer across task domains. In particular, let P and Q represent the set of solutions uniformly and independently sampled from the search space of two different tasks T1 and T2, respectively. Then the mapping M from T1 to T2 is given by
Therefore, the optimized solutions found for different tasks along the evolutionary search can be explicitly transferred across tasks via a simple matrix multiplication operation with the learned M. The authors further improved the explicit knowledge transfer to address combinatorial optimization problems, such as VRPs [112]. In particular, they developed two mechanisms: the weighted l1-norm-regularized learning process for capturing the transfer mapping and the solution-based knowledge transfer process across VRPs.
Aiming to strengthen the knowledge transfer efficiency, a novel genetic transform strategy was proposed and applied in individual reproduction [22]. Given two tasks T1 and T2, two mapping vectors M12 (from T1 to T2) and M21 (from T2 to T1) are calculated as follows:
where and are mean vectors of some selected individuals specific to the two tasks, respectively, and ε represents a small positive number. The operator performs element-wise division of two vectors. Based on two vectors, the parent individuals can be mapped to the vicinity of the other solutions.
It was very recently determined that a novel search space mapping mechanism, namely, subspace alignment (SA) could enable efficient and high-quality knowledge transfer among different tasks [115]. In particular, the SA strategy establishes the connection between two tasks using two transforming matrices, which can reduce the probability of negative transfer. This involves assuming there are two subpopulations P and Q, with each associated with a task. They denote the source data and target data, respectively. and denote the covariance matrices of P and Q, respectively. Then EP and EQ consist of the set of all eigenvectors of WP and WQ, respectively, with one eigenvector per column. From EP and EQ, the eigenvectors corresponding to the largest h eigenvalues that can retain 95% of the information are selected to construct the subspaces of P and Q, that is, SP and SQ. Afterward, the transformation matrix M∗ of mapping SP and SQ is obtained according to Equation (20).
The transferability between two distinct tasks is effectively enhanced with a proper domain adaptation technique. However, the improper pairwise learning fashion may incur a chaotic matching problem, which dramatically degrades the inter-task mapping [110]. Keeping this in mind, a novel rank loss function for acquiring a superior inter-task mapping between the source-target instances was formulated [116]. Then, an evolutionary-path-based probabilistic representation model was proposed to represent the optimization instances. With the proposed representation model, the threat of chaotic matching between the source-target domains is effectively avoided. Finally, with a progressional Gaussian representation model, a closed-form solution of affine transformation for bridging the gap between the source-target instances was mathematically derived from the proposed rank loss function.
Recently, Chen et al. [117] proposed an evolutionary multi-task algorithm with learning task relationships (LTR) for the MOO problem. The decision space of each task is treated as a manifold, and all decision spaces of different tasks are jointly modeled as a joint manifold. The joint mapping matrix composed of multiple mapping functions is then constructed to map the decision spaces of different tasks to the latent space. Finally, the relationships among distinct tasks can be jointly learned so as to promote the optimizing of all the tasks in a MOO problem.
Similarly, Tang et al. [42] also introduced an inter-task knowledge transfer strategy. Specifically, the low-dimension subspaces of task-specific decision spaces are first established via the principal component analysis (PCA) method. Then, the alignment matrix between two subspaces is learned and solved. After that, the corresponding solutions belonging to different tasks are projected into the subspaces. With this, two inter-task reproduction strategies are then designed in the aligned subspaces.
4.4. Balance between Intra-Population Reproduction and Inter-Population Reproduction
As illustrated in Figure 6, the offspring of individuals are generated in two ways: intra-population reproduction and inter-population reproduction. On one hand, the inductive biases transferred from another task are helpful to effectively accelerate convergence. On the other hand, excessive inter-population reproduction may lead to negative genetic transfer across tasks and bad algorithm performance [11,118]. Thus, a natural question in multi-task optimization community is finding a proper balance between intra-population reproduction and inter-population reproduction [51]. Up to now, the proposed approaches have been divided into three groups (fixed parameter, parameter adaptation, and resource reallocating) explained in the following subsections.
4.4.1. Fixed Parameter Strategy
In the original MFEA, the extent of inter-task knowledge transfer is mandated by a scalar parameter defined as the random mating probability (rmp), which is set as a constant of 0.3 [18]. A larger value of rmp induces more exploration of the entire search space, thereby facilitating population diversity. In contrast, a smaller value would encourage the exploitation of current solutions and speed up the population convergence. In TMO-MFEA, a larger rmp is used for diversity-related variables (DV) to enhance its diversity, while a smaller rmp is designed for convergence-related variables (CV) to achieve a better convergence [119,120]. Particularly, rmp for CV equals to 0.3, and rmp for DV equals to 1, which means a random assortative mating.
An appropriate parameter is essential to the efficiency and effectiveness of MTEC algorithm, and vice-versa. However, the user-defined and fixed parameter in MFEA and its variants is likely to have some distinct disadvantages. Firstly, the rmp parameter is manually specified based on the intuition of a decision maker. It is indeed patently clear that such an offline rmp assignment scheme is heavily dependent on the existence of prior knowledge about the different optimization tasks. Given the lack of prior knowledge, particularly in general black-box optimization, inappropriate (blind) rmp values risks the possibility of harmful inter-task knowledge transfers, thereby leading to significant performance slowdowns [41,79,121]. Secondly, the rmp parameter is immutably fixed for all tasks during the optimization process. Similar to biomes symbiosis [122], there are three relationships between source tasks and a target task in an MTO scenario: mutualism, parasitism, and competition. More importantly, the relationship may vary as the population distributions in their corresponding landscapes change. Although this fixed mechanism can make use of the positive knowledge transfer in some very special cases, it may intuitively bring negative effects in general cases [83].
4.4.2. Parameter Adaptation Strategy
If an optimization task is improved more times by the offspring from other tasks, the probability of knowledge transfer should be increased; otherwise, we will decrease this rate [122,123]. Thus, the probability is defined by
where and are the proportions of times that the current best solution in subpopulation Pk is improved by the offspring of the same task and other tasks, respectively. In addition to the transfer rate, the size of the selected candidate solutions also influences the effect of information transfer. An adaptive control mechanism for the size for each task was also devised in [123].
In MPEF (multi-population evolution framework), this parameter was adaptively determined based on evolution status [82,83]:
where srk is the success rate of subpopulation Pk, tsrk is the success rate of that offspring generated with the genetic material transfer, and c is a constant parameter.
A simple random searching method was introduced to adjust this parameter [94]. The current rmp is stored in the candidate list when at least one of K best solutions is updated by a better solution. Otherwise, the parameter is adapted as follows:
where δ is a constant parameter, and N (0,1) is a Gaussian noise with zero mean and unit variance.
Based on the saturation point of the knowledge transfer (SPKT), the knowledge transfer control scheme was proposed to control the generation of hybrid-offspring and alleviate the harmful transferred knowledge [99]. Based on the efficiencies of the global search and local search component, Liu et al. [86] proposed an adaptive control strategy, which can determine whether to perform the global search (DE) or the local search (CMA-ES) during the evolution.
Further, Binh et al. [124] proposed a new method for automatically adjusting rmp parameter. Specifically, the separate rmp value for each task is updated by
where NPi is number of individuals in the current task, is the set of individuals with skill factor and belong to the first nondominated front. The idea behind this definition is that, when most of the individuals are in the first nondominated front, the search process may get stuck in a local nondominated front and then we should increase RMP parameter for the cross-task crossover.
Besides, Zheng et al. [125] defined a novel notion of ability vector to capture the correlations between different tasks and automatically changed the intensity of knowledge transfer across tasks to enhance the performance of MTEC algorithm.
It was very recently reported that an enhanced MFEA called MFEA-II was presented, which enables an online parameter rmp estimation scheme in order to theoretically minimize the negative interactions between distinct optimization tasks [41]. Specifically, the extent of transfer parameter matrix is learned and adapted online based on the optimal blending of probabilistic models in a purely data-driven manner. Bali et al. [79] further presented a realization of a cognizant evolutionary multi-task engine. This framework learns inter-task relationships based on overlaps in the probabilistic search distributions derived from data generated during the search course. Recently, it was also used to solve the operation optimization of integrated energy systems [121].
Some concepts and operators of the parameter adaptation strategy utilized in MFEA-II cannot be directly applied to permutation-based discrete optimization environments, such as parent-centric interactions. Osaba et al. [126] entirely reformulated such concepts, making them suitable to deal with discrete optimization problem without losing the inherent benefits of MFEA-II. Furthermore, dMFEA-II implements a novel and simple strategy for dynamically updating the RMP matrix to the search performance.
4.4.3. Resource Reallocating Strategy
Recently, resource reallocating strategies in MFEA were integrated, which allocate the computational resources according to the complexities of tasks. For example, Wen and Ting [104] proposed an MFEA with resource allocation, named MFEARR. It can determine the occurrence of parting ways during evolution, at which time the effective cross-task knowledge transfer begins to fail. Then, an adaption strategy was proposed, where the transformation frequency is proportional to the probability of positive knowledge transfer. Gong et al. [127] put forward a MTO-DRA algorithm to enable dynamic resources allocation according to task requirements, such that more computing resources are assigned to complex tasks. Motivated by the similar idea that the limited computing resources should be adaptively allocated to different tasks, Yao et al. [128] also proposed dynamic resource allocation strategy. During the evolution of the population, individuals with high scalar fitness will get more investments or rewards, that is, more computing resources are allocated to them, and the scalar fitness of each individual is measured by a utility and updated periodically.
4.5. Evaluation and Selection Strategy
General speaking, the complete definition of a universal selection operator is composed of evaluation, comparison, and selection methods. The individual’s performance can be evaluated directly or indirectly [51]. As an indirect method, the scalar fitness was originally proposed in MFEA and its variants [18,57]. On the other hand, the fitness value of objective function is a nature and typical direct method [82,83,86,88,122]. Note that scalar fitness and function fitness are equivalence relations in a multi-task scenario [51].
After evaluating all individuals’ performances (function fitness or scalar fitness), the next question is the scope or level of comparison objects. In MFEA, the offspring-pop (Rt) and current-pop (Pt) were concatenated and then a sufficient number of individuals were selected to yield a new population [18]. This approach can be called population-based (or all-to-all) comparison. As a contrast, individual-based (or one-to-one) comparison was also utilized [61,82,83,84,88]. Once the offspring individual is generated by intra-population or inter-population reproduction, it is compared with its parent directly and then the better one can remain in the next generation.
For the case of population-based comparison, some alternative strategies were proposed to select the fittest individuals from the joint population. For example, MFEA and its variation follow elitist selection [18], level-based selection [53], and self-adaptive parent selection [129]. Furthermore, it may remove the worse or redundant individuals so as to create more population diversity [61].
The existing MTEC algorithms adopt a fitness-based selection criterion for effectively transferring elite genes across tasks. However, population diversity is necessary when it becomes a bottleneck against the genetic transfer. In [130], Tang et al. proposed a new selection criterion keeping a balance between individual fitness and population diversity as follows:
where is the balance factor, FS is fitness scalar which can adjust factorial cost of individuals evaluated for different tasks to a common scale, and CD is crowding distance which can approximately estimate individual diversity.
5. Related Extension Issues of Multi-Task Evolutionary Computation
5.1. Algorithm Framework
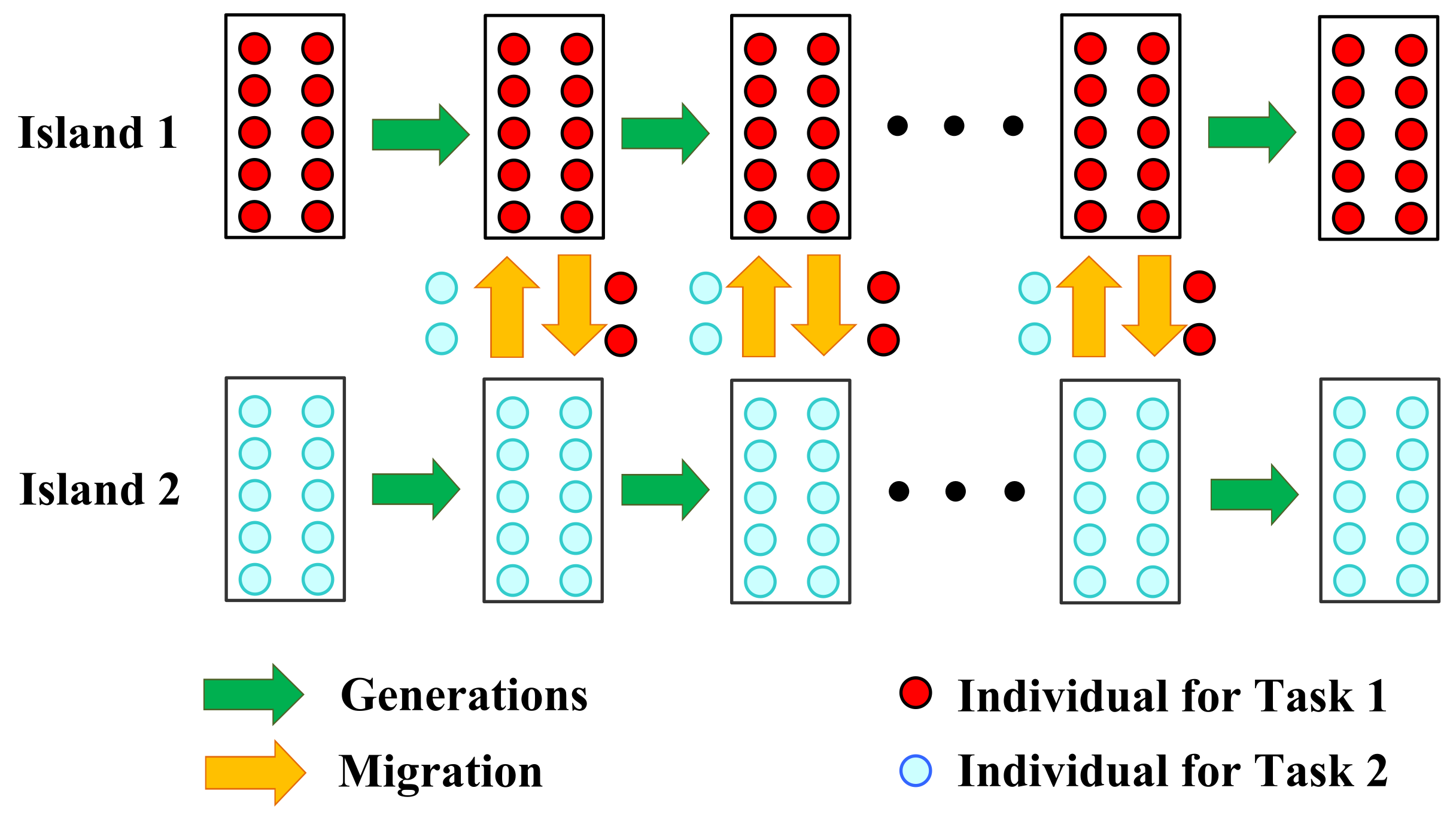
Hashimoto et al. [103] firstly explained that MFEA can be viewed as a special island model and then implemented a simple MTEC framework under the standard island model, as illustrated in Figure 7. Note that, it is essentially an explicit multi-population structure, in which the knowledge transfer across tasks is achieved through migration periodically.
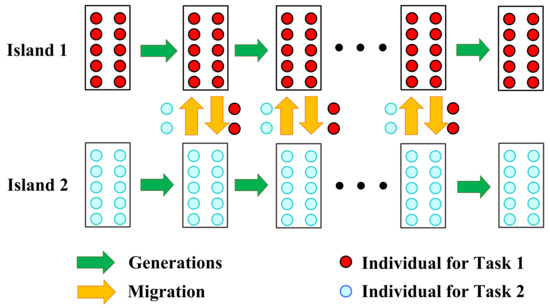
Figure 7.
An illustration of the MTEC framework under the standard island model [103].
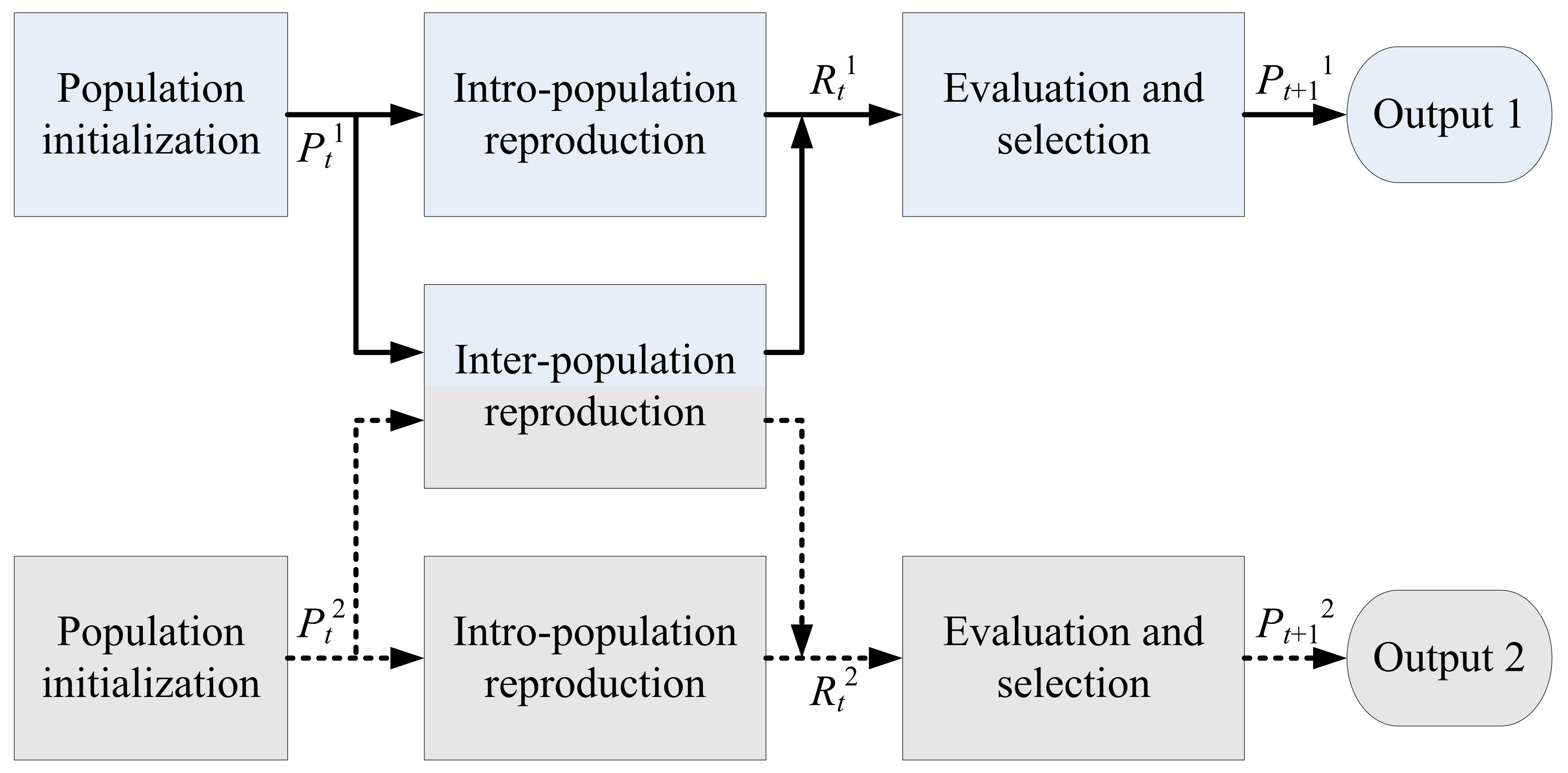
Another multi-population evolution framework (MPEF) was first established for MTO, as shown in Figure 8, wherein each population addressed its own optimization task and genetic material transfer with the other populations can be implemented and controlled in an effective manner [82,83]. Moreover, by adaptively adjusting random mating probability, it is effective for encouraging positive knowledge transfer, while avoiding negative knowledge transfer.
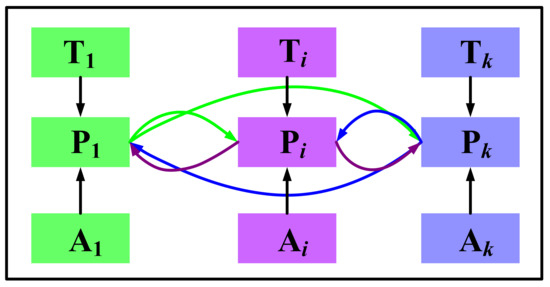
Figure 8.
An illustration of the multi-population evolution framework (MPEF) [83].
Liu et al. [86] proposed an efficient surrogate-assisted multi-task memetic algorithm (SaM-MA) for solving MTO problems. In the proposed method, the population is divided into multiple sub-populations, with each sub-population focusing on solving a task. In addition, a surrogate model with the Gaussian process model is used to predict the best solution, so as to reduce the number of fitness evaluations and to improve the search efficiency.
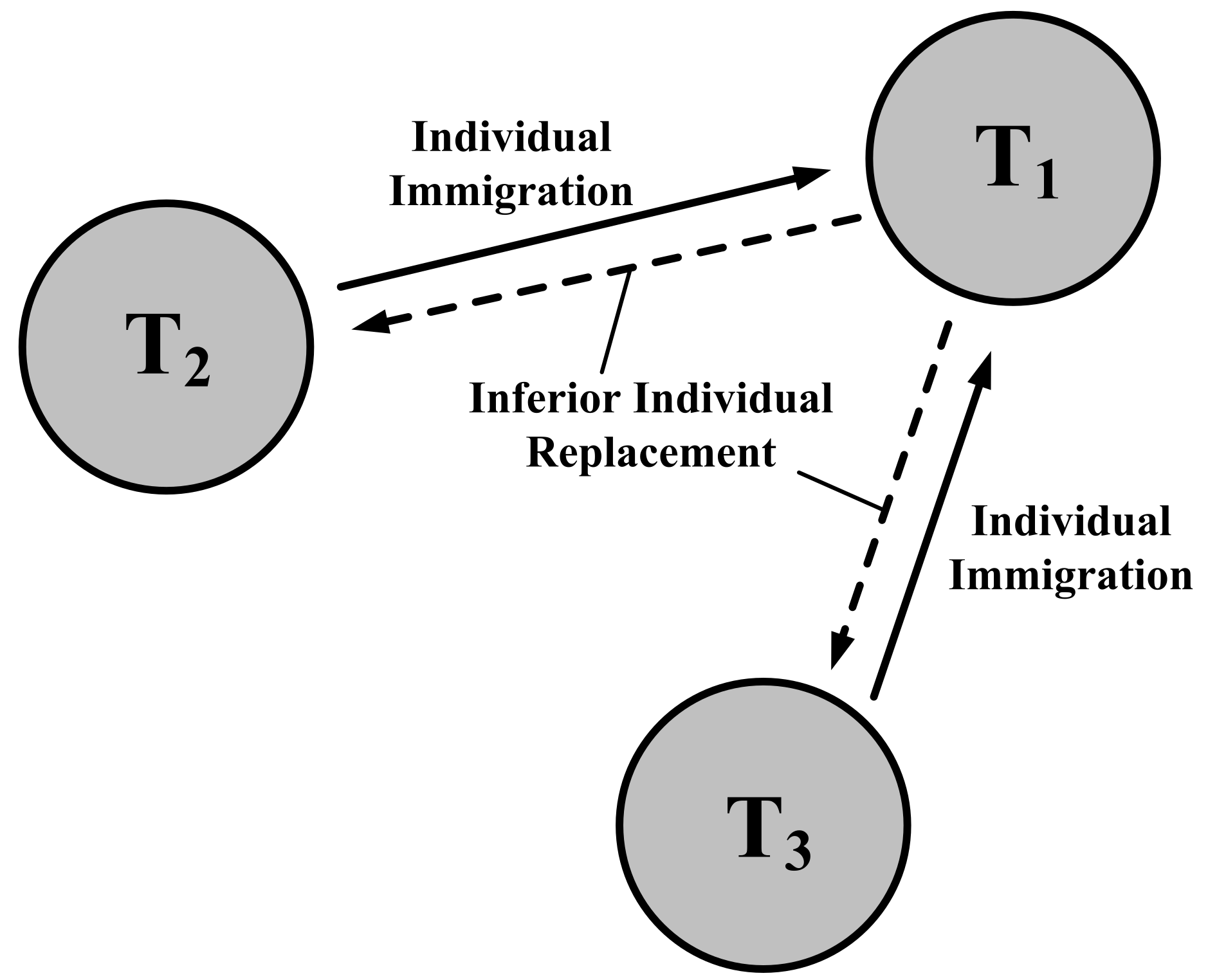
In order to isolate the information of each task, a light-weight multi-population framework was developed, in which each population corresponds to a single task [131]. In the proposed framework depicted in Figure 9, the inter-task knowledge transfer (individual immigration) is employed to generate the offspring, and then the successful individuals (generated from the inter-task crossover and surviving in the next generation) can replace the inferior individuals of the aforementioned task.
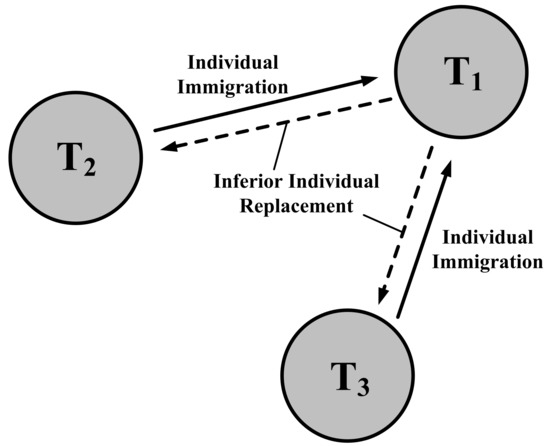
Figure 9.
An illustration of the multipopulation technique for multitask optimization [131].
Besides this, research articles [84,90,100] also proposed the MTEC algorithm based on the multi-population framework, in which the number of populations is equal to the number of tasks to be optimized and each population concentrates on solving a specific task.
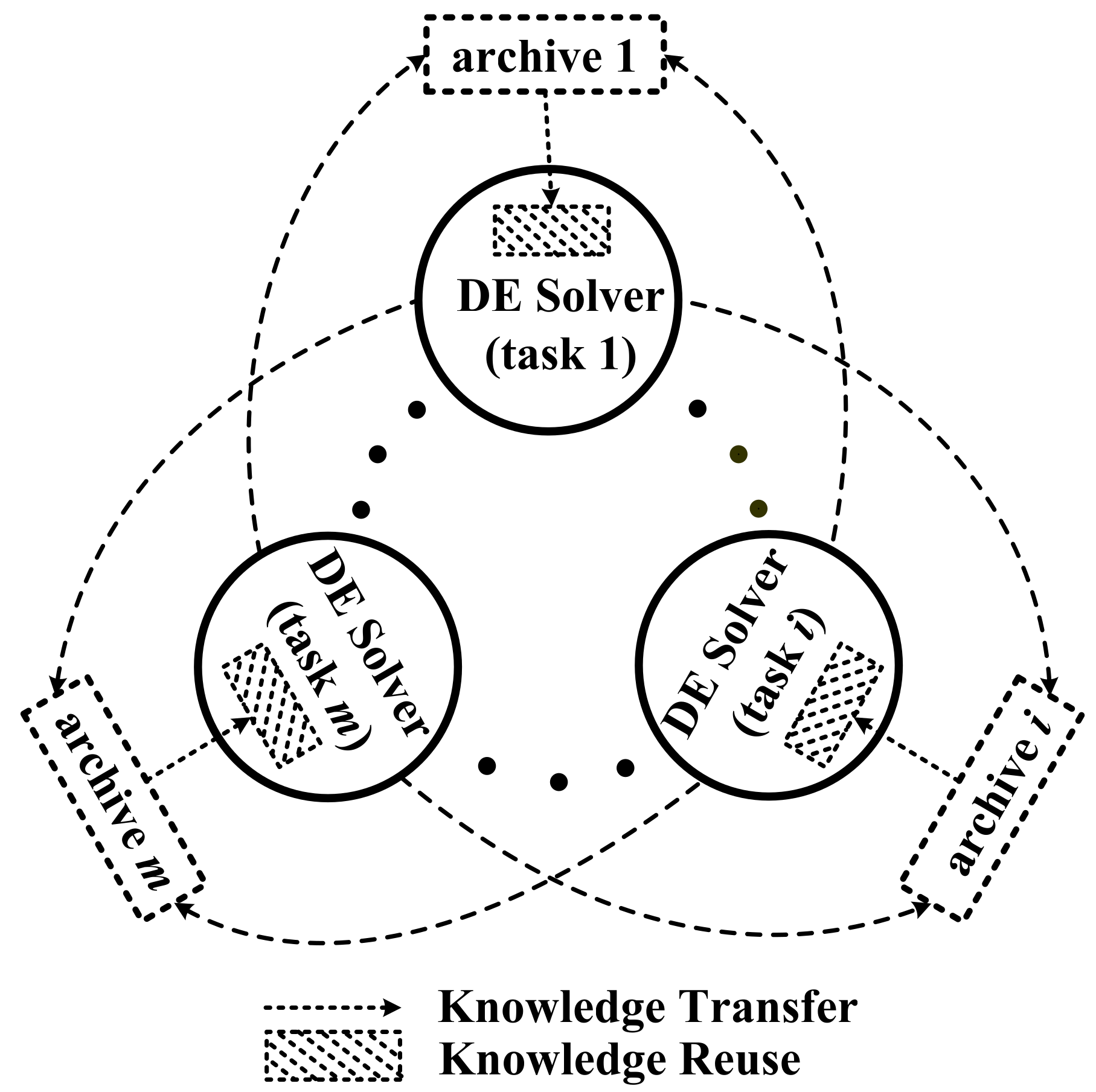
In order to clearly understand the focuses and differences of existing and potential works on MTEC, Jin et al. [132] proposed a general multitasking DE (MTDE) framework, which contains three major components, i.e., DE solver, knowledge transfer, and knowledge reuse. As illustrated in Figure 10, knowledge transfer is defined as both the processes of transferring knowledge out and in, and knowledge reuse as the process of utilizing the knowledge selected from the archive. In addition, two DE-specific knowledge reuse strategies were also studied in [132]: the base vector based strategy and the differential vector based strategy.
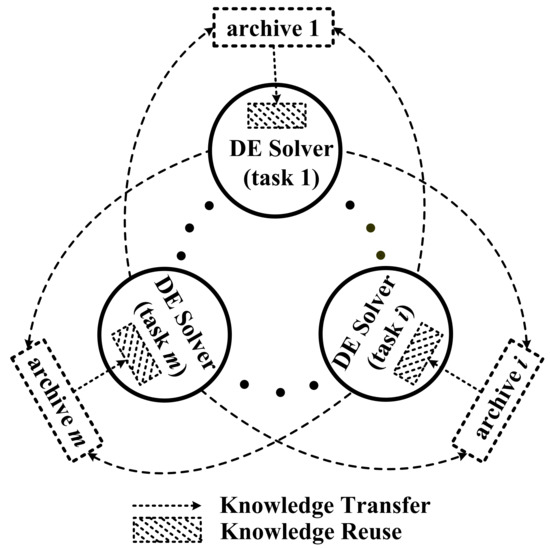
Figure 10.
An illustration of multitasking DE (MTDE) framework [132].
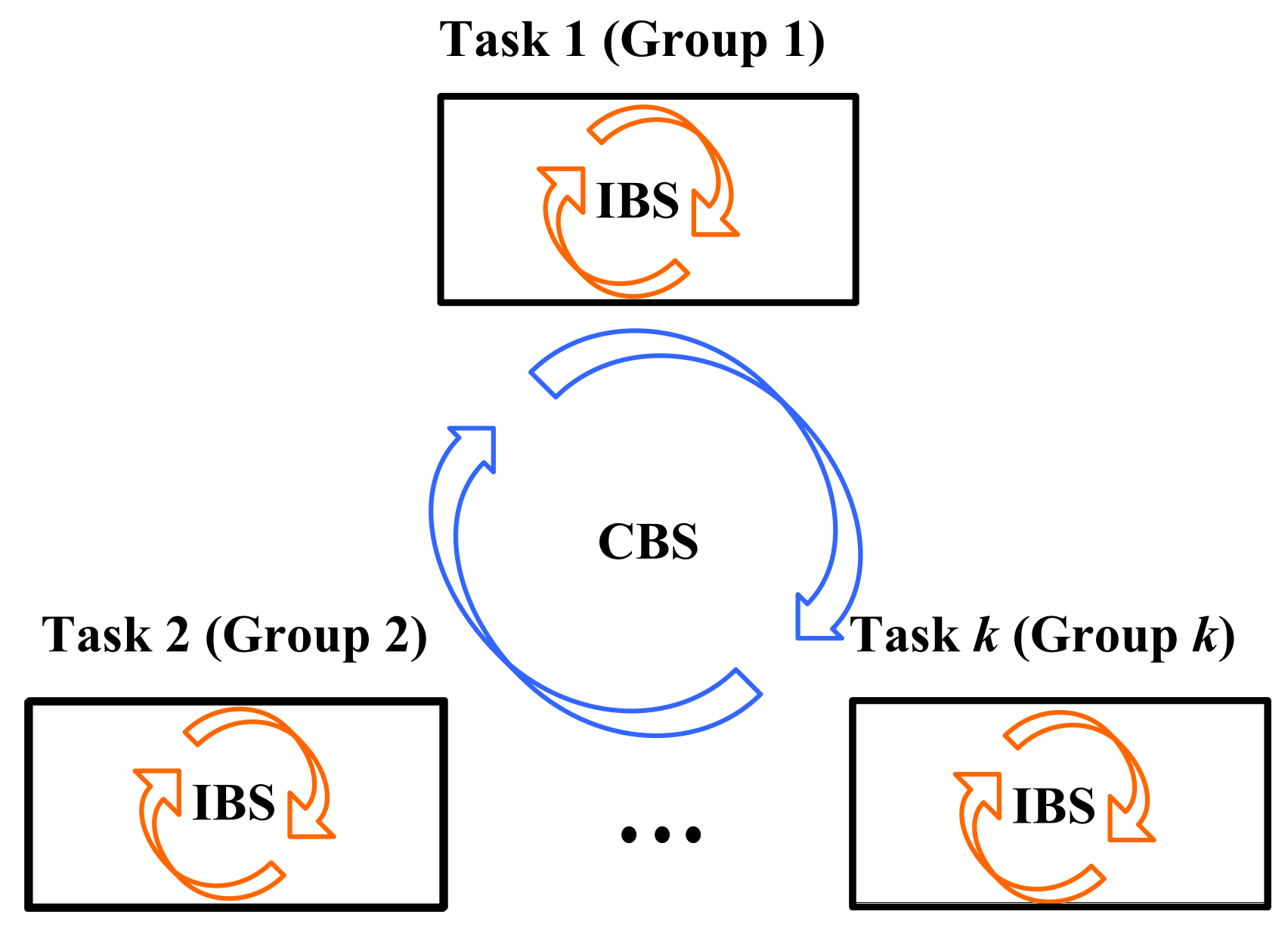
Inspired by the cluster-based search feature of brain storm optimization (BSO), a brain storm multi-task problems solver (BSMTPS) framework was proposed by dividing individuals into several groups [99]. As illustrated in Figure 11, the offspring are generated by the internal brain storm (IBS) and the cross-task brain storm (CBS), achieving knowledge transfer within a special task and across different tasks, respectively. Zheng et al. [98] also employed the clustering technique to cluster similar solutions into one group. In this way, it can avoid the knowledge transfer between dissimilar tasks and speed up the solving process.
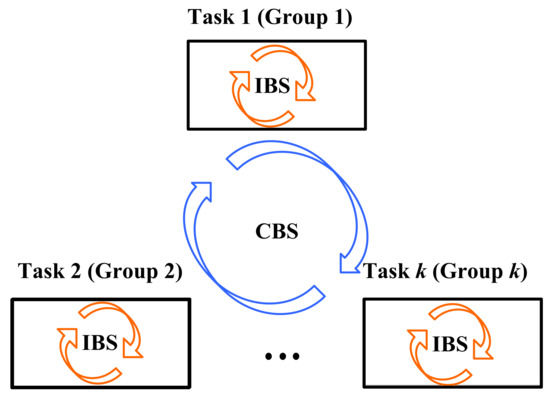
Figure 11.
An illustration of the brain storm multi-task problems solver (BSMTPS) framework [99].
MFEA adopts a simple inter-task knowledge transfer with randomness and tends to suffer from excessive diversity, thereby resulting in a slow convergence speed. To deal with the above issue, a two-level transfer learning framework was proposed for MTO [133]. Particularly, the upper level performs inter-task knowledge transfer via crossover and exploited the knowledge of the elite individuals to enhance the efficiency and effectiveness of genetic transfer. The lower level is an intra-task knowledge transfer, which transmits the beneficial information from one dimension to other dimensions to improve the exploration ability of the proposed algorithm. As a result, the two levels cooperate with each other in a mutually beneficial fashion.
In order to accelerate the algorithm convergence and improve the accuracy of solutions, Xie et al. [134] introduced a hybrid algorithm combining MFEA and PSO, in which the PSO was added after genetic operation of MFEA and applied to the intermediate-pop in each generation. Furthermore, an adaptive variation adjustment factor was proposed to dynamically adjust the velocity of each particle and guarantee that the convergence velocity was not too fast.
5.2. Similarity Measure between Tasks
Some researchers have focused on analyzing and measuring task relatedness [135]. As a pioneering work in [136], the similarity between tasks for MFEA was measured from three different perspectives, i.e., the distance between best solutions, the fitness rank correlation, and the fitness landscape analysis.
Based on a correlation analysis of the objective function landscapes of distinct tasks, Gupta et al. [137] presented a synergy metric (ξ) for capturing and quantifying a promising mode of complementarity between distinct optimization tasks. The metric can explain when and why the notion of implicit genetic transfer of MTEC algorithms may lead to performance enhancements.
For classification tasks, the relatedness between tasks is estimated by comparing their most appropriate patterns [138]. Nguyen et al. [138] proposed a multiple-XOF system, which can dynamically guide the feature transfer among learning classifier systems. The proposed method improves the learning performance of individual tasks when they are related, and reduces harmful signals from other tasks when they are not supportive to a target task.
5.3. Many-Task Optimization Problem
Until now, the existing MTEC approaches mainly focused on solving two optimization tasks simultaneously and few works have been developed solving many-task optimization (MaTO) problems. The work [139] in 2016 is the first attempt to demonstrate its feasibility for solving real-world problems with more than two tasks. In an MaTO environment, a natural idea of knowledge exchange is to select the most matching individuals from all tasks [122,123]. When the number of tasks to be optimized is more than two, in order to avoid this time-consuming approach, it is important to choose the most suitable task (or assisted task) to be paired with the present task (or target task) for effective knowledge transfer. The problem of recommending an internal source task has been considered as an open challenge in a MaTO context [140].
In [102], the roulette method based on the measured similarity of each task pair was used to select the source task. In this way, one task that has high similarity with the target task has a high chance to be selected. This can reduce the harm of negative transfer because only useful knowledge is transferred.
An adaptive mechanism of choosing suitable tasks was also proposed by simultaneously considering the similarity between tasks and the accumulated rewards of knowledge transfer during evolution [141]. Based on the reliable archives storing more sufficient individuals, the similarity between different tasks is measured by the Kullback–Leibler divergence. Inspired by the idea of reinforcement learning, a reward system was further developed in the proposed framework. Finally, the most likely beneficial task is identified and transfers knowledge via a new crossover method.
As task similarity may not capture the useful knowledge between tasks, instead of using similarity measures for task selection, Shang et al. [142] proposed a task selection approach based on credit assignment to conduct positive knowledge transfer. This approach selects the appropriate task according to how good the solutions transferred from different tasks performed along the evolutionary search process. The probability of selecting task Tj to task Ti is defined by:
where an element Wij gives how useful is task Tj for helping task Ti. In addition, the task assigned to individual xi is selected by task selective probability defined by [95]:
where is the degree of how individual xi can handle task Tk, which is defined by
where is the rank of individual xi in task Tk.
Moreover, Tang et al. [130] proposed a group-based MFEA by clustering the similar tasks (tasks with near global optima) and dispersing the dissimilar tasks. More importantly, the genetic materials can only be transferred within the same groups so that negative genetic transfers are eliminated.
Recently, Bali et al. [79] further utilized an RMP matrix in place of a scalar parameter rmp to effectively many-task genetic transfers online. It offers the distinct advantage of adapting the extent of knowledge transmissions between diverse task pairs with possibly nonuniform inter-task similarities.
5.4. Decision Variable Translation Strategy
For MTO problems, the optimal solutions of all constituent tasks tend to be in different locations of the unified search space. Within the range between those optimal solutions of different tasks, the trend of those objective functions may be in different directions. As a result, the effectiveness of knowledge transfer and sharing in MTEC may degrade or even be negative in this case. The main purpose of the decision variable translation strategy is to map the optimal solution of all tasks to the center point of the unified search space so that the growth trends of all tasks are similar and facilitate knowledge transfer during the optimization process [39,143,144].
In generalized MFEA (G-MFEA), each individual in the population was translated to a new location according to Equations (30) and (31):
where pi and opi (i = 1, 2, …, Np) are the ith solution and the corresponding transformed solution, respectively in the unified search space, Np is the population size and the translated value dk is estimated based on the promising solutions of the kth task. Furthermore, mk is the estimated optimum determined by calculating the mean value of the μ percent best solutions of the kth task.
Note that the translated direction and distance are both fixed for all individuals. Unfortunately, it is easy for individuals to go beyond the legal range, and then manual efforts are required to ensure their legality. As a result, the original population distribution is destroyed inevitably. Keeping this in mind, a novel variable transformation strategy and the corresponding inverse transformation were defined as Equations (32) and (33), respectively [143,144]
where cp = (0.5, 0.5, …, 0.5) is the center point of the unified search space, pi = {pi1, pi2, …,piD} is the ith solution in the original unified search space and opi = {opi1, opi2, …,opiD} is the corresponding ith solution in the transformed unified search space. Furthermore, m is the estimated optimal solution, which can be calculated as the mean value of the top μ*Np best solutions in the current generation.
5.5. Decision Variable Shuffling Strategy
In case the dimensions of decision space of different tasks in the MTO problem are different, a fine solution with small dimension may be poor and nonintegrated for task with large dimension, and some decision variables in the latter dimension of solution is always not used for tasks with small dimensions. Thus, the canonical MFEA is inefficient for MTO problems in this particular case.
To address this issue, a decision variable shuffling strategy was introduced [39]. To be specific, this strategy first randomly changes the order of the decision variables of individuals with small dimensions to give each variable an opportunity for knowledge transfer between two tasks. Then, the decision variables of individuals for the small dimensional task that are not in use are replaced with those of individuals for the large dimensional task to ensure the quality of the transferred knowledge.
Zhang and Jiang [145] systematically analyzed the defects of MFEA in dealing with heterogeneous MTO problems, and proposed the concepts of harmful transfer and defective parents. Then hetero-dimensional assortative mating and self-adaption elite replacements were proposed to overcome these issues. On six hetero-dimensional MTO problems, the proposed algorithm performed better than other algorithms.
Generally speaking, the order of decision variables has no significant influence on the single-task EAs. In contrast, the situation is significantly different for MTEC, in which the optimization process of one task more or less influences the optimization process of other tasks. Wang et al. analyzed the influence of the order of decision variables on single-task optimization (STO) and MTO problems, respectively. In addition, three orders of decision variables were proposed in [146,147]: full reverse order, bisection reverse order, and trisection reverse order. An important feature of these orders of decision variables is that an individual can recover as himself after two times of changing the order of decision variables.
5.6. Adaptive Operator Selection Strategy
It has been found that different crossover operators have various capabilities for solving optimization problems. Therefore, the appropriate configuration of crossover is necessary for robust search performance in MFEA. Zhou et al. [148] first investigated how the different types of crossover operator used affect the knowledge transfer in MFEA on both single-objective optimization (SOO) and MOO problems. As an efficient and robust MTEC, a new MFEA with adaptive knowledge transfer (MFEA-AKT) was further proposed, in which the crossover operator employed for knowledge transfer across tasks is self-adapted based on the information collected along the evolutionary search process.
In DE, a mutant vector is obtained by perturbing a base vector with several weighted difference vectors via a certain mutation strategy. Applying different mutation operators on current population can generate different search directions and offspring populations. Multiple commonly-used mutation strategies (DE/rand/1, DE/best/1, DE/current-to-rand/1, DE/current-to-best/1, DE/rand/2, DE/best/2, and DE/best/1 + ρ) were investigated to accelerate the convergence speed in [23,115,149], where DE/best/1 + ρ is defined as follows:
In the proposed mutation strategy, the value of ρ varies from 0 to 1. Its rationale is that the current-found best solution is utilized adequately to guide the search to promising areas in the early phase, while an increased perturbation is also integrated subsequently for a diverse exploration [149]. Note that we selected the suitable mutation strategy randomly in [115] or adaptively according to their success rates in previous generations in [23].
5.7. Multi-Task Optimization under Uncertainties
Optimization problems often have different kinds of uncertainties in practice due to the influence of subjective and objective factors [150,151]. Specifically, the objective and constraint functions across tasks usually contain uncertain variables [152].
The MFEA algorithm was extended to solve the interval MTO problem under uncertainty conditions [44]. In the proposed method, an interval crowding distance based on shape evaluation is calculated to evaluate the interval solutions more comprehensively. In addition, an interval dominance relationship based on the evolutionary state is designed to obtain the interval confidence level, which considers the difference of average convergence levels and the relative size of the potential possibility between individuals.
5.8. Hyper-Heuristic Multi-Task Evolutionary Computation
Instead of searching directly in the solution space like conventional meta-heuristics, hyper-heuristics work at the higher-level search space of a set of low-level heuristics [153,154]. The goal of hyper-heuristics is to solve the problem at hand by selecting existing low-level heuristics or generating new low-level heuristics.
Although hyper-heuristics search in heuristics space, their current paradigms still focus on solving isolated optimization problems independently. To integrate the advantages of MTEC and hyper-heuristics effectively, Hao et al. [78] proposed a unified framework of the evolutionary multi-task graph-based hyper-heuristic (EMHH). Note that, in EMHH, the concept of MTEC and graph heuristics are used as the high-level search methodology and low-level heuristics, respectively. It has been evaluated on examination timetabling and graph coloring problems and the experimental results demonstrate the effectiveness and efficiency of the proposed framework.
5.9. Auxiliary Task Construction
The distinctive performance of MTEC algorithms greatly depends on the similarity of tasks in MTO problem. These methods may fail in cases where no prior knowledge on the task correlations or even no related tasks are existed. Therefore, it is worth noting that constructing the auxiliary and related task for the main task is essential to the improved performance of evolutionary search [155,156].
As the first attempt in this direction, Da et al. [80] solved a complex travel salesman problem (TSP) problem in conjunction with a closely related (but artificially generated) multi-objective optimization task in a multi-task setting. The motivation behind the proposal is that the associated MOO task can often act as a helper task which aids the search process of the original problem by leveraging upon the implicit genetic transfer. Specifically, the MOO task is formulated by decomposing the original TSP problem into two distinct sub-tours.
Similarly, vehicle routing problem with time window (VRPTW) was modeled as a two-task problem in [157], i.e., a MOO version (main task) and a single-objective version (auxiliary task). The auxiliary task provides inspiration for the creation of bone routes and semi-finished product solutions, which work together to speed up the algorithm convergence by using these illegal solutions in the search process.
Feng et al. [111] proposed an evolutionary multitasking assisted random embedding method (EMT-RE) for solving the large-scale optimization problem. Besides the original problem, several low-dimensional auxiliary tasks are constructed by random embedding to assist target optimization in a multi-task scenario.
For a given MOO problem, each single objective problem naturally shares great similarity with it [158]. Therefore, the optimization processes on these single objective functions could generate useful knowledge to enhance the problem solving process on the target MOO problem. Huang et al. [158] treated each single objective problem as a separate task domain and then discussed the detailed designs of building the dynamic domain mapping and conducting knowledge transfer from multiple single objective problems to the multi-objective problem.
In industrial production, excessive process data are generated and collected, even leading to information overload. They are predicted by models with different precision. In [119], the operational indices optimization was first established based on an accurate model (multilayer perception) and two assistant models (the first-order polynomial regression model and the second-order polynomial regression model). Note that the assistant models are alternatively used in the multi-task environment with the accurate model to realize good knowledge transfer from the assistant models to the accurate model.
Inspired by the idea of the weight function, Zheng et al. [159] introduced a new additional helper-task to accelerate the convergence of the main task in multi-task scenario. As expected, the proposed method is beneficial to positive inter-task knowledge transfer by adding possible similar tasks.
6. Applications of Multi-Task Evolutionary Computation
Since the first establishment of MFEA, a number of MTEC algorithms have been proposed and successfully applied in many benchmark problems and real-world problems over the past few years, as summarized in Table 3.

Table 3.
Application domains of MTEC algorithms in the past five years.
6.1. Benchmark Problems
6.1.1. Continuous Optimization Problem
Evolutionary algorithms often lose their effectiveness and efficiency when applied to large-scale optimization problems. Feng et al. [111] presented a primary trial of solving large-scale optimization (up to 2000 dimensions) via the evolutionary multi-task assisted random embedding method.
EAs are not well suited for solving computationally expensive optimization problems, where the evaluation of candidate solutions needs to perform time-consuming numerical simulations or expensive physical experiments. Ding et al. [39] extended the basic MFEA to handle expensive optimization problems by transferring knowledge from multiple computationally cheap tasks to computationally expensive tasks. Similarly, a multi-surrogate based approach was adopted regarding the two surrogates as two related tasks [163]. The global surrogate model (expensive) is trained using all available data, and the local surrogate model (cheap) is trained using only part of the data subsequently selected from the data sorted.
A bi-level optimization problem (BLOP) is defined in the sense that one optimization task (the lower level problem) is nested within another (the upper level problem), which together comprise a pair of objective functions [181]. A multi-task bi-level evolutionary algorithm (M-BLEA) was provided as a promising paradigm to promote solving the upper level problem [37]. In M-BLEA, multiple lower level optimization tasks were to be appropriately solved during every generation of the upper level optimization, thereby facilitating the exploitation of underlying commonalities among them.
Although the original MFEA was designed for SOO problem [18], the idea of knowledge transfer or sharing across constitutive tasks also holds for the MOO problem. As a pioneer in multi-objective MTO, Gupta et al. [38] firstly extended the MFEA framework to the MOO domain. As a key element, a meaningful order of preference among candidate solutions in different tasks was proposed. Notice that for ordering individuals in a population, the binary preference relationship between two individuals satisfies the properties of irreflexivity, asymmetry, and transitivity [38].
Inspired by the division approach, Mo et al. [162] proposed a decomposition-based multi-objective multi-factorial evolutionary algorithm (MFEA/D-M2M). It adopts the M2M approach to decompose the MOO problem into multiple constrained sub-problems in order to enhance the population diversity. Note that a matting pool is also constructed to ensure genetic transfer across different sub-problems.
Yang et al. [120] presented the TMO-MFEA algorithm, in which decision variables were divided into two types, namely, diversity variables and convergence variables. The knowledge transfer on diversity variables is intensified to obtain evenly distributed solutions over the Pareto front (PF), whereas the knowledge transfer on convergence variables is restrained to maintain the convergence of the solution population toward the PF.
In MFEA based on decomposition strategy (MFEA/D), through multiple sets of weight vectors, each multi-objective task was decomposed into a series of SOO subtasks optimized with an independent population [161].
Recently, Ruan et al. [182] investigated when and how knowledge transfer works or fails in dynamic multi-objective optimization. Computationally knowledge transfer works poorly on problems with a fixed Pareto optimal set and under small environmental changes. In addition, the Gaussian kernel function used is not always adequate for the knowledge transfer.
6.1.2. Discrete Optimization Problem
As a preliminary attempt, several NP-hard combinatorial problems were efficiently solved within the MTEC framework, such as the traveling knapsack problem (KP) [18], Sudoku puzzles [48], travel salesman problem (TSP) [56], quadratic assignment problem (QAP) [56], linear ordering problem (LOP) [56], job-scheduling problem (JSP) [56], vehicle routing problems (VRPs) [53], and deceptive trap function (DTF) [164].
Recently, Feng et al. [57] presented a generalized variant of VRPOD, namely, the vehicle routing problem with heterogeneous capacity, time window, and occasional driver (VRPHTO), by taking the capacity heterogeneity and time window of vehicles into consideration. To illustrate its benefit, 56 new VRPHTO instances were further generated based on the existing common vehicle routing benchmarks. In addition, the stochastic team orienteering problem with time windows (TOPTW) models the trip design problem under more realistic settings by incorporating uncertainties. In [167], a new MTEC approach based on island model was developed to effectively enable knowledge sharing and transfer across search spaces.
The CluSTP problem has been solved by MFEA with new genetic operators [62,64]. In [62], the major ideas of the novel genetic operators were first constructing a spanning tree for smallest sub-graph then the spanning tree for larger sub-graph based on the spanning tree for the smaller sub-graph. Thanh et al. [64] also proposed genetic operators based on the Cayley code. Tran et al. [63] proposed a MTEC algorithm to solve multiple instances of minimum routing cost clustered tree problem (CluMRCT) together. Crossover and mutation operators were studied to create a valid solution, and a new method of calculating the CluMRCT solution was also introduced to reduce the consuming resources. More recently, Thanh et al. [68,70] further presented a novel MFEA algorithm for the CluSPT problem. Its notable feature is that the proposed MFEA has two tasks. The goal of the first task is finding the fittest solution as possible for the original problem while the goal of the second one is determining the best tree which enveloped all vertices of the problem.
Rauniyar et al. [166] put forward an MFEA based on NSGA-II to solve the pollution-routing problem (PRP). The authors considered a PRP formulation with two conflicting objectives: minimization of fuel consumption, and minimization of total travel distance.
In the literature, the n-bit parity problem is used to demonstrate the effectiveness and superiority of particular neural network architecture, training algorithms or neuroevolution methods. Chandra et al. [58] presented an evolutionary multi-task learning (EMTL) for feedforward neural networks that evolved modular network topologies for the n-bit parity problem.
6.2. Real-World Problems
6.2.1. Machine Learning
Tang et al. [174] introduced an MTEC algorithm for training multiple extreme learning machines with different number of hidden neurons for classification problem. The proposed method had achieved better quality of solutions even if some hidden neurons and connections were removed. Feature selection is an important data preprocessing technique to reduce the dimensionality in data mining and machine learning. Zhang et al. [89] proposed an ensemble classification framework based on evolutionary feature subspaces generation, which formulated the tasks of searching for the most suitable feature subspace into a MTO problem and solved it via a MTEC optimizer. Recently, MFPSO was also used to solve high-dimensional classification [173]. To be specific, two related tasks with the promising feature subset and the entire features set were developed, respectively. The MTO paradigm naturally fits the multi-classification problem by treating each binary classification problem as an optimization task within certain function evaluations. In the proposed framework, several knowledge transfer strategies (segment-based transfer, DE-based transfer, and feature transfer) were implemented to enable the interaction among the population of each separate binary task [172].
Training a deep neural network (DNN) with sophisticated architectures and a massive amount of parameters is equivalent to solving a highly complex non-convex optimization task. Zhang et al. [170] proposed a novel DNN training framework which formulated multiple related training tasks via a certain sampling method and solved them simultaneously via a MTEC algorithm. During the training process, the intermediate knowledge is identified and shared across all tasks to help their training. Recently, Martinez et al. [171] also presented a MTEC framework to simultaneously optimize multiple deep Q learning (DQL) models.
By identifying the overlaps between communities and active modules, Chen et al. [73] revealed the complex and dynamic mechanisms of high-level biological phenomena that cannot be achieved through identifying them separately. This MTO problem contains two tasks: identification of active modules and division of network into structural communities.
The optimization problem of fuzzy systems is used to optimize the parameters or (and) structure of the fuzzy system. Zhang et al. [72] presented a general framework of the multi-task genetic fuzzy system (MTGFS) to effectively solve this problem. For the sake of better searches in multiple optimization tasks, an efficient assortative mating method (a chromosome-based shuffling strategy and a cross-task bias estimation based on shuffling) was designed according to the specialty of the membership functions.
Shen et al. [169] proposed a novel multi-objective MTEC for learning multiple large-scale fuzzy cognitive maps (FCMs) simultaneously. Each task is treated as a bi-objective problem involving both the differences between the real and learned time series and the sparsity of the whole structure.
6.2.2. Manufacturing Industry
Li et al. [175] established a multi-task sparse reconstruction (MTSR) framework to optimize multiple sparse reconstruction tasks using a single population. The proposed method aims to search the locations of nonzero components or rows instead of searching sparse vectors or matrices directly, and the intra-task and inter-task genetic transfer are employed implicitly. Besides, Zhao et al. [176] successfully handled the endmember selection of hyperspectral images.
Constructing optimal data aggregation trees in wireless sensor networks is an NP-hard problem for larger instances. A new MTEC algorithm was proposed to solve multiple minimum energy cost aggregation tree (MECAT) problems simultaneously [67]. The authors presented crossover and mutation operators, enabling multi-task evolution between instances.
6.2.3. Industrial Engineering
The operational indices optimization is crucial and difficult for the global optimization in beneficiation processes. Yang et al. [17] presented a multi-objective MFEA to solve this problem. Sampath et al. [177] also handled the optimal power flow problems with different load demands on power systems via MTEC framework. The process of continuous annealing production line is very complex in the iron and steel industry. Some environmental parameters and control variables have coupling relationships, which makes it difficult to achieve global optimization with traditional EAs. Wang and Wang [23] proposed an AdaMOMFDE algorithm based on the search mechanism of differential evolution. The optimal operation of integrated energy systems (IES) is of great significance to facilitate the penetration of distributed generators and then improve its overall efficiency. Wu et al. [121] developed a novel grid-connected IES framework by considering the biogas-solar-wind energy complementarities and solved it by MO-MFEA-II. In the Mazda multiple car design benchmark problem, three kinds of cars (SUV, CDW, and C5H) with different sizes and body shapes need to be optimized simultaneously [183]. This MTO problem was solved by two distinct MTEC algorithms [91,95].
6.2.4. Others
Thanks to the effectiveness of MTEC algorithms, they have been successfully applied to tackle other real-world problems in the literature, such as mobile robot path planning [44,107,108], search-based software test data generation [139], the cloud computing service composition problem [74,179], HIV-1 protease cleavage sites prediction [180], and the double-pole balancing problem [61,62,63].
7. Future Works
Although multi-task optimization methodology in the evolutionary community has been a tremendous success, compared with other well-known evolutionary and swarm intelligent methods, it is just at the stage of discipline creation and preliminary exploration in a so far unexplored research direction. Many challenges are yet to be discovered and overcome in the future in theoretical models, efficient algorithms, and engineering applications of this promising paradigm. Based on the literature analysis in the past five years, some opportunities and challenges of MTO and MTEC are summarized as follows [11,184].
7.1. Explore Mechanism of Knowledge Transfer
One of the main features of MTEC algorithms is knowledge transfer from one task to help solve other tasks, which greatly affects the optimization process and algorithm performance. Considering the general process of transfer learning, there are three key issues to be solved serially: (1) when to transfer; (2) what to transfer; (3) how to transfer.
As the original, the first question is to answer when the knowledge transfer is triggered. Theoretically, it is initiated at any stage of optimization process. Thus, the straightforward answer is executing it periodically in a fixed generation interval [21,102]. However, this trial-and-error approach does not properly explain or define the true transfer demands, leading to resource waste. Therefore, we should carefully strike a good balance between transfer cost and transfer effect. One possible and reasonable attempt in the literature is the knowledge transfer across tasks being triggered when the best solutions found so far stagnate for successive generations [88,97].
The second question might seem simple, but it is deceptively difficult. Intuitively, the best solutions found so far are good choices to be transferred. However, it might be counter-productive due to distinctly different search spaces of constitutive tasks. Inspired by biomes symbiosis, three relationships between source tasks and target tasks (mutualism, parasitism, and competition) were summarized in [83] by Li et al. Xu et al. [144] also provided a negative case when the optimal solutions were located in different positions in the unified search space. A potential approach is using the distribution characteristics of population or fitness landscape characteristics of task, instead of a special solution. These characteristics represent a full view of population or task, guiding to the global optimal solutions of each task. More importantly, the MTEC algorithm can learn these characteristics online and then adjust knowledge transfer strategy in a timely manner and properly. As a result, an important research topic is the formulation of approximate online models that can make use of the data generated during the optimization process to somehow quantify the relatedness between tasks.
The research findings of the third question are the most fruitful among three issues. In general, there are two knowledge transfer schemes in multi-task scenario in the literature: implicit transfer and explicit transfer, which are systematically discussed in Section 4.3. Although the experimental results of these schemes are encouraging, it must be kept in mind that the transfer of genetic material across tasks may be pessimistic or negative in some cases. Therefore, the mechanism of knowledge transfer across tasks should be further explored. Only by fully understanding internal mechanisms and external connections of knowledge transfer can we construct novel and positive knowledge transfer strategies.
7.2. Balance Theoretical Analysis and Practical Application
At present, most scholars concentrated mainly on algorithmic advancement and practical application. The superiority of MTEC algorithms is, in most cases, illustrated by simulation results, not by mathematical analysis with some pertinent mathematical concepts and tools. On the other hand, the researchers and practitioners ignore further study on the theoretic analysis of MTO and MTEC, either consciously or unconsciously. The most representative results focused on convergence performance [37,41] and time complexity [46,47] of simplified MFEA, which theoretically explains the superiority of the MTEC algorithm compared with traditional single-task EAs. Comparatively speaking, other theoretical analysis (stability, diversity, etc.) of the MTEC algorithm is very limited and the distinct theoretical framework has not been assessed so far.
As a novel evolution computation paradigm, MTEC has distinct characteristics, such as a unified search space, assortative mating, and selective evaluation, to distinguish it from the single-task EAs. The intensive research of the theoretical models and functioning mechanisms of these key stone characteristics is infrequent. For this reason, the essential and fundamental development of MTO and MTEC has been hard to obtain until now.
7.3. Enhance Effectiveness and Efficiency of MTEC Algorithms
To optimize multiple tasks simultaneously, the effectiveness and adaptation of MTEC algorithm is especially important for a practitioner. In addition to canonical genetic operators (crossover, mutation, and selection), individuals encoding schemes in the unified genotype space and the implicit genetic transfer (via assortative mating and vertical cultural transmission) are the most critical ingredients of the original MFEA [18]. To improve the effectiveness and efficiency, more existing encoding schemes and genetic operators available in the literature need to be tested in a multi-task setting.
On the other hand, the performance of MTEC algorithm mainly depends on the tasks to be optimized. If the adopted methodology does not appropriately suit the behavior or feature of optimization tasks, the optimization process may be counterproductive. Therefore, we should accurately depict and deeply understand the optimization problem we face. As a critical problem to be solved urgently, based on the key feature of each task, a variety of novel encoding schemes and genetic operators can be designed to achieve the active controlling of population diversity and adaptive adjustment over the search direction of the population.
More fundamentally, we can try to modify the basic structure of the MTEC algorithm [185,186]. For instance, Chen et al. [129] introduced a local search strategy based on quasi-Newton, a re-initialization technique of worse individuals, and a self-adapt parent selection strategy to obtain better solutions. Due to the great success of memetic algorithms, incorporating local search to MTEC can also be another possible orientation. The new algorithm framework discussed in Section 5.1 can be seen as a certain positive attempt for this research topic.
7.4. Extend MTEC Algorithmic Advancements
In addition to the core demands of having suitable individuals encoding and the knowledge transfer, the advancements of peripheral elements will certainly play a crucial role in the future progress of MTO and MTEC. In this regard, some potential research prospects are in (a) the many-task optimization problem, (b) uncorrelated optimization tasks, (c) heterogeneous optimization tasks, (d) adaptively selecting the most appropriate genetic operators, (e) the multi-task optimization problem under uncertainties, (f) developing hyper-heuristic MTEC algorithms, and (g) exploring an effective approach to construct auxiliary tasks, as discussed in Section 5.
Without a doubt, these examples studied so far are just the tip of the iceberg. They are simply divided into two groups: issues similar to single-task EAs, such as (e), (f), and (g), and distinct issues in a multi-task scenario, such as (a), (b), (c), (d), and (h). Further, inspired by the single-task EAs, a good deal of similar algorithmic advancements will be explored in a multi-task scenario. For instances, adaptive MTEC is capable of adapting core mechanisms such as genetic operators, population size, and a choice of local search steps. On the other hand, several distinct forms of research in a multi-task scenario should be also conducted in the near future. For example, a natural extension of canonical MTO is effective handling of many tasks or heterogeneous tasks at a time.
7.5. Develop New Science and Engineering Applications
Finally, we believe that the notion of MTO provides a fresh perspective in terms of available knowledge transfer for improved problem solving. Several complex problems in science, engineering, operations research, etc. benefit immensely from the proposed ideas. At present, most applications focus on traditional continuous or discrete optimization fields. Thus, there is still a big gap between MTEC and the practical applications in the real world. As a preliminary attempt in the community of multi-task optimization, Prof. Ong et al. [135,187] have designed two MTO test suites for single-objective and multi-objective continuous optimization tasks, respectively. The test suite for single-objective and multi-objective MTO both contains 10 MTO complex problems, and 10 50-task MTO benchmark problems. Note that the MTO benchmark problems feature different degrees of latent synergy between their involved two component tasks.
Up to now, MTEC has not gained international recognition in community of evolutionary computation, and the reason for this might be just a lack of inspiring results in fundamental, subversive, and pioneering fields. What is more to the point, nobody has carefully and deeply considered why no breakthrough has occurred in such fields, or even summarized the basic features of MTO and MTEC.
7.6. Compare Disparate Algorithms under Different Scenarios
The No Free Lunch (NFL) theory proposed by Wolpert and Macready states that all algorithms are equivalent when their performance is evaluated over all possible problems [188]. Accordingly, each MTEC algorithm with its unique structure and operation strategy always shows different algorithm performance under different scenarios. Although some similar results have been repeatedly confirmed experimentally, it is not enough to draw a conclusion. In order to investigate the sense of the relative strengths and weaknesses of MTEC approaches, disparate strong algorithms based on a novel strategy should be compared directly and thoroughly [189].
As we all know, the overall performance of EAs more or less depends on the tested benchmark problems. Therefore, it is necessary for design diverse benchmark problems to receive a thorough investigation or evaluation. Similarly to the classical EAs, the benchmark problems for MTEC algorithms can be continuous and discrete, unimodal and multimodal, low and high dimension, static and dynamic, non-adaptive and adaptive, and with and without noise instances [152,190]. More importantly, the deviation and complementarity between any two problems should be taken into consideration. Ideally, the benchmark problems should contain various features mentioned above.
8. Conclusions
As a novel optimization paradigm proposed five years ago, with the increasing complexity and volume of data collected in the data-driven world of today, multi-task optimization appears to be an indispensable and competitive tool for the future. Since it has been proposed by Ong in 2015 [24], it has gradually attracted the attention of scholars in the community of evolutionary computation and many good results have been obtained.
To the best of our knowledge, this paper is the first literature review devoted to multi-task optimization and multi-task evolutionary computation. This overview introduced the basic definition of MTO and several confusing concepts of MTO, such as multi-objective optimization, sequential transfer optimization, and multi-form optimization. Some bold theoretical conclusions are also provided, mainly in terms of convergence performance and time complexity of some simplified forms of MFEA. Its goal is theoretically explaining the superiority of the existing MTEC algorithm compared with traditional single-task EAs.
As the core of this review article, a variety of implementation approaches of key components of MTEC are described in Section 4, including a chromosome encoding and decoding scheme, intro-population reproduction, inter-population reproduction, balance between intra-population reproduction and inter-population reproduction, and evaluation and selection strategy. In particular, we provided a clear description of inter-population reproduction, dealing with the when, what, and how of achieving positive knowledge transfer. Further, other related extension issues of MTEC were summarized in Section 5, but they are just preliminary, fragmentary attempts and lack systematization. Next, the applications of MTEC in science and engineering were reviewed, highlighting the theoretical meaning and practical value of each problem.
Finally, a number of trends for further research and challenges that can be undertaken to help move the field forward are discussed. In a word, the future work in MTO and MTEC includes but is not limited to (1) exploring a novel mechanism of positive knowledge transfer, (2) strengthening the theoretical research to set a solid foundation, (3) enhancing the effectiveness and efficiency of MTEC algorithms by various advanced technologies, (4) extend MTEC algorithms in more complex scenarios, such as many-task or uncorrelated optimization problems under uncertainties, (5) developing real-world applications of MTEC, e.g., in machine learning, smart manufacturing [191], and smart logistics [192], and (6) comparing disparate MTEC algorithms under different scenarios.
In short, the purpose of this review article is twofold. For researchers in the evolution computation community, it provides a comprehensive review and examination of MTEC. Further, we hope to encourage more practitioners working in the related fields to become involved in this fascinating territory.
Author Contributions
Conceptualization, methodology, Q.X.; formal analysis, investigation, supervision, project administration, funding acquisition, Q.X., N.W., and L.W.; resources, data curation, W.L. and Q.S.; writing—original draft preparation, Q.X., N.W., L.W., and W.L.; writing—review and editing, Q.X. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the National Science Foundation of China 61773314, Natural Science Basic Research Program of Shaanxi 2019JZ-11 and 2020JM-709, Scientific Research Project of Education Department of Shaanxi Provincial Government 19JC011, and Research Development Foundation of Test and Training Base 23.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Molina, D.; LaTorre, A.; Herrera, F. An insight into bio-inspired and evolutionary algorithms for global optimization: Review, analysis, and lessons learnt over a decade of competitions. Cogn. Comput. 2018, 10, 517–544. [Google Scholar] [CrossRef]
- Lin, M.-H.; Tsai, J.-F.; Yu, C.-S. A review of deterministic optimization methods in engineering and management. Math. Probl. Eng. 2012, 2012, 756023. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Sałabun, W. A new approach to identifying a multi-criteria decision model based on stochastic optimization techniques. Symmetry 2020, 12, 1551. [Google Scholar] [CrossRef]
- Back, T.; Hammel, U.; Schwefel, H.-P. Evolutionary computation: Comments on the history and current state. IEEE Trans. Evol. Comput. 1997, 1, 3–17. [Google Scholar] [CrossRef]
- Jin, Y.C.; Branke, J. Evolutionary optimization in uncertain environments—A survey. IEEE Trans. Evol. Comput. 2005, 9, 303–317. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yang, S.X.; Branke, J. Evolutionary dynamic optimization: A survey of the state of the art. Swarm Evol. Comput. 2012, 6, 1–24. [Google Scholar] [CrossRef]
- Tanabe, R.; Ishibuchi, H. A review of evolutionary multimodal multiobjective optimization. IEEE Trans. Evol. Comput. 2020, 24, 193–200. [Google Scholar] [CrossRef]
- Li, J.; Lei, H.; Alavi, A.H.; Wang, G.-G. Elephant herding optimization: Variants, hybrids, and applications. Mathematics 2020, 8, 1415. [Google Scholar] [CrossRef]
- Bennis, F.; Bhattacharjya, R.K. Nature-Inspired Methods for Metaheuristics Optimization: Algorithms and Applications in Science and Engineering; Springer Nature: Basingstoke, UK, 2020. [Google Scholar]
- Mirjalili, S.; Dong, J.S.; Lewis, A. Nature-Inspired Optimizers: Theories, Literature Reviews and Applications; Springer Nature: Basingstoke, UK, 2020. [Google Scholar]
- Ong, Y.-S.; Gupta, A. Evolutionary multitasking: A computer science view of cognitive multitasking. Cogn. Comput. 2016, 8, 125–142. [Google Scholar] [CrossRef]
- Gupta, A.; Ong, Y.-S.; Feng, L. Insights on transfer optimization: Because experience is the best teacher. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 2, 51–64. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- NIPS*95 Post-Conference Workshop. Available online: http://socrates.acadiau.ca/courses/comp/dsilver/NIPS95_LTL/transfer.workshop.1995.html (accessed on 31 March 2021).
- Caruana, R. Multitask learning. In Learning to Learn; Thrun, S., Pratt, L., Eds.; Springer: New York, NY, USA, 1998; pp. 95–133. [Google Scholar]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D.D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Thrun, S. Is learning the n-th thing any easier than learning the first. In Advances in Neural Information Processing Systems; Mozer, M.C., Jordan, M.I., Petsche, T., Eds.; The MIT Press: Cambridge, MA, USA, 1996; pp. 640–646. [Google Scholar]
- Gupta, A.; Ong, Y.-S.; Feng, L. Multifactorial evolution: Toward evolutionary multitasking. IEEE Trans. Evol. Comput. 2016, 20, 343–357. [Google Scholar] [CrossRef]
- Lin, J.B.; Liu, H.L.; Tan, K.C.; Gu, F.Q. An effective knowledge transfer approach for multiobjective multitasking optimization. IEEE Trans. Cybern. 2020, in press. Available online: https://ieeexplore.ieee.org/document/9032363/ (accessed on 11 March 2020). [CrossRef]
- Min, A.T.W.; Sagarna, R.; Gupta, A.; Ong, Y.-S.; Goh, C.K. Knowledge transfer through machine learning in aircraft design. IEEE Comput. Intell. Mag. 2017, 12, 48–60. [Google Scholar] [CrossRef]
- Feng, L.; Zhou, L.; Zhong, J.H.; Gupta, A.; Ong, Y.-S.; Tan, K.C.; Qin, A.K. Evolutionary multitasking via explicit autoencoding. IEEE Trans. Cybern. 2019, 49, 3457–3470. [Google Scholar] [CrossRef]
- Liang, Z.P.; Zhang, J.; Feng, L.; Zhu, Z.X. A hybrid of genetic transform and hyper-rectangle search strategies for evolutionary multi-tasking. Expert Syst. Appl. 2019, 138, 1–18. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.P. Multiobjective multifactorial operation optimization for continuous annealing production process. Ind. Eng. Chem. Res. 2019, 58, 19166–19178. [Google Scholar] [CrossRef]
- Ong, Y.-S. Towards evolutionary multitasking: A new paradigm in evolutionary computation. In Proceedings of the International Conference on Computational Intelligence, Cyber Security and Computational Models, Coimbatore, India, 17–19 December 2015; pp. 25–26. [Google Scholar]
- Gupta, A.; Da, B.S.; Yuan, Y.; Ong, Y.-S. On the emerging notion of evolutionary multitasking: A computational analog of cognitive multitasking. In Recent Advances in Evolutionary Multi-Objective Optimization; Bechikh, S., Datta, R., Gupta, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 139–157. [Google Scholar]
- Cheng, M.Y. Attribute Selection Method Based on Binary Ant Colony Optimization and Fractal Dimension. Ph.D. Thesis, Hefei University of Technology, Hefei, China, 2017. (In Chinese). [Google Scholar]
- Chen, W.Q. Active Module Identification in Biological Networks. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2018. [Google Scholar]
- Min, A.T.W. Transfer Optimization in Complex Engineering Design. Ph.D. Thesis, Nanyang Technological University, Singapore, 2019. [Google Scholar]
- Da, B.S. Methods in Multi-Source Data-Driven Transfer Optimization. Ph.D. Thesis, Nanyang Technological University, Singapore, 2019. [Google Scholar]
- Gupta, A.; Ong, Y.-S. Back to the roots: Multi-x evolutionary computation. Cogn. Comput. 2019, 11, 1–17. [Google Scholar] [CrossRef]
- Trivedi, A.; Srinivasan, D.; Sanyal, K.; Ghosh, A. A survey of multiobjective evolutionary algorithms based on decomposition. IEEE Trans. Evol. Comput. 2017, 21, 440–462. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Bader, J.; Zitzler, E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.F.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Rice, J.; Cloninger, C.R.; Reich, T. Multifactorial inheritance with cultural transmission and assortative mating. I. Description and basic properties of the unitary models. Am. J. Hum. Genet. 1978, 30, 618–643. [Google Scholar]
- Cloninger, C.R.; Rice, J.; Reich, T. Multifactorial inheritance with cultural transmission and assortative mating. II. A general model of combined polygenic and cultural inheritance. Am. J. Hum. Genet. 1979, 31, 176–198. [Google Scholar]
- Gupta, A.; Mańdziuk, J.; Ong, Y.-S. Evolutionary multitasking in bi-level optimization. Complex Intell. Syst. 2015, 1, 83–95. [Google Scholar] [CrossRef]
- Gupta, A.; Ong, Y.-S.; Feng, L.; Tan, K.C. Multiobjective multifactorial optimization in evolutionary multitasking. IEEE Trans. Cybern. 2017, 47, 1652–1665. [Google Scholar] [CrossRef]
- Ding, J.L.; Yang, C.E.; Jin, Y.C.; Chai, T.Y. Generalized multi-tasking for evolutionary optimization of expensive problems. IEEE Trans. Evol. Comput. 2019, 23, 44–58. [Google Scholar] [CrossRef]
- Bridges, C.L.; Goldberg, D.E. An analysis of reproduction and crossover in a binary-coded genetic algorithm. In Proceedings of the International Conference on Genetic Algorithms and Their Application, Cambridge, MA, USA, 28–31 July 1987; pp. 9–13. [Google Scholar]
- Bali, K.K.; Ong, Y.-S.; Gupta, A.; Tan, P.S. Multifactorial Evolutionary Algorithm with Online Transfer Parameter Estimation: MFEA-II. IEEE Trans. Evol. Comput. 2020, 24, 69–83. [Google Scholar] [CrossRef]
- Tang, Z.D.; Gong, M.G.; Wu, Y.; Liu, W.F.; Xie, Y. Regularized evolutionary multitask optimization: Learning to intertask transfer in aligned subspace. IEEE Trans. Evol. Comput. 2020, 25, 262–276. [Google Scholar] [CrossRef]
- Da, B.S.; Gupta, A.; Ong, Y.-S. Curbing negative influences online for seamless transfer evolutionary optimization. IEEE Trans. Cybern. 2019, 49, 4365–4378. [Google Scholar] [CrossRef]
- Yi, J.; Bai, J.R.; He, H.B.; Zhou, W.; Yao, L.Z. A multifactorial evolutionary algorithm for multitasking under interval uncertainties. IEEE Trans. Evol. Comput. 2020, 24, 908–922. [Google Scholar] [CrossRef]
- Osaba, E.; Martinez, A.D.; Lobo, J.L.; Lana, I.; Ser, J.D. On the transferability of knowledge among vehicle routing problems by using cellular evolutionary multitasking. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems, Rhodes, Greece, 20–23 September 2020; pp. 1–8. [Google Scholar]
- Lian, Y.C.; Huang, Z.X.; Zhou, Y.R.; Chen, Z.F. Improve theoretical upper bound of Jumpk function by evolutionary multitasking. In Proceedings of the High Performance Computing and Cluster Technologies Conference, Guangzhou, China, 22–24 June 2019; pp. 44–50. [Google Scholar]
- Huang, Z.X.; Chen, Z.F.; Zhou, Y.R. Analysis on the efficiency of multifactorial evolutionary algorithms. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Glasgow, UK, 19–24 July 2020; pp. 634–647. [Google Scholar]
- Gupta, A.; Ong, Y.-S. Genetic transfer or population diversification? Deciphering the secret ingredients of evolutionary multitask optimization. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Athens, Greece, 6–9 December 2016; pp. 1–7. [Google Scholar]
- Da, B.S.; Gupta, A.; Ong, Y.-S.; Feng, L. The boon of gene-culture interaction for effective evolutionary multitasking. In Proceedings of the Australasian Conference on Artificial Life and Computational Intelligence, Canberra, Australia, 2–5 February 2016; pp. 54–65. [Google Scholar]
- Peng, D.M.; Cai, Y.Q.; Fu, S.K.; Luo, W. Experimental analysis of selective imitation for multifactorial differential evolution. In Proceedings of the International Conference on Bio-Inspired Computing: Theories and Applications, Zhengzhou, China, 22–25 November 2019; pp. 15–26. [Google Scholar]
- Wang, N.; Xu, Q.Z.; Fei, R.; Yang, J.G.; Wang, L. Rigorous analysis of multi-factorial evolutionary algorithm as multi-population evolution model. Int. J. Comput. Intell. Syst. 2019, 12, 1121–1133. [Google Scholar] [CrossRef]
- Bean, J.C. Genetic algorithms and random keys for sequencing and optimization. Orsa J. Comput. 1994, 6, 154–160. [Google Scholar] [CrossRef]
- Yuan, Y.; Ong, Y.-S.; Gupta, A.; Tan, P.S.; Xu, H. Evolutionary multitasking in permutation-based combinatorial optimization problems: Realization with TSP, QAP, LOP, and JSP. In Proceedings of the IEEE Region 10 Conference, Singapore, 22–25 November 2016; pp. 3157–3164. [Google Scholar]
- Mirabi, M. A novel hybrid genetic algorithm for the multidepot periodic vehicle routing problem. Artif. Intell. Eng. Des. Anal. Manuf. Aiedam 2014, 29, 45–54. [Google Scholar] [CrossRef]
- Prins, C. Two memetic algorithms for heterogeneous fleet vehicle routing problems. Eng. Appl. Artif. Intell. 2009, 22, 916–928. [Google Scholar] [CrossRef]
- Zhou, L.; Feng, L.; Zhong, J.H.; Ong, Y.-S.; Zhu, Z.X.; Sha, E. Evolutionary multitasking in combinatorial search spaces: A case study in capacitated vehicle routing problem. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar]
- Feng, L.; Zhou, L.; Gupta, A.; Zhong, J.H.; Zhu, Z.X.; Tan, K.C.; Qin, K. Solving generalized vehicle routing problem with occasional drivers via evolutionary multitasking. IEEE Trans. Cybern. 2019, in press. Available online: https://ieeexplore.ieee.org/document/8938734 (accessed on 23 December 2019). [CrossRef]
- Chandra, R.; Gupta, A.; Ong, Y.-S.; Goh, C.K. Evolutionary multi-task learning for modular training of feedforward neural networks. In Proceedings of the International Conference on Neural Information Processing, Kyoto, Japan, 16–21 October 2016; pp. 37–46. [Google Scholar]
- Wen, Y.-W.; Ting, C.-K. Learning ensemble of decision trees through multifactorial genetic programming. In Proceedings of the IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 24–29 July 2016; pp. 5293–5300. [Google Scholar]
- Zhong, J.H.; Ong, Y.-S.; Cai, W.T. Self-learning gene expression programming. IEEE Trans. Evol. Comput. 2016, 20, 65–80. [Google Scholar] [CrossRef]
- Zhong, J.H.; Feng, L.; Cai, W.T.; Ong, Y.-S. Multifactorial genetic programming for symbolic regression problems. IEEE Trans. Syst. ManCybern. Syst. 2020, 50, 4492–4505. [Google Scholar] [CrossRef]
- Binh, H.T.T.; Thanh, P.D.; Trung, T.B.; Thao, L.P. Effective multifactorial evolutionary algorithm for solving the cluster shortest path tree problem. In Proceedings of the IEEE Congress on Evolutionary Computation, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Trung, T.B.; Thanh, L.T.; Hieu, L.T.; Thanh, P.D.; Binh, H.T.T. Multifactorial evolutionary algorithm for clustered minimum routing cost problem. In Proceedings of the International Symposium on Information and Communication Technology, Hanoi, Vietnam, 4–6 December 2019; pp. 170–177. [Google Scholar]
- Thanh, P.D.; Dung, D.A.; Tien, T.N.; Binh, H.T.T. An effective representation scheme in multifactorial evolutionary algorithm for solving cluster shortest-path tree problem. In Proceedings of the IEEE Congress on Evolutionary Computation, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Thanh, P.D.; Binh, H.T.T.; Trung, T.B.; Long, N.B. Multifactorial evolutionary algorithm for solving clustered tree problems: Competition among Cayley codes. Memetic Comput. 2020, 12, 185–217. [Google Scholar]
- Raidl, G.R.; Julstrom, B.A. Edge sets: An effective evolutionary coding of spanning trees. IEEE Trans. Evol. Comput. 2003, 7, 225–239. [Google Scholar] [CrossRef]
- Tam, N.T.; Tuan, T.Q.; Binh, H.T.T.; Swami, A. Multifactorial evolutionary optimization for maximizing data aggregation tree lifetime in wireless sensor networks. In Proceedings of the Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications II, Online Only, CA, USA, 27 April–9 May 2020; pp. 114130Z:1–114130Z:14. [Google Scholar]
- Thanh, P.D.; Binh, H.T.T.; Trung, T.B. An efficient strategy for usingmultifactorial optimization to solve the clustered shortest path tree problem. Appl. Intelliigence 2020, 50, 1233–1258. [Google Scholar] [CrossRef]
- Binh, H.T.T.; Thanh, P.D.; Thang, T.B. New approach to solving the clustered shortest-path tree problem based on reducing the search space of evolutionary algorithm. Knowl. -Based Syst. 2019, 180, 12–25. [Google Scholar] [CrossRef]
- Binh, H.T.T.; Thanh, P.D. Two levels approach based on multifactorial optimization to solve the clustered shortest path tree problem. Evol. Intell. 2020, in press. Available online: https://link.springer.com/article/10.1007/s12065-020-00501-w (accessed on 14 October 2020).
- Binh, H.T.T.; Thang, T.B.; Long, N.B.; Hoang, N.V.; Thanh, P.D. Multifactorial evolutionary algorithm for inter-domain path computation under domain uniqueness constraint. In Proceedings of the IEEE Congress on Evolutionary Computation, Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Zhang, K.; Hao, W.N.; Yu, X.H.; Jin, D.W.; Zhang, Z.H. A multitasking genetic algorithm for mamdani fuzzy system with fully overlapping triangle membership functions. Int. J. Fuzzy Syst. 2020, 22, 2449–2465. [Google Scholar] [CrossRef]
- Chen, W.Q.; Zhu, Z.X.; He, S. MUMI: Multitask module identification for biological networks. IEEE Trans. Evol. Comput. 2020, 24, 765–776. [Google Scholar] [CrossRef]
- Wang, C.; Ma, H.; Chen, G.; Hartmann, S. Evolutionary multitasking for semantic web service composition. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 2490–2497. [Google Scholar]
- Wang, C.; Ma, H.; Chen, A.; Hartmann, S. Comprehensive quality-aware automated semantic web service composition. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–20 August 2017; pp. 195–207. [Google Scholar]
- Wang, T.-C.; Liaw, R.-T. Multifactorial genetic fuzzy data mining for building membership functions. In Proceedings of the IEEE Congress on Evolutionary Computation, Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Ting, C.-K.; Wang, T.-C.; Liaw, R.-T.; Hong, T.-P. Genetic algorithm with a structure-based representation for genetic-fuzzy data mining. Soft Comput. 2017, 21, 2871–2882. [Google Scholar] [CrossRef]
- Hao, X.X.; Qu, R.; Liu, J. A unified framework of graph-based evolutionary multitasking hyper-heuristic. IEEE Trans. Evol. Comput. 2021, 25, 35–47. [Google Scholar] [CrossRef]
- Bali, K.K.; Gupta, A.; Ong, Y.-S.; Tan, P.S. Cognizant multitasking in multiobjective multifactorial evolution: MO-MFEA-II. IEEE Trans. Cybern. 2020, 51, 1784–1796. [Google Scholar] [CrossRef]
- Da, B.S.; Gupta, A.; Ong, Y.-S.; Feng, L. Evolutionary multitasking across single and multi-objective formulations for improved problem solving. In Proceedings of the IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 24–29 July 2016; pp. 1695–1701. [Google Scholar]
- Tuan, N.Q.; Hoang, T.D.; Binh, H.T.T. A guided differential evolutionary multi-tasking with powell search method for solving multi-objective continuous optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Li, G.H.; Zhang, Q.F.; Gao, W.F. Multipopulation evolution framework for multifactorial optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 215–216. [Google Scholar]
- Li, G.H.; Lin, Q.Z.; Gao, W.F. Multifactorial optimization via explicit multipopulation evolutionary framework. Inf. Sci. 2020, 512, 1555–1570. [Google Scholar] [CrossRef]
- Chen, Y.L.; Zhong, J.H.; Tan, M.K. A fast memetic multi-objective differential evolution for multi-tasking optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Feng, L.; Zhou, W.; Zhou, L.; Jiang, S.W.; Zhong, J.H.; Da, B.S.; Zhu, Z.X.; Wang, Y. An empirical study of multifactorial PSO and multifactorial DE. In Proceedings of the IEEE Congress on Evolutionary Computation, San Sebastian, Spain, 5–8 June 2017; pp. 921–928. [Google Scholar]
- Liu, D.N.; Huang, S.J.; Zhong, J.H. Surrogate-assisted multi-tasking memetic algorithm. In Proceedings of the IEEE Congress on Evolutionary Computation, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Cai, Y.Q.; Peng, D.M.; Fu, S.K.; Tian, H. Multitasking differential evolution with difference vector sharing mechanism. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Xiamen, China, 6–9 December 2019; pp. 3309–3346. [Google Scholar]
- Cheng, M.Y.; Gupta, A.; Ong, Y.-S.; Ni, Z.W. Coevolutionary multitasking for concurrent global optimization: With case studies in complex engineering design. Eng. Appl. Artif. Intell. 2017, 64, 13–24. [Google Scholar] [CrossRef]
- Zhang, B.Y.; Qin, A.K.; Sellis, T. Evolutionary feature subspaces generation for ensemble classification. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 577–584. [Google Scholar]
- Song, H.; Qin, A.K.; Tsai, P.-W.; Liang, J.J. Multitasking multi-swarm optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 1937–1944. [Google Scholar]
- Xiao, H.; Yokoya, G.; Hatanaka, T. Multifactorial PSO-FA hybrid algorithm for multiple car design benchmark. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Bari, Italy, 6–9 October 2019; pp. 1926–1931. [Google Scholar]
- Cheng, M.Y.; Qian, Q.; Ni, Z.W.; Zhu, X.H. Co-evolutionary particle swarm optimization for multitasking. Pattern Recognit. Artif. Intell. 2018, 31, 322–334. (In Chinese) [Google Scholar]
- Cheng, M.Y.; Qian, Q.; Ni, Z.W.; Zhu, X.H. Information exchange particle swarm optimization for multitasking. Pattern Recognit. Artif. Intell. 2019, 32, 385–397. (In Chinese) [Google Scholar]
- Tang, Z.D.; Gong, M.G. Adaptive multifactorial particle swarm optimisation. Caai Trans. Intell. Technol. 2019, 4, 37–46. [Google Scholar] [CrossRef]
- Yokoya, G.; Xiao, H.; Hatanaka, T. Multifactorial optimization using artificial bee colony and its application to car structure design optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 3404–3409. [Google Scholar]
- Xu, Z.W.; Zhang, K.; Xu, X.; He, J.J. A fireworks algorithm based on transfer spark for evolutionary multitasking. Front. Neurorobotics 2020, 13, 109. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Qian, Q.; Ni, Z.W.; Zhu, X.H. Self-organized migrating algorithm for multi-task optimization with information filtering. J. Comput. Appl. 2020, in press. Available online: http://www.joca.cn/CN/10.11772/j.issn.1001-9081.2020091390 (accessed on 26 November 2020). (In Chinese).
- Zheng, X.L.; Lei, Y.; Gong, M.G.; Tang, Z.D. Multifactorial brain storm optimization algorithm. In Proceedings of the International Conference on Bio-inspired Computing: Theories and Applications, Xi’an, China, 28–30 October 2016; pp. 47–53. [Google Scholar]
- Lyu, C.; Shi, Y.H.; Sun, L.J. A novel multi-task optimization algorithm based on the brainstorming process. IEEE Access 2020, 8, 217134–217149. [Google Scholar] [CrossRef]
- Osaba, E.; Ser, J.D.; Yang, X.S.; Iglesias, A.; Galvez, A. COEBA: A coevolutionary bat algorithm for discrete evolutionary multitasking. In Proceedings of the International Conference on Computational Science, Amsterdam, The Netherlands, 3–5 June 2020; pp. 244–256. [Google Scholar]
- Chen, Q.J.; Ma, X.L.; Zhu, Z.X.; Sun, Y.W. Evolutionary multi-tasking single-objective optimization based on cooperative co-evolutionary memetic algorithm. In Proceedings of the International Conference on Computational Intelligence and Security, Hong Kong, China, 15–18 December 2017; pp. 197–201. [Google Scholar]
- Liang, J.; Qiao, K.J.; Yuan, M.H.; Yu, K.J.; Qu, B.Y.; Ge, S.L.; Li, Y.X.; Chen, G.L. Evolutionary multi-task optimization for parameters extraction of photovoltaic models. Energy Convers. Manag. 2020, 207, 112509. [Google Scholar] [CrossRef]
- Hashimoto, R.; Ishibuchi, H.; Masuyama, N.; Nojima, Y. Analysis of evolutionary multi-tasking as an island model. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 1894–1897. [Google Scholar]
- Wen, Y.-W.; Ting, C.-K. Parting ways and reallocating resources in evolutionary multitasking. In Proceedings of the IEEE Congress on Evolutionary Computation, San Sebastian, Spain, 5–8 June 2017; pp. 2404–2411. [Google Scholar]
- Zheng, X.L.; Lei, Y.; Qin, A.K.; Zhou, D.Y.; Shi, J.; Gong, M.G. Differential evolutionary multi-task optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 1914–1921. [Google Scholar]
- Lin, J.B.; Liu, H.L.; Xue, B.; Zhang, M.J.; Gu, F.Q. Multi-objective multi-tasking optimization based on incremental learning. IEEE Trans. Evol. Comput. 2020, 24, 824–838. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Wang, T.H.; Peng, X.G. MFEA-IG: A multi-task algorithm for mobile agents path planning. In Proceedings of the IEEE Congress on Evolutionary Computation, Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Hu, H.; Zhou, Y.J.; Wang, T.H.; Peng, X.G. A multi-task algorithm for autonomous underwater vehicles 3D path planning. In Proceedings of the International Conference on Unmanned Systems, Harbin, China, 27–28 November 2020; pp. 972–977. [Google Scholar]
- Min, A.T.W.; Ong, Y.-S.; Gupta, A.; Goh, C.K. Multiproblem surrogates: Transfer evolutionary multiobjective optimization of computationally expensive problems. IEEE Trans. Evol. Comput. 2019, 23, 15–28. [Google Scholar] [CrossRef]
- Yin, J.; Zhu, A.M.; Zhu, Z.X.; Yu, Y.N.; Ma, X.L. Multifactorial evolutionary algorithm enhanced with cross-task search direction. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 2244–2251. [Google Scholar]
- Feng, Y.L.; Feng, L.; Hou, Y.Q.; Tan, K.C. Large-scale optimization via evolutionary multitasking assisted random embedding. In Proceedings of the IEEE Congress on Evolutionary Computation, Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Feng, L.; Huang, Y.X.; Zhou, L.; Zhong, J.H.; Gupta, A.; Tang, K.; Tan, K.C. Explicit evolutionary multitasking for combinatorial optimization: A case study on capacitated vehicle routing problem. IEEE Trans. Cybern. 2020, in press. Available online: https://ieeexplore.ieee.org/document/9023952/ (accessed on 4 March 2020). [CrossRef] [PubMed]
- Bali, K.K.; Gupta, A.; Feng, L.; Ong, Y.-S.; Tan, P.S. Linearized domain adaptation in evolutionary multitasking. In Proceedings of the IEEE Congress on Evolutionary Computation, San Sebastian, Spain, 5–8 June 2017; pp. 1295–1302. [Google Scholar]
- Shang, Q.X.; Zhou, L.; Feng, L. Multi-task optimization algorithm based on denoising auto-encoder. J. Dalian Univ. Technol. 2019, 59, 417–426. (In Chinese) [Google Scholar]
- Liang, Z.P.; Dong, H.; Liu, C.; Liang, W.Q.; Zhu, Z.X. Evolutionary multitasking for multiobjective optimization with subspace alignment and adaptive differential evolution. IEEE Trans. Cybern. 2020, in press. Available online: https://ieeexplore.ieee.org/document/9123962/ (accessed on 24 June 2020). [CrossRef]
- Xue, X.M.; Zhang, K.; Tan, K.C.; Feng, L.; Wang, J.; Chen, G.D.; Zhao, X.G.; Zhang, L.M.; Yao, J. Affine transformation-enhanced multifactorial optimization for heterogeneous problems. IEEE Trans. Cybern. 2020, in press. Available online: https://ieeexplore.ieee.org/document/9295394/ (accessed on 15 December 2020). [CrossRef] [PubMed]
- Chen, Z.F.; Zhou, Y.R.; He, X.Y.; Zhang, J. Learning task relationships in evolutionary multitasking for multiobjective continuous optimization. IEEE Trans. Cybern. 2020, in press. Available online: https://ieeexplore.ieee.org/document/9262898/ (accessed on 18 November 2020). [CrossRef]
- Xu, Q.Z.; Zhang, J.H.; Fei, R.; Li, W. Parameter analysis on multifactorial evolutionary algorithm. J. Eng. 2020, 2020, 620–625. [Google Scholar] [CrossRef]
- Yang, C.E.; Ding, J.L.; Jin, Y.C.; Wang, C.Z.; Chai, T.Y. Multitasking multiobjective evolutionary operational indices optimization of beneficiation processes. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1046–1057. [Google Scholar] [CrossRef]
- Yang, C.E.; Ding, J.L.; Tan, K.C.; Jin, Y.C. Two-stage assortative mating for multi-objective multifactorial evolutionary optimization. In Proceedings of the IEEE 56th Annual Conference on Decision and Control, Melbourne, Australia, 12–15 December 2017; pp. 76–81. [Google Scholar]
- Wu, T.; Bu, S.Q.; Wei, X.; Wang, G.B.; Zhou, B. Multitasking multi-objective operation optimization of integrated energy system considering biogas-solar-wind renewables. Energy Convers. Manag. 2021, 229, 113736. [Google Scholar] [CrossRef]
- Liaw, R.-T.; Ting, C.-K. Evolutionary many-tasking based on biocoenosis through symbiosis: A framework and benchmark problems. In Proceedings of the IEEE Congress on Evolutionary Computation, San Sebastian, Spain, 5–8 June 2017; pp. 2266–2273. [Google Scholar]
- Liaw, R.-T.; Ting, C.-K. Evolution of biocoenosis through symbiosis with fitness approximation formany-tasking optimization. Memetic Comput. 2020, 12, 399–417. [Google Scholar] [CrossRef]
- Binh, H.T.T.; Tuan, N.Q.; Long, D.C.T. A multi-objective multi-factorial evolutionary algorithm with reference-point-based approach. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 2824–2831. [Google Scholar]
- Zheng, X.L.; Qin, A.K.; Gong, M.G.; Zhou, D.Y. Self-regulated evolutionary multi-task optimization. IEEE Trans. Evol. Comput. 2020, 24, 16–28. [Google Scholar] [CrossRef]
- Osaba, E.; Martinez, A.D.; Galvez, A.; Iglesias, A.; Ser, J.D. dMFEA-II: An adaptive multifactorial evolutionary algorithm for permutation-based discrete optimization problems. In Proceedings of the Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; pp. 1690–1696. [Google Scholar]
- Gong, M.G.; Tang, Z.D.; Li, H.; Zhang, J. Evolutionary multitasking with dynamic resource allocating strategy. IEEE Trans. Evol. Comput. 2019, 23, 858–869. [Google Scholar] [CrossRef]
- Yao, S.S.; Dong, Z.M.; Wang, X.P.; Ren, L. A Multiobjective multifactorial optimization algorithm based on decomposition and dynamic resource allocation strategy. Inf. Sci. 2020, 511, 18–35. [Google Scholar] [CrossRef]
- Chen, Q.J.; Ma, X.L.; Sun, Y.W.; Zhu, Z.X. Adaptive memetic algorithm based evolutionary multi-tasking single-objective optimization. In Proceedings of the Asia-Pacific Conference on Simulated Evolution and Learning, Shenzhen, China, 10–13 November 2017; pp. 462–472. [Google Scholar]
- Tang, J.; Chen, Y.K.; Deng, Z.X.; Xiang, Y.P.; Joy, C.P. A group-based approach to improve multifactorial evolutionary algorithm. In Proceedings of the International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 3870–3876. [Google Scholar]
- Tang, Z.D.; Gong, M.G.; Jiang, F.L.; Li, H.; Wu, Y. Multipopulation optimization for multitask optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 1906–1913. [Google Scholar]
- Jin, C.; Tsai, P.-W.; Qin, A.K. A study on knowledge reuse strategies in multitasking differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 1564–1571. [Google Scholar]
- Ma, X.L.; Chen, Q.J.; Yu, Y.N.; Sun, Y.W.; Ma, L.J.; Zhu, Z.X. A two-level transfer learning algorithm for evolutionary multitasking. Front. Neurosci. 2020, 13, 1408. [Google Scholar] [CrossRef]
- Xie, T.; Gong, M.G.; Tang, Z.D.; Lei, Y.; Liu, J.; Wang, Z. Enhancing evolutionary multifactorial optimization based on particle swarm optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 24–29 July 2016; pp. 1658–1665. [Google Scholar]
- Da, B.S.; Ong, Y.-S.; Feng, L.; Qin, A.K.; Gupta, A.; Zhu, Z.X.; Ting, C.-K.; Tang, K.; Yao, X. Evolutionary Multitasking for Single-Objective Continuous Optimization: Benchmark Problems, Performance Metric and Baseline Results; Technical Report; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Zhou, L.; Feng, L.; Zhong, J.H.; Zhu, Z.X.; Da, B.S.; Wu, Z. A study of similarity measure between tasks for multifactorial evolutionary algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 229–230. [Google Scholar]
- Gupta, A.; Ong, Y.-S.; Da, B.S.; Feng, L.; Handoko, S.D. Landscape synergy in evolutionary multitasking. In Proceedings of the IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 24–29 July 2016; pp. 3076–3083. [Google Scholar]
- Nguyen, T.B.; Browne, W.N.; Zhang, M.J. Relatedness measures to aid the transfer of building blocks among multiple tasks. In Proceedings of the Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; pp. 377–385. [Google Scholar]
- Sagarna, R.; Ong, Y.-S. Concurrently searching branches in software tests generation through multitask evolution. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar]
- Scott, E.O.; De Jong, K.A. Automating knowledge transfer with multi-task optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 2252–2259. [Google Scholar]
- Chen, Y.L.; Zhong, J.H.; Feng, L.; Zhang, J. An adaptive archive-based evolutionary framework for many-task optimization. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 369–384. [Google Scholar] [CrossRef]
- Shang, Q.; Zhang, L.; Feng, L.; Hou, Y.; Zhong, J.; Gupta, A.; Tan, K.C.; Liu, H.L. A preliminary study of adaptive task selection in explicit evolutionary many-tasking. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 2153–2159. [Google Scholar]
- Xu, Q.Z.; Tian, B.L.; Wang, L.; Sun, Q.; Zou, F. An effective variable transfer strategy in multitasking optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; pp. 59–60. [Google Scholar]
- Xu, Q.Z.; Wang, L.; Yang, J.G.; Wang, N.; Fei, R.; Sun, Q. An effective variable transformation strategy in multitasking evolutionary algorithms. Complexity 2020, 2020, 8815117. [Google Scholar] [CrossRef]
- Zhang, D.Q.; Jiang, M.Y. Hetero-dimensional multitask neuroevolution for chaotic time series prediction. IEEE Access 2020, 8, 123135–123150. [Google Scholar] [CrossRef]
- Wang, L.; Sun, Q.; Xu, Q.Z.; Tian, B.L.; Li, W. On the order of variables for multitasking optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; pp. 57–58. [Google Scholar]
- Wang, L.; Sun, Q.; Xu, Q.Z.; Li, W.; Jiang, Q.Y. Analysis of multitasking evolutionary algorithms under the order of solution variables. Complexity 2020, 2020, 4609489. [Google Scholar] [CrossRef]
- Zhou, L.; Feng, L.; Tan, K.C.; Zhong, J.H.; Zhu, Z.X.; Liu, K.; Chen, C. Toward adaptive knowledge transfer in multifactorial evolutionary computation. IEEE Trans. Cybern. 2020, in press. Available online: https://ieeexplore.ieee.org/document/9027113/ (accessed on 6 March 2020). in press. [CrossRef]
- Zhou, L.; Feng, L.; Liu, K.; Chen, C.; Deng, S.J.; Xiang, T.; Jiang, S.W. Towards effective mutation for knowledge transfer in multifactorial differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 1541–1547. [Google Scholar]
- Gong, D.W.; Xu, B.; Zhang, Y.; Guo, Y.N.; Yang, S.X. A similarity-based cooperative co-evolutionary algorithm for dynamic interval multiobjective optimization problems. IEEE Trans. Evol. Comput. 2020, 24, 142–156. [Google Scholar] [CrossRef]
- Gong, D.W.; Sun, J.; Miao, Z. A set-based genetic algorithm for interval many-objective optimization problems. IEEE Trans. Evol. Comput. 2018, 22, 47–60. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Kołodziejczyk, J. The search of the optimal preference values of the characteristic objects by using particle swarm optimization in the uncertain environment. In Proceedings of the 12th KES International Conference on Intelligent Decision Technologies, Split, Croatia, 17–19 June 2020; pp. 353–363. [Google Scholar]
- Burke, E.; Kendall, G.; Newall, J.; Hart, E.; Ross, P.; Schulenburg, S. Hyper-heuristics: An emerging direction in modern search technology. In Handbook of Metaheuristics; Glover, F.W., Kochenberger, G.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 457–474. [Google Scholar]
- Pillay, N.; Qu, R. Hyper-Heuristics: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Więckowski, J.; Kizielewicz, B.; Kołodziejczyk, J. Application of hill climbing algorithm in determining the characteristic objects preferences based on the reference set of alternatives. In Proceedings of the 12th KES International Conference on Intelligent Decision Technologies, Split, Croatia, 17–19 June 2020; pp. 341–351. [Google Scholar]
- Więckowski, J.; Kizielewicz, B.; Kołodziejczyk, J. Finding an approximate global optimum of characteristic objects preferences by using simulated annealing. In Proceedings of the 12th KES International Conference on Intelligent Decision Technologies, Split, Croatia, 17–19 June 2020; Springer: Singapore, 2020; pp. 365–375. [Google Scholar]
- Zhou, Z.F.; Ma, X.L.; Liang, Z.P.; Zhu, Z.X. Multi-objective multi-factorial memetic algorithm based on bone route and large neighborhood local search for VRPTW. In Proceedings of the IEEE Congress on Evolutionary Computation, Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Huang, L.Y.; Feng, L.; Wang, H.D.; Hou, Y.Q.; Liu, K.; Chen, C. A preliminary study of improving evolutionary multi-objective optimization via knowledge transfer from single-objective problems. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Toronto, ON, Canada, 11–14 October 2020; pp. 1552–1559. [Google Scholar]
- Zheng, Y.J.; Zhu, Z.X.; Qi, Y.T.; Wang, L.; Ma, X.L. Multi-objective multifactorial evolutionary algorithm enhanced with the weighting helper-task. In Proceedings of the International Conference on Industrial Artificial Intelligence, Shenyang, China, 23–25 October 2020; pp. 1–6. [Google Scholar]
- Yu, Y.N.; Zhu, A.M.; Zhu, Z.X.; Lin, Q.Z.; Yin, J.; Ma, X.L. Multifactorial differential evolution with opposition-based learning for multi-tasking optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 1898–1905. [Google Scholar]
- Yao, S.S.; Dong, Z.M.; Wang, X.P. A multiobjective multifactorial evolutionary algorithm based on decomposition. Control Decis. 2021, 36, 637–644. (In Chinese) [Google Scholar]
- Mo, J.J.; Fan, Z.; Li, W.J.; Fang, Y.; You, Y.G.; Cai, X.Y. (2017) Multi-factorial evolutionary algorithm based on M2M decomposition. In Proceedings of the Asia-Pacific Conference on Simulated Evolution and Learning, Shenzhen, China, 10–13 November 2017; pp. 134–144. [Google Scholar]
- Liao, P.; Sun, C.L.; Zhang, G.C.; Jin, Y.C. Multi-surrogate multi-tasking optimization of expensive problems. Knowl.-Based Syst. 2020, 205, 106262. [Google Scholar] [CrossRef]
- Binh, H.T.T.; Thanh, P.D.; Trung, T.B.; Thanh, L.C.; Phong, L.M.H.; Swami, A.; Lam, B.T. A multifactorial optimization paradigm for linkage tree genetic algorithm. Inf. Sci. 2020, 540, 325–344. [Google Scholar]
- Park, J.; Mei, Y.; Nguyen, S.; Chen, G.; Zhang, M.J. Evolutionary multitask optimisation for dynamic job shop scheduling using niched genetic programming. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Wellington, New Zealand, 11–14 December 2018; pp. 739–751. [Google Scholar]
- Rauniyar, A.; Nath, R.; Muhuri, P.K. Multi-factorial evolutionary algorithm based novel solution approach for multi-objective pollution routing problem. Comput. Ind. Eng. 2019, 130, 757–771. [Google Scholar] [CrossRef]
- Karunakaran, D.; Mei, Y.; Zhang, M.J. Multitasking genetic programming for stochastic team orienteering problem with time windows. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Xiamen, China, 6–9 December 2019; pp. 1598–1605. [Google Scholar]
- Zhuang, Z.Y.; Wei, C.; Li, B.; Xu, P.; Guo, Y.F.; Ren, J.C. Performance prediction model based on multi-task learning and co-evolutionary strategy for ground source heat pump system. IEEE Access 2019, 7, 117925–117933. [Google Scholar] [CrossRef]
- Shen, F.; Liu, J.; Wu, K. Evolutionary multitasking fuzzy cognitive map learning. Knowl. -Based Syst. 2019, 192, 105294. [Google Scholar] [CrossRef]
- Zhang, B.Y.; Qin, A.K.; Pan, H.; Sellis, T. A novel DNN training framework via data sampling and multi-task optimization. In Proceedings of the International Joint Conference on Neural Networks, Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Martinez, A.D.; Osaba, E.; Ser, J.D.; Herrera, F. Simultaneously evolving deep reinforcement learning models using multifactorial optimization. In Proceedings of the IEEE Conference on Evolutionary Computation, Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Wei, T.Y.; Zhong, J.H. A preliminary study of knowledge transfer in multi-classification using gene expression programming. Front. Neurosci. 2020, 13, 1396. [Google Scholar] [CrossRef]
- Chen, K.; Xue, B.; Zhang, M.J.; Zhou, F.Y. An evolutionary multitasking-based feature selection method for high-dimensional classification. IEEE Trans. Cybern. 2020. Available online: https://ieeexplore.ieee.org/document/9311803/ (accessed on 31 December 2020).
- Tang, Z.D.; Gong, M.G.; Zhang, M.Y. Evolutionary multi-task learning for modular extremal learning machine. In Proceedings of the IEEE Congress on Evolutionary Computation, San Sebastian, Spain, 5–8 June 2017; pp. 474–479. [Google Scholar]
- Li, H.; Ong, Y.-S.; Gong, M.G.; Wang, Z.K. Evolutionary multitasking sparse reconstruction: Framework and case study. IEEE Trans. Evol. Comput. 2019, 23, 733–747. [Google Scholar] [CrossRef]
- Zhao, Y.Z.; Li, H.; Wu, Y.; Wang, S.F.; Gong, M.G. Endmember selection of hyperspectral images based on evolutionary multitask. In Proceedings of the IEEE Congress on Evolutionary Computation, Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Sampath, L.P.M.I.; Gupta, A.; Ong, Y.-S.; Gooi, H.B. Evolutionary multitasking to support optimal power flow under rapid load variations. South. Power Syst. Technol. 2017, 11, 103–114. [Google Scholar]
- Liu, J.W.; Li, P.L.; Wang, G.B.; Zha, Y.X.; Peng, J.C.; Xu, G. A multitasking electric power dispatch approach with multi-objective multifactorial optimization algorithm. IEEE Access 2020, 8, 155902–155910. [Google Scholar] [CrossRef]
- Bao, L.; Qi, Y.T.; Shen, M.Q.; Bu, X.X.; Yu, J.S.; Li, Q.; Chen, P. An evolutionary multitasking algorithm for cloud computing service composition. In Proceedings of the World Congress on Services, Seattle, WA, USA, 25–30 June 2018; pp. 130–144. [Google Scholar]
- Singh, D.; Sisodia, D.S.; Singh, P. Compositional framework for multitask learning in the identification of cleavage sites of HIV-1 protease. J. Biomed. Inform. 2020, 102, 103376. [Google Scholar] [CrossRef]
- Sinha, A.; Malo, P.; Deb, K. Unconstrained scalable test problems for single-objective bilevel optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Ruan, G.; Minku, L.L.; Menzel, S.; Sendhoff, B.; Yao, X. When and how to transfer knowledge in dynamic multi-objective optimization. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Xiamen, China, 6–9 December 2019; pp. 2034–2041. [Google Scholar]
- Kohira, T.; Akira, O.; Kemmotsu, H.; Tatsukawa, T. Proposal of benchmark problem based on real-world car structure design optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 183–184. [Google Scholar]
- Xu, Q.Z.; Yang, H.; Wang, N.; Wu, G.H.; Jiang, Q.Y. Recent advances in multifactorial evolutionary algorithm. Comput. Eng. Appl. 2018, 54, 15–20. (In Chinese) [Google Scholar]
- Hao, G.-S.; Wang, G.-G.; Zhang, Z.-J.; Zou, D.-X. Optimization of the high order problems in evolutionary algorithms: An application of transfer learning. Int. J. Wirel. Mob. Comput. 2018, 14, 56–63. [Google Scholar] [CrossRef]
- Wang, G.-G.; Tan, Y. Improving metaheuristic algorithms with information feedback models. IEEE Trans. Cybern. 2019, 49, 542–555. [Google Scholar] [CrossRef]
- Yuan, Y.; Ong, Y.-S.; Feng, L.; Qin, A.K.; Gupta, A.; Da, B.S.; Zhang, Q.F.; Tan, K.C.; Jin, Y.C.; Ishibuchi, H. Evolutionary Multitasking for Multiobjective Continuous Optimization: Benchmark Problems, Performance Metrics and Baseline Results; Technical Report; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Sands, T. Comparison and interpretation methods for predictive control of mechanics. Algorithms 2019, 12, 232. [Google Scholar] [CrossRef]
- Sałabun, W.; Wątróbski, J.; Shekhovtsov, A. Are MCDA methods benchmarkable? A comparative study of TOPSIS, VIKOR, COPRAS, and PROMETHEE II methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- Jiang, S.W.; Xu, C.; Gupta, A.; Feng, L.; Ong, Y.-S.; Zhang, A.N.; Tan, P.S. Complex and intelligent systems in manufacturing. IEEE Potentials 2016, 35, 23–28. [Google Scholar] [CrossRef]
- Sands, T. Development of deterministic artificial intelligence for unmanned underwater vehicles (UUV). J. Mar. Sci. Eng. 2020, 8, 578. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).