1. Introduction
“The history of science” writes Abraham Kaplan ([
1], p. 354) “is a history of the successive replacement of one explanation by another.” There is perhaps no clearer manifestation of this observation in the field of security studies than the attempts by game and decision theorists to explain the Cuban missile crisis, an event whose significance in international affairs almost defies hyperbole.
More than fifty years have passed since the crisis was settled; in the interim researchers have gained access to a growing collection of primary sources. Key documents from the Soviet archives have been released and secret recordings of the deliberations of the Kennedy administration have been made public.
1 In light of developments, one might well expect that explanations of the crisis have been adjusted and refined. Indeed, this has been the case in both the general literature of the crisis (e.g., Allison and Zelikow, [
4]; Fursenko and Naftali, [
5,
6]) and in the explanations constructed by game theorists. But the parallel game-theoretic literature also reflects controversies and refinements within game theory itself. As game theory has evolved, so have the explanations fashioned by its practitioners. The purpose of this essay is to trace these explanatory refinements using the Cuban crisis as a mooring and to briefly outline a new interpretation of the crisis that exploits both the advances in game theory over time and the expanded evidentiary base.
Before beginning, however, two preliminary questions must be addressed. The first, of course, is what is to be explained? There appears to be wide consensus in the literature on this issue. Three questions are key: First, why did the crisis take place in the first place? (i.e., why did the Soviets install medium- and intermediate-range missiles in Cuba?) Second, why was the US response measured? (i.e., why did the United States respond with a blockade and not an air strike or an invasion?) And third, why was the crisis resolved short of war? (i.e., why did the Soviets remove the missiles?) The surveyed explanations will be evaluated by the extent to which all three of these questions are answered. As will be seen, partial or incomplete explanations are the norm.
There is also a consensus in both the wider and the game-theoretic literature that the bargain that resolved the crisis was a compromise (Gaddis, [
7], p. 261). In return for a public US pledge not to invade Cuba and a private assurance that US controlled missiles in Turkey would eventually be dismantled, the Soviets agreed to withdraw the missiles. Though there are some who argue otherwise (e.g., Sorensen, [
8]), this analysis will take as its starting point the fact that there was no clear winner of the crisis, that the key event to be explained was a political bargain in which both sides gave way. As will be seen, coding the outcome a “compromise”, confounds explanation. One-sided victories are much easier to explain game-theoretically.
2Second, what constitutes an explanation? An explanation, according to Kaplan ([
1], p. 339), “shows that, on the basis of what we know, the something cannot be otherwise.” Within game theory, this task is delegated to the game’s equilibria, which are particular combinations of strategy choices such that no one player has an incentive to abandon its strategy given that none of the other players switch to another strategy at the same time. As Riker ([
10], p. 175) explains: “equilibria are … identified consequences of decisions that are necessary and sufficient to bring them about. An explanation is … the assurance that an outcome must be the way it is because of antecedent conditions. This is precisely what an equilibrium provides.”
It is easy to understand Riker’s reasoning. Game theory takes as axiomatic the rationality of the players. Of all the outcomes in a game, only the equilibria are consistent with rational choices by all of the players. The assumption that the players in a game are rational, therefore, leads naturally to the expectation that they will make choices that are associated with some equilibrium outcome. Game-theoretic explanations and predictions derive from this expectation. When players in a real-world game make choices that can plausibly be associated with an equilibrium outcome, a game-theoretic explanation has been uncovered. Similarly, game-theoretic predictions about future play presume rational choice—that is, the assumption is that an equilibrium choice will be made by each of the players.
The precise definition of an equilibrium depends on whether the game’s depiction is dynamic or static and on whether the players have complete or incomplete information about one another’s preferences. In what follows the technical details between different types of equilibria will be suppressed whenever possible. The interested reader should consult Morrow [
11] or another standard source on game theory for any omitted particulars.
2. Thomas Schelling and the Threat-That-Leaves-Something-to-Chance
The benchmark against which all other explanations of the crisis should be measured is Thomas Schelling’s. Schelling was the first game theorist to explore the strategic dynamic of the crisis and, if one takes the derivative literature seriously, his initial characterization was, and still is, the standard interpretation of the dénouement of crisis (Dodge, [
12]; Hesse, [
13]).
Strictly speaking, however, Schelling never actually offered a fully formed explanation of the missile crisis. In fact, in the “Preface” to his widely read and most influential 1966 book,
Arms and Influence [
14], he claimed that all of the real world examples he discussed were meant merely “to illustrate some point or tactic … [and that] … mention does not mean approval, even when a policy was successful.” Nonetheless, an explanation can be pieced together from several lengthy passages about the crisis in the book. Trachtenberg ([
15], p. 162) refers to this composite view as an explanation “à la Thomas Schelling”.
Schelling ([
14], pp. 96, 176) saw the Cuban crisis, indeed, all crises, as a “competition in risk-taking”. Lurking beneath this view of intense interstate confrontations are the structural dynamics of the 2 × 2 normal- (or strategic-) form game of Chicken (see
Figure 1). In Chicken, the two players, be they teen drivers or generic States, A and B, are on a “collision course”. A
Win in this game occurs when one of the players cooperates (or swerves) by choosing C when the other defects from cooperation (or does not swerve) by choosing D. A
Compromise is reached if both cooperate. And finally, a disaster (
i.e.,
Conflict) results if and when neither player cooperates.
In Chicken, the assumption is that each player most-prefers to win and, failing that, to compromise. Chicken’s defining characteristic, however, is the further assumption that Conflict is a mutually worst outcome. In other words, each player’s preference is to back off and allow the other player to win rather than crash head on.
In
Figure 1 these (ordinal) utility assumptions are reflected in the ordered pair in each cell of the matrix. The first entry in each cell indicates the payoff to State A, the second to State B. Each player’s highest ranked outcome is indicated by a rank of “4”, the next most-preferred by “3”, and so on. The outcome called
Conflict is the lowest ranked outcome (
i.e., “1”) of both players.
From a game-theoretic perspective, Chicken presents a number of perplexing analytic problems. There are two (pure strategy) Nash equilibria in Chicken (as indicated by the asterisks in
Figure 1).
3 A Nash equilibrium is the accepted measure of rational behavior in normal-form games with complete information.
4 But the two Nash equilibria are neither
equivalent—that is, they are associated with different payoffs to the players—nor
interchangeable in the sense that the strategies associated with them may not have identical consequences. Needless to say, the existence of two or more non-equivalent and/or non-interchangeable equilibria, Nash or otherwise, confounds game-theoretic explanations and predictions (Harsanyi, [
16], pp. 3–4). This is especially true in Chicken where the players have symmetric roles. On what basis might one make a prediction and how, after the fact, might one explain why one player rather than the other has prevailed when more than one outcome consistent with rational choice exists?
Schelling’s answer [
14] to both questions is that the player who is the first to commit to driving straight on will force the other player to (rationally) swerve, and will thereby gain the advantage.
5 In a chapter appropriately entitled “The Art of Commitment” [
14] he offered several examples of commitment artists at work. Prime among them was President Kennedy’s televised speech to the nation on October 22. Schelling characterized Kennedy’s promise of an automatic response against the Soviet Union should any nuclear missile be launched from Cuba “effective”.
Schelling went on to note, however, that a firm commitment was probably not necessary. Kennedy’s threat might still have been effective if he had merely raised “the possibility that a single Cuban missile, if it contained a nuclear warhead and exploded on the North American continent, could have triggered the full frantic fury of all-out war” (Schelling, [
14], p. 41). In other words, one might win simply by increasing the risk of war. Of course, what is true for one player is also true for the other in any symmetric game, which is why Schelling came to view intense interstate crises such as Cuba as risk taking contests.
One of the analogies that Schelling ([
14], p. 123; [
18], p. 196) used to make this point was of two men “fighting in a canoe”. If the ship goes down, both players could drown. Worse still, once the canoe starts to wobble, neither might be able to stabilize it. Thus, in any crisis, there was an autonomous risk of war, a risk of things spiraling out of control. Schelling’s ([
18], Ch. 8) intuition led him to argue that this was a type of risk that could be used to successfully manage an intense interstate conflict. Thus was conceived the “threat-that-leaves-something-to-chance”.
6 Schelling ([
14], p. 96) saw just such a threat implicit in the blockade even though “there was nothing about the blockade of Cuba that could have led straightforwardly into general war”. But the blockade, as measured as it was, still carried with it the possibility of an inadvertent nuclear exchange. And it is precisely because President Kennedy successfully manipulated this autonomous risk that he won the war of nerves with Premier Khrushchev and was able to get the better of the Soviet Union in 1962 [
14].
Schelling was not the only one to code the outcome of the crisis as a “win” for the United States and to attribute it to President Kennedy’s adroit brinkmanship. Consider, for example, Arthur Schlesinger’s ([
22], p. 767) summary description of Kennedy’s diplomatic performance:
“From the moment of challenge the American President never had a doubt about the need for a hard response. But throughout the crisis he coolly and exactly measured the level of force necessary to deal with the level of threat. Defining a clear and limited objective, he moved with mathematical precision to accomplish it. At every stage he gave his adversary time for reflection and reappraisal, taking care not to force him into ‘spasm’ reactions or to cut off his retreat.”
Schlesinger’s interpretation of the crisis and, by extension, Schelling’s, has not withstood the test of time and informed historical scrutiny. Michael Dobbs [
23], for example, recently noted that “the White House tapes demonstrate that Kennedy was a good deal more nuanced, and skeptical, about the value of ‘red lines’ than his political acolytes were. He saw the blockade—or ‘quarantine’ as he preferred to call it—as an opportunity to buy time for a
negotiated settlement” (emphasis added. See also Dobbs, [
24]). Similarly, after reviewing the transcripts of White House deliberations, Marc Trachtenberg ([
15], p. 162) concluded that the documentary record does not support a view of “the crisis as a ‘competition in risk-taking’ à la Thomas Schelling”. Speaking about US decision-makers as a group, Trachtenberg [
15] noted that “no one wanted to keep upping the ante, to keep outbidding the Soviets in ‘resolve,’ as the way of triumphing in the confrontation”.
Both Dobbs and Trachtenberg, then, find little evidence of the mathematically precise manipulation of threat levels that Schlesinger wrote about.
7 Of course, their empirical observations do not necessarily mean that Schelling’s view of the crisis as a competition in risk taking can be cast aside. As the astrophysicist Carl Sagan once noted: “the absence of evidence is not the evidence of absence.” Thus, before rejecting Schelling’s explanation of the missile crisis, a more compelling reason would have to be given.
In the years immediately after Schelling wrote, a determinative assessment of his interpretation of the crisis was problematic. The main reason was that his approach, which Young ([
28], p. 318) labels “manipulative bargaining theory” had “not yet yielded much in the way of deductively derived propositions that can be subjected to empirical validation”. Some years later Achen and Snidal ([
29], p. 159) made the same point when they pointed out that “Schelling’s ‘threat that leaves something to chance’ has yet to be given a coherent statement within rational choice theory.”
At about the same time that Achen and Snidal wrote, however, Robert Powell [
30,
31] developed a two-person sequential game model that nicely filled the theoretical void.
8 In Powell’s model one player begins play by deciding whether to accept the status quo, to escalate the contest by challenging it, or to attack. If that player chooses not to contest the status quo or to attack, the game ends. But if escalation is chosen, the other player is faced with similar choices. Significantly, the four possible outcomes in this model are the same as in Chicken. If the player choosing first does not escalate or attack, the status quo prevails. If one player escalates and the other does not, the escalating player wins. If either player attacks, the game ends in disaster. And if both players escalate, the game continues until one player submits or until the game “gets out of control” and culminates in disaster. Powell assumes that by choosing to escalate, a player unleashes an autonomous risk, beyond its control, of an all-out war. Thus, his model captures well Schelling’s view of a nuclear crisis as a “competition in risk taking”.
Given these assumptions, Powell [
30] shows that the existence of a crisis equilibrium, that is, a stable outcome that arises after a challenge by one player and resistance by the other, depends on incomplete information, that is, each side’s lack of information about the values of its opponent.
9 But once a crisis occurs the game can only end in one of three ways: a victory for the first player, a victory for the second, or a head-on collision.
10 The clear implication is that the political bargain that brought the Cuban crisis to a close cannot be adequately explained by a mutual fear that things might spiral out of control. If the Cuban crisis were truly a
competition in risk taking, there could have been no compromise; there would either have been a clear “winner” or a thermonuclear war.
To put this in a slightly different way, Schelling’s interpretation [
14] of the Cuban missile crisis and, arguably, of most other intense major power disputes,
11 is game-theoretically inconsistent with what is now a strong consensus among historians and foreign policy analysts that the resolution of the crisis was a political compromise or draw. When former US Secretary of State Dean Rusk learned on October 24 that several Soviet ships that were approaching Cuba had either turned around or stopped dead in the water he is said to have remarked that “We are eyeball to eyeball, and I think the other fellow just blinked” (May and Zelikow, [
3], p. 358). Rusk was probably correct. But in this regard the Soviets were not alone. The historical record shows not only that President Kennedy was more than eager to compromise, but that he was also willing to offer much more than he did to end the high stakes stalemate that the Soviets referred to as the Caribbean crisis.
The lack of fit between Schelling’s theoretical explanation and the resolution of the crisis is indeed disturbing. But when this discrepancy is coupled with the absence of any compelling empirical trace that either President Kennedy or Premier Khrushchev carefully calibrated his threats in order to manipulate the other’s behavior and induce the other’s concession, it becomes difficult to sustain what has become the conventional interpretation of the crisis, that is, an explanation “à la Thomas Schelling”.
3. Nigel Howard and the Theory of Metagames
After Schelling, the next noteworthy attempt by a game theorist to explain the missile crisis was Nigel Howard’s [
34]. Howard’s analysis begins on Tuesday October 16, the day that President Kennedy was told that the Soviets were installing missiles in Cuba. As Howard saw things, once the missiles were discovered, the United States had only two viable options: either to cooperate by
Blockading (B) Cuba or to desist from cooperation by attempting to remove the missiles with a “surgical”
Air Strike (A). On October 22, after a full review of US options, Kennedy announce the blockade. According to Howard, once this announcement was made, the Soviet Union also had only two broad strategic choices: to either cooperate by
Withdrawing (W) the missiles or to not cooperate by
Maintaining (M) them. These policy options give rise to a 2 × 2 normal-form game. Like Schelling [
14] and most other strategic analysts of this era, Howard assumes a payoff structure that defines the crisis as a game of Chicken. Recall that in Chicken,
Conflict is the worst outcome, and
Compromise is second-best outcome, for both players.
In Howard’s representation [
34], an all-out
Conflict would ensue if the Soviet Union decided to maintain the missiles and the United States launched an air strike to remove them. By contrast, a
Compromise would be reached if the United States decided to blockade Cuba and the Soviets responded by agreeing to withdraw their missiles.
12 Of course, this is what happened so Howard, unlike Schelling [
14], implicitly accepts what is now the standard understanding of the crisis’s resolution, that is, that it was a draw.
As noted above, the existence of two non-equivalent and non-interchangeable Nash equilibria in Chicken, each with equal status as a solution candidate, confounds a game-theoretic analysis. But Howard’s interpretation [
34] of the game’s outcome creates an additional stumbling block: since the
Compromise outcome is not a Nash equilibrium, how can its persistence be explained?
13 Why, in other words, didn’t just one of the superpowers blink, as both Powell’s model [
30] and a standard interpretation would suggest?
To answer this and related questions, Howard developed the
theory of metagames [
34]. Building on an idea first suggested by von Neumann and Morgenstern ([
37], pp. 100–106), Howard altered the underlying game to reflect the possibility that the players might be able to anticipate each other’s strategy choice. Presuming that each player bases its own strategy choice on the strategy it expects the other to select, a new game—the
metagame—is rendered and played “in the heads” of the players prior to the play of the actual game. In the metagame, players choose
metastrategies rather than strategies. Stable outcomes of the metagame are termed
metaequilibria.
14 One way to think about Howard’s reformulation of classical game theory [
34] is as a theory of equilibrium selection. In the metagame, the metastrategies can be interpreted as signals that the players send to one another
before the game begins.
15 These signals, verbal or otherwise, allow each of the players to anticipate the other’s strategy choice. In other words, the theory of metagames attempts to model the impact of preplay communication in a non-cooperative game environment. Howard’s goal is to identify those communication patterns that are consistent with rational choice, that is, are associated with the metaequilibria. Within the theoretical confines of the theory of metagames, an explanation is uncovered when a plausible connection is made between a communication pattern, a pair of metastrategies, and an observed metaequilibrium. Because preplay communication allows the players to form a common conjecture about the way the game will be played, the problem of multiple non-interchangeable and non-equivalent equilibria is potentially rendered moot.
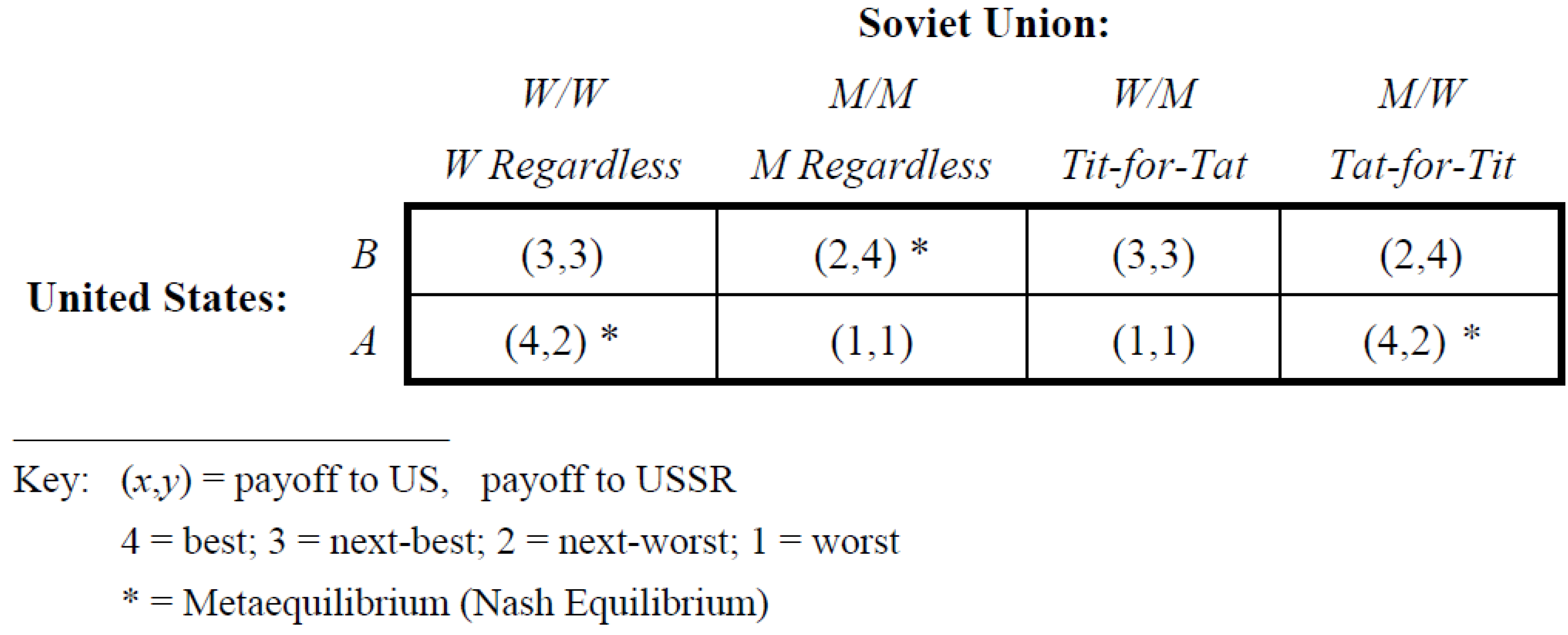
To illustrate, assume that, as the crisis unfolded, the Soviet leadership believed that it could correctly anticipate the strategy choice of the United States. If this were the case, the range of choices available to the Soviet Union would expand. Rather than having just two strategies (
i.e.,
W or
M), it would now have 2 × 2 = 4 metastrategies:
W/W: choose W regardless of the US choice (Withdraw Regardless)
M/M: choose M regardless of the US choice (Maintain Regardless)
W/M: choose W if the US chooses B, M if the US chooses A (tit-for-tat)
M/W: choose M if the US chooses B, W if the US chooses A (tat-for-tit),
which gives rise to the 2 × 4
first-level metagame shown in
Figure 2. Notice that the third metastrategy (tit-for-tat) of the Soviet Union is conditionally cooperative. It implies Soviet cooperation (W) if and only if Soviet leaders believe that the United States intends to cooperate (B).
Figure 2.
First-level metagame of the Cuban missile crisis (Chicken).
Figure 2.
First-level metagame of the Cuban missile crisis (Chicken).
There are three metaequilibria in the first-level metagame. Two correspond to the Nash equilibria in the original (simultaneous choice) Chicken game while the third—(A, M/W)—is strictly a product of the metagame. The additional metaequilibrium, however, does not materially expand the set of distinct rational strategic possibilities, i.e., it is repetitive. In consequence, the central explanatory problem remains: the compromise outcome (3,3) continues to be (at least for now) an irrational event, that is, it is not a metaequilibrium of the first-level metagame.
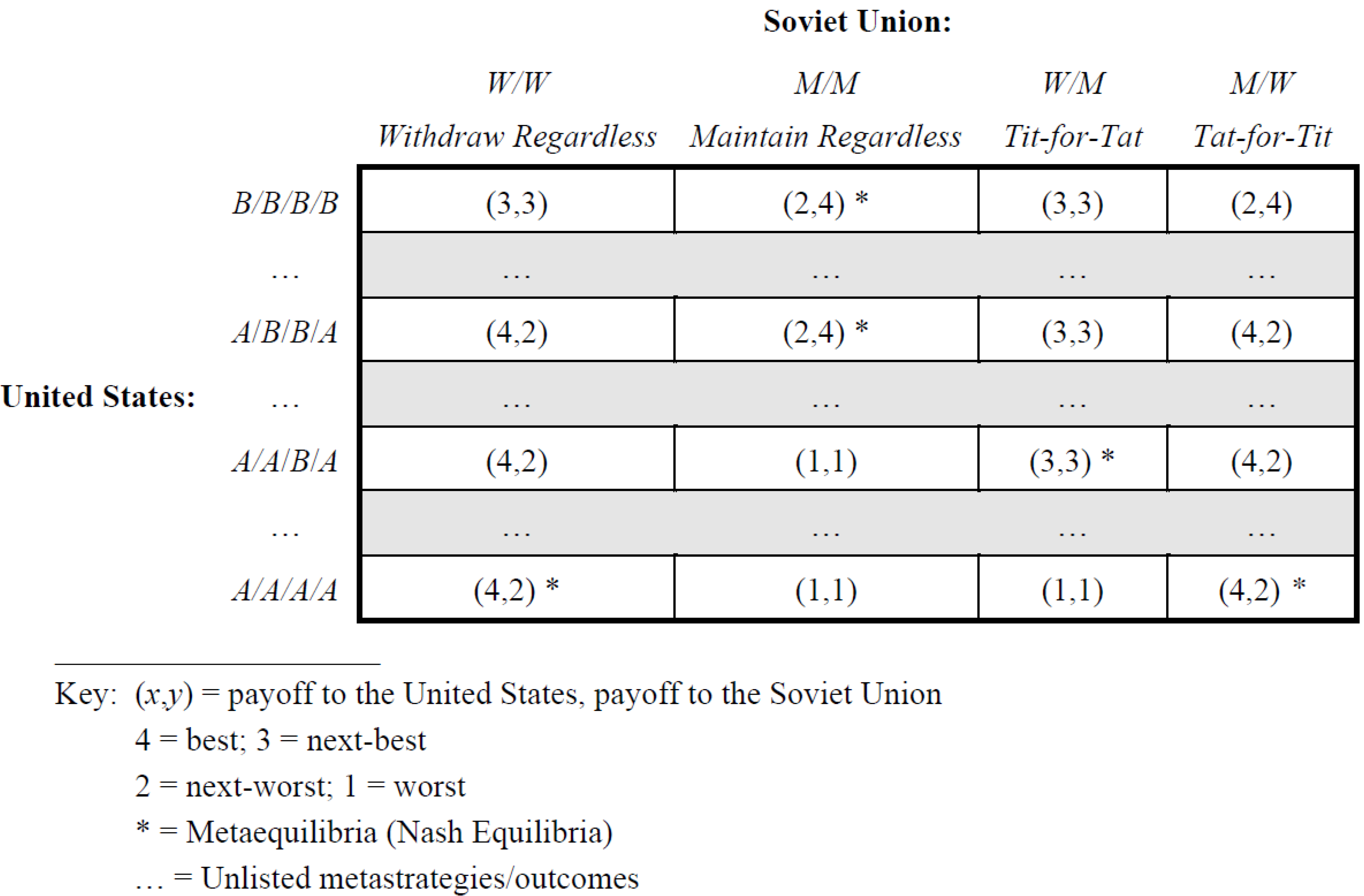
But Howard [
34] continues. What if, he asks, the United States could predict the metastrategy of the Soviet Union and then based its choice on that prediction? If the United States was able to condition its strategy choice on the Soviets metastrategy, it could choose either
B or
A for each of the four Soviet metastrategies, which gives it 2 × 2 × 2 × 2 = 16
second-level metastrategies. For instance, the second-level metastrategy
A/A/B/A requires the United States to:
Choose A if the Soviet Union chooses W/W (WRegardless)
Choose A if the Soviet Union chooses M/M (MRegardless)
Choose B if the Soviet Union chooses W/M (Tit-for-Tat)
Choose A if the Soviet Union chooses M/W (Tat-for-Tit).
Notice that this metastrategy is also conditionally cooperative. It implies US cooperation (B) if and only if US leaders believe that the Soviet Union is itself conditionally cooperative (
i.e., selects its tit-for-tat metastrategy).
The 16 second-level metastrategies of the United States and the 4 first-level metastrategies of the Soviet Union imply a 16 × 4 = 64 outcome metagame. An abbreviated version of this matrix, listing only non-repetitive metaequilibria, is given in
Figure 3. As before a number of new metaequilibria appear. Among them is one that corresponds to the
Compromise outcome (3,3). To support this outcome in equilibrium, however, each player must intend to choose conditionally cooperative metastrategies (
W/M for the Soviet Union and
A/A/B/A for the United States) and convey this intention to the other. Specifically, the Soviet Union must intend to cooperate (by withdrawing the missiles) if (and only if) the United States cooperates by not using force to remove the missiles (
i.e., by blockading Cuba). And the United States must intend to cooperate by blockading Cuba if (and only if) the Soviet Union cooperates by withdrawing the missiles.
This is an interesting and potentially important theoretical result. If it stands a logically consistent rational choice explanation of the political bargain that ended the missile crisis will have been developed. Whether it stands, however, depends on the interpretation of the metaequilibria.
Figure 3.
Second-level metagame of Cuban missile crisis (Chicken).
Figure 3.
Second-level metagame of Cuban missile crisis (Chicken).
Howard’s construction [
34] is strictly
descriptive: metaequilibria are established as theoretical possibilities only, and the metastrategies are theoretical statements about the content of the communication necessary to lead to some outcome in equilibrium. In Howard’s view, no particular metaequilibrium has special status. Each, therefore, describes a logical possibility in a game between rational players. Which metaequilibrium eventually comes into play depends on what the players expect from one another, or what they communicate to each other, in pre-play bargaining and discussion.
In the present example, then, a bargain was struck not only because both players were prepared to cooperate but also because both indicated that they were willing to run the risk of all-out war (the Soviets by maintaining their missiles and the United States by using an air strike to remove them) if the other was unwilling to cooperate. Of course, there were other rational strategic possibilities. As Howard notes [
34], if only one of the players was willing to risk war, that player would have won. For instance, if the Soviet Union limits itself to the two metastrategies that do not admit the possibility of the
Conflict (1,1) outcome, Withdraw Regardless (
W/W) and Tat-for Tit (
W/M), the only remaining metaequilibria are associated with a victory for the United States.
Howard’s explanation [
34], however, merely begs the question: why that communication pattern, why that particular metaequilibrium? Worse still, there is a compelling strategic rationale that suggests that the metastrategies required to effect a compromise would
not be selected by rational agents. Notice that the metastrategy
A/B/B/A—or what Howard refers to as the “sure-thing” metastrategy—is weakly dominant for the United States, giving the Soviet Union good reason to suspect that the United States would choose it; and since
M Regardless is the Soviet Union’s best response to
A/B/B/A, the United States would have had a good reason to suspect that the Soviets were going to choose it. All of which suggests that the metaequilibrium associated with these two metastrategies, which would bring about a Soviet victory, might well evolve in an actual play of the metagame.
Howard, however, rejects this outcome as
the solution to the metagame, and denies that any particular reason exists for singling it out. In fact, he argues it would be
foolish for the United States to select its sure-thing metastrategy because it induces a worse outcome than its “retaliatory” metastrategy
A/A/B/A. Or in Howard’s ([
39], p. 730) own words, the sure-thing metastrategy is “the strategy of a ‘sucker’ who invites, and is ready to yield before, the most extreme ultimatum in the possession of his opponent, and is thus willing to surrender his position before any bargaining begins”.
Harsanyi [
40], however, argues convincingly that the use of any dominated metastrategy is irrational and, hence,
incredible. Since a player with a dominant metastrategy always maximizes its expected utility by choosing it, there is no good reason for an opponent to believe that any other metastrategy would be chosen. This, in turn, implies that a player with a dominant metastrategy should choose it.
16 To do otherwise would be to invite calamity. Specifically, if the United States were to select its retaliatory metastrategy
A/
A/
B/
A and the Soviet Union, anticipating the sure-thing metastrategy
A/
B/
B/
A, selects
M Regardless, each player’s worst outcome,
Conflict, results.
It is difficult to ignore Harsanyi’s admonition not to abandon the use of even a weakly dominant strategy. To be sure, Howard’s metagame theory provides insight into the conditions that are both necessary and sufficient to effect a political compromise during a crisis. But, because it lacks a normative foundation, at least according to Howard, an explanation of the missile crisis within its theoretical confines can only be considered weak and incomplete.
4. Fraser, Hipel and the Analysis of Options Technique
Niall Fraser and Keith Hipel’s [
45] explanation of the Cuban missile crisis begins where Howard’s leaves off. Like Howard’s theory of metagames, Fraser and Hipel’s
analysis of options (or
improved metagame)
technique should be interpreted, at least in part, as a proto-theory of equilibrium selection. But unlike Howard’s attempt [
34] to reformulate classical game theory, Fraser and Hipel’s subtle refinement of Nash’s equilibrium concept adds a distinctly dynamic element into the analysis of complex conflicts.
As its name suggests, Fraser and Hipel’s [
45] innovative methodology explores the stability characteristics of every feasible combination of strategy choices in a game and suggests a path leading to the selection of one equilibrium when multiple equilibria exist. Like Howard [
34], their analysis of the Cuban crisis begins with the discovery of the missiles on October 16. Stepping away from the narrow confines of a 2 × 2 normal-form game and the standard Chicken analogy, however, they consider three options for the United States:
Perform no aggressive action, either by doing nothing or by using normal diplomatic channels to try to induce the Soviets to remove the missiles,
Destroy the missile sites with an air strike, or
Blockade Cuba;
and three for the Soviet Union:
Clearly, some of these options are mutually exclusive, while other could be selected concurrently. For instance, the Soviets could not both withdraw and maintain the missiles, although the United States could blockade and attack the missiles sites at the same time. After eliminating the mutually exclusive combinations of options, twelve feasible combinations and, hence, twelve different outcomes, remain. These combinations are listed as columns in
Table 1. To facilitate a computer implementation of their technique, Fraser and Hipel [
45] convert each outcome into a binary number, that is, they are “decimalized”. These numbers, which range from 0 to 11 and which are arrayed in the last row of Table, can also be considered numerical labels for the various outcomes.
Table 1.
Players, Options and Outcomes for the Cuban Missile Crisis (Fraser and Hipel, [
45]).
Table 1.
Players, Options and Outcomes for the Cuban Missile Crisis (Fraser and Hipel, [45]).
| | Outcomes |
|---|
| US |
| Air Strike | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| Blockade | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| USSR |
| Withdraw | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Escalate | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Decimalized | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Opposite two of the US and two of the Soviet options in
Table 1 are eleven columns that contain either a one (1) or a zero (0). A “1” indicates that the option has been selected, a “0” that it has not been selected. For instance, one option for the United States is to “do nothing”, that is, neither blockading nor striking. This “do nothing” option is captured by the two zeros next to the other two US options above the decimalized outcome 0 in
Table 1.
To explore the stability characteristics of the set of feasible outcomes they start with preference assumptions.
17 In
Table 2, US preferences are given, from best to worst, in the second row of its part of the array; Soviet preferences by the second row of its part of the array. Specifically, Fraser and Hipel [
45] assume that the United States most-prefers outcome 4 (which is brought about when it does nothing and the Soviets withdraw their missiles) to outcome 6 (in which the Soviets withdraw their missiles in response to a blockade), and so on. Next, they ask whether any of the outcomes offer either player a “unilateral improvement” (or UI), which is defined as a better outcome a player can induce by unilaterally changing its strategy.
Table 2 lists all possible UIs, in descending order of preference, in the three rows beneath the preference vector of the United States and the two rows beneath the preference vector of the Soviet Union. For example, the United States has a unilateral improvement from outcome 6, its second-best outcome, to outcome 4, its most-preferred outcome. And since it can induce outcome 4 from 6 simply by switching from its blockade only option to its do nothing option, a unilateral improvement from 6 to 4 is listed below its preference vector in
Table 2.
Table 2.
Stability analysis tableau for the Cuban Missile Crisis (Fraser and Hipel, [
45]).
Table 2.
Stability analysis tableau for the Cuban Missile Crisis (Fraser and Hipel, [45]).
| | E | E | X | X | X | X | X | X | X | X | X | X | Overall Stability |
|---|
| US | r | s | u | u | r | u | u | u | r | u | u | u | Player Stability |
| 4 | 6 | 5 | 7 | 2 | 1 | 3 | 0 | 11 | 9 | 10 | 8 | Preference Vector |
| | 4 | 4 | 4 | | 2 | 2 | 2 | | 11 | 11 | 11 | UI |
| | | 6 | 6 | | | 1 | 1 | | | 9 | 9 | UI |
| | | | 5 | | | | 3 | | | | 10 | UI |
| USSR | r | s | r | u | r | u | r | u | u | u | u | u | Player Stability |
| 0 | 4 | 6 | 2 | 5 | 1 | 7 | 3 | 11 | 9 | 10 | 8 | Preference Vector |
| | 0 | | 6 | | 5 | | 7 | 7 | 5 | 6 | 0 | UI |
| | | | | | | | | 3 | 1 | 2 | 4 | UI |
To determine which of the twelve outcomes are in equilibrium, a multi-step search procedure is necessary. These steps involve characterizing the stability, or lack thereof, of each outcome. In this regard, Fraser and Hipel identify three types of outcomes:
rational,
sanctioned, and
unstable.
18 Rational outcomes are those for which a player has no unilateral improvements.
19 Rational outcomes are indicated by an “r” above each player’s preference vector in
Table 2. Clearly, the most-preferred outcome of the United States (
i.e., 4) and of the Soviet Union (
i.e., 0) are rational and are labeled as such in
Table 2.
Sanctioned outcomes, designated by an “s” in the row above each player’s preference vector, are those for which the other player can credibly induce a worse outcome for a player who acts on a unilateral improvement. A credible action is one which brings about a better outcome for the sanctioning player. For example, the unilateral improvement of the United States from outcome 6 to outcome 4 is sanctioned by the Soviet Union since the Soviets can unilaterally induce outcome 0, which it prefers and which the United States does not prefer, to outcome 4. Unstable outcomes, designated by a “u”, are those with an unsanctioned unilateral improvement. Any outcome that is not unstable for both players is in equilibrium. Only outcomes 4 and 6 pass this test and are denoted with an “E” in the first row of
Table 2. Non-equilibria are indicated by an “X”.
To choose between these competing equilibria, Fraser and Hipel [
45] examine the game’s status quo outcome, outcome 0, which was the state of the world on October 15, the day before the missiles were discovered. This is the outcome that obtains when the Soviets maintain their missiles and the United States does nothing. Although outcome 0 is rational for the Soviet Union, it is unstable for the United States, which can induce three other outcomes it prefers to outcome 0 simply by switching to another course of action. Of these three unilateral improvements, outcome 2 would be the US preference. Outcome 2 is induced by blockading Cuba. Hence, the US reaction.
The likely Soviet response to the blockade can be also deduced from its incentive structure. At outcome 2, the Soviets have a unilateral improvement to outcome 6, which it can bring about by withdrawing the missiles. Outcome 6, of course is an equilibrium. Since, by definition, neither player can do better at an equilibrium by unilaterally switching to another course of action, the game would rationally end there. Thus, Fraser and Hipel [
45] are able to successfully explain why the United States blockaded Cuba and why the Soviets responded by withdrawing the missiles.
What they are unable to explain, however, is why the dynamic process they explore did not stop at that point. Notice that the United States has a unilateral improvement from outcome 6 to outcome 4, which is also an equilibrium. Moreover, not only is outcome 4 Pareto-superior to outcome 6, but it is in fact a more accurate description of the flow of events that brought the crisis to a close. After all, once the Soviets withdrew their missiles, the United States dropped the blockade.
Fraser and Hipel’s [
45] are unable to reach this seemingly straightforward conclusion, and it is easy to understand why: their definition of an equilibrium is constrained by an arbitrary stopping rule. Recall that a unilateral improvement from an outcome is sanctioned for a player if the other player has a credible (
i.e., rational) response that leaves the player acting on the unilateral improvement worse off. In effect, this criterion limits each player’s foresight to a single move and counter-move. Thus, in their view the United States would not act on its unilateral improvement from outcome 6 to outcome 4 simply because it is sanctioned by the Soviet Union (one move and one counter-move). But why would the Soviets sanction that move by acting on its own unilateral improvement from outcome 4 back to outcome 0, the original status quo? The obvious answer is that they would not because a move from 4 to 0 would lead to a counter-countermove by the United States to outcome 2, which would be worse for the Soviets (assuming for the sake of argument that the process would stop there). But this answer (or any other) would require that the United States consider the consequences of three moves (or more) rather than just two. With laudable but nonetheless perplexing consistency, then, Fraser and Hipel [
45] fail to fully extend the strategic logic of their model. In consequence, their explanation of the missile crisis necessarily falls short of the mark.
20 5. Steven J. Brams and the Theory of Moves
Perhaps sensing this, Steven J. Brams developed a more general dynamic modeling framework called the “Theory of Moves” (or TOM) and used it to offer several (plausible) explanations of the crisis (Brams, [
35], pp. 48–62; [
46], pp. 226–240). Here I concentrate on the theoretical core of all his explanations and ignore the subtle differences that set the various explanations apart.
21Like Fraser and Hipel [
45], Brams [
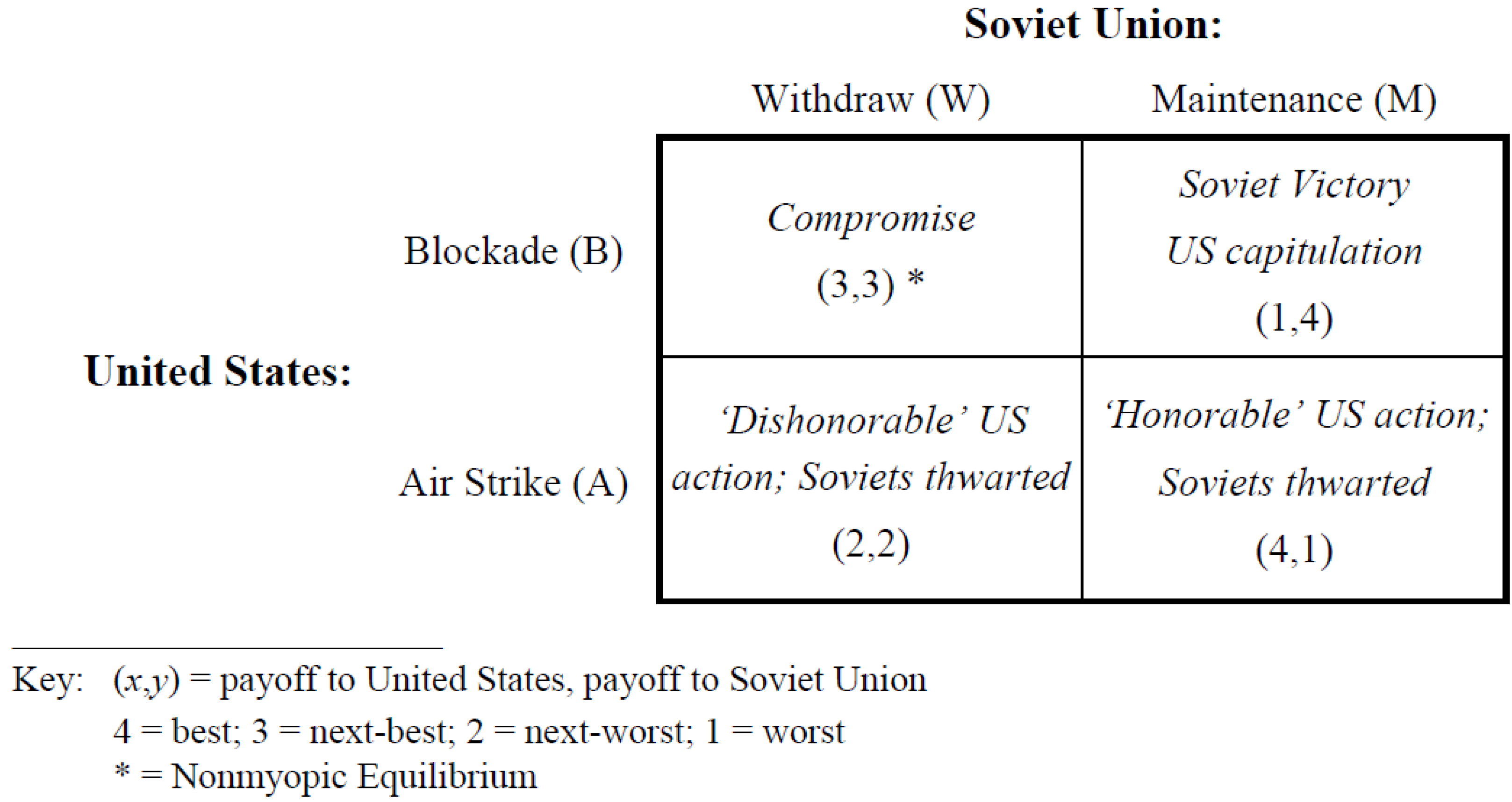
35] abandons both a normal-form representation and the standard Chicken analogy. Instead he begins by considering the “payoff matrix” given by
Figure 4. The cells of this graphical summary of the crisis represent possible states of the world (or outcomes). The ordered pair in each cell of the matrix reflects Brams’ understanding of the relative ranking of the four possible outcomes by the United States and the Soviet Union, respectively. Brams assumes that once a game begins either player can move from whatever outcome is the initial state (or status quo outcome) and, if it does, the other can respond, the first can counter-respond, and so on. The process continues until one player decides not to respond, and the outcome that they are at is the final outcome. Any outcome from which neither player, looking ahead indefinitely, has an incentive to move to another state of the world, including the initial state, is said to be a
nonmyopic equilibrium (Brams, [
47]).
Figure 4.
The Cuban Missile as seen by Brams [
35].
Figure 4.
The Cuban Missile as seen by Brams [
35].
When Kennedy announced the blockade on October 22, the Soviet missiles were already being installed in Cuba. This, the initial state of the world, was the worst for the United States and best for the Soviet Union. Thus this outcome is labeled “Soviet Victory”. Brams [
35] suggests several reasons why the Soviet Union would then withdraw the missiles and induce its next-best outcome, the Compromise outcome, rather than stick with its initial choice. For example, if the United States had what he calls
moving power, which is the ability to continue moving in a game when the other player cannot, it could induce the Soviet Union to end the game at (3,3) by forcing it to choose between (3,3) and (4,1). Or, if the United States possessed
threat power, which is the ability to threaten a mutually disadvantageous outcome in the first play of a repeated game, it could similarly induce the Soviet Union to withdraw the missiles by threatening to remove them with an air strike if they did not.
But regardless of the reason why the Soviets decided to withdraw the missiles, once they did, the game ended. Brams’ explanation [
35] is that the Compromise outcome is a nonmyopic equilibrium, that is, neither player can do better by moving the game to another state of the world by changing its strategy choice, given that the other might then switch to another strategy, it might then be forced to also change its strategy, and so on.
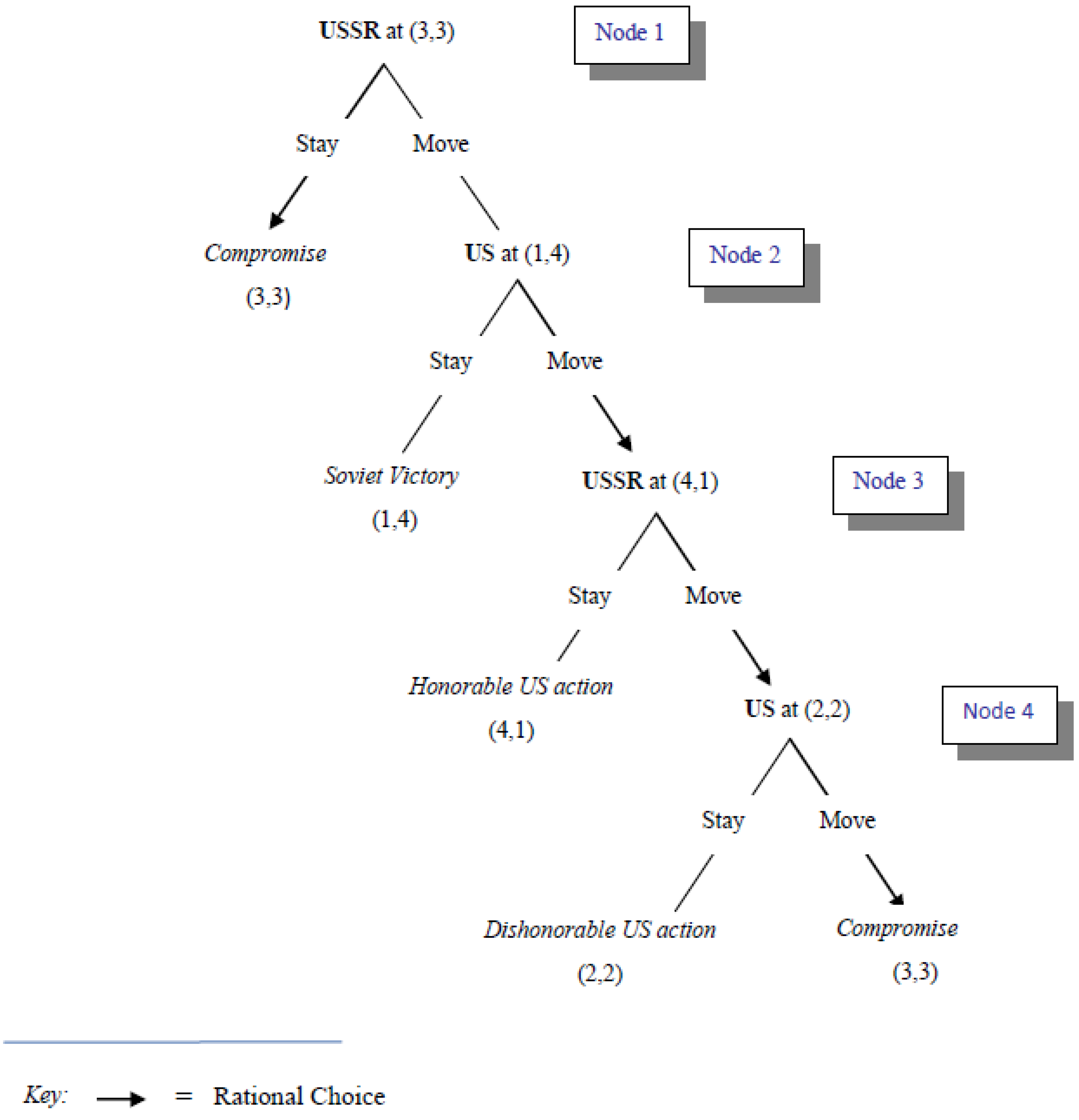
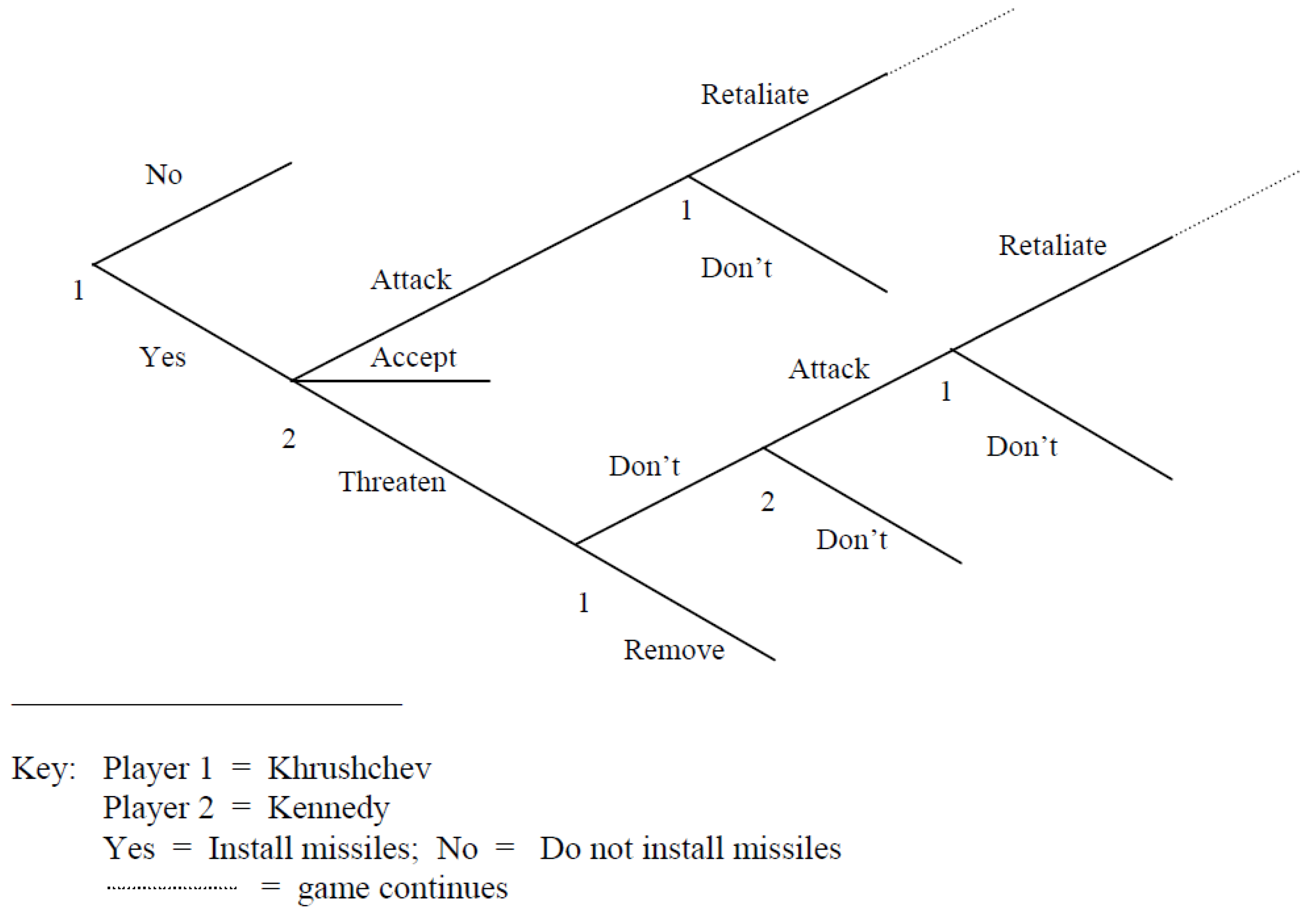
To see this, consider
Figure 5 which lists the sequence of moves and countermoves away from the Compromise outcome that would be touched off if the Soviet Union reversed its course and decided to maintain the missiles after all. At the last node of this tree, the United States has a choice of staying at its second-worst outcome or cycling back to the Compromise outcome, its second-best. As indicated by the arrow, the United States would rationally move.
Similarly, at the previous node, the Soviet Union would move away from (4,1) its least-preferred outcome to its next-worst outcome (2,2). But it would do so not because it prefers (2,2) to (4,1)—which it does—but because it would anticipate the outcome induced by the American choice at the subsequent node which is better still. Counter-intuitively, perhaps, the United States would, at the second node of the tree, also rationally move to its best outcome, not because it is its best outcome, but because it prefers to cycle back to the Compromise outcome, which is its second-best, to terminating the game at (1,4), its least-preferred outcome.
Finally, Brams argues that the Soviet Union would stick with its choice (at the top of the tree) to withdraw the missiles simply because, by not doing so, it would only cycle back to the Compromise outcome. As Brams [
48] asks, “what is the point of initiating the move-countermove process if play simply returns to ‘square one’?”
Figure 5.
Moves and Countermoves during the Cuban Missile Crisis, starting with the Soviet Union at the Compromise Outcome (3,3).
Figure 5.
Moves and Countermoves during the Cuban Missile Crisis, starting with the Soviet Union at the Compromise Outcome (3,3).
It would be a straightforward exercise to show that there is also no incentive for the United States to precipitate the move-countermove process once the Compromise outcome is reached. And since neither player has a long-term incentive to move away from this outcome if and when it is reached, it constitutes a nonmyopic equilibrium.
22 Brams’ explanation [
35] proceeds from this fact. As an equilibrium the Compromise outcome is, by definition, consistent with the rationality postulate. And since it is the only nonmyopic equilibrium in the matrix of
Figure 4, it is the only outcome that can persist under rational play. All of which is another way of saying that the Soviet Union withdrew the missiles because, looking ahead, they believed that maintaining them would not be in their long-term interest. Given the American blockade and the incentive structure of the game, they simply could not win.
There is obviously much to like about the Theory of Moves framework. Indeed, I have used it myself to explore the dynamics of both one-sided and two-sided deterrence relationships and to analyze a number of acute interstate crises (Zagare, [
49]). The Theory of Moves is a simple and extremely intuitive methodology for analyzing complex interstate conflicts like the missile crisis; it is also more general than the analysis of options technique developed by Fraser and Hipel [
45]; its major solution concepts are easy to calculate and interpret; and since it is based only on ordinal utilities, it requires fewer “heroic assumptions” than many other game-theoretic frameworks.
In the case of the missile crisis, however, its strengths are also it weaknesses. Since the concept of a nonmyopic equilibrium has not as yet been successfully defined in games in which the players have more than two strategies each, it can only be used to assess the rationality of four outcomes at a time. This limitation explains why Brams starts his analysis on October 22, the day that Kennedy announced the blockade. In consequence its theoretical range is restricted. Why did the Soviets precipitate the crisis by installing the missiles in the first place and why did the United States then respond by blockading Cuba? These are questions that Brams does not address and, in fact, cannot address within the confines of a single integrated game model using the Theory of Moves framework. Thus, while his analysis of the end-game of the crisis is both insightful and penetrating, his explanation remains incomplete.
7. The Asymmetric Escalation Game
Elsewhere I have developed an explanation of the crisis that, at least in my opinion, overcomes the limitations implicit in Wagner’s approach (Zagare, [
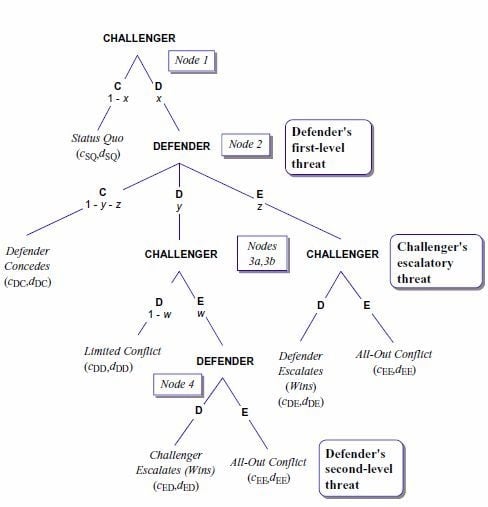
59]). That explanation is developed in the context of a single integrated game model of interstate conflict initiation, limitation and escalation called the Asymmetric Escalation Game (see
Figure 7). Since the empirical fit between this model and the strategic dynamic of the missile crisis is especially close, I claim that it is able to generate a more complete and a more satisfying explanation of the crisis than any of the attempts evaluated in this essay. More specifically, there is a perfect Bayesian equilibrium of this incomplete information model that is uniquely consistent with the beliefs and the action choices of the United States and the Soviet Union and, significantly, with the eventual resolution of the crisis. In consequence, this equilibrium, which is a member of a family of perfect Bayesian equilibria called the Constrained Limited Response family, is able to address all of the foundational questions associated with the crisis.
For example, why did the Soviet Union precipitate a crisis by installing nuclear capable missiles in Cuba? The strategic properties of a Constrained Limited-Response equilibrium (for the details, see Zagare and Kilgour, [
33]) provides a succinct answer: Soviet actions were motivated, at least in part, by the clear expectation that the United States would not respond, either because it was thought that the Kennedy administration would be unwilling to respond forcefully or, more likely, because it would be too late to do so if and when the missiles were discovered.
Figure 7.
The Asymmetric Escalation Game (Zagare and Kilgour, [
33]).
Figure 7.
The Asymmetric Escalation Game (Zagare and Kilgour, [
33]).
Why was the response of the United States measured and not escalatory? Within the theoretical confines of the Asymmetric Escalation Game model, the answer is clear: US decision-makers believed that it was the course of action “most likely to secure our limited objective—removal of the missiles—at the lowest cost” (Sorensen, [
8], p. 782). By contrast, an air strike and/or an invasion carried with it an unacceptably high risk of a superpower war. Kennedy famously estimated this risk to be “somewhere between one out of three and even” (Sorensen, [
8], p. 795). Needless to say, the strong belief that that an escalatory response was likely to lead to an all-out conflict is required for a limited conflict to occur under any Constrained Limited-Response equilibrium. Wagner, of course, reaches the same conclusion but constructs an equilibrium to conform to the fact rather than deducing the fact as a theoretical implication of a general model of interstate conflict initiation.
Finally, why was the settlement of the crisis a political compromise under which the Soviets withdrew their missiles in exchange for a public US promise and a private US assurance? The short answer is that the Soviets got the message implicit in the blockade and the other signals, intended or not, sent by the United States. All of which is to say that the Soviet decision to withdraw the missiles was the rational response to the additional information they acquired about US preferences while the crisis was playing out.
Clearly, space and other considerations preclude either a full description of the model or a detailed discussion of the explanation derived from it. Suffice it to say that the explanation implicit in the equilibrium structure of the model is neither ad hoc or post hoc; rather it is flows naturally from the model’s a priori theoretical expectations. And while it is not necessarily at odds with most of the other game-theoretic explanations discussed in this essay, it is more general.
28 To be sure, this is a strong claim. Unfortunately, it is also a claim that must be evaluated in a different venue, and by others.
8. Conclusions
This study surveys and evaluates previous attempts to use game theory to explain the strategic dynamic of the Cuban missile crisis, a crisis that has been characterized, without exaggeration, as the “defining event of the nuclear age” (Allison and Zelikow, [
4]). All the attempts were judged to be either incomplete or deficient in some other way. The earliest, most well-known, and most enduring interpretation of the crisis has drawn its inspiration from the pioneering work of Thomas Schelling [
14]. Schelling’s “threat-that-leave-something-to-chance”, however, fails as an explanation on both theoretical and empirical grounds. Formal analyses of this bargaining tactic reveal it to be inconsistent with the consensus interpretation of the crisis’ outcome. Equally troubling is the scant empirical evidence that the Kennedy administration either manipulated the risk of war during the crisis with “mathematical precision”, as Schlesinger ([
22], p. 767) and some other insider accounts have claimed, or successfully made use of any related brinkmanship tactics that resulted in a clear US victory. The crisis ended only when
both sides “blinked”.
Nigel Howard’s metagame analysis [
34] of the missile crisis also fails to provide a compelling explanation. To be sure, Howard [
34] shows the superpower compromise that settled the crisis is a meta-equilibrium in his game model and, consequently, consistent with a minimal definition of rational behavior. However, since the normative foundation of the compromise meta-equilibrium is more than suspect, Howard is unable to explain why rational agents would settle on it, other than by observing that one of the players in his model (
i.e., the United States) would lose if it were “perfectly” rational. Needless to say, rational choice explanations that reject even some of the logical imperatives of the rationality postulate are less than satisfying.
Similarly, the improved metagame technique of Fraser and Hipel [
45] falls short of the explanatory mark. Like Howard [
34], Fraser and Hipel [
45] find that the compromise outcome is an equilibrium in their dynamic model, but are unable to explain, at least game-theoretically, why it, and not another co-existing equilibrium, ended the crisis. Making matters worse, the co-existing equilibrium is in fact a more accurate descriptor of the eventual resolution of the crisis than is the equilibrium implied by their modeling technique. Finally, since their description of the crisis begins after the missiles were installed, they fail to address one of the three critical questions that a complete explanation of the crisis requires.
Brams’ theory of moves framework [
47] avoids the arbitrary foresight limitation that Fraser and Hipel [
45] assume of the players in their model. It also mitigates some of the problems associated with the existence of multiple, co-existing equilibria. However, Brams [
35] take as his starting point the announcement of the blockade on October 22. As a result his explanation, like Fraser and Hipel’s [
45], is incomplete. Specifically, Brams [
35] is unable to explain why the Soviet Union decided to challenge the status quo by installing the missiles; and why the “initial” step taken by the United States was not an escalatory choice?
Wagner’s model [
54], which makes use of the modern methodology of games of incomplete information, does in fact address all of the central questions about the crisis. Wagner’s model [
54] is carefully constructed from the facts of the crisis as they were known to him at the time. As such, it can be considered a concise and even a more than plausible
description of the events of October 1962. But the explanatory power of his model is suspect. Theories and models that are constructed from facts cannot but fail to explain those facts. In consequence, explanations like Wagner’s that verge on the tautological, are, ultimately, unconvincing (King, Keohane and Verba, [
60], pp. 19–23; Morrow, [
11], p. 22).