1. Introduction
Underwater light is an important environmental variable because its low availability limits the photosynthetic activity, and thereby the primary production of the aquatic ecosystem [
1]. Light is attenuated by water molecules, suspended particulate matter (SPM), colored dissolved organic matter (CDOM, yellow substances), and chlorophyll along with other photosynthetic pigments of living phytoplankton. Each of these components attenuates light from different wavelengths, and some components are primarily absorbers and some scatterers. For example, dissolved substances primarily absorb light, suspended particles scatter, and photosynthesizing cells do both [
1].
Due to the efficient attenuation in natural waters, the illuminated surface layer, and consequently the potential zone for photosynthesis, is relatively thin. The thickness of the photosynthetically active water layer can be assessed by comparing the amounts of photoautotrophic production and heterotrophic consumption, but it can also be roughly estimated by measuring the amount of light in the water column, e.g., [
1]. A common variable is the euphotic depth (
Zeu), which is relatively easy and accurate to determine [
2] by measuring the depth in which 1% of the photosynthetically active radiation (PAR, 400–700 nm) entering the water remains.
Another way to evaluate the underwater light penetration is to measure the Secchi depth (
ZSD), which is the depth in which a white Secchi disc disappears from sight.
ZSD is a visual measure to provide a numerical variable that describes the clarity of the water [
3]. The use of Secchi disc measurements is a traditional and common practice in marine observation and monitoring programs. It is an easy, inexpensive, and straightforward method, and thus often included in a field program—if not as a main focus of the particular study, at least as a background variable describing the prevailing conditions. The method is, however, rather coarse. Compared to direct PAR measurements, Secchi readings are more prone to measurement inaccuracies caused by, for example, surface roughness, general illumination conditions or human interpretation. The potential sources of error need to be acknowledged before making any comparisons.
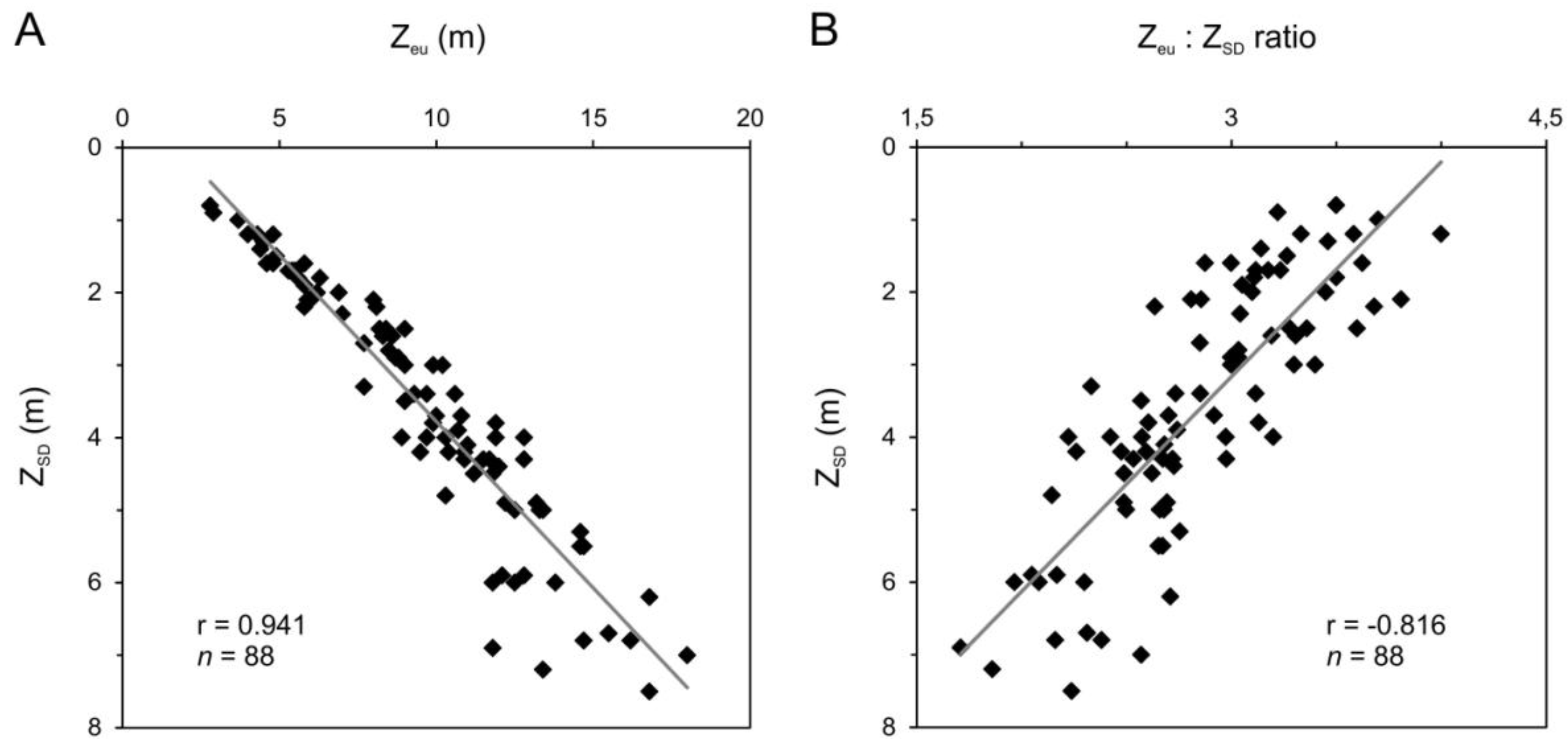
The Secchi disc readings and underwater light sensors react differently to changes in the absorption/scattering balance,
i.e., changes in the relative amounts of, for example, SPM and CDOM in water ([
4] and references therein). Consequently, the relationship between the optical parameters, or in this case the
Zeu:
ZSD ratio, varies according to the changes in the optical properties of water, e.g., [
1,
4,
5,
6]. The correlation between the parameters is, in its simplest form, expressed as follows:
The reported values of the conversion coefficient,
m, usually range from less than 1 up to 5, or even 10 ([
4] and references therein). Holmes [
7], for example, suggests a factor of 3 to be a suitable general coefficient in turbid waters, but, at the same time, he adds that a higher factor would be better for more turbid waters, and a lower one for clearer waters.
Preisendorfer [
3] has criticized the attempts to create coefficients to convert
ZSD to
Zeu. He rationalizes that, if instruments for higher quality optical measurements are needed in assessing the factors, they should be used to measure the underwater light field directly. This is a valid statement. However, since underwater PAR measurements require specific instruments and knowledge, and despite their increasing popularity in routine ocean surveys, they are still performed less frequently than
ZSD measurements. Instead, Secchi depth measurements continue to be a normal procedure within any marine sampling campaign. In addition, the history of the
ZSD method is much longer than that of the modern optical measurement techniques; the first measurements were made already at the early 19th century [
8]. Whenever and wherever Secchi disc measurements are the only optical data available, they are highly valuable, since they provide—as opposed to nothing—at least some information about the underwater light conditions.
All in all,
ZSD data are much more plentiful on both spatial and temporal dimension than data on euphotic depths or attenuation coefficients [
8]. By defining the quantitative linkage between
ZSD and other parameters, the excessive, already existing, and continuously accumulating
ZSD data can be utilized more efficiently. Holmes [
7] pointed out that biologists may not need the same high degree of accuracy and precision required by optical oceanographers, and thus the
ZSD conversions—despite their limitations—might be useful in certain study types. Moreover, in highly variable, constantly fluctuating coastal conditions, the absolute accuracy of point measurements can even be seen as rather irrelevant if they only represent very local and highly momentary conditions [
9].
Due to the reasons mentioned above, researchers will undoubtedly continue to convert ZSD measurements to Zeu estimates. In some cases, such as the historic Secchi data dating before the availability of remote sensing data or underwater light sensors, the ZSD to Zeu conversion is the only way to obtain information about the euphotic depth. While it is advisable to use optical equipment whenever possible, it is still inevitable that ZSD will be, by far, the most common measure of underwater light conditions also in the future. Rather than trying to suppress the common practice, we find it important to aim at its optimization. The indirect conversion results provide more reliable information about the thickness of the productive layer than using the Secchi depth as such.
Geographical information systems (GIS) are widely utilized in marine research, especially in coastal areas. Spatial data and modeling methods add to the understanding of the marine ecosystems from the littoral to the benthic environments. Characteristic to the shallow coastal seas, the euphotic zone regulates the occurrence and depth distribution of seafloor habitats. For instance, in our study area, the euphotic seafloor area fluctuates approximately 100% from yearly minimum to maximum [
10]. As
Zeu is a key variable in any model concerning the marine environment, its use also in GIS modeling is increasing. This calls for optimized parameterization of the phenomenon, including improved understanding of the spatial characteristics of the water transparency and its driving forces.
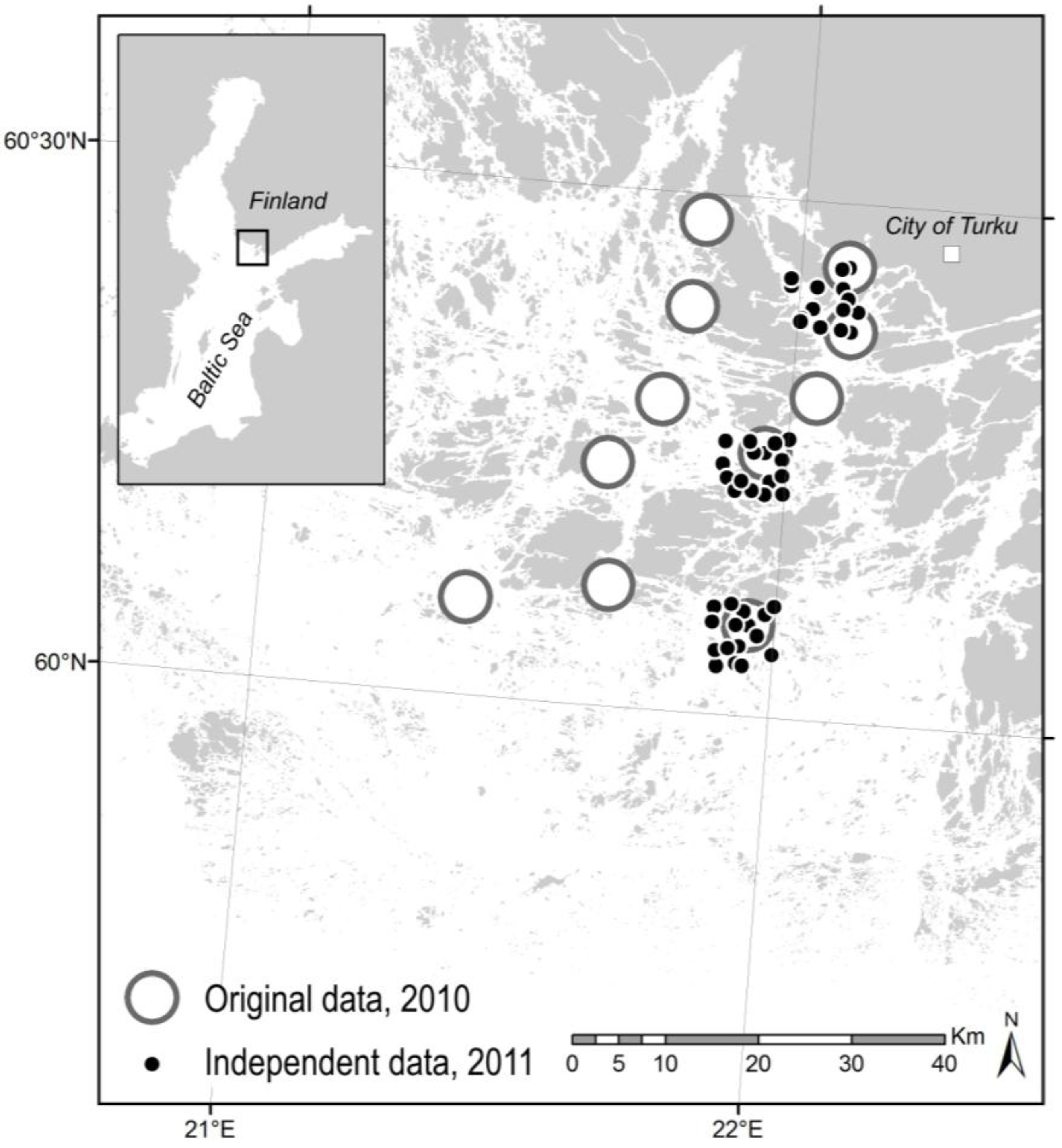
In this paper, we compare alternative methods for determining the coefficients between ZSD and Zeu, using our own in situ data from the Baltic Sea archipelago coast of SW Finland. The aim is to assess, which is the most suitable criterion to base the coefficient on. As it is vital to understand the importance of local empirical calibration, we do not present any general coefficients. Instead, we study our empirical data in detail and urge researchers to critically consider the most suitable conversion method for their particular study areas. The conversion procedure may be rather straightforward in oceanic offshore conditions, but we would like to pay more attention to transitional coastal environments with more varying water quality.
4. Discussion
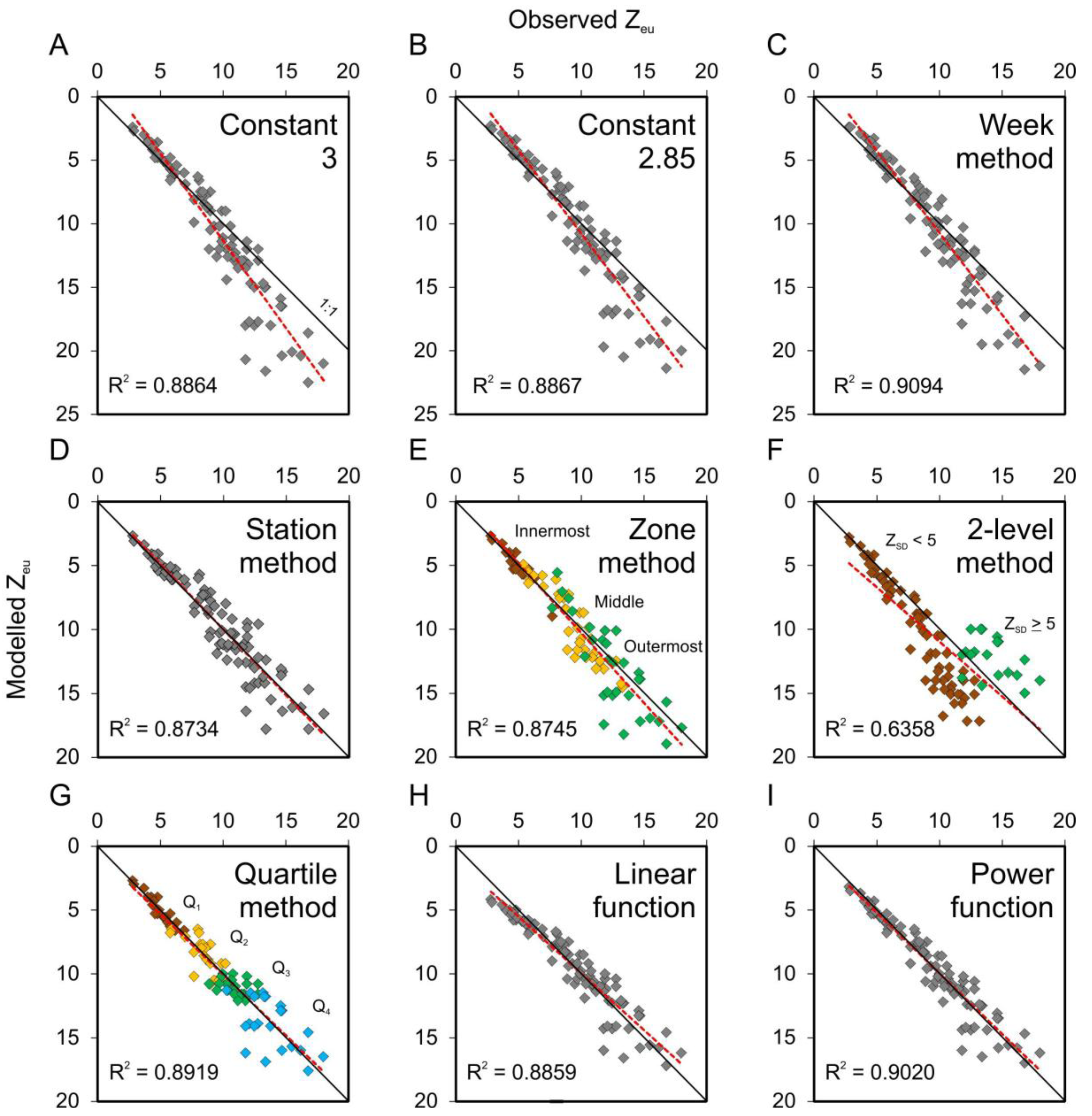
The aim of the study was to compare methods for determining the coefficients between ZSD and Zeu. We assessed different criteria to base the coefficient on, and managed to significantly improve the accuracy—in this case to halve the mean absolute error of the original training data, and to double the success rate for the independent testing data—by choosing a more appropriate conversion method than a fixed constant coefficient. The best results were achieved with the function methods that performed well in the accuracy tests of both of the datasets.
As suggested in literature, and supported by our data, the conversion coefficient changes as a function of water transparency change. The conversion functions process this transition as a continuum, and they do not require the sometimes problematic procedure of pre-classifying the data. According to the error indicators, the power function is the best performing conversion method in our study—even though there were only minor differences in the performance among the most accurate methods. Furthermore, the scatter plot illustrating the modeling accuracy of the power function revealed a relatively good fit of model throughout the entire data range. The same applies for the linear function in high Zeu values, but in less transparent water, the values were notably exaggerated.
The other option, besides using functions, is to use fixed or scalable coefficients. They, however, may be problematic, as always when compressing data into averages, some information is lost. Therefore, the values closer to the mean of the respective group are more accurate than the values approaching the limits of the class. Conversions based on averaged coefficients tend to overestimate the modeled Zeu values in clearer waters, and underestimate them in less transparent waters. This is most clearly seen when using only one fixed coefficient, but the phenomenon is also relevant with the scalable coefficients that divide the input data into subgroups—despite the absolute data ranges of the classes. Furthermore, the limiting values are always artificial, whether they are drawn based on pure mathematics, or on the estimates by the researcher—no matter how well established they are.
Xu
et al. [
16] stated in their studies—where they tried to estimate the connection between Secchi depth and attenuation coefficient in the Chesapeake Bay—that the bulk relationships fitted over many months and large areas possibly fail because the light controlling dependences change considerably in time and space. Likewise, this applies to our study area, where the optical properties of the less transparent inner archipelago waters and the clearer outer archipelago waters differ notably, and the seasonal differences are also distinctive [
12,
15].
These extremes in water quality can be separated by dividing the area geographically into fixed zones. A more flexible and efficient baseline is to divide the data according to water quality itself. A pre-classification of the original
ZSD data before the actual conversion procedure has been suggested before. The 2-level water transparency division suggested by Holmes [
7] already in the early 70s was tested in this study, but the results for our dataset were poor. We found the difference between the two coefficient values rather notable, causing a great gap between the modeled values around the border of the two classes. In a recent study by Liu
et al. [
17] the NTD675 water classification method was used as a baseline for pre-classification to allow more precise assessment of optical properties of water. However, few researchers who convert
ZSD to
Zeu have access to such data or instruments. This highlights the convenience of the
ZSD-based pre-classification method, the quartile method, as, after the calibration procedure, no other data or instruments are needed beside the
ZSD values themselves.
The functions do not require any decision-making in the execution phase of the conversion procedure, and thus their usage is rather unambiguous. Likewise, when using the quartile method, it is straightforward to select the appropriate coefficient according to the quartile in which the ZSD reading in question belongs to. These properties are advantageous, for example, when sampling transitional areas between coastal zones. In other words, one avoids the problem of choosing an appropriate zonal coefficient and consequently a formation of imaginary boundaries into sea areas which actually face gradual changes in water quality.
Furthermore, the conversion procedure ought to be flexible when the water quality does not remain stable. High spatio-temporal variability might be left unrecognized by using coefficients that are fixed for timings or locations, such as measurement weeks, stations, or the archipelago zones. They on the other hand require either locally or temporally restricted calibration procedures, but at the same time, they face the bulk problem on the other dimension. In contrast, the quartile method avoids the bulk problem in both of the dimensions. By choosing an appropriate conversion coefficient according to the water transparency, more flexibility is allowed for the procedure as certain areas or timings are not permanently fixed with certain coefficients. Actually, our results show that this flexibility is valuable, as for all the original stations—with only one exception—several of the four coefficients based on ZSD quartiles were used at different occasions during the growing season.
The accuracy of all the models depends on the success of their calibration. The coverage of the calibration data needs to be sufficient and suitable for the purpose. Preisendorfer [
3] found the empirically defined conversion coefficients frustrating as the statistical links between the Secchi and euphotic depth may dissolve in time. He rationalized that even though the changes in water quality tend to be periodic, there is always some randomness caused by, for example, climatic or anthropogenic factors, which changes the optical composition of water. Due to the random variability in water quality, the pre-defined conversion coefficients may not be trustworthy after completing the calibration.
Consequently, we urge the use of spatio-temporally comprehensive data when calibrating the coefficients. Including as wide and as variable data as possible in the calibration phase, the coefficients are more likely to perform well also in situations outside the calibration procedure. The link may well be untrustworthy if the coefficients are created based on data collected within a narrow time window, for example during cyanobacteria blooms, and if these coefficients are then used during the water transparency maximum. Instead, our data cover variation in both time and space, and thus the spatio-temporal differences are already included in the coefficients.
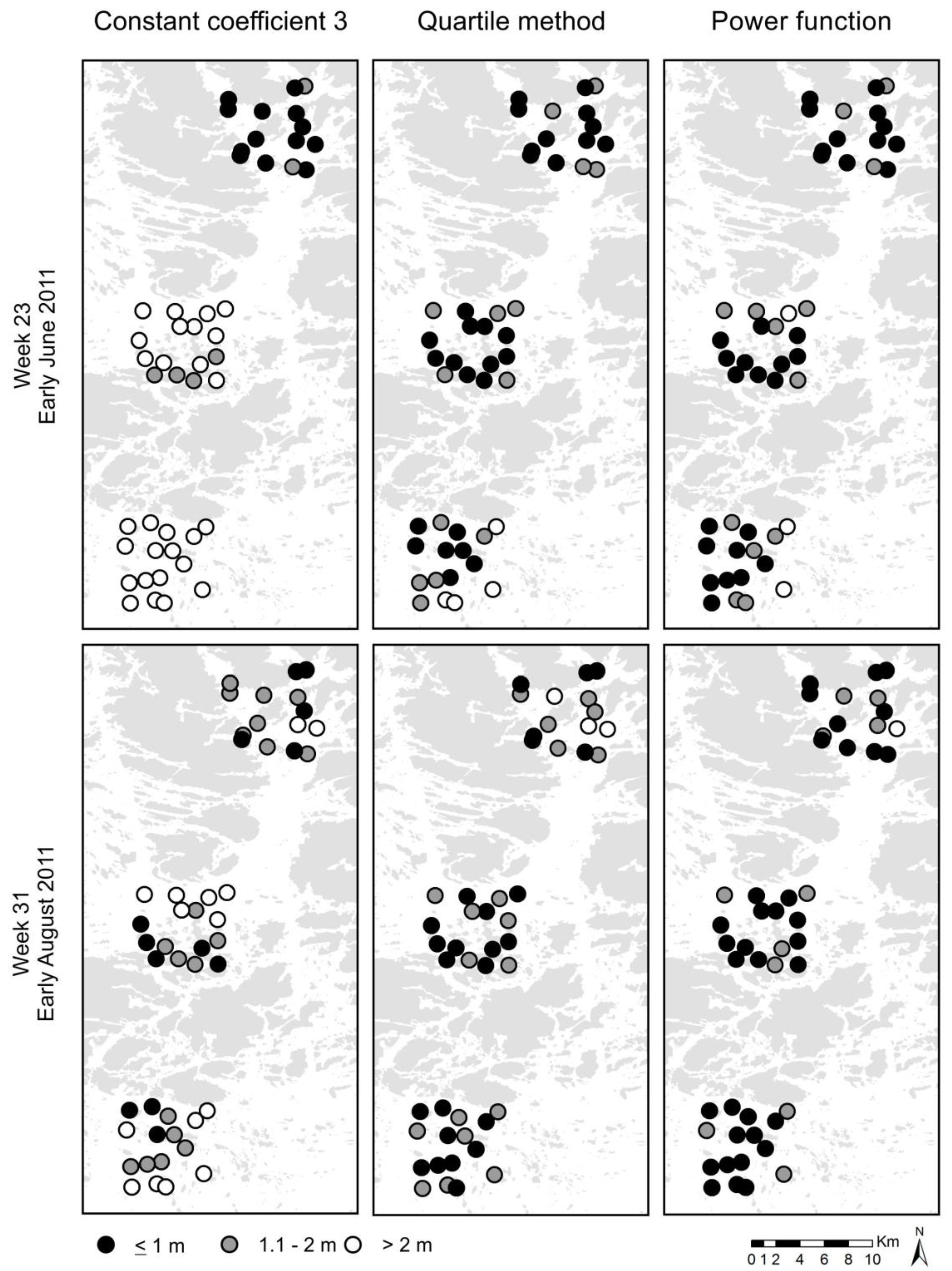
Nonetheless, there were spatio-temporal differences in the quality assessment made with the independent testing data (from year 2011). During the first test week, the accuracy improved towards the mainland, while in the second week, it improved towards the open sea. One possible explanation for the poorer performance in the outer archipelago during the first week is the high transparency of waters. Some of the ZSD values in 2011 were notably greater than any ZSD values in 2010, and thus fell outside the original training data range. The quartile method presumably requires a new water transparency class for waters clearer than the ones used in our current classification. The functions, on the other hand, performed better as they rather accurately succeeded in extrapolating the ZSD-Zeu correlation also outside the original data range.
In our study, the method based on water transparency quartiles modeled the Zeu values in the original training data very well, and in the independent testing data with moderate accuracy. The method is assumed to work with sufficient accuracy whenever the calibration data, i.e., the computed coefficients, are derived at the same sea area, or at least from optically similar waters—it is not necessary to use exactly the same locations. Nevertheless, it is important to consider what kind of waters are in question. Coefficients defined in very turbid waters will presumably not work well in optically very different waters, such as very clear waters, or waters in which the attenuation is strongly dominated by organic material.
As geographical information is increasingly demanded in coastal research and administration, also euphotic depth data are needed. The applications for spatial Zeu data range from studies of phytoplankton and macrophyte ecology to the planning work related to integrated coastal zone management (ICZM) and marine spatial planning (MSP). In each case, it is crucial to operate with data which reflect the true euphotic depth as well as possible. Instead of using one or few measured ZSD values to represent a certain coastal area, we urge to study the area comprehensively. As a part of this, an optimized ZSD to Zeu conversion will often notably improve the results of the coastal GIS work.