Quantum Mechanical Modeling: A Tool for the Understanding of Enzyme Reactions
Abstract
:1. Introduction
2. Models
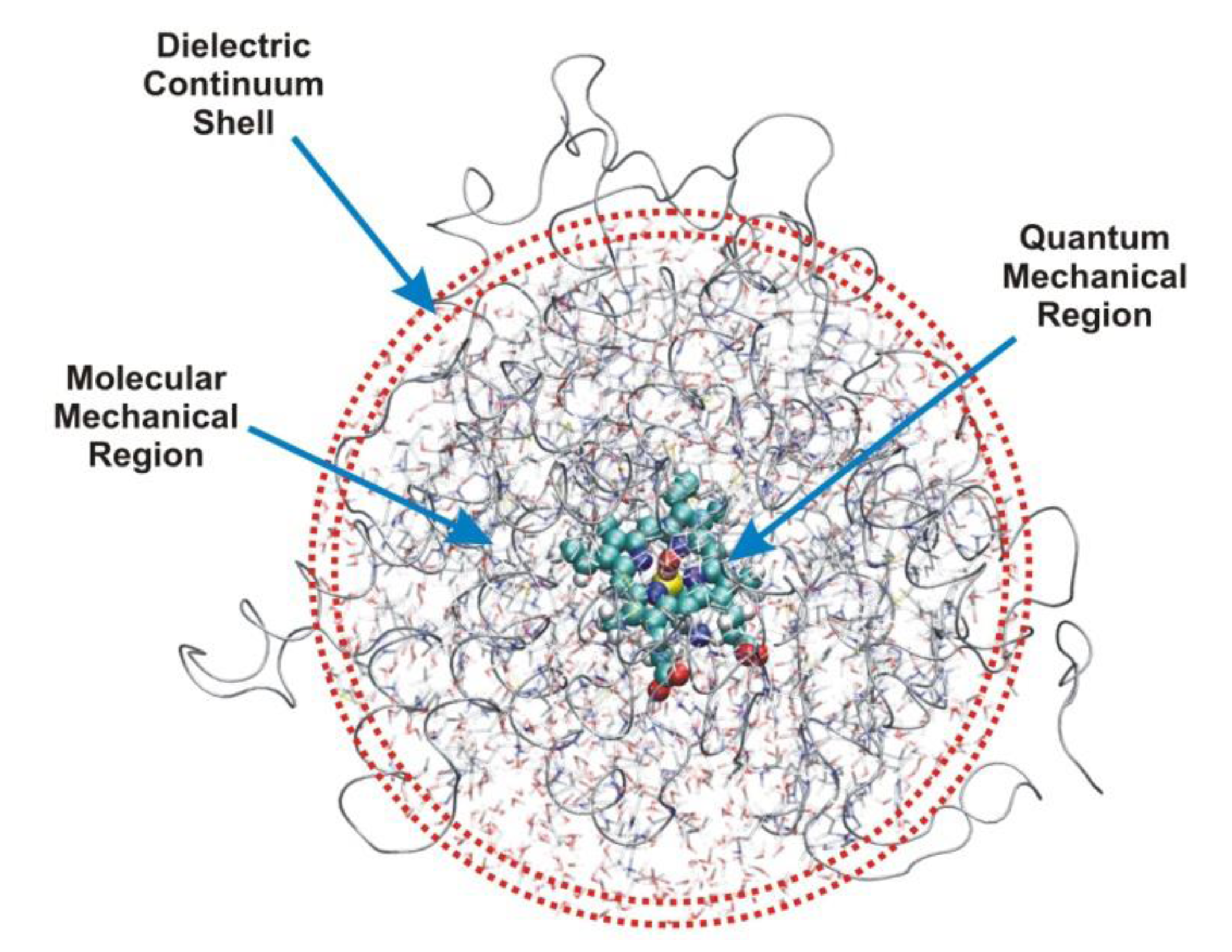
3. Methods
4. Case studies
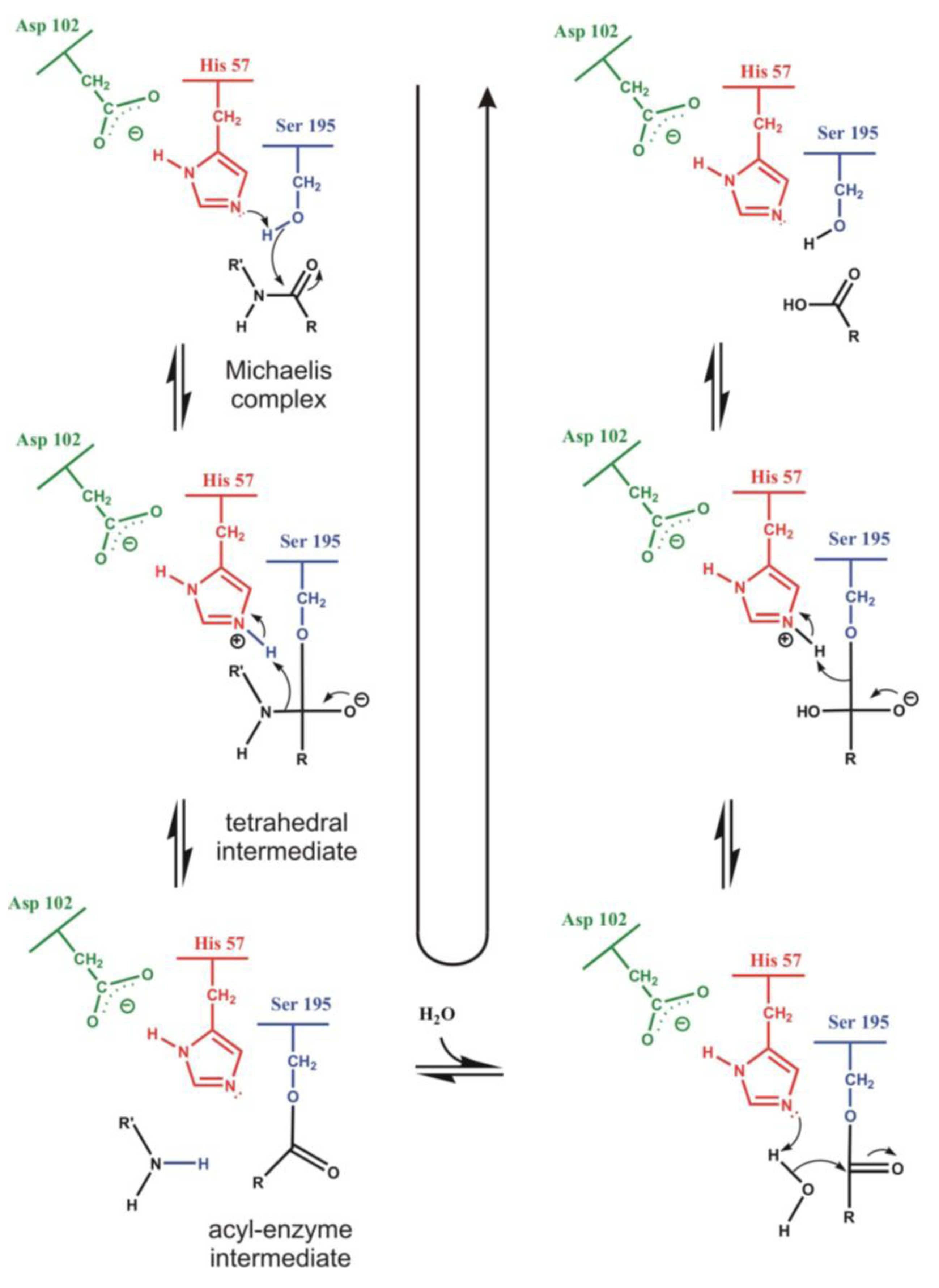
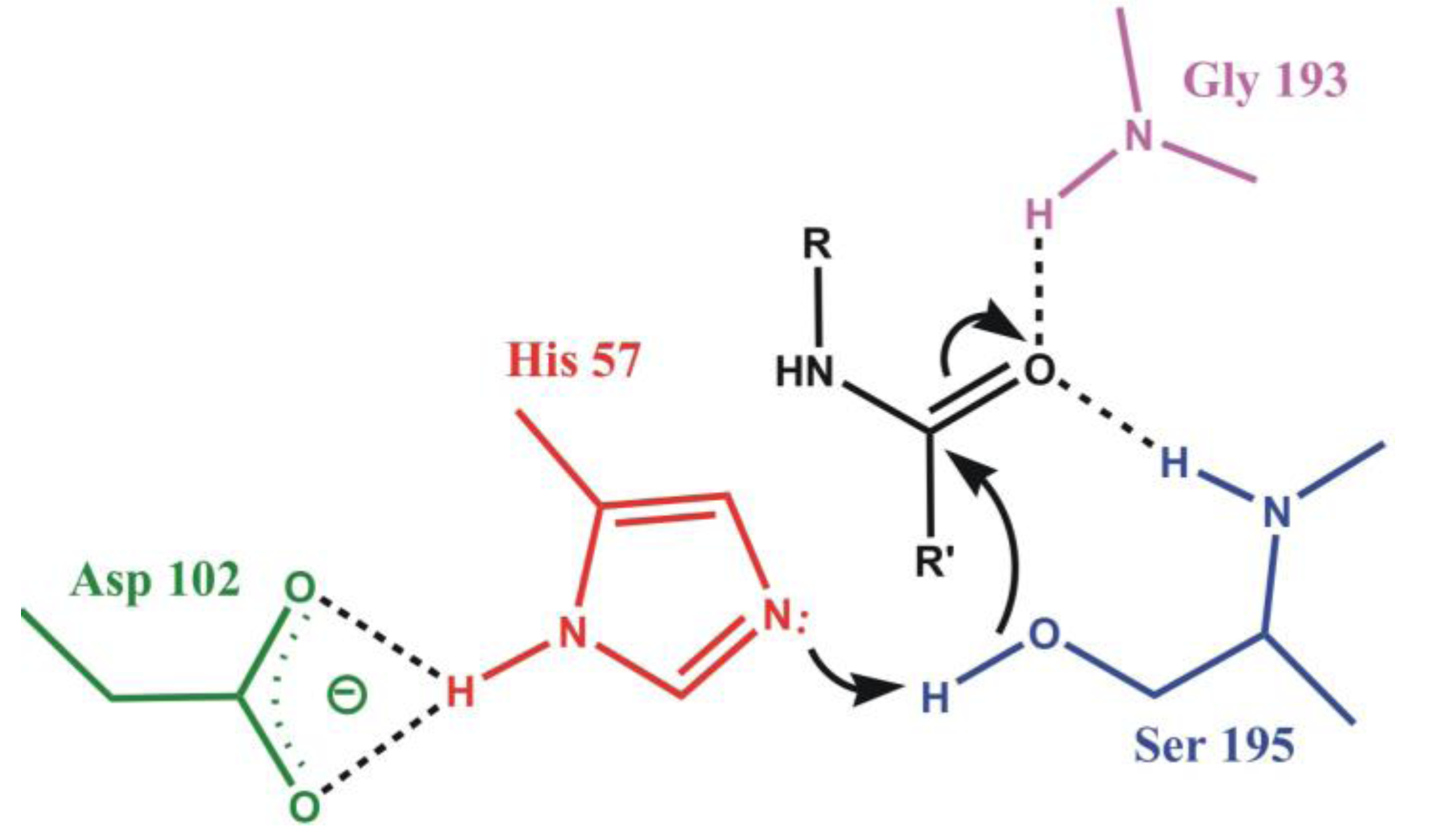
4.1. Electrostatic Catalysis: Serine Proteases
| Enzyme | Calculated | Experimental |
|---|---|---|
| subtilisin Carlsberg | −102.6 | −36.5 |
| α-chymotrypsin | −71.9 | −34.2 |
| subtilisin NOVO | −62.1 | −31.6 |
| β-trypsin | −40.7 | −26.7 |
| α-lytic protease | 9.3 | 0.3 |

4.2. Phosphoryl Transfer

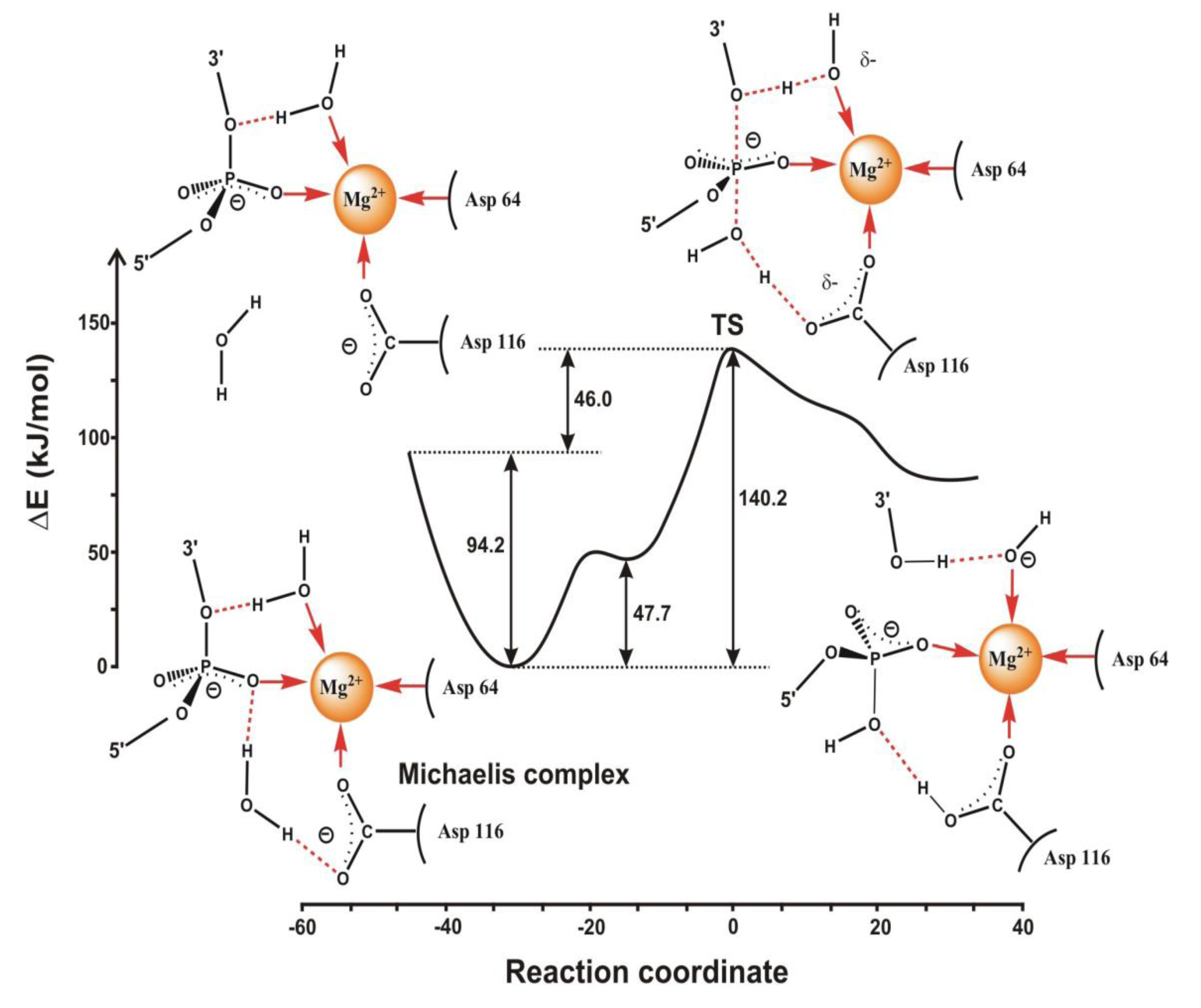
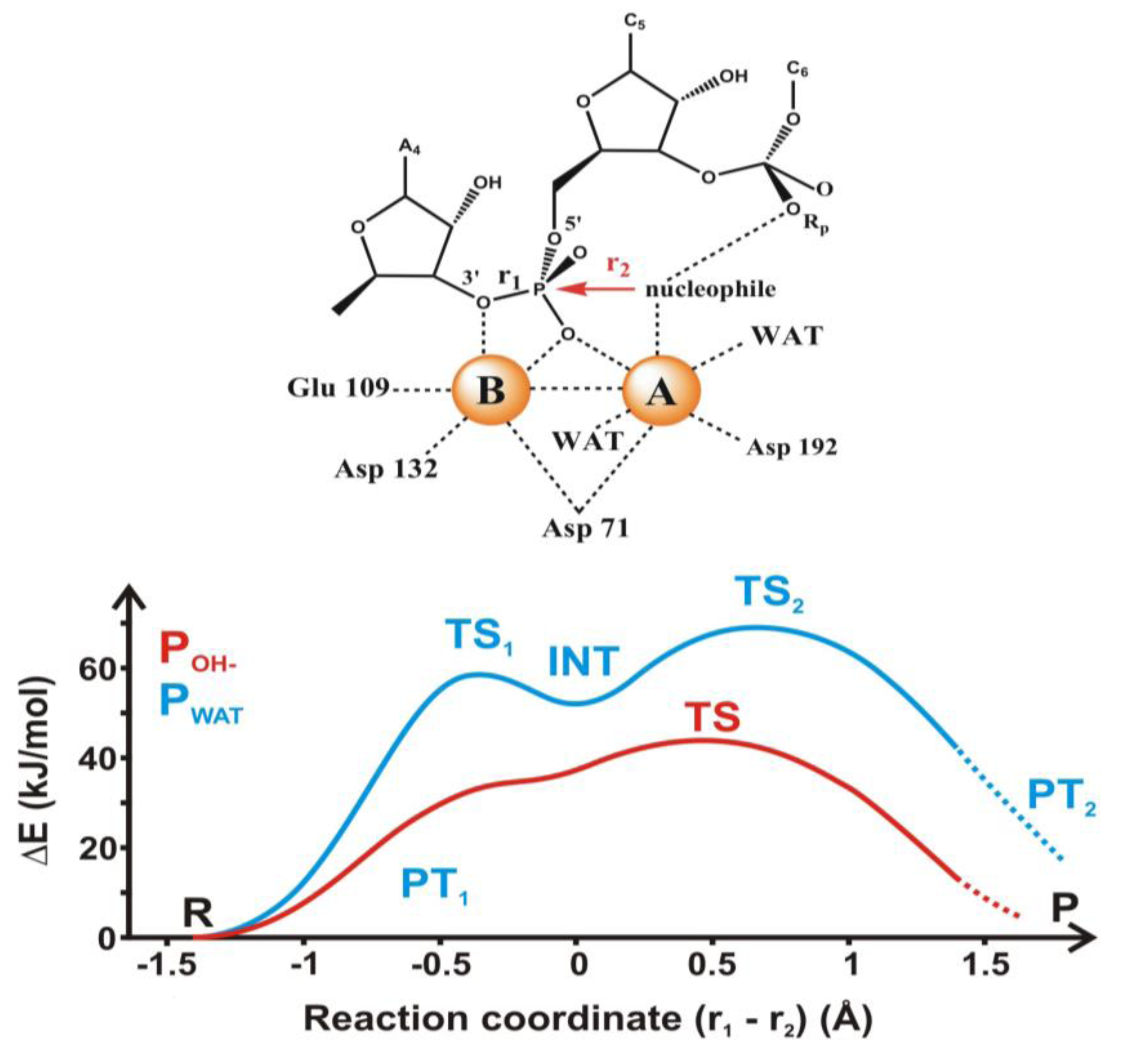
4.3. Long-Range Electron Transfer in Heme Peroxidases
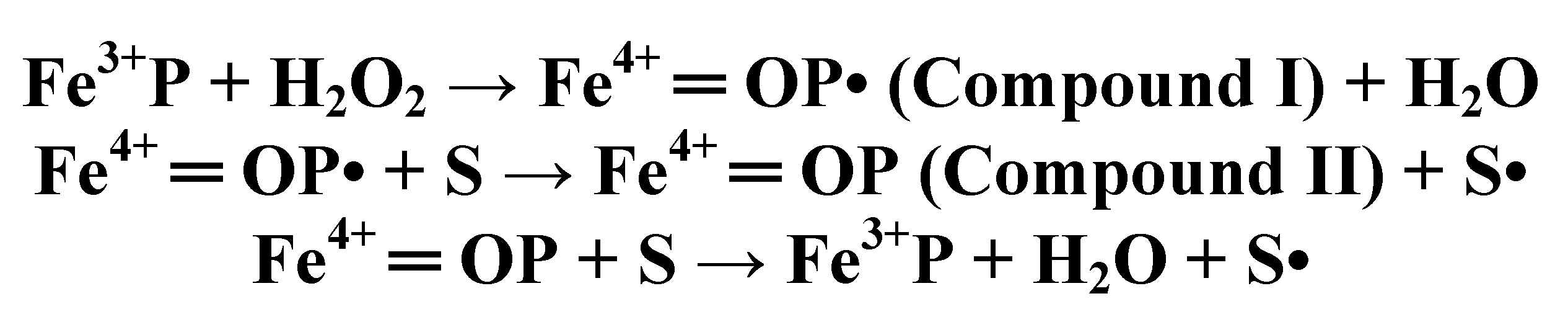
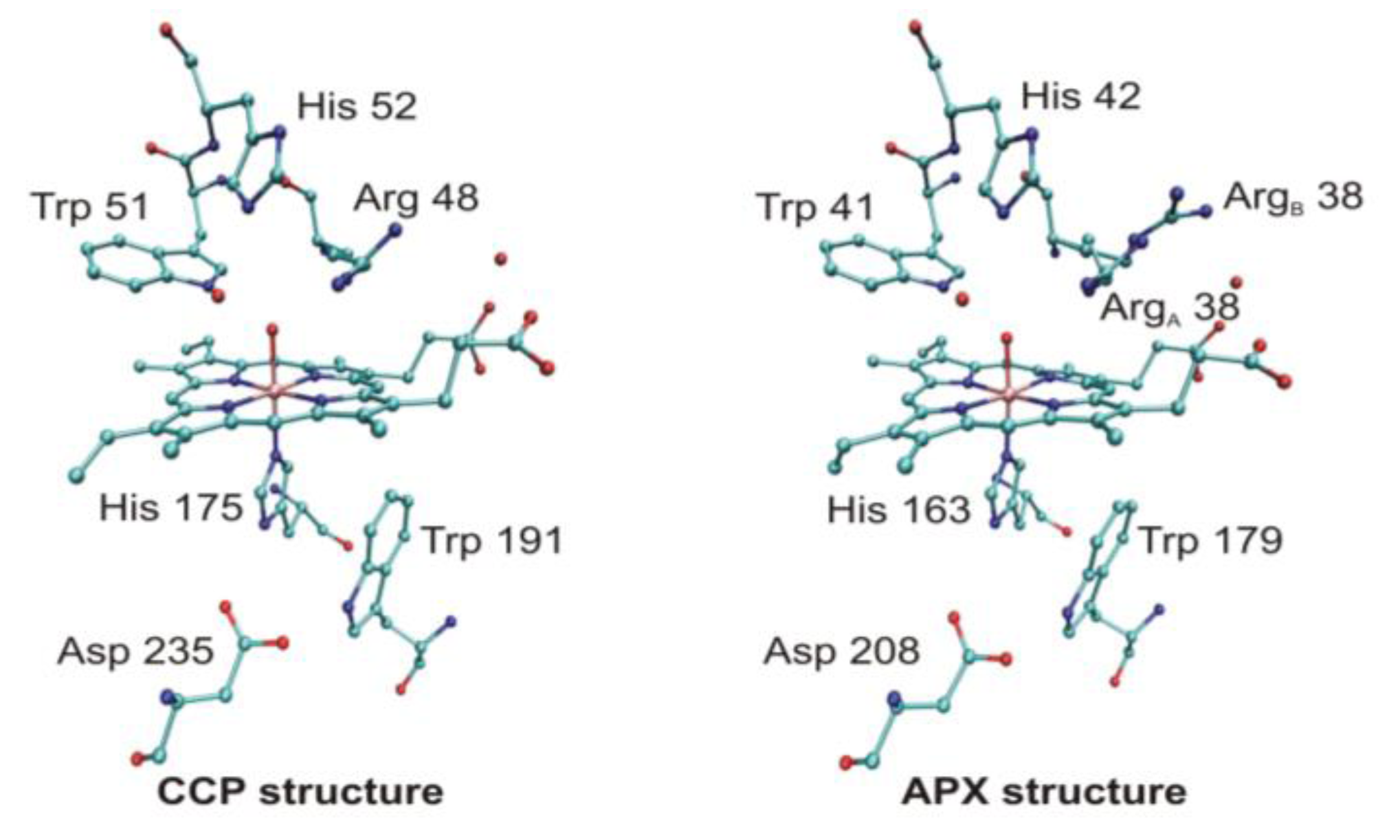
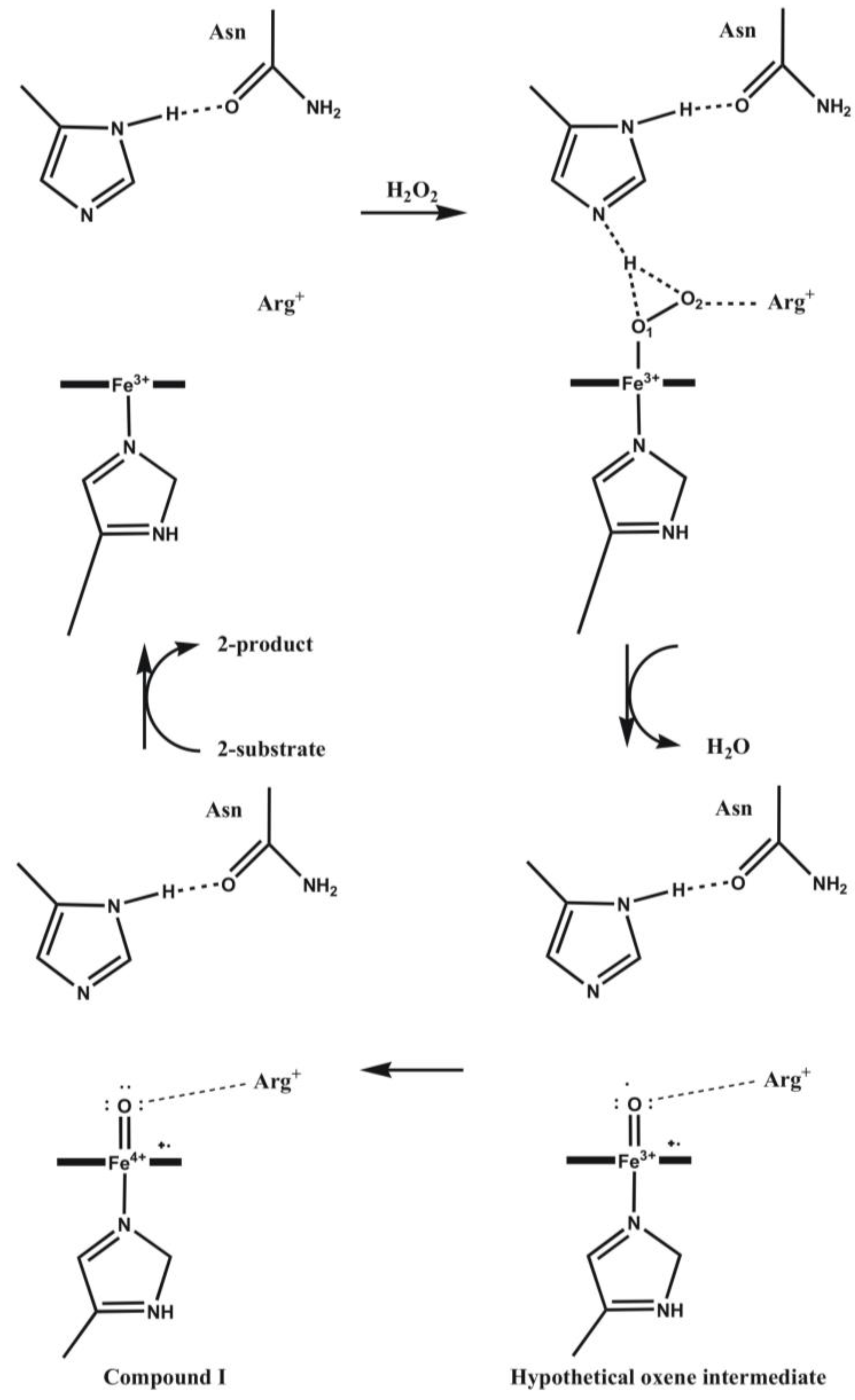
4.4. Cytochrome P450 Enzymes
4.4.1. Is the Oxidizing Power of Active Species of Various P450 Isoforms the Same?
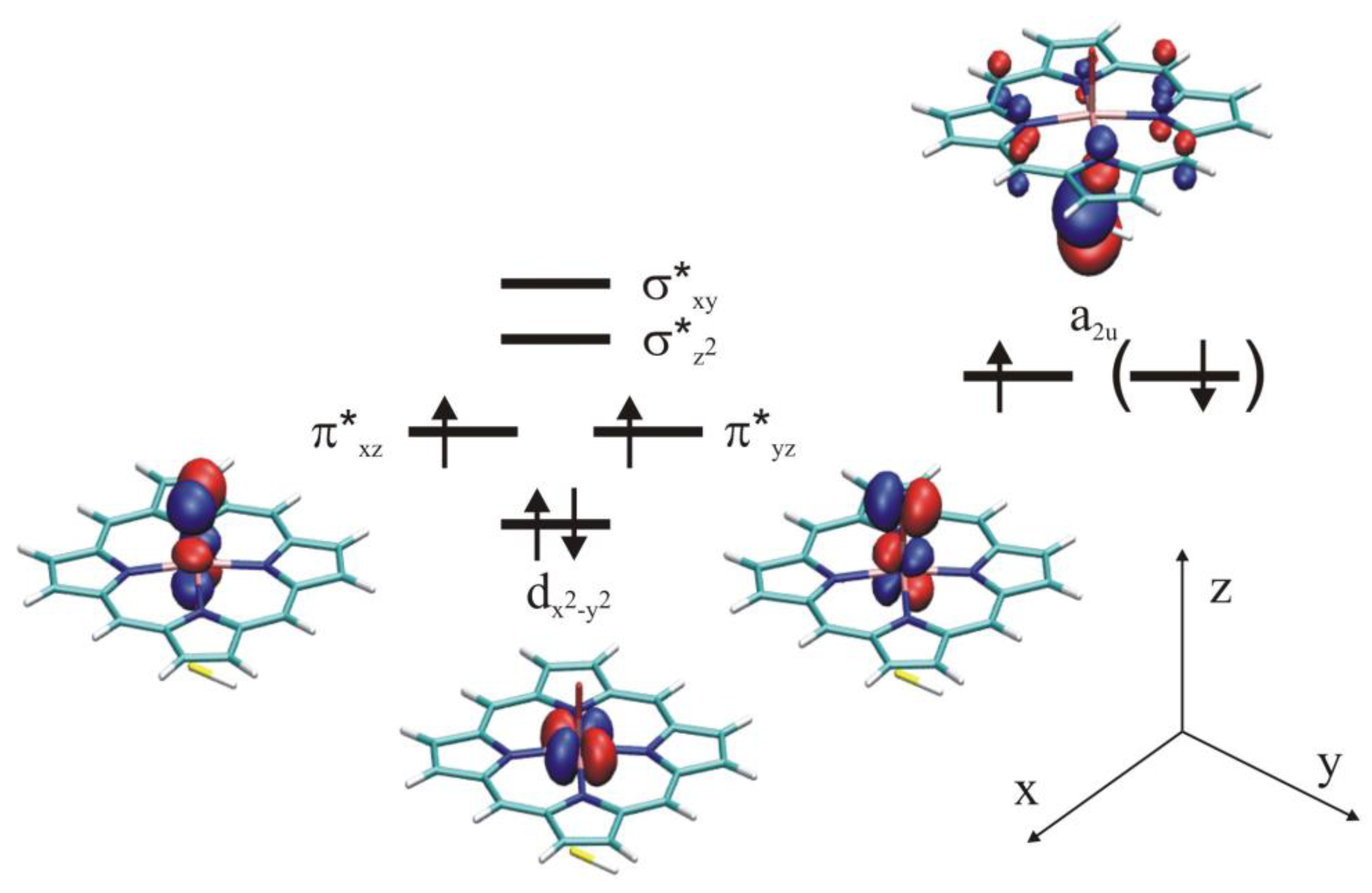
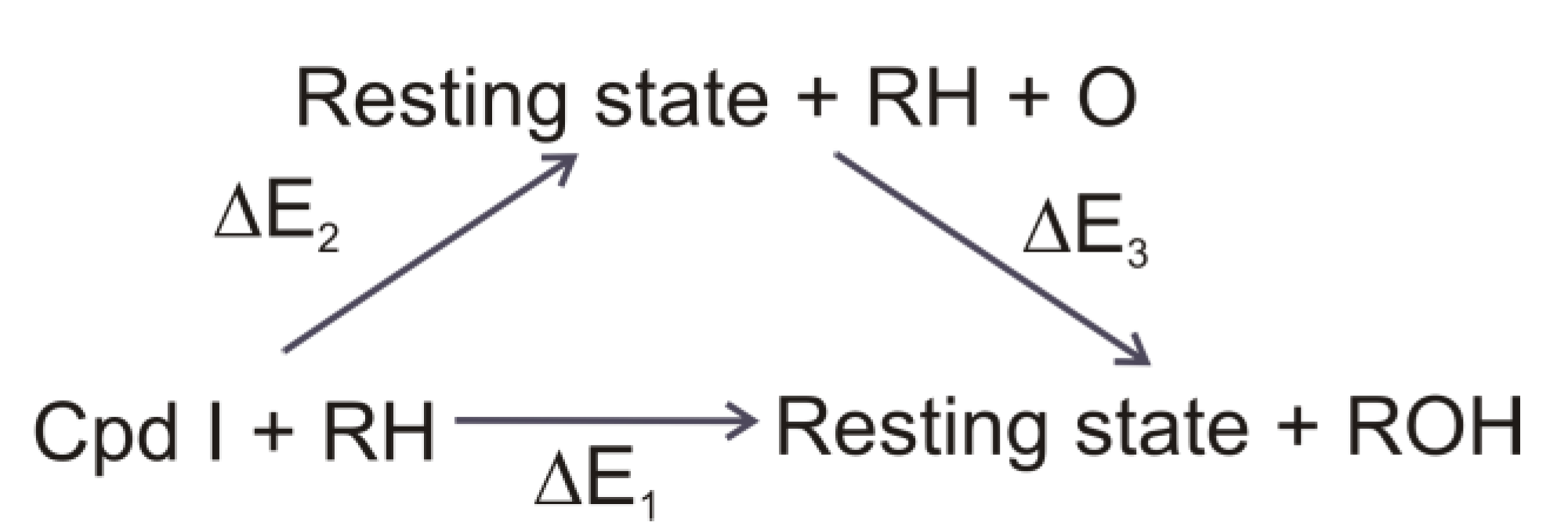
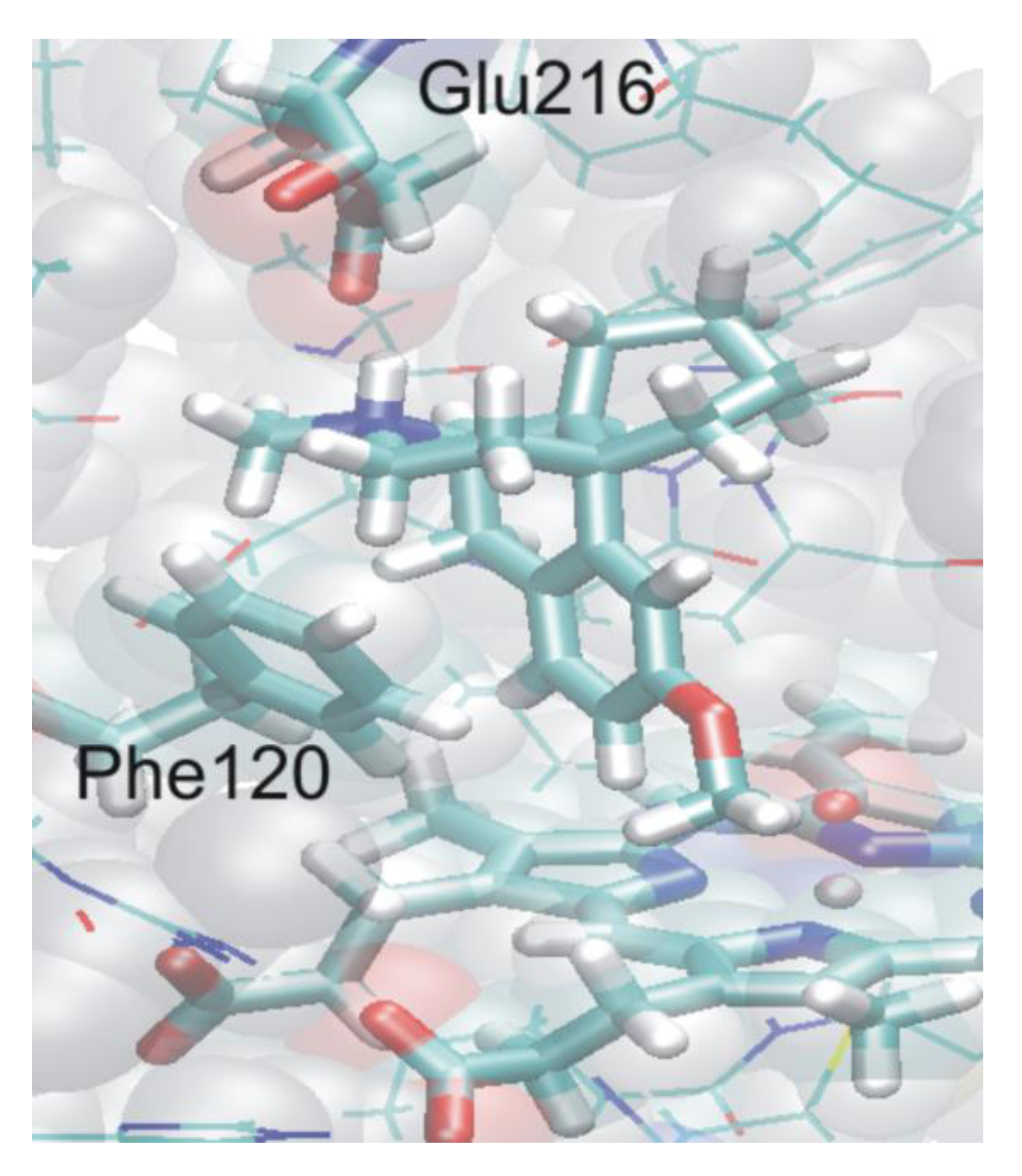
4.4.2. Metabolism of Dextromethorphan by P450 2D6: What Drives the Regioselectivity of the Enzymes?
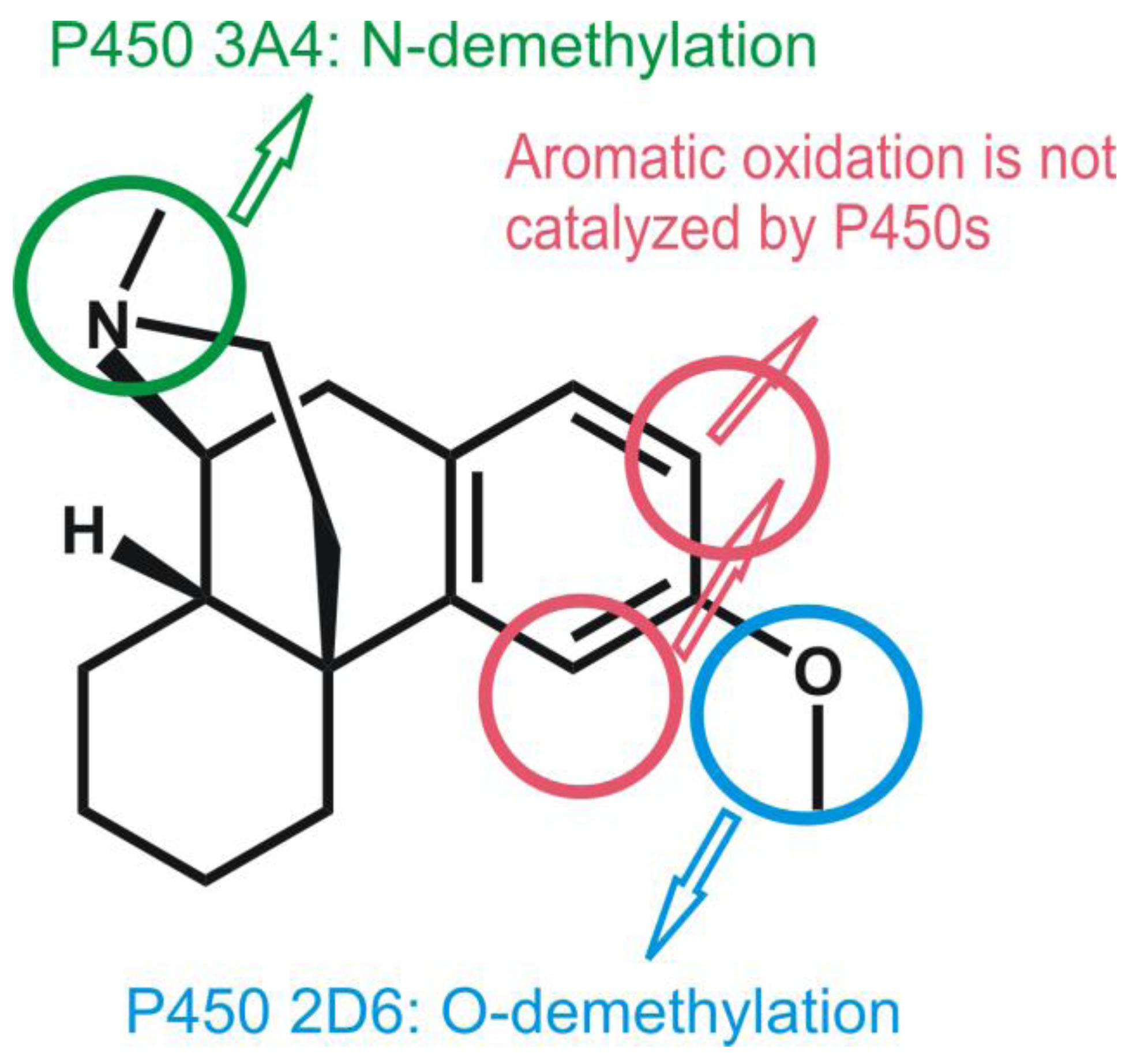
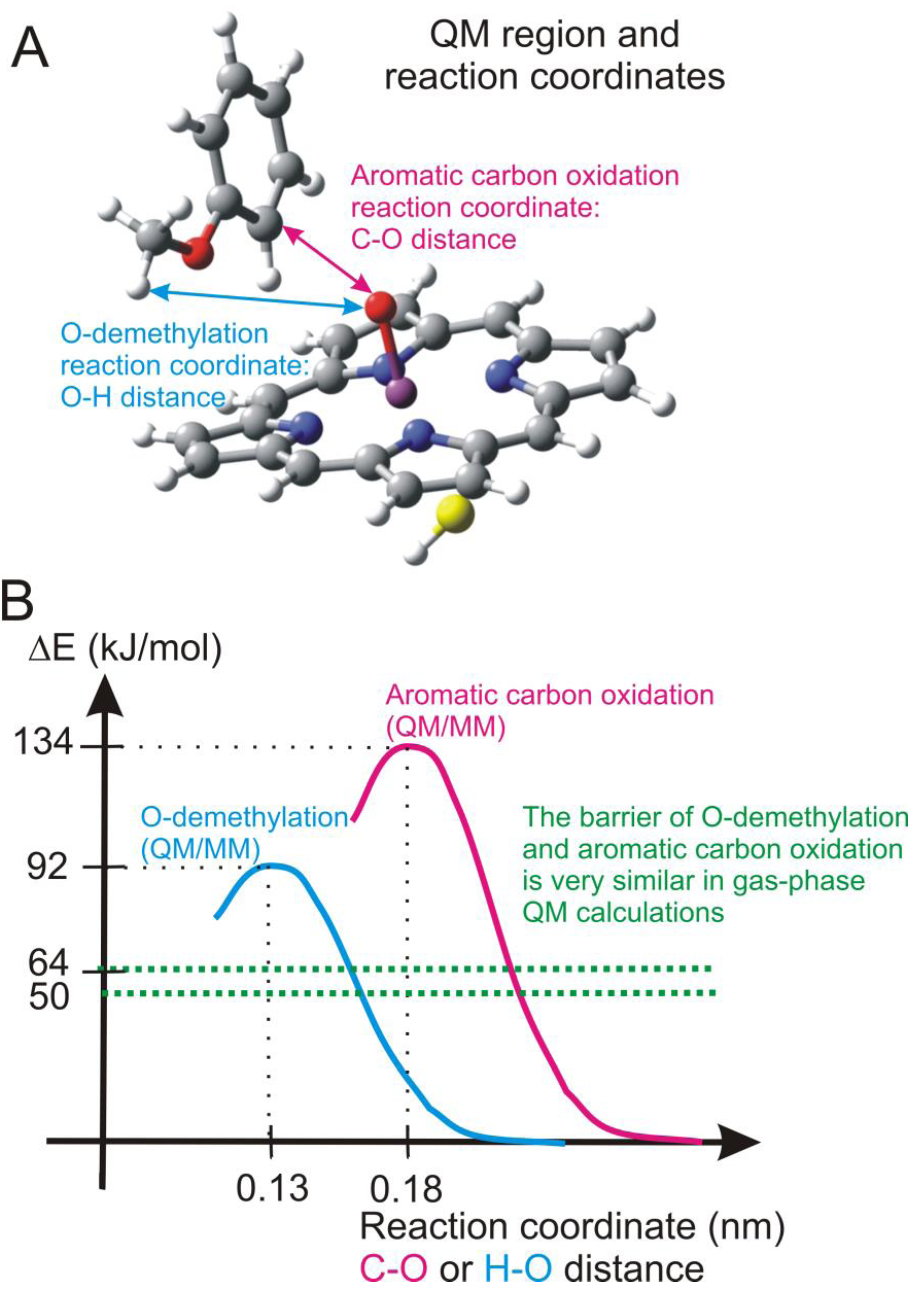
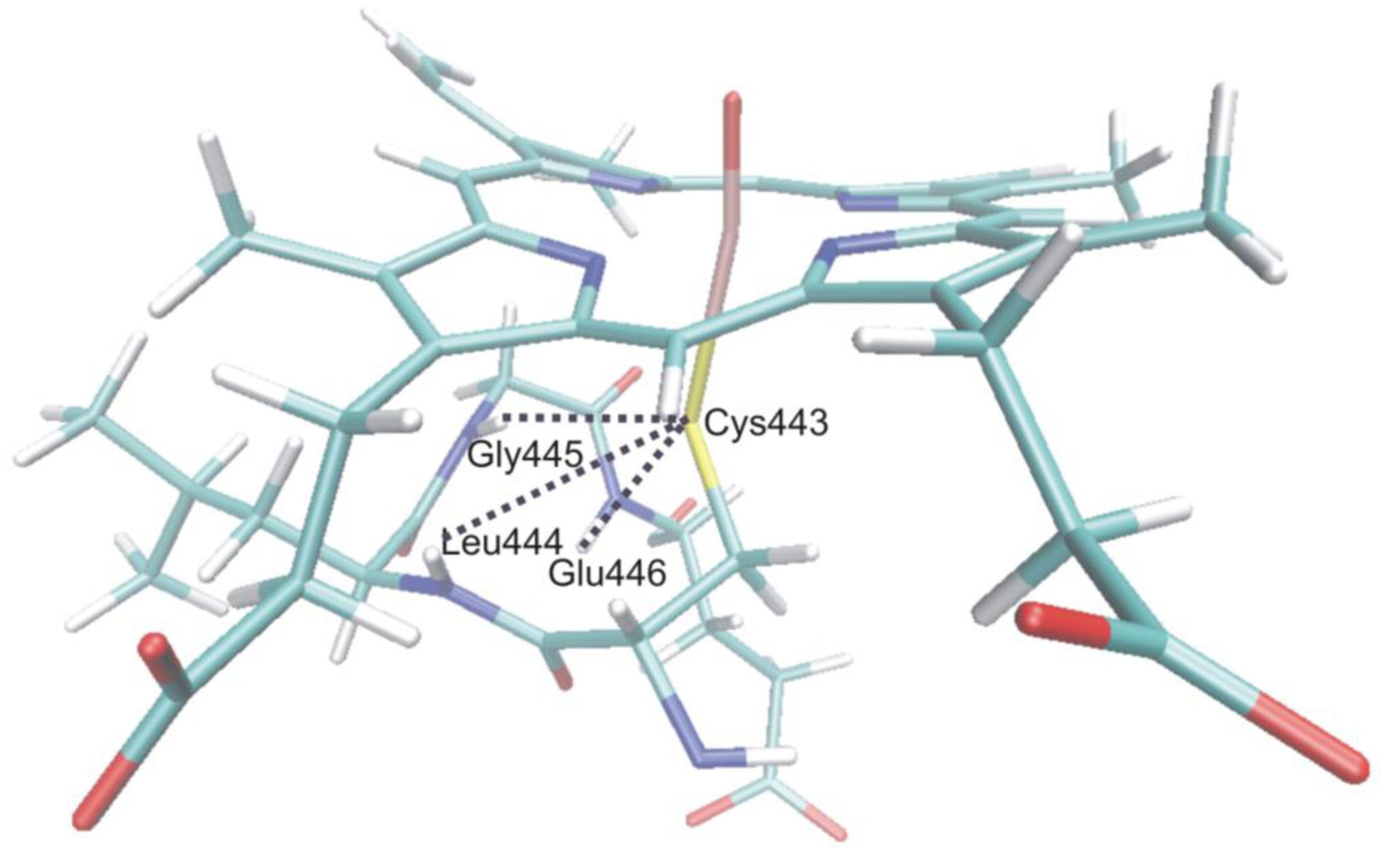
4.4.3. Reactivity of the P450nor Enzyme
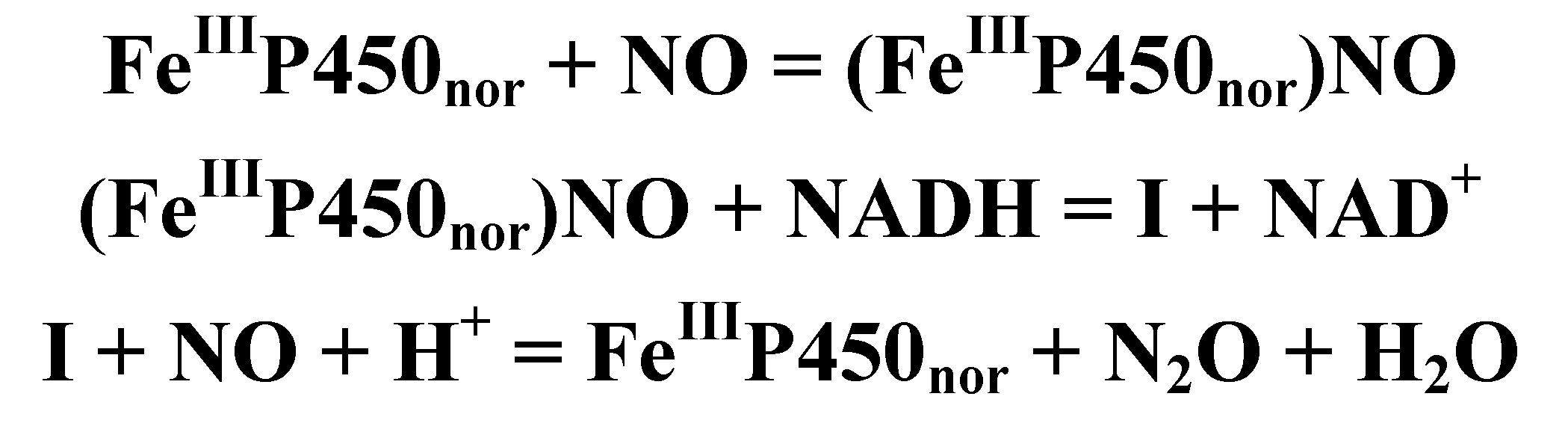
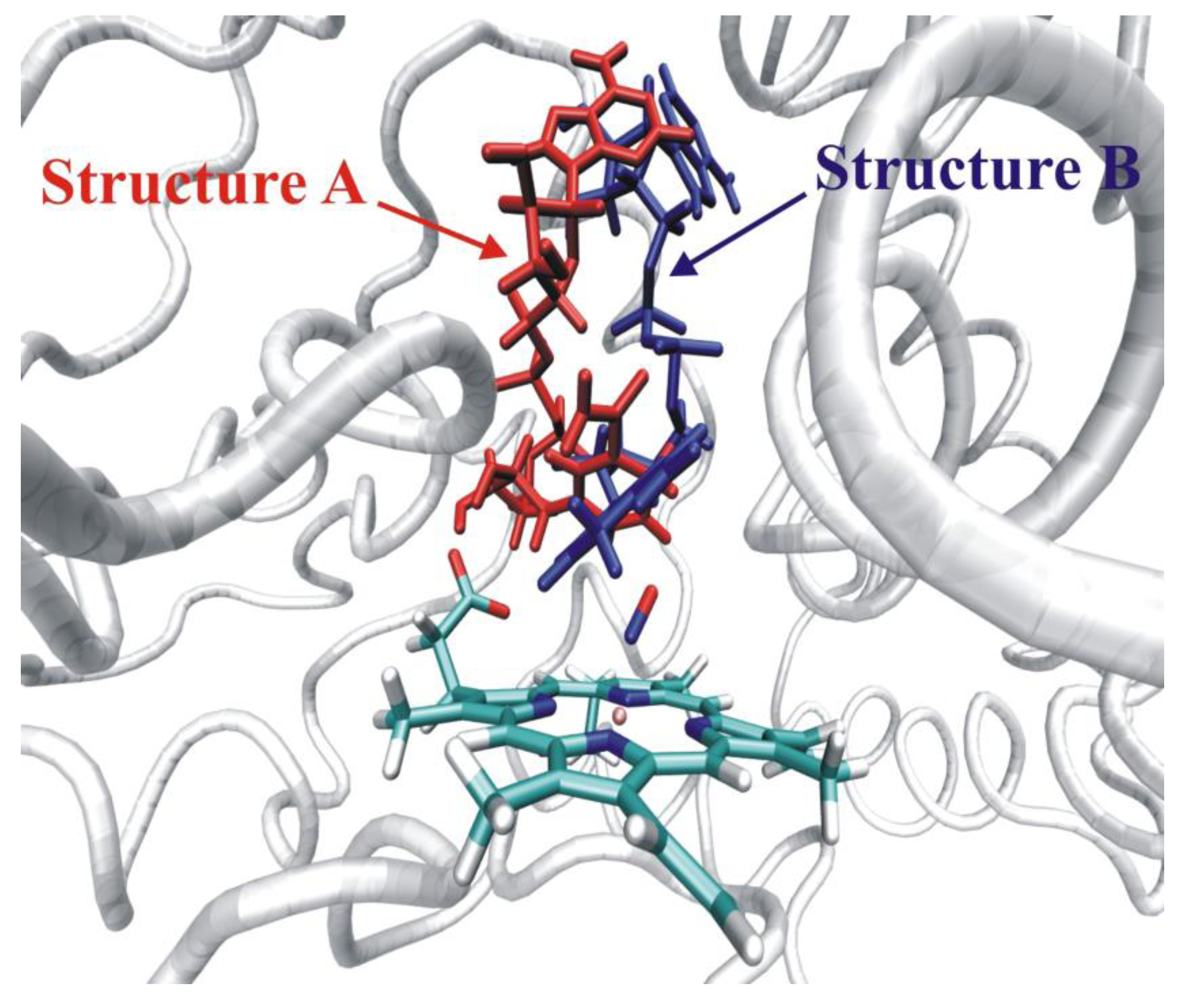
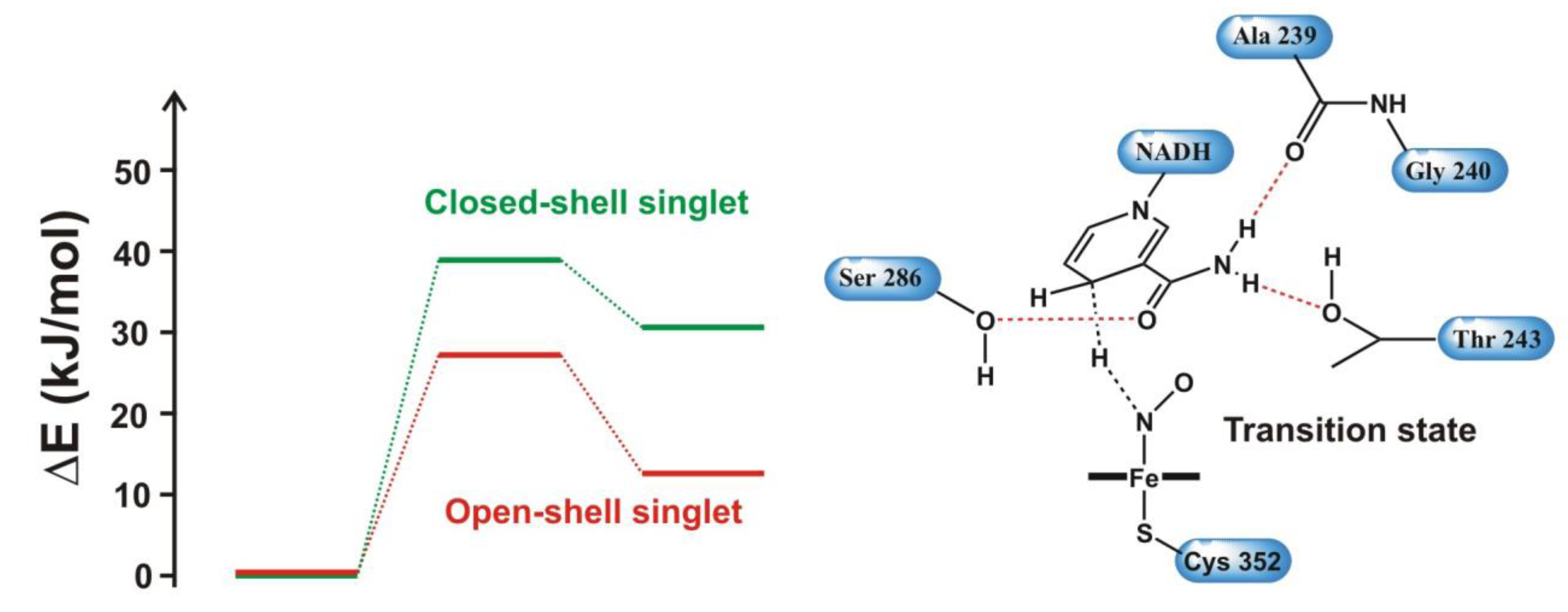
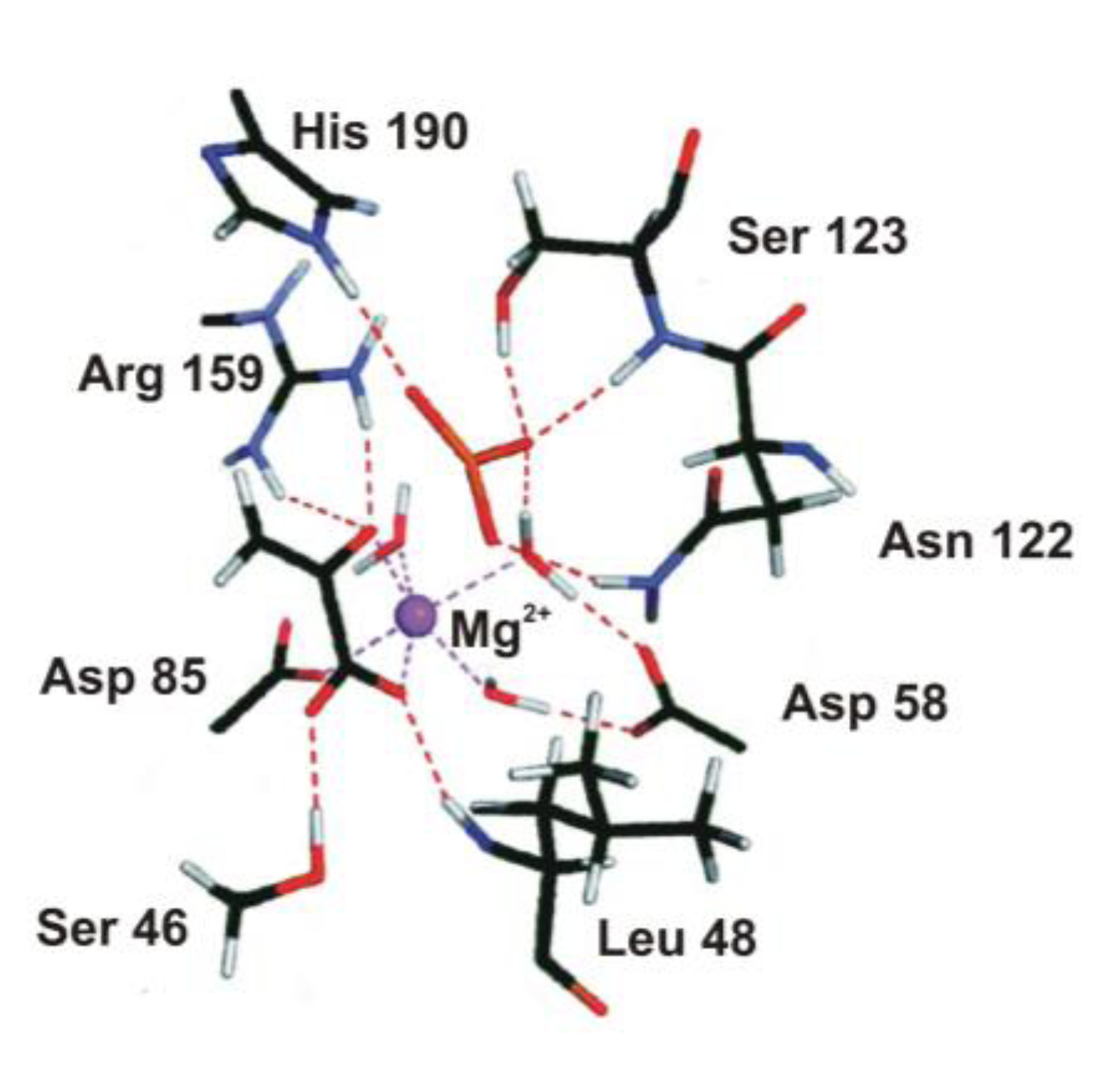
4.5. Xylose Isomerase

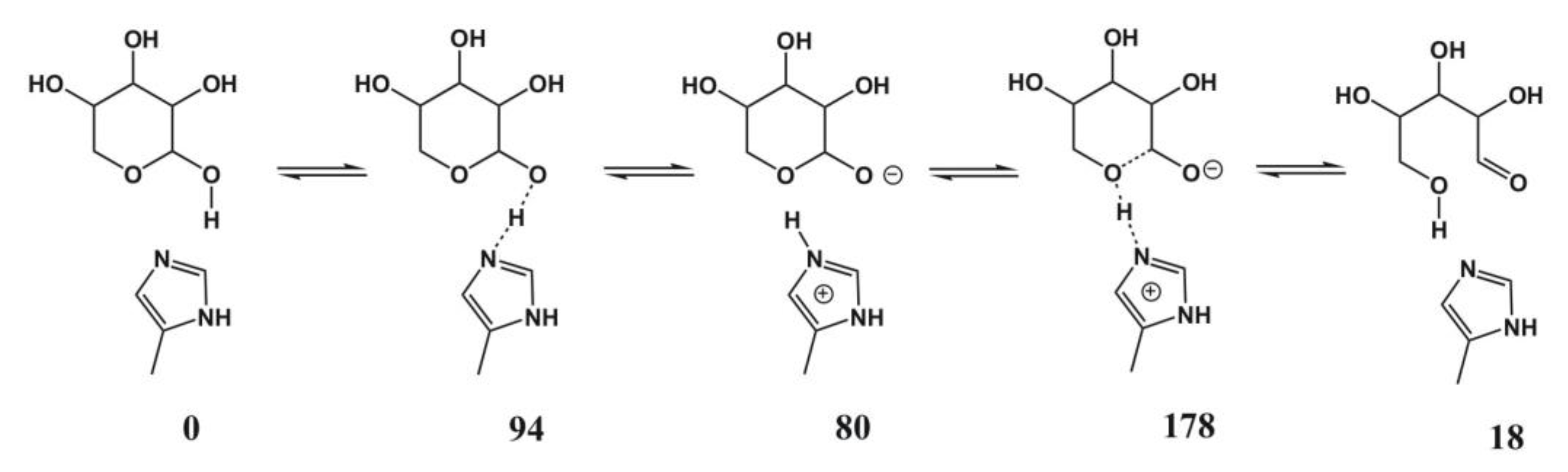
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Claeyssens, F.; Harvey, J.N.; Manby, F.R.; Mata, R.A.; Mulholland, A.J.; Ranaghan, K.E.; Schütz, M.; Thiel, S.; Thiel, W.; Werner, H.J. High-accuracy computation of reaction barriers in enzymes. Angew. Chem. 2006, 118, 7010–7013. [Google Scholar] [CrossRef]
- Matthews, B.W.; Sigler, P.B.; Henderson, R.; Blow, D.M. Three-Dimensional structure of tosyl α-chymotrypsin. Nature 1967, 214, 652–656. [Google Scholar] [CrossRef]
- Hedström, L. Serine protease mechanism and specificity. Chem. Rev. 2002, 102, 4501–4523. [Google Scholar] [CrossRef]
- Lassila, J.K.; Zalatan, J.G.; Herschlag, D. Biological phosphoryl-transfer reactions: Understanding mechanism and catalysis. Annu. Rev. Biochem. 2011, 80, 669–702. [Google Scholar] [CrossRef]
- Asbóth, B.; Náray-Szabó, G. Mechanism of action of d-xylose isomerase. Curr. Protein Pept. Sci. 2000, 1, 237–254. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- Wade, R.C.; Luty, B.A.; Demchuk, E.; Madura, J.D.; Davis, M.E.; Briggs, J.M.; McCammon, J.A. Simulation of enzyme-substrate encounter with gated active sites. Nat. Struct. Biol. 1994, 1, 65–69. [Google Scholar] [CrossRef]
- Hammes-Schiffer, S.; Benkovic, S.J. Relating protein motion to catalysis. Annu. Rev. Biochem. 2006, 75, 519–541. [Google Scholar] [CrossRef]
- McGeagh, J.D.; Ranaghan, K.E.; Mulholland, A.J. Protein dynamics and enzyme catalysis: Insights from simulations. Biochim. Biophys. Acta 2011, 1814, 1077–1092. [Google Scholar] [CrossRef]
- Warshel, A. Computer Modeling of Chemical Reactions in Enzymes and Solutions; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Ranaghan, K.E.; Mulholland, A.J. Investigations of enzyme-catalysed reactions with combined quantum mechanics/molecular mechanics (QM/MM) methods. Int. Rev. Phys. Chem. 2010, 29, 65–133. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory; Dover Publications: Mineola, NY, USA, 1996. [Google Scholar]
- Jacobsen, H.; Cavallo, L. Directions for Use of Density Functional Theory: A Short Introduction Manual for Chemists. In Handbook of Computational Chemistry; Leszczynski, J., Ed.; Springer: Berlin, Germany, 2011; pp. 97–133. [Google Scholar]
- Vreven, T.; Morokuma, K. Hybrid methods: ONIOM(QM:MM) and QM/MM. Annu. Repts Comput. Chem. 2006, 2, 35–51. [Google Scholar] [CrossRef]
- Poltev, V. Molecular Mechanics: Method and Applications. In Handbook of Computational Chemisry; Leszczynski, J., Ed.; Springer: Berlin, Germany, 2011; pp. 260–291. [Google Scholar]
- Case, D.A.; Darden, T.A.; Cheatham, T.E., III; Simmerling, C.L.; Wang, J.; Duke, R.E.; Luo, R.; Walker, R.C.; Zhang, W.; Merz, K.M.; et al. AMBER 11. University of California: San Francisco, 2010. [Google Scholar]
- Christen, M.; Hunenberger, P.H.; Bakowies, D.; Baron, R.; Bürgi, R.; Geerke, D.P.; Heinz, T.N.; Kastenholz, M.A.; Krautler, V.; Oostenbrink, C.; et al. The gromos software for biomolecular simulation: Gromos05. J. Comp. Chem. 2005, 26, 1719–1751. [Google Scholar] [CrossRef]
- Available online: http://www.gromacs.org/ (accessed on 6 August 2013).
- Brooks, B.R.; Brooks, C.L., III; Mackerell, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comp. Chem. 2009, 30, 1545–1615. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Tirado-Rives, J. Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Natl. Acad. Sci. USA 2005, 102, 6665–6670. [Google Scholar] [CrossRef]
- Nowak, W. Applications of Computational Methods to Simulations of Proteins Dynamics. In Handbook of Computational Chemistry; Leszczynski, J., Ed.; Springer: Berlin, Germany, 2011; pp. 1129–1155. [Google Scholar]
- Marx, D.; Hutter, J. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Röthlisberger, D.; Khersonsky, O.; Wollacott, A.M.; Jiang, J.; DeChancie, J.; Betker, J.; Gallaher, J.L.; Althoff, E.A.; Zanghellini, A.; Dym, O.; et al. Kemp elimination catalysts by computational enzyme design. Nature 2008, 453, 190–195. [Google Scholar] [CrossRef]
- Náray-Szabó, G.; Surján, P.R. Bond orbital framework for rapid calculation of environmental effects on molecular potential energy surfaces. Chem. Phys. Lett. 1983, 96, 499–501. [Google Scholar] [CrossRef]
- Hu, H.; Yang, W. Free energies of chemical reactions in solution and in enzymes with ab initio quantum mechanics/molecular mechanics methods. Annu. Rev. Phys. Chem. 2008, 59, 573–560. [Google Scholar] [CrossRef]
- Warshel, A.; Florian, J. Empirical Valence Bond and Related Approaches; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Kamerlin, S.C.L.; Cao, J.; Rosta, E.; Warshel, A. On unjustifiably misrepresenting the EVB approach while simultaneously adopting it. J. Phys. Chem. B 2009, 113, 10905–10915. [Google Scholar] [CrossRef]
- Bentzien, J.; Muller, R.P.; Florián, J.; Warshel, A. Hybrid ab initio quantum mechanics/molecular mechanics calculations of free energy surfaces for enzymatic reactions: The nucleophilic attack in subtilisin. J. Phys. Chem B 1998, 102, 2293–2301. [Google Scholar] [CrossRef]
- Rocchia, W.; Alexov, E.; Honig, B. Extending the applicability of the nonlinear poisson-boltzmann equation: Multiple dielectric constants and multivalent ions. J. Phys. Chem. B 2001, 105, 6507–6514. [Google Scholar] [CrossRef]
- Sarkar, S.; Witham, S.; Zhang, J.; Zhenirovskyy, M.; Rocchia, W.; Alexov, E. DelPhi Web Server: A comprehensive online suite for electrostatic calculations of biological macromolecules and their complexes. Comm. Comp. Phys. 2013, 13, 269–284. [Google Scholar]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Polgár, L. Mechanisms of Protease Action; CRC Press: Boca Raton, FL, USA, 1989. [Google Scholar]
- Brenner, S. The molecular evolution of genes and proteins: A tale of two serines. Nature 1988, 334, 528–530. [Google Scholar] [CrossRef]
- Asbóth, B.; Polgár, L. Transition-state stabilization at the oxyanion binding sites of serine and thiol proteinases: Hydrolyses of thiono and oxygen esters. Biochemistry 1983, 22, 117–122. [Google Scholar] [CrossRef]
- Carter, P.; Wells, J.A. Functional interaction among catalytic residues in subtilisin BPN’. Proteins Struct. Funct. Genet. 1990, 7, 335–342. [Google Scholar] [CrossRef]
- Blow, D.M.; Birktoft, J.J.; Hartley, B.S. Role of a buried acid group in the mechanism of action of chymotrypsin. Nature 1969, 221, 337–340. [Google Scholar] [CrossRef]
- Polgár, L.; Bender, M.L. The nature of general base-general acid catalysis in serine proteases. Proc. Natl. Acad. Sci. USA 1969, 64, 1335–1342. [Google Scholar] [CrossRef]
- Bachovchin, W.W. Confirmation of the assignment of the low-field proton resonance of serine proteases by using specifically nitrogen-15 labeled enzyme. Proc. Natl. Acad. Sci. USA 1985, 82, 7948–7951. [Google Scholar] [CrossRef]
- Kossiakoff, A.A.; Spencer, S.A. Direct determination of the protonation states of aspartic acid-102 and histidine-57 in the tetrahedral intermediate of the serine proteases: Neutron structure of trypsin. Biochemistry 1981, 20, 6462–6474. [Google Scholar] [CrossRef]
- Sprang, S.; Standing, T.; Fletterick, R.J.; Stroud, R.M.; Finer-Moore, J.; Xuong, N.H.; Hamlin, R.; Rutter, W.J.; Craik, C.S. The Three-dimensional structure of Asn102 mutant of trypsin: Role of Asp102 in serine protease catalysis. Science 1987, 237, 905–909. [Google Scholar]
- Szeltner, Z.; Rea, D.; Renner, V.; Fülöp, V.; Polgár, L. Electrostatic effects and binding determinants in the catalysis of prolyl oligopeptidase. Site specific mutagenesis at the oxyanion binding site. J. Biol. Chem. 2002, 277, 42613–42622. [Google Scholar]
- Warshel, A.; Náray-Szabó, G.; Sussman, F.; Hwang, J.K. How do serine proteases really work? Biochemistry 1989, 28, 3629–3637. [Google Scholar] [CrossRef]
- Warshel, A. Electrostatic origin of the catalytic power of enzymes and the role of preorganized active sites. J. Biol. Chem. 1998, 273, 27035–27038. [Google Scholar] [CrossRef]
- Kamerlin, S.C.L.; Sharma, P.K.; Chu, Z.T.; Warshel, A. Ketosteroid isomerase provides further support for the idea that enzymes work by electrostatic preorganization. Proc. Natl. Acad. Sci. USA 2010, 107, 4075–4080. [Google Scholar] [CrossRef]
- Gérczei, T.; Asbóth, B.; Náray-Szabó, G. Conservative electrostatic potential patterns at enzyme active sites. The anion-cation-anion triad. J. Chem. Inf. Comput. Sci. 1999, 39, 310–315. [Google Scholar] [CrossRef]
- Náray-Szabó, G.; Fuxreiter, M.; Warshel, A. Electrostatic Basis of Enzyme Catalysis. In Computational Approaches to Biochemical Reactivity; Warshel, A., Náray-Szabó, G., Eds.; Kluwer: Dordrecht, The Netherlands, 1997; pp. 237–293. [Google Scholar]
- Umeyama, H.; Nakagawa, S.; Kudo, T. Role of Asp102 in the enzymatic reaction of bovine beta-trypsin. A molecular orbital study. J. Mol. Biol. 1981, 150, 409–421. [Google Scholar] [CrossRef]
- Náray-Szabó, G. Electrostatic effect on catalytic rate enhancement in serine proteinases. Int. J. Quant. Chem. 1982, 22, 575–582. [Google Scholar] [CrossRef]
- Ishida, T.; Kato, S. Theoretical perspectives on the reaction mechanism of serine proteases: The reaction free energy profiles of the acylation process. J. Am. Chem. Soc. 2003, 125, 12035–12048. [Google Scholar] [CrossRef]
- Topf, M.; Richards, W.G. Theoretical studies on the deacylation step of serine protease catalysis in the gas phase, in solution, and in elastase. J. Am. Chem. Soc. 2004, 126, 14631–14641. [Google Scholar] [CrossRef]
- Hudáky, P.; Perczel, A. A self-stabilized model of the chymotrypsin catalytic pocket. The energy profile of the overall catalytic cycle. Proteins Struct. Funct. Bioinf. 2006, 62, 749–759. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y. Serine protease acylation proceeds with a subtle re-orientation of the histidine ring at the tetrahedral intermediate. Chem. Commun. 2011, 47, 1577–1579. [Google Scholar] [CrossRef]
- Florián, J.; Warshel, A. Phosphate ester hydrolysis in aqueous solution: Associative versus dissociative mechanisms. J. Phys. Chem. B 1998, 102, 719–734. [Google Scholar] [CrossRef]
- Bernardi, F.; Bottoni, A.; de Vivo, M.; Garavelli, M.; Keserű, G.; Náray-Szabó, G. A hypothetical mechanism for HIV-1 integrase catalytic action: DFT modelling of a bio-mimetic environment. Chem. Phys. Lett. 2002, 362, 1–7. [Google Scholar] [CrossRef]
- Franzini, E.; Fantucci, P.; de Gioia, L. Density functional theory investigation of guanosine triphosphate models. Catalytic role of Mg2+ ions in phosphate ester hydrolysis. J. Mol. Catal. A 2003, 204, 409–417. [Google Scholar]
- Lahiri, S.D.; Zhang, G.; Dunaway-Mariano, D.; Allen, K.N. The pentacovalent phosphorus intermediate of a phosphoryl transfer reaction. Science 2003, 299, 2067–2071. [Google Scholar] [CrossRef]
- Blackburn, G.M.; Williams, N.H.; Gamblin, S.J.; Smerdon, S.J. The pentacovalent phosphorus intermediate of a phosphoryl transfer reaction. Science 2003, 301, 1184c. [Google Scholar] [CrossRef]
- Baxter, N.J.; Bowler, M.W.; Alizadeh, T.; Cliff, M.J.; Hounslow, A.M.; Wu, B.; Berkowitz, D.B.; Williams, N.H.; Blackburn, G.M.; Waltho, J.P. Atomic details of near-transition state conformers for enzyme phosphoryl transfer revealed by MgF3- rather than by phosphoranes. Proc. Natl. Acad. Sci. USA 2010, 107, 4555–4560. [Google Scholar] [CrossRef]
- Webster, C.E. High-energy intermediate or stable transition state analogue: Theoretical perspective of the active site and mechanism of β-phosphoglucomutase. J. Am. Chem. Soc. 2004, 126, 6840–6841. [Google Scholar] [CrossRef]
- Berente, I.; Beke, T.; Náray-Szabó, G. Quantum mechanical studies on the existence of a trigonal bipyramidal phosphorane intermediate in enzymatic phosphate ester hydrolysis. Theor. Chem. Acc. 2007, 118, 129–134. [Google Scholar] [CrossRef]
- Barabás, O.; Pongrácz, V.; Kovári, J.; Wilmanns, M.; Vértessy, B.G. Structural insights into the catalytic mechanism of phosphate ester hydrolysis by dUTPase. J. Biol. Chem. 2004, 279, 42907–42915. [Google Scholar]
- Ivanov, I.; Tainer, J.A.; McCammon, J.A. Unraveling the three-metal-ion catalytic mechanism of the DNA repair enzyme endonuclease IV. Proc. Natl. Acad. Sci. USA 2007, 104, 1465–1470. [Google Scholar] [CrossRef]
- Cavalli, A.; de Vivo, M.; Recanatini, M. Computational study of the phosphoryl transfer catalyzed by a cyclin-dependent kinase. Chem. Eur. J. 2007, 13, 8437–8444. [Google Scholar] [CrossRef]
- Smith, G.K.; Ke, Z.; Guo, H. Insights into the phosphoryl transfer mechanism of cyclin-dependent protein kinases from ab initio QM/MM free-energy studies. J. Phys. Chem. B 2011, 115, 13713–13722. [Google Scholar] [CrossRef]
- Kamerlin, S.C.L.; McKenna, C.E.; Goodman, M.F.; Warshel, A. A computational study of the hydrolysis of dGTP analogues with halomethylene-modified leaving groups in solution: Implications for the mechanism of DNA polymerases. Biochemistry 2009, 48, 5963–5971. [Google Scholar] [CrossRef]
- Wong, K.-Y.; Gao, J. Insight into the phosphodiesterase mechanism from combined QM/MM free energy simulations. FEBS J. 2011, 278, 2579–2595. [Google Scholar] [CrossRef]
- Lior-Hoffmann, L.; Wang, L.; Wang, S.; Geacintov, N.E.; Broyde, S.; Zhang, Y. Preferred WMSA catalytic mechanism of the nucleotidyl transfer reaction in human DNA polymerase κ elucidates error-free bypass of a bulky DNA lesion. Nucleic Acids Res. 2012, 40, 9193–9205. [Google Scholar] [CrossRef]
- Xu, D.; Guo, H. Ab initio QM/MM studies of the phosphoryl transfer reaction catalyzed by PEP Mutase suggest a dissociative metaphosphate transition state. J. Phys. Chem. B 2008, 112, 4102–4108. [Google Scholar] [CrossRef]
- Xu, D.; Guo, H.; Liu, Y.; York, D.M. Theoretical studies of dissociative phosphoryl transfer in interconversion of phosphoenolpyruvate to phosphonopyruvate: Solvent effects, thio effects, and implications for enzymatic reactions. J. Phys. Chem. B 2005, 109, 13827–13834. [Google Scholar] [CrossRef]
- De Vivo, M.; Dal Peraro, M.; Klein, M.L. Phosphodiester cleavage in ribonuclease H occurs via an associative two-metal-aided catalytic mechanism. J. Am. Chem. Soc. 2008, 130, 10955–10962. [Google Scholar] [CrossRef]
- Rosta, E.; Woodcock, H.L.; Brooks, B.R.; Hummer, G. Artificial reaction coordinate “Tunneling” in free-energy calculations: The catalytic reaction of RNase H. J. Comput. Chem. 2009, 30, 1634–1641. [Google Scholar] [CrossRef]
- Schlichting, I.; Reinstein, J. pH influences fluoride coordination number of the AIFx phosphoryl transfer transition state analog. Nat. Struct. Biol. 1999, 6, 721–723. [Google Scholar] [CrossRef]
- De Vivo, M.; Ensing, B.; Dal Peraro, M.; Gomez, G.A.; Christianson, D.W.; Klein, M.L. Proton shuttles and phosphatase activity in soluble epoxide hydrolase. J. Am. Chem. Soc. 2007, 129, 387–394. [Google Scholar] [CrossRef]
- Ram Prasad, B.; Plotnikov, N.V.; Warshel, A. Addressing open questions about phosphate hydrolysis pathways by careful free energy mapping. J. Phys. Chem. B 2013, 117, 153–163. [Google Scholar]
- Kamerlin, S.C.L.; Florián, J.; Warshel, A. Associative versus dissociative mechanisms of phosphate monoester hydrolysis: On the interpretation of activation entropies. ChemPhysChem 2008, 9, 1767–1773. [Google Scholar] [CrossRef]
- Finzel, B.C.; Poulos, T.L.; Kraut, J. Crystal structure of yeast cytochrome c peroxidase refined at 1.7 Å resolution. J. Biol. Chem. 1984, 269, 32759–32767. [Google Scholar]
- Poulos, T.L.; Edwards, S.L.; Wariishi, H.; Gold, M.H. Crystallographic Refinement of lignin peroxidase at 2 Å. J. Biol. Chem. 1993, 268, 4429–4440. [Google Scholar]
- Patterson, W.R.; Poulos, T.L.; Goodin, D.B. Identification of a porphyrin Pi cation radical in ascorbate peroxidase compound I. Biochemistry 1995, 34, 4342–4345. [Google Scholar] [CrossRef]
- Gajhede, M.; Schuller, D.J.; Henriksen, A.; Smith, A.T.; Poulos, T.L. Crystal structure of horseradish peroxidase C at 2.15 Å resolution. Nat. Struct. Biol. 1997, 4, 1032–1038. [Google Scholar] [CrossRef]
- Patterson, W.R.; Poulos, T.L. Crystal structure of recombinant pea cytosolic ascorbate peroxidase. Biochemistry 1995, 34, 4331–4341. [Google Scholar] [CrossRef]
- Menyhárd, D.K.; Náray-Szabó, G. Electrostatic effect on electron transfer at the active site of heme peroxidases: A comparative molecular orbital study on Cytochrome C peroxidase and ascorbate peroxidase. J. Phys. Chem. B 1999, 103, 227–233. [Google Scholar] [CrossRef]
- Jensen, G.M.; Bunte, S.W.; Warshel, A.; Goodin, D.B. Energetics of cation radical formation at the proximal active site tryptophan of cytochrome c peroxidase and ascorbate peroxidase. J. Phys. Chem. 1998, 102, 8221–8228. [Google Scholar]
- Wirstam, M.; Blomberg, M.R.A.; Siegbahn, P.E.M. Reaction mechanism of compound i formation in heme peroxidases: A density functional theory study. J. Am. Chem. Soc. 1999, 121, 10178–10185. [Google Scholar] [CrossRef]
- Hiner, A.N.; Martínez, J.I.; Arnao, M.B.; Acosta, M.; Turner, D.D.; Lloyd Raven, E.; Rodríguez-López, J.N. Detection of a tryptophan radical in the reaction of ascorbate peroxidase with hydrogen peroxide. Eur. J. Biochem. 2001, 268, 3091–3098. [Google Scholar] [CrossRef]
- Heimdal, J.; Rydberg, P.; Ryde, U. Protonation of the proximal histidine ligand in heme peroxidases. J. Phys. Chem. B 2008, 112, 2501–2510. [Google Scholar] [CrossRef]
- De Visser, S.P. What affects the quartet-doublet energy splitting in peroxidase enzymes? J. Phys. Chem. A 2005, 109, 11050–11057. [Google Scholar] [CrossRef]
- Bathelt, C.M.; Mulholland, A.J.; Harvey, J.N. QM/MM studies of the electronic structure of the compound I intermediate in cytochrome c peroxidase and ascorbate peroxidase. J. Chem. Soc. Dalton Trans. 2005, 3470–3476. [Google Scholar]
- Derat, E.; Cohen, S.; Shaik, S.; Altun, A.; Thiel, W. Principal active species of horseradish peroxidase compound I: A hybrid quantum mechanical/molecular mechanical study. J. Am. Chem. Soc. 2005, 127, 13611–13621. [Google Scholar] [CrossRef]
- Jensen, K.P.; Ryde, U. Importance of proximal hydrogen bonds in haem proteins. Mol. Phys. 2003, 101, 2003–2018. [Google Scholar] [CrossRef]
- Guallar, V.; Wallrapp, F.H. QM/MM methods: Looking inside heme proteins biochemisty. Biophys. Chem. 2010, 149, 1–11. [Google Scholar] [CrossRef]
- Vlasitsa, J.; Jakopitscha, C.; Bernroitnera, M.; Zamockya, M.; Furtmüllera, P.G.; Obingera, C. Mechanisms of catalase activity of heme peroxidases. Arch. Biochem. Biophys. 2010, 500, 74–81. [Google Scholar] [CrossRef]
- Harris, D.L.; Loew, G.H. Proximal ligand effects on electronic structure and spectra of compound I of peroxidases. J. Porphyr. Phthalocyanins 2001, 5, 334–344. [Google Scholar] [CrossRef]
- Nelson, D.R.; Goldstone, J.V.; Stegeman, J.J. The cytochrome P450 genesis locus: The origin and evolution of animal cytochrome P450s. Phil. Trans. R. Soc. B 2013, 368, 20120474. [Google Scholar] [CrossRef]
- Guengerich, F.P. Chapter 10 (6.45). In Cytochrome P450: Structure, Mechanism, and Biochemistry, 2nd ed.; Ortiz de Montellano, P.R., Ed.; Plenum Press: New York, NY, USA, 1995; pp. 450–452. [Google Scholar]
- Shaik, S.; Kumar, D.; de Visser, S.P.; Altun, A.; Thiel, W. Theoretical perspective on the structure and mechanism of cytochrome P450 enzymes. Chem. Rev. 2005, 105, 2279–2328. [Google Scholar] [CrossRef]
- Rittle, J.; Green, M.T. Cytochrome P450 Compound I: Capture, characterization, and C-H Bond activation kinetics. Science 2010, 330, 933–937. [Google Scholar] [CrossRef]
- De Visser, S.P.; Ogliaro, F.; Sharma, P.K.; Shaik, S. Hydrogen bonding modulates the selectivity of enzymatic oxidation by P450: A chameleon oxidant behavior by compound I. Angew. Chem. Int. Ed. 2002, 41, 1947–1951. [Google Scholar] [CrossRef]
- De Visser, S.P.; Ogliaro, F.; Sharma, P.K.; Shaik, S. What factors affect the regioselectivity of oxidation by cytochrome p450? A DFT study of allylic hydroxylation and double bond epoxidation in a model reaction. J. Am. Chem. Soc. 2002, 124, 11809–11826. [Google Scholar] [CrossRef]
- Ogliaro, F.; Cohen, S.; de Visser, S.P.; Shaik, S. Medium polarization and hydrogen bonding effects on compound I of cytochrome P450: What kind of a radical it really is? J. Am. Chem. Soc. 2000, 122, 12892–12893. [Google Scholar] [CrossRef]
- Lonsdale, R.; Oláh, J.; Mulholland, A.J.; Harvey, J.N. Does compound I vary significantly between isoforms of cytochrome P450? J. Am. Chem. Soc. 2011, 133, 15464–15474. [Google Scholar] [CrossRef]
- Schmider, J.; Greenblatt, D.J.; Fogelman, S.M.; von Moltke, L.L.; Shader, R.I. Metabolism of dextromethorphan in vitro: Involvement of cytochromes P450 2D6 and 3A3/4, with a possible role of 2E1. Biopharm. Drug. Dispos. 1997, 18, 227–240. [Google Scholar] [CrossRef]
- Daly, J. Metabolism of acetanilides and anisoles with rat liver microsomes. Biochem. Pharmacol. 1970, 19, 2979–2993. [Google Scholar] [CrossRef]
- Bray, H.G.; James, S.P.; Thorpe, W.V.; Wasdell, M.R. The metabolism of ethers in the rabbit. 1. anisole and diphenyl ether. Biochem. J. 1953, 54, 547–551. [Google Scholar]
- Olsen, L.; Rydberg, P.; Rod, T.H.; Ryde, U. Prediction of activation energies for hydrogen abstraction by cytochrome P450. J. Med. Chem. 2006, 49, 6489–6499. [Google Scholar] [CrossRef]
- Oláh, J.; Mulholland, A.J.; Harvey, J.N. Determinants of selectivity in drug metabolism by cytochrome P450: QM/MM modeling of dextromethorphan oxidation by CYP2D6. Proc. Natl. Acad. Sci. USA 2011, 108, 6050–6055. [Google Scholar]
- Ingelman-Sundberg, M. Genetic polymorphisms of cytochrome P450 2D6 (CYP2D6): Clinical consequences, evolutionary aspects and functional diversity. Pharmacogenomics J. 2005, 5, 6–13. [Google Scholar] [CrossRef]
- Rowland, P.; Blaney, F.E.; Smyth, M.G.; Jones, J.J.; Leydon, V.R.; Oxbrow, A.K.; Lewis, C.J.; Tennant, M.G.; Modi, S.; Eggleston, D.S.; et al. Crystal structure of human cytochrome P450 2D6. J. Biol. Chem. 2006, 281, 7614–7622. [Google Scholar] [CrossRef]
- McLaughlin, L.A.; Paine, M.J.I.; Kemp, C.A.; Maréchal, J.D.; Flanagan, J.U.; Ward, R.; Sutcliffe, M.J.; Roberts, G.C.K.; Wolf, C.R. Why is quinidine an inhibitor of cytochrome P450 2D6? The role of key active-site residues in quinidine binding. J. Biol. Chem. 2005, 280, 38617–38624. [Google Scholar] [CrossRef]
- Flanagan, J.U.; Maréchal, J.D.; Ward, R.; Kemp, C.A.; McLaughlin, L.A.; Sutcliffe, M.J.; Roberts, G.C.K.; Paine, M.J.I.; Wolf, C.R. Phe120 contributes to the regiospecificity of cytochrome P450 2D6: Mutation leads to the formation of a novel dextromethorphan. Biochem. J. 2004, 380, 353–360. [Google Scholar] [CrossRef]
- Lonsdale, R.; Houghton, K.T.; Żurek, J.; Bathelt, C.M.; Foloppe, N.; de Groot, M.J.; Harvey, J.N.; Mulholland, A.J. Quantum mechanics/molecular mechanics modeling of regioselectivity of drug metabolism in cytochrome P450 2C9. J. Am. Chem. Soc. 2013, 135, 8001–8015. [Google Scholar] [CrossRef]
- Zhang, L.; Kudo, T.; Takaya, N.; Shoun, H. The B′ helix determines cytochrome P450nor specificity for the electron donors NADH and NADPH. J. Biol. Chem. 2002, 277, 33842–33847. [Google Scholar]
- De Vries, S.; Schröder, I. Comparison between the nitric oxide reductase family and its aerobic relatives, the cytochrome oxidases. Biochem. Soc. Trans. 2002, 30, 662–667. [Google Scholar]
- Richardson, D.; Felgate, H.; Watmough, N.; Thomson, A.; Baggs, E. Mitigating release of the potent greenhouse gas N(2)O from the nitrogen cycle - could enzymic regulation hold the key? Trends Biotechnol. 2009, 27, 388–397. [Google Scholar] [CrossRef]
- Wink, D.A.; Hines, H.B.; Cheng, R.Y.S.; Switzer, C.H.; Flores-Santana, W.; Vitek, M.P.; Ridnour, L.A.; Colton, C.A.J. Nitric oxide and redox mechanisms in the immune response. Leukocyte Biol. 2011, 89, 873–891. [Google Scholar] [CrossRef]
- Chao, L.Y.; Rine, J.; Marletta, M.A. Spectroscopic and kinetic studies of nor1, a cytochrome p450 nitric oxide reductase from the fungal pathogen Histoplasma capsulatum. Arch. Biochem. Biophys. 2008, 480, 132–137. [Google Scholar] [CrossRef]
- Shiro, Y.; Fujii, M.; Iizuka, T.; Adachi, S.; Tsukamoto, K.; Nakahara, K.; Shoun, H. Spectroscopic and kinetic studies on reaction of cytochrome P450nor with nitric oxide. Implication for its nitric oxide reduction mechanism. J. Biol. Chem. 1995, 270, 1617–1623. [Google Scholar]
- Harris, D.L. Cytochrome P450nor: A nitric oxide reductase - structure, spectra, and mechanism. Int. J. Quantum Chem. 2002, 288, 183–200. [Google Scholar] [CrossRef]
- Tsukamoto, K.; Nakamura, S.; Shimizu, K. SAM1 semiempirical calculations on the catalytic cycle of nitric oxide reductase from Fusarium oxysporum. J. Mol. Struct. (THEOCHEM) 2003, 624, 309–322. [Google Scholar] [CrossRef]
- Averill, B.A. Dissimilatory nitrite and nitric oxide reductases. Chem. Rev. 1996, 96, 2951–2964. [Google Scholar] [CrossRef]
- Daiber, A.; Nauser, T.; Takaya, N.; Kudo, T.; Weber, P.; Hultschig, C.; Shoun, H.; Ullrich, V. Isotope effects and intermediates in the reduction of NO by P450NOR. J. Inorg. Biochem. 2002, 88, 343–352. [Google Scholar] [CrossRef]
- Lehnert, N.; Praneeth, V.K.K.; Paulat, F. Electronic structure of Fe(II)-porphyrin nitroxyl complexes: Molecular mechanism of fungal nitric oxide reductase (P450nor). J. Comput. Chem. 2006, 27, 1338–1351. [Google Scholar] [CrossRef]
- Krámos, B.; Menyhárd, D.K.; Oláh, J. Direct hydride shift mechanism and stereoselectivity of P450nor confirmed by QM/MM calculations. J. Phys. Chem. B 2012, 116, 872–885. [Google Scholar] [CrossRef]
- Suzuki, N.; Higuchi, T.; Urano, Y.; Kikuchi, K.; Uchida, T.; Mukai, M.; Kitagawa, T.; Nagano, T. First synthetic no-heme-thiolate complex relevant to nitric oxide synthase and cytochrome P450nor. J. Am. Chem. Soc. 2000, 122, 12059–12060. [Google Scholar] [CrossRef]
- Shimizu, H.; Obayashi, E.; Gomi, Y.; Arakawa, H.; Park, S.Y.; Nakamura, H.; Adachi, S.; Shoun, H.; Shiro, Y. Proton delivery in no reduction by fungal nitric-oxide reductase. cryogenic crystallography, spectroscopy, and kinetics of ferric-no complexes of wild-type and mutant enzymes. J. Biol. Chem. 2000, 275, 4816–4826. [Google Scholar] [CrossRef]
- Menyhárd, D.K.; Keserű, G.M. Binding mode analysis of the NADH cofactor in nitric oxide reductase: A theoretical study. J. Mol. Graphics Model. 2006, 25, 363–372. [Google Scholar] [CrossRef]
- Oshima, R.; Fushinobu, S.; Su, F.; Zhang, L.; Takaya, N.; Shoun, H. Structural evidence for direct hydride transfer from NADH to cytochrome P450nor. J. Mol. Biol. 2004, 342, 207–217. [Google Scholar] [CrossRef]
- Riplinger, C.; Neese, F. The reaction mechanism of cytochrome P450 NO reductase: A detailed quantum mechanics/molecular mechanics study. ChemPhysChem 2011, 12, 3192–3203. [Google Scholar] [CrossRef]
- Callens, M.; Tomme, P.; Kerstens-Hilderson, H.; Cornelis, W.; Vangrysperre, W.; de Bruyne, C.K. Metal ion binding to d-xylose isomerase from streptomyces violaceoruber. Biochem. J. 1988, 250, 285–291. [Google Scholar]
- Farber, G.K.; Machin, P.; Almo, S.C.; Petsko, G.A.; Hajdu, J. X-ray laue diffraction from crystals of xylose isomerase. Proc. Natl. Acad. Sci. USA 1988, 85, 112–118. [Google Scholar] [CrossRef]
- Collyer, C.A.; Henrick, K.; Blow, D.M. Mechanism for aldose-ketose interconversion by D-Xylose isomerase involving ring opening followed by a 1,2-hydride shift. J. Mol. Biol. 1990, 212, 211–235. [Google Scholar] [CrossRef]
- Jenkins, J.; Janin, J.; Rey, F.; Chidmi, M.; Tilbeurgh, H.; Lasters, I.; Maeyer, M.; Belle, D.; Wodak, S.; Lauwereys, M.; et al. Protein engineering of xylose (Glucose) isomerase from actinoplanes missouriensis. 1. Crystallography and site-directed mutagenesis of metal binding sites. Biochemistry 1992, 31, 5449–5458. [Google Scholar] [CrossRef]
- Hu, H.; Liu, H.; Shi, Y. The reaction pathway of the isomerization of d-xylose catalyzed by the enzyme d-xylose isomerase: A theoretical study. Proteins Struct. Funct. Genet. 1997, 27, 545–555. [Google Scholar] [CrossRef]
- Fuxreiter, M.; Farkas, Ö.; Náray-Szabó, G. Molecular modeling of xylose isomerase catalysis: The role of electrostatics and charge transfer to metals. Protein Eng. 1995, 8, 925–933. [Google Scholar] [CrossRef]
- Fábián, P.; Asbóth, B.; Náray-Szabó, G. The role of electrostatics in the ring-opening step of xylose isomerase catalysis. J. Mol. Struct. Theochem. 1994, 307, 171–178. [Google Scholar] [CrossRef]
- Lambeir, A.M.; Lauwereys, M.; Stanssens, P.; Mrabet, N.T.; Snauwaert, J.; van Tilbeurgh, H.; Matthyssens, G.; Lasters, I.; de Maeyer, M.; Wodak, S.J.; et al. Protein engineering of xylose (glucose) isomerase from actinoplanes missouriensis. 3. Changing metal specificity and the PH profile by site-directed mutagenesis. Biochemistry 1992, 31, 5459–5466. [Google Scholar] [CrossRef]
- Garcia-Viloca, M.; Alhambra, C.; Truhlar, D.G.; Gao, J. Quantum dynamics of hydride transfer catalyzed by bimetallic electrophilic catalysis: Synchronous motion of Mg2+ and H- in xylose isomerase. J. Am. Chem. Soc. 2002, 124, 7268–7269. [Google Scholar] [CrossRef]
- Garcia-Viloca, M.; Alhambra, C.; Truhlar, D.G.; Gao, J. Hydride transfer catalyzed by xylose isomerase: Mechanism and quantum effects. J. Comput. Chem. 2003, 24, 177–190. [Google Scholar] [CrossRef]
- Masgrau, L.; Roujeinikova, A.; Johannissen, L.O.; Hothi, P.; Basran, J.; Ranaghan, K.E.; Mulholland, A.J.; Sutcliffe, M.J.; Scrutton, N.S.; Leys, D. Atomic description of an enzyme reaction dominated by proton tunneling. Science 2006, 312, 237–241. [Google Scholar] [CrossRef]
- Iyengar, S.S.; Sumner, I.; Jakowski, J. Hydrogen tunneling in an enzyme active site: A quantum wavepacket dynamical perspective. J. Phys. Chem. B 2008, 112, 7601–7613. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Náray-Szabó, G.; Oláh, J.; Krámos, B. Quantum Mechanical Modeling: A Tool for the Understanding of Enzyme Reactions. Biomolecules 2013, 3, 662-702. https://doi.org/10.3390/biom3030662
Náray-Szabó G, Oláh J, Krámos B. Quantum Mechanical Modeling: A Tool for the Understanding of Enzyme Reactions. Biomolecules. 2013; 3(3):662-702. https://doi.org/10.3390/biom3030662
Chicago/Turabian StyleNáray-Szabó, Gábor, Julianna Oláh, and Balázs Krámos. 2013. "Quantum Mechanical Modeling: A Tool for the Understanding of Enzyme Reactions" Biomolecules 3, no. 3: 662-702. https://doi.org/10.3390/biom3030662
APA StyleNáray-Szabó, G., Oláh, J., & Krámos, B. (2013). Quantum Mechanical Modeling: A Tool for the Understanding of Enzyme Reactions. Biomolecules, 3(3), 662-702. https://doi.org/10.3390/biom3030662