Current-Perpendicular-to-Plane Magnetoresistance in Chemical Vapor Deposition-Grown Multilayer Graphene
Abstract
:1. Introduction
2. Experimental Section

2.1. Growth of Multilayer Graphene (MLG) on Ni and Cu Substrates Using CVD
2.2. Oxygen Plasma Etching of MLG and Device Patterning
2.3. Transfer of MLG on SiO2/Si
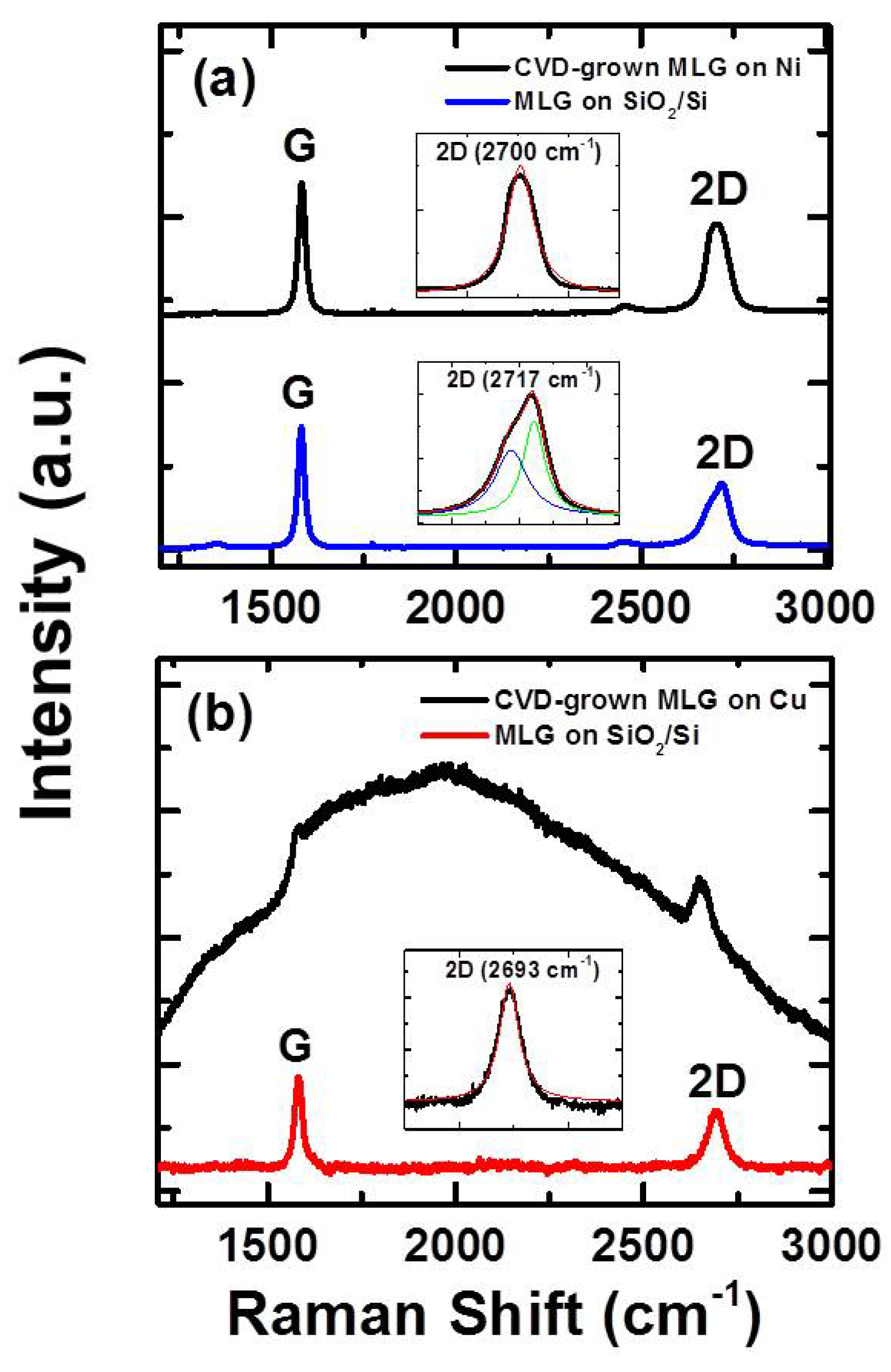
3. Results and Discussion
 I (i.e., θ = π/2).
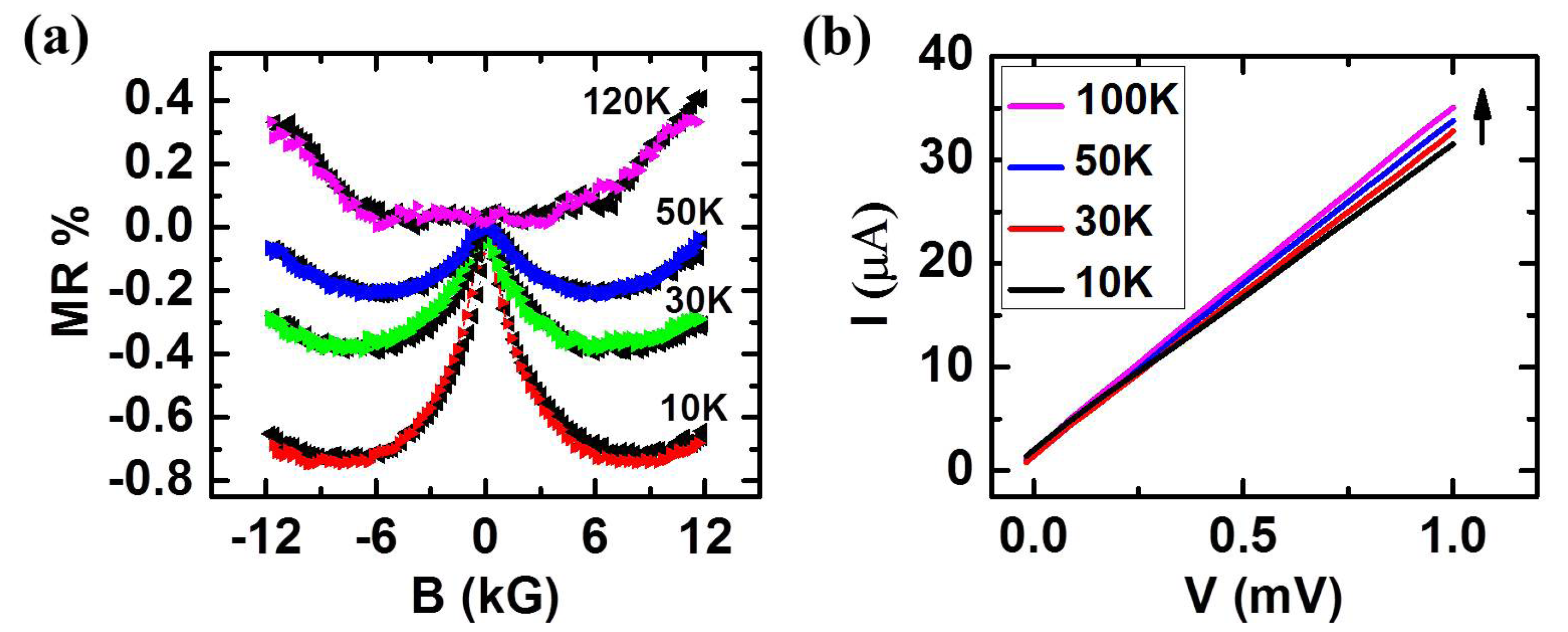
I (i.e., θ = π/2). geometry (i.e., “field-in-plane” or θ = π/2), a weak, positive MR is observed (insets of Figure 3a–d), which gradually disappears as the temperature increases. This positive MR has been observed before and is the result of the bending of carrier trajectories, due to classical Lorentz force [20]. Surprisingly, in B || I geometry (i.e., “field normal to the plane” or θ = 0), a sharp decrease in resistance (a factor of three) at around 3 kG is observed as the magnetic field is increased. Such a large change in resistance cannot be explained by semiclassical models, since the Lorentz force on charge carriers is zero in B || I geometry. Both scan directions up to ±1 Tesla are presented to demonstrate the reproducibility of the data and the absence of any hysteresis. We note from the MR data of several nominally identical samples that the observed effect is almost independent of temperature, which sometimes even persists at room temperature. The room temperature MR data from another sample is shown in Figure 3e. The change in resistance is large, around 3 kG, which has been observed in several nominally identical samples (~20) at a similar temperature range. A maximum of a two orders of magnitude change in negative MR has been observed in some of the samples. No hysteretic MR has been observed in any of the samples.
geometry (i.e., “field-in-plane” or θ = π/2), a weak, positive MR is observed (insets of Figure 3a–d), which gradually disappears as the temperature increases. This positive MR has been observed before and is the result of the bending of carrier trajectories, due to classical Lorentz force [20]. Surprisingly, in B || I geometry (i.e., “field normal to the plane” or θ = 0), a sharp decrease in resistance (a factor of three) at around 3 kG is observed as the magnetic field is increased. Such a large change in resistance cannot be explained by semiclassical models, since the Lorentz force on charge carriers is zero in B || I geometry. Both scan directions up to ±1 Tesla are presented to demonstrate the reproducibility of the data and the absence of any hysteresis. We note from the MR data of several nominally identical samples that the observed effect is almost independent of temperature, which sometimes even persists at room temperature. The room temperature MR data from another sample is shown in Figure 3e. The change in resistance is large, around 3 kG, which has been observed in several nominally identical samples (~20) at a similar temperature range. A maximum of a two orders of magnitude change in negative MR has been observed in some of the samples. No hysteretic MR has been observed in any of the samples.  I) is shown. The left inset in (d) shows the temperature dependence of CPP resistance at zero and high magnetic fields; (e) room temperature large, negative MR data observed in another MLG on Ni sample; (f) Rzz vs. B for Ni-grown MLG after transferring on the Cu substrate. No negative MR is observed. (Inset) Optical microscopic image of MLG transferred on the Cu substrate. A constant current bias of 1 mA is applied for all resistance measurements. Each resistance value is an average of 50 readings. Both scan directions are presented, and no MR hysteresis is observed.
I) is shown. The left inset in (d) shows the temperature dependence of CPP resistance at zero and high magnetic fields; (e) room temperature large, negative MR data observed in another MLG on Ni sample; (f) Rzz vs. B for Ni-grown MLG after transferring on the Cu substrate. No negative MR is observed. (Inset) Optical microscopic image of MLG transferred on the Cu substrate. A constant current bias of 1 mA is applied for all resistance measurements. Each resistance value is an average of 50 readings. Both scan directions are presented, and no MR hysteresis is observed.
 I) is shown. The left inset in (d) shows the temperature dependence of CPP resistance at zero and high magnetic fields; (e) room temperature large, negative MR data observed in another MLG on Ni sample; (f) Rzz vs. B for Ni-grown MLG after transferring on the Cu substrate. No negative MR is observed. (Inset) Optical microscopic image of MLG transferred on the Cu substrate. A constant current bias of 1 mA is applied for all resistance measurements. Each resistance value is an average of 50 readings. Both scan directions are presented, and no MR hysteresis is observed.
I) is shown. The left inset in (d) shows the temperature dependence of CPP resistance at zero and high magnetic fields; (e) room temperature large, negative MR data observed in another MLG on Ni sample; (f) Rzz vs. B for Ni-grown MLG after transferring on the Cu substrate. No negative MR is observed. (Inset) Optical microscopic image of MLG transferred on the Cu substrate. A constant current bias of 1 mA is applied for all resistance measurements. Each resistance value is an average of 50 readings. Both scan directions are presented, and no MR hysteresis is observed. 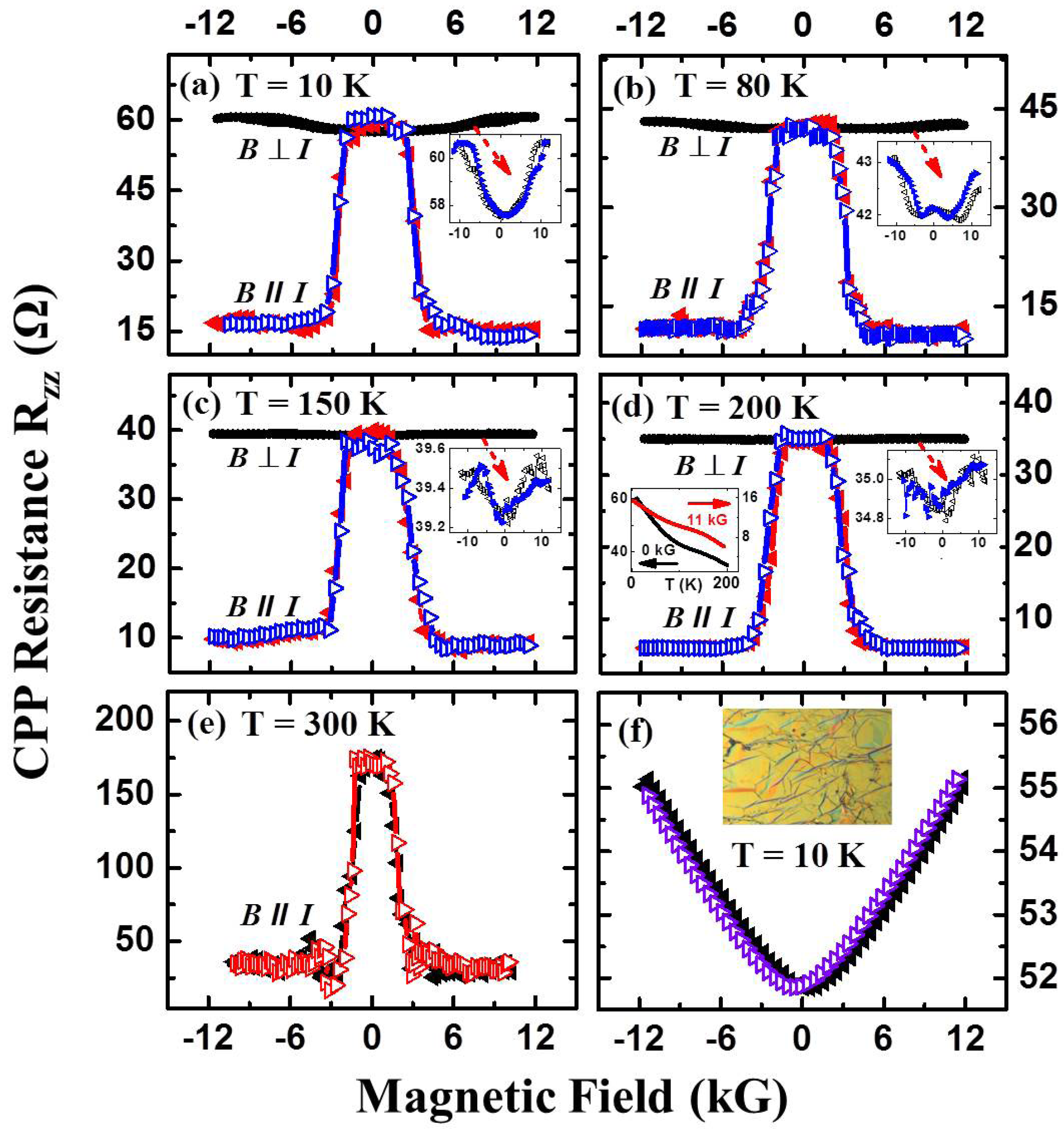
4. Conclusions
Appendix
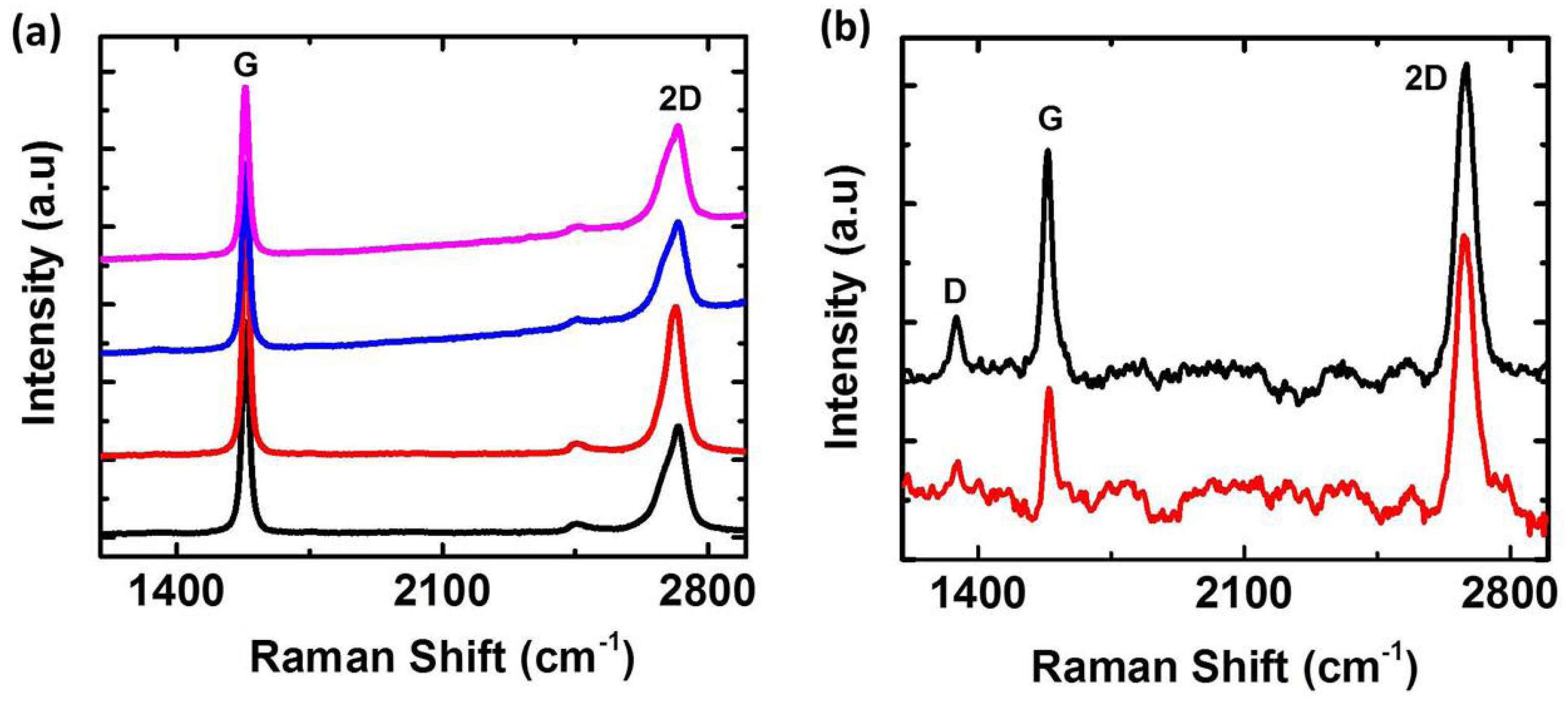
I. Raman Spectroscopic Characterization of Grain Boundaries of CVD-grown Multilayer Graphene (MLG)
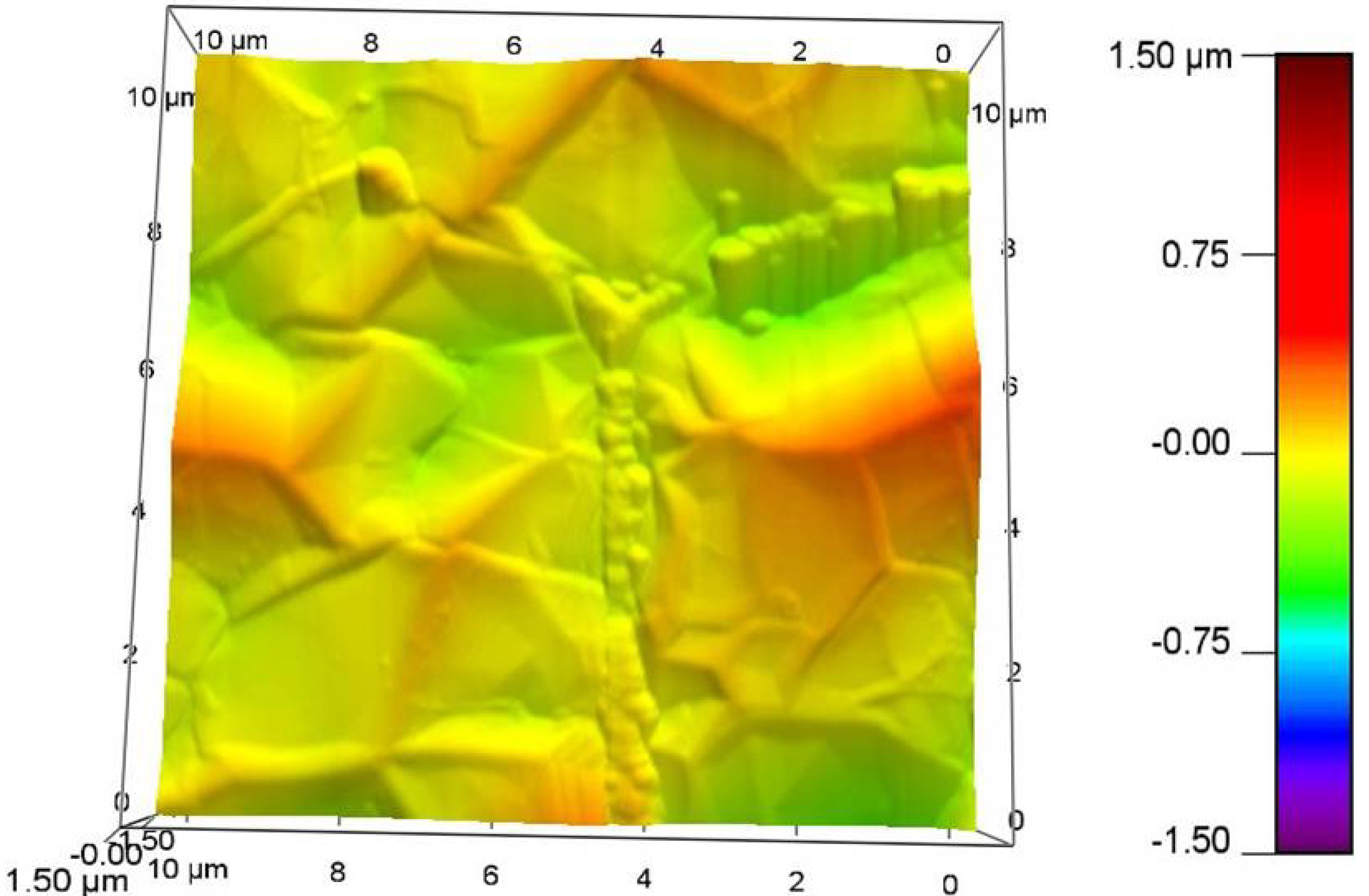
II. AFM Image of Multilayer Graphene on Ni Foil
Conflicts of Interest
References
- Nickel, J. Magnetoresistance Overview; Hewlett-Packard Laboratories, Technical Publications Department: Palo Alto, CA, USA, 1995. [Google Scholar]
- Chappert, C.; Fert, A.; Dau, F.N.V. The emergence of spin electronics in data storage. Nat. Mater. 2007, 6, 813–823. [Google Scholar] [CrossRef]
- McGuire, T.; Potter, R. Anisotropic magnetoresistance in ferromagnetic 3d alloys. IEEE Trans. Magn. 1975, 11, 1018–1038. [Google Scholar]
- Bergmann, G. Weak localization in thin films: A time-of-flight experiment with conduction electrons. Phys. Rep. 1984, 107, 1–58. [Google Scholar]
- Wan, C.; Zhang, X.; Gao, X.; Wang, J.; Tan, X. Geometrical enhancement of low-field magnetoresistance in silicon. Nature 2011, 477, 304–307. [Google Scholar]
- Francis, T.L.; Mermer, Ö.; Veeraraghavan, G.; Wohlgenannt, M. Large magnetoresistance at room temperature in semiconducting polymer sandwich devices. New J. Phys. 2004, 6, 185–185. [Google Scholar]
- Ramirez, A.P. Colossal magnetoresistance. J. Phys. Condens. Matter 1997, 9, 8171–8199. [Google Scholar]
- Biskupski, G. Positive and negative magnetoresistance in the variable-range-hopping regime of doped semiconductors. Philos. Mag. Part B 1992, 65, 723–728. [Google Scholar]
- Novoselov, K.S.; Jiang, Z.; Zhang, Y.; Morozov, S.V.; Stormer, H.L.; Zeitler, U.; Maan, J.C.; Boebinger, G.S.; Kim, P.; Geim, A.K. Room-temperature quantum hall effect in graphene. Science 2007, 315, 1379–1379. [Google Scholar] [CrossRef] [Green Version]
- Dean, C.R.; Young, A.F.; Cadden-Zimansky, P.; Wang, L.; Ren, H.; Watanabe, K.; Taniguchi, T.; Kim, P.; Hone, J.; Shepard, K.L. Multicomponent fractional quantum hall effect in graphene. Nat. Phys. 2011, 7, 693–696. [Google Scholar]
- Kempa, H.; Esquinazi, P.; Kopelevich, Y. Field-induced metal-insulator transition in the c-axis resistivity of graphite. Phys. Rev. B 2002, 65, 241101. [Google Scholar] [CrossRef]
- Zhi-Ming, W.; Ding-Yu, X.; Shi-Yuan, Z.; Qing-Yu, X.; VanBael, M.; You-Wei, D. Magnetic-field-induced semimetal-insulator-like transition in highly oriented pyrolitic graphite. Chin. Phys. Lett. 2007, 24, 199–202. [Google Scholar] [CrossRef]
- Khveshchenko, D.V. Magnetic-field-induced insulating behavior in highly oriented pyrolitic graphite. Phys. Rev. Lett. 2001, 87, 206401. [Google Scholar] [CrossRef]
- Khveshchenko, D.V. Ghost excitonic insulator transition in layered graphite. Phys. Rev. Lett. 2001, 87, 246802. [Google Scholar] [CrossRef]
- Kempa, H.; Semmelhack, H.; Esquinazi, P.; Kopelevich, Y. Absence of metal-insulator transition and coherent interlayer transport in oriented graphite in parallel magnetic fields. Solid State Commun. 2003, 125, 1–5. [Google Scholar] [CrossRef]
- Liu, Y.; Lew, W.S.; Sun, L. Enhanced weak localization effect in few-layer graphene. Phys. Chem. Chem. Phys. 2011, 13, 20208. [Google Scholar] [CrossRef]
- Wu, X.; Li, X.; Song, Z.; Berger, C.; de Heer, W.A. Weak Antilocalization in epitaxial graphene: Evidence for chiral electrons. Phys. Rev. Lett. 2007, 98, 136801. [Google Scholar] [CrossRef]
- Tikhonenko, F.V.; Kozikov, A.A.; Savchenko, A.K.; Gorbachev, R.V. Transition between electron localization and antilocalization in graphene. Phys. Rev. Lett. 2009, 103, 226801. [Google Scholar] [CrossRef]
- Matis, B.R.; Bulat, F.A.; Friedman, A.L.; Houston, B.H.; Baldwin, J.W. Giant negative magnetoresistance and a transition from strong to weak localization in hydrogenated graphene. Phys. Rev. B 2012, 85, 195437. [Google Scholar]
- Liao, Z.-M.; Wu, H.-C.; Kumar, S.; Duesberg, G.S.; Zhou, Y.-B.; Cross, G.L.W.; Shvets, I.V.; Yu, D.-P. Large magnetoresistance in few layer graphene stacks with current perpendicular to plane geometry. Adv. Mater. 2012, 24, 1862–1866. [Google Scholar] [CrossRef]
- Friedman, A.L.; Tedesco, J.L.; Campbell, P.M.; Culbertson, J.C.; Aifer, E.; Perkins, F.K.; Myers-Ward, R.L.; Hite, J.K.; Eddy, C.R.; Jernigan, G.G.; et al. Quantum linear magnetoresistance in multilayer epitaxial graphene. Nano Lett. 2010, 10, 3962–3965. [Google Scholar] [CrossRef]
- Cobas, E.; Friedman, A.L.; van’t Erve, O.M.J.; Robinson, J.T.; Jonker, B.T. Graphene as a tunnel barrier: Graphene-based magnetic tunnel junctions. Nano Lett. 2012, 12, 3000–3004. [Google Scholar] [CrossRef]
- Van’t Erve, O.M.J.; Friedman, A.L.; Cobas, E.; Li, C.H.; Robinson, J.T.; Jonker, B.T. Low-resistance spin injection into silicon using graphene tunnel barriers. Nat. Nanotechnol. 2012, 7, 737–742. [Google Scholar]
- Schmidt, G.; Molenkamp, L.W. Spin injection into semiconductors, physics and experiments. Semicond. Sci. Technol. 2002, 17, 310–321. [Google Scholar] [CrossRef]
- Dlubak, B.; Martin, M.-B.; Weatherup, R.S.; Yang, H.; Deranlot, C.; Blume, R.; Schloegl, R.; Fert, A.; Anane, A.; Hofmann, S.; et al. Graphene-passivated nickel as an oxidation-resistant electrode for spintronics. ACS Nano 2012, 6, 10930–10934. [Google Scholar]
- Friedman, A.L.; Robinson, J.T.; Perkins, F.K.; Campbell, P.M. Extraordinary magnetoresistance in shunted chemical vapor deposition grown graphene devices. Appl. Phys. Lett. 2011, 99, 022108:1–022108:3. [Google Scholar]
- Karpan, V.M.; Giovannetti, G.; Khomyakov, P.A.; Talanana, M.; Starikov, A.A.; Zwierzycki, M.; van den Brink, J.; Brocks, G.; Kelly, P.J. Graphite and graphene as perfect spin filters. Phys. Rev. Lett. 2007, 99, 176602. [Google Scholar] [CrossRef]
- Karpan, V.M.; Khomyakov, P.A.; Starikov, A.A.; Giovannetti, G.; Zwierzycki, M.; Talanana, M.; Brocks, G.; van den Brink, J.; Kelly, P.J. Theoretical prediction of perfect spin filtering at interfaces between close-packed surfaces of Ni or Co and graphite or graphene. Phys. Rev. B 2008, 78, 195419. [Google Scholar] [CrossRef]
- Dedkov, Y.S.; Fonin, M.; Rüdiger, U.; Laubschat, C. Rashba effect in the graphene/Ni(111) system. Phys. Rev. Lett. 2008, 100, 107602. [Google Scholar] [CrossRef]
- Wintterlin, J.; Bocquet, M.-L. Graphene on metal surfaces. Surf. Sci. 2009, 603, 1841–1852. [Google Scholar] [CrossRef]
- Gong, C.; Lee, G.; Shan, B.; Vogel, E.M.; Wallace, R.M.; Cho, K. First-principles study of metal-graphene interfaces. J. Appl. Phys. 2010, 108, 123711:1–123711:8. [Google Scholar]
- Giovannetti, G.; Khomyakov, P.A.; Brocks, G.; Karpan, V.M.; van den Brink, J.; Kelly, P.J. Doping graphene with metal contacts. Phys. Rev. Lett. 2008, 101, 026803. [Google Scholar] [CrossRef]
- Xu, Z.; Buehler, M.J. Interface structure and mechanics between graphene and metal substrates: A first-principles study. J. Phys. Condens. Matter 2010, 22, 485301. [Google Scholar] [CrossRef]
- Nouchi, R.; Shiraishi, M.; Suzuki, Y. Transfer characteristics in graphene field-effect transistors with Co contacts. Appl. Phys. Lett. 2008, 93, 152104:1–152104:3. [Google Scholar]
- Park, N.; Kim, B.-K.; Lee, J.-O.; Kim, J.-J. Influence of metal work function on the position of the Dirac point of graphene field-effect transistors. Appl. Phys. Lett. 2009, 95, 243105:1–243105:3. [Google Scholar]
- Zhang, Y.; Gomez, L.; Ishikawa, F.N.; Madaria, A.; Ryu, K.; Wang, C.; Badmaev, A.; Zhou, C. Comparison of graphene growth on single-crystalline and polycrystalline Ni by chemical vapor deposition. J. Phys. Chem. Lett. 2010, 1, 3101–3107. [Google Scholar] [CrossRef]
- Yu, Q.; Lian, J.; Siriponglert, S.; Li, H.; Chen, Y.P.; Pei, S.-S. Graphene segregated on Ni surfaces and transferred to insulators. Appl. Phys. Lett. 2008, 93, 113103:1–113103:3. [Google Scholar]
- Reina, A.; Jia, X.; Ho, J.; Nezich, D.; Son, H.; Bulovic, V.; Dresselhaus, M.S.; Kong, J. Large area, few-layer graphene films on arbitrary substrates by chemical vapor deposition. Nano Lett. 2008, 9, 30–35. [Google Scholar]
- Kim, K.S.; Zhao, Y.; Jang, H.; Lee, S.Y.; Kim, J.M.; Kim, K.S.; Ahn, J.-H.; Kim, P.; Choi, J.-Y.; Hong, B.H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710. [Google Scholar] [CrossRef]
- Dzemiantsova, L.V.; Karolak, M.; Lofink, F.; Kubetzka, A.; Sachs, B.; von Bergmann, K.; Hankemeier, S.; Wehling, T.O.; Frömter, R.; Oepen, H.P.; Lichtenstein, A.I.; Wiesendanger, R. Multiscale magnetic study of Ni(111) and graphene on Ni(111). Phys. Rev. B 2011, 84, 205431. [Google Scholar] [CrossRef]
- Gong, S.J.; Li, Z.Y.; Yang, Z.Q.; Gong, C.; Duan, C.-G.; Chu, J.H. Spintronic properties of graphene films grown on Ni(111) substrate. J. Appl. Phys. 2011, 110, 043704:1–043704:5. [Google Scholar]
- Chae, S.J.; Güneş, F.; Kim, K.K.; Kim, E.S.; Han, G.H.; Kim, S.M.; Shin, H.-J.; Yoon, S.-M.; Choi, J.-Y.; Park, M.H.; et al. Synthesis of large-area graphene layers on poly-nickel substrate by chemical vapor deposition: Wrinkle formation. Adv. Mater. 2009, 21, 2328–2333. [Google Scholar] [CrossRef]
- Li, X.; Cai, W.; An, J.; Kim, S.; Nah, J.; Yang, D.; Piner, R.; Velamakanni, A.; Jung, I.; Tutuc, E.; et al. Large-Area synthesis of high-quality and uniform graphene films on copper foils. Science 2009, 324, 1312–1314. [Google Scholar] [CrossRef]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–87. [Google Scholar] [CrossRef]
- Charlier, J.; Eklund, P.; Zhu, J.; Ferrari, A. Electron and Phonon Properties of Graphene: Their Relationship with Carbon Nanotubes. In Carbon Nanotubes; Springer: Berlin/Heidelberg, Germany, 2008; Volume 111, pp. 673–709. [Google Scholar]
- Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S.; Cancado, L.G.; Jorio, A.; Saito, R. Studying disorder in graphite-based systems by Raman spectroscopy. Phys. Chem. Chem. Phys. 2007, 9, 1276–1290. [Google Scholar] [CrossRef]
- Latil, S.; Meunier, V.; Henrard, L. Massless fermions in multilayer graphitic systems with misoriented layers: Ab initio calculations and experimental fingerprints. Phys. Rev. B 2007, 76, 201402. [Google Scholar] [CrossRef]
- Lenski, D.R.; Fuhrer, M.S. Raman and optical characterization of multilayer turbostratic graphene grown via chemical vapor deposition. J. Appl. Phys. 2011, 110, 013720:1–013720:4. [Google Scholar]
- Faugeras, C.; Nerrière, A.; Potemski, M.; Mahmood, A.; Dujardin, E.; Berger, C.; de Heer, W.A. Few-layer graphene on SiC, pyrolitic graphite, and graphene: A Raman scattering study. Appl. Phys. Lett. 2008, 92, 011914:1–011914:3. [Google Scholar]
- Ni, Z.H.; Wang, Y.Y.; Yu, T.; Shen, Z.X. Raman spectroscopy and imaging of graphene. Nano Res. 2008, 1, 273–291. [Google Scholar] [CrossRef]
- Osada, T. Negative interlayer magnetoresistance and zero-mode landau level in multilayer dirac electron systems. J. Phys. Soc. Jpn. 2008, 77, 084711. [Google Scholar] [CrossRef]
- Morinari, T.; Tohyama, T. Crossover from positive to negative interlayer magnetoresistance in multilayer massless dirac fermion system with non-vertical interlayer tunneling. J. Phys. Soc. Jpn. 2010, 79, 044708. [Google Scholar] [CrossRef]
- Tajima, N.; Sugawara, S.; Kato, R.; Nishio, Y.; Kajita, K. Effect of the zero-mode landau level on interlayer magnetoresistance in multilayer massless dirac fermion systems. Phys. Rev. Lett. 2009, 102, 176403. [Google Scholar]
- Tajima, N.; Sato, M.; Sugawara, S.; Kato, R.; Nishio, Y.; Kajita, K. Spin and valley splittings in multilayered massless Dirac fermion system. Phys. Rev. B 2010, 82, 121420. [Google Scholar] [CrossRef]
- Bright, A.A. Negative magnetoresistance of pregraphitic carbons. Phys. Rev. B 1979, 20, 5142–5149. [Google Scholar] [CrossRef]
- Matsubara, K.; Sugihara, K.; Tsuzuku, T. Electrical resistance in the c direction of graphite. Phys. Rev. B 1990, 41, 969–974. [Google Scholar] [CrossRef]
- Venugopal, G.; Jung, M.-H.; Suemitsu, M.; Kim, S.-J. Fabrication of nanoscale three-dimensional graphite stacked-junctions by focused-ion-beam and observation of anomalous transport characteristics. Carbon 2011, 49, 2766–2772. [Google Scholar] [CrossRef]
- Acik, M.; Chabal, Y.J. Nature of graphene edges: A review. Jpn. J. Appl. Phys. 2011, 50, 070101. [Google Scholar] [CrossRef]
- Yu, Q.; Jauregui, L.A.; Wu, W.; Colby, R.; Tian, J.; Su, Z.; Cao, H.; Liu, Z.; Pandey, D.; Wei, D.; et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nat. Mater. 2011, 10, 443–449. [Google Scholar] [CrossRef]
- Lahiri, J.; Lin, Y.; Bozkurt, P.; Oleynik, I.I.; Batzill, M. An extended defect in graphene as a metallic wire. Nat. Nanotechnol. 2010, 5, 326–329. [Google Scholar] [CrossRef]
- Kopelevich, Y.; da Silva, R.R.; Pantoja, J.C.M.; Bratkovsky, A.M. Negative c-axis magnetoresistance in graphite. Phys. Lett. 2010, 374, 4629–4632. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bodepudi, S.C.; Singh, A.P.; Pramanik, S. Current-Perpendicular-to-Plane Magnetoresistance in Chemical Vapor Deposition-Grown Multilayer Graphene. Electronics 2013, 2, 315-331. https://doi.org/10.3390/electronics2030315
Bodepudi SC, Singh AP, Pramanik S. Current-Perpendicular-to-Plane Magnetoresistance in Chemical Vapor Deposition-Grown Multilayer Graphene. Electronics. 2013; 2(3):315-331. https://doi.org/10.3390/electronics2030315
Chicago/Turabian StyleBodepudi, Srikrishna C., Abhay P. Singh, and Sandipan Pramanik. 2013. "Current-Perpendicular-to-Plane Magnetoresistance in Chemical Vapor Deposition-Grown Multilayer Graphene" Electronics 2, no. 3: 315-331. https://doi.org/10.3390/electronics2030315



