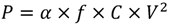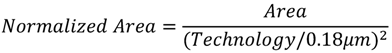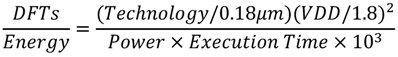1. Introduction
Recently, the rapid growth of multimedia and wireless communication technologies has enabled the integration of various audio coding standards in a multimedia platform for audio applications. Digital Radio Mondiale (DRM) [
1] is a digital broadcasting system for radio frequencies of below 30 MHz. DRM Plus (DRM
+) is the technology extending the DRM system to the VHF bands up to 174 MHz. It is a new standard of the European Telecommunication Standards Institute (ETSI ES 201 980). DRM offers the possibility to use various audio codecs, such as High Efficiency Advanced Audio Coding (HE-AAC), MPEG-4 Code-excited linear prediction (CELP), MPEG-4 Harmonic Vector Excitation Coding (HVXC), and MPEG Surround,
etc., to their broadcasting system. The discrete Fourier transform (DFT) and inverse modified cosine transform (IMDCT) have been, respectively, applied to realize the coded orthogonal frequency division multiplexing (COFDM) and the synthesis filterbank of advanced audio coding (AAC) in DRM specification. In a DRM and DRM
+ receiver, the COFDM adopts the non-power-of-two and power-of-two DFT whose transform lengths are specified to 288, 256, 176, 112, and 27. For a HE-AAC decoder, it also requires 1920- and 240-point IMDCT computations.
Previously, the issue of a common architecture design of fast Fourier transform (FFT) and IMDCT has been developed in [
2,
3,
4,
5] for a digital audio broadcasting (DAB) system [
6,
7]. The specified transform lengths of both FFT and IMDCT are all power of two, and it is very suitable for parallel design to implement the common architecture of FFT and IMDCT [
2,
3,
4] or FFT-based IMDCT [
5]. However, it would be a great challenge to design a flexible FFT or IMDCT accelerator with the transform lengths of power-of-two and non-power-of-two. Currently, Lai
et al. [
8] propose a recursive DFT (RDFT) to compute IMDCT coefficients. Due to the nature of recursive structure, Lai
et al.’s hardware accelerator can arbitrarily switch transform length between power-of-two and non-power-of-two without any extra hardware processing units. Additionally, the results indicate that it achieves lower computational complexity than recursive DCT-based designs [
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. Since the FFT (or RDFT) can be further used for computing the IMDCT, the transform length of IMDCT is shortened from
N to
N/4. It exactly reduces the iteration loops for recursively computing IMDCT coefficients; however, compared with Lei
et al.’s IMDCT [
19], this method, which adopted one-dimension (1-D) RDFT as a unified kernel, would not gain better performance. This implies that it still has a bottleneck on using a 1-D RDFT to compute the IMDCT coefficients.
In 2004, Wolkotte
et al. [
20] presented a detailed analysis for computational complexity in a DRM receiver and clearly showed that the DFT block took 50.51% of all computations. To meet the specification that requires non-power-of-two transform lengths, RDFT approaches [
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32] and recursive IMDCT approaches [
9,
10,
11,
12,
13,
14,
15,
16,
17,
18] have been suggested for area-efficient implementations. The major limitation of RDFT is on the issue of long computational cycle,
i.e., long processing time. To overcome this shortcoming, a 2-D RDFT structure design with prime factor algorithm has been presented in [
30,
31,
32]. Compared with other RDFT approaches [
21,
22,
23,
24,
25,
26], Lai
et al. [
29,
30,
31,
32] have a greater improvement in terms of computational complexity and latency. However, the computational complexity of 256-point RDFT based on Lai
et al.’s algorithm [
32] still takes more multiplications and additions, because the transform length only has one prime factor so that we only can adopt three 1-D RDFT hardware accelerators to simultaneously compute all 256-point DFT coefficients. Another issue that arises in [
30,
32] is that, in order to decompose the
N-point RDFT into
c- and
m-point sub-RDFTs, a great number of register files would be inserted between the first-stage and second-stage RDFTs for buffering temporal data. It makes the chip size become much larger, and consumes much power on memory access. Recently, a FFT design consisted of memory, control unit, and various mixed-radix butterfly modules has been presented in [
33]. Hsiao
et al. merge prime factor and common factor concepts to realize the proposed accelerator, and propose an efficient address generator to avoid the memory access conflict. However, it still requires many radix-r processing units to support the FFT computations. Due to the nature of RDFT, we can apply the variable-length and low-cost advantages to save these processing units. Thus, high-performance RDFT architecture is proposed to enhance our previous works [
29,
30,
31,
32] in this paper.
The rest of this paper is organized as follows:
Section 2 takes an overview for our previous works [
29,
30,
31,
32] first, and then proposes a new concept to integrate them by applying the common factor DFT (CF-DFT) algorithm.
Section 3 demonstrates the compact architecture design of the proposed RDFT, and then
Section 4 introduces the low-power optimizations of VLSI implementation for the proposed hardware accelerator.
Section 5 compares and contrasts the differences in performance for various approaches. Finally, conclusions are outlined in
Section 6.
2. The Proposed Compact RDFT with Prime Factor and Common Factor Algorithms
The
N-point DFT formula is defined as Equation (1). According to the derivation of Lai
et al. [
29], it can be found that the transfer function
![Jlpea 03 00099 i001]()
is obtained as Equation (2).
Equation (2) can be easily mapped into a hardware accelerator. To reduce the number of multiplications, both coefficients of
![Jlpea 03 00099 i004]()
and
![Jlpea 03 00099 i005]()
can be computed by one multiplication and a simple shift operation. To reduce the usage of multipliers in implementation, a multiplier-sharing scheme is proposed and applied in [
23,
24,
26,
29,
30,
31,
32] for this recursive structure. Hence, the multiplication of cosine and sine can be computed by the same multiplier with one clock cycle delay in realization. By adopting the hardware-sharing scheme and register-shifting concept, the RDFT circuit of Lai
et al. [
29] can be further improved.
Figure 1 shows the compact RDFT circuit. The detailed control rules of multiplexers are shown in
Figure 1b.
Figure 1.
Proposed compact architecture of recursive discrete Fourier transform (RDFT) module. (a) The computational circuit of X[0] and X[N/2]; (b) The computational circuit design of X[1] to X[N/2 − 1].
Figure 1.
Proposed compact architecture of recursive discrete Fourier transform (RDFT) module. (a) The computational circuit of X[0] and X[N/2]; (b) The computational circuit design of X[1] to X[N/2 − 1].
Compared with our previous work [
29], this design only takes eight multiplexers, four adders and two multipliers in RDFT implementation. To lower the computational complexity and cycle, Lai
et al. proposed a new algorithm using the Chinese Reminder Theorem (CRT),
i.e., prime factor algorithm, in [
30,
31,
32]. In this algorithm, the input sequence length (
N) can be factored into two mutually prime factors (
c and
m), and then the change of the variables is computed as Equation (3), where
![Jlpea 03 00099 i006]()
.
For this mappings to be unique, the condition A, B, C, and D are chosen such that:
Thus, the DFT algorithm with the CRT scheme, which is also called the prime factor DFT (PF-DFT) algorithm, can be defined as
By adopting the RDFT in
Figure 1 to the Equation (5), the low-cost and reconfigurable two-dimension RDFT algorithm can be easily obtained. For a DRM system, the transform length of 288 (
N) can be divided into 32 (
c) and 9 (
m) where factors of
c and
m are co-prime. The conditions of (
A,
B,
C,
D) are then chosen as (9, 32, 64, 225). Similarly, the conditions of (
A,
B,
C,
D) for the frame size of 176, 112, 480, 60 can be chosen as (11, 16, 33, 144), (7, 16, 49, 64), (15, 32, 225, 256), and (5, 12, 25, 36), respectively. Note that the details for the selection of these conditions are introduced in the section III of Lai
et al. [
30]. However, the PF-DFT algorithm cannot be applied to compute the 256-point DFT coefficients, because the transform length only has one prime,
i.e., 256 = 2
8. Thus, we should adopt an efficient method called the CF-DFT algorithm to solve this problem. Assume that the input sequence length (
N) can be also factored into two common factors (
c and
m), and
By taking Equation (6) into Equation (1), we can obtain the CF-DFT algorithm as Equation (7):
The difference between Equations (5) and (7) is the twiddle factor
![Jlpea 03 00099 i012]()
. It implies that the computation between
c-point DFT and
m-point DFT has a complex multiplication. Additionally, it requires extra adders, multipliers and ROMs for the operations of twiddle factors in implementation. On the other hand, it will also increase the number of multiplications and additions in algorithm. Although the CF-DFT algorithm would take a fewer costs than PF-DFT, it can be applied to compute the one-prime-length DFT coefficients. To reduce the growth of coefficients with the variable-length DFT for DRM specification, Lai
et al. proposes a coefficient-free algorithm in [
31,
32]. The two major coefficients in Equation (2),
i.e.,
![Jlpea 03 00099 i004]()
and
![Jlpea 03 00099 i013]()
, can be respectively calculated by using the trigonometric identities Equations (9,10) [
31]. The detailed computations have been introduced in section 2.C of Lai
et al.’s paper [
31]. It is also applied to generate the coefficients of twiddle factors in this paper. Note that it only takes two computational cycles to generate the twiddle factors by using two multipliers in one RDFT kernel.
5. Comparison and Discussion
In this section, we make a completed comparison for various performance evaluations in terms of computational complexity, computational cycle, time cost per transformation (TCPT), and hardware costs. Since the proposed method adopted CF and PF algorithms to speed up the traditional RDFT computation, the factor selection would be greatly impact on the performance of the proposed RDFT. Here, we compare all lists of the required DFT transform lengths in the OFDM of DRM standard,
i.e., 288, 256, 176, 112, and 27.
Table 1 lists the suitable
c and
m factors for the proposed RDFT. Both
c and
m factors are corresponding to the number of computational complexity and the number of computational cycle. To avoid the twiddle factor multiplications in the proposed hardware design, the transform lengths of 288, 176, and 112 are calculated by PFA. Only 256- and 27-point DFT are computed by CFA.
Table 1.
Factor selection for the proposed RDFT.
Table 1.
Factor selection for the proposed RDFT.
| Length | 288 | 256 * | 176 | 112 | 27 * | 480 | 60 |
|---|
| c | 32 | 16 | 16 | 16 | 9 | 32 | 12 |
| m | 9 | 16 | 11 | 7 | 3 | 15 | 5 |
| A | 9 | 1 | 11 | 7 | 1 | 15 | 5 |
| B | 32 | m | 16 | 16 | m | 32 | 12 |
| C | 64 | c | 144 | 64 | c | 256 | 36 |
| D | 255 | 1 | 33 | 49 | 1 | 255 | 25 |
Table 2 demonstrates a comparison of computational complexity for various RDFTs with different transform lengths. Van
et al.’s method [
26] takes (2
N2 + 6
N) multiplications and (4
N2 + 8
N) additions to compute N-point DFT coefficients. On the other hand, Lai
et al. [
9] proposes a much simpler structure, and it takes (
N2 –
N − 2) multiplications and (2
N2 + 7
N − 2) additions in
N-point DFT computation. Furthermore, Lai
et al. proposed two low-complexity methods [
30,
32] to reduce the numbers of multiplication and addition. It only takes [2
N(
m +
c + 2)] multiplications and [4
N(
m +
c + 2)] additions in [
30]. For the proposed PF-RDFT algorithm,
i.e., in case of 288-point DFT computations, the number of multiplications would, respectively, take [2
m(
c + 1)(
c/2 − 1)] and [2
c(
m + 1)(
m − 1)/2] for
c-point and
m-point RDFT computations as shown in (5), where (
c/2 − 1) and [(
m − 1)/2] are the corresponding number of recursive loops, respectively, for even and odd-point RDFT. In addition, [2
m(
c + 1)] and [2
c(
m + 1)] are respectively the number of multiplications per recursive loop, where the scale “2” means the multiplication required for complex input sequence. The total number of additions would, respectively, take [4
N(
c/2 − 1) + 4
c] and [4
N(
m − 1)/2 + 4
m] for
c-point and
m-point RDFT computations, where (4
N) is the number of additions per recursive loop in
Figure 1b, and (4
c) is the total number of additions only for
Figure 1a under consideration of the case of
c-point RDFT computations. About the proposed CF-RDFT algorithm,
i.e., in case of 256-point DFT computations as shown in Equation (7), it requires extra multiplications and additions for the twiddle factor operation more than that of the proposed PF-RDFT algorithm. However, the twiddle factor operation only takes (4
N) multiplications and (2
N) additions.
Since the proposed method has a compact and high-throughput RDFT circuit as well as our previous work [
32], we can further calculate the desired coefficients with much lower complexity by combining PF and CF algorithms with RDFT. The result shows that the proposed method can, respectively, reduce the numbers of multiplications and additions by 97.40% and 94.31% for 256-point DFT computation while the CFA is adopted.
Table 2.
Computational complexity of various RDFT algorithms for 288- and 256-point computations.
Table 2.
Computational complexity of various RDFT algorithms for 288- and 256-point computations.
| Method | Multiplications | Additions |
|---|
| N = 288 | N = 256 | N = 288 | N = 256 |
|---|
| [26] * | 167,616 | 132,608 | 334,080 | 264,192 |
| [27] | 41,464 | 32,760 | 85,658 | 67,946 |
| [29] | 82,654 | 65,278 | 167,902 | 132,862 |
| [30] | 24,768 | 332,928 | 49,536 | 263,168 |
| [32] | 12,704 | 332,928 | 25,984 | 263,168 |
| Proposed | 11,470 | 8,640 | 22,034 | 14,976 |
To evaluate the latency of various algorithms, we make a comparison of computational cycle with five transform lengths specified in DRM system. Van
et al. [
26] and Lai
et al. [
29] require (
N2/2) and [(
N2 –
N − 1)/2] cycles, respectively, to compute the
N-point DFT coefficients. In
Table 3, Meher
et al. [
27] has the lowest computational cycle but requires most hardware resources to implement the systolic structure. Since PFA can be applied to speed up the conventional RDFT and makes the
N-point DFT to be
c- and
m-point sub-DFTs, Lai
et al. [
30,
32] have a lower latency in computation. For example, Lai
et al. [
30] only requires [(
c + 1)
N + (
m + 1)
m] cycles to calculate all coefficients for 288, 176, and 112 transform lengths. Due to the difference of RDFT kernel design, the result shows that the number of computational cycle for our previous works [
30,
32] is relatively different. In this work, we propose a memory-based structure with a single and compact RDFT processing unit to compute variable-length transform. The results show that the proposed method has a lower latency compared with previous works [
26,
29,
30]. Compared to [
32], although the proposed method requires more latency for 288-, 176-, 112-, and 27-point DFT, it still shows a greater performance in terms of 256-point DFT computation, and dramatically reduces the computational cycle by 46.50%. In addition, the hardware costs of this work can be greatly improved, as shown in
Table 4.
Table 3.
Computational cycle of various RDFT algorithms.
Table 3.
Computational cycle of various RDFT algorithms.
| Method | Transform length |
|---|
| 288 | 256 | 176 | 112 | 27 |
|---|
| [26] | 41,472 | 32,768 | 15,488 | 6,272 | N/A |
| [27] | 431 | 383 | 263 | 167 | N/A |
| [29] | 41,327 | 32,639 | 15,399 | 6,215 | 364 |
| [30] | 9,594 | 32,896 | 3,124 | 1,960 | N/A |
| [32] | 4,842 | 11,137 | 1,594 | 1,006 | N/A |
| Proposed | 6,693 | 5,958 | 2,865 | 1,609 | 346 |
For hardware cost comparison, we use items such as a multiplier, adder, buffer, coefficient-ROM, and data throughput per transformation (DTPT) to evaluate the existing RDFT designs in
Table 4. For the temporal buffer, Meher
et al. [
27] require (
N/4 − 2) latch cells and each latch cell takes four latches to store the data. By the way, Lai
et al. [
30] and [
32], respectively, require (4 × 11) and (8 × 15) register files. On the other hand, for the number of coefficients stored in the ROM, Van
et al. [
26] and Lai
et al. [
29], respectively require (
N) and (
N − 2) coefficients for each
N-point DFT computation, but Meher
et al. [
27] require (3
N − 2) coefficients. It can be observed that Lai
et al. [
32] have more hardware costs than previous works [
26,
29,
30] do; however, the complexity and latency of [
32] have a better improvement according to
Table 2,
Table 3. To make the design balance in realization,
i.e., cost and performance, the proposed method adopts only one RDFT module to implement the memory-based DFT processor. Thus, it does not require extra buffer for temporal data as is the case with Meher
et al. [
27] and Lai
et al. [
30,
32]. Additionally, we adopt on-line coefficient generator [
31,
32] to avoid coefficient-ROM using in chip implementation and maintain the same DTPT as well as [
29]. The overall comparisons and considerations are clearly indicated that the proposed solution would be a low-cost and high-performance design for variable-length DFT computations.
Table 4.
Hardware cost for various RDFT algorithms.
Table 4.
Hardware cost for various RDFT algorithms.
| Method | Multiplier | Adder | Buffer | ROM | DTPT |
|---|
| [26] | 10 | 17 | No | Yes | 1 |
| [27] | N + 4 | N + 18 | Yes | Yes | 4 |
| [29] | 2 | 13 | No | Yes | 2 |
| [30] | 4 | 8 | Yes | Yes | 1 |
| [32] | 6 | 18 | Yes | No | 4 |
| Proposed | 2 | 4 | No | No | 2 |
The time cost per transformation (TCPT) of various-length DFTs specified by DRM standard is summarized in
Table 5. Based on the results of
Table 3, the TCPT of the proposed design can be estimated while the operating frequency rate is set to 25 MHz. In addition, the RAM access time per transformation (RAM_ATPT) is used to calculate the data loading into DFT accelerator and storing back to the system bus, since the proposed design would be an IP in a system. The results show that it can easily achieve real-time requirement of DRM standard and saves over 98.91% of time cost. It implies that we can adjust the operation frequency down to 273 kHz to achieve the requirement of low power consumption. According to NanoSim simulation results, the power consumption for the 288- and 256-point DFT computations are, respectively, 0.105 mW and 0.1176 mW at 273 kHz.
Table 5.
Time cost per transformation for the proposed method.
Table 5.
Time cost per transformation for the proposed method.
| Length | 288 | 256 | 176 | 112 | 27 |
|---|
| DRM Spec. (ms) | <26.7 | <26.7 | <20 | <16.7 | <2.5 |
| Proposed (us) | 267.72 | 238.32 | 114.60 | 64.36 | 13.84 |
| RAM_ATPT(us) | 23.04 | 20.48 | 14.08 | 8.96 | 2.16 |
| Reduction (%) | 98.91 | 99.03 | 99.36 | 99.56 | 99.36 |
Table 6 summarizes the comparisons between the proposed design and other RDFT processors for DRM receiver in the literature. For the purpose of fair comparison with different process technologies, we employ Baas’ normalization Equations (9) and (10) [
35] to normalize the area and DFTs/Energy.
Table 6.
Comparison of chip feature for previous works and this work.
Table 6.
Comparison of chip feature for previous works and this work.
| Design | [29 | [30 | [33] | This work |
|---|
| Technology | 0.18 μm | 0.18 μm | 0.18 μm | 0.18 μm |
| Internal/Coeff. word lengths | 24/24 (bits) | 21/16 (bits) | 24/24 (bits) | 24/24 (bits) |
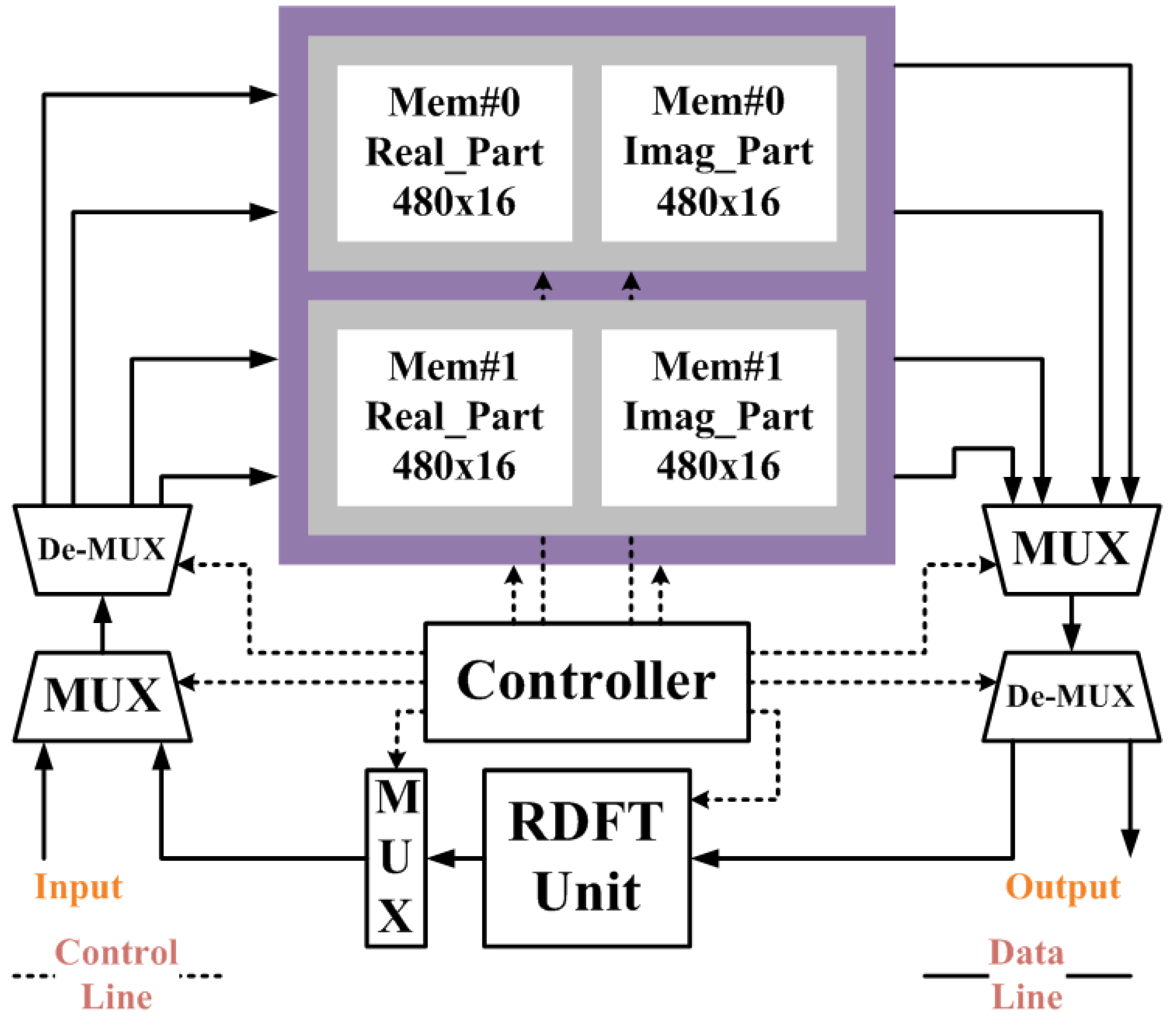
| Data Memory (bits) | Excluded | Excluded | Excluded | 2 × 480 × 32 |
| Coefficient Memory | Excluded | Coeff.-free | Coeff.-free | Coeff.-free |
| Supply Voltage | 1.98 v | 1.98 v | 1.98 v | 1.7 v (opt.) |
| Clock Rate | 25 MHz | 25 MHz | 25 MHz | 25 MHz |
| Supporting DFT | 288, 256, 176, | 288, 256, 176, | 288, 256, 176, | 288, 256, 176, |
| Transform-Length | 112, 212, 106 | 112 | 112, 480, 60 | 112, 480, 60 |
| Executing Time for 288-point | 1.65 ms | 384 μs | 193.68 μs | 267.72 μs |
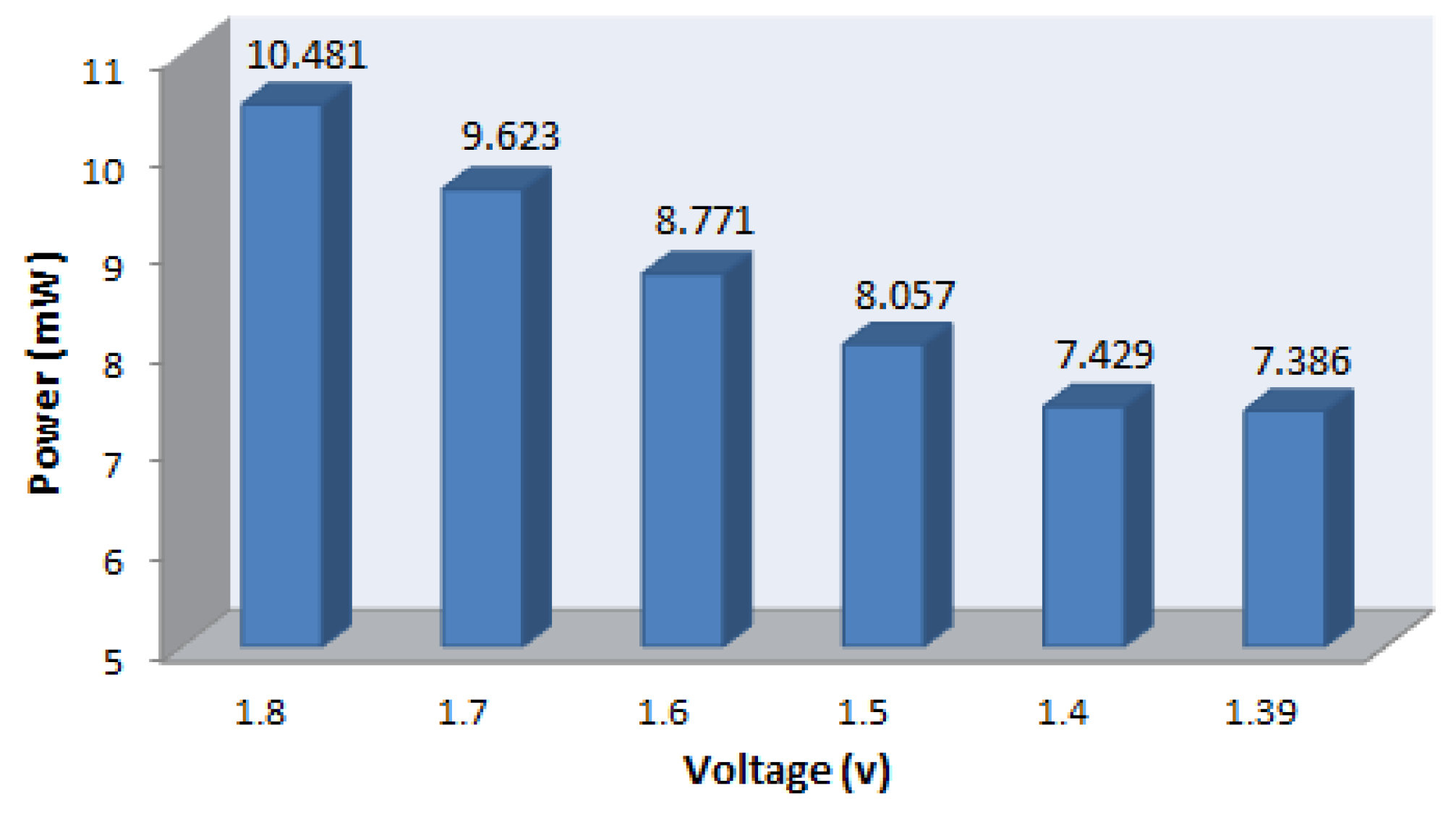
| Power Consumption | Circuit | 5.98 mW | 8.44 mW | 14.3 mW | 9.62 mW(opt.) |
| Data Memory | 5.53 mW * | 5.53 mW* | 5.53 mW * |
| Core Area | Circuit | 0.154 mm2 | 0.265 mm2 | 0.746 mm2 | 0.714 mm2 |
| Data Memory | 0.347 mm2 | 0.347 mm2 | 0.347 mm2 |
| Normalized DFTs/Energy | 63.71 | 225.56 | 315.05 | 346.34 (opt.) |
Note that the memory unit excluded in these literatures. Van
et al.’s algorithm [
26] has a number of
N2/2 computational cycles as well as Lai
et al.’s [
29], but the implementation chip of Van
et al. is only designed to DTMF application. For DRM applications, previous works [
30,
32] have a better performance in terms of normalized DFTs per energy; however, these designs do not include the data memory to buffer the input and out sequence. This implies that these two designs would occupy most bandwidth of system bus, since they are hard intellectual properties (IPs) in an embedded system. Form the system view to consider this problem, the area and power consumption of data memory (RAM) should not be neglected.
Table 2 clearly shows that the proposed design is a smaller than previous work [
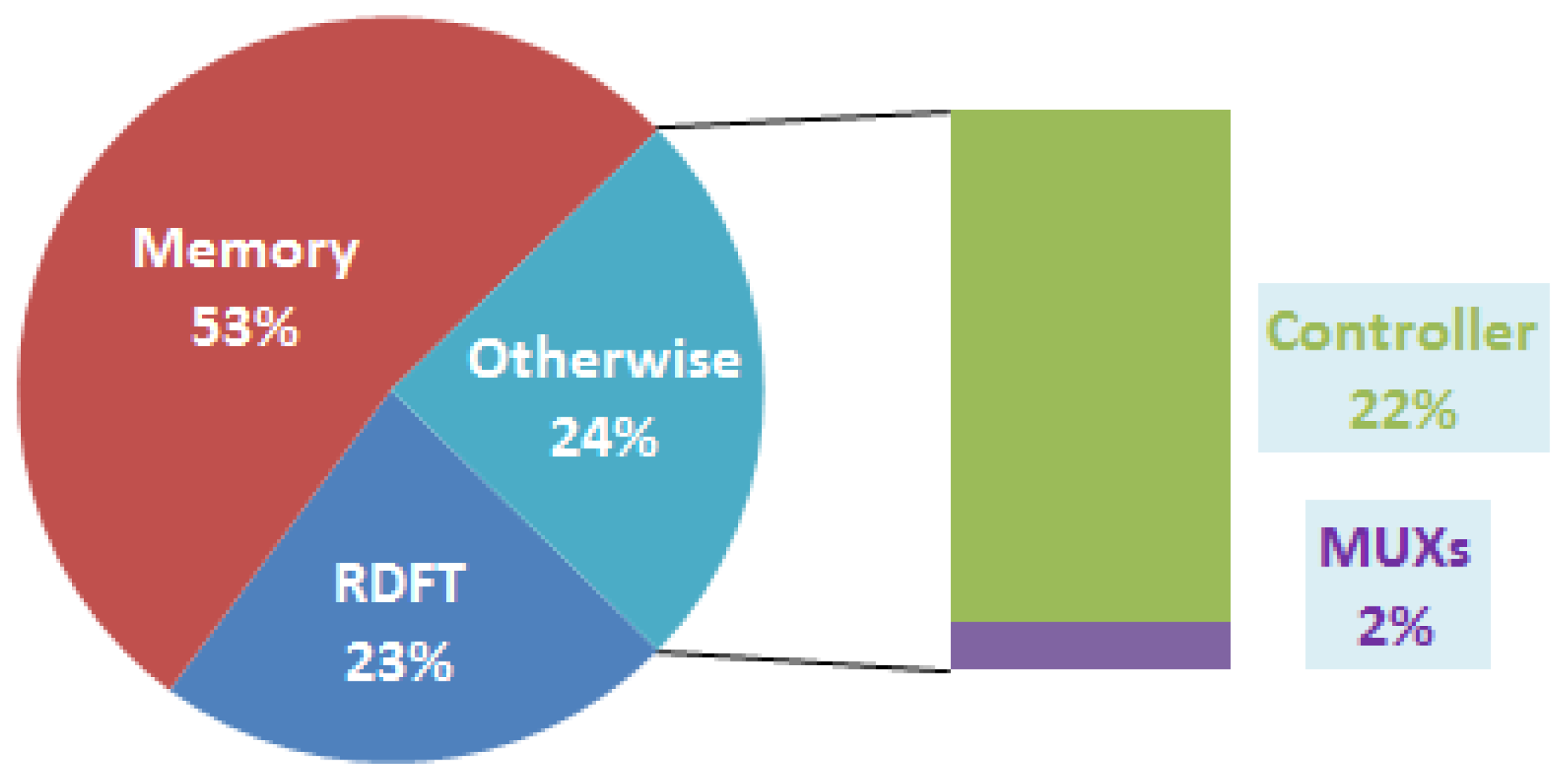
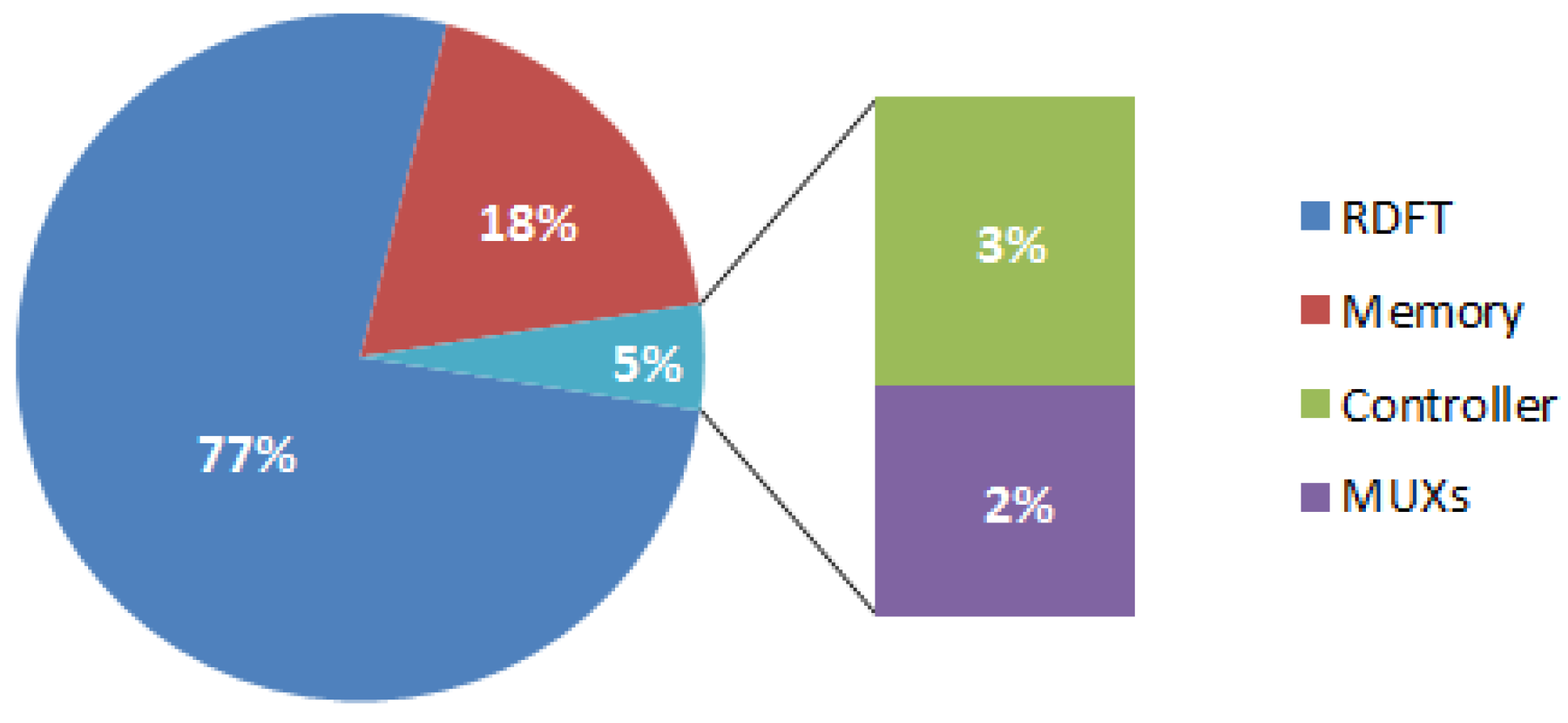
32], although it seems to lose its advantage in power consumption. Here, we also provide a power consumption result simulated by NanoSim. The result shows that the proposed design consumes 10.693 mW @ 25 MHz. The percentage of power dissipation is as shown in
Figure 6. We can see that it consumes the most of power in RDFT module, and the power consumption of memory module is 1.925 mW. Based on
Figure 4,
Figure 6, we know that the memory module consumes approximately a fifth of total power, and takes more chip area over 50% of total gate counts.
Figure 6.
Percentage of power dissipation for the proposed design by Prime Power.
Figure 6.
Percentage of power dissipation for the proposed design by Prime Power.
 is obtained as Equation (2).
is obtained as Equation (2).
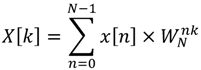
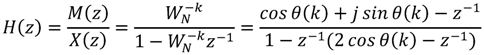
 and
and  can be computed by one multiplication and a simple shift operation. To reduce the usage of multipliers in implementation, a multiplier-sharing scheme is proposed and applied in [23,24,26,29,30,31,32] for this recursive structure. Hence, the multiplication of cosine and sine can be computed by the same multiplier with one clock cycle delay in realization. By adopting the hardware-sharing scheme and register-shifting concept, the RDFT circuit of Lai et al. [29] can be further improved. Figure 1 shows the compact RDFT circuit. The detailed control rules of multiplexers are shown in Figure 1b.
can be computed by one multiplication and a simple shift operation. To reduce the usage of multipliers in implementation, a multiplier-sharing scheme is proposed and applied in [23,24,26,29,30,31,32] for this recursive structure. Hence, the multiplication of cosine and sine can be computed by the same multiplier with one clock cycle delay in realization. By adopting the hardware-sharing scheme and register-shifting concept, the RDFT circuit of Lai et al. [29] can be further improved. Figure 1 shows the compact RDFT circuit. The detailed control rules of multiplexers are shown in Figure 1b.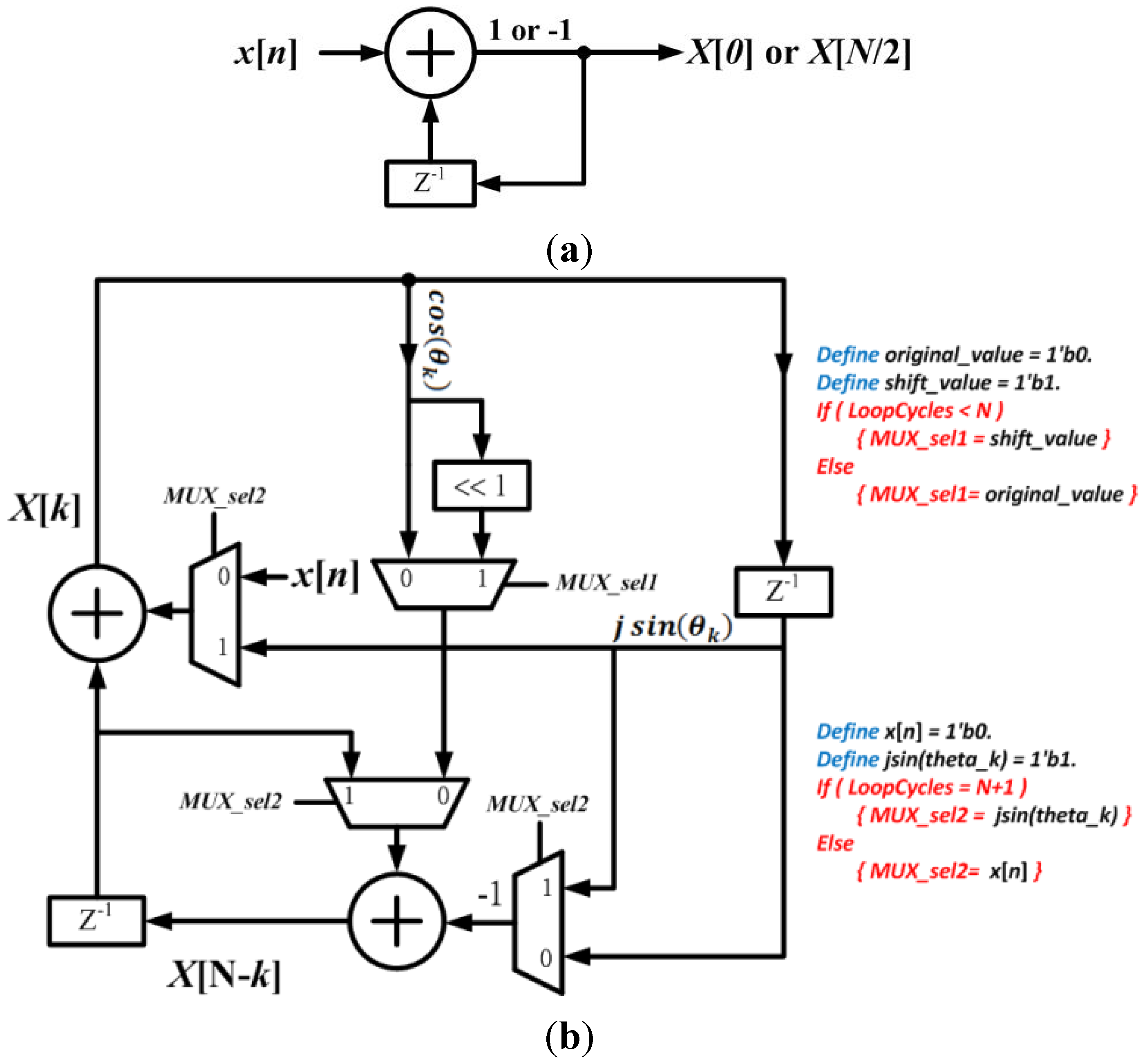
 .
.
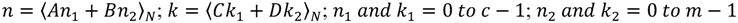
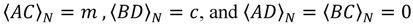
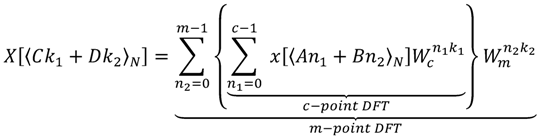
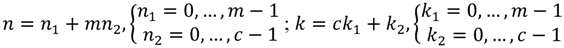
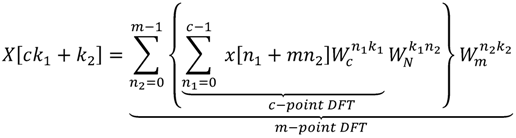
 . It implies that the computation between c-point DFT and m-point DFT has a complex multiplication. Additionally, it requires extra adders, multipliers and ROMs for the operations of twiddle factors in implementation. On the other hand, it will also increase the number of multiplications and additions in algorithm. Although the CF-DFT algorithm would take a fewer costs than PF-DFT, it can be applied to compute the one-prime-length DFT coefficients. To reduce the growth of coefficients with the variable-length DFT for DRM specification, Lai et al. proposes a coefficient-free algorithm in [31,32]. The two major coefficients in Equation (2), i.e.,
. It implies that the computation between c-point DFT and m-point DFT has a complex multiplication. Additionally, it requires extra adders, multipliers and ROMs for the operations of twiddle factors in implementation. On the other hand, it will also increase the number of multiplications and additions in algorithm. Although the CF-DFT algorithm would take a fewer costs than PF-DFT, it can be applied to compute the one-prime-length DFT coefficients. To reduce the growth of coefficients with the variable-length DFT for DRM specification, Lai et al. proposes a coefficient-free algorithm in [31,32]. The two major coefficients in Equation (2), i.e.,  and
and  , can be respectively calculated by using the trigonometric identities Equations (9,10) [31]. The detailed computations have been introduced in section 2.C of Lai et al.’s paper [31]. It is also applied to generate the coefficients of twiddle factors in this paper. Note that it only takes two computational cycles to generate the twiddle factors by using two multipliers in one RDFT kernel.
, can be respectively calculated by using the trigonometric identities Equations (9,10) [31]. The detailed computations have been introduced in section 2.C of Lai et al.’s paper [31]. It is also applied to generate the coefficients of twiddle factors in this paper. Note that it only takes two computational cycles to generate the twiddle factors by using two multipliers in one RDFT kernel.