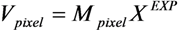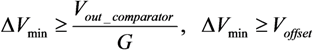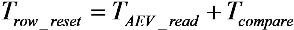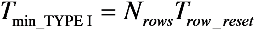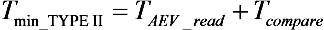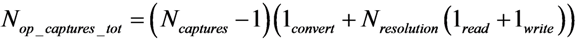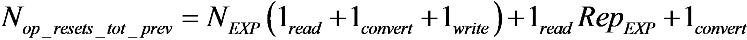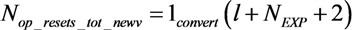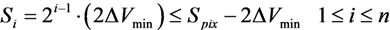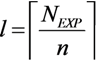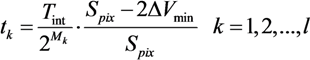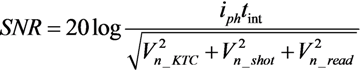2.2. The Proposed Solution
Our solution is based upon “ranging” and AEV concepts. The purpose of this solution is to reduce DR processing times and to omit the memory unit. In addition, we have presented the solution architecture and the flow.
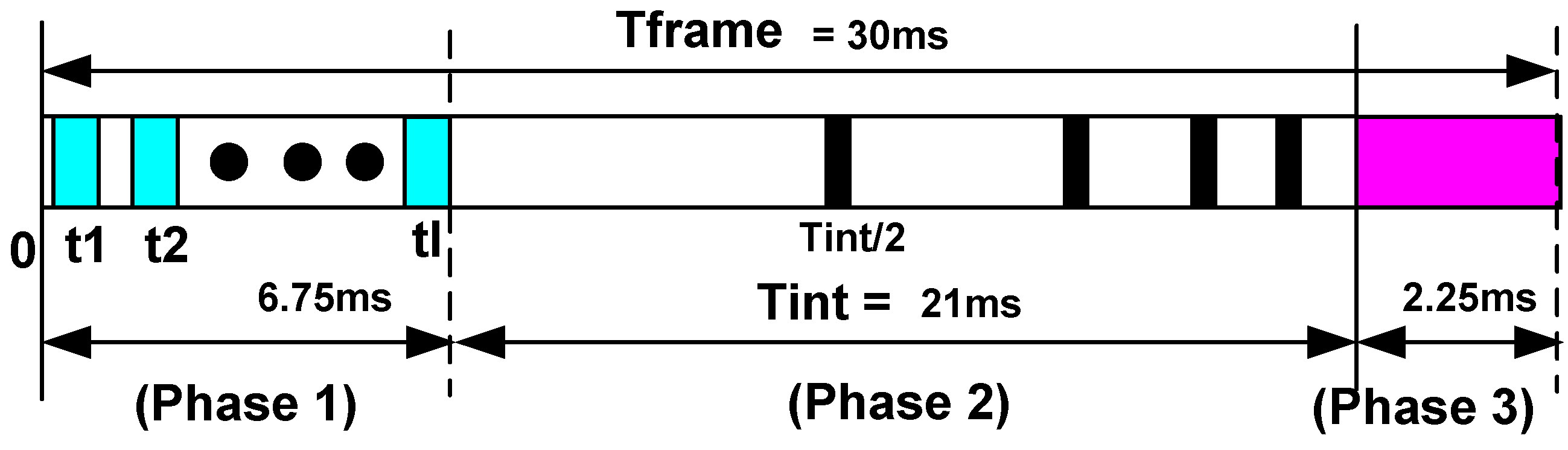
We have divided the WDR algorithm into three phases (
Figure 1). During Phase 1, the
EXP values are produced and memorized inside each pixel in a format of analog encoding voltage
AEV. This assignment, which precedes the saturation checks, is called “ranging”, since it “coarsely” quantizes [
23] the pixel signal. In fact, the
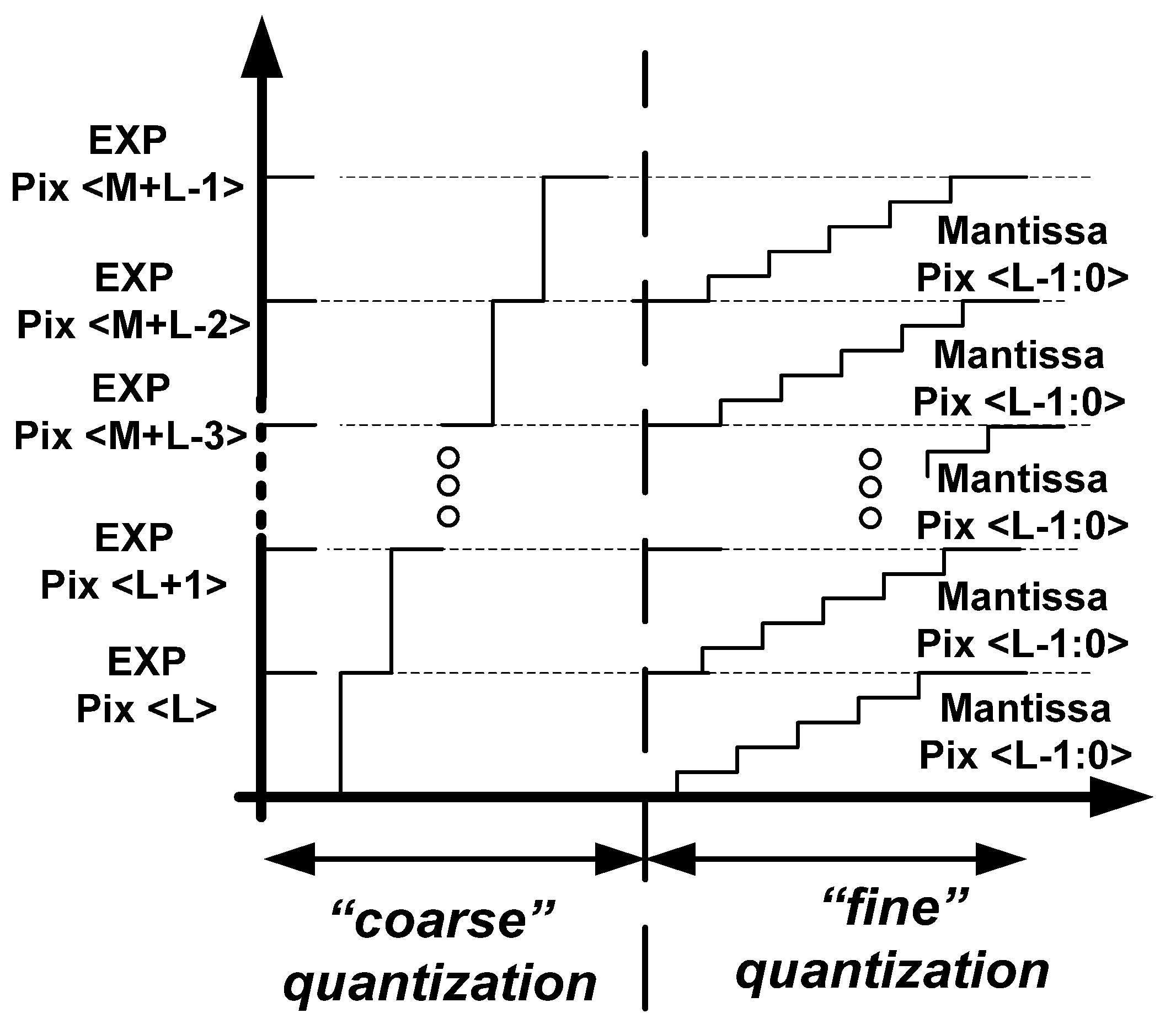
AEV value produced in this quantization, contains the most significant bits of pixel signal
Pix<
M + L − 1:
L> (
Figure 2); whereas the
Mantissa obtained at the end of the next phase contains the least significant bits
Pix<
L − 1:0>. In this way, each pixel is given its valid integration time for the current frame before the saturation checks start.
Figure 1.
Three Phases of the proposed WDR algorithm.
Figure 1.
Three Phases of the proposed WDR algorithm.
During Phase 2, the pixel integrates in accordance with its AEV. Since the integration time is already known, there is no need to retrieve the last reset information or to refresh information for the current check as was performed in our previous solutions; we merely compare the AEV to the global reference. In case the AEV is below the reference, the pixel will be reset; if not, the pixel will remain untouched till the next frame.
Figure 2.
Digital Pixel Value: Mantissa and the EXP bits.
Figure 2.
Digital Pixel Value: Mantissa and the EXP bits.
During Phase 3, both the
AEV and
Mantissa are digitized in a single slope analog to a digital conversion (ADC) (
Figure 3). For this purpose, the
AEV and
Mantissa are read separately and converted with different resolutions. The
AEV is digitized with a “coarse” resolution; whereas the
Mantissa is converted by a ramp with a “fine” resolution.
Figure 3.
The Coarse and Fine Quantization of the Pixel Signal.
Figure 3.
The Coarse and Fine Quantization of the Pixel Signal.
In general, the three phases can overlap each other. However, in this study, we present the first version of the algorithm; therefore, we assume that each phase is completely separated from the others. In future works we will demonstrate how these phases can be overlaid on each other. We assessed the duration of each phase in accordance with further presented simulation results. In
Figure 1, we present the division of a single frame (30 ms) into three phases as if the algorithm is applied on a 1000 × 1000 pixel array. In spite of all the phases being separate, it is important to note that the maximal integration time (Phase 2) still occupies the major part of the frame, whereas the overall integration times in the rest of the phases 1 and 3 are substantially shorter.
2.6. TYPE I Pixel
For most applications the required dynamic range (DR) does not exceed 120 dBs, so the pixel structure can be straightforward. In our case, all we need is to accommodate the
AEV and the pixel
Mantissa on two separate capacitors and to add a readout chain and conditional access circuitry (
Figure 5) to each of them. Since the pixel structure here is not complex and the DR extension is typical, this design is named
TYPE I.
Figure 5.
Schematic of TYPE I Pixel.
Figure 5.
Schematic of TYPE I Pixel.
The functionality of the TYPE I pixel is implemented with 11 transistors only. They can be divided into two groups: the first processes the data received from the pinned photodiode (PPD) M1–M6; and the second is responsible for the AEV handling M7–M11.
The charge transfer from the
PPD is bidirectional, similar to [
25]. In this way, we can deliberately dump the generated charge to drain the photo-diode through
M1 or we can transfer the charge for further processing to
Cs through
M2. We use a simple conditional reset scheme, implemented by
M3 and
M4 transistors, to implement the multiple resets algorithm. By activating the
Row_Reset signal, the required pixel row is chosen and then, by means of the
C_Reset signal, driven by the column-wise comparators, is conditionally reset to
Vrst. Transistors
M5,
M6 form a traditional source follower to handle the
CS readout [26].
AEV processing inside the pixel is very simple as well. The
AEV value is fed to the pixel from the column-wise bus
AEV_In. The write operation of the input
AEV into the pixel dynamic memory is conditional and is implemented by using a trivial stacked scheme
M7 and
M8. By activating the
Wr_AEV signal, a required row is accessed; while the
Logic Decision signal, driven by column-wise comparators, enables the MOS capacitor
CAEV to sample the
AEV_In bus. It is important to note that aside from its simplicity, this stacked scheme also minimizes the possible leakage from the
AEV capacitor, thus maintaining the data integrity till the readout. The readout of the
AEV is performed through a separate source follower, implemented by
M10 and
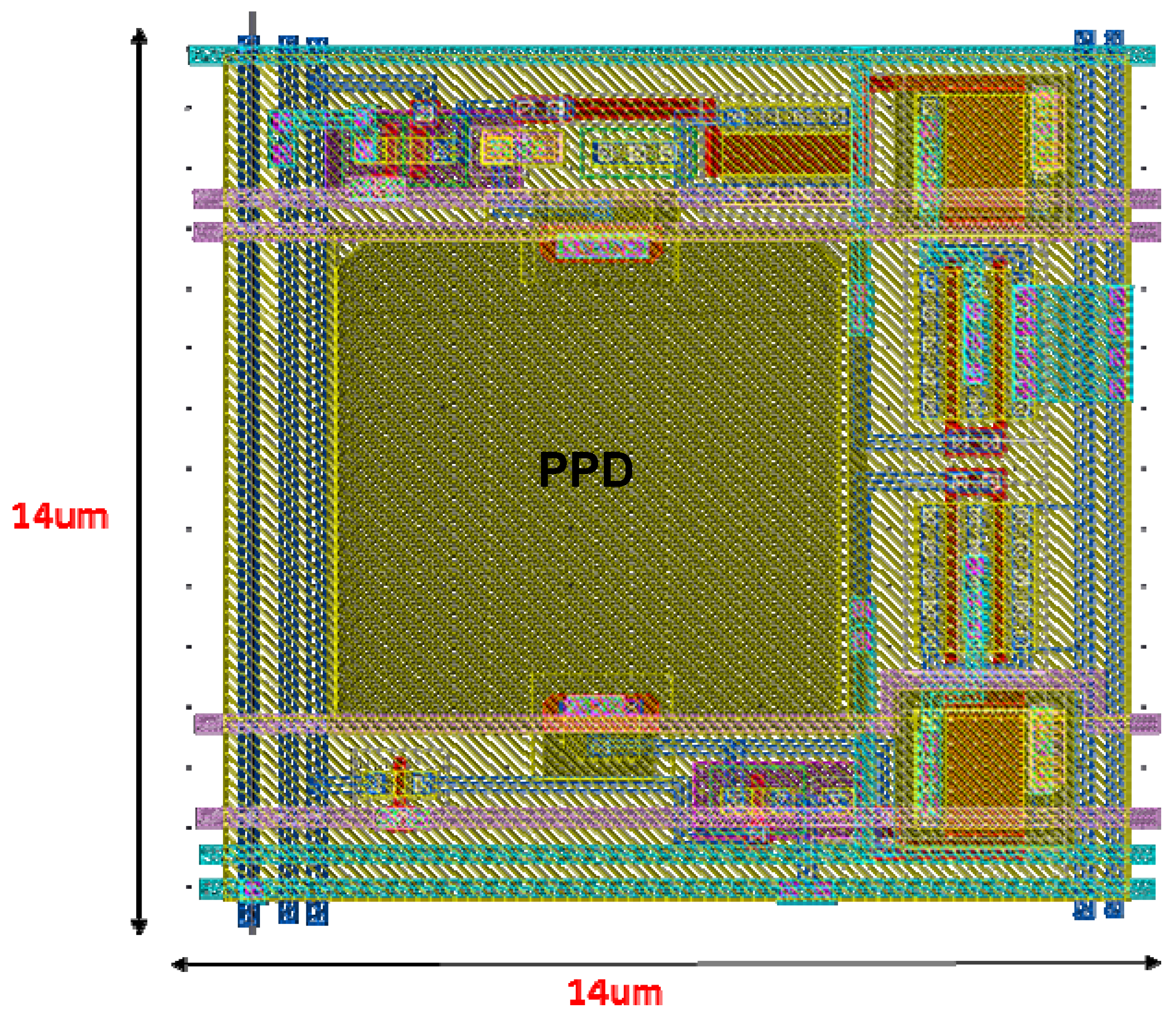
M11. This relatively simple pixel was implemented in layout using 0.18 µm CMOS technology, with 14 µm pitch and 40% fill factor (FF) (
Figure 6).
Figure 6.
Layout of TYPE I Pixel.
Figure 6.
Layout of TYPE I Pixel.
Figure 7.
Phase 1 TYPE I pixel.
Figure 7.
Phase 1 TYPE I pixel.
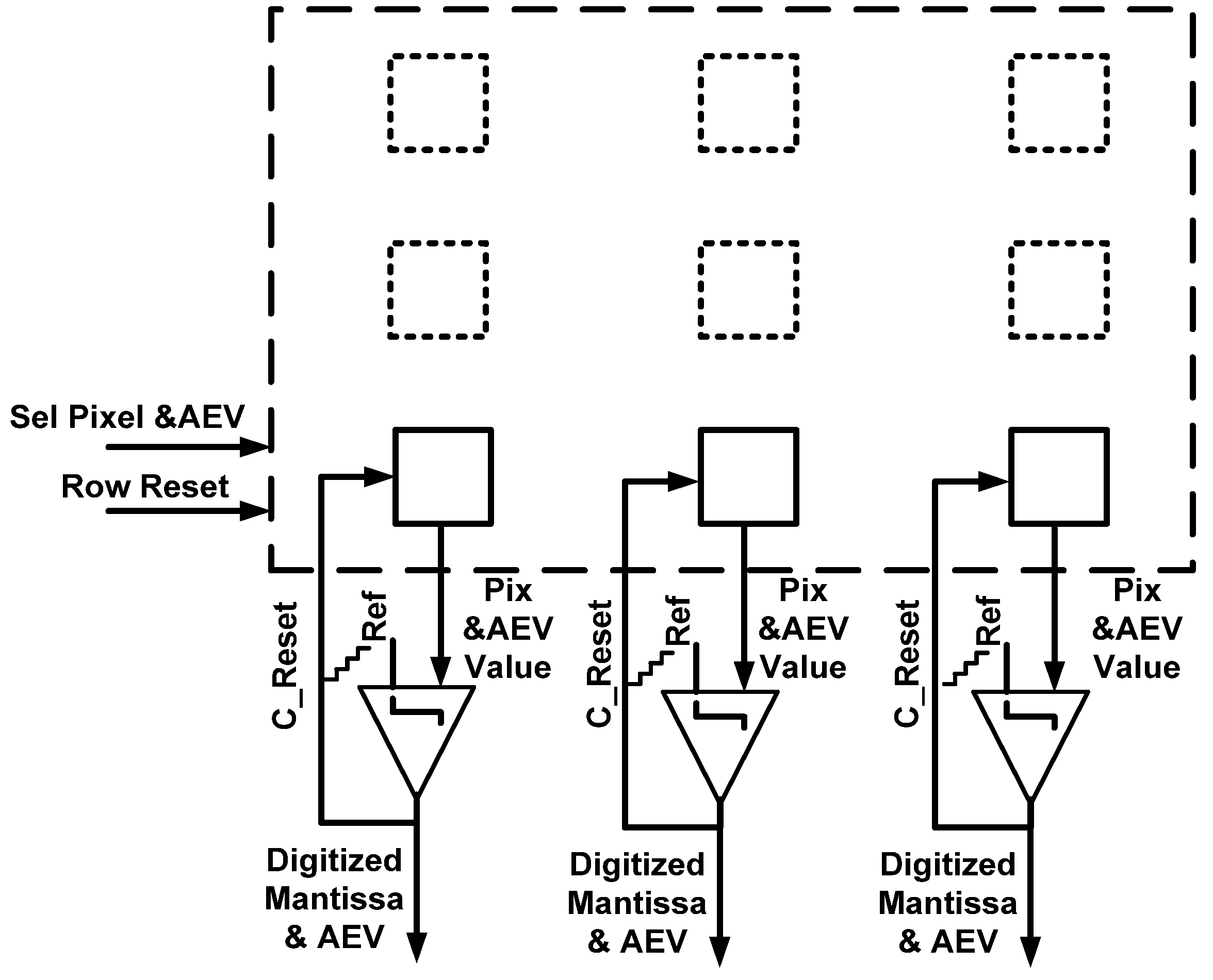
Figure 7 depicts Phase 1 for the
TYPE I pixel. At each span, the pixel (
Pix value) is being accessed by election of a specific row and is being compared to the reference signal
Ref.
After Phase 1 is completed, Phase 2 begins. During this phase, each pixel integrates in accordance to the assigned
AEV. After a certain integration slot (3) elapses, the
AEV’s within each row are selected and compared with the
Ref, which now reflects the reference values of integration times (
Figure 8).
Figure 8.
Phase 2 TYPE I pixel.
Figure 8.
Phase 2 TYPE I pixel.
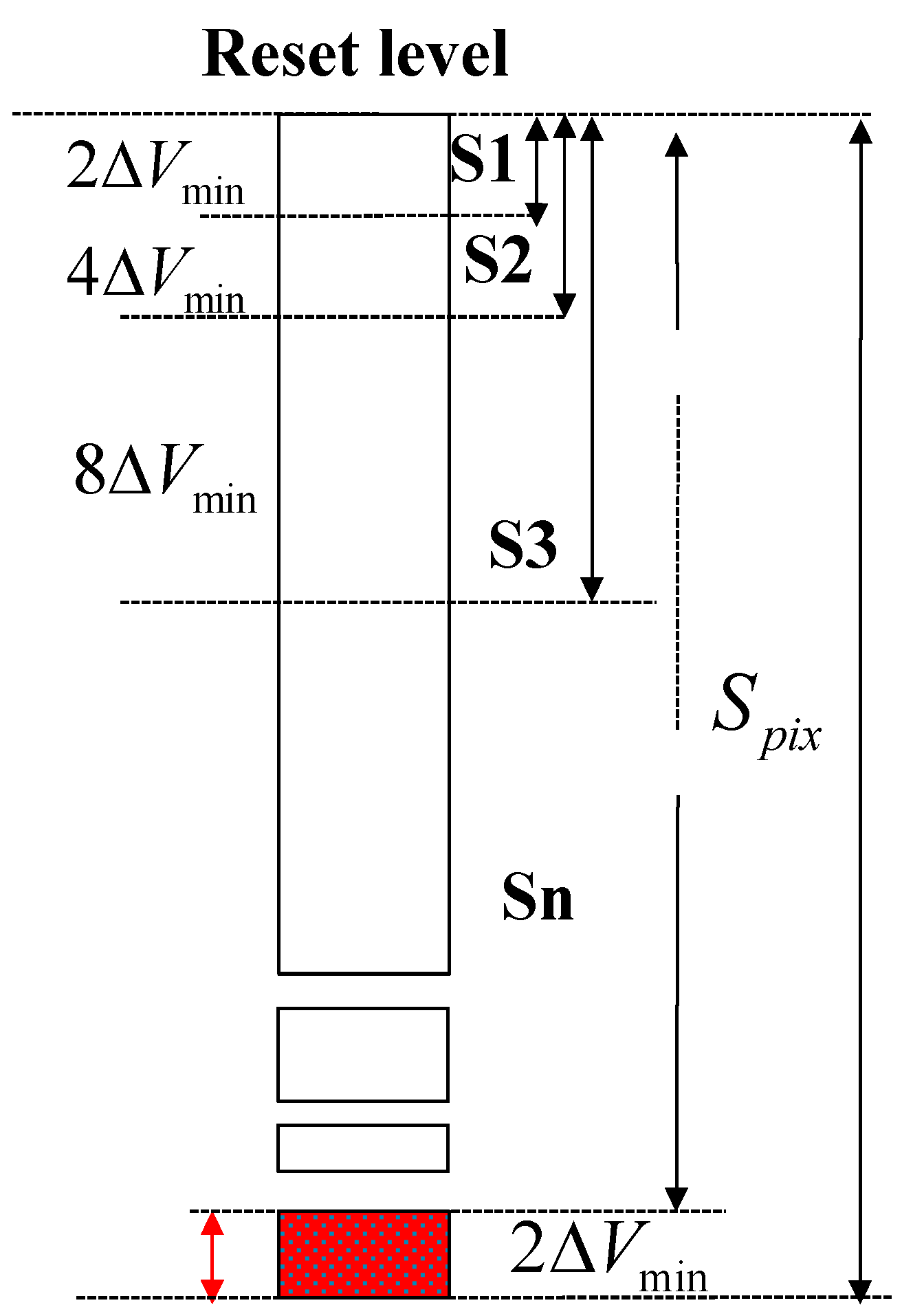
In our solution, the pixel is reset as long as its AEV is lower than the reference value.
In a
TYPE I solution, the conditional resets are applied to each pixel row sequentially. The processing time, which takes to apply the conditional reset a single pixel row
Trow_reset, is given by:
where
TAEV_read and
Tcompare are the time to sample the
AEV and to decide to reset or not the referred pixel, respectively. Since two saturation checks cannot overlap each other, the time it takes to complete a single one sets the minimal integration time
Tmin_TYPE I:
Given the minimal integration time, we can easily calculate the maximal possible DR extension factor (DRF) [
8]. Through the performed simulations, we learned that the minimal integration time
Tmin_TYPE I is 112 µs. Assuming the maximal integration time is 30 ms, we have obtained a DR extension factor equal to 256 (48 dB). The expected intrinsic DR
i.e., before the extension is 60 dBs, consequently the total DR equals 108 dBs.
In the last phase of the frame (
Figure 9), the accumulated data are accessed for the final ADC. By activating two separate select signals
Sel_Pix and
Sel_AEV, the pixel and the
AEV, respectively, are digitized using the same comparators as in Phase 1
The TYPE I design was successfully tested in various post-layout simulations, which proved its feasibility. To reduce the length of this work, we present only the post-layout simulation results of the TYPE II design because it is much more complex. To conclude, CMOS sensor based upon the presented TYPE I pixel is capable of providing a DR of almost 5 decades operating at video frame rate and providing an image with a decent resolution.
Figure 9.
Phase 3 TYPE I pixel.
Figure 9.
Phase 3 TYPE I pixel.
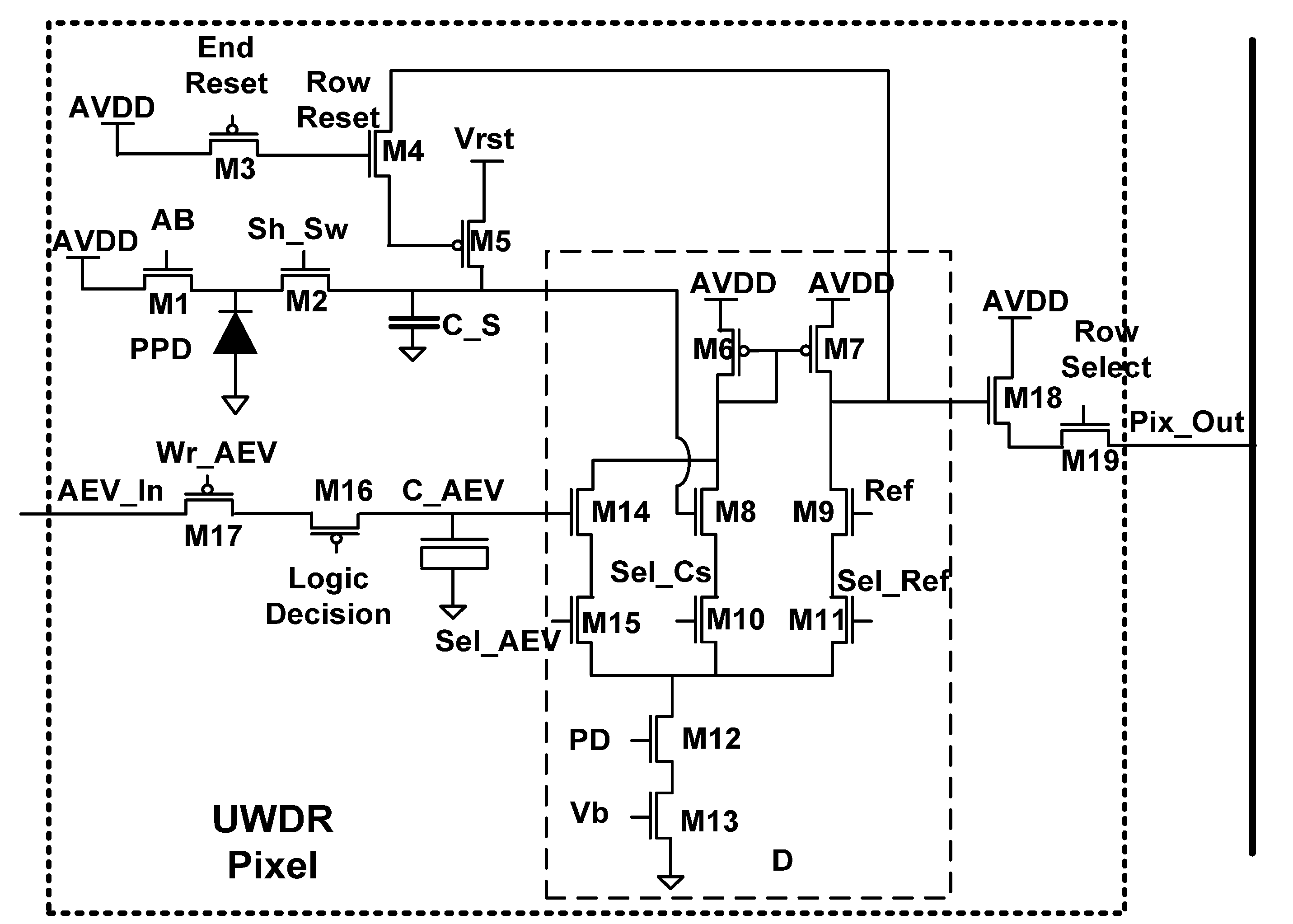
2.7. Ultra WDR (TYPE II) Pixel
The main difference between the Ultra WDR (
TYPE II) pixel and the previous
TYPE I solution lies in its accommodating a differential stage (
D) within the pixel (
Figure 10).
Figure 10.
Schematic of TYPE II Pixel.
Figure 10.
Schematic of TYPE II Pixel.
The inputs to this stage are: the pixel integration time represented by AEV (M14); the photo-generated signal (M8); and the global reference signal Ref (M9). These inputs are sampled from CAEV, CS, and Ref, respectively. By means of Sel_AEV (M15) or Sel_Cs (M10), the differential stage compares the AEV or the photo-generated signal, to the Ref. the transistor M11, controlled by Sel_Ref signal, was added to ensure an optimal matching within the differential amplifier. The bias point is controlled by an analog signal Vb (M13), which sets the current magnitude throughout the amplifier branches. To facilitate the power reduction, we inserted an additional transistor M12 in the series to the current source in order to shut down the entire stage, when no comparison is needed. The load of the D stage is implemented by two PMOS transistors: M6 and M7. The drain of the latter is connected to the drain of M4, forming a self-reset structure.
The self-reset feature of the D amplifier enables the application of the conditional reset operation during a saturation check simultaneously to every pixel within the array rather than row by row. At each saturation check, the Row Reset (M4) is raised globally, connecting the output of the D stage to the reset transistor M5. Obviously, when the amplifier’s output is low, the Cs capacitance is reset to Vrst, otherwise Cs remains without a change. To stop the reset cycle, regardless of the differential stage output, we use End Reset signal (M3), which forces AVDD on the gate of the reset transistor M5.
AEV assignments are done row by row as will be explained further. Before the assignment operation, the first AEV is asserted onto the AEV_In bus. Then, the signal Wr_AEV (M17) selects the appropriate pixels’ row. The Logic Decision signal (M16), which is driven by the column-wise common source amplifiers, enables the corresponding AEV to be sampled by the CAEV capacitor. The charge flow from the PPD is the same as in the TYPE I design throughout the whole frame.
At the end of the frame, both the AEV and the photo-generated charge are sampled nondestructively through the source follower (SF) (M18 and M19) and converted by column-wise amplifiers, as will be explained later.
Figure 11.
Layout of the TYPE II Pixel.
Figure 11.
Layout of the TYPE II Pixel.
The
TYPE II pixel was implemented in a 0.18 CMOS process (
Figure 11). All the control signals were divided into two groups: 7 analog signals, and 10 logic signals. To reduce the coupling between the control lines, we used extensive orthogonal patterning, so that part of the signals was routed along the X axis, whereas another part was laid along the Y axis. The analog signals were implemented in Metal1 and placed along the Y axis to the left and to the right of the
PPD. Such an arrangement reduced the coupling between the analog lines themselves and created a substantial separation from the rest logic signals, which were laid along the X axis. Moreover, all the signals, which were running horizontally, were implemented in Metal 3, which reduced the coupling between the pixel analog and logic lines even further. Due to the dense layout, we successfully implemented the described pixel with 17 µm pitch and 25% fill factor FF (
Figure 11).
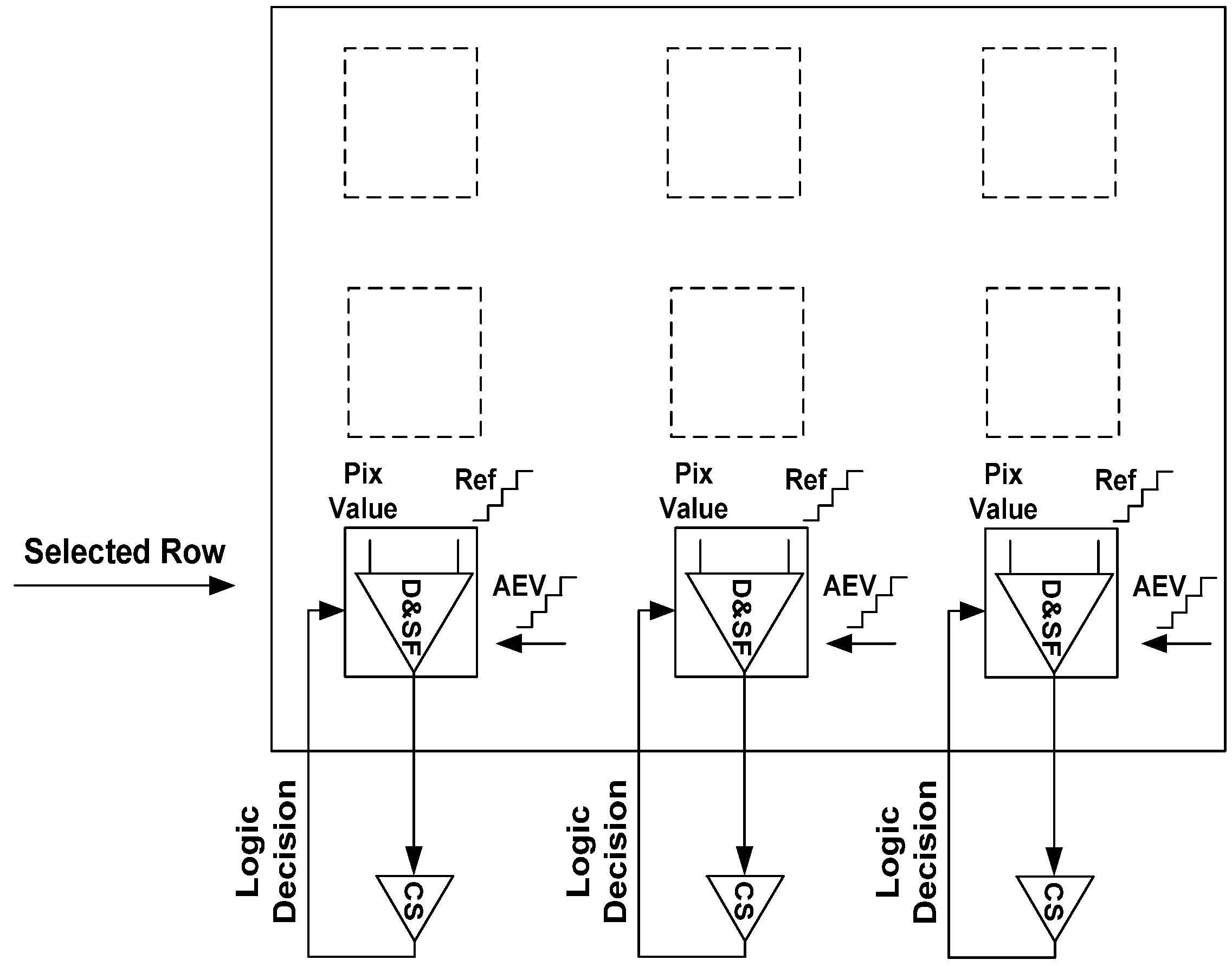
The three phases in the
TYPE II solution are described in detail below. The
AEV assignment that occurs in Phase 1 requires a high gain comparator. Since the gain of the in-pixel differential amplifier is not high enough, we added an external common source (
CS) amplifier (
Figure 12). In this way, we obtained the three stage high gain comparator: (1)
D; (2)
SF; (3)
CS, respectively. The
Pix Value is compared to
Ref inside each pixel of the selected row. The final amplification is performed by
CS, which drives the
Logic Decision signal (
Figure 12). This signal stamps the appropriate
AEV value onto
CAEV capacitance inside each pixel.
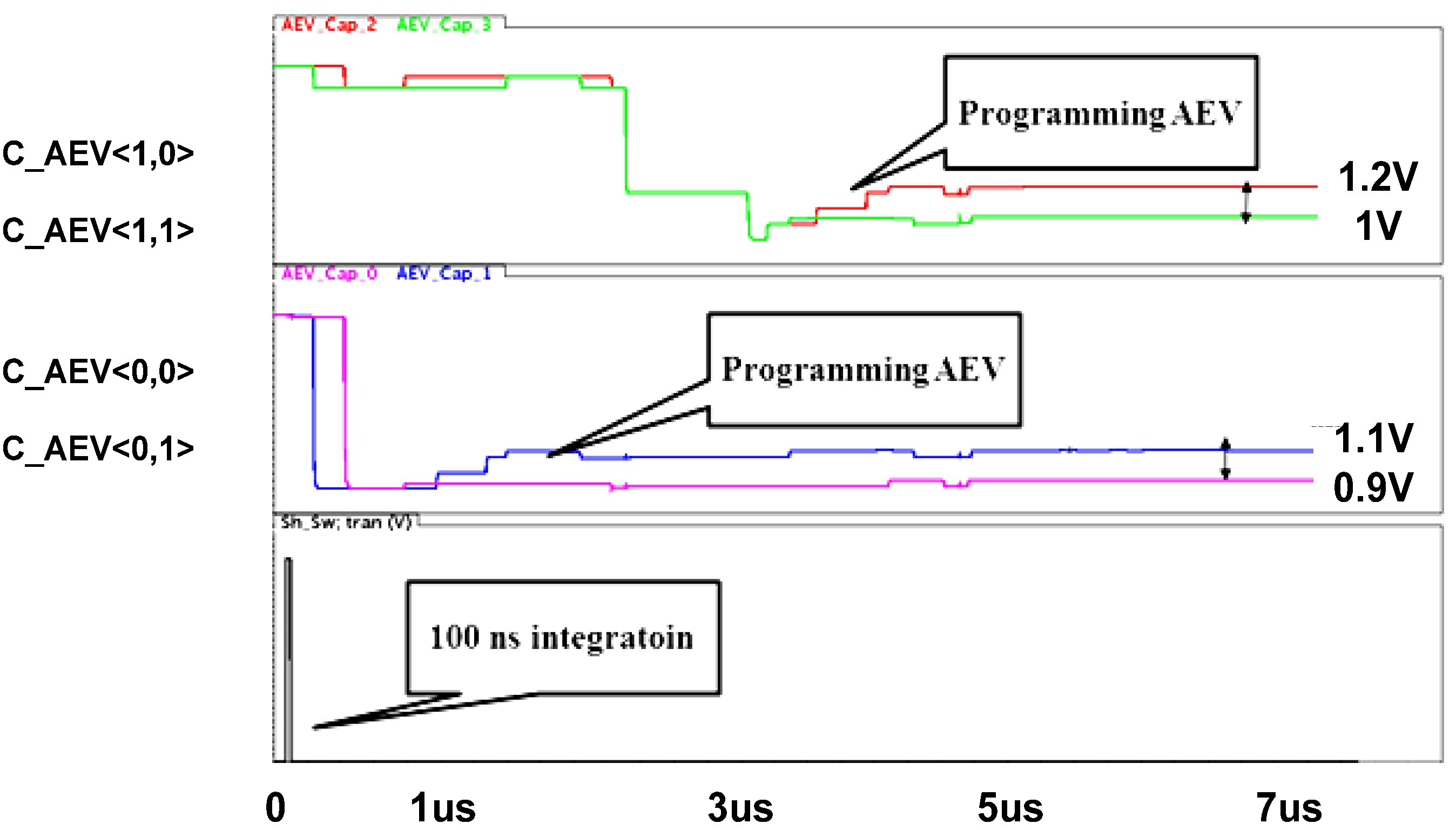
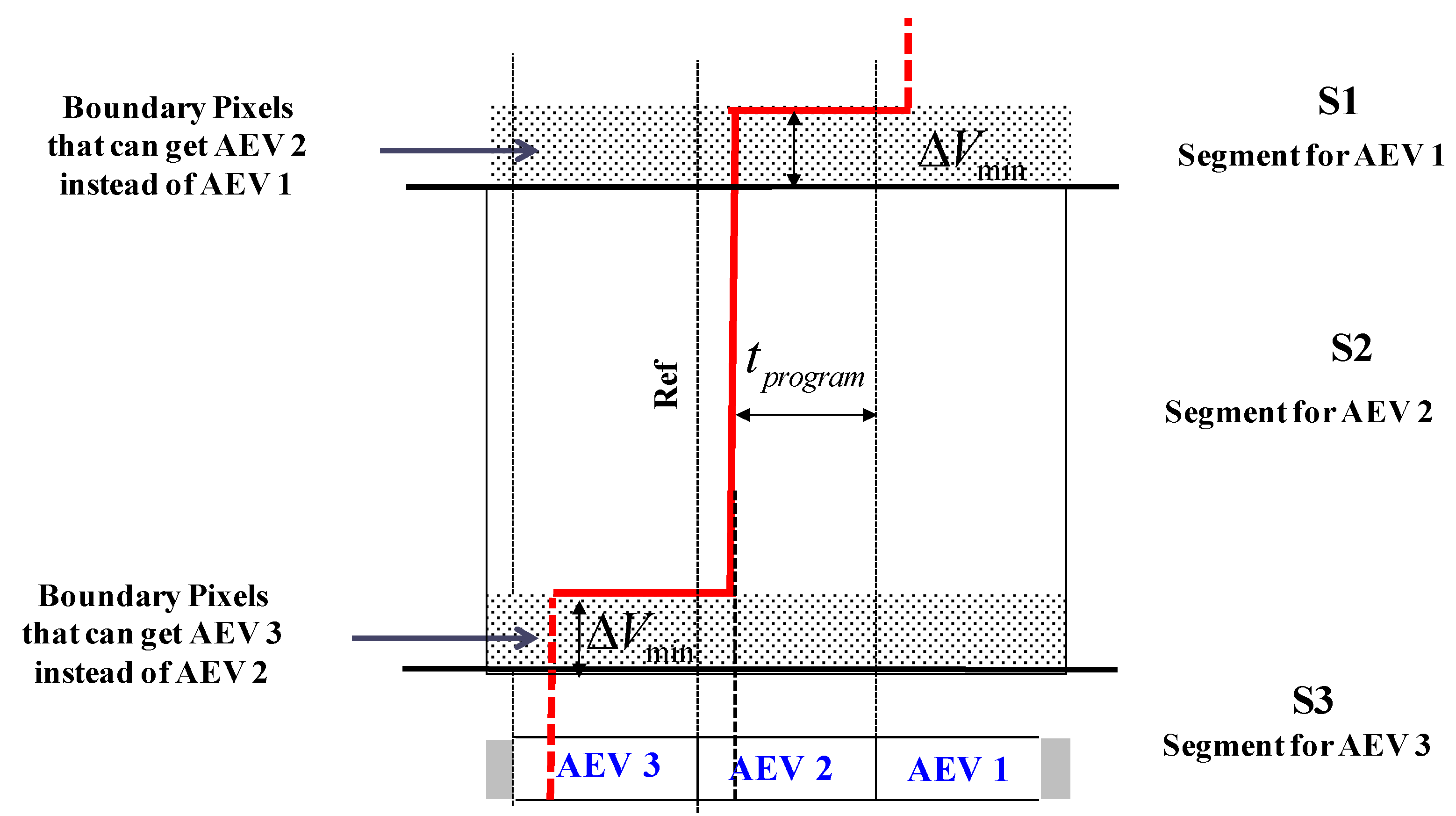
Figure 13 illustrates the flow of the
AEV assignment to a pixel matrix of 2 × 2 at the first span. Each pixel within the matrix has its own coordinates: the first denotes the row and the second denotes the column. We performed the simulation as if each pixel within this matrix receives a different incoming signal. Therefore, we stimulated the pixels with different current sources, imitating different discharge rates. The
AEV values were generated by a piecewise ascending ramp voltage ranging from 0.9 V up to 2.6 V, corresponding to 18 different values distanced by 0.1 V from each other. The first span occurs after 100ns. Then, the photo-generated charge is transferred to
CS simultaneously within the whole matrix and is compared row by row with the reference, thus causing the corresponding
AEV to be written onto
CAEV capacitance (
Figure 10). Capacitances
CAEV<0,0> and
CAEV<0,1>, found at the row <0>, are processed first, whereas row <1> capacitances are programmed after the completion of row <0> programming.
Figure 12.
Phase 1 of TYPE II Pixel.
Figure 12.
Phase 1 of TYPE II Pixel.
Figure 13.
Post-Layout Simulation of Phase 1 of TYPE II Pixel.
Figure 13.
Post-Layout Simulation of Phase 1 of TYPE II Pixel.
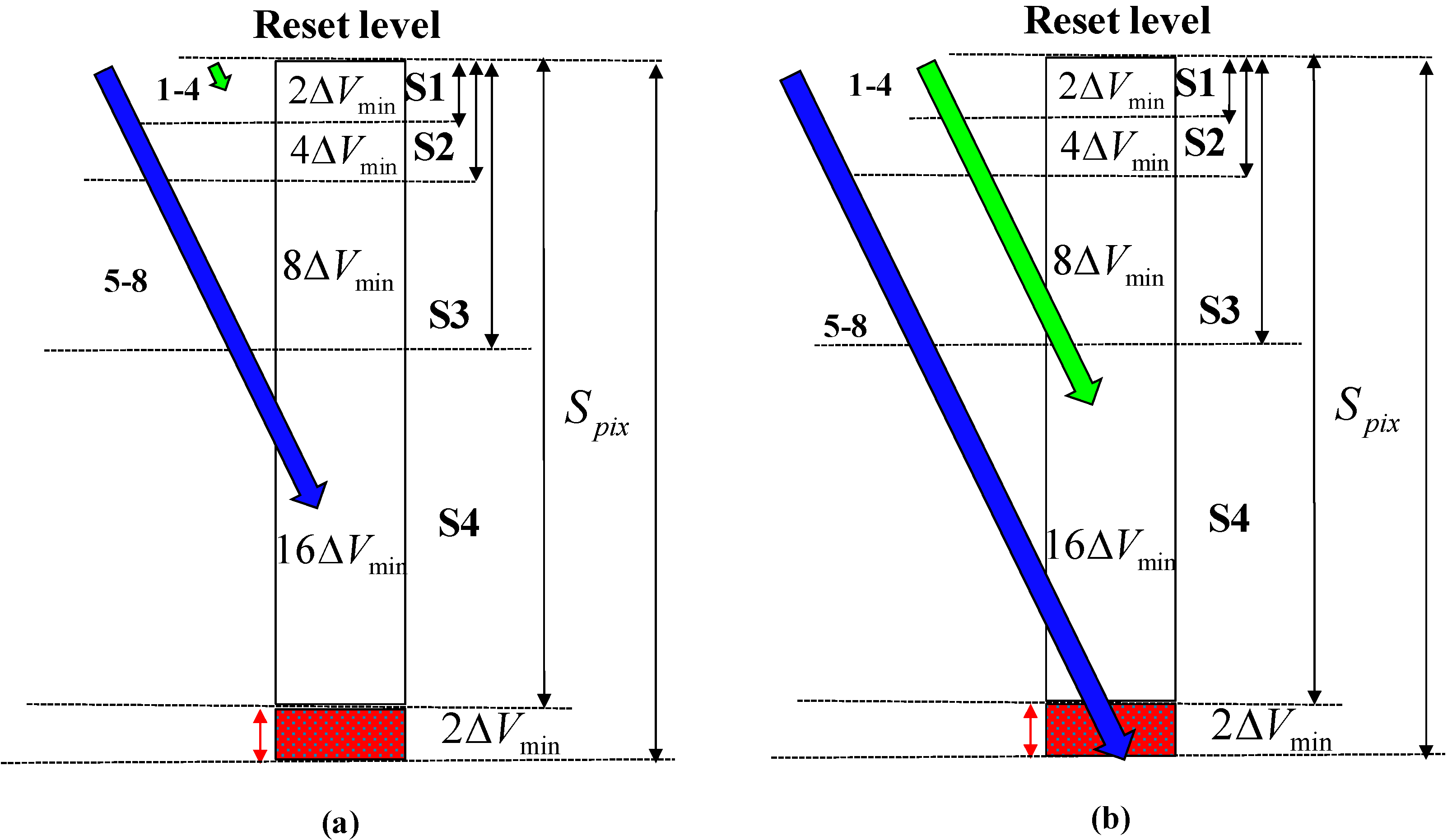
In the illustrated case, there are four different photo-generated signals, falling within four different segments; therefore every pixel is assigned a different AEV from 0.9 V to 1.2 V. The lowest AEV is assigned to the most illuminated pixel, i.e., to CAEV<0,1>, whereas the rest of the AEV’s: 1 V, 1.1 V, and 1.2 V are assigned to less illuminated pixels CAEV<1,1>, CAEV<0,0>, CAEV<1,0>, respectively. It is important to note that the adjacent AEV values differ from each other by 2∆Vmin, which is 0.1 V in this case, and this difference stays intact after the AEV’s were written to CAEV. In such a case, decoding the analog data at the end of the frame will be easy; otherwise the final pixel value will be erroneous due to a possible shift of the stored AEV values.
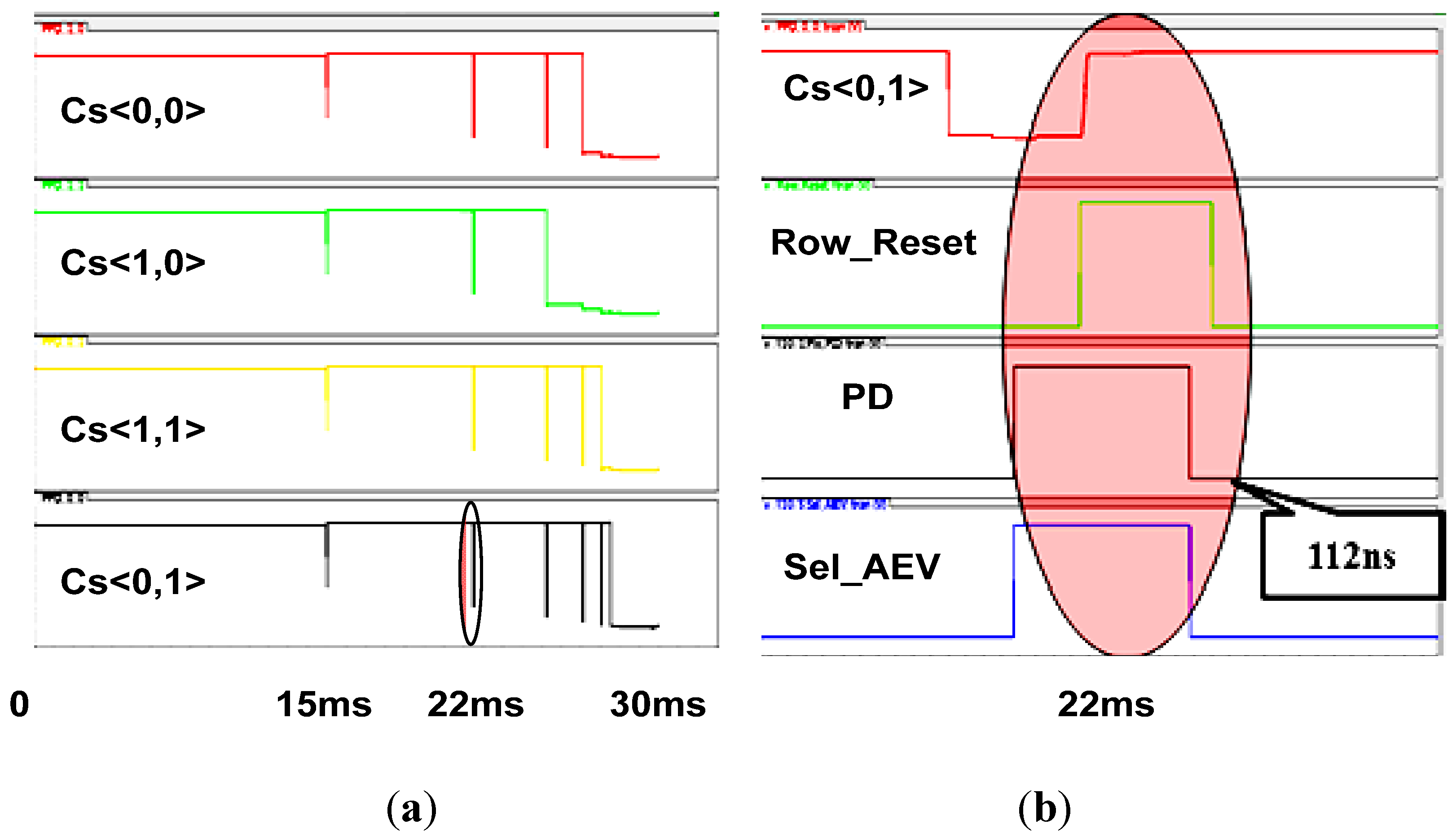
It is important to understand that the time of the first span is shorter than the minimal integration time, since, during all the spans, the available signal to be accumulated is lower than the pixel swing by 2ΔVmin. However, during the next phase the entire pixel swing is available, thus the real integration period will be somewhat higher. In the specific example we have discussed, the minimal integration time will be not 100 ns, but rather 112 ns.
Phase 2 in a
TYPE II pixel is ultra-fast. Due to its self-reset ability, the reset decision inside each pixel is autonomously fed from the differential stage through
M4 to the gate of
M5 (
Figure 10). Consequently, each pixel is reset independently upon the comparison of its own
AEV with the global reference
Ref (
Figure 14). Therefore, the minimal integration time for this design is:
Figure 14.
Phase 2 of TYPE II Pixel.
Figure 14.
Phase 2 of TYPE II Pixel.
Equation (6), which describes the minimal pixel conditional reset time, sets the minimal integration time and, as such, defines the available DR extension. In this case, the minimal integration times can be set as low as 112ns, which enables the DR to be extended by over five decades.
Figure 15a,b illustrates the flow of Phase 2 on a matrix of 2 × 2 pixels. There are four different illuminated pixels, each with its own
AEV in Phase 1. At Phase 2, every pixel is reset in accordance with its
AEV (
Figure 15a). The bottom pixel,
CS<0,1>, has the lowest
AEV and therefore it is reset for five times; whereas the pixel
CS<1,0>with the highest
AEV is reset only twice. A close–up of the typical reset sequence is presented in
Figure 15b. First, the differential stage inside the pixel is activated by raising the
PD signal; then, the
AEV is compared to a reference by raising
Sel_AEV. After this, the bias point of the amplifier stabilizes, the
Row Reset signal is activated, which enables the decision to reach the reset transistor. In the specific case we have presented, the reset decision is positive and therefore the capacitance
Cs<0,1> is charged up. The whole sequence lasts for 112 ns; thus, by assuming a typical frame time of 30 ms, we obtain DR extension of 109 dB [8]. Adding to this the intrinsic DR of 60 dBs (10 bits), we obtain overall DR of 170 dB approximately.
Figure 15.
Post-Layout simulation of: (a) 4 different pixel signals during Phase 1; (b) a close up of a single self-reset cycle.
Figure 15.
Post-Layout simulation of: (a) 4 different pixel signals during Phase 1; (b) a close up of a single self-reset cycle.
The final A/D conversion occurs at Phase 3. We use the same comparator configuration as depicted in
Figure 12 to perform a single slope conversion to a photo-generated signal (
Mantissa) and to an
AEV.
Figure 16 depicts the process of A/D conversion to the stored
AEV and the pixel
Mantissa. First, the pixel
AEV is converted using a ramp with reduced (“coarse”) resolution. It can easily be observed that the
Ref signal spans the
AEV domain in a reduced number of steps, which corresponds to the “coarse” conversion; whereas, the pixel
Mantissa is spanned by the reference with a much higher (“fine”) resolution. As a matter of fact, after the
Mantissa is converted, the capacitance
CS storing it is being reset for the next frame. The capacitance holding the
AEV is not necessary to be reset, since it will be assigned the new
AEV in Phase 1 of the subsequent frame in any case.
Figure 16.
Post-Layout Simulation of Phase 3 of TYPE II pixel.
Figure 16.
Post-Layout Simulation of Phase 3 of TYPE II pixel.
In conclusion, the relatively complex structure of the
TYPE II pixel has enabled a very large DR extension and has substantially simplified the second and the third phases of the proposed algorithm.
Figure 15,
Figure 16 prove the feasibility of the
TYPE II design and indicate that sensor based upon a
TYPE II pixel can be successfully implemented in a silicon process.
2.8. A Power Profile of TYPE I and TYPE II Designs
Another important factor is the examination of the power performance of the TYPE I and TYPE II designs, since, if they were power hungry, it would be pointless using them. We made both of the designs optimized for low power using the following methods: the two stacked transistors scheme, and multiple power supplies. The result was that the leakage within the pixels was successfully minimized, and the power supplies could be lowered easily without degrading the anticipated sensor's performance.
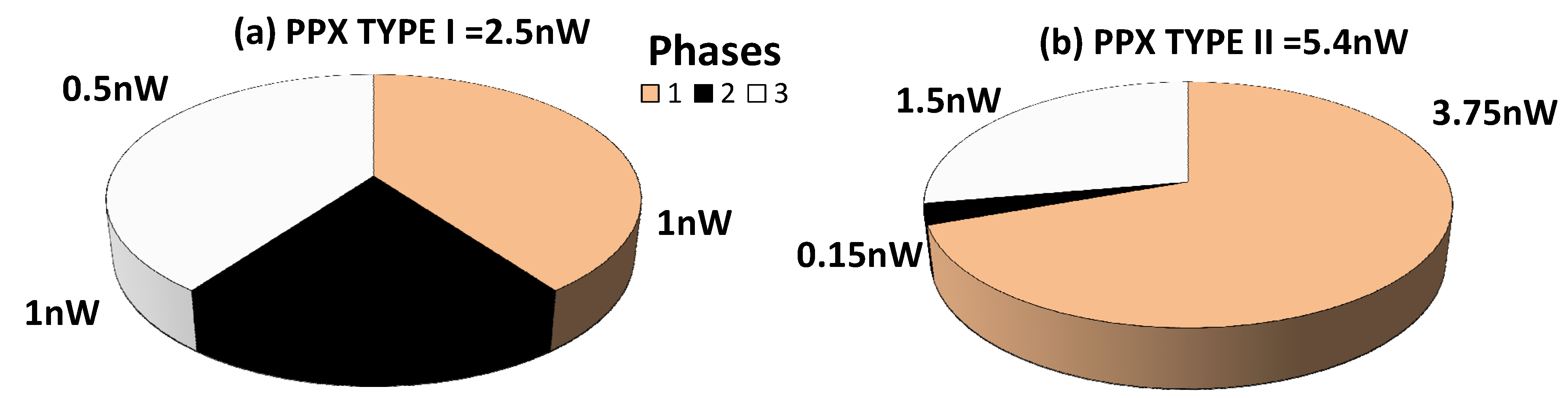
In analyzing the
TYPE I power per pixel (
PPX), we have concluded that most of the power is consumed during the
AEV assignment (Phase 1) and the A/D conversion (Phase 3), because these two operations require activating the comparators for a longer period of time than in Phase 2 (
Figure 17a).
In
TYPE II, the relative power contribution of Phase 2 is also the lowest, in comparison with the two other phases, as its overall effective duration is the shortest one (
Figure 17b). Most of the power is consumed during Phase 1, which contains an increased number of spans and, thereby, in aggregate, lasts longer than Phase 3. Phase 3’s contribution to
PPX, is almost the same as in the
TYPE I case due to similar flow of the data conversion.
Based on these simulations, we have concluded that the two presented designs consume power of 2.5 nW and 5.4 nW, respectively. Taking into account the anticipated extraordinary DR extension they provide, we have found that the power budget is low and definitely appropriate to the state-of-the art CMOS image sensors [
25].
Figure 17.
Power per Pixel Distribution of TYPE I and TYPE II Designs. (a) PPX TYPE I = 2.5 nW; (b) PPX TYPE I = 5.4 nW.
Figure 17.
Power per Pixel Distribution of TYPE I and TYPE II Designs. (a) PPX TYPE I = 2.5 nW; (b) PPX TYPE I = 5.4 nW.
To summarize the anticipated performance of the proposed designs, we provide
Table 1, where different state-of-the art WDR solutions are compared with respect to several key attributes such as fabrication technology, WDR technique (WDR T.), pixel size, fill factor (FF), DR, SNR, power per pixel (PPX), and frame rate (FR).
Table 1.
Comparison between state-of-the art WDR image sensors.
Table 1.
Comparison between state-of-the art WDR image sensors.
| Parameter | [11] | [5] | [12] | [14] | [21] | TYPE I | TYPE II |
|---|
| Technology | 0.18 µm | 0.09 µm | 0.18 µm | 0.35 µm | 0.18 µm | 0.18 µm | 0.18 µm |
| WDR T. | Well Cap.Adjustment | Well Cap.Adjustment | Frequency | TFS | Multiple Capt. | Multiple Resets | Multiple Resets |
| Pixel Size | 3 µm × 3 µm | 5.86 µm × 5.86 µm | 23 µm × 23 µm | 81.5 µm × 76.5 µm | 5.6 µm × 5.6 µm | 14 µm × 14 µm | 17 µm × 17 µm |
| FF | - | - | 25% | 2% | 45% | 40% | 25% |
| DR | 100 dB | 83 dB | 130 dB | 100 dB | 99d B | 108 dB | 170 dB |
| SNR | 48 dB* | 48 dB * | - | - | - | 48 dB * | 48 dB * |
| PPX | - | 400 nW ** | 250 nW | ≤6.4 µW ** | 10 nW ** | 2.5 nW | 5.4 nW |
| FR | - | 30 | - | - | 15 | 33 | 33 |
From
Table 1, we can understand that the pixel sizes of pixels presented in our work are mediocre. They are substantially larger than those associated with well capacity adjustment and multiple captures, but much smaller than frequency and TFS based sensors. Important to note that both of our designs maintain a decent FF relatively other listed solutions due to area effective layout. The DR of proposed herein designs emphasizes the extraordinary ability of multiple resets algorithm to extend the pixel dynamic range.
TYPE I provides remarkable DR, whilst
TYPE II brings it to extreme values. Moreover, such DR is obtained, maintaining excellent SNR (see Appendix B). Not less important to note that both of proposed designs operate at video frame rate and present the best power performance.