Development of a Kelp-Type Structure Module in a Coastal Ocean Model to Assess the Hydrodynamic Impact of Seawater Uranium Extraction Technology
Abstract
:1. Introduction
2. Methodology
2.1. Kelp-Type Structure Module Development

 = velocity vector (m/s).
= velocity vector (m/s).






2.2. Module Validation
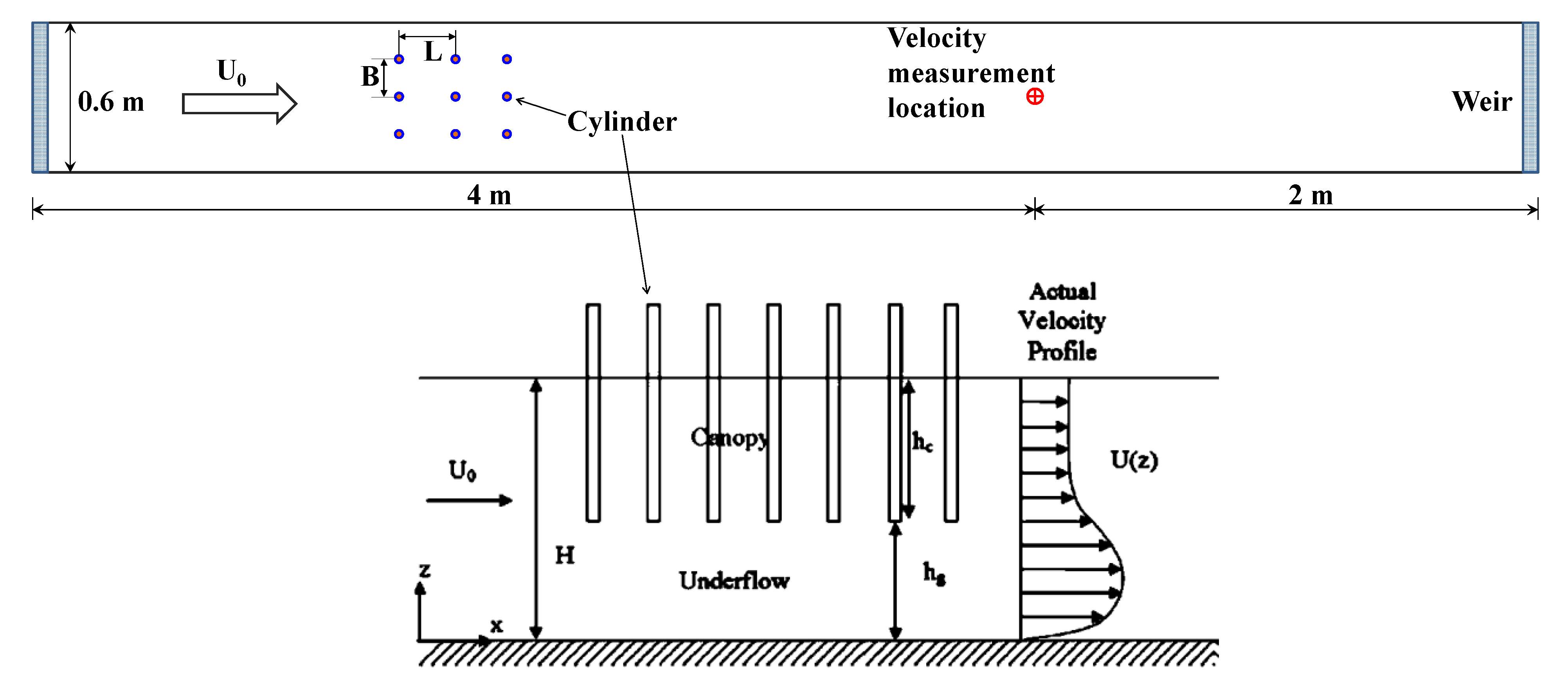
| Validation Run | H (mm) | hg (mm) | L (mm) | B (mm) | a (m−1) | Q (L/s) |
|---|---|---|---|---|---|---|
| A | 200 | 100 | 100 | 50 | 1.908 | 10.5 |
| B | 200 | 100 | 150 | 50 | 1.272 | 10.1 |
| C | 200 | 100 | 200 | 50 | 0.954 | 10.1 |
| D | 200 | 100 | 200 | 100 | 0.477 | 10.3 |

3. Results and Discussion
3.1. Kelp-Type Module Validation
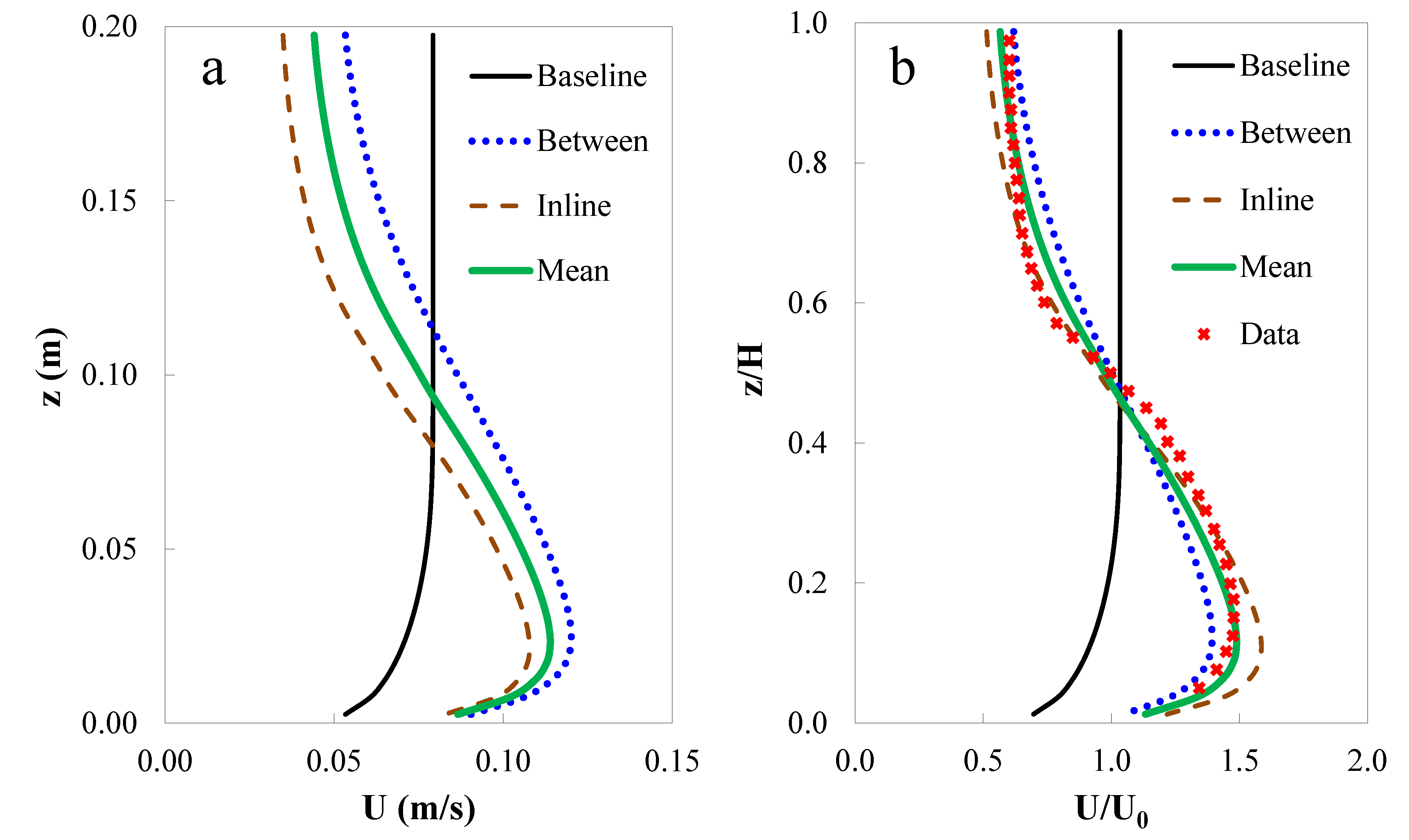

 , where ηm and η° stand for model predictions and laboratory observations, respectively, ηo is the mean of observations).
, where ηm and η° stand for model predictions and laboratory observations, respectively, ηo is the mean of observations).
| Validation Run | Velocity | Turbulent Stress | ||
|---|---|---|---|---|
| R2 | RE (%) | R2 | RE (%) | |
| A | 0.98 | 1.2 | 0.94 | 6.0 |
| B | 0.98 | 1.4 | 0.98 | 3.6 |
| C | 0.98 | 1.7 | 0.94 | 5.5 |
| D | 0.97 | 2.5 | 0.93 | 5.0 |

3.2. Module Applications—Kelp Forest and Braid Adsorbent Farm Simulation

4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Bardi, U. Extracting minerals from seawater: An energy analysis. Sustainability 2010, 2, 980–992. [Google Scholar] [CrossRef]
- Davies, R.V.; Kennedy, J.; McIlroy, R.W.; Spence, R.; Hill, K.M. Extraction of uranium from sea water. Nature 1964, 203, 1110–1115. [Google Scholar] [CrossRef]
- Annual Report: Powerful Partnerships: The Federal Role in International Cooperation on Energy Innovation; Office of the President of the United States: Washington, DC, USA, June 1999.
- Tamada, M.; Seko, N.; Kasai, N.; Shimizu, T. Cost estimation of uranium recovery from seawater with system of braid type adsorbent. Trans. Atomic Energy Soc. Jpn. 2006, 5, 358–363. [Google Scholar]
- Sugo, T.; Tamada, M.; Seguchi, T.; Shimizu, T.; Uotani, M.; Kashima, R. Recovery system for uranium from seawater with fibrous adsorbent and its preliminary cost estimation. J. Atomic Energy Soc. Jpn. 2001, 43, 1010–1016. [Google Scholar] [CrossRef]
- Jackson, G.A. Currents in the high drag environment of a coastal kelp stand off California. Cont. Shelf Res. 1998, 17, 1913–1928. [Google Scholar] [CrossRef]
- Grant, J.; Bacher, C. A numerical model of flow modification induced by suspended aquaculture in a Chinese Bay. Can. J. Fish. Aquat. Sci. 2001, 58, 1003–1011. [Google Scholar] [CrossRef]
- Plew, D.R. Shellfish farm-induced changes to tidal circulation in an embayment, and implications for seston depletion. Aquac. Environ. Interact. 2011, 1, 201–214. [Google Scholar] [CrossRef]
- Struve, J.; Falconer, R.A.; Wu, Y. Influence of model mangrove trees on the hydrodynamics in a flume. Estuar. Coast. Shelf Sci. 2003, 58, 163–171. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured, finite-volume, three-dimensional, primitive equation ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Chen, C.; Huang, H.; Beardsley, R.; Liu, H.; Xu, Q.; Cowles, G. A finite volume numerical approach for coastal ocean circulation studies: Comparisons with finite difference models. J. Geophys. Res. 2007, 112, C03018. [Google Scholar] [CrossRef]
- Ji, R.; Davis, C.; Chen, C.; Beardsley, R. Influence of local and external processes on the annual nitrogen cycle and primary productivity on Georges Bank: A 3-D biological-physical modeling study. J. Mar. Syst. 2008, 73, 31–47. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, T.; Copping, A.E. Modeling tidal stream energy extraction and its effects on transport processes in a tidal channel and bay system using a three-dimensional coastal ocean model. Renew. Energy 2013, 50, 605–613. [Google Scholar] [CrossRef]
- Chen, C.; Beardsley, R.C.; Cowles, G. An Unstructured Grid, Finite-Volume Coastal Ocean Model: FVCOM User Manual; School for Marine Science and Technology, University of Massachusetts Dartmouth: North Dartmouth, MA, USA, 2006; p. 315. [Google Scholar]
- Plew, D.R. Depth-averaged drag coefficient for modeling flow through suspended canopies. J. Hydraul. Eng. 2011, 137, 234–247. [Google Scholar]
- Li, C.; Yan, K. Numerical investigation of wave-current-vegetation interaction. J. Hydraul. Eng. 2007, 133, 794–803. [Google Scholar] [CrossRef]
- Sheng, Y.P.; Lapetina, A.; Ma, G. The reduction of storm surge by vegetation canopies—three-dimensional simulations. Geophys. Res. Lett. 2012, 39, L20601. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S.Y. A depth-averaged two-dimensional numerical model of flow and sediment transport in open channels with vegetation. In Riparian Vegetation and Fluvial Geomorphology; American Geophysical Union: Washington, DC, USA, 2004. [Google Scholar]
- Schlichting, H. Boundary Layer Theory; McGraw Hill Book Co.: New York, NY, USA, 1968. [Google Scholar]
- Jackson, G.A.; Winant, C.D. Effect of a kelp forest on coastal currents. Cont. Shelf Res. 1983, 20, 75–80. [Google Scholar] [CrossRef]
- Rosman, J.H.; Koseff, J.R.; Monismith, S.G.; Grover, J. A field investigation into the effects of a kelp forest (Macrocystis pyrifera) on coastal hydrodynamics and transport. J. Geophys. Res. 2007, 112, C02016. [Google Scholar] [CrossRef]
- Tegner, M.J.; Dayton, P.K.; Edwards, P.B.; Riser, K.L.; Chadwick, D.B.; Dean, T.A.; Deysher, L. Effects of a large sewage spill on a kelp forest community: Catastrophe or disturbance? Mar. Environ. Res. 1995, 40, 181–224. [Google Scholar]
- Katul, G.G.; Mahrt, L.; Poggi, D.; Sanz, C. One- and two-equation models for canopy turbulence. Bound. Layer Meteorol. 2004, 113, 81–109. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, T.; Khangaonkar, T.; Long, W.; Gill, G. Development of a Kelp-Type Structure Module in a Coastal Ocean Model to Assess the Hydrodynamic Impact of Seawater Uranium Extraction Technology. J. Mar. Sci. Eng. 2014, 2, 81-92. https://doi.org/10.3390/jmse2010081
Wang T, Khangaonkar T, Long W, Gill G. Development of a Kelp-Type Structure Module in a Coastal Ocean Model to Assess the Hydrodynamic Impact of Seawater Uranium Extraction Technology. Journal of Marine Science and Engineering. 2014; 2(1):81-92. https://doi.org/10.3390/jmse2010081
Chicago/Turabian StyleWang, Taiping, Tarang Khangaonkar, Wen Long, and Gary Gill. 2014. "Development of a Kelp-Type Structure Module in a Coastal Ocean Model to Assess the Hydrodynamic Impact of Seawater Uranium Extraction Technology" Journal of Marine Science and Engineering 2, no. 1: 81-92. https://doi.org/10.3390/jmse2010081





