Integration of Epidemiological Evidence in a Decision Support Model for the Control of Campylobacter in Poultry Production
Abstract
:1. Introduction
2. Materials and Methods
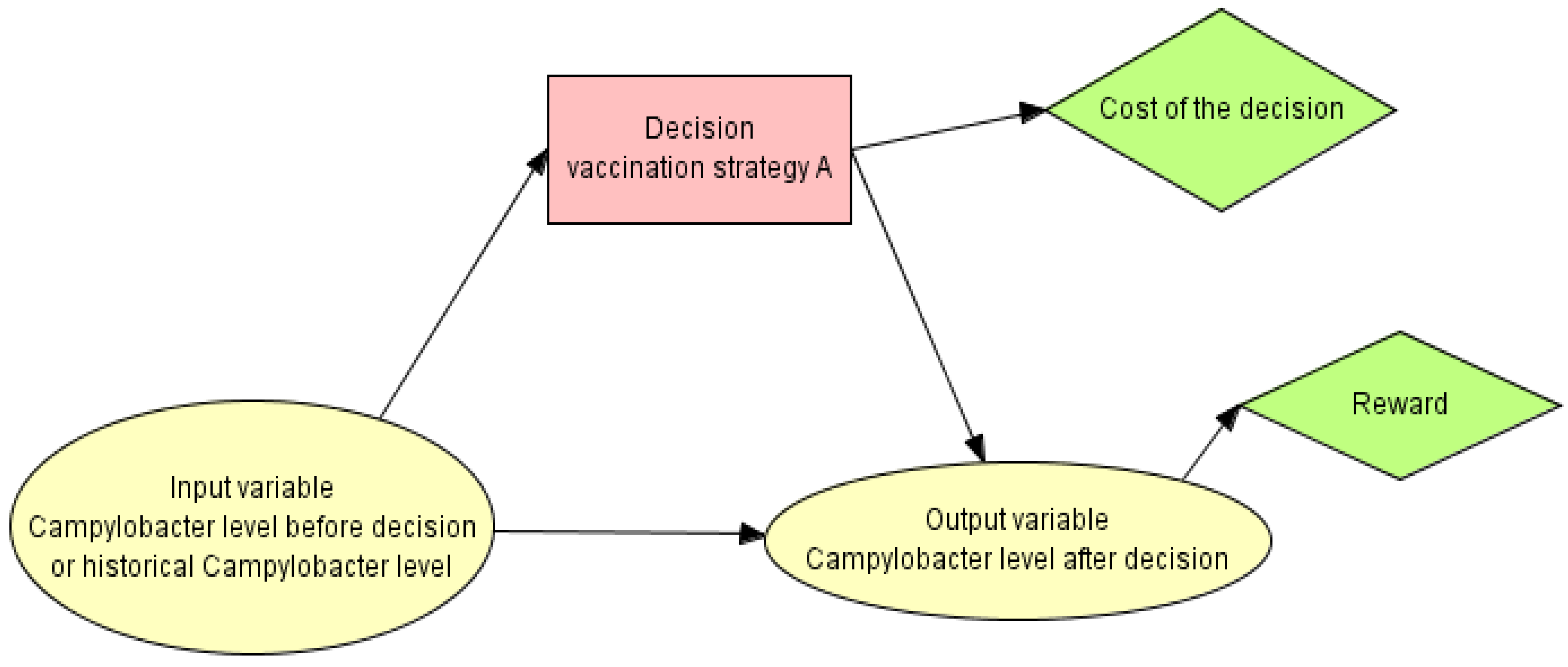
2.1. Probabilistic Graphical Models (PGMs)
| No vaccination Posterior probabilities related to expected Campylobacter levels: | Vaccination strategy A Posterior probabilities related to expected Campylobacter levels: |
|---|---|
| 0–2 logs (7%) | 0–2 logs (52%) |
| 2–4 logs (20%) | 2–4 logs (18%) |
| 4–6 logs (23%) | 4–6 logs (12%) |
| 6–8 logs (24%) | 6–8 logs (10%) |
| 8–10 logs (26%) | 8–10 logs (8%) |
| Expected cost-reward balance: | Expected cost-reward balance: |
| +0.36 euros/chicken | +0.44 euros/chicken |
| Expected cost-reward balance (gross profit) for an average flock with 20,000 chickens: 7200 euros | Expected cost-reward balance (gross profit) for an average flock with 20,000 chickens: 8800 euros |
2.2. Case Study Model
2.2.1. Current Knowledge Related to Poultry Management Factors
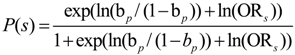
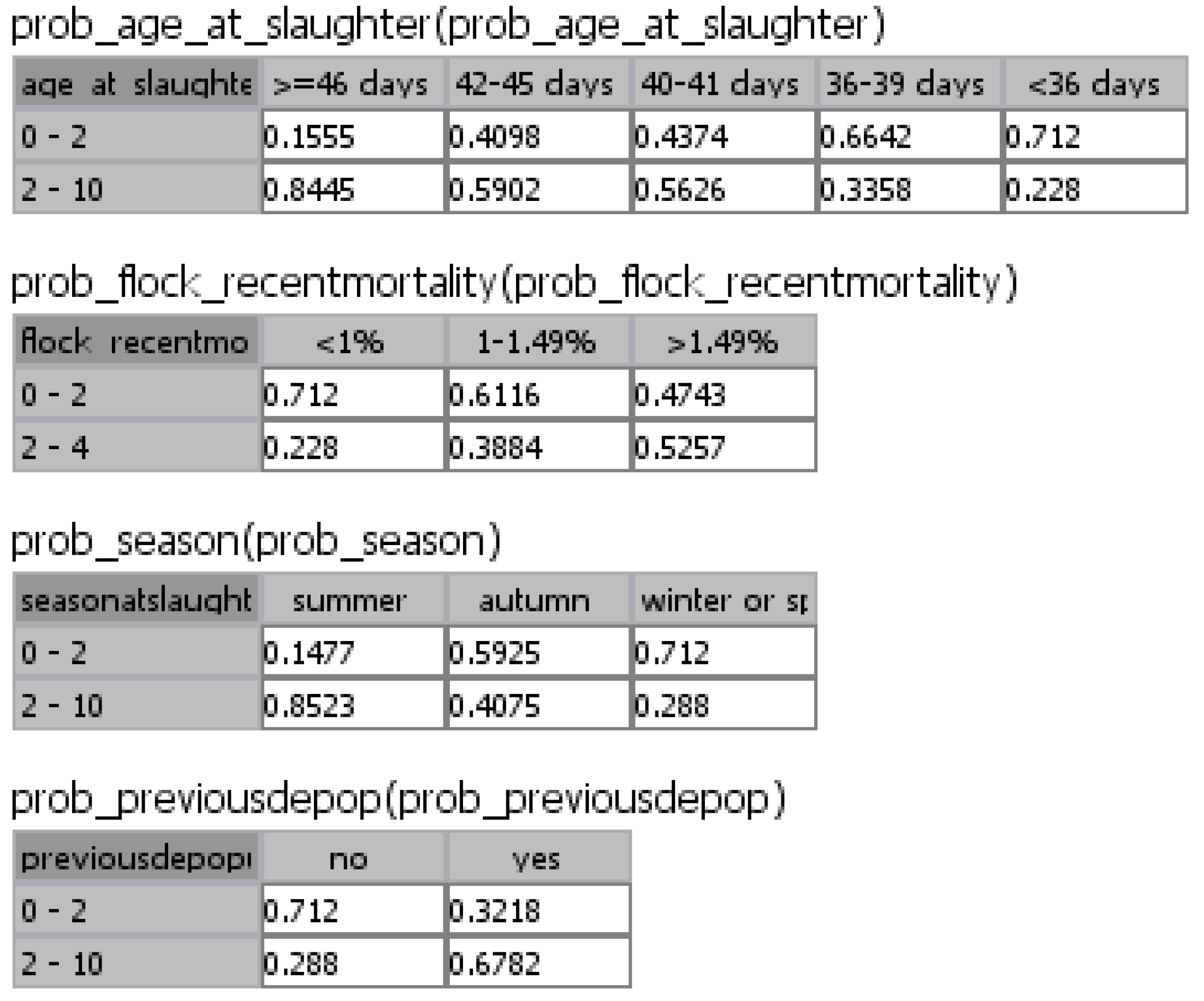
| Risk factor and frequency of occurrence | Odds Ratio (95% CI) | Probability of a Campylobacter positive flock * due to the presence of specific risk factors |
|---|---|---|
| Season | ||
| Summer (26.32%) | 14.27 (7.83–26.02) | 0.85 |
| Autumn (25.38%) | 1.70 (1.21–2.37) | 0.41 |
| Spring or winter a (48.3%) | 1 | |
| Age of broilers | ||
| ≥46 days (19.59%) | 13.43 (7.40–24.35) | 0.85 |
| 42–45 days (15.67%) | 3.56 (2.39–5.29) | 0.59 |
| 40–41 days (18.57%) | 3.18 (1.42–7.12) | 0.57 |
| 36–39 days (21.98%) | 1.25 (0.86–1.81) | 0.34 |
| <36 days a (24.19%) | 1 | |
| Flock recent mortality | ||
| >1.49% (32.22%) | 2.74 (1.18–6.40) | 0.53 |
| 1.00%–1.49% (29.35%) | 1.57 (1.12–2.21) | 0.39 |
| <1.00% a (38.43%) | 1 | |
| Previous partial depopulation | ||
| Yes (64.94%) | 5.21 (2.89–9.38) | 0.68 |
| No a (35.06%) | 1 |
2.2.2. Cost-Reward Function
| Campylobacter numbers (logs) | 0–2 | 2–4 | 4–6 | 6–8 | 8–10 |
|---|---|---|---|---|---|
| Gross profit (£/chicken) | 0.52 | 0.43 | 0.36 | 0.29 | 0.23 |
2.2.3. Designing the PGM
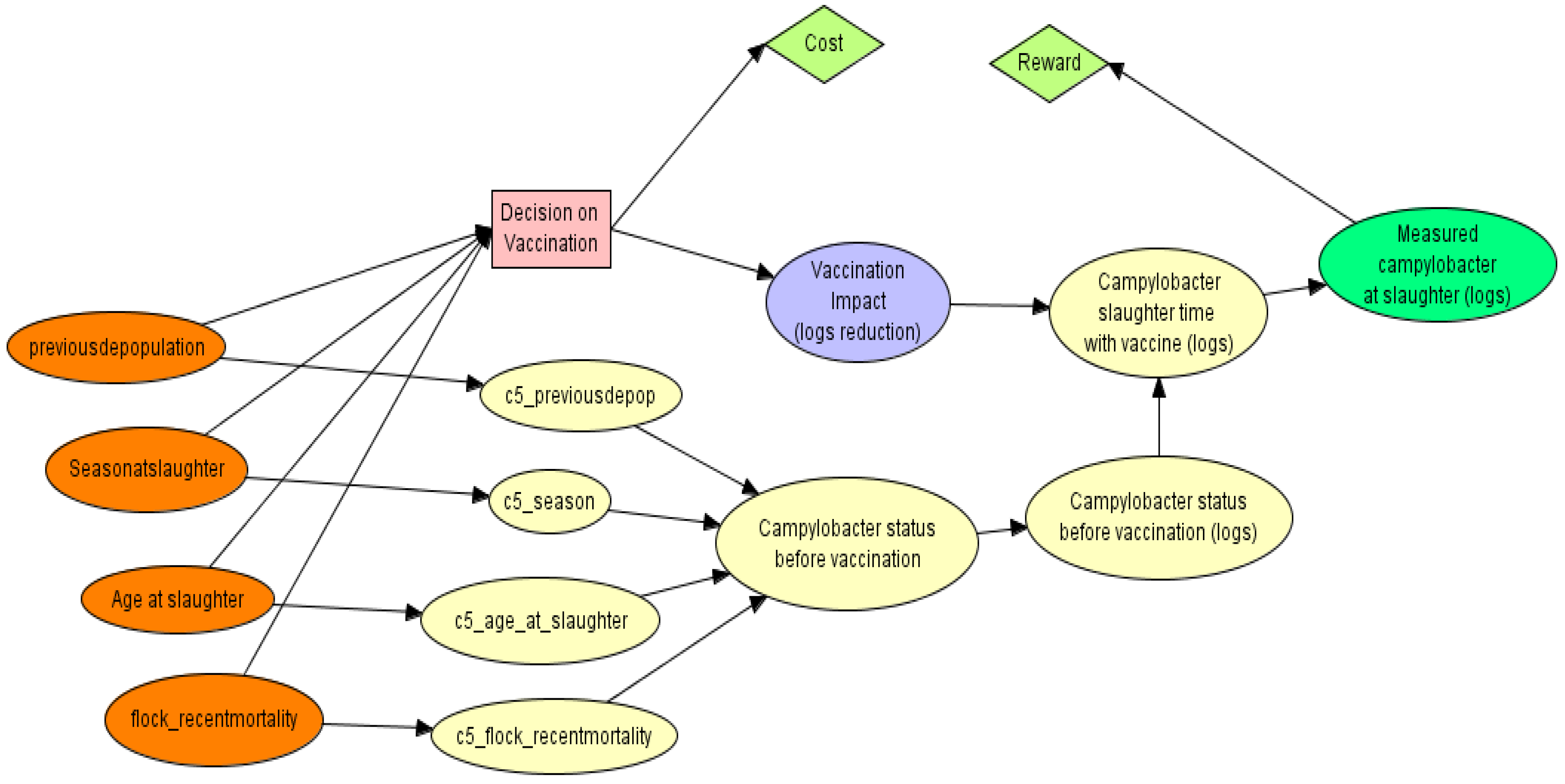
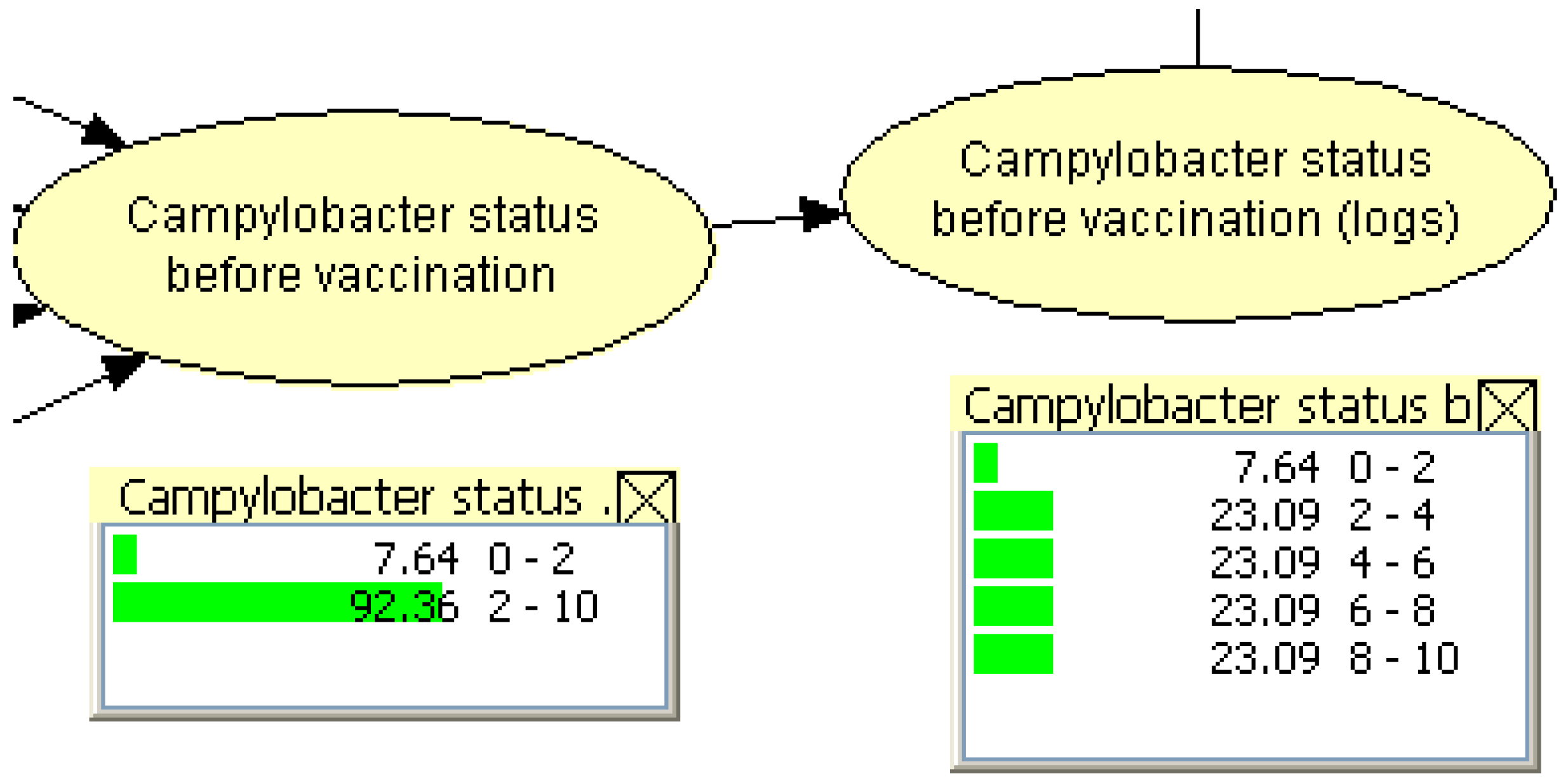
2.2.4. Sensitivity Analyses
3. Results
3.1. Results from the Model Commercial Broilers Vaccination UK Model (ComBVacUK)
| Best-case scenario | Worst-case scenario | “Most likely” scenario (based on study data [35]) |
|---|---|---|
| Spring or winter (100%) | Summer (100%) | Season |
| Summer (26.32%) | ||
| Autumn (25.38%) | ||
| Spring or winter a (48.3%) | ||
| Age of broilers | Age of broilers | Age of broilers |
| ≤36 days (100%) | ≥46 days (100%) | ≥46 days (19.59%) |
| 42–45 days (15.67%) | ||
| 40–41 days (18.57%) | ||
| 36–39 days (21.98%) | ||
| <36 days a (24.19%) | ||
| Flock recent mortality | Flock recent mortality | Flock recent mortality |
| <1.00% (100%) | >1.49% (100%) | >1.49% (32.22%) |
| 1.00%–1.49% (29.35%) | ||
| <1.00% a (38.43%) | ||
| Previous partial depopulation | Previous partial depopulation | Previous partial depopulation |
| No (100%) | Yes (100%) | Yes (64.94%) |
| No a (35.06%) |
| Scenarios | |||
|---|---|---|---|
| Best-case scenario | Worst-case scenario | “Most likely” scenario (based on study data from the UK [35]) | |
| Posterior probabilities related to expected Campylobacter levels when implementing no additional protective measure | 0–2 logs (25.70%) | 0–2 logs (0.35%) | 0–2 logs (7.27%) |
| 2–4 logs (18.58%) | 2–4 logs (24.91%) | 2–4 logs (23.18%) | |
| 4–6 logs (18.58%) | 4–6 logs (24.91%) | 4–6 logs (23.18%) | |
| 6–8 logs (18.58%) | 6–8 logs (24.91%) | 6–8 logs (23.18%) | |
| 8–10 logs (18.58%) | 8–10 logs (24.91%) | 8–10 logs (23.18%) | |
| Cost-reward balance: 0.38 £/chicken | Cost-reward balance: 0.33 £/chicken | Cost-reward balance: 0.34 £/chicken | |
| Flock with 50,000 chickens = 19,000 £ | Flock with 50,000 chickens = 16,500 £ | Flock with 50,000 chickens = 17,000 £ | |
| Posterior probabilities related to expected Campylobacter levels after the implementation of a decision (Vaccine B) | Vaccine B | Vaccine B | Vaccine B |
| 0–2 logs (35%) | 0–2 logs (12.82%) | 0–2 logs (18.87%) | |
| 2–4 logs (18.59%) | 2–4 logs (24.94%) | 2–4 logs (23.21%) | |
| 4–6 logs (17.67%) | 4–6 logs (23.70%) | 4–6 logs (22.05%) | |
| 6–8 logs (15.81%) | 6–8 logs (21.21%) | 6–8 logs (19.74%) | |
| 8–10 logs (12.93%) | 8–10 logs (17.34%) | 8–10 logs (16.14%) | |
| Expected cost-reward balance: 0.38 £/chicken | Expected cost-reward balance: 0.34 £/chicken | Expected cost-reward balance: 0.35 £/chicken | |
| Flock with 50,000 chickens = 19,000 £ | Flock with 50,000 chickens = 17,000 £ | Flock with 50,000 chickens = 17,500 £ | |
3.2. Results from the Sensitivity Analyses
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Pebody, R.G.; Ryan, M.J.; Wall, P.G. Outbreaks of Campylobacter infection: Rare events for a common pathogen. Commun. Dis. Rep. CDR Rev. 1997, 7, 33–37. [Google Scholar]
- Neimann, J.; Engberg, J.; Molbak, K.; Wegener, H.C. A case-control study of risk factors for sporadic Campylobacter infections in Denmark. Epidemiol. Infect. 2003, 130, 353–366. [Google Scholar]
- Bouwknegt, M.; van de Giessen, A.W.; Dam-Deisz, W.D.; Havelaar, A.H.; Nagelkerke, N.J.; Henken, A.M. Risk factors for the presence of Campylobacter spp. in Dutch broiler flocks. Prev. Vet. Med. 2004, 62, 35–49. [Google Scholar] [CrossRef]
- Wingstrand, A.; Neimann, J.; Engberg, J.; Nielsen, E.M.; Gerner-Smidt, P.; Wegener, H.C.; Mølbak, K. Fresh chicken as main risk factor for Campylobacteriosis, Denmark. Emerg. Infect. Dis. 2006, 12, 280–285. [Google Scholar] [CrossRef]
- Arsenault, J.; Letellier, A.; Quessy, S.; Normand, V.; Boulianne, M. Prevalence and risk factors for Salmonella spp. and Campylobacter spp. caecal colonization in broiler chicken and turkey flocks slaughtered in Quebec, Canada. Prev. Vet. Med. 2007, 81, 250–264. [Google Scholar] [CrossRef]
- Wilson, D.J.; Gabriel, E.; Leatherbarrow, A.J.; Cheesbrough, J.; Gee, S.; Bolton, E.; Fox, A.; Fearnhead, P.; Hart, C.A.; Diggle, P.J. Tracing the source of Campylobacteriosis. PLoS. Genet. 2008, 4, e1000203. [Google Scholar] [CrossRef]
- Sheppard, S.K.; Dallas, J.F.; Strachan, N.J.; MacRae, M.; McCarthy, N.D.; Wilson, D.J.; Gormley, F.J.; Falush, D.; Ogden, I.D.; Maiden, M.C.; et al. Campylobacter genotyping to determine the source of human infection. Clin. Infect. Dis. 2009, 48, 1072–1078. [Google Scholar] [CrossRef]
- Sears, A.; Baker, M.G.; Wilson, N.; Marshall, J.; Muellner, P.; Campbell, D.M.; Lake, R.J.; French, N.P. Marked Campylobacteriosis decline after interventions aimed at poultry, New Zealand. Emerg. Infect. Dis. 2011, 17, 1007–1015. [Google Scholar] [CrossRef]
- Ansari-Lari, M.; Hosseinzadeh, S.; Shekarforoush, S.S.; Abdollahi, M.; Berizi, E. Prevalence and risk factors associated with Campylobacter infections in broiler flocks in Shiraz, southern Iran. Int. J. Food. Microbiol. 2011, 144, 475–479. [Google Scholar] [CrossRef]
- Reich, F.; Atanassova, V.; Haunhorst, E.; Klein, G. The effects of Campylobacter numbers in caeca on the contamination of broiler carcasses with Campylobacter. Int. J. Food. Microbiol. 2008, 127, 116–120. [Google Scholar] [CrossRef]
- Van Deun, K.; Pasmans, F.; Ducatelle, R.; Flahou, B.; Vissenberg, K.; Martel, A.; van den Broeck, W.; van Immerseel, F.; Haesebrouck, F. Colonization strategy of Campylobacter jejuni results in persistent infection of the chicken gut. Vet. Microbiol. 2008, 130, 285–297. [Google Scholar] [CrossRef]
- Jacobs-Reitsma, W. Aspects of epidemiology of Campylobacter in poultry. Vet. Q. 1997, 19, 113–117. [Google Scholar] [CrossRef]
- Rosenquist, H.; Sommer, H.; Nielsen, N.; Christensen, B. The effect of slaughter operations on the contamination of chicken carcasses with thermotolerant Campylobacter. Int. J. Food. Microbiol. 2006, 108, 226–232. [Google Scholar] [CrossRef]
- Stas, T.; Jordan, F.T.W.; Woldehiwet, Z. Experimental infection of chickens with Campylobacter jejuni: Strains differ in their capacity to colonize the intestine. Avian Pathol. 1999, 28, 61–64. [Google Scholar] [CrossRef]
- Sahin, O.; Morishita, T.; Zhang, Q. Campylobacter colonization in poultry: Sources of infection and modes of transmission. Animal Health Res. Rev. 2002, 3, 95–105. [Google Scholar] [CrossRef]
- Lütticken, D.; Segers, R.; Visser, N. Veterinary vaccines for public health and prevention of viral and bacterial zoonotic diseases. Rev. Sci. Tech. 2007, 26, 165–177. [Google Scholar]
- Black, R.E.; Levine, M.M.; Clements, M.L.; Hughes, T.P.; Blaser, M.J. Experimental Campylobacter jejuni infection in humans. J. Infect Dis. 1988, 157, 472–479. [Google Scholar] [CrossRef]
- Janssen, R.; Krogfelt, K.A.; Cawthraw, S.A.; van Pelt, W.; Wagenaar, J.A.; Owen, R.J. Host-pathogen interactions in Campylobacter infections: The host perspective. Clin. Microbiol. Rev. 2008, 21, 505–518. [Google Scholar] [CrossRef]
- The CamVac Project. Campylobacter Vaccination of Poultry. 2012. Available online: http://www.camvac.dk/ (accessed on 21 September 2012).
- Rosenquist, H.; Nielsen, N.L.; Sommer, H.M.; Nørrung, B.; Christensen, B. Quantitative risk assessment of human Campylobacteriosis associated with thermophilic Campylobacter species in chickens. Int. J. Food. Microbiol. 2003, 83, 87–103. [Google Scholar] [CrossRef]
- Van de Giessen, A.W.; Tilburg, J.J.H.C.; Ritmeester, W.S.; van der Plas, J. Reduction of Campylobacter infections in broiler flocks by application of hygiene measures. Epidemiol. Infect. 1998, 121, 57–66. [Google Scholar] [CrossRef]
- Evans, S.J.; Sayers, A.R. A longitudinal study of Campylobacter infection of broiler flocks in Great Britain. Prev. Vet. Med. 2000, 46, 209–223. [Google Scholar] [CrossRef]
- Newell, D.G.; Fearnley, C. Sources of Campylobacter colonization in broiler chickens. Appl. Environ. Microbiol. 2003, 69, 4343–4351. [Google Scholar] [CrossRef]
- Messens, W.; Hartnett, E.; Gellynck, X.; Viaene, J.; Halet, D.; Herman, L.; Grijspeerdt, K. Quantitative Risk Assessment of Human Campylobacteriosis through the Consumption of Chicken Meat in Belgium. In Proceedings of the XVIII European Symposium on the Quality of Poultry Meat and the XII European Symposium on the Quality of Eggs and Egg products, Ghent University Academy, Prague, Czech Republic, 2–5 September 2007; pp. 167–168.
- Lin, J. Novel approaches for Campylobacter control in poultry. Foodborne Pathog. Dis. 2009, 12, 755–765. [Google Scholar] [CrossRef]
- Hilmarsson, H.; Thormar, H.; Thrainsson, J.H.; Gunnarsson, E.; Dadadottir, S. Effect of 20 glycerol monocaprate (monocaprin) on broiler chickens: An attempt at reducing intestinal Campylobacter infection. Poult. Sci. 2006, 85, 588–592. [Google Scholar]
- Hermans, D.; Martel, A.; van Deun, K.; Verlinden, M.; van Immerseel, F.; Garmyn, A.; Messens, W.; Heyndrickx, M.; Haesebrouck, F.; Pasmans, F. Intestinal mucus protects Campylobacter jejuni in the ceca of colonized broiler chickens against the bactericidal effects of medium-chain fatty acids. Poult. Sci. 2010, 89, 1144–1155. [Google Scholar] [CrossRef]
- El-Shibiny, A.; Scott, A.; Timms, A.; Metawea, Y.; Connerton, P.; Connerton, I. Application of a group II Campylobacter bacteriophage to reduce strains of Campylobacter jejuni and Campylobacter coli colonizing broiler chickens. J. Food Prot. 2009, 72, 733–740. [Google Scholar]
- Garcia, A.B.; Bahrndorff, S.; Hald, B.; Hoorfar, J.; Madsen, M.; Vigre, H. Design and data analysis of experimental trials to test vaccine candidates against zoonotic pathogens in animals: The case of a clinical trial against Campylobacter in broilers. Expert Rev. Vaccines 2012, 11, 1179–1188. [Google Scholar] [CrossRef]
- Sandberg, M. Personal Communication. Danish Agriculture and Food Council, 2013. [Google Scholar]
- Greenland, S. Bayesian perspectives for epidemiological research: I. Foundations and basic methods. Int. J. Epidemiol. 2006, 35, 765–775. [Google Scholar] [CrossRef]
- Roberts, J.A.; Cumberland, P.; Sockett, P.N.; Wheeler, J.G.; Rodrigues, L.C.; Sethi, D.; Roderick, J. The study of infectious intestinal disease in England: Socio-economic impact. Epidemiol. Infect. 2003, 130, 1–11. [Google Scholar]
- Bronzwaer, S.; Hugas, M.; Collins, J.D.; Newell, D.G.; Robinson, T.; Mäkelä, P.; Havelaar, A. EFSA’s 12th Scientific Colloquium—Assessing health benefits of controlling Campylobacter in the food chain. Int. J. Food Microb. 2009, 131, 284–285. [Google Scholar] [CrossRef]
- Laboratory Reports of Campylobacter sp in England and Wales 2000–2011. Available online: http://www.hpa.org.uk/Topics/InfectiousDiseases/InfectionsAZ/Campylobacter/EpidemiologicalData/campyDataEw/ (accessed on 20 December 2012).
- Lawes, J.R.; Vidal, A.; Clifton-Hadley, F.A.; Sayers, R.; Rodgers, J.; Snow, L.; Evans, S.J.; Powell, L.F. Investigation of prevalence and risk factors for Campylobacter in broiler flocks at slaughter: Results from a UK survey. Epidemiol. Infect. 2012, 140, 1725–1737. [Google Scholar] [CrossRef]
- Heckerman, D.; Mamdani, A.; Wellman, M.P. Real-world applications of Bayesian networks. Commun. ACM 1995, 38, 24–68. [Google Scholar] [CrossRef]
- Deeks, J.J.; Altman, D.G.; Bradburn, M.J. Statistical Methods for Examining Heterogeneity and Combining Results from Several Studies in Meta-Analysis. In Systematic Reviews in Health Care: Meta-analysis in Context, 2nd ed.; Egger, M., Davey Smith, G., Altman, D.G., Eds.; BMJ Publication Group: London, UK, 2001. [Google Scholar]
- Deeks, J.J.; Higgins, J.P.T.; Altman, D.G. Chapter 9: Analysing Data and Undertaking Meta-Analyses. Available online: http://hiv.cochrane.org/sites/hiv.cochrane.org/files/uploads/Ch09_Analysing.pdf (accessed on 16 November 2012).
- Howard, R.A.; Matheson, J.E. Influence Diagrams. In Readings in Decision Analysis; Strategic Decisions Group: Menlo Park, CA, USA, 1981; pp. 763–771. [Google Scholar]
- Annan-Prah, A.; Janc, M. The mode of spread of Campylobacter jejuni/coli to broiler flocks. J. Vet. Med. 1988, 35, 11–18. [Google Scholar] [CrossRef]
- Stern, N.J. Reservoirs for C. jejuni and Approaches for Intervention in Poultry. In Campylobacter jejuni: Current Status and Future Trends; Nachamkin, I., Blaser, M.J., Tompkins, L.S., Eds.; American Society for Microbiology: Washington, DC, USA, 1992; pp. 49–60. [Google Scholar]
- Rice, B.; Rollins, D.; Mallinson, E.; Carr, L.; Joseph, S. Campylobacter jejuni in broiler chickens: Colonization and humoral immunity following oral vaccination and experimental infection. Vaccine 1997, 15, 1922–1932. [Google Scholar] [CrossRef]
- Food Survey Information Sheet 04/09. A UK Survey of Campylobacter and Salmonella Contamination of Fresh Chicken at Retail Sale. Available online: http://www.food.gov.uk/multimedia/pdfs/fsis0409.pdf (accessed on 3 December 2012).
- Crane, R.; Davenport, R.; Vaughan, R. Farm Business Survey 2009/2010. Poultry Production in England. Available online: http://www.fbspartnership.co.uk/documents/2009_10/PoultryProduction_2009_10.pdf (accessed on 14 January 2012).
- Dianova. Available online: http://www.dianova.dk/ (accessed on 17 June 2013).
- European Food Safety Authority (EFSA). Analysis of the baseline survey on the prevalence of Campylobacter in broiler batches and of Campylobacter and Salmonella on broiler carcasses, in the EU, 2008—Part A: Campylobacter and Salmonella prevalence estimates. EFSA J. 2010, 8, 1503–1550. [CrossRef]
- Allen, V.M.; Bull, S.A.; Corry, J.E.; Domingue, G.; Jorgensen, F.; Frost, J.A.; Whyte, R.; Gonzalez, A.; Elviss, N.; Humphrey, T.J. Campylobacter spp. contamination of chicken carcasses during processing in relation to flock colonisation. Int. J. Food Microb. 2007, 113, 54–61. [Google Scholar] [CrossRef]
- Brelade, S.; Harman, C. Practical Guide to Knowledge Management; Thorogood Publishing: London, UK, 2003. [Google Scholar]
- Firestone, J.; McElroy, M. Has Knowledge Management Been Done; Emerald Group Publishing Limited: Bradford, UK, 2005. [Google Scholar]
- Madsen, A.L.; Karlsen, M.; Barker, G.C.; Garcia, A.B.; Hoorfar, J.; Jensen, F.; Vigre, H. An Architecture for Web Deployment of Decision Support Systems Based on Probabilistic Graphical Models with Applications; Tech Report TR-12-001; Department of Computer Science, Aalborg University: Aalborg, Denmark, 2012. [Google Scholar]
- HUGIN EXPERT. The Leading Decision Support Tool. Available online: http://www.hugin.com/ (accessed on 26 September 2012).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Garcia, A.B.; Madsen, A.L.; Vigre, H. Integration of Epidemiological Evidence in a Decision Support Model for the Control of Campylobacter in Poultry Production. Agriculture 2013, 3, 516-535. https://doi.org/10.3390/agriculture3030516
Garcia AB, Madsen AL, Vigre H. Integration of Epidemiological Evidence in a Decision Support Model for the Control of Campylobacter in Poultry Production. Agriculture. 2013; 3(3):516-535. https://doi.org/10.3390/agriculture3030516
Chicago/Turabian StyleGarcia, Ana B., Anders L. Madsen, and Håkan Vigre. 2013. "Integration of Epidemiological Evidence in a Decision Support Model for the Control of Campylobacter in Poultry Production" Agriculture 3, no. 3: 516-535. https://doi.org/10.3390/agriculture3030516




