Diffraction Focal Position and Vector Diffraction Theory for Micro Holographic Storage Systems
Abstract
:1. Introduction
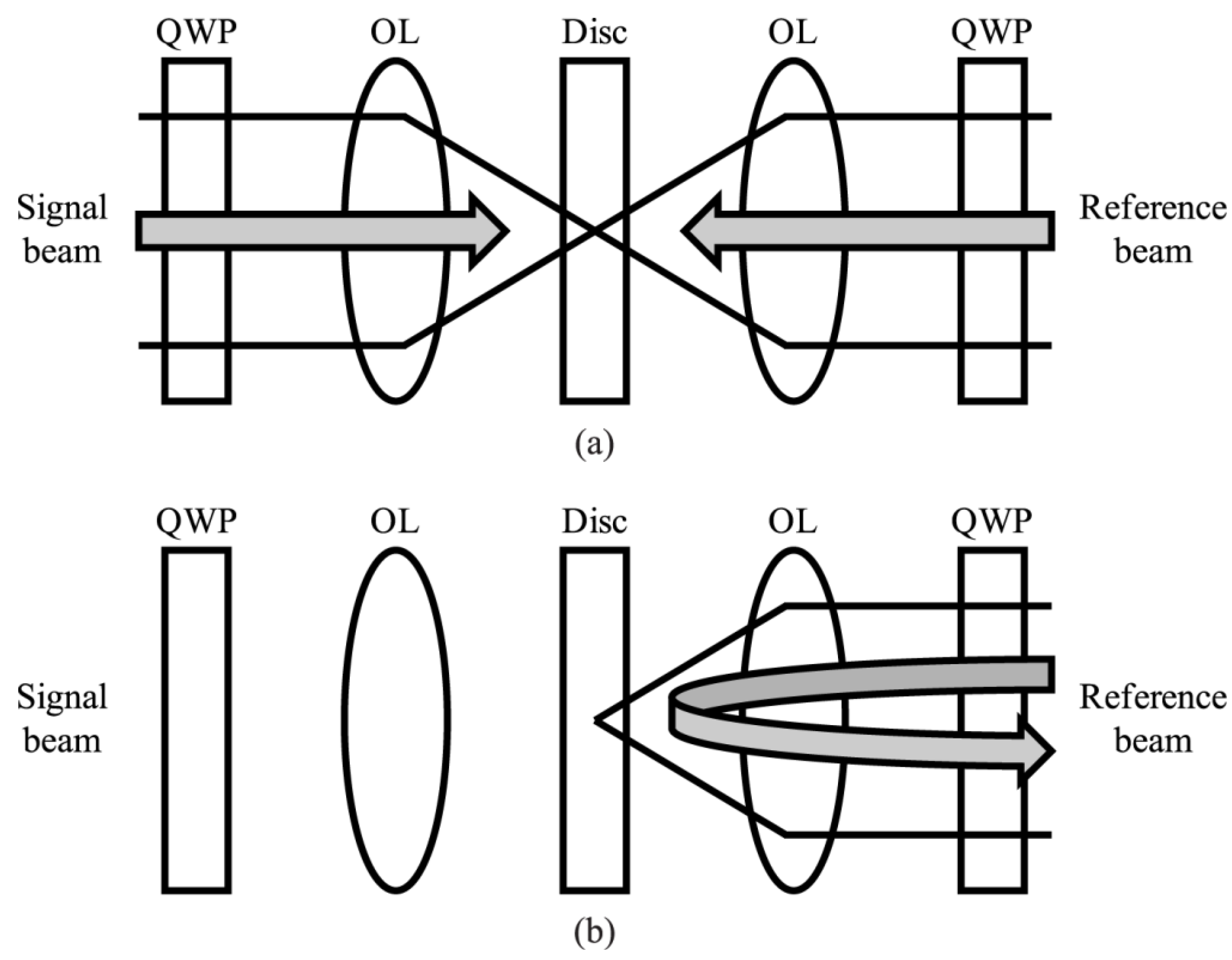
2. Micrograting of a Micro Holographic Storage System
2.1. Vector Diffraction Theory for Micrograting

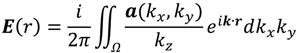
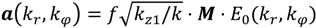 with f corresponding to the focal length of the lens system, and the general lens matrix incorporating possible layer transitions, as derived and summarized in reference [12].
with f corresponding to the focal length of the lens system, and the general lens matrix incorporating possible layer transitions, as derived and summarized in reference [12].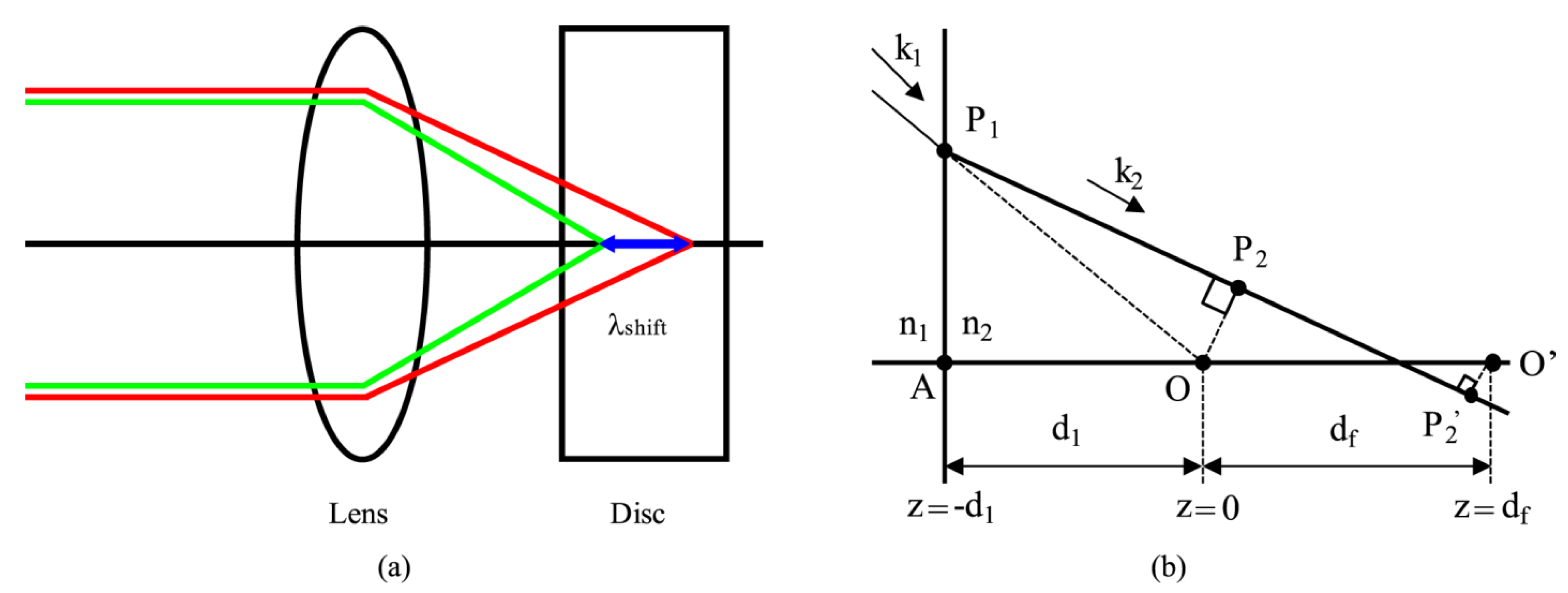
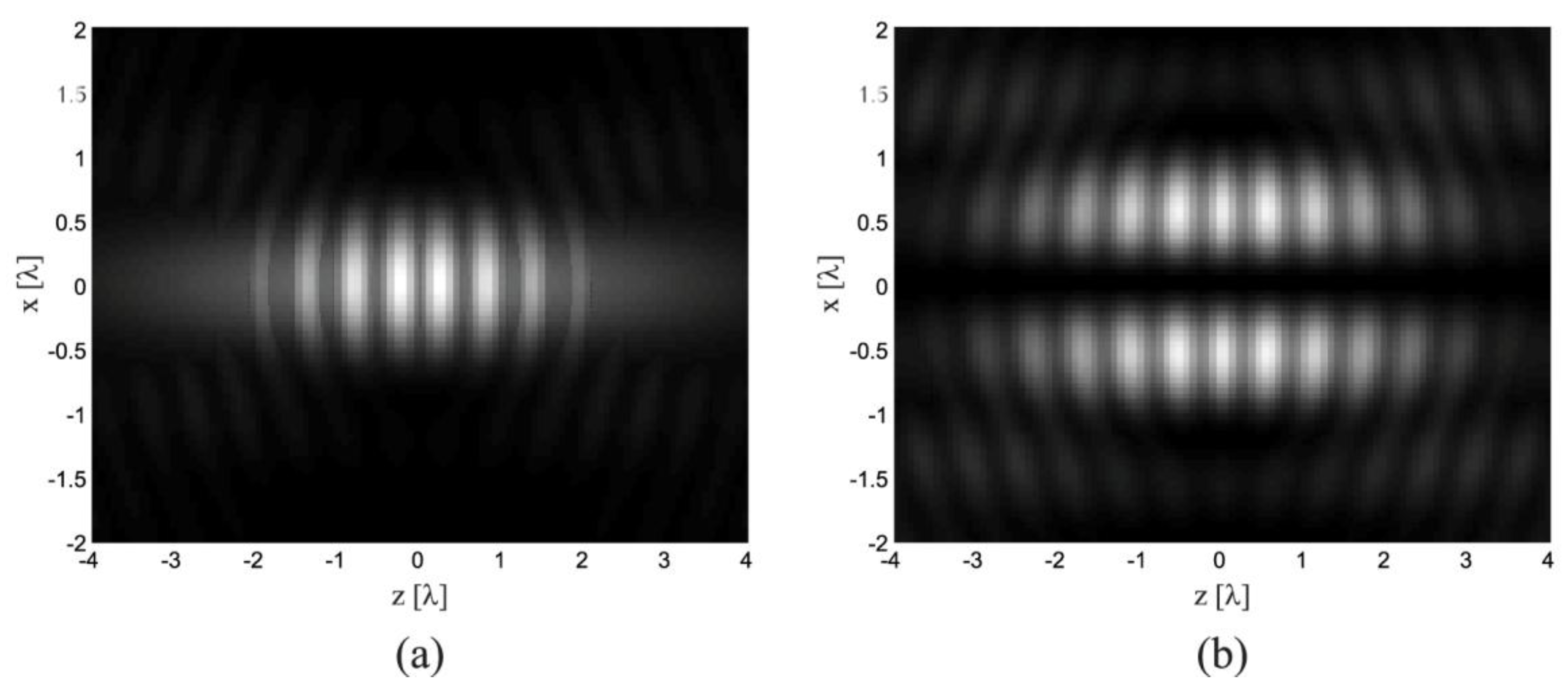
2.2. Numerical Results for Micrograting
| Effective NA | 0.6/0.7/0.8 | |
|---|---|---|
| Polarization | Circular | |
| Media | Recording | Photopolymer n = 1.53, Thickness = 400 μm |
| Substrate | Glass n = 1.53, Top = 600 μm, Bottom = 600 μm | |
| Wavelength | 405/532/633 nm | |
| λ (nm) | NA | λ/(2NA) (nm) | Scalar (nm) | Vector (nm) | |
|---|---|---|---|---|---|
| Transverse | Total | ||||
| 532 | 0.6 | 443 | 457 | 444 | 458 |
| 0.7 | 380 | 390 | 405 | 422 | |
| 0.8 | 332 | 342 | 325 | 349 | |
| 405 | 0.6 | 337 | 348 | 338 | 349 |
| 0.7 | 289 | 297 | 308 | 321 | |
| 0.8 | 253 | 260 | 248 | 266 | |

3. Experimental Section
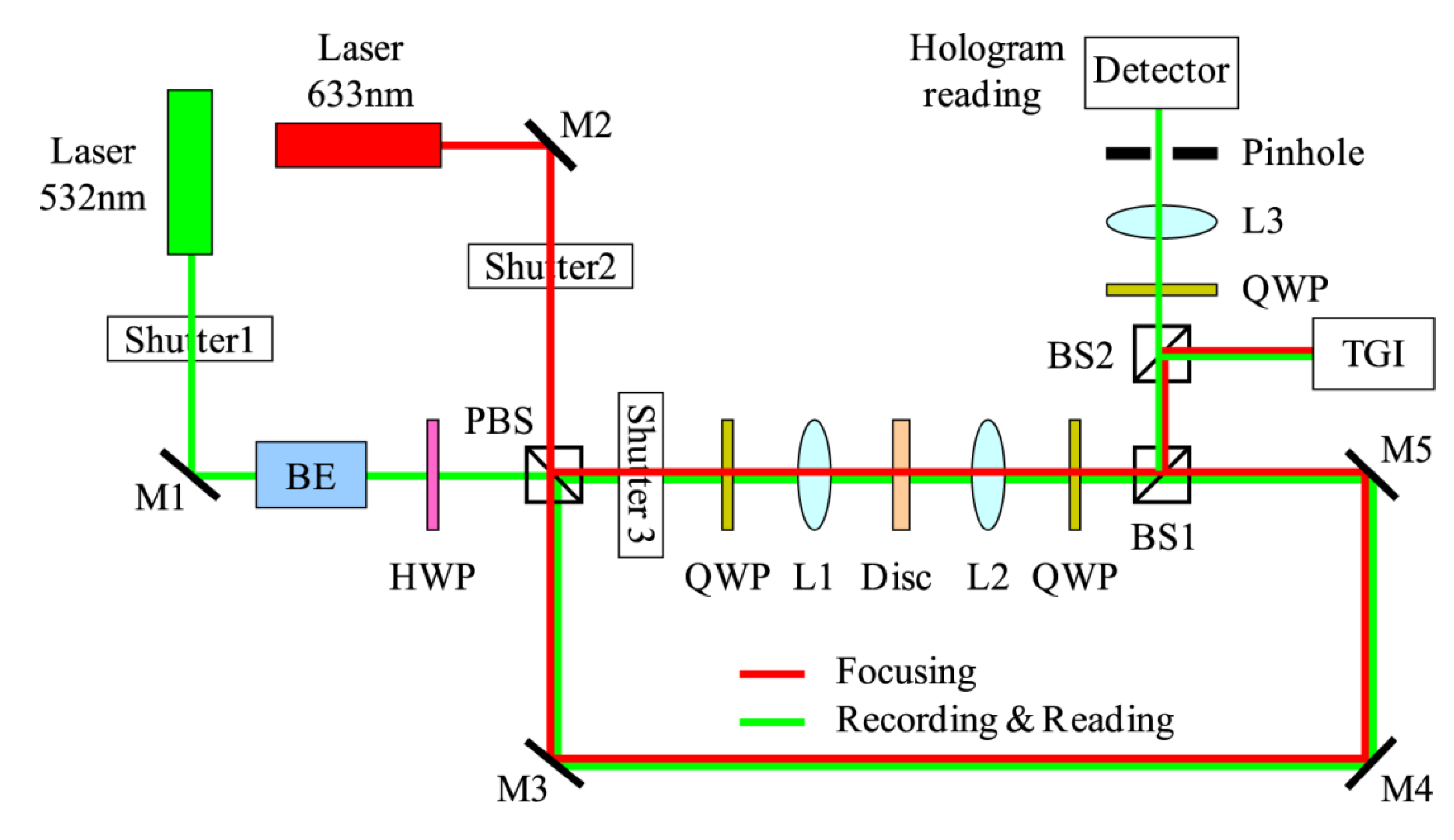
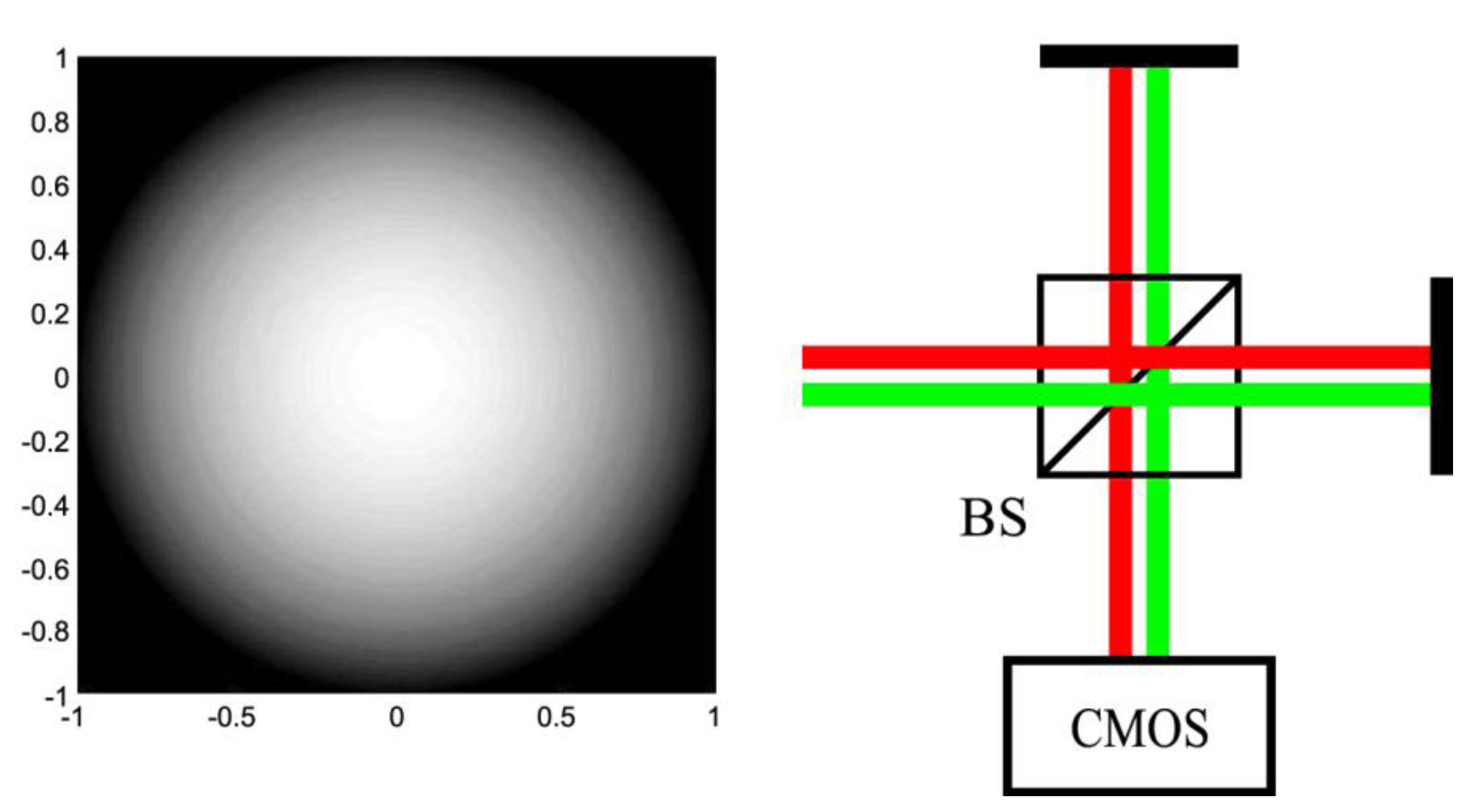

4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Eichler, H.J.; Kuemmel, P.; Orlic, S.; Wappelt, A. High-density disk storage by multiplexed microholograms. IEEE J. Sel. Top. Quantum Electron. 1998, 4, 840–848. [Google Scholar] [CrossRef]
- Boden, E.P.; Chan, K.P.; Dylov, D.V.; Kim, E.M.; Lorraine, P.W.; McCloskey, P.J.; Misner, M.J.; Natarajan, A.; Ostroverkhov, V.; Pickett, J.E.; et al. Recent progress in micro-holographic storage. In Proceedings of NLO & ISOM/ODS 2011 The Optical Society (OSA), Kauai, HI, USA, 17–22 July 2011.
- Ostroverkhov, V.; Lawrence, B.L.; Shi, X.; Boden, E.P.; Erben, C. Micro-holographic storage and threshold holographic recording materials. Jpn. J. Appl. Phys. 2009, 48, 03A035. [Google Scholar]
- Mikami, H.; Osawa, K.; Tatsu, E.; Watanabe, K. Experimental demonstration of optical phase multilevel recording in microhologram. Jpn. J. Appl. Phys. 2012, 51, 08JD01. [Google Scholar] [CrossRef]
- Jallapuram, R.; Naydenova, I.; Martin, S.; Howard, R.; Toal, V.; Frohmann, S.; Orlic, S.; Eichler, H.J. Acrylamide-based photopolymer for microholographic data storage. Opt. Mater. 2006, 28, 1329–1333. [Google Scholar] [CrossRef]
- Mikami, H.; Osawa, K.; Watanabe, K. Optical phase multi-level recording in microhologram. Proc. SPIE 2010, 7730. [Google Scholar] [CrossRef]
- Orlic, S.; Ulm, S.; Eichler, H.J. 3D bit-oriented optical storage in photopolymers. J. Opt. A. 2001, 3, 72–81. [Google Scholar] [CrossRef]
- McLeod, R.R.; Daiber, A.J.; McDonald, M.E.; Robertson, T.L.; Slagle, T.; Sochava, S.L.; Hesselink, L. Microholographic multilayer optical disk data storage. Appl. Opt. 2005, 44, 3197–3207. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, G.; Tan, W.; Shi, L.; Chong, T. Spot size and depth of focus in optical data storage systems. Opt. Eng. 2007, 46, 065201. [Google Scholar] [CrossRef]
- Wei, X.; Wachters, A.J.H.; Urbach, H.P. Finite-element model for three-dimensional optical scattering problems. J. Opt. Soc. Am. A 2007, 24, 866–881. [Google Scholar]
- Kelly, J.V.; Gleeson, M.R.; Close, C.E.; O’Neill, F.T.; Sheridan, J.T. Temporal analysis of grating formation in photopolymer using the nonlocal polymerization-driven diffusion model. Opt. Express 2005, 13, 6990–7004. [Google Scholar] [CrossRef]
- Van de Nes, A.S.; Braat, J.J.M.; Pereira, S.F. High-density optical data storage. Rep. Prog. Phys. 2006, 69, 2323–2363. [Google Scholar] [CrossRef]
- Flagello, D.G.; Milster, T.; Rosenbluth, A.E. Theory of high-NA imaging in homogeneous thin films. J. Opt. Soc. Am. A 1996, 13, 53–64. [Google Scholar] [CrossRef]
- Van Haver, S.; Braat, J.J.M.; Dirksen, P.; Janssen, A.J.E.M. High-NA aberration retrieval with the extended Nijboer-Zernike vector diffraction theory. J. Eur. Opt. Soc. 2006, 1, 06004. [Google Scholar] [CrossRef]
- Van Haver, S.; Braat, J.J.M.; Dirksen, P.; Janssen, A.J.E.M. High-NA aberration retrieval with the Extended Nijboer-Zernike vector diffraction theory: Erratum. J. Eur. Opt. Soc. 2007, 2, 07011e. [Google Scholar] [CrossRef]
- Stallinga, S. Compact description of substrate-related aberrations in high numerical-aperture optical disk readout. Appl. Opt. 2005, 44, 849–858. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Min, C.-K.; Moon, H.; Kim, D.-H.; Park, N.-C.; Park, K.-S.; Park, Y.-P. Diffraction Focal Position and Vector Diffraction Theory for Micro Holographic Storage Systems. Appl. Sci. 2014, 4, 57-65. https://doi.org/10.3390/app4010057
Min C-K, Moon H, Kim D-H, Park N-C, Park K-S, Park Y-P. Diffraction Focal Position and Vector Diffraction Theory for Micro Holographic Storage Systems. Applied Sciences. 2014; 4(1):57-65. https://doi.org/10.3390/app4010057
Chicago/Turabian StyleMin, Cheol-Ki, Hyungbae Moon, Do-Hyung Kim, No-Cheol Park, Kyoung-Su Park, and Young-Pil Park. 2014. "Diffraction Focal Position and Vector Diffraction Theory for Micro Holographic Storage Systems" Applied Sciences 4, no. 1: 57-65. https://doi.org/10.3390/app4010057




