Guideline for Forming Stiffened Panels by Using the Electromagnetic Forces
Abstract
:1. Introduction
2. Material and Methods
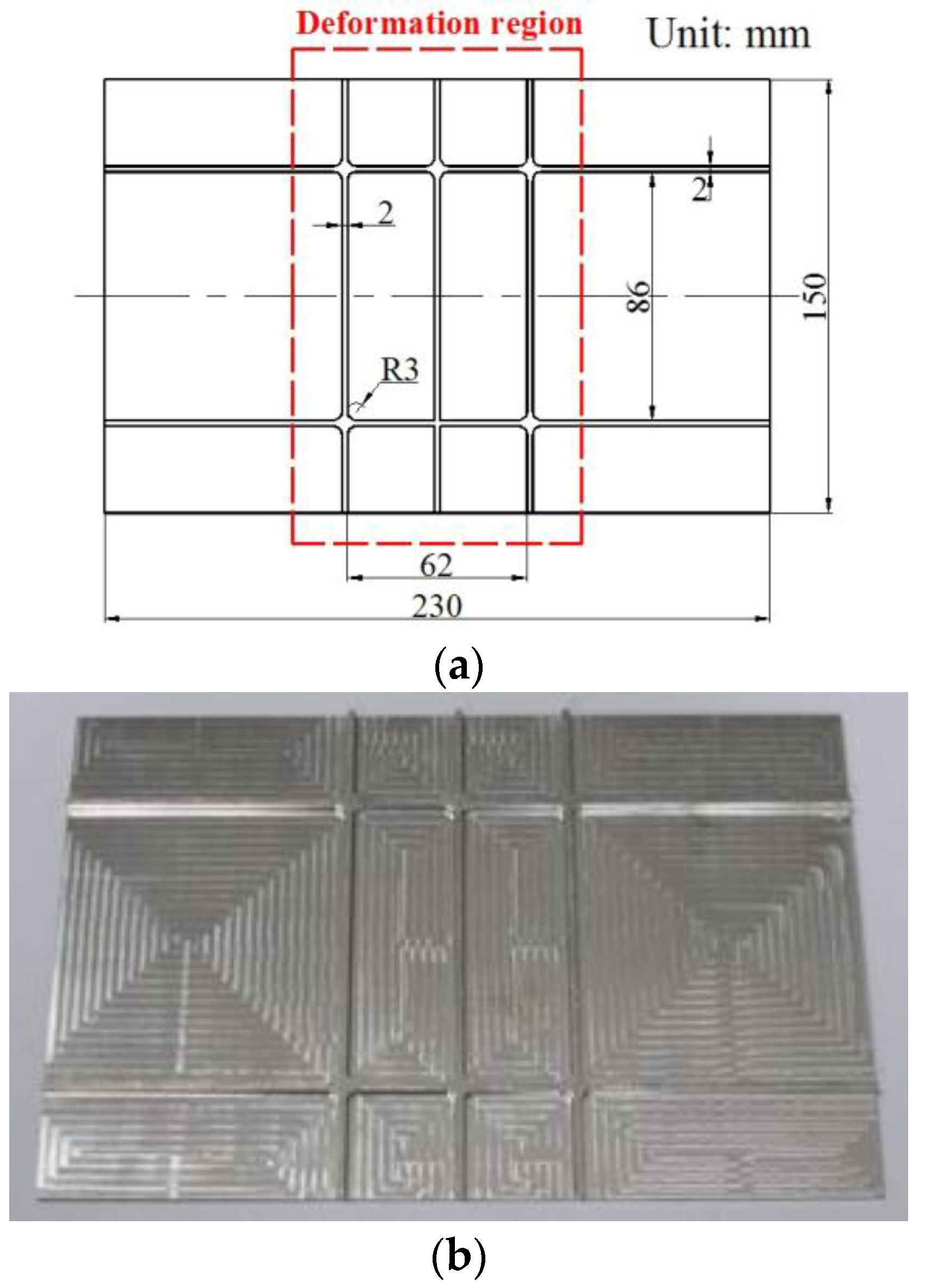
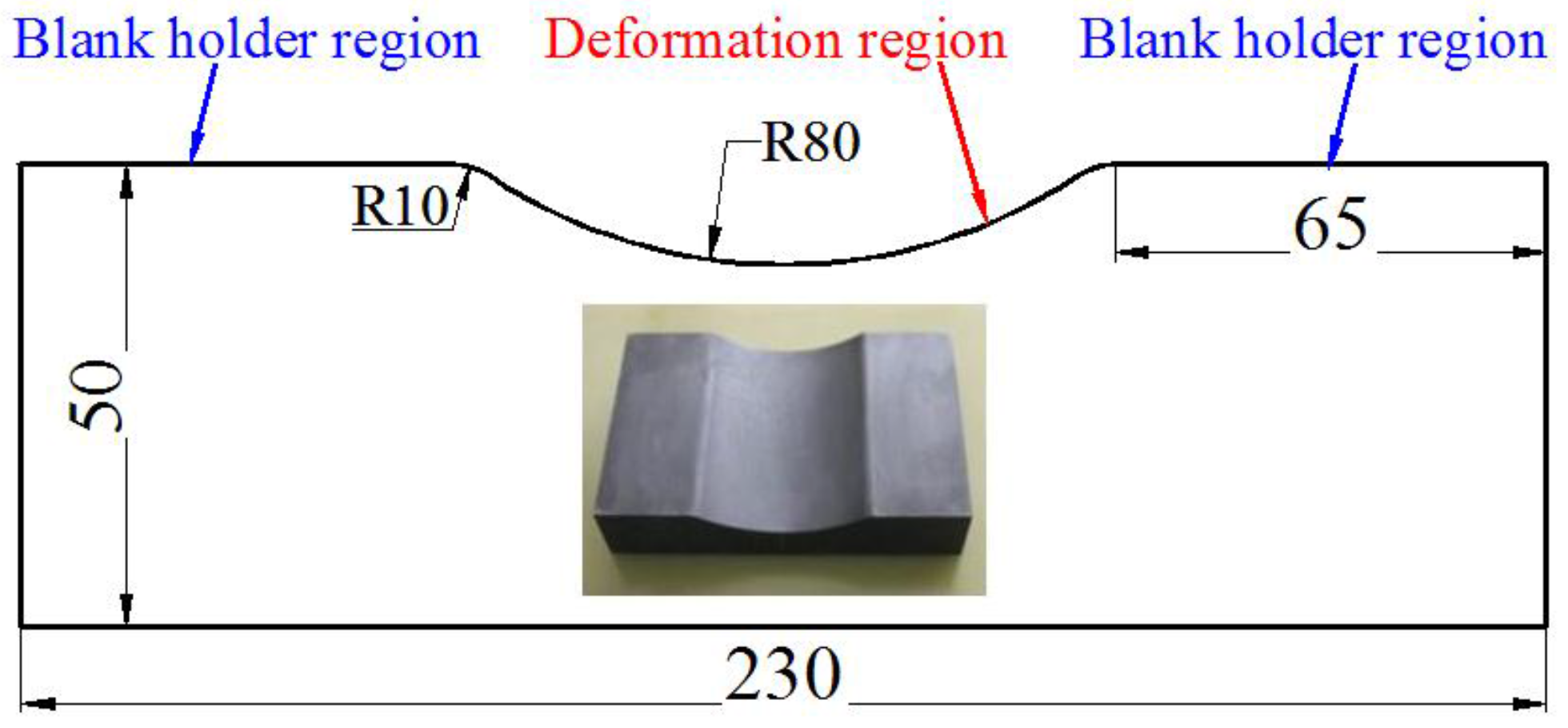
2.1. Material and Blank
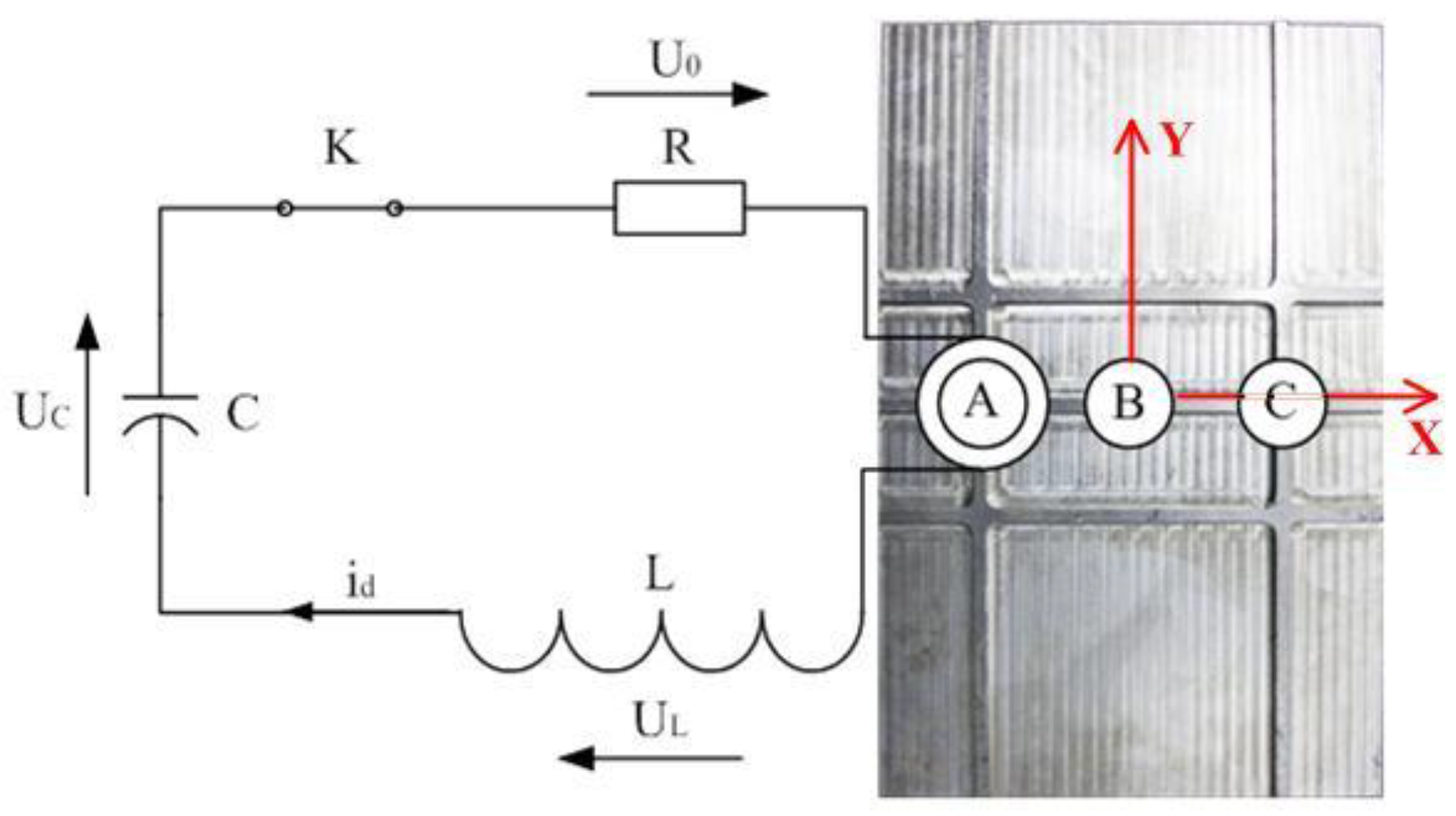
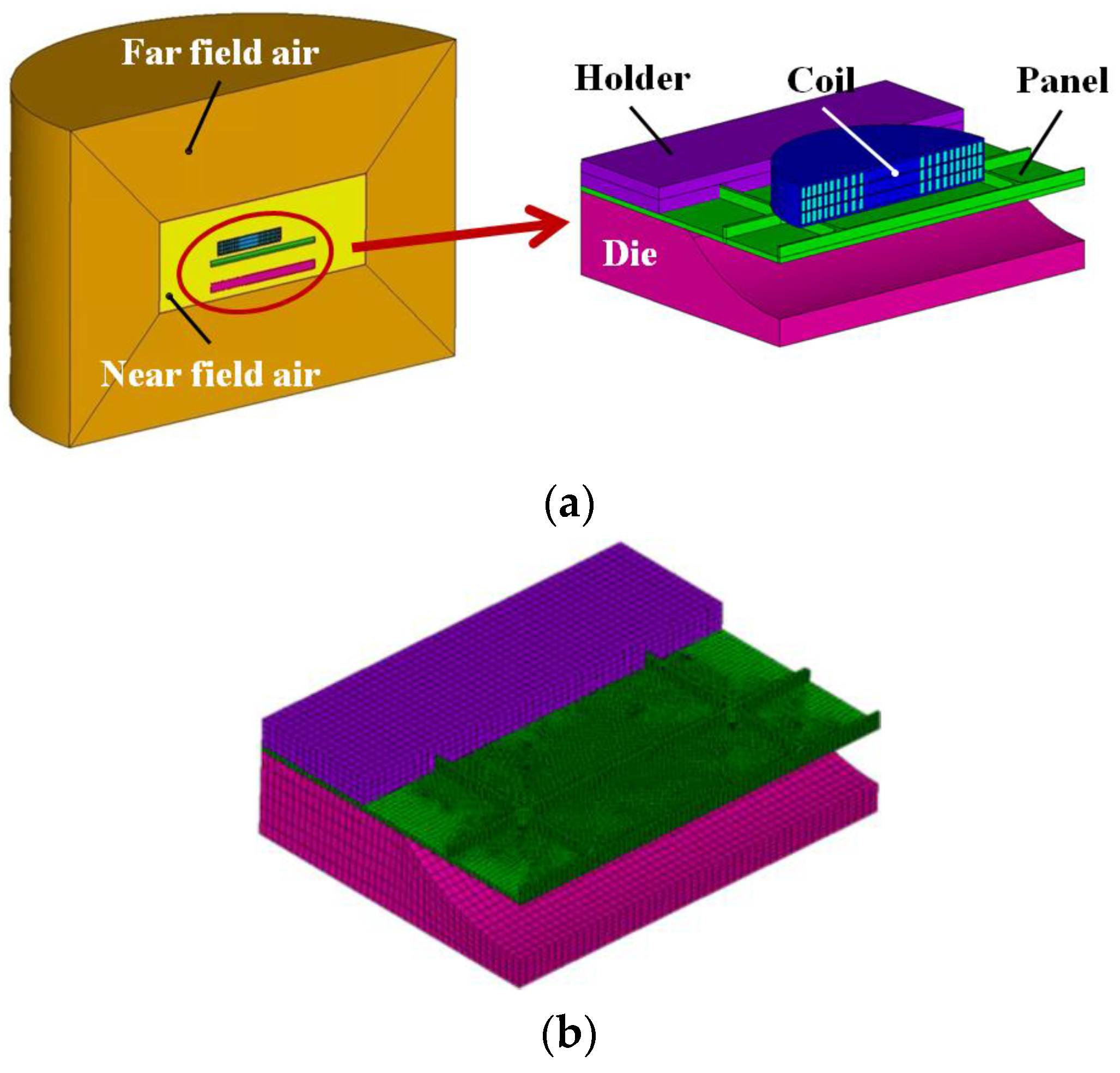
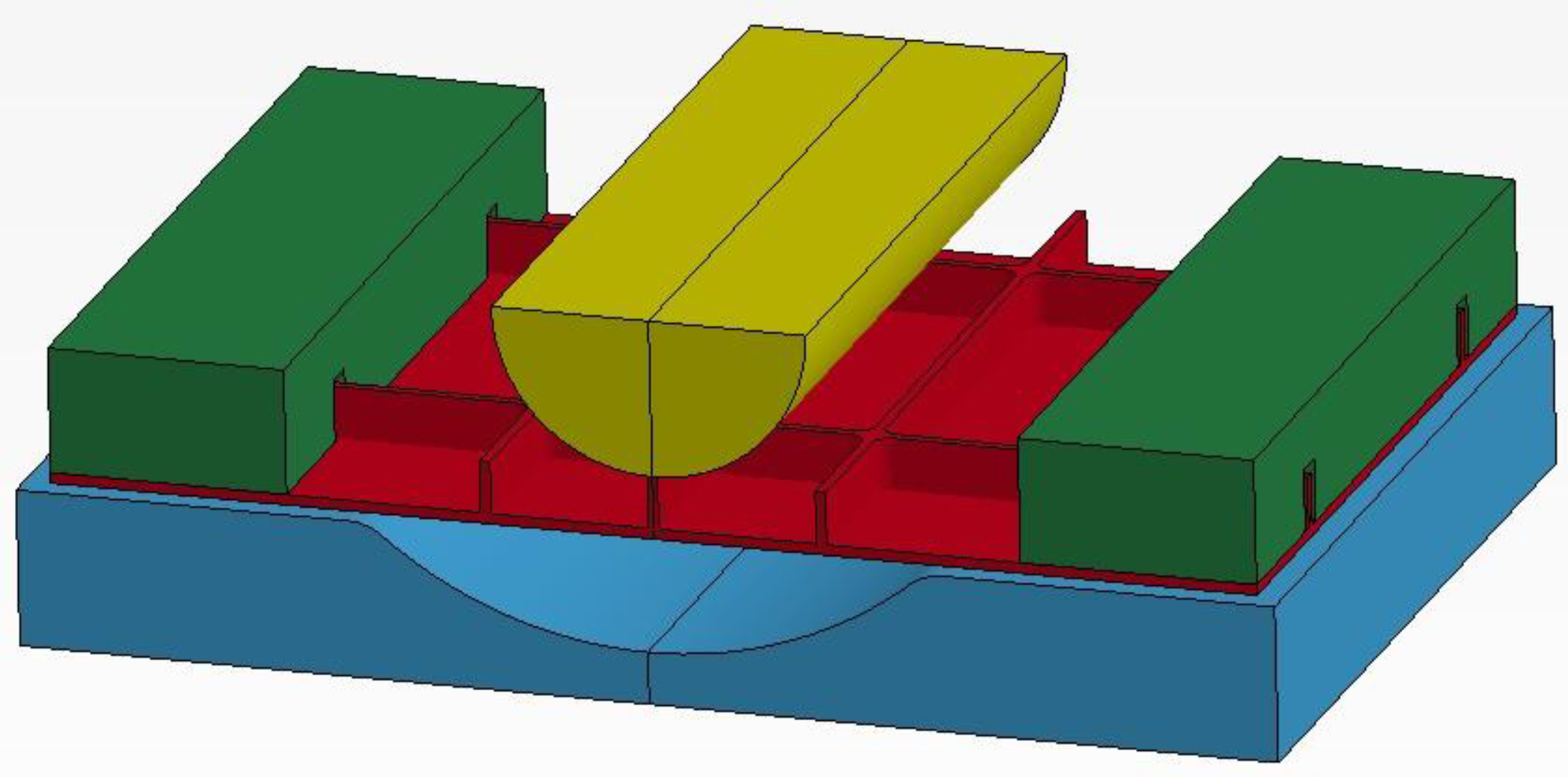
2.2. Forming Set-Up
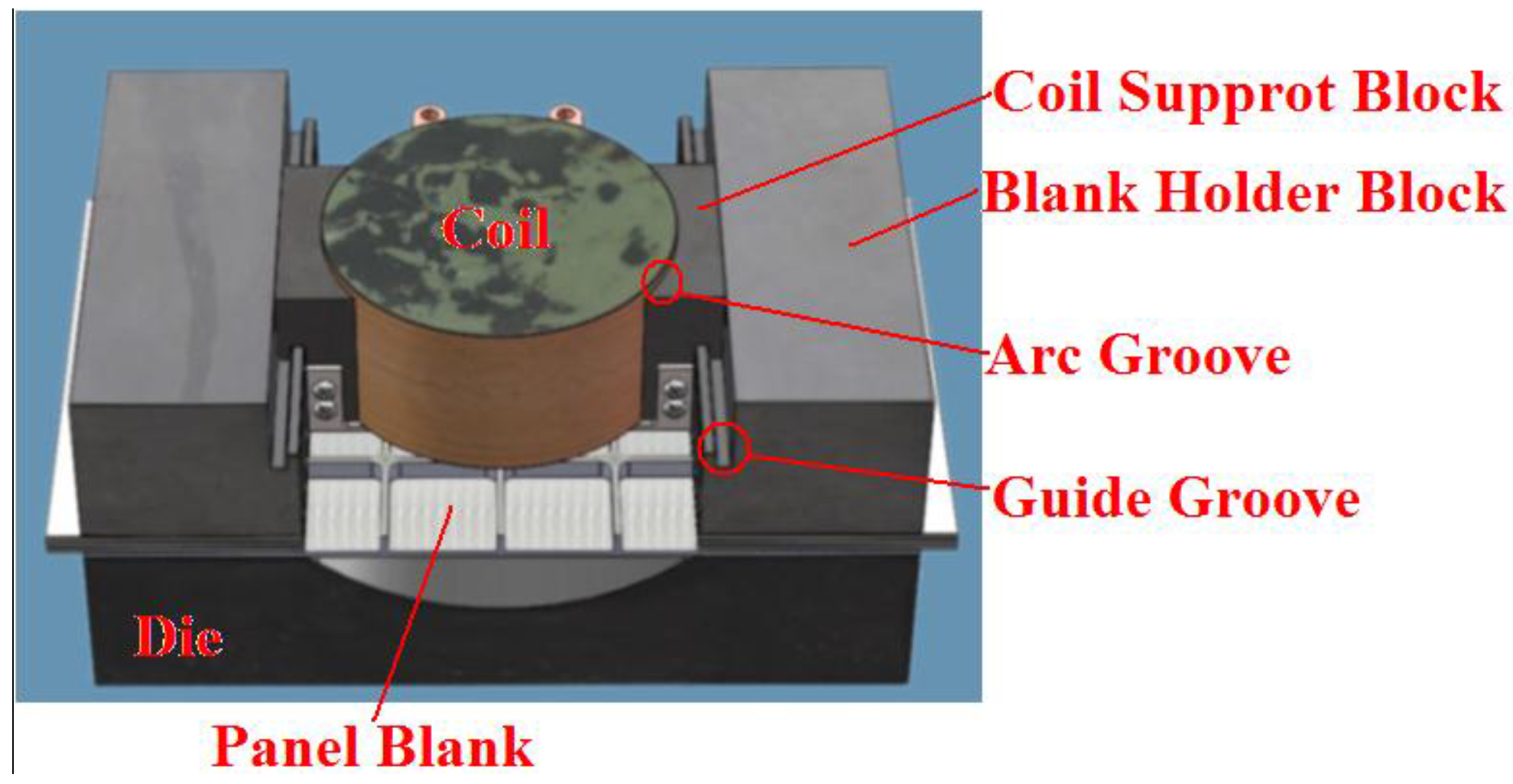
2.2.1. Die
2.2.2. Coil
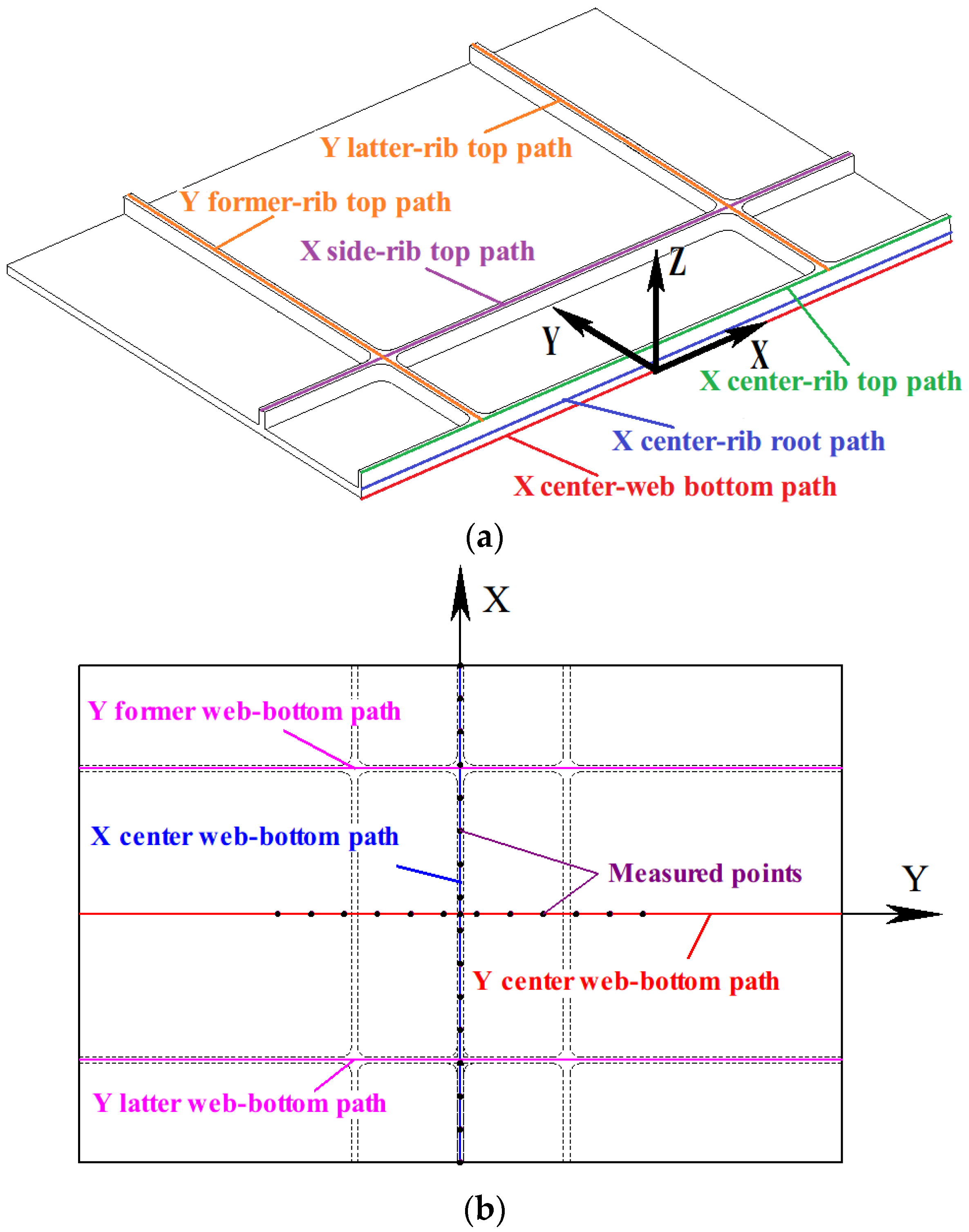
2.3. Forming Stations and Coil Paths
3. Numerical Simulation
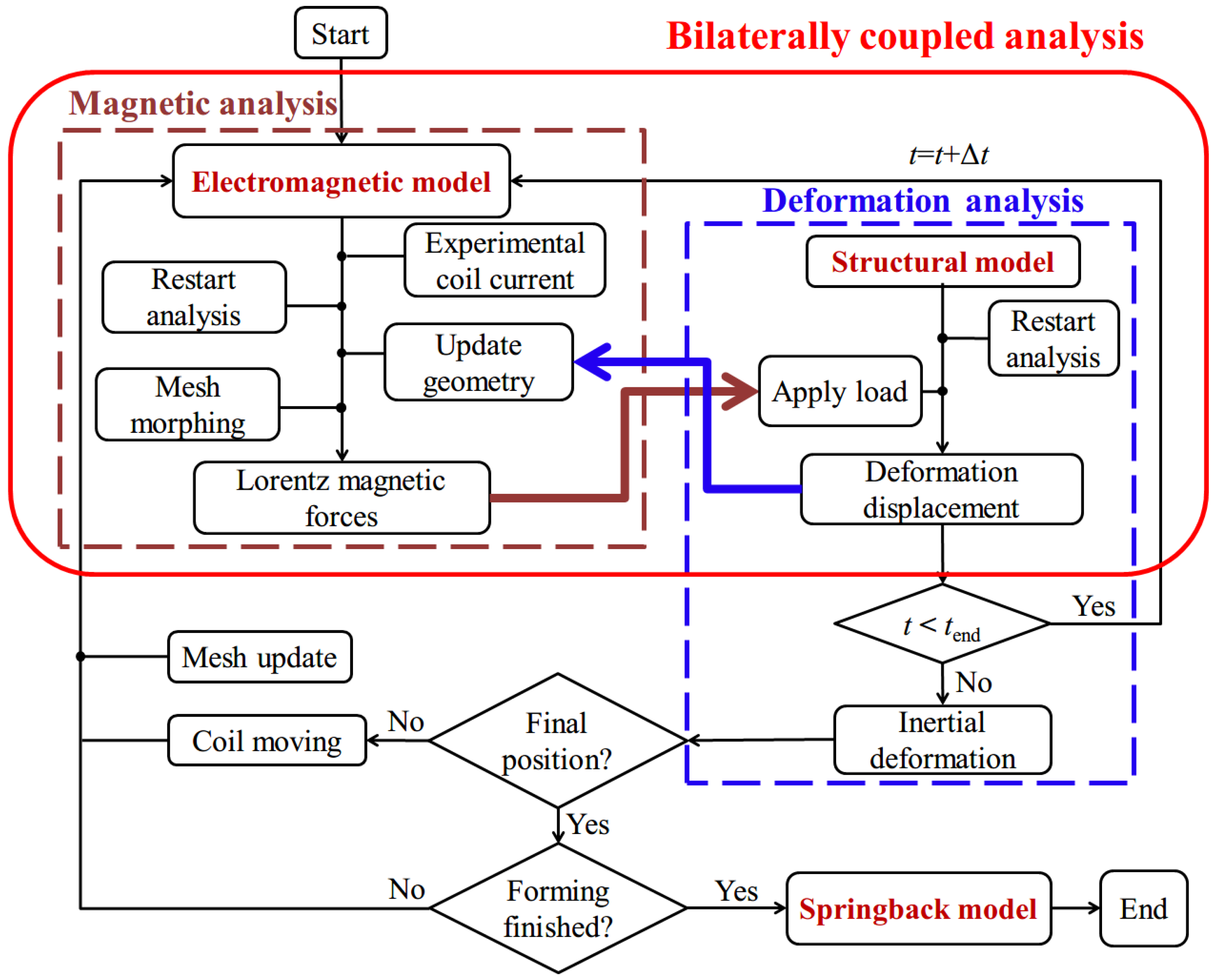
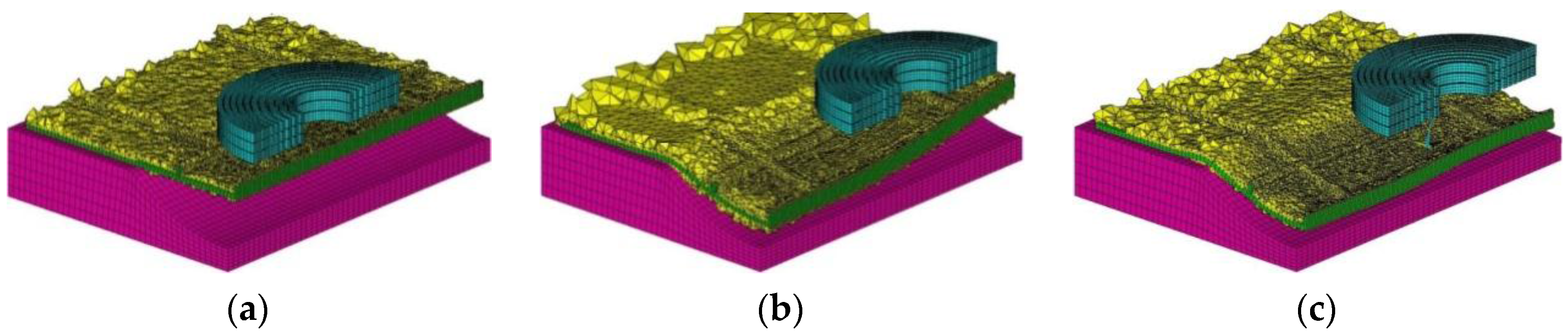
3.1. Establishment of the FE Model
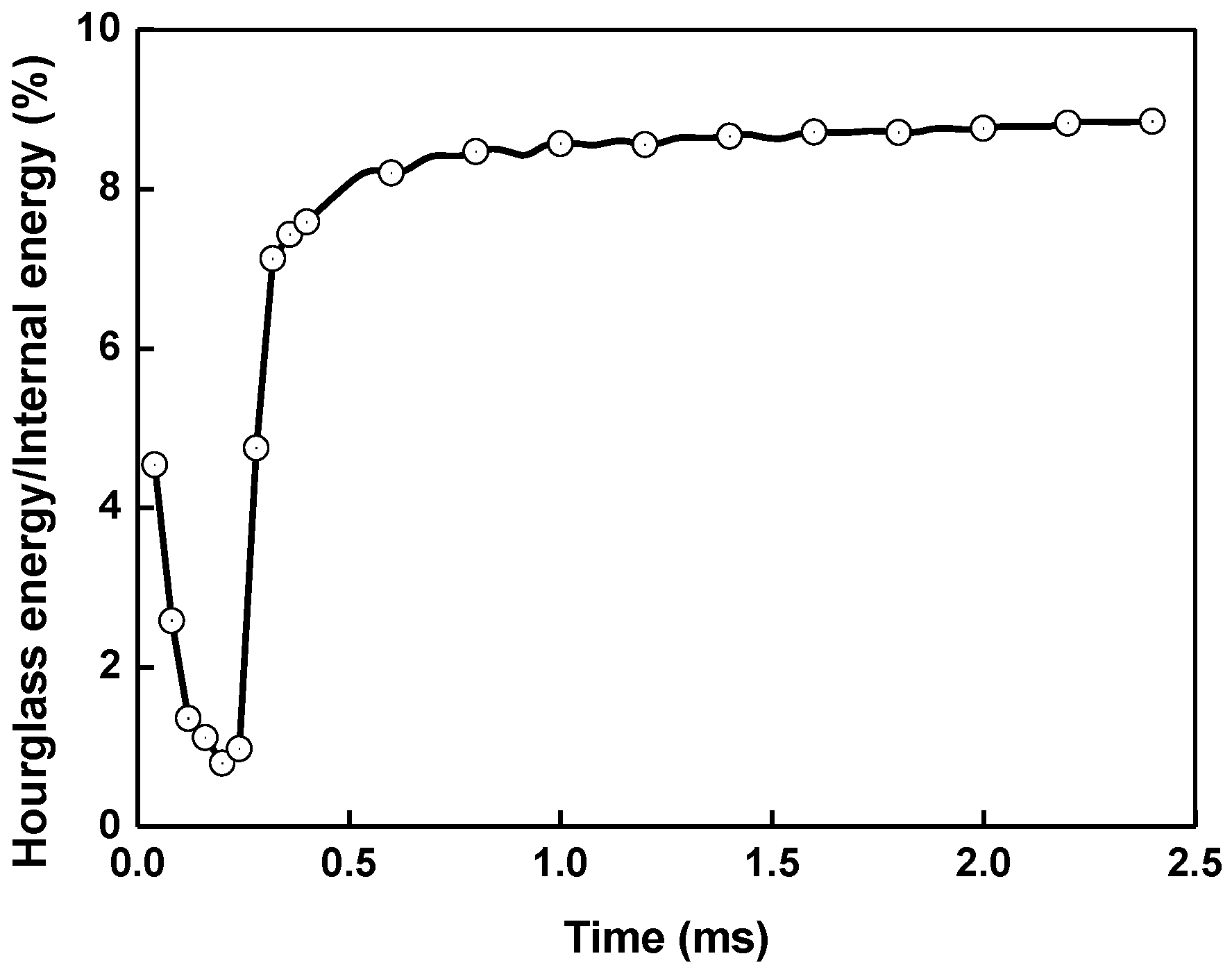
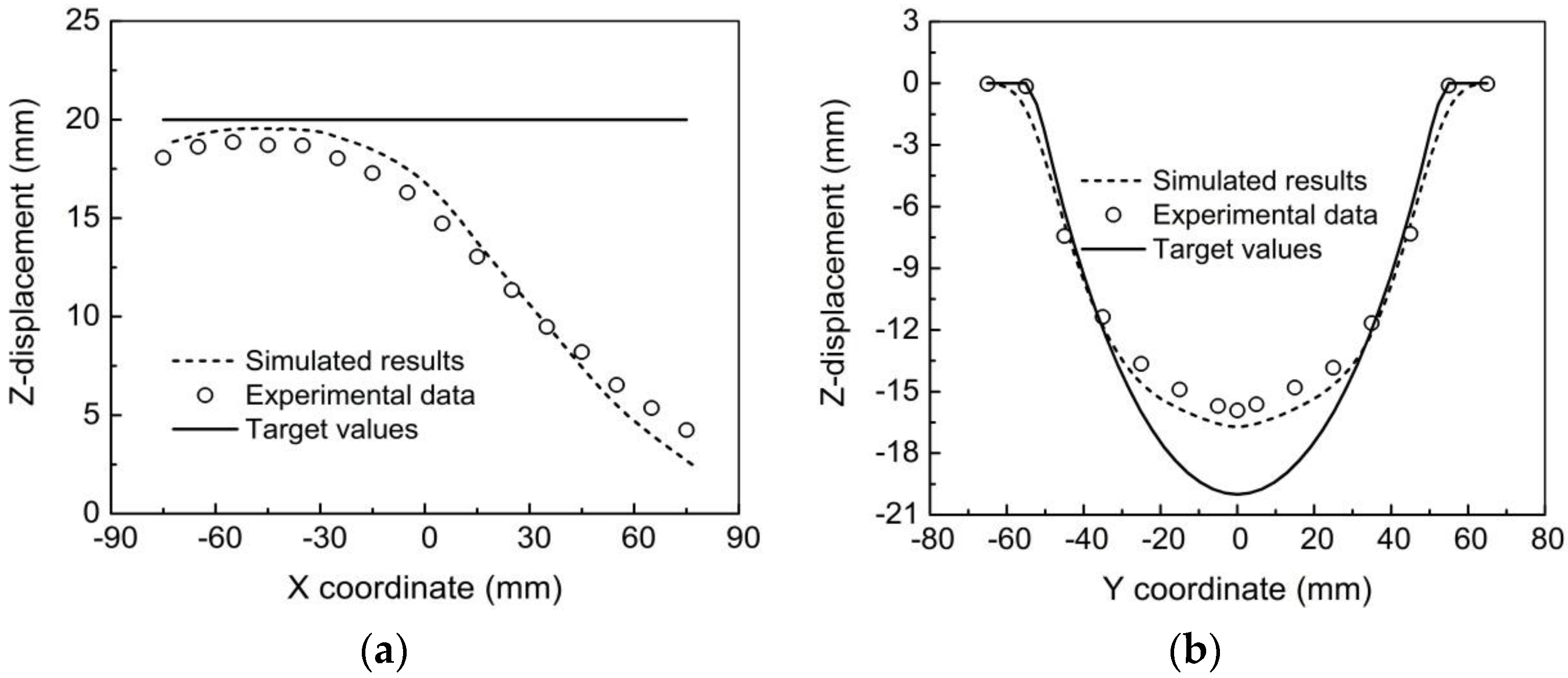
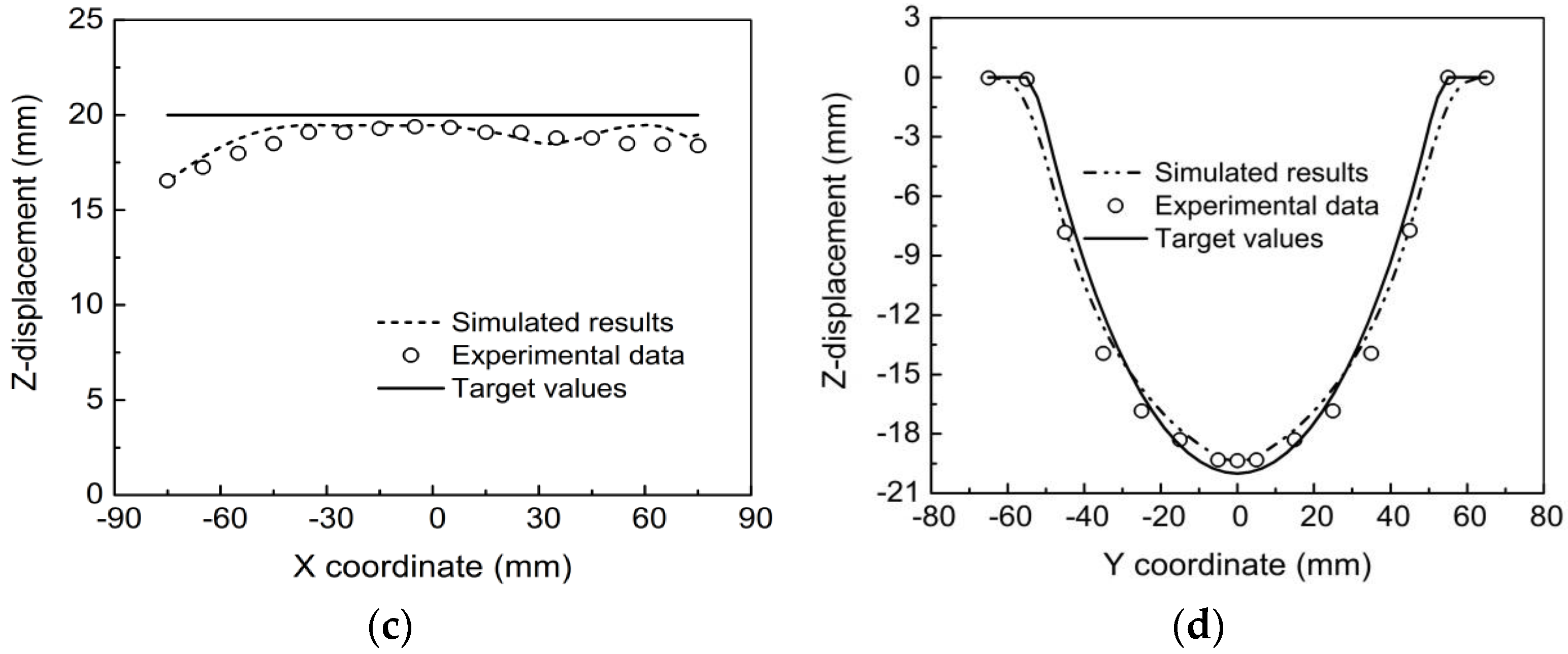
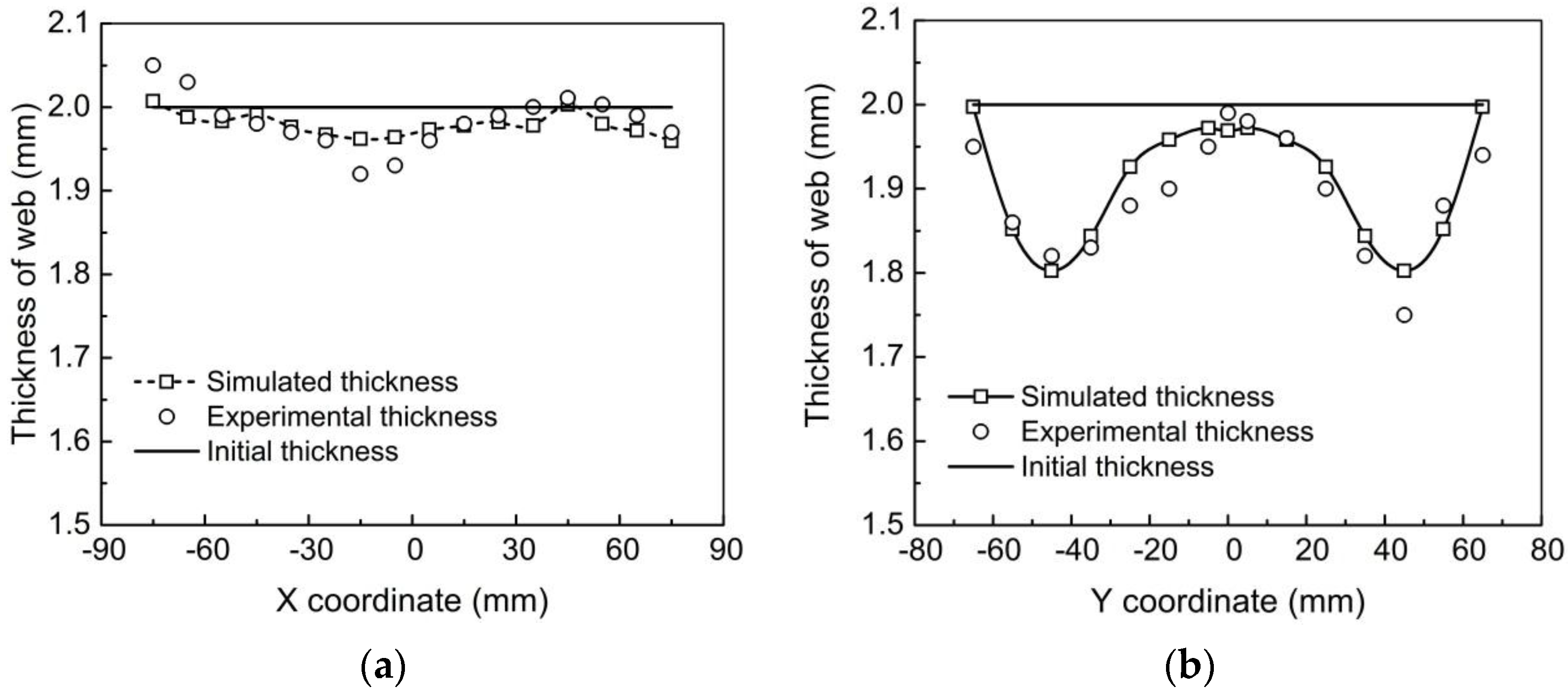
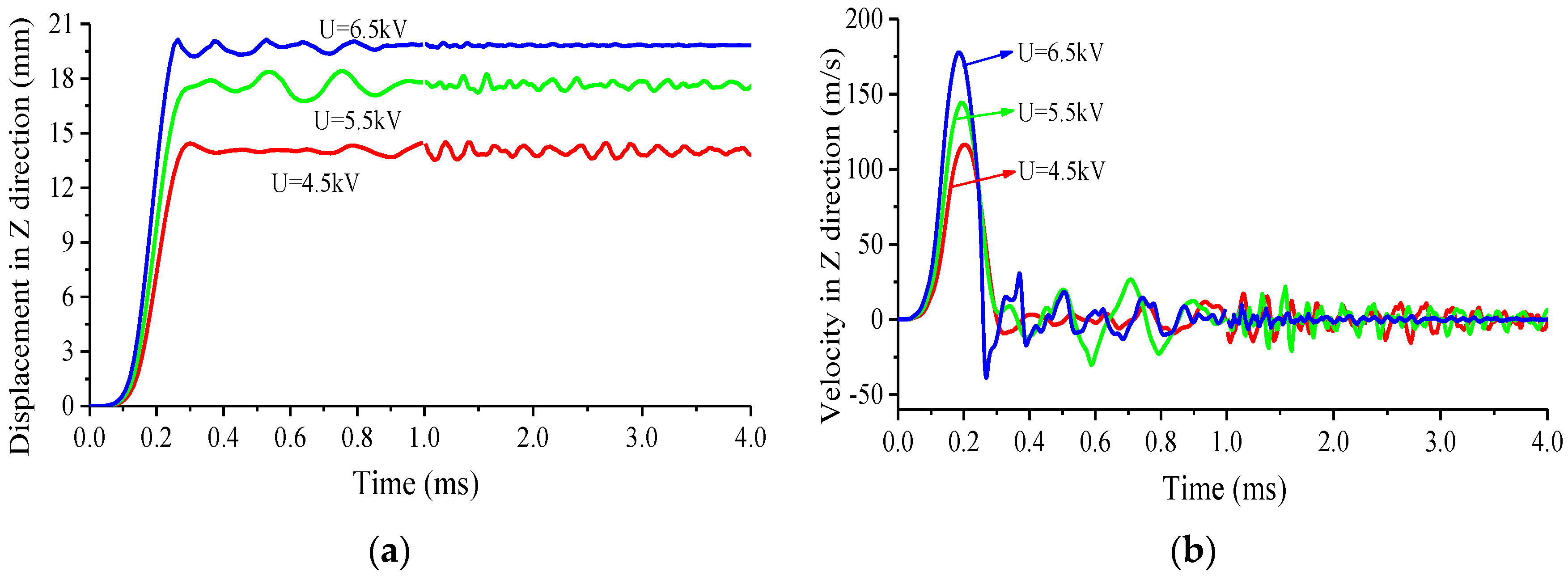
3.2. Verification of the FE Model
- (1)
- The capacitance is 160 μF.
- (2)
- For station A: X coordinate is −28 mm and the voltage is 7 kV. For station C, X coordinate is 28 mm and the voltage is 9.8 kV.
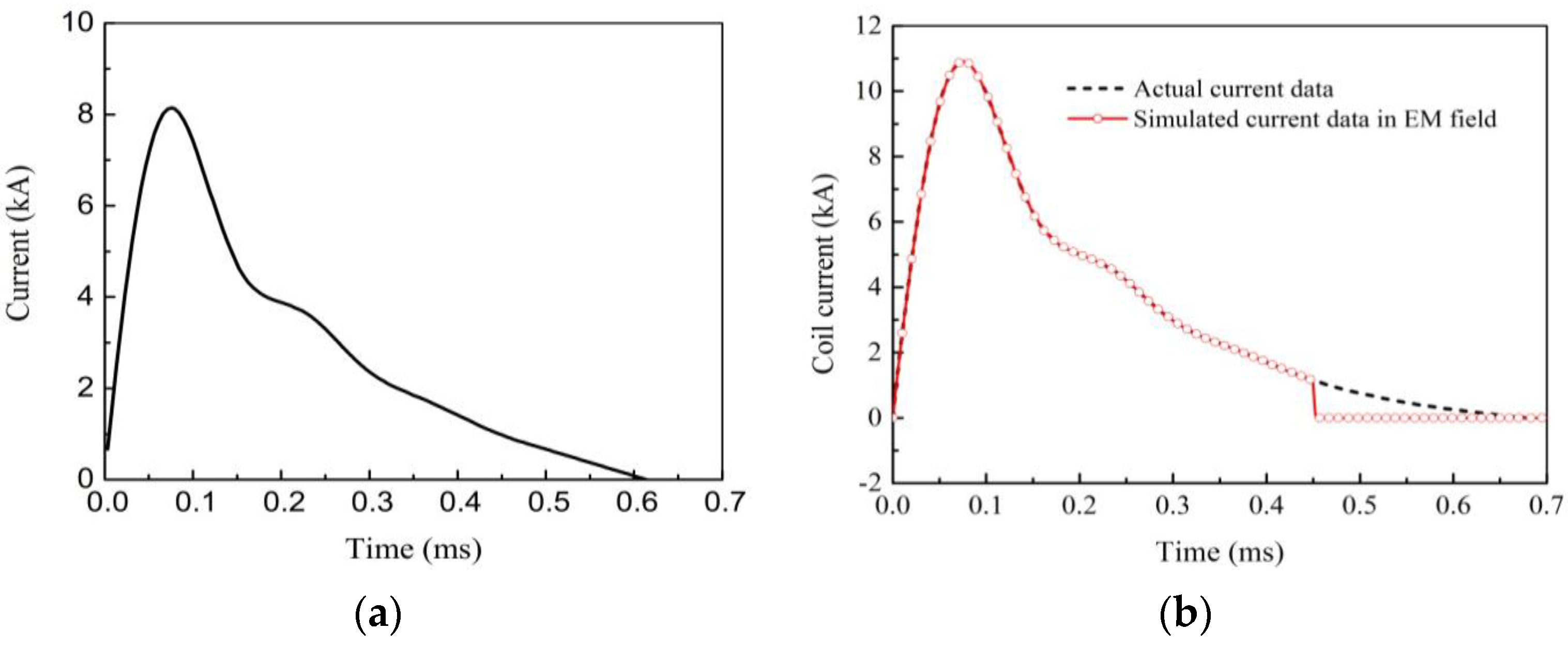
3.3. Determination of the Discharge Time and Deformation Time
4. Results and Discussion
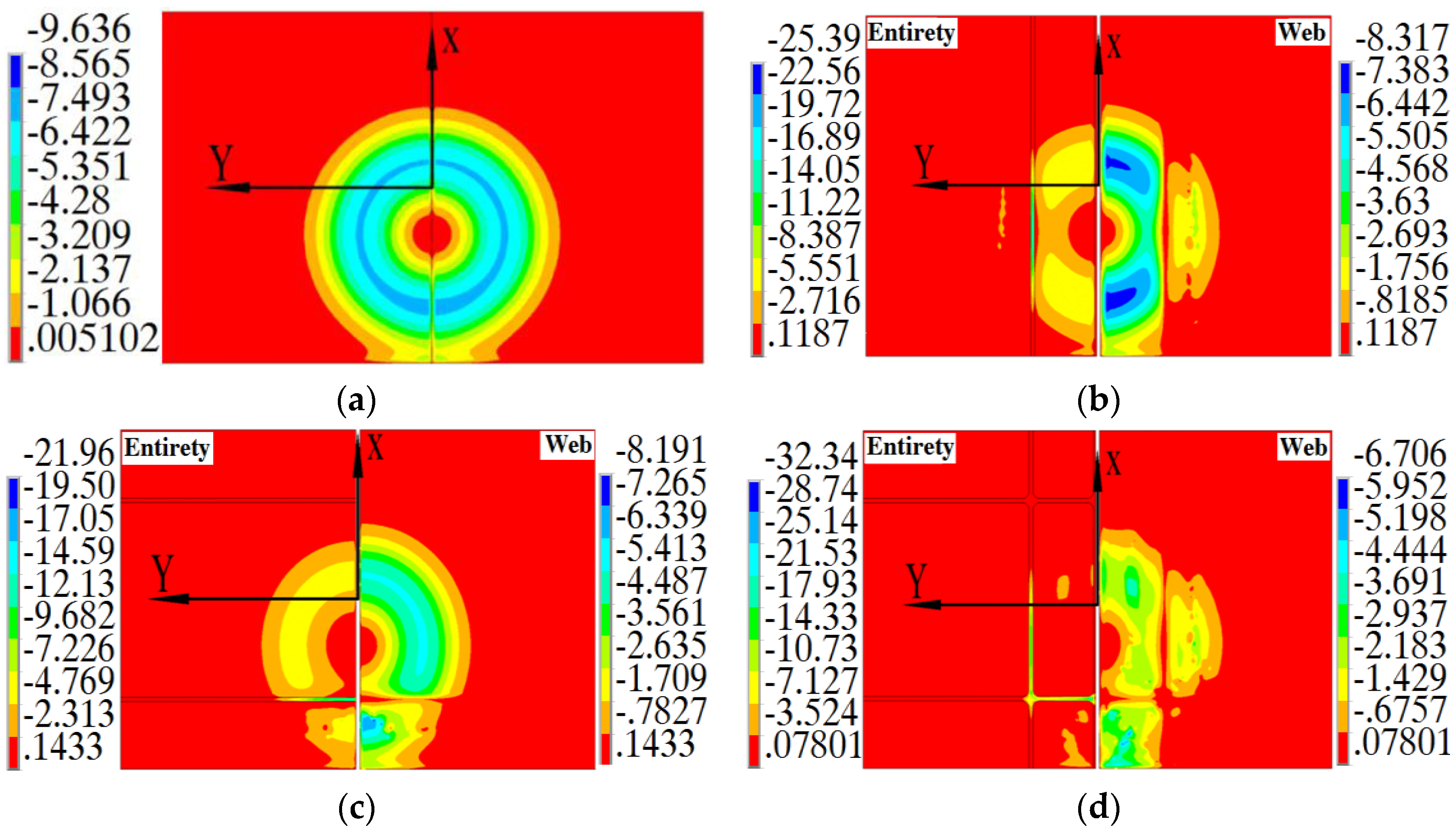
4.1. Electromagnetic Force Distribution
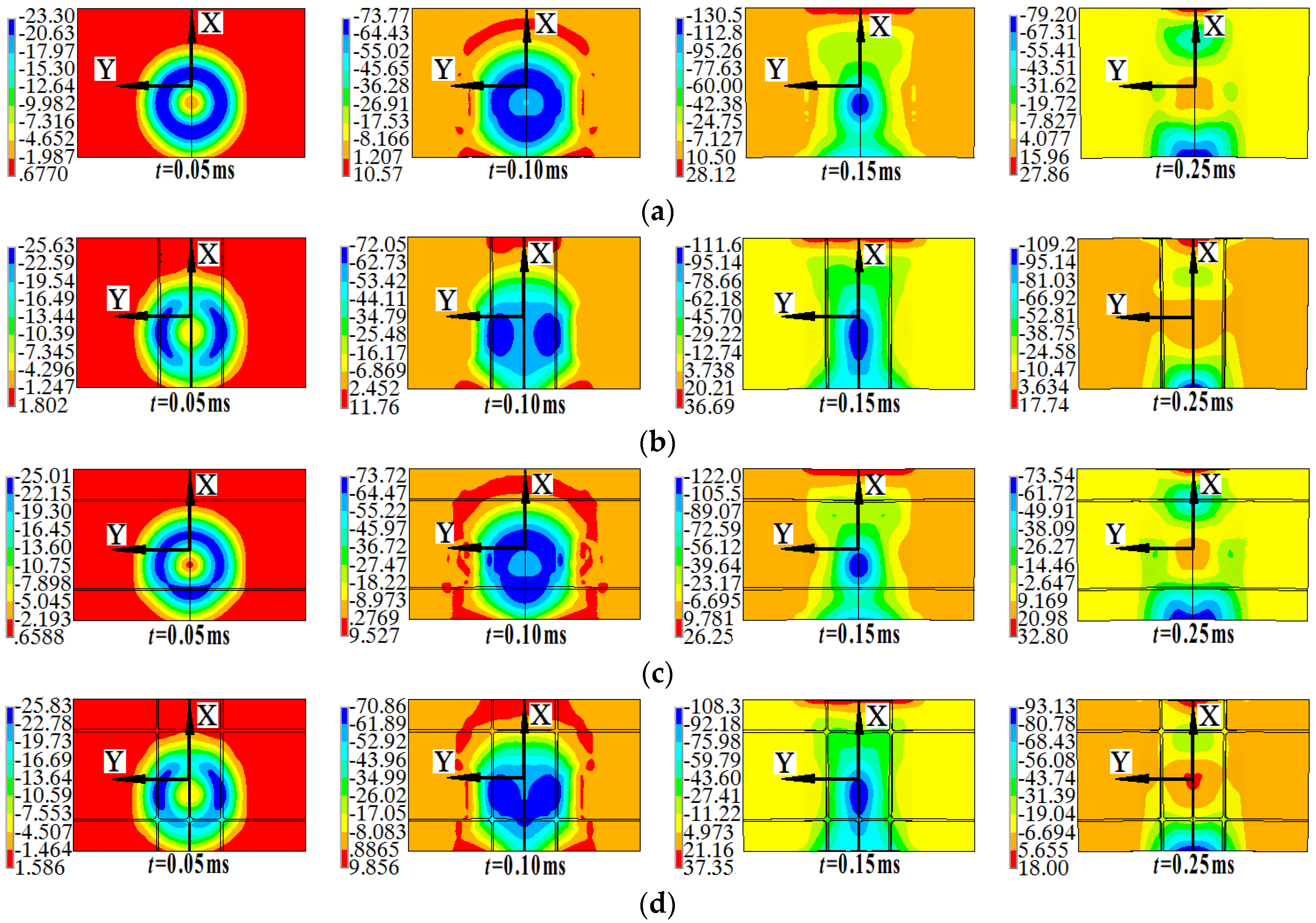
4.2. Velocity Distribution
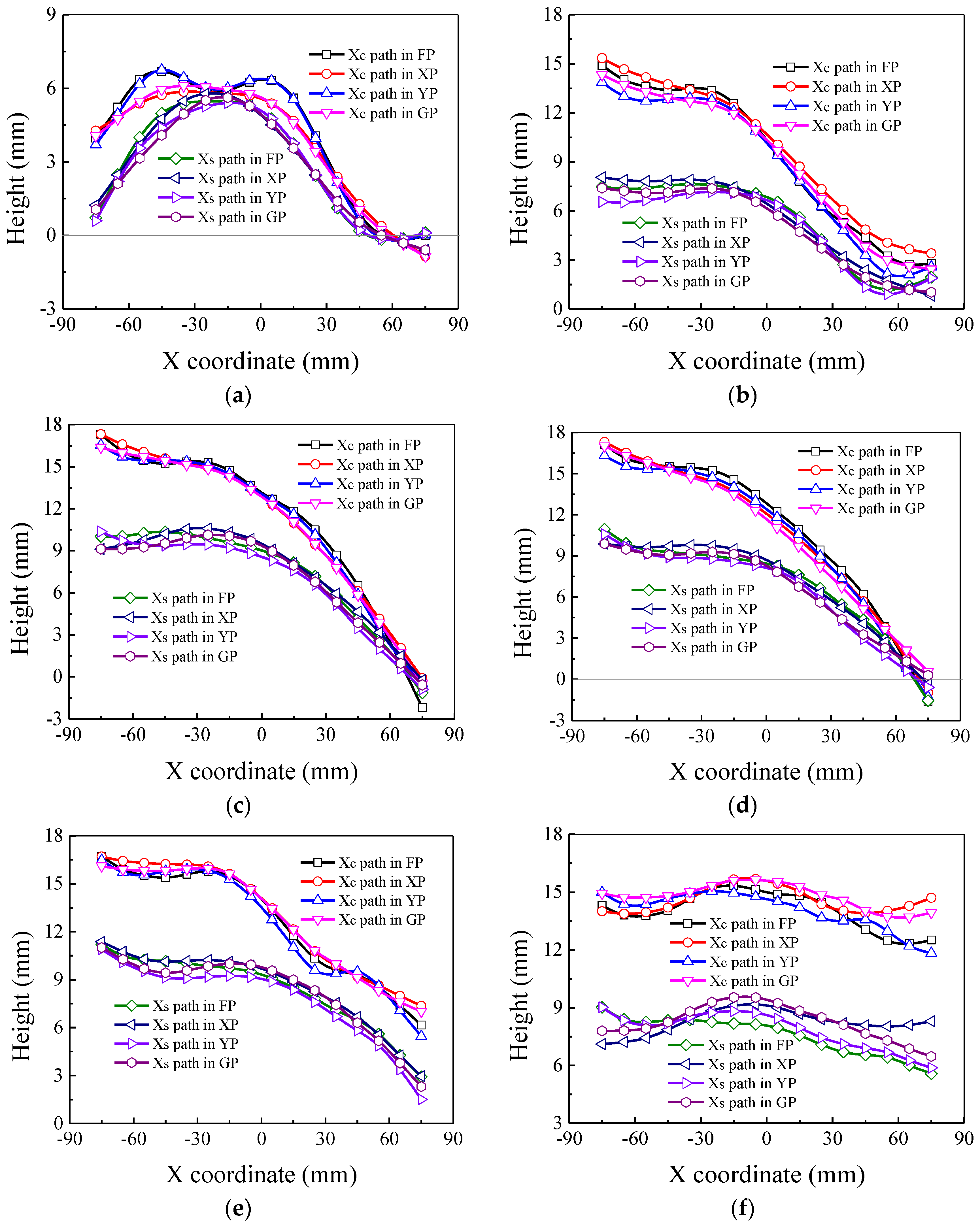
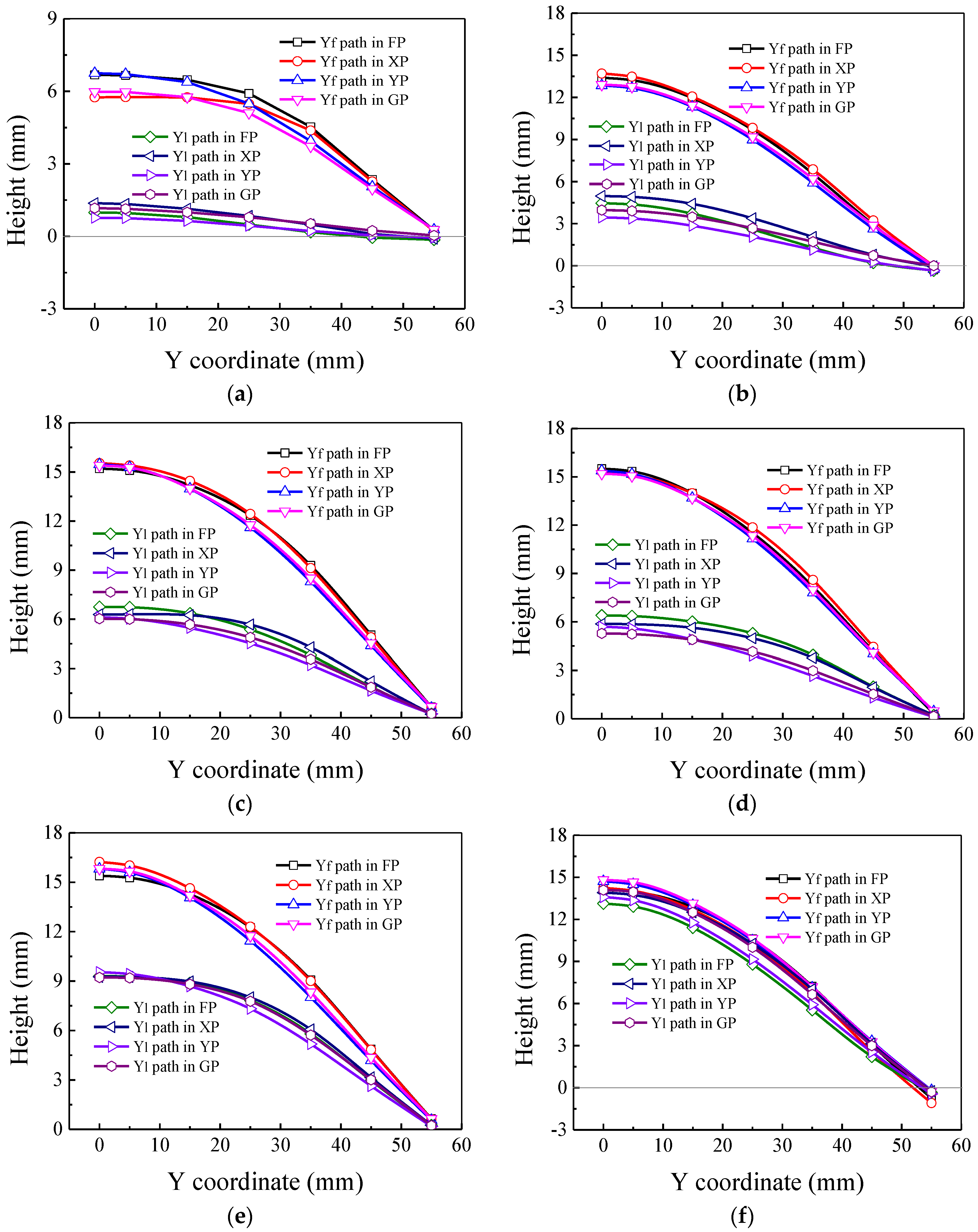
4.3. Forming Height
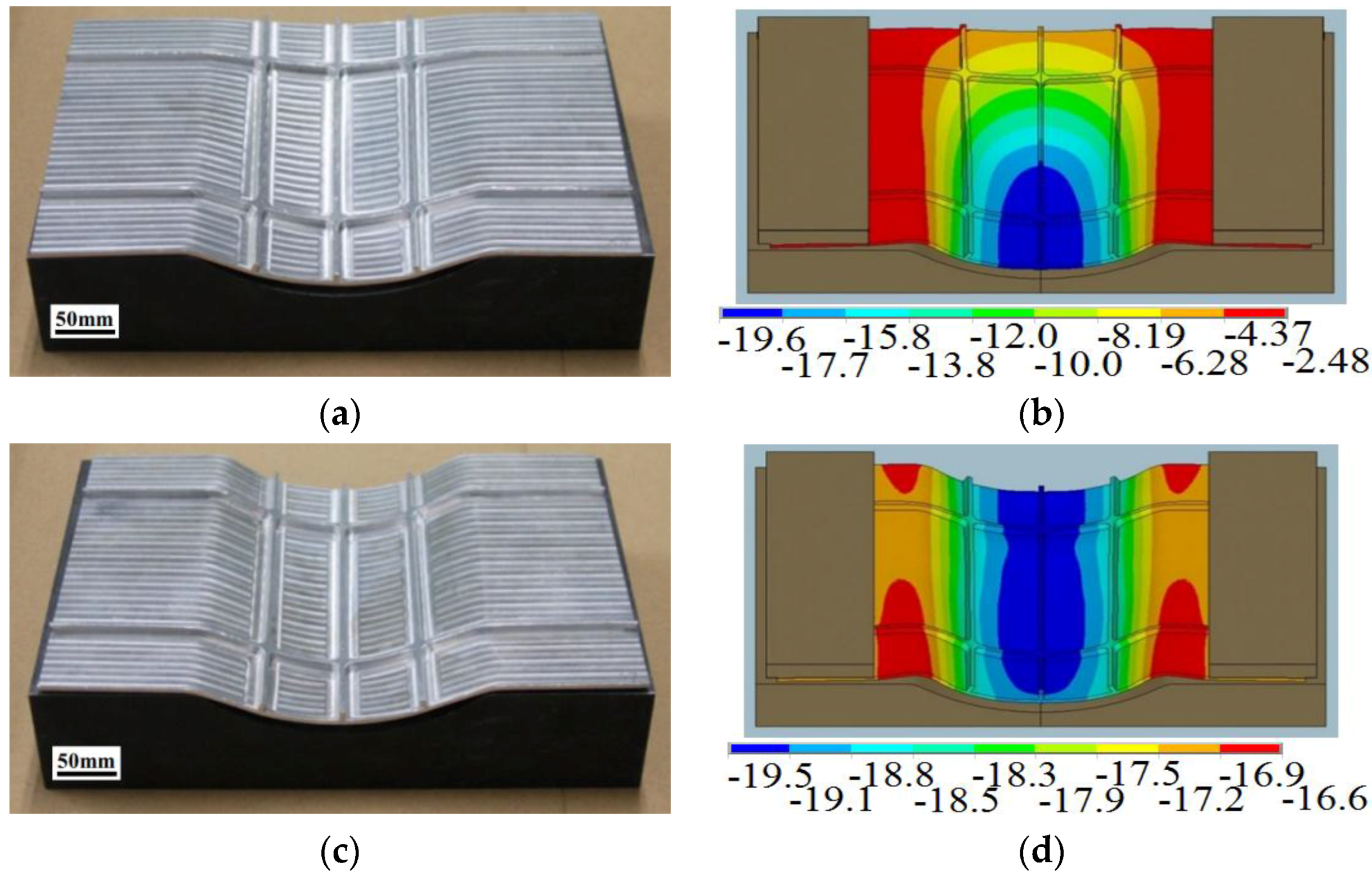
4.4. Comparison with Brake Forming
5. Conclusions
- (1)
- Different from traditional stiffened panels forming process, there are electromagnetic body forces loading in the ribs and webs simultaneously, which increases the forming ability of the stiffened panels. The large force of GP concentrates in both the two direction ribs, indicating the superposition effect of the two direction ribs.
- (2)
- The velocity distribution of the grid-rib panel is mainly affected by the X-direction ribs, next is the Y-direction ribs; the ribs along the bending direction and the flat panel promote the velocity attenuation while the ribs perpendicular to the bending direction prevent the velocity attenuation. For the grid-rib panel, it can be seen as the superposition of the X-direction ribs and the Y-direction ribs.
- (3)
- The decrease of the forming height at the free ends of the four panels at the end of each pass indicates that the mutual influence exists between the region undergoing deformation and the deformed or undeformed regions; the reverse velocity distribution exists for all the panels during the EMIF process, which mainly locates in the two free ends and thus is harmful for improving the forming height. Therefore, the reverse velocity should be avoided.
- (4)
- The comparison of the simulation results with the brake forming to those with the electromagnetic forming shows that EMF has a small elastic deformation in the web and a smaller plastic deformation in the ribs in the deformation region, which helps prevent or reduce the defects, such as springback and buckling that commonly happen in the traditional brake forming process.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Munroe, J.; Wilkins, K.; Gruber, M. Integral Airframe Structures (IAS)—Validated Feasibility Study of Integrally Stiffened Metallic Fuselage Panels for Reducing Manufacturing Costs; Boeing Commercial Airplane Group: Seattle, WA, USA, 2000. [Google Scholar]
- Zhan, L.H.; Lin, J.G.; Dean, T.A. A review of the development of creep age forming: Experimentation, modeling and applications. Int. J. Mach. Tools Manuf. 2011, 51, 1–17. [Google Scholar] [CrossRef]
- Erbel, F.; Gardiner, S.; Campanile, G.; Surdon, G.; Venmans, M.; Prangnell, P. Ageformable panels for commercial aircraft. J. Aerosp. Eng. 2008, 222, 873–886. [Google Scholar]
- Ho, K.C.; Lin, J.G.; Dean, T.A. Modelling of springback in creep forming thick aluminum sheet. Int. J. Plast. 2004, 20, 733–754. [Google Scholar] [CrossRef]
- Lam, A.C.L.; Shi, Z.S.; Yang, H.L.; Wan, L.; Davies, C.M.; Lin, J.G.; Zhou, S.J. Creep-age forming AA2219 plates with different stiffener designs and pre-form age conditions: Experimental and finite element studies. J. Mater. Proc. Technol. 2015, 219, 155–163. [Google Scholar] [CrossRef]
- Ribeiro, F.C.; Marinho, E.P.; Inforzato, D.J.; Costa, P.R.; Batalha, G.F. Creep age forming: A short review of fundaments and applications. J. Achiev. Mater. Manuf. Eng. 2010, 43, 353–361. [Google Scholar]
- Yamada, Y.; Takahashi, T.; Ikeda, M.; Sugimoto, S.; Ohta, T. Development of shot peening for wing integral skin for continental business jets. Mitsubishi Heavy Ind. Tech. Rev. 2002, 39, 57–61. [Google Scholar]
- Miao, H.Y.; Demers, D.; Larose, S.; Perron, C.; Levesque, M. Experimental study of shot peening and stress peen forming. J. Mater. Proc. Technol. 2010, 210, 2089–2102. [Google Scholar] [CrossRef]
- Wang, X.F.; Guo, X.L.; Chen, G.N.; Silvanus, J. Remark of integral panel forming. Mod. Manuf. Technol. Equip. 2008, 3, 1–4. [Google Scholar]
- Lai, S.B.; Chen, T.X.; Yu, D.Y. Dynamic explicit analysis method for roll bending forming of integrally stiffened panel with rubber filler. Spacecr. Eng. 2012, 3, 41–47. [Google Scholar]
- Yan, Y.; Wan, M.; Wang, H.B.; Huang, L. Design and optimization of press bend forming path for producing aircraft integral panels with compound curvatures. Chin. J. Aeronaut. 2010, 23, 274–282. [Google Scholar]
- Yu, Y.; Wang, H.B.; Min, M. Prediction of stiffener buckling in press bend forming of integral panels. Trans. Nonferr. Met. Soc. China 2011, 21, 2459–2465. [Google Scholar]
- Yu, Y.; Wang, H.B.; Min, M. FEM modeling for press bend forming of doubly curved integrally stiffened aircraft panel. Trans. Nonferr. Met. Soc. China 2012, 22, s39–s47. [Google Scholar]
- Daehn, G.S. High Velocity Metal Forming. In ASM Handbook, Volume 14B, Metalworking: Sheet Forming; ASM International: Columbus, OH, USA, 2006; pp. 405–418. [Google Scholar]
- Psyk, V.; Risch, D.; Kinsey, B.L.; Tekkaya, A.E.; Kleiner, M. Electromagnetic forming—A review. J. Mater. Proc. Technol. 2011, 211, 787–829. [Google Scholar] [CrossRef]
- Cui, X.H.; Mo, J.H.; Li, J.J.; Zhao, J.; Xiao, S.J. Produce a large aluminum alloy sheet metal using electromagnetic-incremental (EM-IF) forming method: Experiment and Numerical simulation. In Proceedings of the 5th International Conference on High Speed Forming, Dortmund, Germany, 24–26 April 2012; pp. 59–70.
- Kamal, M.; Daehn, G.S. A uniform pressure electromagnetic actuator for forming flat sheets. J. Manuf. Sci. Eng. 2007, 129, 369–379. [Google Scholar] [CrossRef]
- Zhao, J.; Mo, J.H.; Cui, X.H.; Qiu, L. Research on numerical simulation and forming uniformity of electromagnetic incremental tube bulging. J. Plast. Eng. 2012, 19, 92–99. (In Chinese) [Google Scholar]
- Cui, X.H.; Mo, J.H.; Li, J.J.; Zhao, J.; Zhu, Y.; Huang, L.; Li, Z.W.; Zhong, K. Electromagnetic incremental forming (EMIF): A novel aluminum alloy sheet and tube forming technology. J. Mater. Proc. Technol. 2014, 214, 409–427. [Google Scholar] [CrossRef]
- Fenton, G.K.; Daehn, G.S. Modeling of electromagnetically formed sheet metal. J. Mater. Proc. Technol. 1998, 75, 6–16. [Google Scholar] [CrossRef]
- Ma, S.G.; Zhan, M.; Tan, J.Q.; Zhang, P.P. 3D sequentially coupled model to simulate electromagnetic sheet forming. J. Plast. Eng. 2012, 19, 54–58. (In Chinese) [Google Scholar]
- Oliveira, D.A.; Worswick, M. Electromagnetic forming of aluminium alloy sheet. J. Phys. IV France 2003, 110, 293–298. [Google Scholar] [CrossRef]
- Yu, H.P.; Li, C.F.; Deng, J.H. Sequential coupling simulation for electromagnetic mechanical tube compression by finite element analysis. J. Mater. Proc. Technol. 2009, 209, 707–713. [Google Scholar]
- Cui, X.H.; Mo, J.H.; Xiao, S.J.; Du, E.H. Numerical simulation of electromagnetic sheet bulging based on FEM. Int. J. Adv. Manuf. Technol. 2011, 57, 127–134. [Google Scholar] [CrossRef]
- ISO 209:2007. Aluminium and Aluminum Alloy—Chemical Composition; ISO: Geneva, Switzerland, 2007. [Google Scholar]
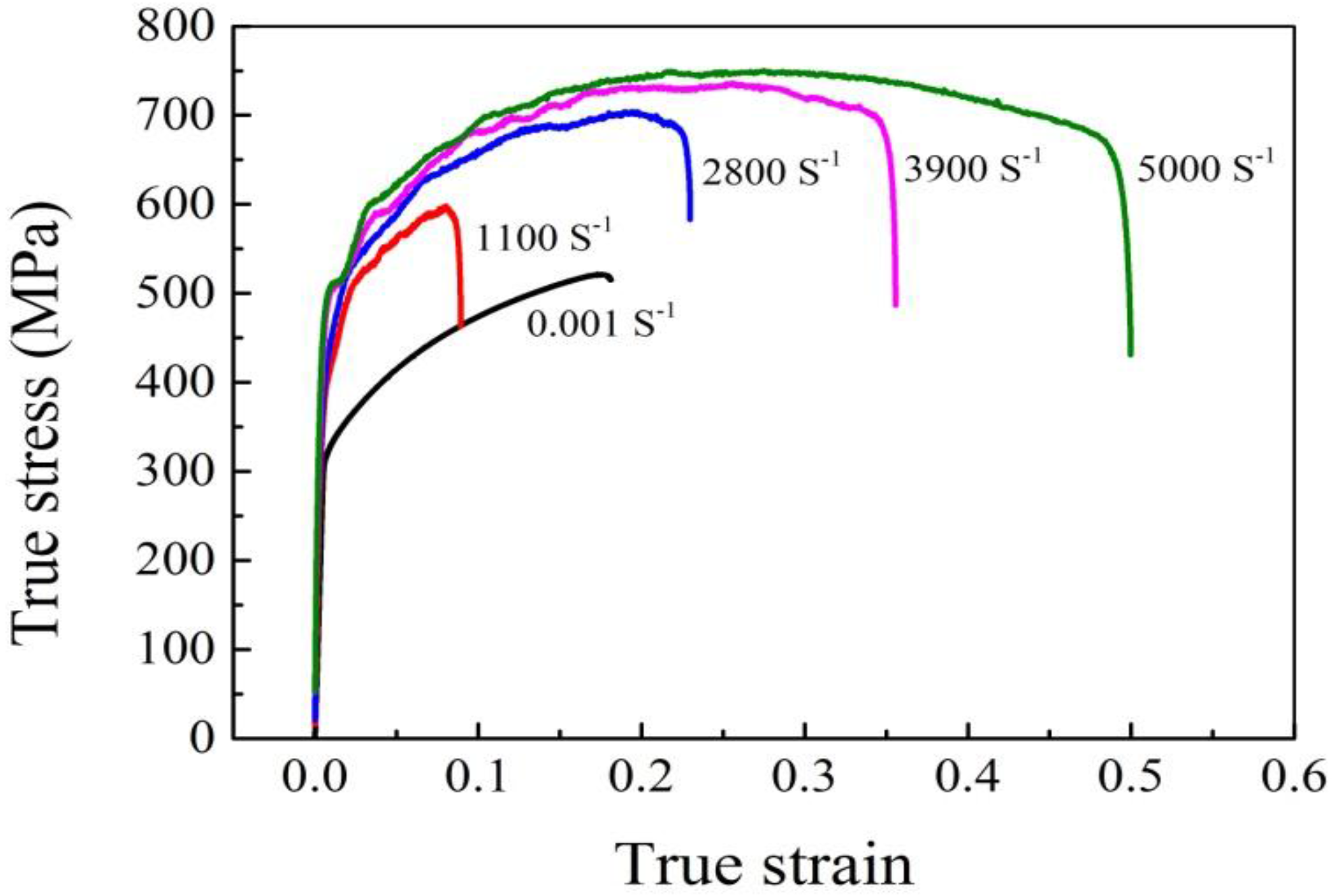
- Tan, J.Q.; Zhan, M.; Liu, S.; Huang, T.; Guo, J.; Yang, H. A modified Johnson-cook model for tensile flow behaviors of 7050-T7451 aluminum alloy at high strain rates. Mater. Sci. Eng. A 2015, 631, 214–219. [Google Scholar] [CrossRef]
- ISO 6892-1:2009. Metallic Materials-Tensile Testing. Part 1: Method of Test at Room Temperature; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- Cao, Q.L.; Han, X.T.; Lai, Z.P.; Xiong, Q.; Zhang, X.; Chen, Q.; Xiao, H.X.; Li, L. Analysis and reduction of coil temperature rise in electromagnetic forming. J. Mater. Proc. Technol. 2015, 225, 185–194. [Google Scholar] [CrossRef]
- Liu, D.H.; Zhou, W.H.; Li, C.F. Influence of body force effect of the pulsed magnetic forces of the dynamic forming limits of AA5052 sheets. J. Plast Eng. 2013, 6, 62–67. [Google Scholar]
- Neugebauer, R.; Bouzakis, K.D.; Denkena, B.; Klocke, F.; Sterzing, A.; Tekkaya, A.E.; Wertheim, R. Velocity effects in metal forming and machining processes. CIRP Ann. Manuf. Technol. 2011, 2, 627–650. [Google Scholar] [CrossRef]
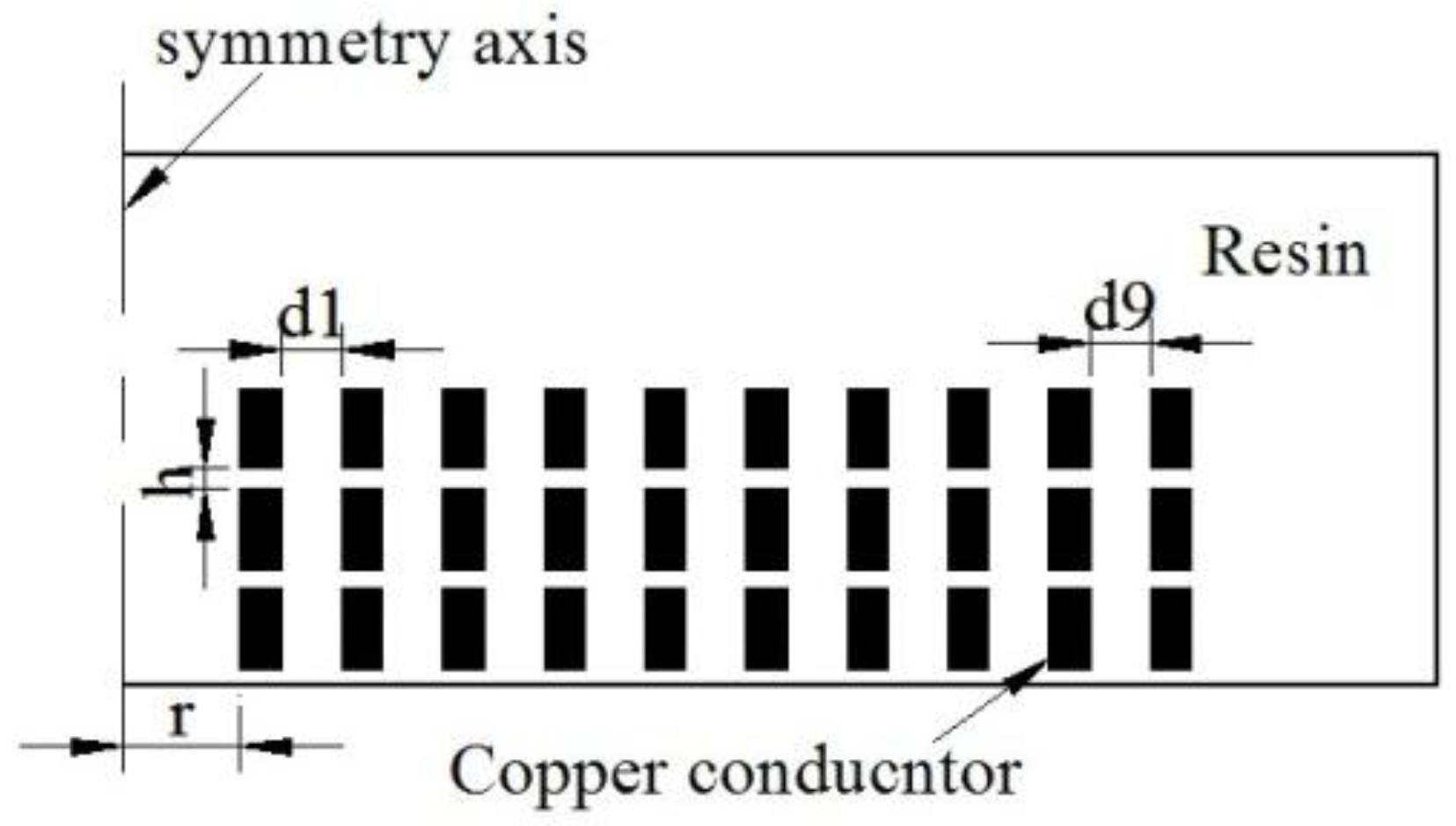


| Parameters | Value | Parameters | Value | Parameters | Value |
|---|---|---|---|---|---|
| Rectangular section | 2 mm × 4 mm | Layer gap h | 0.4 mm | Turn gap d5 | 0.95 mm |
| Total turns N | 30 | Turn gap d1 | 1.8 mm | Turn gap d6 | 0.95 mm |
| Layers | 3 | Turn gap d2 | 1.8 mm | Turn gap d7 | 0.7 mm |
| Inner radius R | 7 mm | Turn gap d3 | 1.7 mm | Turn gap d8 | 0.7 mm |
| Height H | 12.8 mm | Turn gap d4 | 1.2 mm | Turn gap d9 | 0.7 mm |
| Blank Form | Rib Height (mm) | Rib Width (mm) | Web Thickness (mm) |
|---|---|---|---|
| Flat panel (FP) | 0 | 0 | 2 |
| X-rib panel (XP) | 4 | 2 | 2 |
| Y-rib panel (YP) | 4 | 2 | 2 |
| Grid-rib panel (GP) | 4 | 2 | 2 |
| Materials & Boundary Condition | Parameter | Value |
|---|---|---|
| Air Coil (copper) | Relative permeability Relative permeability Resistance Inductance Reference resistivity Density Elastic modulus Poisson’s ratio | 1 1 20 mΩ 15 μH 1.7 × 10−8 Ω·m 8.9 × 103 kg/m3 90 GPa 0.33 |
| Panel (2A12-T4 Al alloy) | Relative permeability Reference resistivity Density Elastic modulus Poisson’s ratio Yield strength Ultimate strength | 1 3 × 10−8 Ω·m 2.77 × 103 kg/m3 69 GPa 0.31 284 MPa 495 MPa |
| Die/Blank holder block (42CrMo4) | Relative permeability Density Elastic modulus Poisson’s ratio | 1 7.85 × 103 kg/m3 206 GPa 0.3 |
| Circuit line | Line resistance Line inductance | 25 mΩ 6.5 μH |
| Contact set (Blank holder block-Panel) | Static friction factor Dynamic friction factor | 0.17 0.15 |
| Contact set (Die-Panel) | Static friction factor Dynamic friction factor | 0.17 0.15 |
| Discharge Capacity (μF) | X Coordinate at the 1st Pass (mm) | Voltage at the 1st Pass (kV) | X Coordinate at the 2nd Pass (mm) | Voltage at the 2nd Pass (kV) | X Coordinate at the 3rd Pass (mm) | Voltage at the 3rd Pass (kV) |
|---|---|---|---|---|---|---|
| 80 | −20 | 9.9 | −20 | 12 | +20 | 12 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, J.; Zhan, M.; Liu, S. Guideline for Forming Stiffened Panels by Using the Electromagnetic Forces. Metals 2016, 6, 267. https://doi.org/10.3390/met6110267
Tan J, Zhan M, Liu S. Guideline for Forming Stiffened Panels by Using the Electromagnetic Forces. Metals. 2016; 6(11):267. https://doi.org/10.3390/met6110267
Chicago/Turabian StyleTan, Jinqiang, Mei Zhan, and Shuai Liu. 2016. "Guideline for Forming Stiffened Panels by Using the Electromagnetic Forces" Metals 6, no. 11: 267. https://doi.org/10.3390/met6110267





