Modelling of Violent Water Wave Propagation and Impact by Incompressible SPH with First-Order Consistent Kernel Interpolation Scheme
Abstract
:1. Introduction
2. ISPH Methodology
2.1. Governing Equations and Solution Algorithms
2.2. Calculation of Spatial Derivatives
2.3. Free Surface and Solid Boundary Conditions
3. Improved First-Order Derivative Scheme
3.1. Simplified Finite Difference Interpolation (SFDI) Scheme
3.2. Moving Least Square (MLS) Method
3.3. First-Order Consistent Kernel Interpolation (C1_KI) Scheme
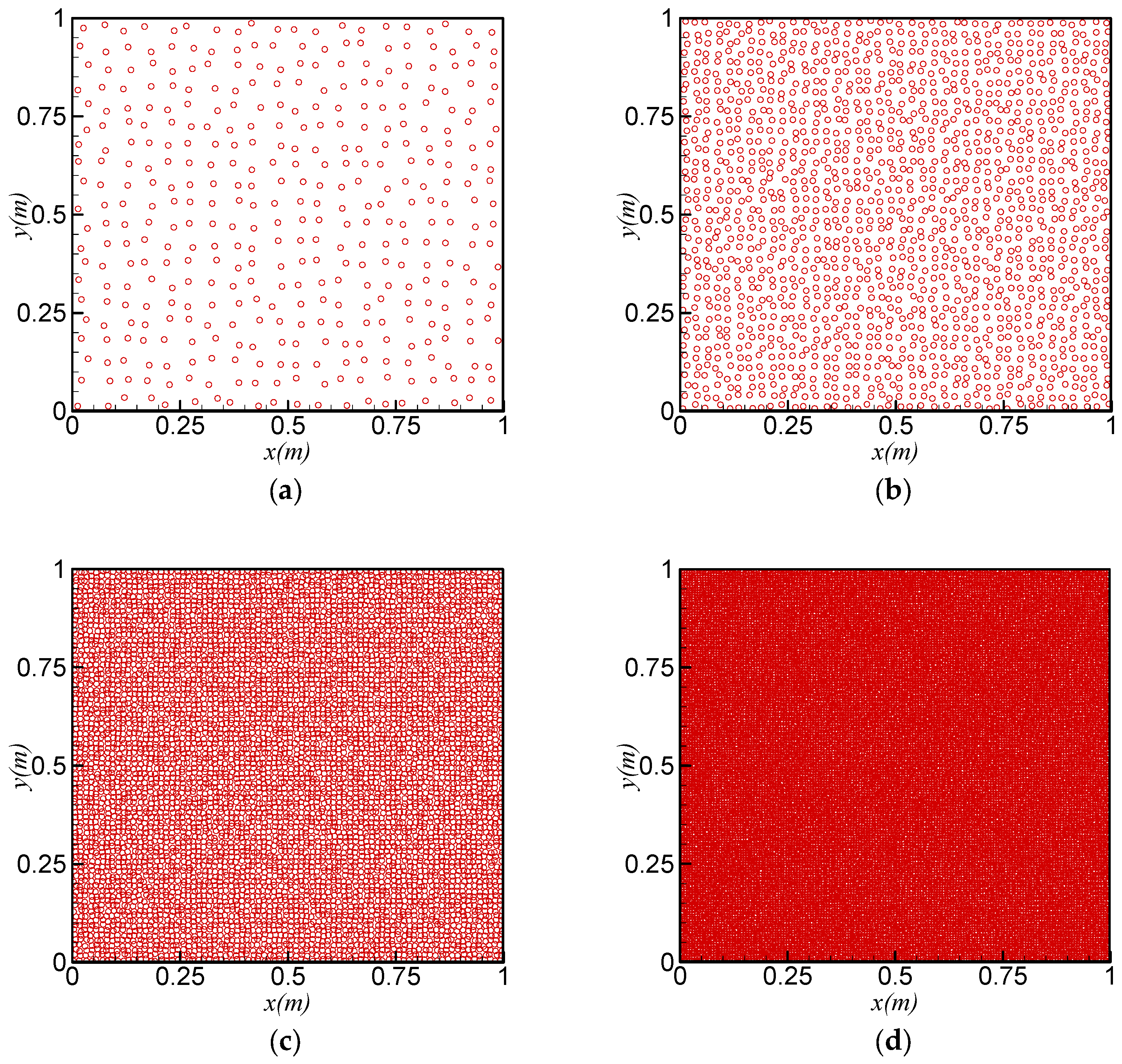
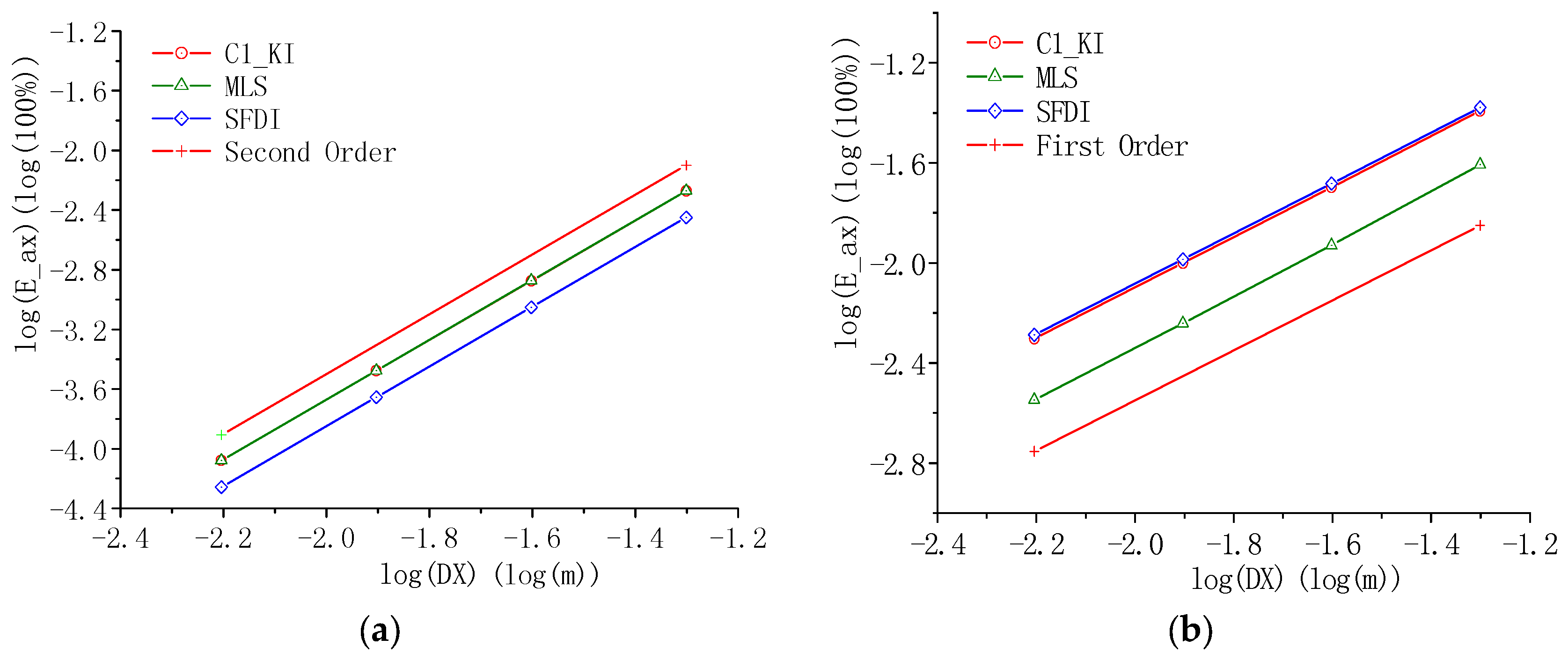
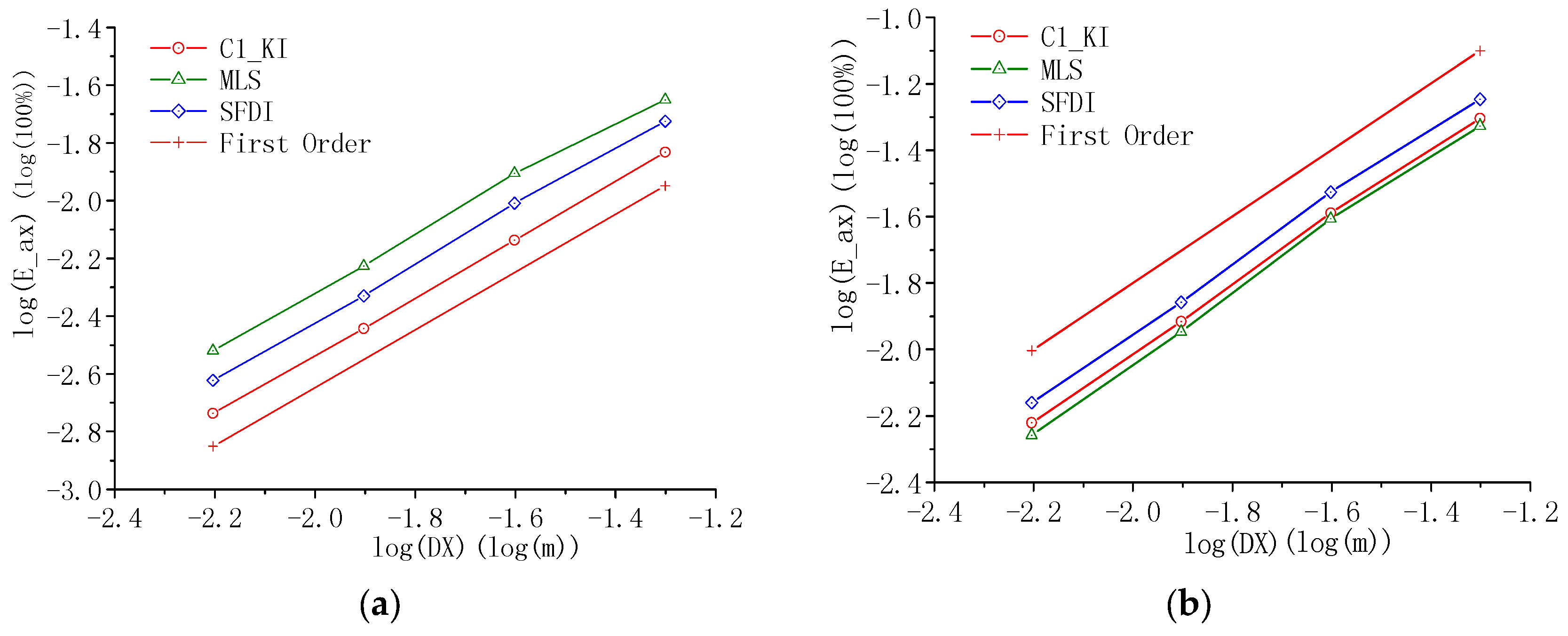
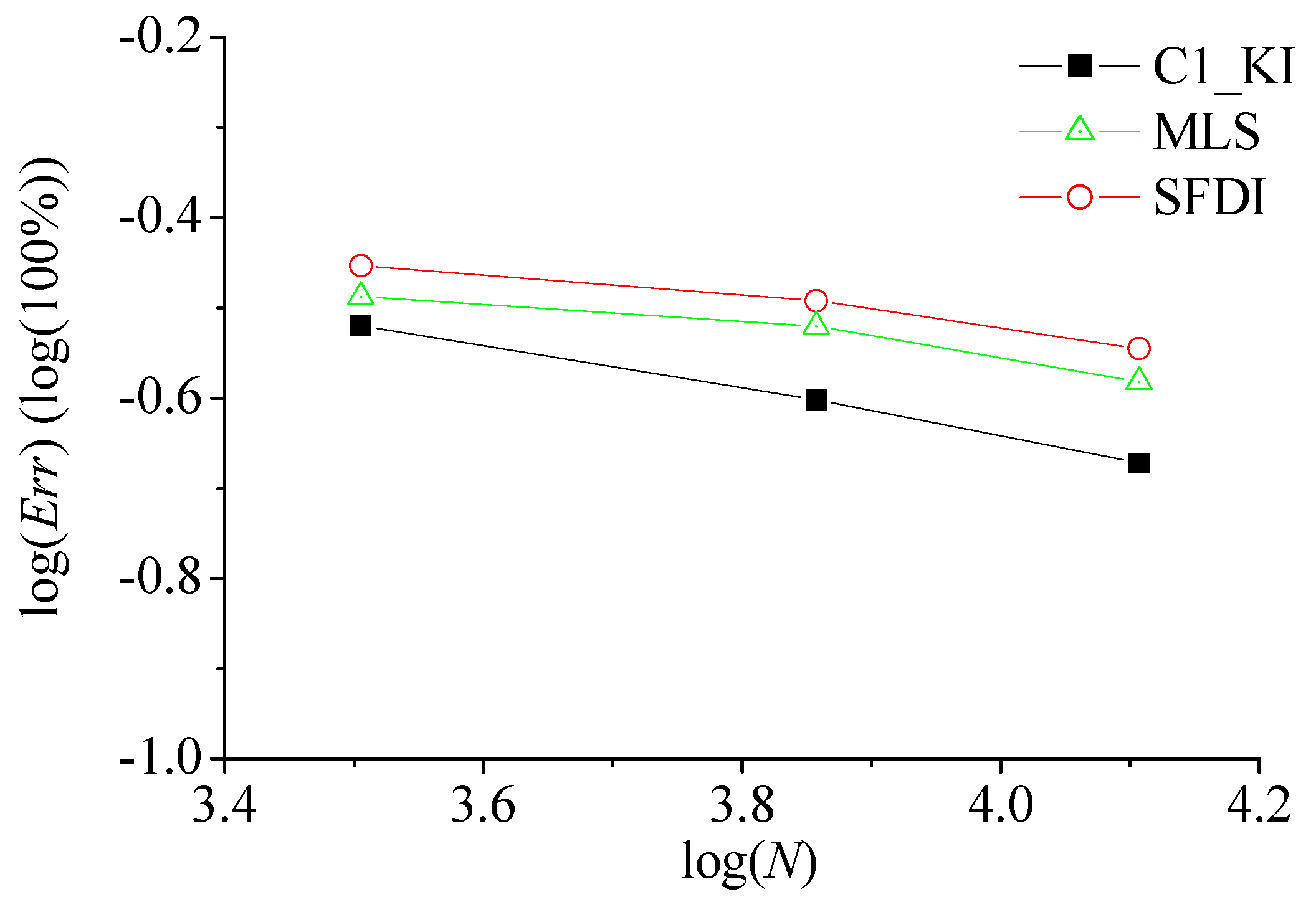
4. Convergence and Accuracy of Different Pressure Gradient Models
5. Model Applications in Water Wave Modelling
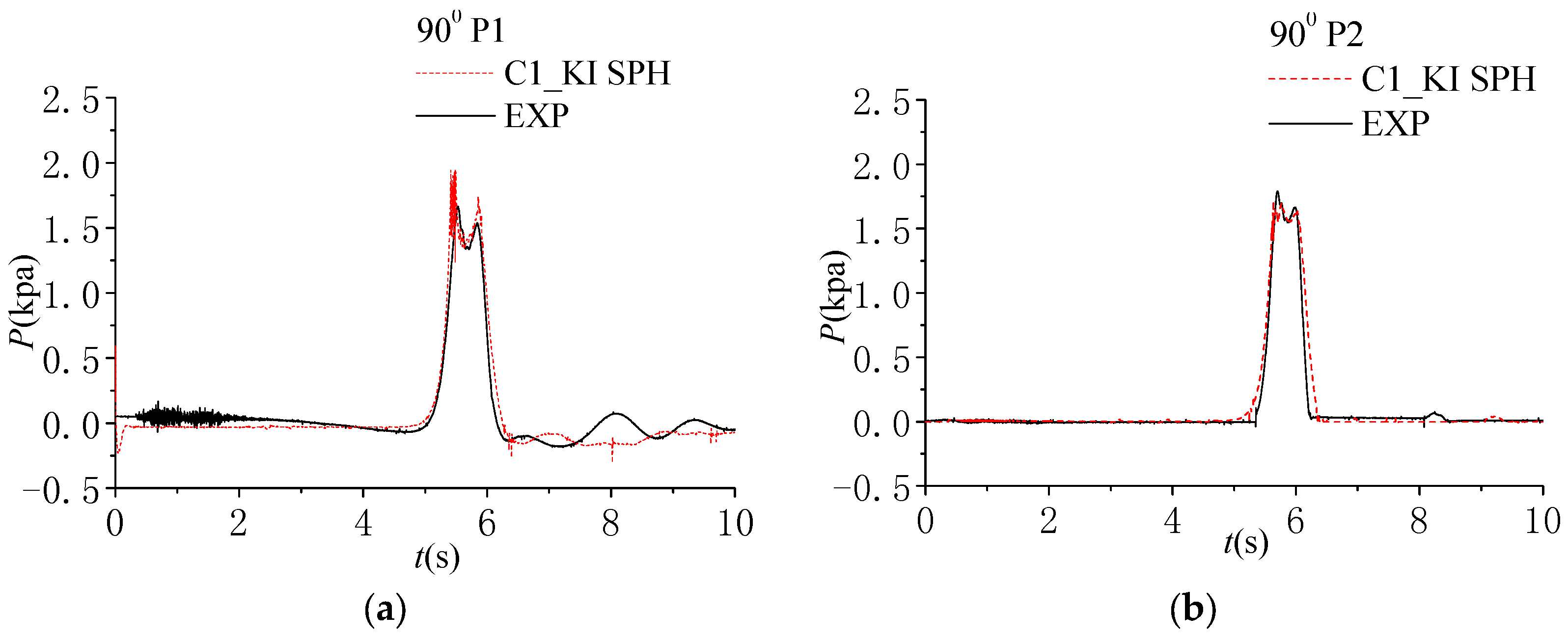
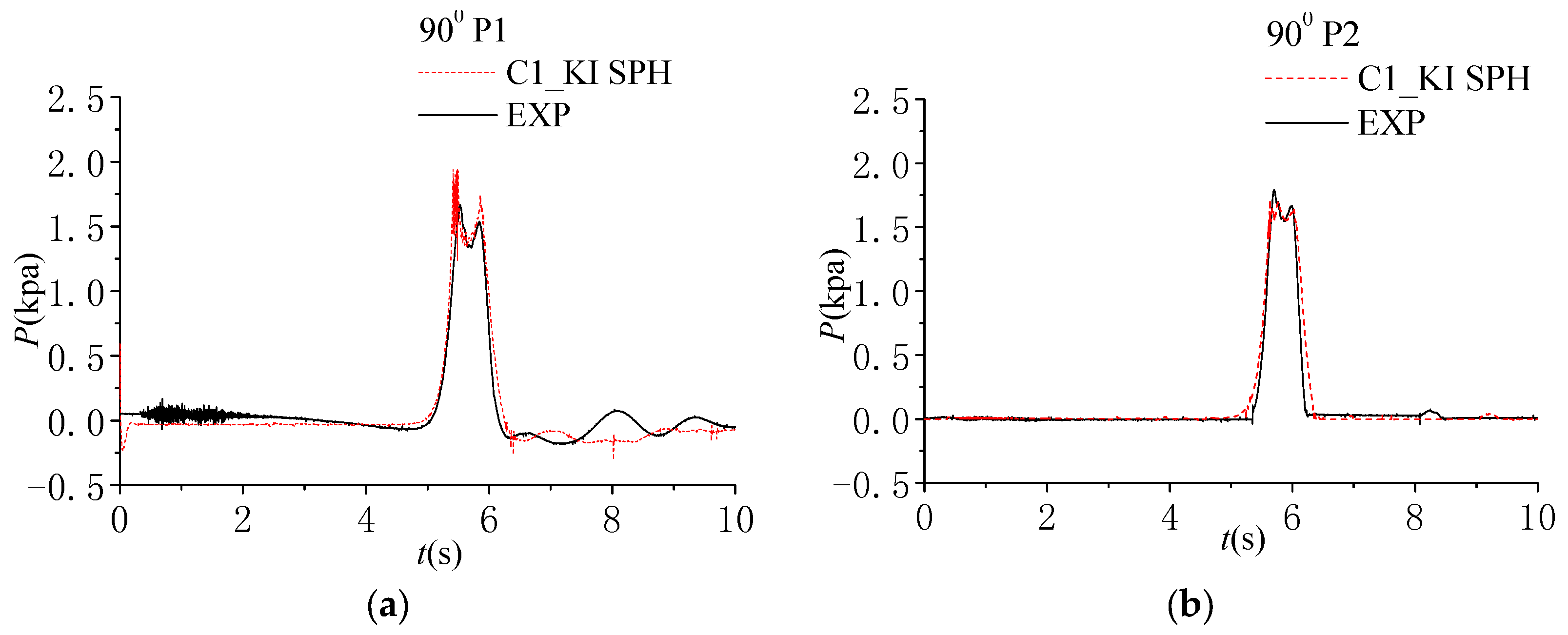
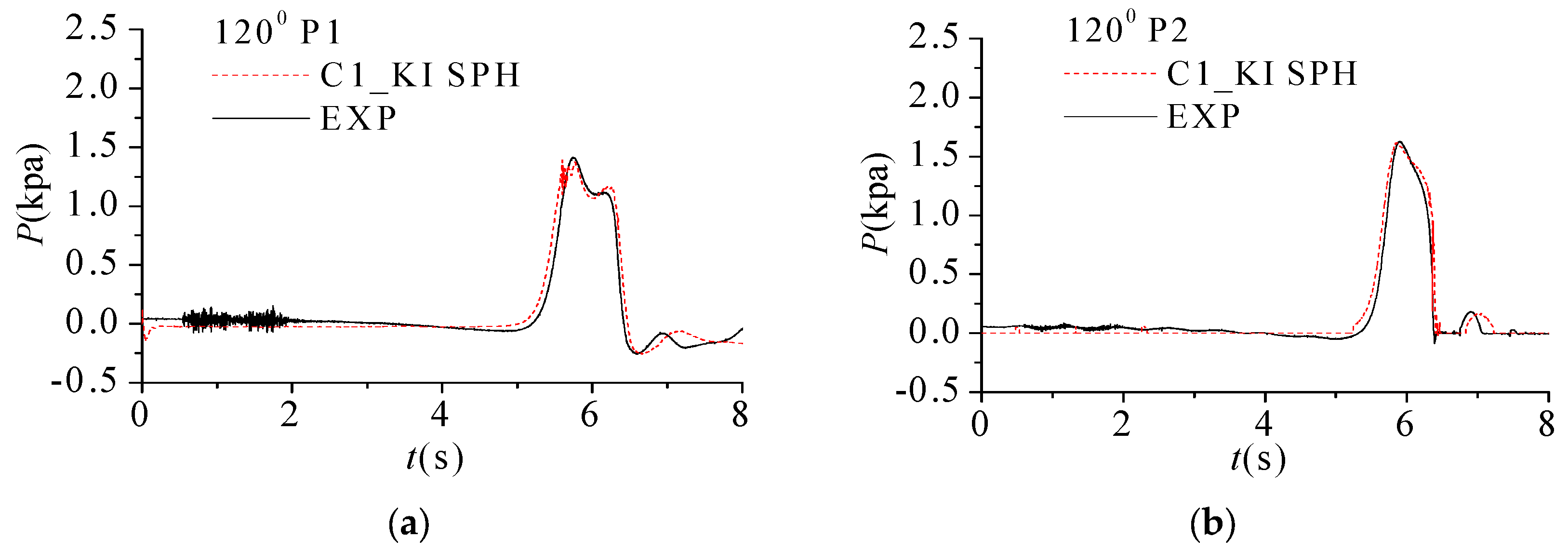
5.1. Dam Break Wave Impact on a Vertical Wall
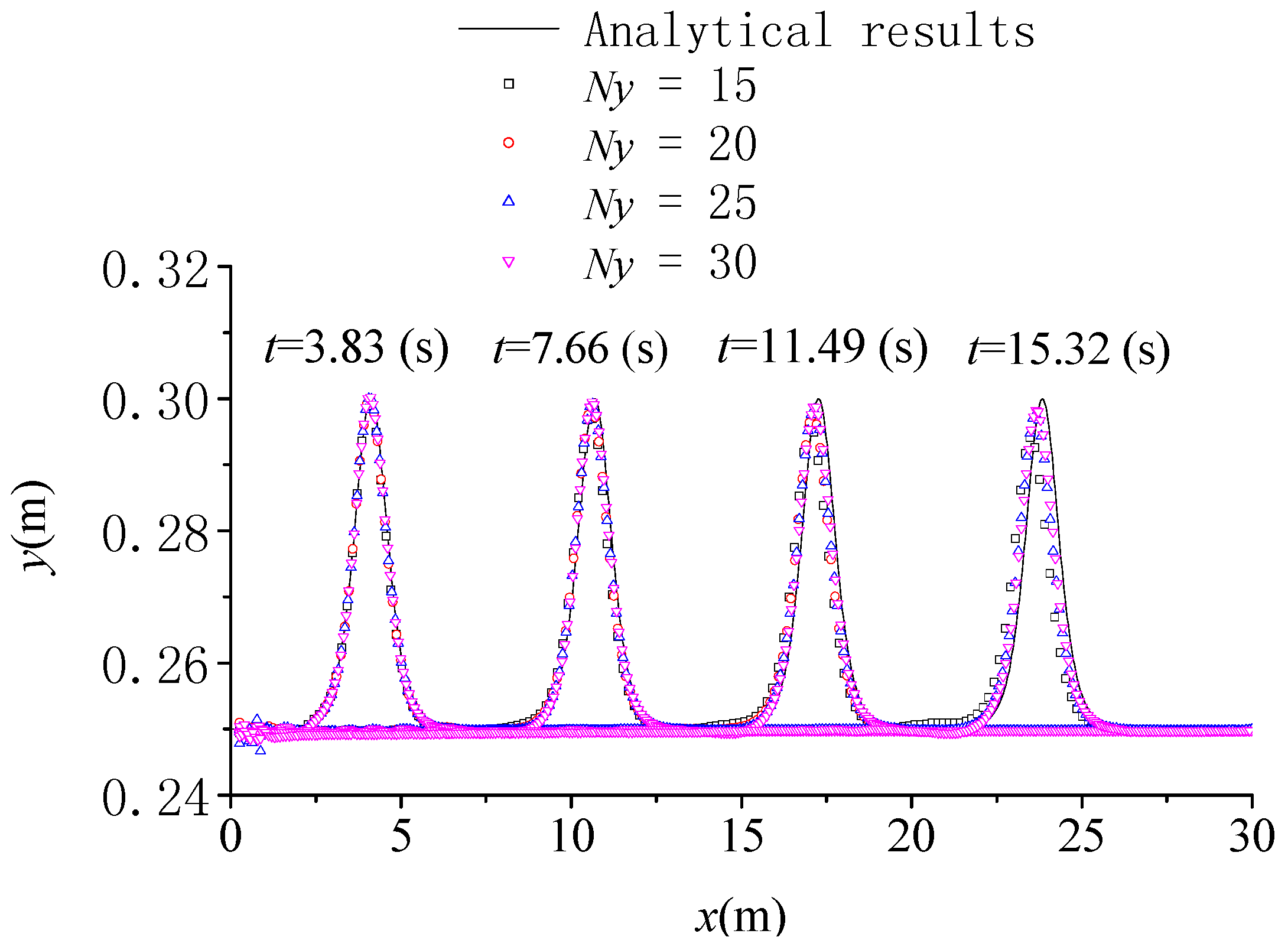
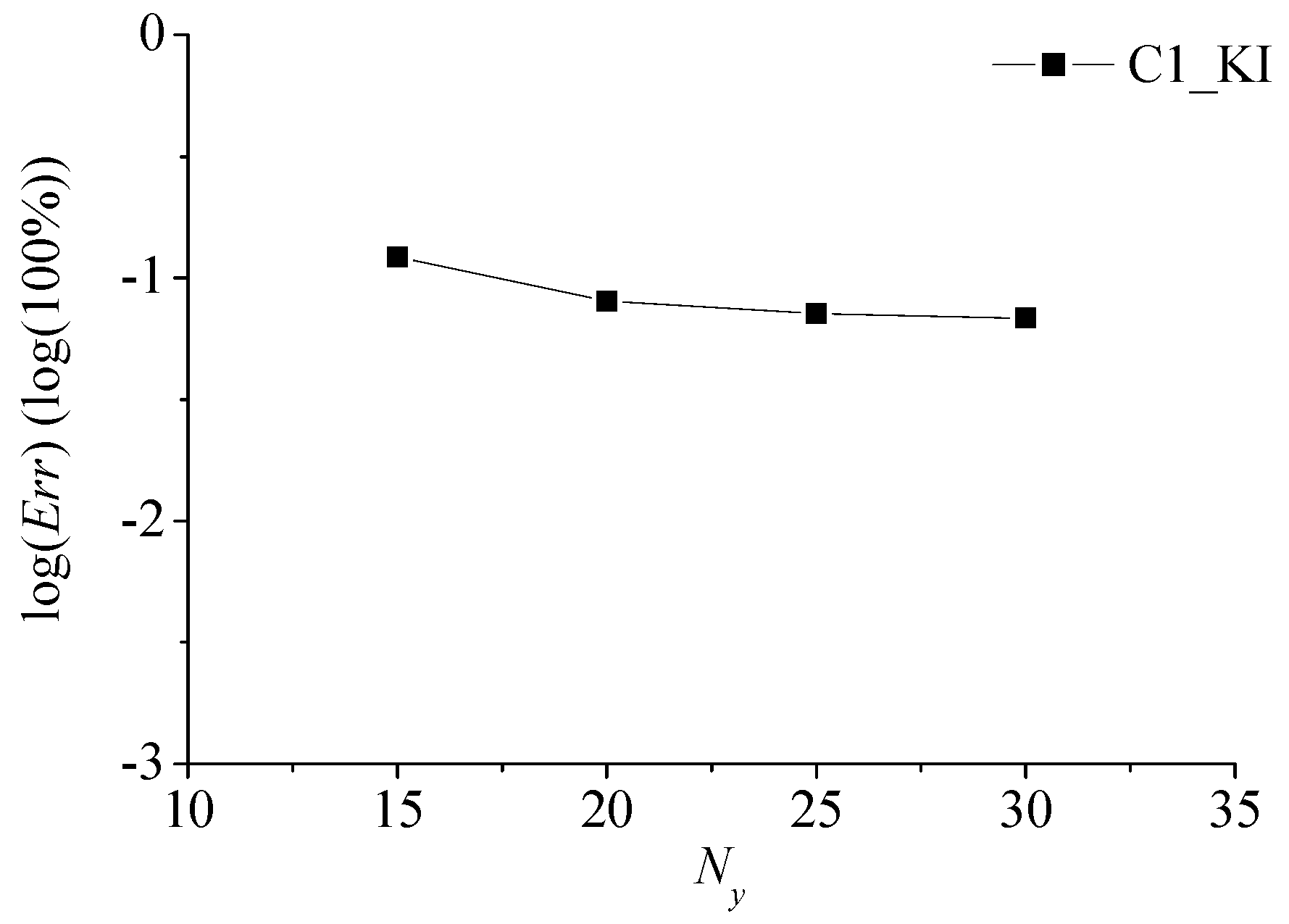
5.2. Solitary Wave Propagation over a Constant Depth
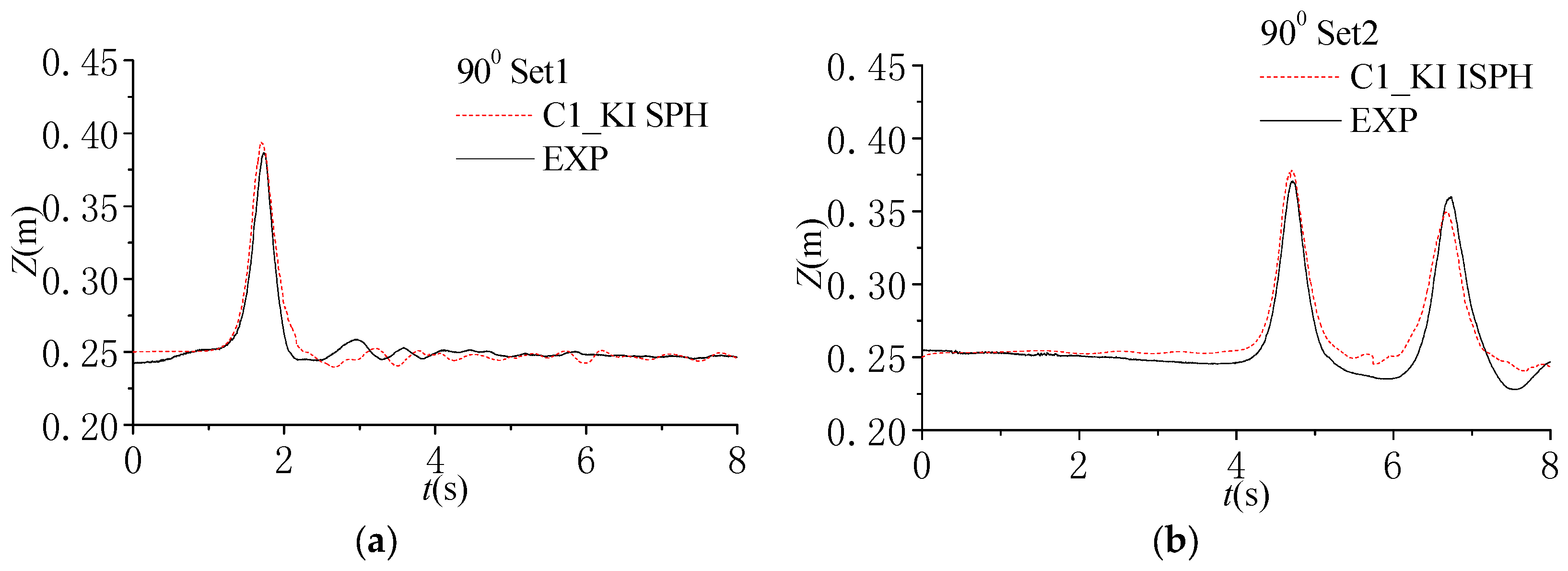
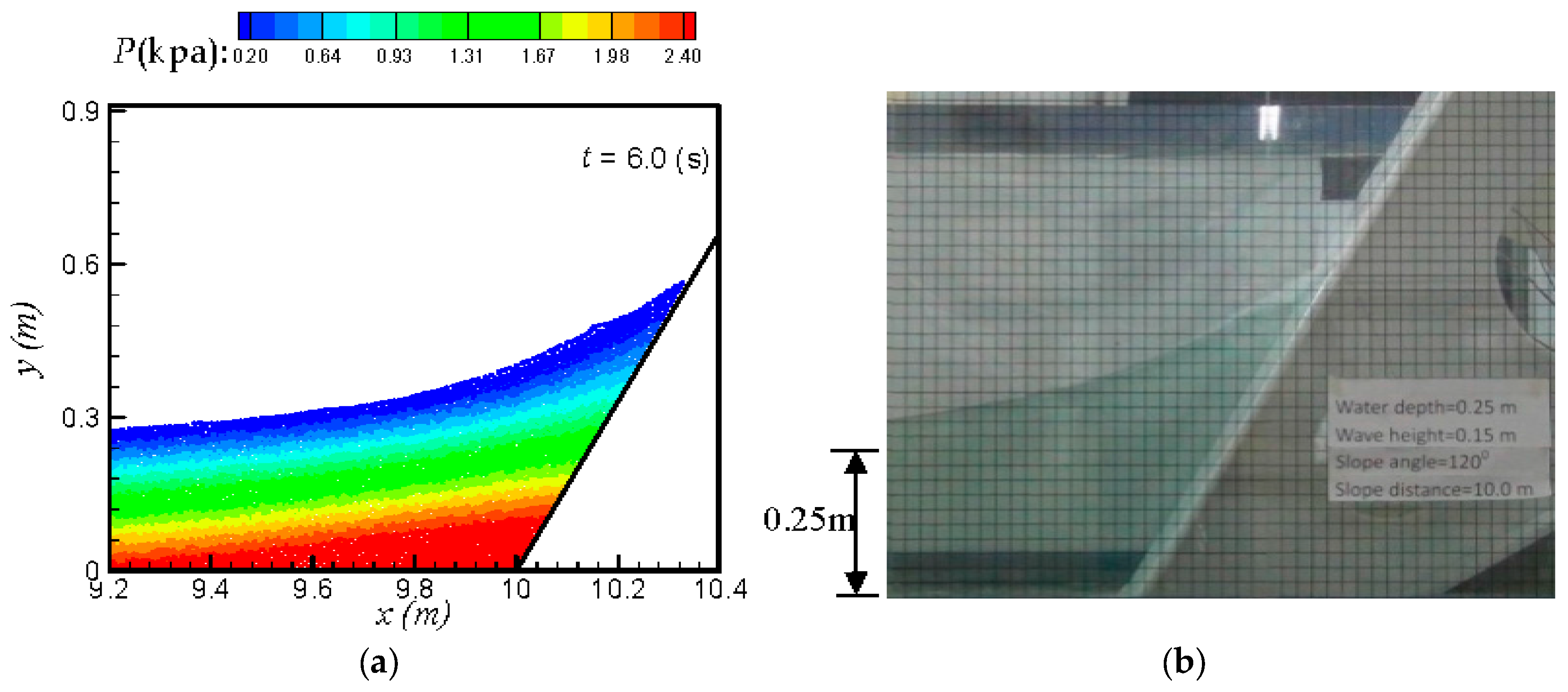
5.3. Solitary Wave Impacting on Vertical and Inclined Walls
6. Conclusions and Discussions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Grilli, S.T.; Guyenne, P.; Dias, F. A fully nonlinear model for three-dimensional overturning waves over arbitrary bottom. Int. J. Numer. Methods Fluids 2001, 35, 829–867. [Google Scholar] [CrossRef]
- Celebi, M.S.; Kim, M.H.; Beck, R.F. Fully nonlinear 3D numerical wave tank simulation. J. Ship Res. 1998, 42, 33–45. [Google Scholar]
- Ma, Q.W.; Wu, G.X.; Eatock Taylor, R. Finite element simulation of fully non-linear interaction between vertical cylinders and steep waves. Part 2: Numerical results and validation. Int. J. Numer. Methods Fluids 2001, 36, 287–308. [Google Scholar] [CrossRef]
- Yue, W.; Lin, C.L.; Patel, V.C. Numerical simulation of unsteady multidimensional free surface motions by level set method. Int. J. Numer. Methods Fluids 2003, 42, 853–884. [Google Scholar] [CrossRef]
- Greaves, D.M. Simulation of interface and free surface flows in a viscous fluid using adaptive quadtree grids. Int. J. Numer. Methods Fluids 2004, 44, 1093–1117. [Google Scholar] [CrossRef]
- Wang, P.; Yao, Y.; Tulin, M. An efficient numerical tank for nonlinear water waves, based on the multi-subdomain approach with BEM. Int. J. Numer. Methods Fluids 1995, 20, 1315–1336. [Google Scholar] [CrossRef]
- Wu, G.X.; Hu, Z.Z. Simulation of nonlinear interactions between waves and floating bodies through a finite-element-based numerical tank. Proc. R. Soc. A 2004, 460, 3037–3058. [Google Scholar] [CrossRef]
- Stansby, P. Solitary wave runup and overtopping by a semi-implicit finite volume shallow-water Boussinesq model. J. Hydraulic Res. 2003, 41, 639–647. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of fusion process. Astron. J. 1977, 88, 1013–1024. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Cerqueiroa, D.; Crespo, C.; Dalrymple, R.A. Green water overtopping analyzed with a SPH model. Ocean Eng. 2005, 32, 223–238. [Google Scholar] [CrossRef]
- Koshizuka, S.; Oka, Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid. Nucl. Sci. Eng. 1996, 123, 421–434. [Google Scholar]
- Cummins, S.J.; Rudman, M. An SPH projection method. J. Comput. Phys. 1999, 152, 584–607. [Google Scholar] [CrossRef]
- Shao, S.D.; Lo, E.Y.M. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Resour. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Shao, S.D. Corrected incompressible SPH method for accurate water-surface tracking in breaking waves. Coast. Eng. 2008, 55, 236–250. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Dominguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Aristodemo, F.; Meringolo, D.D.; Groenenboom, P.; Lo Schiavo, A.; Veltri, P.; Veltri, M. Assessment of dynamic pressures at vertical and perforated breakwaters through diffusive SPH schemes. Math. Probl. Eng. 2015, 2015, 305028. [Google Scholar] [CrossRef]
- Meringolo, D.D.; Aristodemo, F.; Veltri, P. SPH numerical modeling of wave-perforated breakwater interaction. Coast. Eng. 2015, 101, 48–68. [Google Scholar] [CrossRef]
- Meringolo, D.D.; Colagrossi, A.; Marrone, S.; Aristodemo, F. On the filtering of acoustic components in weakly-compressible SPH simulations. J. Fluids Struct. 2017, 70, 1–23. [Google Scholar] [CrossRef]
- Marrone, S.; Colagrossi, A.; Di Mascio, A.; Le Touzé, D. Prediction of energy losses in water impacts using incompressible and weakly compressible models. J. Fluids Struct. 2015, 54, 802–822. [Google Scholar] [CrossRef]
- Zheng, X.; Ma, Q.W.; Duan, W.Y. Comparative study of different SPH schemes on simulating violent water wave impact flows. China Ocean Eng. 2014, 28, 791–806. [Google Scholar] [CrossRef]
- Zheng, X.; Ma, Q.W.; Duan, W.Y. Incompressible SPH method based on Rankine source solution for violent water wave simulation. J. Comput. Phys. 2014, 276, 291–314. [Google Scholar] [CrossRef]
- Sriram, V.; Ma, Q.W. Improved MLPG_R method for simulating 2D interaction between violent waves and elastic structures. J. Comput. Phys. 2012, 231, 7650–7670. [Google Scholar] [CrossRef]
- Ma, Q.W. A new meshless interpolation scheme for MLPG_R method. CMES Comput. Model. Eng. Sci. 2008, 23, 75–89. [Google Scholar]
- Aturi, S.N.; Shen, S. The Meshless Local Petrove-Galerkin (MLPG) method: A simple & less-costly alternative to the finite element and boundary element methods. CMES Comput. Model. Eng. Sci. 2002, 3, 11–52. [Google Scholar]
- Zheng, X.; Duan, W.Y.; Ma, Q.W. Comparison of improved meshless interpolation schemes for SPH method and accuracy analysis. Int. J. Mar. Sci. Appl. 2010, 9, 223–230. [Google Scholar] [CrossRef]
- Yang, J.Y.; Zhao, Y.M.; Liu, N.; Bu, W.P.; Xu, T.L.; Tang, Y.F. An implicit MLS meshless method for 2-D time dependent fractional diffusion-wave equation. Appl. Math. Model. 2015, 39, 1229–1240. [Google Scholar] [CrossRef]
- Martin, J.C.; Moyce, W.J. Part IV. An experimental study of the collapse of liquid columns on a rigid horizontal plane. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1952, 244, 312–324. [Google Scholar] [CrossRef]
- Zhou, Z.Q.; De Kat, J.O.; Buchner, B. A nonlinear 3-D approach to simulate green water dynamics on deck. In Proceedings of the 7th International Conference on Numerical Ship Hydrodynamics, Nantes, France, 19–22 July 1999; pp. 1–15. [Google Scholar]
- Khayyer, A.; Gotoh, H.; Shimizu, Y.; Gotoh, K. On enhancement of energy conservation properties of projection-based particle methods. Eur. J. Mech. B/Fluids 2017, in press. Available online: http://dx.doi.org/10.1016/j.euromechflu.2017.01.014 (accessed on 3 June 2017).
- Liang, D.F.; Thusyanthan, I.; Madabhushi, S.P.G.; Tang, H. Modelling solitary waves and its impact on coastal houses with SPH method. China Ocean Eng. 2010, 24, 353–368. [Google Scholar]
- Lin, P.Z.; Liu, X.; Zhang, J. The simulation of a landside-induced surge wave and its overtopping of a dam using a coupled ISPH model. Eng. Appl. Comput. Fluid Mech. 2015, 9, 432–444. [Google Scholar]
- Zheng, X.; Shao, S.D.; Khayyer, A.; Duan, W.Y.; Ma, Q.W.; Liao, K.P. Corrected first-order derivative ISPH in water wave simulations. Coast. Eng. J. 2017, 59, 1750010. [Google Scholar] [CrossRef]
- Ma, Q.W.; Zhou, J. MLPG_R method for numerical simulation of 2D breaking waves. CMES Comput. Model. Eng. Sci. 2009, 43, 277–304. [Google Scholar]
- Zheng, X.; Hu, Z.H.; Ma, Q.W.; Duan, W.Y. Incompressible SPH based on rankine source solution for water wave impact simulation. Procedia Eng. 2015, 126, 650–654. [Google Scholar] [CrossRef]
- Liang, D.F.; Jian, W.; Shao, S.D.; Chen, R.D.; Yang, K.J. Incompressible SPH simulation of solitary wave interaction with movable seawalls. J. Fluids Struct. 2017, 69, 72–88. [Google Scholar] [CrossRef]

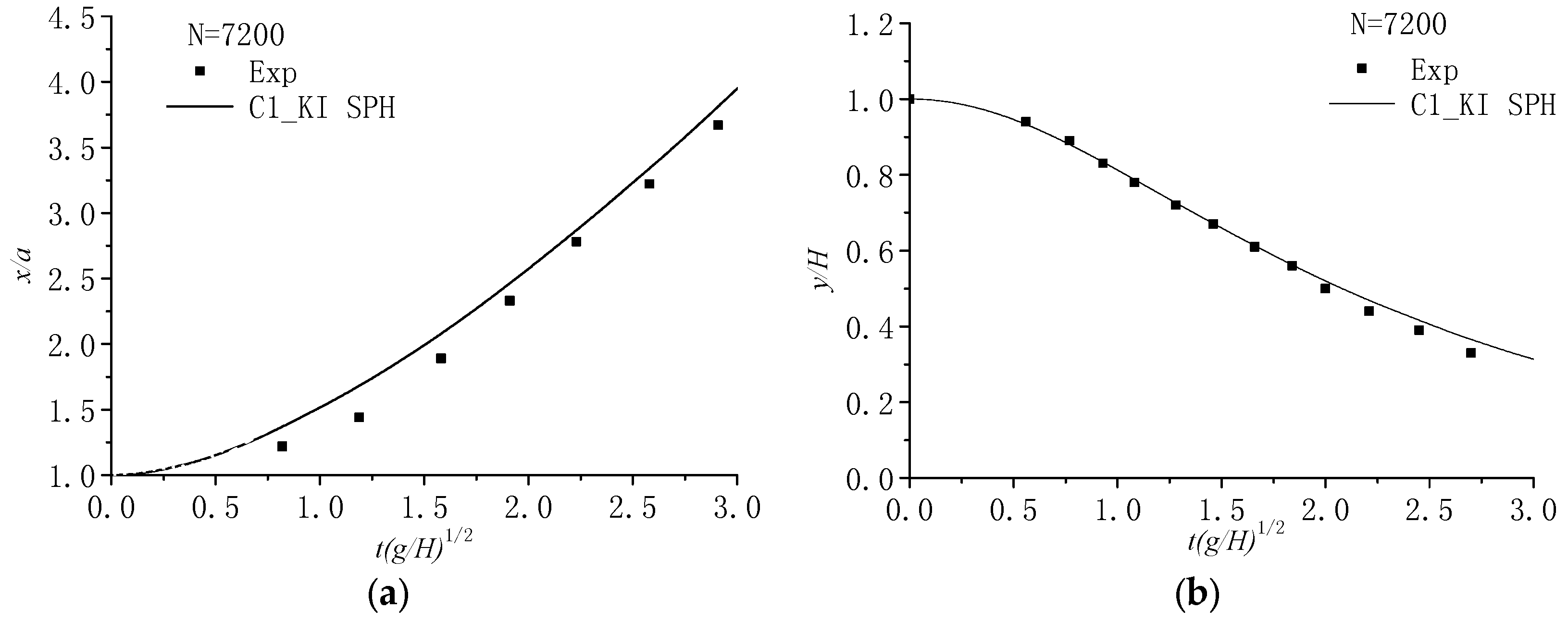




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Ma, Q.; Shao, S.; Khayyer, A. Modelling of Violent Water Wave Propagation and Impact by Incompressible SPH with First-Order Consistent Kernel Interpolation Scheme. Water 2017, 9, 400. https://doi.org/10.3390/w9060400
Zheng X, Ma Q, Shao S, Khayyer A. Modelling of Violent Water Wave Propagation and Impact by Incompressible SPH with First-Order Consistent Kernel Interpolation Scheme. Water. 2017; 9(6):400. https://doi.org/10.3390/w9060400
Chicago/Turabian StyleZheng, Xing, Qingwei Ma, Songdong Shao, and Abbas Khayyer. 2017. "Modelling of Violent Water Wave Propagation and Impact by Incompressible SPH with First-Order Consistent Kernel Interpolation Scheme" Water 9, no. 6: 400. https://doi.org/10.3390/w9060400




