Assessing the Impacts of Sea Level Rise on Salinity Intrusion and Transport Time Scales in a Tidal Estuary, Taiwan
Abstract
:1. Introduction
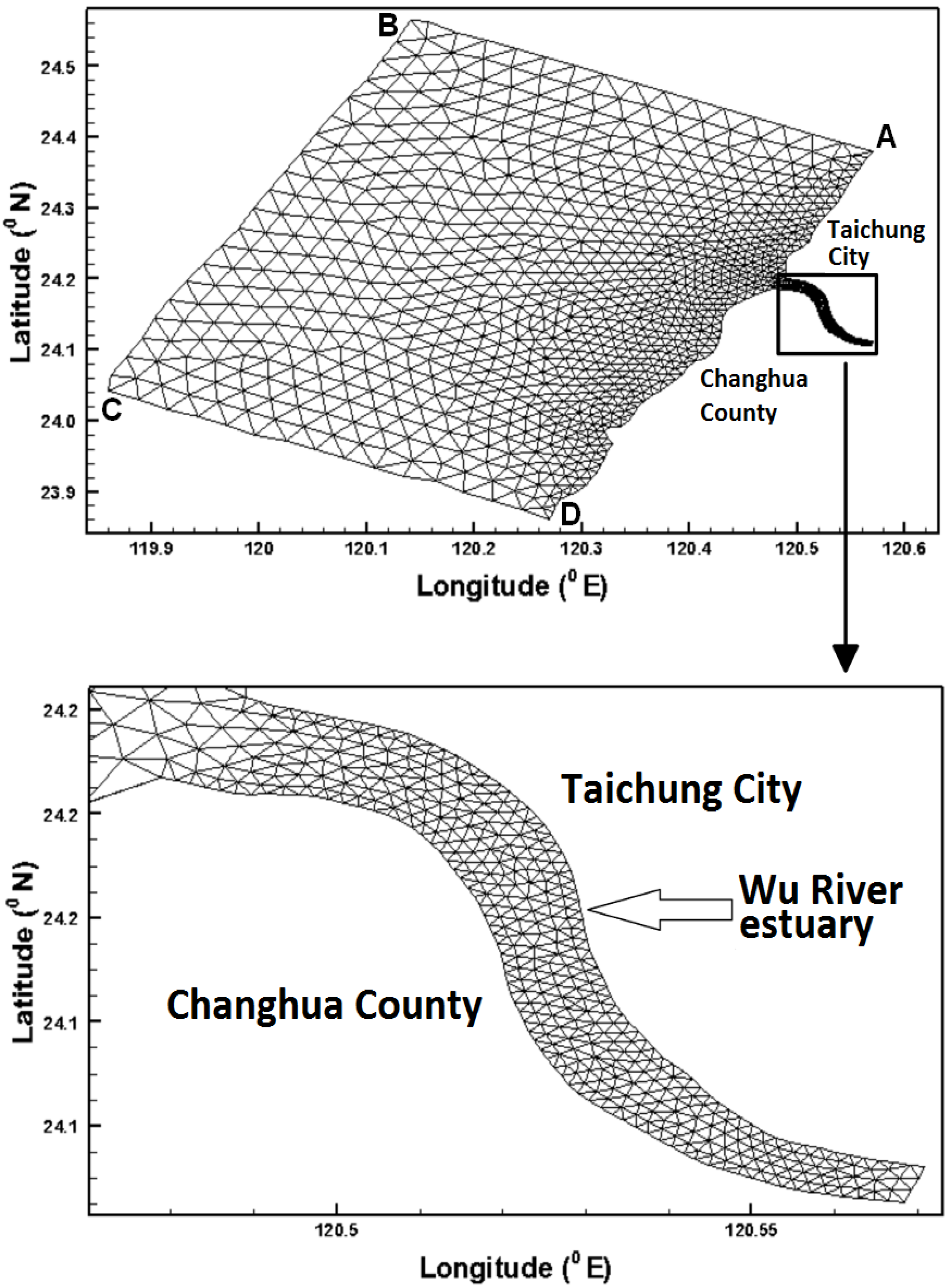
2. Study Area
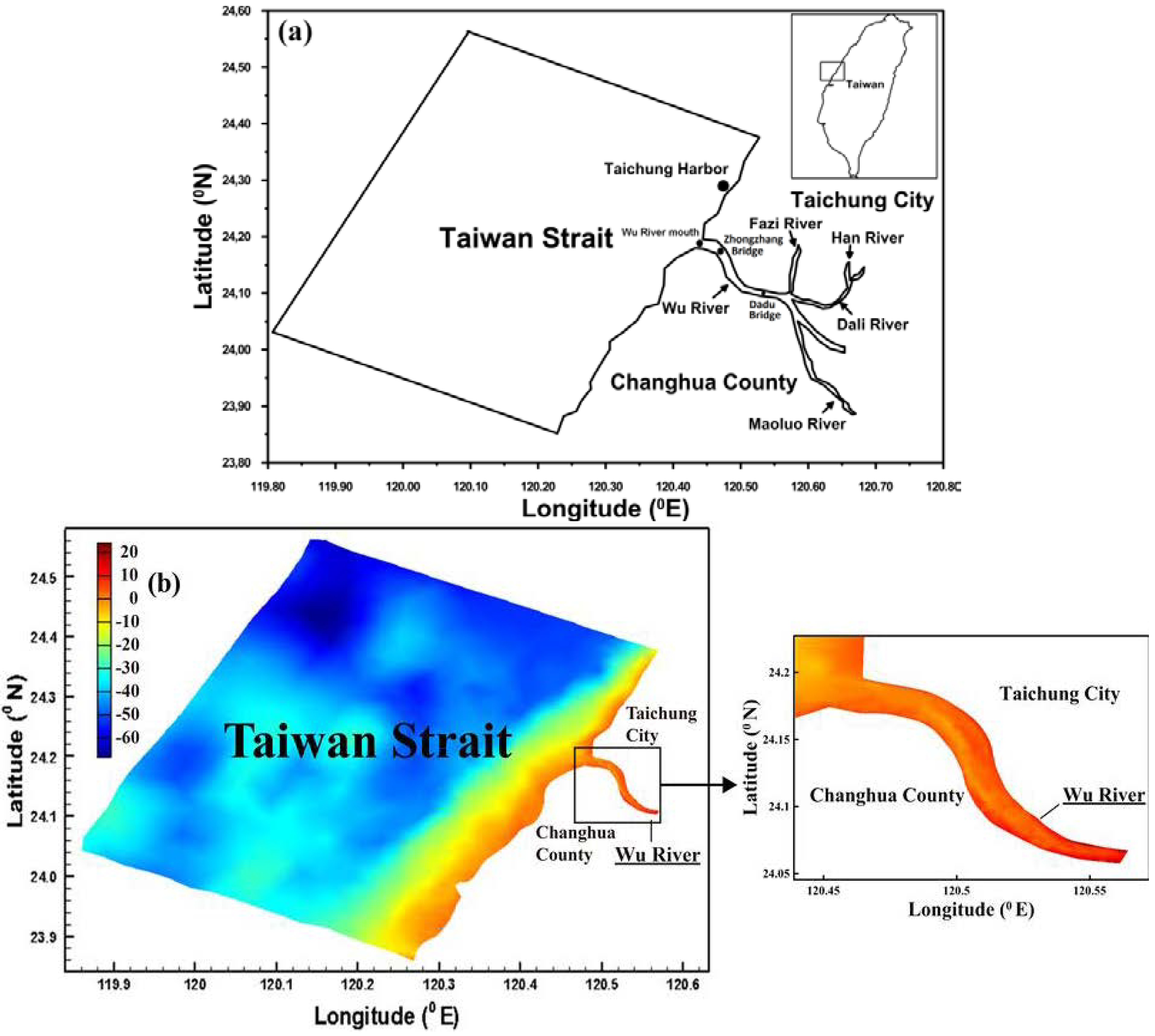
3. Materials and Methods
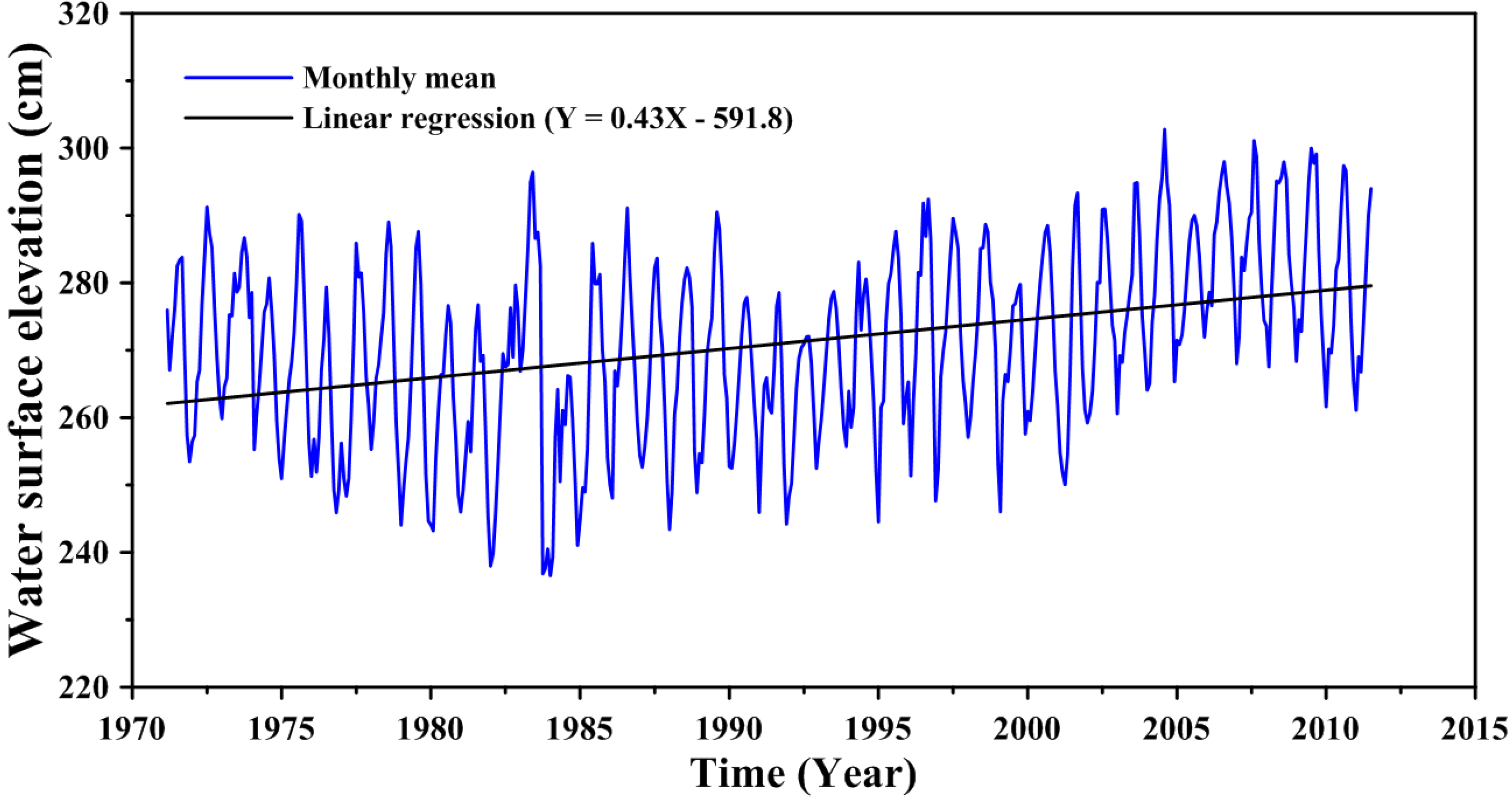
3.1. Sea Level Rise Projection
3.2. Three-Dimensional Hydrodynamic Model
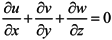
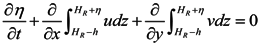
 is the water density, of which the default reference value; ρo, is set to 1,025 kg/ m3; Pa(x,y,t) is the atmospheric pressure at the free surface; p is the pressure; v is the vertical eddy viscosity; S is the salinity; Kv is the vertical eddy diffusivity for salinity and Fs is the horizontal diffusion for the transport equation.
is the water density, of which the default reference value; ρo, is set to 1,025 kg/ m3; Pa(x,y,t) is the atmospheric pressure at the free surface; p is the pressure; v is the vertical eddy viscosity; S is the salinity; Kv is the vertical eddy diffusivity for salinity and Fs is the horizontal diffusion for the transport equation.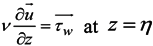
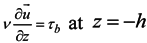
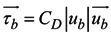 .
.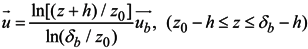
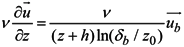
3.3. Computation of Flushing Time
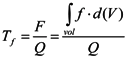
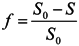
3.4. Computation of Residence Time
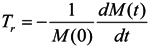
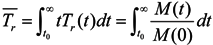
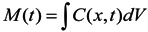
3.5. Model Schematization
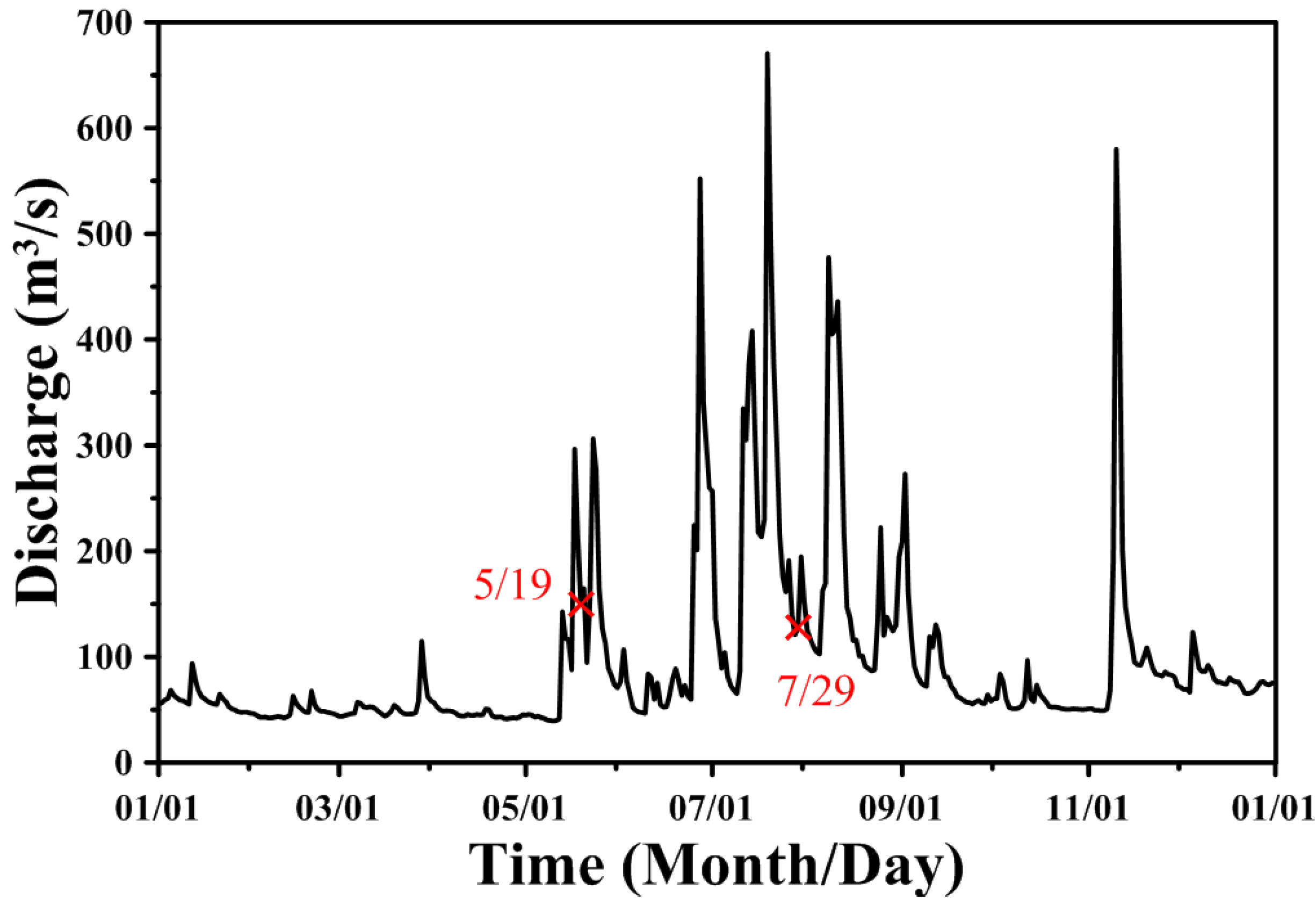
4. Model Calibration and Verification
4.1. Calibration with Amplitudes and Phases
| Constituent | Boundary at Point A | Boundary at Point B | Boundary at Point C | Boundary at Point D | ||||
|---|---|---|---|---|---|---|---|---|
| Amplitude (m) | Phase (°) | Amplitude (m) | Phase (°) | Amplitude (m) | Phase (°) | Amplitude (m) | Phase (°) | |
| M2 | 1.82 | 266.06 | 1.88 | 266.91 | 1.60 | 272.39 | 1.57 | 267.23 |
| S2 | 0.51 | 14.45 | 0.53 | 16.34 | 0.44 | 26.29 | 0.43 | 20.55 |
| N2 | 0.25 | 28.89 | 0.26 | 29.77 | 0.22 | 36.02 | 0.21 | 31.15 |
| K1 | 0.27 | 161.62 | 0.29 | 160.20 | 0.29 | 167.21 | 0.28 | 167.16 |
| O1 | 0.21 | 279.53 | 0.22 | 277.24 | 0.23 | 283.55 | 0.22 | 284.03 |
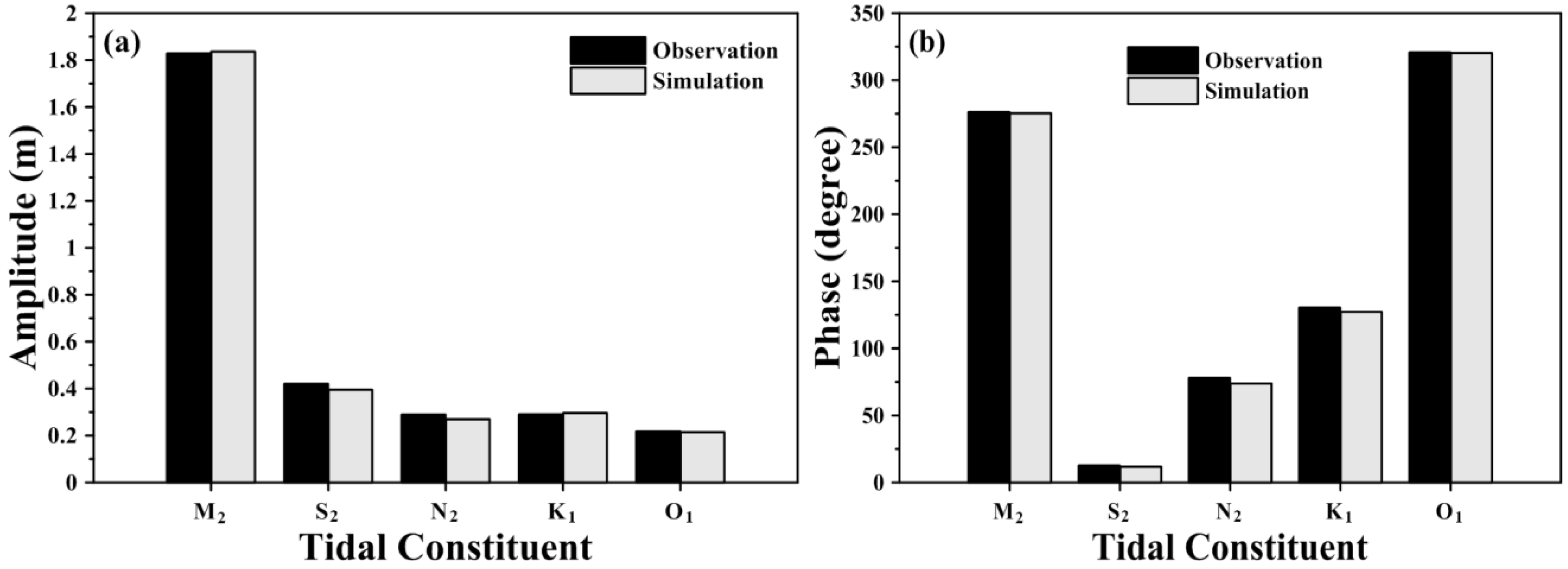
4.2. Verification of Water Surface Elevation

4.3. Calibration and Verification of Salinity Distribution

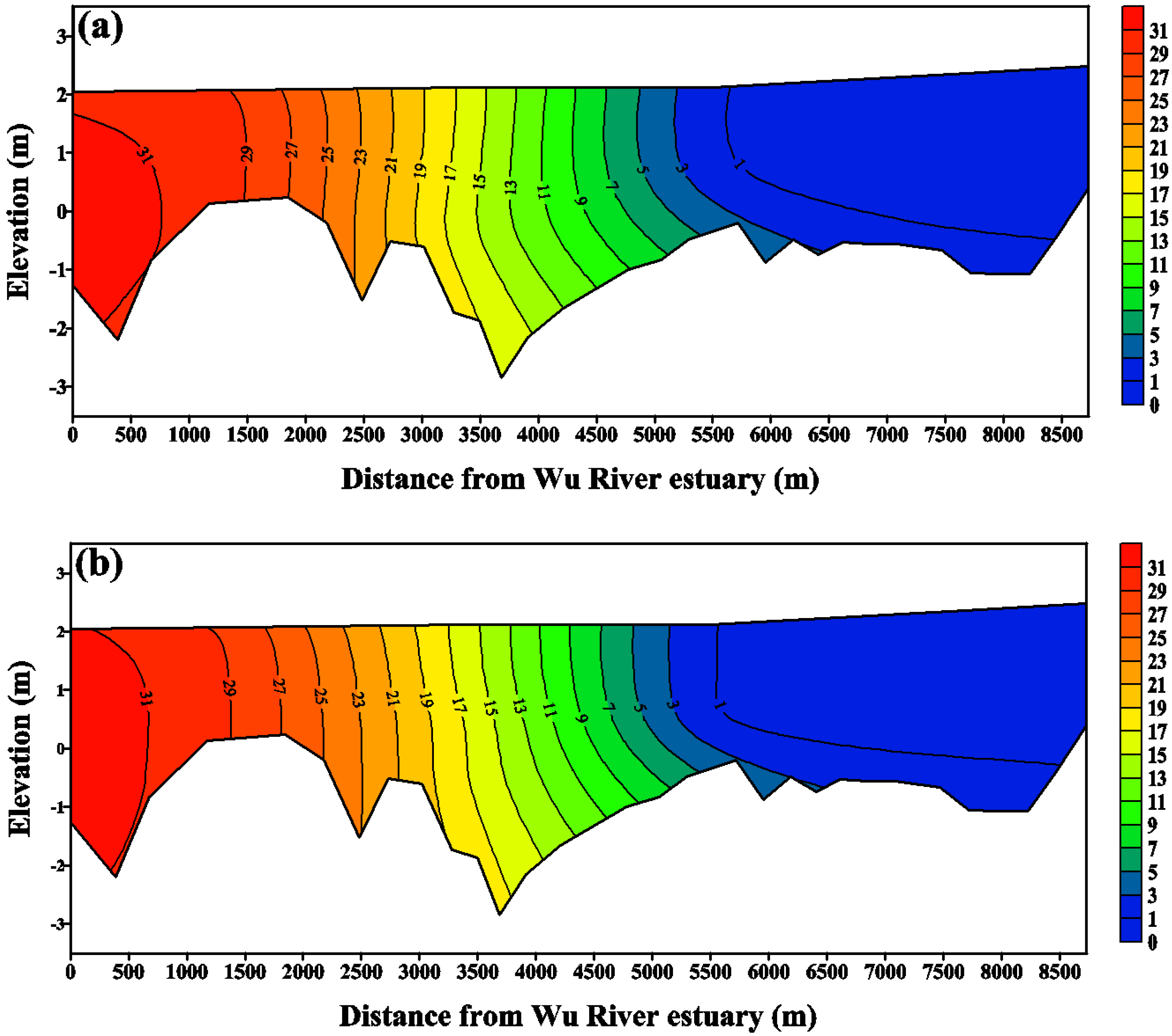
5. Results and Discussion
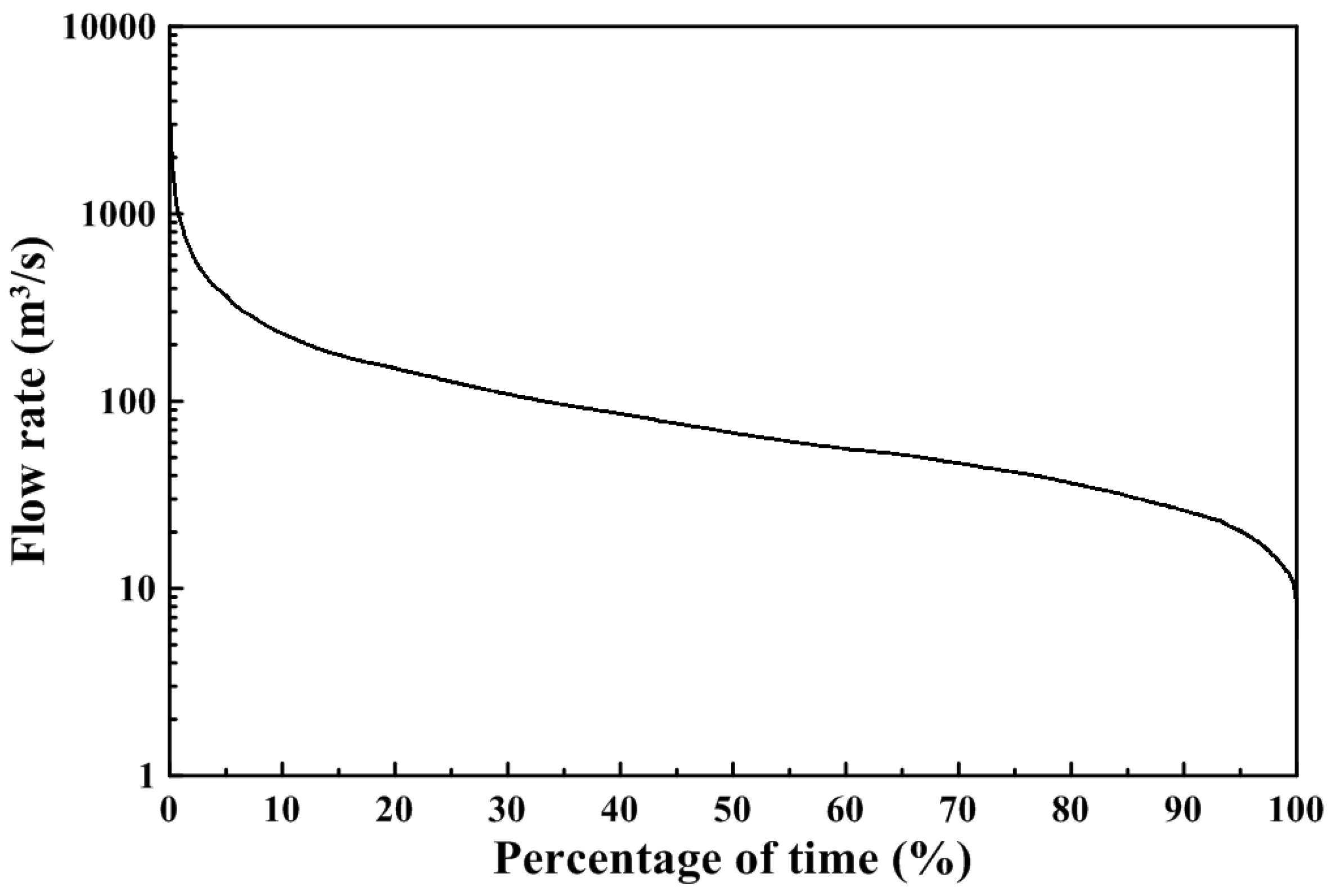
| Freshwater discharge | Flow rate at Dadu Bridge (m3/s) |
|---|---|
| Q10 | 229.0 |
| Q20 | 149.0 |
| Q30 | 108.7 |
| Q40 | 85.6 |
| Q50 | 67.5 |
| Q60 | 55.5 |
| Q70 | 46.5 |
| Q80 | 36.5 |
| Q90 | 26.0 |
5.1. Sea Level Rise Effects on Salinity Distribution
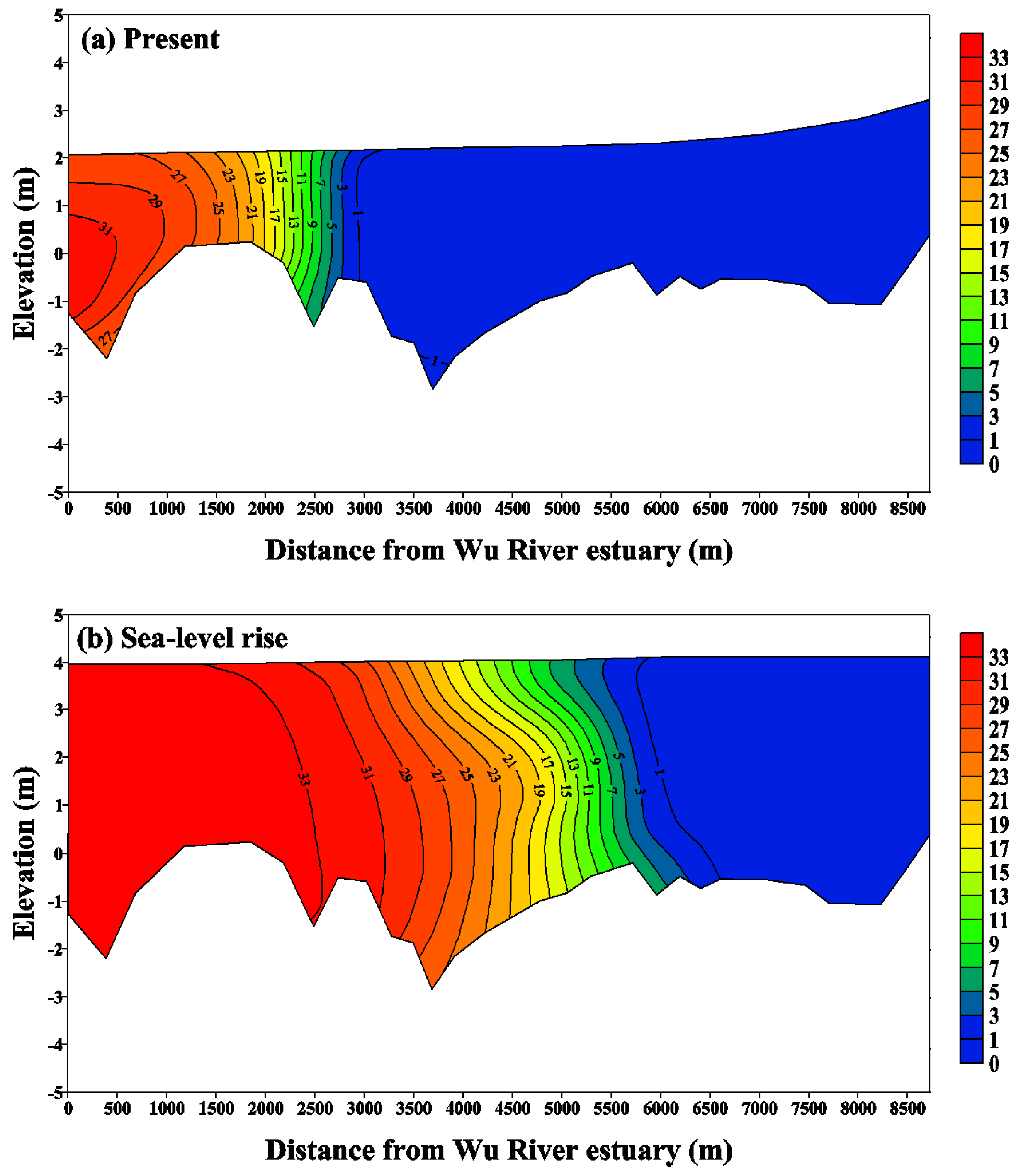
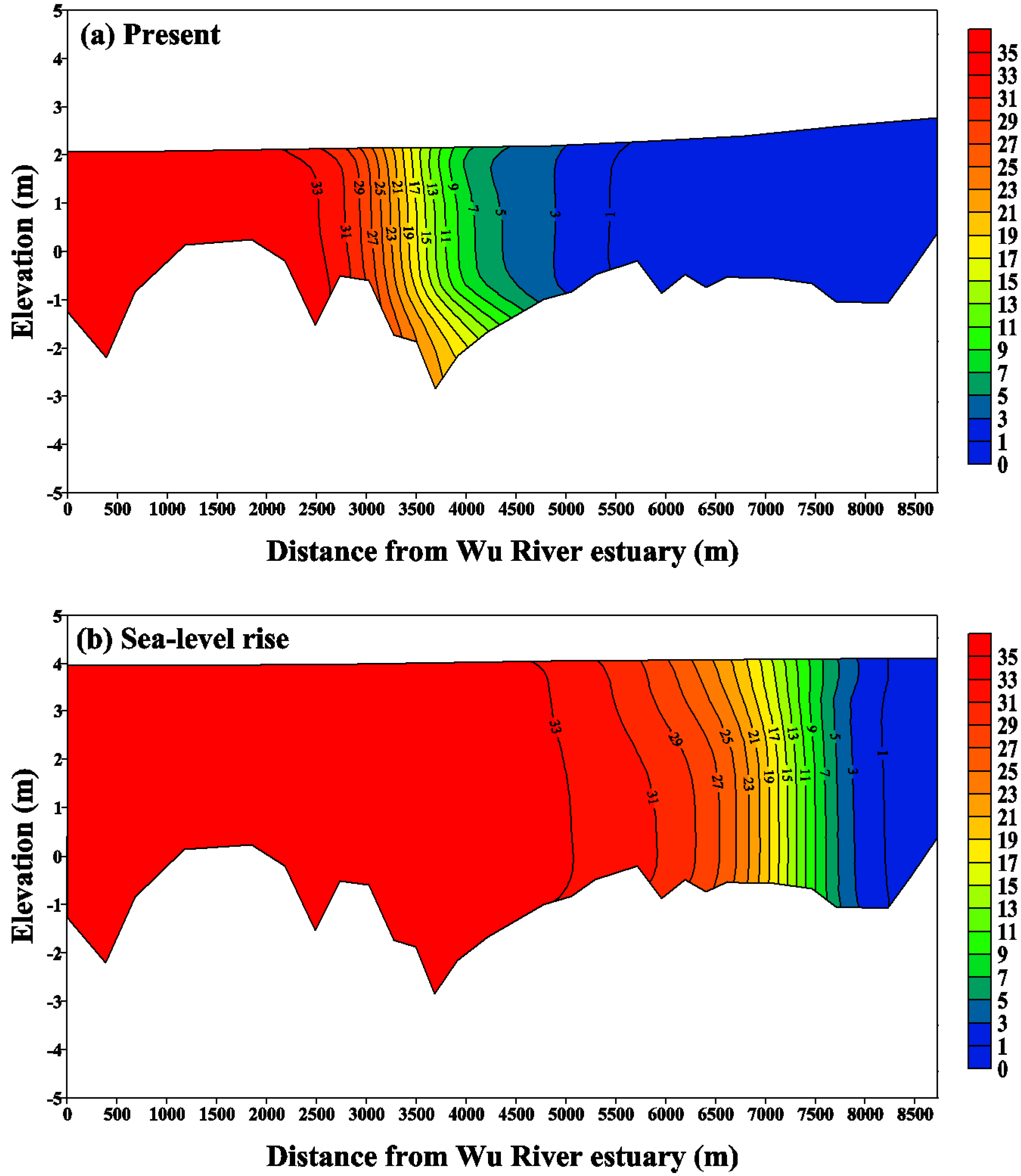
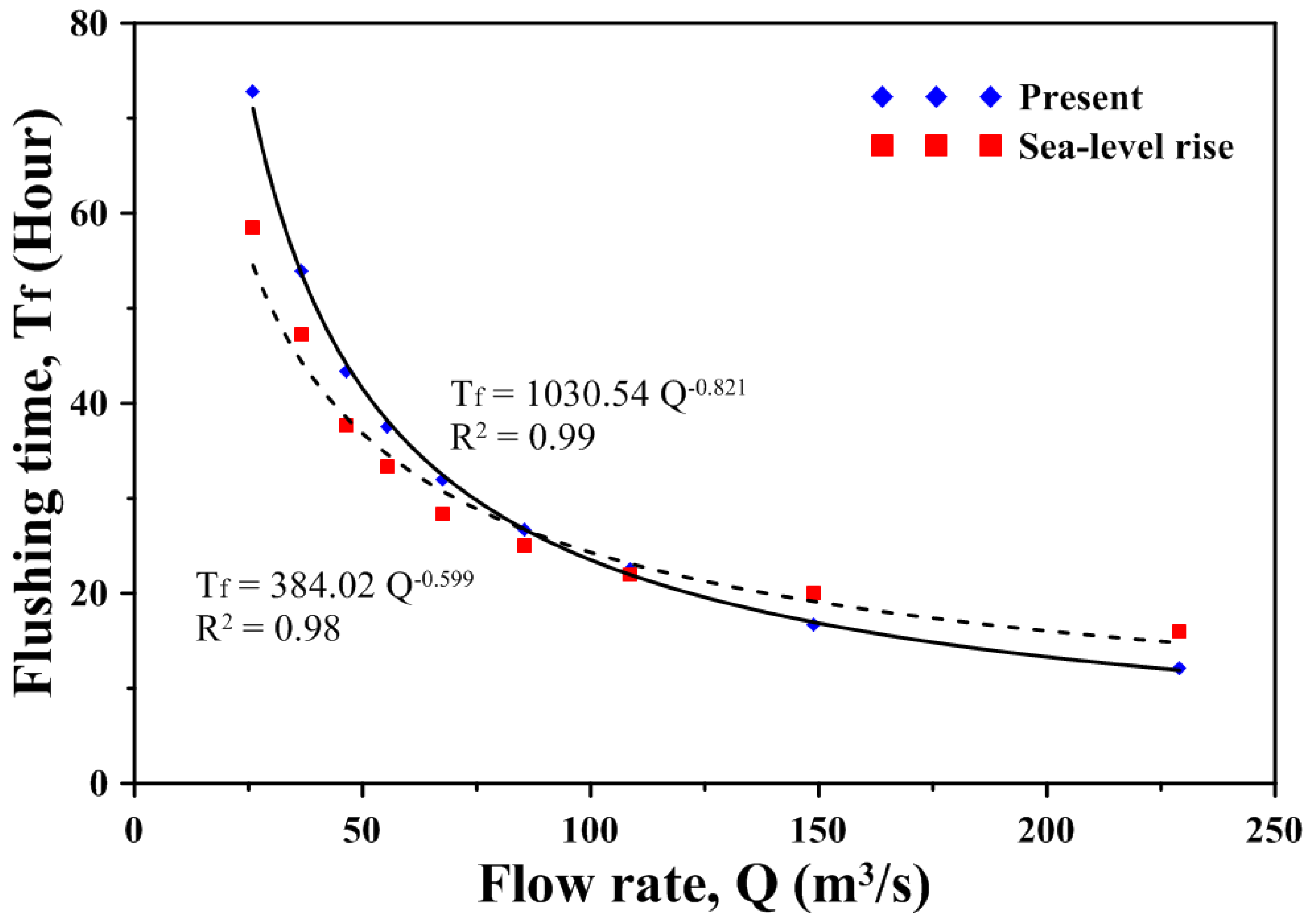
5.2. Flushing Time in Response to Sea Level Rise
5.3. Residence Time in Response to Sea Level Rise

6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Yu, Y.F.; Yu, Y.X.; Zuo, J.C.; Wan, Z.W.; Chen, Z.Y. Effect of sea level variation on tidal characteristic values for the East China Sea. China Ocean Eng. 2003, 17, 369–382. [Google Scholar]
- IPCC. Climate Change 2007: The Physical Science Basis. In Contribution of Working Group 1 to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, S., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Hsu, H.H.; Chen, C.T. Observed and projected climate change in Taiwan. Meteorol. Atmos. Phys. 2002, 79, 87–104. [Google Scholar] [CrossRef]
- Yu, P.S.; Yang, T.C.; Kuo, C.C. Evaluating long-term trends in annual and seasonal precipitation in Taiwan. Water Resour. Manag. 2006, 20, 1007–1023. [Google Scholar] [CrossRef]
- Chiu, M.C. Relationship of Stream Insects with Flooding and Dippers in Wuling Area. Master Thesis, National Chung Hsing University, Taichung, Taiwan, 2009. [Google Scholar]
- Poff, N.L.; Brinson, M.M.; Day, J.W., Jr. Aquatic Ecosystems and Global Climate Change; Pew Center on Global Change: Arlington, VA, USA, 2002; p. 45. [Google Scholar]
- Hilton, T.W.; Najjar, R.G.; Zhong, L.; Li, M. Is there a signal of sea level rise in Chesapeake Bay salinity? J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Bhuiyan, M.J.A.N.; Dutta, D. Assessing impacts of sea level rise on river salinity in the Gorai river network, Bangladesh. Estuar. Coast. Shelf Sci. 2012, 96, 219–227. [Google Scholar] [CrossRef]
- Hong, B.; Shen, J. Responses of estuarine salinity and transport processes to potential future sea level rise in the Chesapeake Bay. Estuar. Coast. Shelf Sci. 2012, 104–105, 33–45. [Google Scholar] [CrossRef]
- Lucas, L.V. Implications of Estuarine Transport for Water Quality. In Contemporary Issues in Estuarine Physics; Valle-Levinson, A., Ed.; Cambridge University Press: Cambridge, UK, 2010; pp. 273–306. [Google Scholar]
- Hull, C.H.J.; Tortoriello, R. Sea Level Trend and Salinity in the Delaware Estuary; Staff Report; Delaware Basin Commission: West Trenton, NJ, USA, 1979. [Google Scholar]
- Grabemann, H.; Grabemann, I.; Herbers, D.; Muller, A. Effects of a specific climate scenario on the hydrograph and transport of conservative substances in the Weser estuary, Germany: A case study. Clim.Res. 2001, 18, 77–87. [Google Scholar] [CrossRef]
- Chua, V.P.; Fringer, O.B.; Monismith, S.G. Influence of sea level rise on salinity in San Francisco Bay. 2011; unpublished work. [Google Scholar]
- Rice, K.C.; Hong, B.; Shen, J. Assessment of salinity intrusion in the James and Chickahominy Rivers as a result of simulated sea level rise in Chesapeake Bay, East Coast, USA. J. Environ. Manag. 2012, 111, 61–69. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Wu, C.Y. Coupling of a one-dimensional river routing model and a three-dimensional ocean model to predict overbank flows in a complex river-ocean system. Appl. Math. Model. 2013, 37, 6163–6176. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. Sea level rise from the late 19th to the early 21st century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Snay, R.; Cline, M.; Dillinger, W.; Foote, R.; Hilla, S.; Kass, W.; Ray, J.; Rohde, J.; Sella, G.; Soler, T. Using global positions system-derived crustal velocities to estimate rates of absolute sea level change from North American tidal gauge records. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Cazenave, A. Sea level rise and its impact on coastal zone. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef]
- Tseng, Y.H.; Breaker, L.C.; Cheng, T.Y. Sea level variations in the regional seas around Taiwan. J. Oceanogr. 2010, 66, 27–39. [Google Scholar] [CrossRef]
- Huang, C.J.; Hsu, T.W.; Wu, L.C. Application of Tide-Gauge and Satellite AltimetryData to Estimate Sea Level Rise; Report to Water Resources Agency: Taipei, Taiwan, 2009. [Google Scholar]
- Zhang, Y.L.; Baptista, A.M. SELFE: A semi-implicit Eulerian-Lagrangian finite-element model for cross-scale ocean circulation. Ocean Model. 2008, 21, 71–96. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhao, M.; Dickinson, R.E. Intercomparison of bulk aerodynamic algorithms for the computation of sea surface fluxes using TOGA COARE and TAO data. J. Clim. 1998, 11, 2628–2644. [Google Scholar] [CrossRef]
- Umlauf, L.; Buchard, H. A. generic length-scale equation for geophysical turbulence models. J. Mar. Res. 2003, 61, 235–265. [Google Scholar] [CrossRef]
- Lauff, G.E. Lyered Sediments of Tidal Flats, Beaches, and Shelf Bottoms of the North Sea. In American Association for the Advancement of Science Publication No. 83; American Association for the Advancement of Science: Washington, DC, USA, 1967. [Google Scholar]
- Dyer, K.R. Estuaries: A Physical Introduction, 2nd ed.; John Wiley: London, UK, 1977; p. 195. [Google Scholar]
- Liu, W.C.; Hsu, M.H.; Kuo, A.Y.; Kuo, J.T. The influence of river discharge on salinity intrusion in the Tanshui Estuary, Taiwan. J. Coast. Res. 2001, 17, 544–552. [Google Scholar]
- Huang, W.; Spaulding, M. Modelling residence-time response to freshwater input in Apalachicola Bay, Florida, USA. Hydrol. Process. 2002, 16, 3051–3064. [Google Scholar] [CrossRef]
- De Brye, B.; de Brauwere, A.; Gourge, O.; Delhez, E.J.M.; Deleersnijder, E. Water renewal timescales in the Scheldt Estuary. J. Mar. Syst. 2012, 94, 74–86. [Google Scholar] [CrossRef]
- Zimmerman, J.T.F. Mixing and flushing of tidal embayment in the western Dutch Wadden Sea. Part I: Description of salinity and calculation of mixing time scales. Neth. J. Sea Res. 1976, 10, 149–191. [Google Scholar] [CrossRef]
- Takeoka, H. Fundamental concepts of exchange and transport time scales in a coastal sea. Cont. Shelf Res. 1984, 3, 311–326. [Google Scholar] [CrossRef]
- Liu, W.C.; Chen, W.B.; Kuo, J.T.; Wu, C. Numerical determination of residual time and age in a partially mixed estuary using three-dimensional hydrodynamic model. Cont. Shelf Res. 2008, 28, 1068–1088. [Google Scholar] [CrossRef]
- Zhang, W.G.; Wilkin, J.L.; Schofield, O.M.E. Simulation of water age and residence time in the New York Bight. J. Phys. Oceanogr. 2010, 40, 965–982. [Google Scholar] [CrossRef]
- De Brauwere, A.; de Brye, B.; Blaise, S.; Deleersnijder, E. Residence time, exposure time and connectivity in the Scheldt Estuary. J. Mar. Syst. 2011, 84, 85–95. [Google Scholar] [CrossRef]
- Kenov, I.A.; Garcia, A.C.; Neves, R. Residence time of water in the Mondego estuary (Portugal). Estuar. Coast. Shelf Sci. 2012, 106, 13–22. [Google Scholar] [CrossRef]
- Shi, J.; Li, G.; Wang, P. Anthropogenic influences on the tidal prism and water exchange in Jiaozhou Bay, Qingdao, China. J. Coast. Res. 2011, 27, 57–72. [Google Scholar] [CrossRef]
- Hsu, M.H.; Kuo, A.Y.; Kuo, J.T.; Liu, W.C. Procedure to calibrate and verify numerical models of estuarine hydrodynamics. J. Hydraul. Eng. ASCE 1999, 125, 166–182. [Google Scholar] [CrossRef]
- Officer, C.B. Physical Oceanography of Estuaries (and Associated Coastal Waters); Wiley: New York, NY, USA, 1976. [Google Scholar]
- Geyer, W.R. Influence of wind on dynamics and flushing of shallow estuaries. Estuar. Coast. Shelf Sci. 1997, 44, 713–722. [Google Scholar] [CrossRef]
- Huang, W. Hydrodynamic modeling of flushing time in small estuary of North Bay, Florida, USA. Estuar. Coast. Shelf Sci. 2007, 74, 722–731. [Google Scholar] [CrossRef]
- Huang, W.; Liu, X.; Chen, X.; Flannery, M.S. Critical flow for water management in a shallow tidal river based on estuarine residence time. Water Resour. Manag. 2011, 25, 2367–2385. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, W.-C.; Liu, H.-M. Assessing the Impacts of Sea Level Rise on Salinity Intrusion and Transport Time Scales in a Tidal Estuary, Taiwan. Water 2014, 6, 324-344. https://doi.org/10.3390/w6020324
Liu W-C, Liu H-M. Assessing the Impacts of Sea Level Rise on Salinity Intrusion and Transport Time Scales in a Tidal Estuary, Taiwan. Water. 2014; 6(2):324-344. https://doi.org/10.3390/w6020324
Chicago/Turabian StyleLiu, Wen-Cheng, and Hong-Ming Liu. 2014. "Assessing the Impacts of Sea Level Rise on Salinity Intrusion and Transport Time Scales in a Tidal Estuary, Taiwan" Water 6, no. 2: 324-344. https://doi.org/10.3390/w6020324
APA StyleLiu, W.-C., & Liu, H.-M. (2014). Assessing the Impacts of Sea Level Rise on Salinity Intrusion and Transport Time Scales in a Tidal Estuary, Taiwan. Water, 6(2), 324-344. https://doi.org/10.3390/w6020324






