A Non-Stationary and Directional Probabilistic Analysis of Coastal Storms in the Greek Seas
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Studies
2.2. Wave Climate Description
2.3. Methodology
2.3.1. Summary
2.3.2. Non-Stationary Directional Extreme Value Analysis (NS-DEVA)
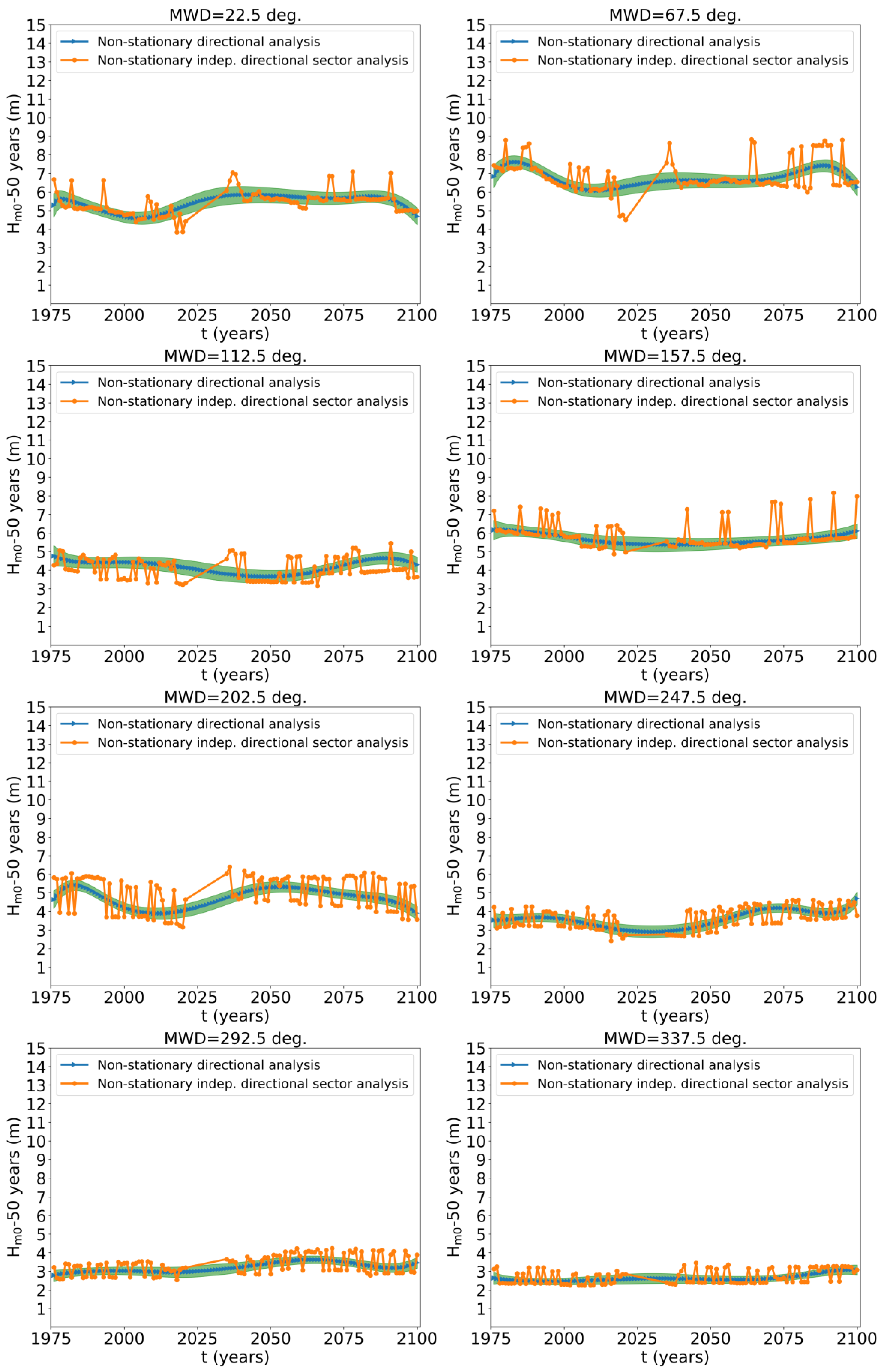
2.3.3. Incorporating a Directional Model into the Extreme Value Analysis (DEVA)
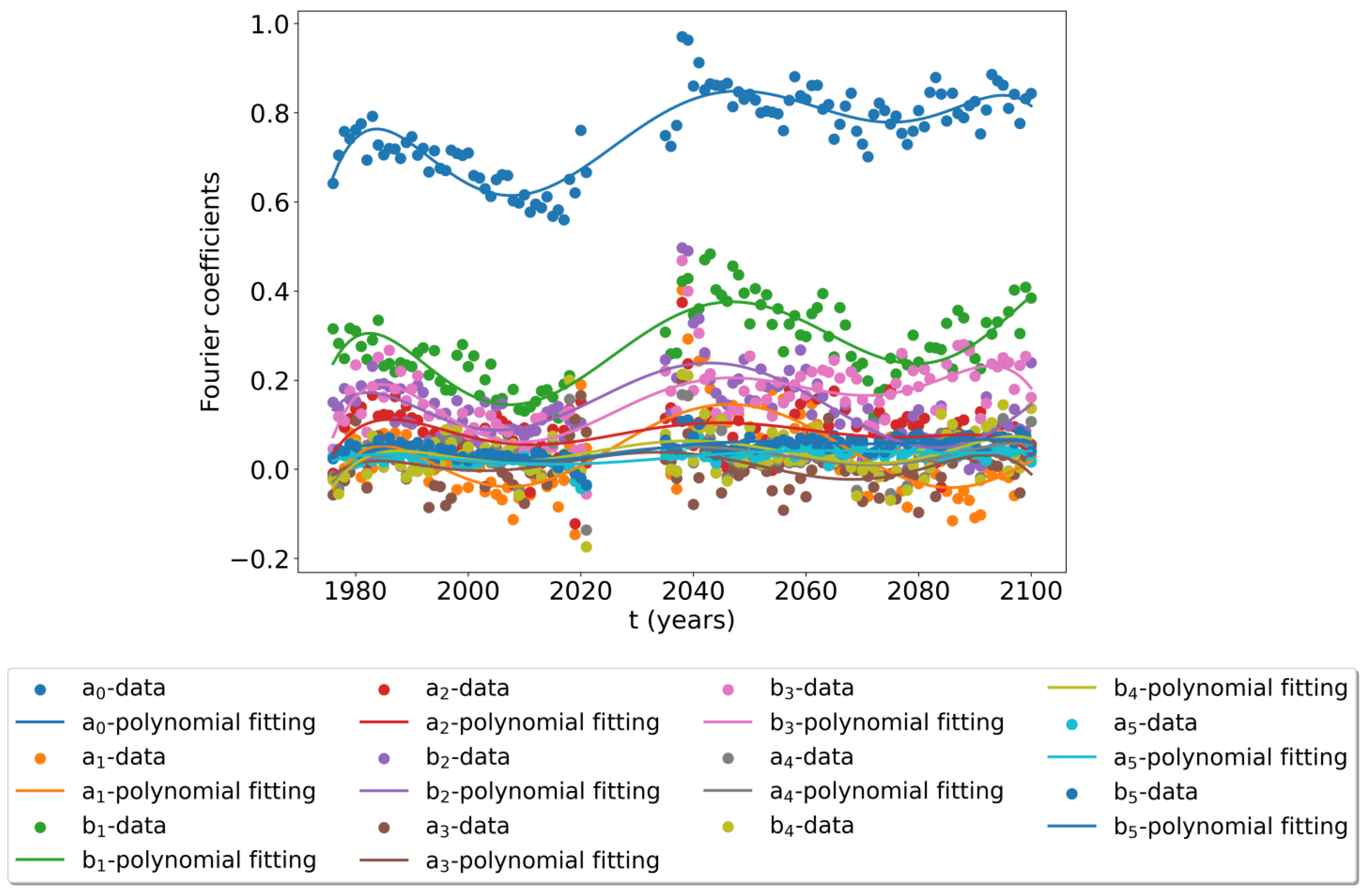
2.3.4. Trend Analysis in the NS-DEVA
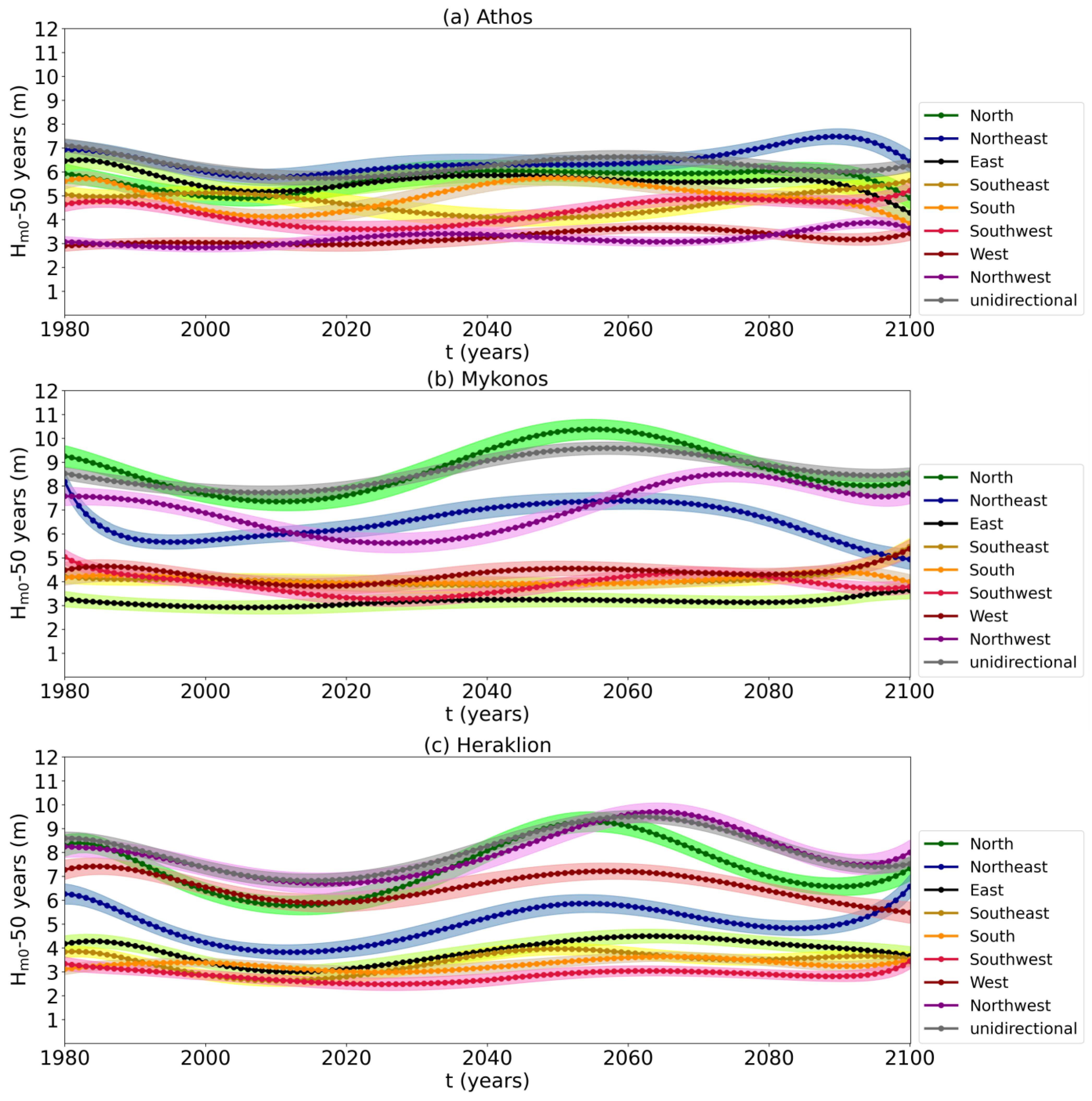
3. Results and Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. Intergovernmental Panel on Climate Change (IPCC). Climate change 2007: The scientifc basis. In Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Field, C.B.; Barros, V.; Stocker, T.F.; Dahe, Q.; Intergovernmental Panel on Climate Change (IPCC). Managing the risks of extreme events and disasters to advance climate change adaptation. In A Special Report of Working Groups I and II of the Inter-Governmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Field, C.B.; Barros, V.R.; Dokken, D.J.; Mach, K.J.; Mastrandrea, M.D.; Intergovernmental Panel on Climate Change (IPCC). Climate change 2014: Impacts, adaptation and vulnerability. In Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Daneshfaraz, R.; Norouzi, R.; Ebadzadeh, P.; Di Francesco, S.; Abraham, J.P. Experimental Study of Geometric Shape and Size of Sill Effects on the Hydraulic Performance of Sluice Gates. Water 2023, 15, 314. [Google Scholar] [CrossRef]
- Marcos, M.; Tsimplis, M.N. Coastal sea level trends in Southern Europe. Geophys. J. Int. 2008, 175, 70–82. [Google Scholar] [CrossRef] [Green Version]
- Somot, S.; Sevault, F.; Déqué, M.; Crépon, M. 21st century climate change scenario for the Mediterranean using a coupled atmosphere-ocean regional climate model. Glob. Planet. Change 2008, 63, 112–126. [Google Scholar] [CrossRef] [Green Version]
- Carillo, A.; Sannino, G.; Artale, V.; Ruti, P.M.; Calmanti, S.; Dell’Aquila, A. Steric sea level rise over the Mediterranean Sea: Present climate and scenario simulations. Clim. Dyn. 2012, 39, 2167–2184. [Google Scholar] [CrossRef]
- Tsimplis, M.N.; Calafat, F.M.; Marcos, M.; Jordà, G.; Gomis, D.; Fenoglio-Marc, L.; Struglia, M.V.; Josey, S.A.; Chambers, D.P. The effect of the NAO on sea level and on mass changes in the Mediterranean Sea. J. Geophys. Res. Ocean. 2013, 118, 944–952. [Google Scholar] [CrossRef] [Green Version]
- Adloff, F.; Somot, S.; Sevault, F.; Jordà, G.; Aznar, R.; Déqué, M.; Herrmann, M.; Marcos, M.; Dubois, C.; Padorno, E.; et al. Mediterranean Sea response to climate change in an ensemble of twenty first century scenarios. Clim. Dyn. 2015, 45, 2775–2802. [Google Scholar] [CrossRef]
- Lionello, P.; Cogo, S.; Galati, M.B.; Sanna, A. The Mediterranean surface wave climate inferred from future scenario simulations. Glob. Planet. Change 2008, 63, 152–162. [Google Scholar] [CrossRef]
- Martucci, G.; Carniel, S.; Chiggiato, J.; Sclavo, M.; Lionello, P.; Galati, M.B. Statistical trend analysis and extreme distribution of significant wave height from 1958 to 1999—An application to the Italian Seas. Ocean Sci. 2010, 6, 525–538. [Google Scholar] [CrossRef] [Green Version]
- Benetazzo, A.; Fedele, F.; Carniel, S.; Ricchi, A.; Bucchignani, E.; Sclavo, M. Wave climate of the Adriatic Sea: A future scenario simulation. Nat. Hazards Earth Syst. Sci. 2012, 12, 2065–2076. [Google Scholar] [CrossRef] [Green Version]
- Androulidakis, Y.S.; Kombiadou, K.D.; Makris, C.V.; Baltikas, V.N.; Krestenitis, Y.N. Storm surges in the Mediterranean Sea: Variability and trends under future climatic conditions. Dyn. Atmos. Ocean. 2015, 71, 56–82. [Google Scholar] [CrossRef]
- Galiatsatou, P.; Anagnostopoulou, C.; Prinos, P. Modeling nonstationary extreme wave heights in present and future climates of Greek Seas. Water Sci. Eng. 2016, 9, 21–32. [Google Scholar] [CrossRef] [Green Version]
- Galiatsatou, P.; Makris, C.; Prinos, P.; Kokkinos, D. Nonstationary joint probability analysis of extreme marine variables to assess design water levels at the shoreline in a changing climate. Nat. Hazards 2019, 98, 1051–1089. [Google Scholar] [CrossRef]
- Makris, C.; Galiatsatou, P.; Tolika, K.; Anagnostopoulou, C.; Kombiadou, K.; Prinos, P.; Velikou, K.; Kapelonis, Z.; Tragou, E.; Androulidakis, Y.; et al. Climate change effects on the marine characteristics of the Aegean and Ionian Seas. Ocean Dyn. 2016, 66, 1603–1635. [Google Scholar] [CrossRef]
- Makris, C.V.; Tolika, K.; Baltikas, V.N.; Velikou, K.; Krestenitis, Y.N. The impact of climate change on the storm surges of the Mediterranean Sea: Coastal sea level responses to deep depression atmospheric systems. Ocean Model. 2023, 181, 102149. [Google Scholar] [CrossRef]
- Mazas, F.; Hamm, L. A multi-distribution approach to POT methods for determining extreme wave heights. Coast. Eng. 2011, 58, 385–394. [Google Scholar] [CrossRef]
- Mazas, F. Extreme events: A framework for assessing natural hazards. Nat. Hazards 2019, 98, 823–848. [Google Scholar] [CrossRef]
- Martzikos, N.T.; Prinos, P.E.; Memos, C.D.; Tsoukala, V.K. Statistical analysis of Mediterranean coastal storms. Oceanologia 2021, 63, 133–148. [Google Scholar] [CrossRef]
- Martzikos, N.; Malliouri, D.; Tsoukala, V. Shape investigation and probabilistic representation of coastal storms. Applications to Mykonos and Barcelona. Appl. Ocean Res. 2023, 135, 103563. [Google Scholar] [CrossRef]
- Malliouri, D.I.; Memos, C.D.; Soukissian, T.H.; Tsoukala, V.K. Assessing failure probability of coastal structures based on probabilistic representation of sea conditions at the structures’ location. Appl. Math. Model. 2021, 89, 710–730. [Google Scholar] [CrossRef]
- Radfar, S.; Galiatsatou, P. Influence of nonstationarity and dependence of extreme wave parameters on the reliability assessment of coastal structures—A case study. Ocean Eng. 2023, 273, 113862. [Google Scholar] [CrossRef]
- Radfar, S.; Shafieefar, M.; Akbari, H.; Galiatsatou, P.A.; Mazyak, A.R. Design of a rubble mound breakwater under the combined effect of wave heights and water levels, under present and future climate conditions. Appl. Ocean Res. 2021, 112, 102711. [Google Scholar] [CrossRef]
- Malliouri, D.; Martzikos, N.; Tsoukala, V. Fully probabilistic reliability and resilience analysis of coastal structures based on damage evolution simulation. In Proceedings of the 39th IAHR World Congress, International Association for Hydro-Environment Engineering and Research (IAHR), Granada, Spain, 19–24 June 2022; pp. 5908–5916. [Google Scholar]
- Tsoukala, V.K.; Chondros, M.; Kapelonis, Z.G.; Martzikos, N.; Lykou, A.; Belibassakis, K.; Makropoulos, C. An integrated wave modelling framework for extreme and rare events for climate change in coastal areas—The case of Rethymno, Crete. Oceanologia 2016, 58, 71–89. [Google Scholar] [CrossRef] [Green Version]
- Gad, F.-K.; Chatzinaki, M.; Vandarakis, D.; Kyriakidou, C.; Kapsimalis, V. Assessment of Wave Storm-Induced Flood Vulnerability in Rhodes Island, Greece. Water 2020, 12, 2978. [Google Scholar] [CrossRef]
- Dissanayake, P.; Brown, J.; Wisse, P.; Karunarathna, H. Effects of storm clustering on beach/dune evolution. Mar. Geol. 2015, 370, 63–75. [Google Scholar] [CrossRef]
- Dissanayake, P.; Brown, J.; Sibbertsen, P.; Winter, C. Using a two-step framework for the investigation of storm impacted beach/dune erosion. Coast. Eng. 2021, 168, 103939. [Google Scholar] [CrossRef]
- Karathanasi, F.; Soukissian, T.; Belibassakis, K. Directional Extreme Value Models in Wave Energy Applications. Atmosphere 2020, 11, 274. [Google Scholar] [CrossRef] [Green Version]
- Coles, S.G. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Mentaschi, L.; Vousdoukas, M.; Voukouvalas, E.; Sartini, L.; Feyen, L.; Besio, G.; Alfieri, L. The transformed-stationary approach: A generic and simplified methodology for non-stationary extreme value analysis. Hydrol. Earth Syst. Sci. 2016, 20, 3527–3547. [Google Scholar] [CrossRef] [Green Version]
- Galiatsatou, P.; Makris, C.; Krestenitis, Y.; Prinos, P. Nonstationary Extreme Value Analysis of Nearshore Sea-State Parameters under the Effects of Climate Change: Application to the Greek Coastal Zone and Port Structures. J. Mar. Sci. Eng. 2021, 9, 817. [Google Scholar] [CrossRef]
- Ewans, K.; Jonathan, P. The Effect of Directionality on Northern North Sea Extreme Wave Design Criteria. J. Offshore Mech. Arct. Eng. 2008, 130. [Google Scholar] [CrossRef]
- Barlow, A.M.; Mackay, E.; Eastoe, E.; Jonathan, P. A penalised piecewise-linear model for non-stationary extreme value analysis of peaks over threshold. Ocean Eng. 2023, 267, 113265. [Google Scholar] [CrossRef]
- Caires, S.; Yan, K. Ocean Surface Wave Time Series for the European Coast from 1976 to 2100 Derived from Climate Projections. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/sis-ocean-wave-timeseries?tab=overview (accessed on 1 January 2023).
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.-F.; et al. The representative concentration pathways: An overview. Clim. Change 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Thomson, A.M.; Calvin, K.V.; Smith, S.J.; Kyle, G.P.; Volke, A.; Patel, P.; Delgado-Arias, S.; Bond-Lamberty, B.; Wise, M.A.; Clarke, L.E.; et al. RCP4.5: A pathway for stabilization of radiative forcing by 2100. Clim. Change 2011, 109, 77–94. [Google Scholar] [CrossRef] [Green Version]
- Pielke, R., Jr.; Burgess, M.G.; Ritchie, J. Plausible 2005–2050 emissions scenarios project between 2 °C and 3 °C of warming by 2100. Environ. Res. Lett. 2022, 17, 024027. [Google Scholar] [CrossRef]
- Höök, M.; Sivertsson, A.; Aleklett, K. Validity of the Fossil Fuel Production Outlooks in the IPCC Emission Scenarios. Nat. Resour. Res. 2010, 19, 63–81. [Google Scholar] [CrossRef] [Green Version]
- Fisher, N.I. Statistical Analysis of Circular Data; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Arguez, A.; Vose, R.S. The Definition of the Standard WMO Climate Normal: The Key to Deriving Alternative Climate Normals. Bull. Am. Meteorol. Soc. 2011, 92, 699–704. [Google Scholar] [CrossRef] [Green Version]
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kim, H.; Kanae, S. Global flood risk under climate change. Nat. Clim. Change 2013, 3, 816–821. [Google Scholar] [CrossRef]
- Bender, J.; Wahl, T.; Jensen, J. Multivariate design in the presence of non-stationarity. J. Hydrol. 2014, 514, 123–130. [Google Scholar] [CrossRef]
- Hipel, K.; McLeod, A. Time Series Modelling of Water Resources and Environmental Systems; Electronic Reprint of Our Book Originally Published in 1994; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Rutkowska, A. Properties of the Cox–Stuart Test for Trend in Application to Hydrological Series: The Simulation Study. Commun. Stat. Simul. Comput. 2015, 44, 565–579. [Google Scholar] [CrossRef]
- Sanuy, M.; Duo, E.; Jäger, W.S.; Ciavola, P.; Jiménez, J.A. Linking source with consequences of coastal storm impacts for climate change and risk reduction scenarios for Mediterranean sandy beaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 1825–1847. [Google Scholar] [CrossRef] [Green Version]
- Duo, E.; Sanuy, M.; Jiménez, J.A.; Ciavola, P. How good are symmetric triangular synthetic storms to represent real events for coastal hazard modelling. Coast. Eng. 2020, 159, 103728. [Google Scholar] [CrossRef]
- Langousis, A.; Mamalakis, A.; Puliga, M.; Deidda, R. Threshold detection for the generalized Pareto distribution: Review of representative methods and application to the NOAA NCDC daily rainfall database. Water Resour. Res. 2016, 52, 2659–2681. [Google Scholar] [CrossRef] [Green Version]
- Davison, A.C.; Smith, R.L. Models for Exceedances Over High Thresholds. J. R. Stat. Soc. Ser. B 1990, 52, 393–425. [Google Scholar] [CrossRef]
- Hall, W.; Weller, J. Mean residual life. In Statistics and Related Topics; Csorgo, M., Dawson, D.A., Rao, J.N.K., Saleh, A.K.M.E., Eds.; Norrh-Holland Publishing Company: Amsterdam, The Netherlands, 1981; pp. 169–184. [Google Scholar]
- Eastoe, E.F.; Tawn, J.A. Modelling the distribution of the cluster maxima of exceedances of subasymptotic thresholds. Biometrika 2012, 99, 43–55. [Google Scholar] [CrossRef]
- Grabemann, I.; Weisse, R. Climate change impact on extreme wave conditions in the North Sea: An ensemble study. Ocean Dyn. 2008, 58, 199–212. [Google Scholar] [CrossRef] [Green Version]
- Benito, S.; López-Martín, C.; Navarro, M.Á. Assessing the importance of the choice threshold in quantifying market risk under the POT approach (EVT). Risk Manag. 2023, 25, 6. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D.; Makropoulos, C. How extreme is extreme? An assessment of daily rainfall distribution tails. Hydrol. Earth Syst. Sci. 2013, 17, 851–862. [Google Scholar] [CrossRef] [Green Version]
- Ochi, M.K. Ocean Waves—The Stochastic Approach; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Malliouri, D.I.; Memos, C.D.; Tampalis, N.D.; Soukissian, T.H.; Tsoukala, V.K. Integrating short- and long-term statistics for short-crested waves in deep and intermediate waters. Appl. Ocean Res. 2019, 82, 346–361. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Parameter and Quantile Estimation for the Generalized Pareto Distribution. Technometrics 1987, 29, 339–349. [Google Scholar] [CrossRef]
- Moharram, S.H.; Gosain, A.K.; Kapoor, P.N. A comparative study for the estimators of the Generalized Pareto distribution. J. Hydrol. 1993, 150, 169–185. [Google Scholar] [CrossRef]
- Castillo, E.; Hadi, A.S. Fitting the Generalized Pareto Distribution to Data. J. Am. Stat. Assoc. 1997, 92, 1609–1620. [Google Scholar] [CrossRef]
- Robinson, M.E.; Tawn, J.A. Statistics for Extreme Sea Currents. J. R. Stat. Soc. Ser. C Appl. Stat. 1997, 46, 183–205. [Google Scholar] [CrossRef]
- Green, P.J.; Silverman, B.W. Nonparametric Regression and Generalized Linear Models; Chapman and Hall/CRC: New York, NY, USA, 1993; ISBN 9780429161056. [Google Scholar]
- Jonathan, P.; Ewans, K. The effect of directionality on extreme wave design criteria. Ocean Eng. 2007, 34, 1977–1994. [Google Scholar] [CrossRef]
- Chambers, J. Chapter 4 of statistical models in S. In Linear Models; Chambers, J., Hastie, T., Eds.; Wadsworth & Brooks/Cole: Nashville, TN, USA, 1992. [Google Scholar]
- Galiatsatou, P.; Prinos, P. Joint probability analysis of extreme wave heights and storm surges in the Aegean Sea in a changing climate. E3S Web Conf. 2016, 7, 02002. [Google Scholar] [CrossRef]
- Casas-Prat, M.; Sierra, J.P. Projected future wave climate in the NW Mediterranean Sea. J. Geophys. Res. Ocean. 2013, 118, 3548–3568. [Google Scholar] [CrossRef]
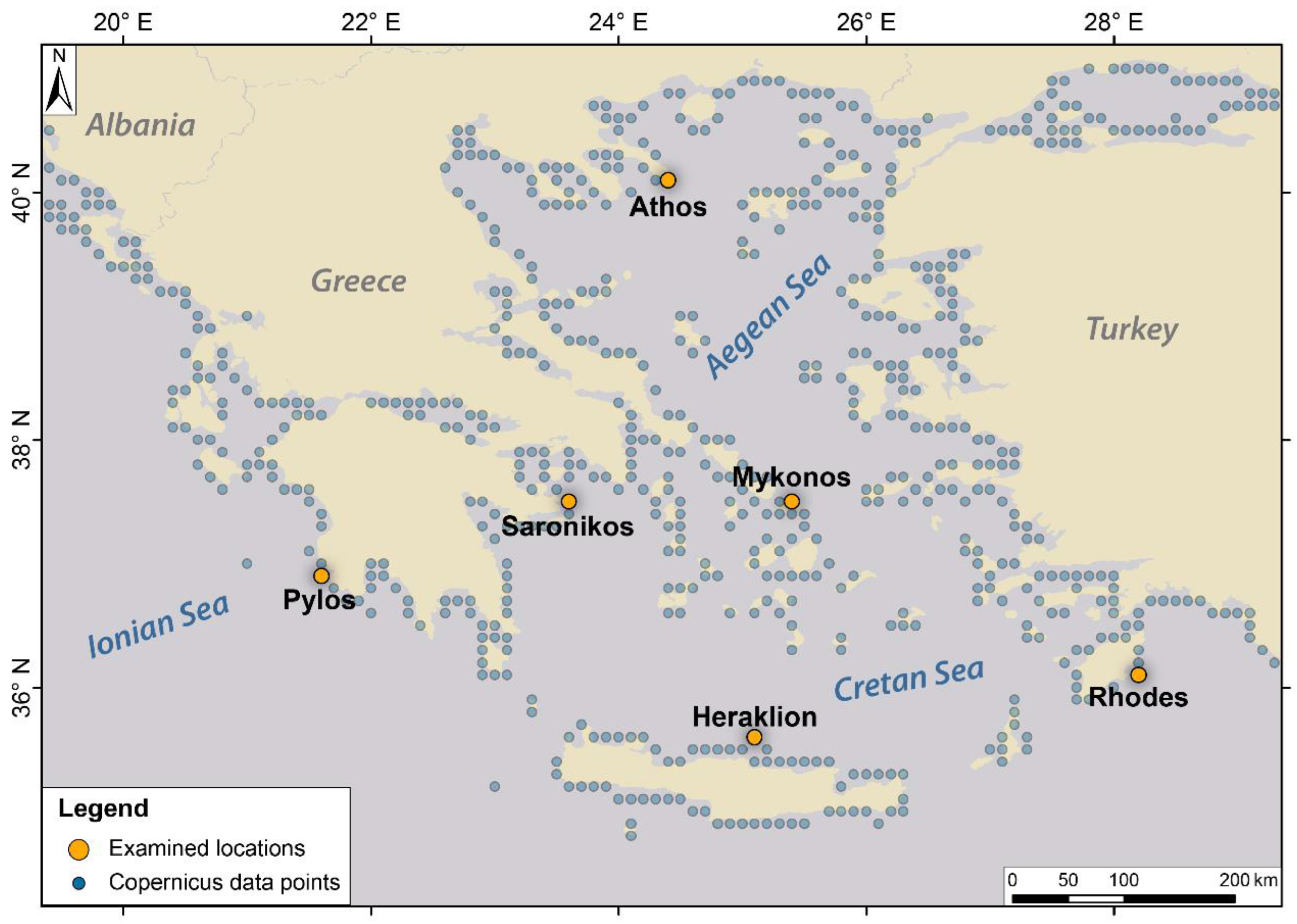





| s/n | Area | Latitude, Longitude (°) | Water Depth (m) |
|---|---|---|---|
| 1 | Athos | 40.1 N, 24.4 E | 840 |
| 2 | Mykonos | 37.5 N, 25.4 E | 32 |
| 4 | Heraklion | 35.6 N, 25.1 E | 650 |
| 4 | Rhodes | 36.1 N, 28.2 E | 1080 |
| 5 | Saronikos | 37.5 N, 23.6 E | 135 |
| 6 | Pylos | 36.9 N, 21.6 E | 710 |
| s/n | Location | Mean (m) | Median (m) | Max. (m) | Stand. Dev. (m) | Mean (deg.) | Stand. Dev. (deg.) |
|---|---|---|---|---|---|---|---|
| 1 | Athos | 0.69 | 0.46 | 6.94 | 0.68 | 77.35 | 80.81 |
| 2 | Mykonos | 0.95 | 0.76 | 9.03 | 0.74 | 355.57 | 74.36 |
| 4 | Heraklion | 0.94 | 0.77 | 8.44 | 0.70 | 328.05 | 55.54 |
| 4 | Rhodes | 0.58 | 0.43 | 6.37 | 0.52 | 236.90 | 83.71 |
| 5 | Saronikos | 0.49 | 0.35 | 5.44 | 0.46 | 26.89 | 97.66 |
| 6 | Pylos | 0.88 | 0.63 | 9.03 | 0.75 | 280.29 | 55.80 |
| Interest Point | |
|---|---|
| Athos | 0.0006 ± 0.0003 |
| Mykonos | 0.0007 ± 0.0005 |
| Heraklion | 0.0004 ± 0.0002 |
| Rhodes | 0.0002 ± 0.0001 |
| Saronikos | 0.0004 ± 0.0001 |
| Pylos | 0.0006 ± 0.0004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malliouri, D.I.; Moraitis, V.; Petrakis, S.; Vandarakis, D.; Hatiris, G.-A.; Kapsimalis, V. A Non-Stationary and Directional Probabilistic Analysis of Coastal Storms in the Greek Seas. Water 2023, 15, 2455. https://doi.org/10.3390/w15132455
Malliouri DI, Moraitis V, Petrakis S, Vandarakis D, Hatiris G-A, Kapsimalis V. A Non-Stationary and Directional Probabilistic Analysis of Coastal Storms in the Greek Seas. Water. 2023; 15(13):2455. https://doi.org/10.3390/w15132455
Chicago/Turabian StyleMalliouri, Dimitra I., Vyron Moraitis, Stelios Petrakis, Dimitrios Vandarakis, Georgios-Angelos Hatiris, and Vasilios Kapsimalis. 2023. "A Non-Stationary and Directional Probabilistic Analysis of Coastal Storms in the Greek Seas" Water 15, no. 13: 2455. https://doi.org/10.3390/w15132455







