A Coarse-Grained DNA Model Parameterized from Atomistic Simulations by Inverse Monte Carlo
Abstract
:1. Introduction
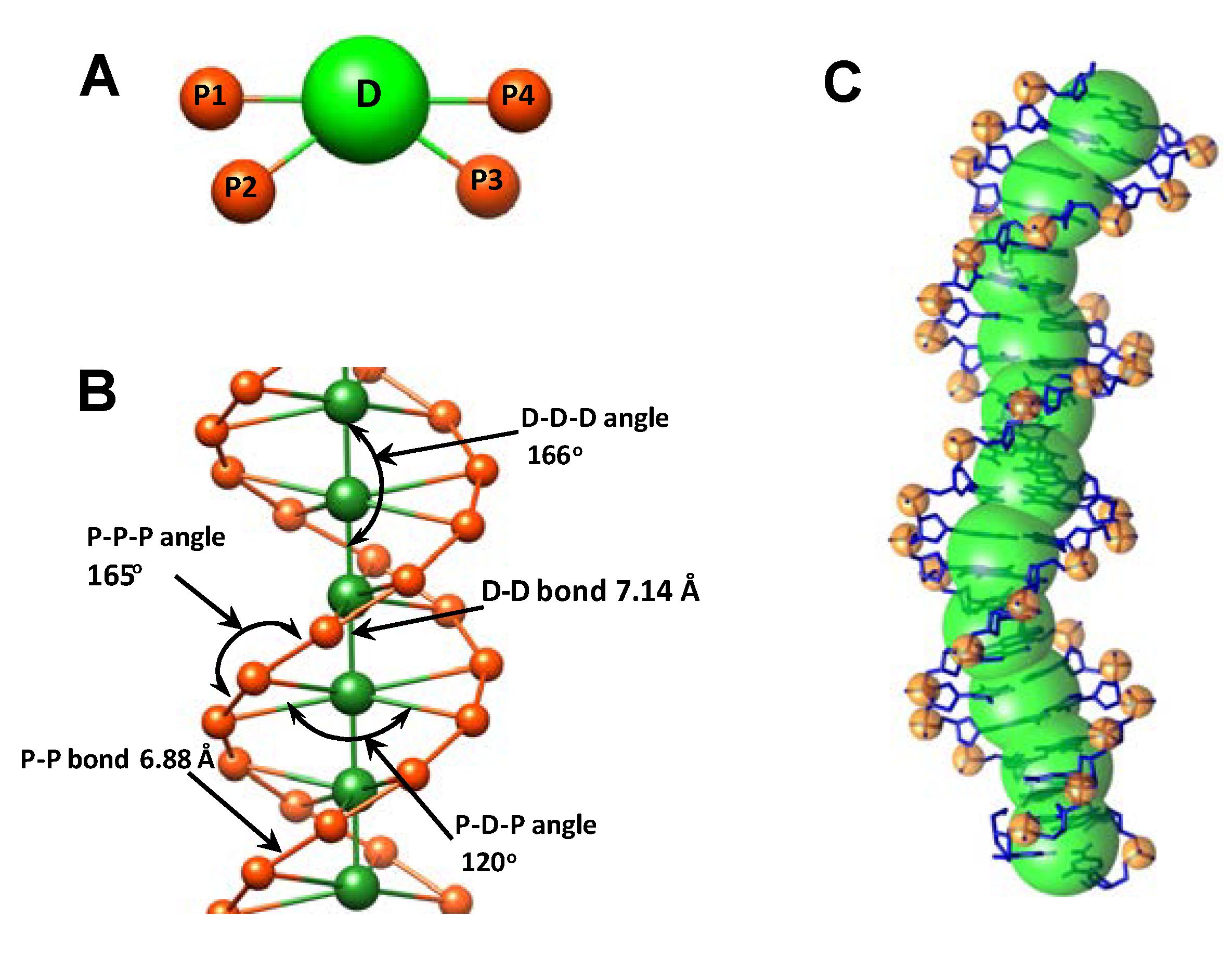
2. Methodology
2.1. Design of the Flexible CG DNA Model and Principles of Its Parameterization
| Type of bond/angle | Equilibrium distance/angle | IMC derived force constant (kBT·Å−2 or kBT·rad−2) |
|---|---|---|
| D–D bond | 7.14 Å | 14.8 |
| D–P bond | 9.04 Å | 9.7 |
| P–P bond | 6.88 Å | 19.4 |
| D–D–D angle | 166.00° | 37.0 |
| P–D–P angle | 119.50° | 100.0 |
| P–P–P angle | 165.00° | 32.0 |
2.2. Atomistic Molecular Dynamics Simulations
2.3. Coarse-Grained DNA and Computations of Effective Potentials
2.4. Coarse-Grained DNA Model: Large-Scale Simulations
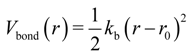
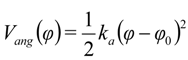
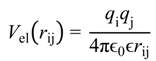
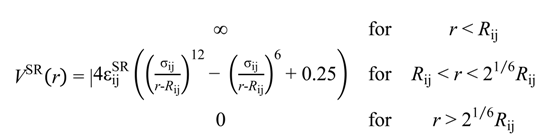
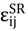 were set to σij = 4 Å and
were set to σij = 4 Å and 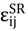 = 1 (kBT units) for all interactions. Thus, the effective radius of each particle was determined by a sum of the soft radius of σij/2 = 2 Å and the hard radius Ri which was defined separately for each particle type. The hard radii Ri as well as charges qi are given in Table 2. The charges were obtained by summation of partial charges of the corresponding CG groups of the CHARMM27 force field. Thus, the total interaction potential (potential energy) of the system is:
= 1 (kBT units) for all interactions. Thus, the effective radius of each particle was determined by a sum of the soft radius of σij/2 = 2 Å and the hard radius Ri which was defined separately for each particle type. The hard radii Ri as well as charges qi are given in Table 2. The charges were obtained by summation of partial charges of the corresponding CG groups of the CHARMM27 force field. Thus, the total interaction potential (potential energy) of the system is:
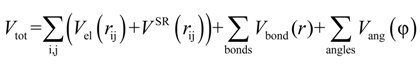
| Site | Charge | Radius Ri (Å) |
|---|---|---|
| D (DNA) | +0.8 | 4.0 |
| P (DNA) | −1.2 | 1.0 |
| K+ (ion) | +1.0 | 0.0 |
| Cl− (ion) | −1.0 | 0.0 |
| Ionic strength | Box size (Å) | Number of cations (K+) | Number of anions (Cl−) |
|---|---|---|---|
| Uncharged 1 | 800 | 300 | 300 |
| 100.0 mM | 500 | 7900 | 7500 |
| 30.0 mM | 500 | 2650 | 2250 |
| 10.0 mM | 800 | 3400 | 3000 |
| 3.0 mM | 800 | 1300 | 900 |
| 1.0 mM | 800 | 700 | 300 |
| 0.3 mM | 1400 | 900 | 500 |
| 0.1 mM | 1420 | 580 | 180 |
3. Results and Discussion
3.1. Harmonic Approximation for Internal Potentials
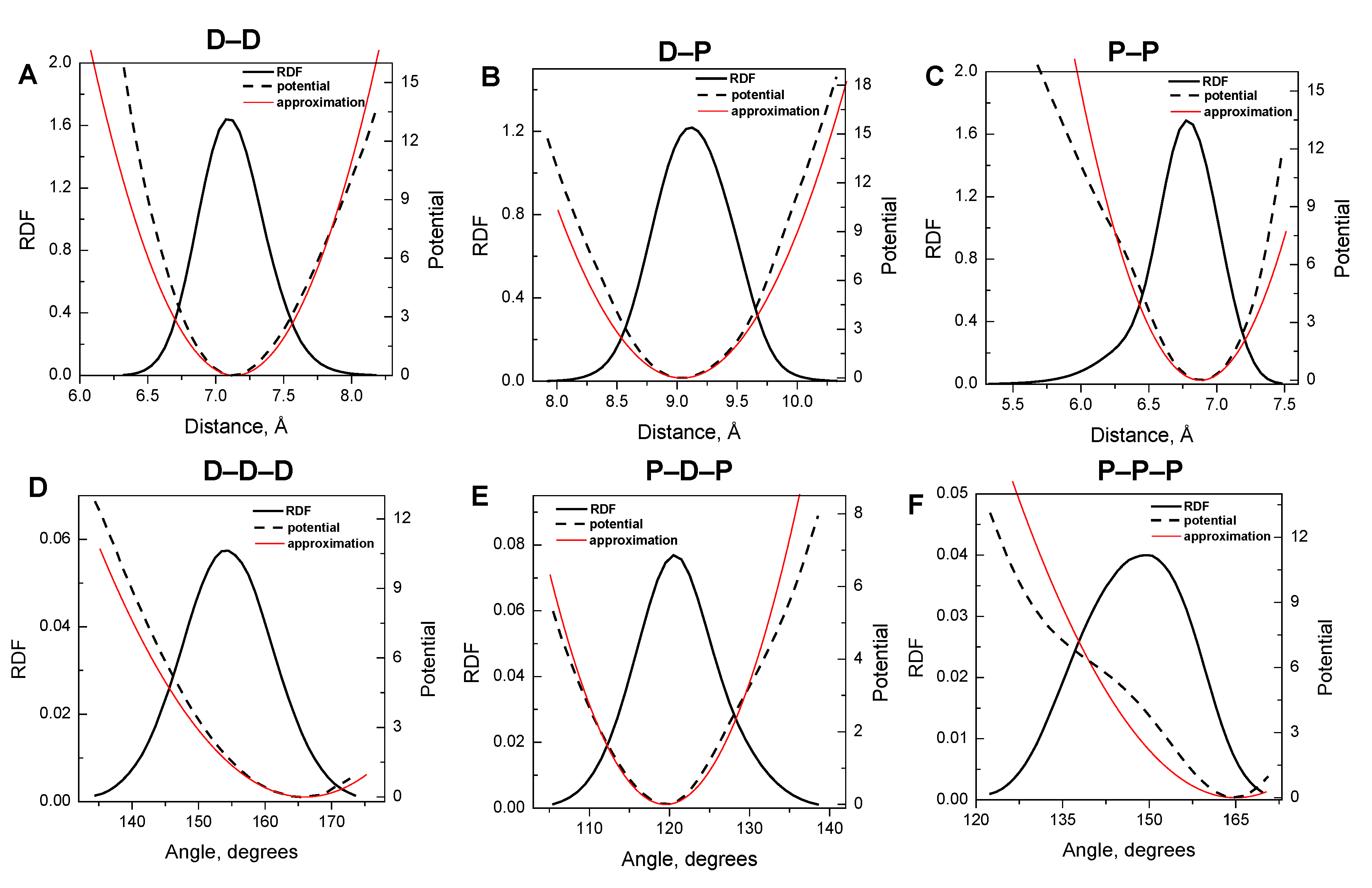
3.2. Validation of the CG-Model: Salt Dependence of DNA Persistence Length
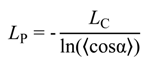
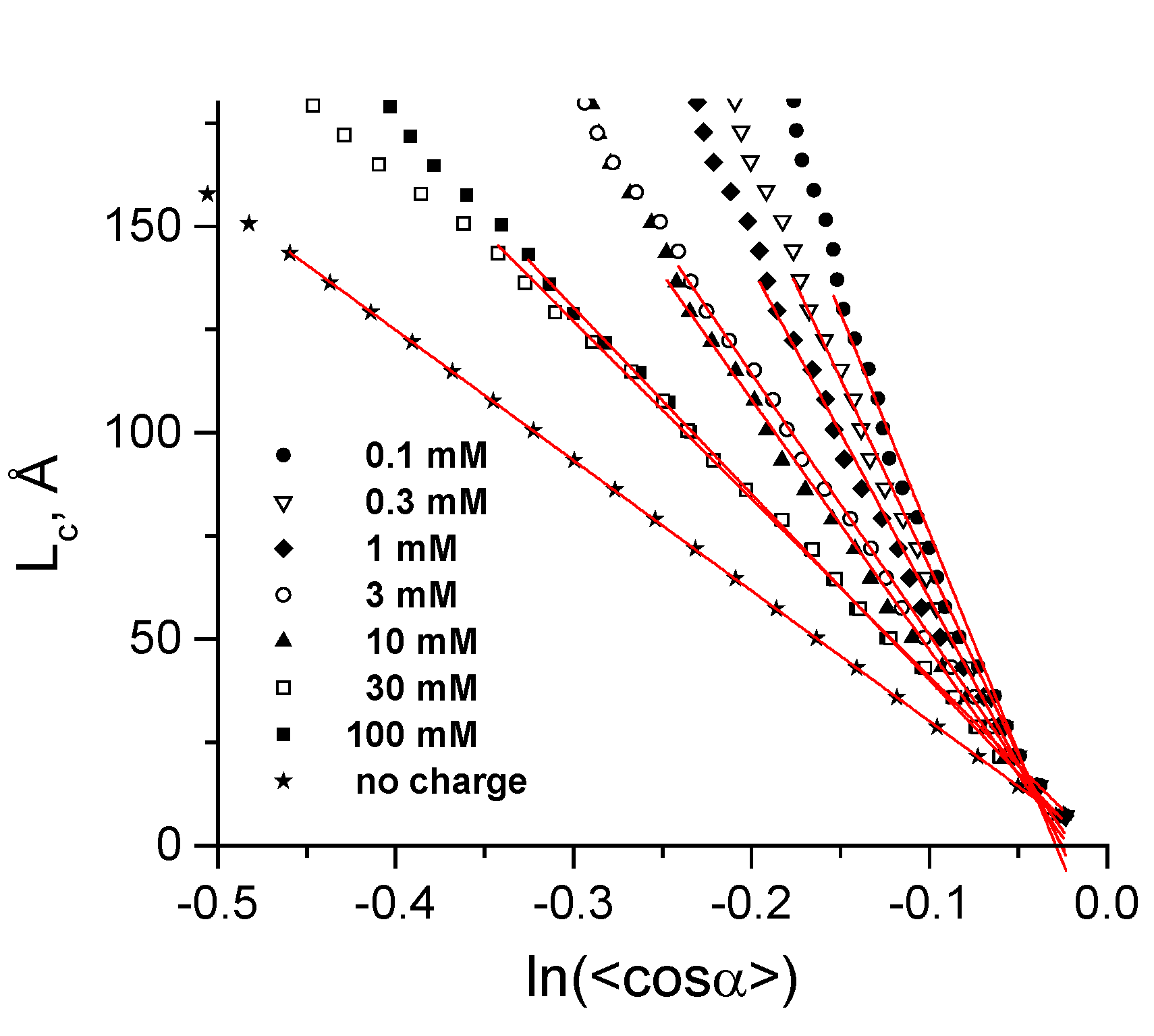
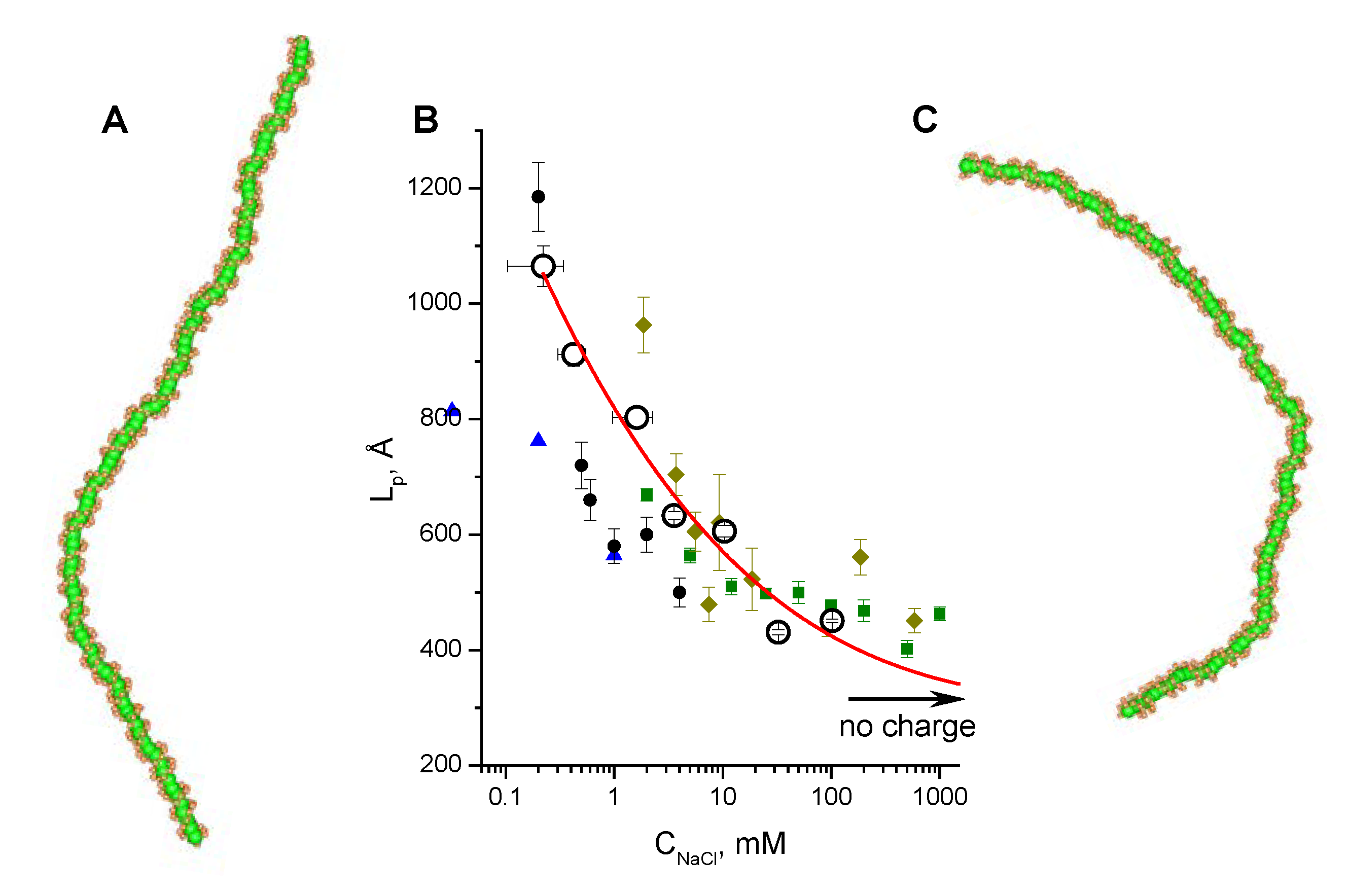
| Cation concentration 1, (mM) | Persistent length, LC (Å) | Torsional persistence length, LT (Å) |
|---|---|---|
| 0.104–0.340 | 1065 ± 35 | 1446 |
| 0.303–0.545 | 912 ± 20 | 1461 |
| 0.970–2.270 | 803 ± 17 | 1415 |
| 2.910–4.210 | 633 ± 7 | 1463 |
| 9.730–11.030 | 606 ± 10 | 1409 |
| 29.800–35.200 | 431 ± 4 | 1424 |
| 99.600–105.000 | 451 ± 3 | 1399 |
| No charge | 316 ± 1 | 1349 |
3.3. Calculation of Torsion Persistence Length of the DNA CG-Model
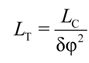
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Widom, J. Physicochemical studies of the folding of the 100 A nucleosome filament into the 300 A filament. Cation dependence. J. Mol. Biol. 1986, 190, 411–424. [Google Scholar] [CrossRef]
- Clark, D.J.; Kimura, T. Electrostatic mechanism of chromatin folding. J. Mol. Biol. 1990, 211, 883–896. [Google Scholar]
- Korolev, N.; Vorontsova, O.V.; Nordenskiöld, L. Physicochemical analysis of electrostatic foundation for DNA-protein interactions in chromatin transformations. Prog. Biophys. Mol. Biol. 2007, 95, 23–49. [Google Scholar] [CrossRef]
- Korolev, N.; Berezhnoy, N.V.; Eom, K.D.; Tam, J.P.; Nordenskiöld, L. A universal description for the experimental behavior of salt-(in)dependent oligocation-induced DNA condensation. Nucleic Acids Res. 2009, 37, 7137–7150. [Google Scholar] [CrossRef]
- Bloomfield, V.A. DNA condensation. Curr. Opin. Struct. Biol. 1996, 6, 334–341. [Google Scholar] [CrossRef]
- Iwaki, T.; Saito, T.; Yoshikawa, K. How are small ions involved in the compaction of DNA molecules? Surf. B Biointerf. 2007, 56, 126–133. [Google Scholar] [CrossRef] [Green Version]
- Ray, J.; Manning, G.S. Effect of counterion valence and polymer charge density on the pair potential of two polyions. Macromol. 1997, 30, 5739–5744. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Nordenskiöld, L. Monte Carlo simulation study of ion distribution and osmotic pressure in hexagonally oriented DNA. J. Phys. Chem. 1995, 99, 10373–10382. [Google Scholar] [CrossRef]
- Gronbech-Jensen, N.; Mashl, R.J.; Bruinsma, R.F.; Gelbart, W.M. Counterion-induced attraction between rigid polyelectrolytes. Phys. Rev. Lett. 1997, 78, 2477–2480. [Google Scholar] [CrossRef]
- Guldbrand, L.; Nilsson, L.G.; Nordenskiöld, L. A Monte Carlo simulation study of electrostatic forces between hexagonally packed DNA double helices. J. Chem. Phys. 1986, 85, 6686–6698. [Google Scholar] [CrossRef]
- Nilsson, L.G.; Guldbrand, L.; Nordenskiöld, L. Evaluation of the electrostatic osmotic pressure in an infinite system of hexagonally oriented DNA molecules. A Monte Carlo simulation study. Mol. Phys. 1991, 72, 177–192. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Nordenskiöld, L. Monte Carlo simulation study of DNA polyelectrolyte properties in the presence of multivalent polyamine ions. J. Phys. Chem. B 1997, 101, 4335–4342. [Google Scholar] [CrossRef]
- Arya, G.; Schlick, T. Role of histone tails in chromatin folding revealed by a mesoscopic oligonucleosome model. Proc. Natl. Acad. Sci. USA. 2006, 103, 16236–16241. [Google Scholar] [CrossRef]
- Arya, G.; Schlick, T. A tale of tails: How histone tails mediate chromatin compaction in different salt and linker histone environments. J. Phys. Chem. A 2009, 113, 4045–4059. [Google Scholar] [CrossRef]
- Muhlbacher, F.; Schiessel, H.; Holm, C. Tail-induced attraction between nucleosome core particles. Phys. Rev. E 2006, 74. [Google Scholar] [CrossRef]
- Saunders, M.G.; Voth, G.A. Coarse-graining of multiprotein assemblies. Curr. Opin. Struct. Biol. 2012, 22, 144–150. [Google Scholar] [CrossRef]
- Takada, S. Coarse-grained molecular simulations of large biomolecules. Curr. Opin. Struct. Biol. 2012, 22, 130–137. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Laaksonen, A. Calculation of effective interaction potentials from radial distribution functions: A reverse Monte Carlo approach. Phys. Rev. E 1995, 52, 3730–3737. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Mirzoev, A.; Chen, L.J.; Laaksonen, A. Systematic coarse-graining of molecular models by the Newton inversion method. Faraday Discuss. 2010, 144, 43–56. [Google Scholar] [CrossRef]
- Izvekov, S.; Voth, G.A. Multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B 2005, 109, 2469–2473. [Google Scholar] [CrossRef]
- Ayton, G.S.; Noid, W.G.; Voth, G.A. Multiscale modeling of biomolecular systems: In serial and in parallel. Curr. Opin. Struct. Biol. 2007, 17, 192–198. [Google Scholar] [CrossRef]
- Chaimovich, A.; Shell, M.S. Coarse-graining errors and numerical optimization using a relative entropy framework. J. Chem. Phys. 2011, 134. [Google Scholar] [CrossRef]
- Rudzinski, J.F.; Noid, W.G. Coarse-graining entropy, forces, and structures. J. Chem. Phys. 2011, 135. [Google Scholar] [CrossRef]
- Savelyev, A.; Papoian, G.A. Molecular renormalization group coarse-graining of polymer chains: application to double-stranded DNA. Biophys. J. 2009, 96, 4044–4052. [Google Scholar] [CrossRef]
- Savelyev, A.; Papoian, G.A. Chemically accurate coarse graining of double-stranded DNA. Proc. Natl. Acad. Sci. USA 2010, 107, 20340–20345. [Google Scholar] [CrossRef]
- Potoyan, D.A.; Savelyev, A.; Papoian, G.A. Recent successes in coarse-grained modeling of DNA. WIREs Comput. Mol. Sci. 2013, 3, 69–83. [Google Scholar] [CrossRef]
- Dans, P.D.; Zeida, A.; MacHado, M.R.; Pantano, S. A coarse grained model for atomic-detailed DNA simulations with explicit electrostatics. J. Chem. Theory Comput. 2010, 6, 1711–1725. [Google Scholar]
- Demille, R.C.; Cheatham, T.E.; Molinero, V. A coarse-grained model of DNA with explicit solvation by water and ions. J. Phys. Chem. B 2011, 115, 132–142. [Google Scholar] [CrossRef]
- Cao, Q.; Zuo, C.; Ma, Y.; Li, L.; Zhang, Z. Interaction of double-stranded DNA with a nanosphere: A coarse-grained molecular dynamics simulation study. Soft Matter 2011, 7, 506–514. [Google Scholar]
- Freeman, G.S.; Hinckley, D.M.; de Pablo, J.J. A coarse-grain three-site-per-nucleotide model for DNA with explicit ions. J. Chem. Phys. 2011, 135. [Google Scholar] [CrossRef]
- Hinckley, D.M.; Freeman, G.S.; Whitmer, J.K.; de Pablo, J.J. An experimentally-informed coarse-grained 3-site-per-nucleotide model of DNA: Structure, thermodynamics, and dynamics of hybridization. J. Chem. Phys. 2013, 139. [Google Scholar] [CrossRef]
- Cragnolini, T.; Derreumaux, P.; Pasquali, S. Coarse-grained simulations RNA and DNA duplexes. J. Phys. Chem. B 2013, 117, 8047–8060. [Google Scholar] [CrossRef]
- Doye, J.P.; Ouldridge, T.E.; Louis, A.A.; Romano, F.; Šulc, P.; Matek, C.; Snodin, B.E.; Rovigatti, L.; Schreck, J.S.; Harrison, R.M.; et al. Coarse-graining DNA for simulations of DNA nanotechnology. Phys. Chem. Chem. Phys. 2013, 15, 20395–20414. [Google Scholar] [CrossRef]
- Ouldridge, T.E.; Louis, A.A.; Doye, J.P.K. DNA nanotweezers studied with a coarse-grained model of DNA. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef]
- Ouldridge, T.E.; Louis, A.A.; Doye, J.P.K. Structural, mechanical, and thermodynamic properties of a coarse-grained DNA model. J. Chem. Phys. 2011, 134. [Google Scholar] [CrossRef]
- Muhlbacher, F.; Holm, C.; Schiessel, H. Controlled DNA compaction within chromatin: the tail-bridging effect. Europhys. Lett. 2006, 73, 135–141. [Google Scholar] [CrossRef]
- Wedemann, G.; Langowski, J. Computer simulation of the 30-nanometer chromatin fiber. Biophys. J. 2002, 82, 2847–2859. [Google Scholar] [CrossRef]
- Korolev, N.; Lyubartsev, A.P.; Nordenskiöld, L. Computer modeling demonstrates that electrostatic attraction of nucleosomal DNA is mediated by histone tails. Biophys. J. 2006, 90, 4305–4316. [Google Scholar] [CrossRef]
- Langowski, J. Polymer chain models of DNA and chromatin. Eur. Phys. J. E 2006, 19, 241–249. [Google Scholar] [CrossRef]
- Voltz, K.; Trylska, J.; Tozzini, V.; Kurkal-Siebert, V.; Langowski, J.; Smith, J. Coarse-grained force field for the nucleosome from self-consistent multiscaling. J. Comp. Chem. 2008, 29, 1429–1439. [Google Scholar] [CrossRef]
- Langowski, J.; Schiessel, H. Chromatin Simulations. from DNA to Chromatin Fibers. In Computational Studies of RNA and DNA; Šponer, J., Lankaš, F., Eds.; Springer: Dordrecht, the Netherlands, 2006; pp. 605–634. [Google Scholar]
- Arya, G.; Schlick, T. Efficient global biopolymer sampling with end-transfer configurational bias Monte Carlo. J. Chem. Phys. 2007, 126, 044107. [Google Scholar] [CrossRef]
- Langowski, J.; Heermann, D.W. Computational modeling of the chromatin fiber. Semin. Cell Dev. Biol. 2007, 18, 659–667. [Google Scholar] [CrossRef]
- Kepper, N.; Foethke, D.; Stehr, R.; Wedemann, G.; Rippe, K. Nucleosome geometry and internucleosomal interactions control the chromatin fiber conformation. Biophys. J. 2008, 95, 3692–3705. [Google Scholar] [CrossRef]
- Stehr, R.; Kepper, N.; Rippe, K.; Wedemann, G. The effect of internucleosomal interaction on folding of the chromatin fiber. Biophys. J. 2008, 95, 3677–3691. [Google Scholar] [CrossRef]
- Grigoryev, S.A.; Arya, G.; Correll, S.; Woodcock, C.L.; Schlick, T. Evidence for heteromorphic chromatin fibers from analysis of nucleosome interactions. Proc. Natl. Acad. Sci. USA 2009, 106, 13317–13322. [Google Scholar]
- Yang, Y.; Lyubartsev, A.P.; Korolev, N.; Nordenskiöld, L. Computer modeling reveals that modifications of the histone tail charges define salt-dependent interaction of the nucleosome core particles. Biophys. J. 2009, 96, 2082–2094. [Google Scholar] [CrossRef]
- Stehr, R.; Schöpflin, R.; Ettig, R.; Kepper, N.; Rippe, K.; Wedemann, G. Exploring the conformational space of chromatin fibers and their stability by numerical dynamic phase diagrams. Biophys. J. 2010, 98, 1028–1037. [Google Scholar] [CrossRef]
- Kepper, N.; Ettig, R.; Stehr, R.; Marnach, S.; Wedemann, G.; Rippe, K. Force spectroscopy of chromatin fibers: Extracting energetics and structural information from Monte Carlo simulations. Biopolymers 2011, 95, 435–447. [Google Scholar] [CrossRef]
- Materese, C.K.; Savelyev, A.; Papoian, G.A. Counterion atmosphere and hydration patterns near a nucleosome core particle. J. Am. Chem. Soc. 2009, 131, 15005–15013. [Google Scholar] [CrossRef]
- Voltz, K.; Trylska, J.; Calimet, N.; Smith, J.C.; Langowski, J. Unwrapping of nucleosomal DNA ends: A multiscale molecular dynamics study. Biophys. J. 2012, 102, 849–858. [Google Scholar] [CrossRef]
- Hess, B.; Holm, C.; van der Vegt, N. Modeling multibody effects in ionic solutions with a concentration dependent dielectric permittivity. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef]
- Korolev, N.; Lyubartsev, A.P.; Nordenskiöld, L. Cation-induced polyelectrolyte-polyelectrolyte attraction in solutions of DNA and nucleosome core particles. Adv. Coll. Interf. Sci. 2010, 158, 32–47. [Google Scholar] [CrossRef]
- Korolev, N.; Allahverdi, A.; Yang, Y.; Fan, Y.; Lyubartsev, A.P.; Nordenskiöld, L. Electrostatic origin of salt-induced nucleosome array compaction. Biophys. J. 2010, 99, 1896–1905. [Google Scholar] [CrossRef]
- Allahverdi, A.; Yang, R.; Korolev, N.; Fan, Y.; Davey, C.A.; Liu, C.F.; Nordenskiöld, L. The effects of histone H4 tail acetylations on cation-induced chromatin folding and self-association. Nucleic Acids Res. 2011, 39, 1680–1691. [Google Scholar] [CrossRef]
- Fan, Y.; Korolev, N.; Lyubartsev, A.P.; Nordenskiöld, L. An advanced coarse-grained nucleosome core particle model for computer simulations of nucleosome-nucleosome interactions under varying ionic conditions. PLoS One 2013, 8, e54228. [Google Scholar]
- Bertin, A.; Mangenot, S.; Renouard, M.; Durand, D.; Livolant, F. Structure and phase diagram of nucleosome core particles aggregated by multivalent cations. Biophys. J. 2007, 93, 3652–3663. [Google Scholar] [CrossRef]
- Leforestier, A.; Dubochet, J.; Livolant, F. Bilayers of nucleosome core particles. Biophys. J. 2001, 81, 2114–2421. [Google Scholar]
- Mangenot, S.; Leforestier, A.; Durand, D.; Livolant, F. Phase diagram of nucleosome core particles. J. Mol. Biol. 2003, 333, 907–916. [Google Scholar] [CrossRef]
- Li, G.; Levitus, M.; Bustamante, C.; Widom, J. Rapid spontaneous accessibility of nucleosomal DNA. Nat. Struct. Mol. Biol. 2005, 12, 46–53. [Google Scholar] [CrossRef]
- Böhm, V.; Hieb, A.R.; Andrews, A.J.; Gansen, A.; Rocker, A.; Tóth, K.; Luger, K.; Langowski, J. Nucleosome accessibility governed by the dimer/tetramer interface. Nucleic Acids Res. 2011, 39, 3093–3102. [Google Scholar] [CrossRef]
- Mirzoev, A.; Lyubartsev, A.P. MagiC: Software package for multiscale modeling. J. Chem. Theory Comput. 2013, 9, 1512–1520. [Google Scholar] [CrossRef]
- Mirzoev, A.; Lyubartsev, A.P. Systematic implicit solvent coarse graining of DMPC lipids. J. Comput. Chem. 2014, in press. [Google Scholar]
- Korolev, N.; Lyubartsev, A.P.; Rupprecht, A.; Nordenskiöld, L. Experimental and Monte Carlo simulation studies on the competitive binding of Li+, Na+, and K+ ions to DNA in oriented DNA fibers. J. Phys. Chem. B 1999, 103, 9008–9019. [Google Scholar] [CrossRef]
- Korolev, N.; Lyubartsev, A.P.; Rupprecht, A.; Nordenskiöld, L. Competitive binding of Mg2+, Ca2+, Na+, and K+ to DNA in oriented DNA fibers: Experimental and Monte Carlo simulation results. Biophys. J. 1999, 77, 2736–2749. [Google Scholar] [CrossRef]
- Montoro, J.C.G.; Abascal, J.L.F. Ionic distribution around simple DNA models. I. Cylindrically averaged properties. J. Chem. Phys. 1995, 103, 8273–8284. [Google Scholar] [CrossRef]
- Macke, T.; Case, D.A. Modeling unusual nucleic acid structures. In Molecular Modeling of Nucleic Acids; Leontes, N.B., SantaLucia, J., Eds.; ACS Publications: Washington, DC, USA, 1998; pp. 379–393. [Google Scholar]
- van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible and free. J. Comp. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Lindahl, E.; Hess, B.; van der Spoel, D. Gromacs 3.0: A package for molecular simulations and trajectory analysis. J. Mol. Mod. 2001, 7, 306–317. [Google Scholar]
- Foloppe, N.; MacKerell, A.D., Jr. All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comp. Chem. 2000, 21, 86–104. [Google Scholar] [CrossRef]
- MacKerell, A.D., Jr.; Banavali, N. All-atom empirical force field for nucleic acids: II. Application to molecular dynamics simulations of DNA and RNA in solution. J. Comp. Chem. 2000, 21, 105–120. [Google Scholar]
- Hart, K.; Foloppe, N.; Baker, C.M.; Denning, E.J.; Nilsson, L.; MacKerell, A.D., Jr. Optimization of the CHARMM additive force field for DNA: Improved treatment of the BI/BII conformational equilibrium. J. Chem. Theory Comput. 2012, 8, 348–362. [Google Scholar]
- Mark, P.; Nilsson, L. Structure and dynamics of liquid water with different long range interaction truncation and temperature control methods in molecular dynamics simulations. J. Comp. Chem. 2002, 23, 1211–1219. [Google Scholar] [CrossRef]
- Mark, P.; Nilsson, L. Structure and dynamics of the TIP3P, SPC, and SPC/E water models at 298 K. J. Phys. Chem. A 2001, 105, 9954–9960. [Google Scholar] [CrossRef]
- Darden, T.; York, D.M.; Pedersen, L.G. Particle mesh Ewald: An N-log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Korolev, N.; Yu, H.; Lyubartsev, A.P.; Nordenskiöld, L. Molecular dynamics simulations demonstrate the regulation of DNA-DNA attraction by H4 histone tail acetylations and mutations. Biopolymers 2014, in press. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Laaksonen, A. Osmotic and activity coefficient from effective potentials for hydrated ions. Phys. Rev. E 1997, 55, 5689–5696. [Google Scholar]
- Rashin, A.A.; Bukatin, M.A. A view of thermodynamics of hydration emerging from continuum studies. Biophys. Chem. 1994, 51, 167–190. [Google Scholar] [CrossRef]
- Koehl, P. Electrostatics calculations: Latest methodological advance. Curr. Opin. Struct. Biol. 2006, 16, 142–151. [Google Scholar] [CrossRef]
- Korolev, N.; Allahverdi, A.; Lyubartsev, A.P.; Nordenskiöld, L. The polyelectrolyte properties of chromatin. Soft Matter 2012, 8, 9322–9333. [Google Scholar] [CrossRef]
- Korolev, N.; Fan, Y.; Lyubartsev, A.P.; Nordenskiöld, L. Modelling chromatin structure and dynamics: status and prospects. Curr. Opin. Struct. Biol. 2012, 22, 151–159. [Google Scholar] [CrossRef]
- Korolev, N.; Lyubartsev, A.P.; Rupprecht, A.; Nordenskiöld, L. Competitive substitution of hexammine cobalt(III) for Na+ and K+ ions in oriented DNA fibers. Biopolymers 2001, 58, 268–278. [Google Scholar] [CrossRef]
- Korolev, N.; Lyubartsev, A.P.; Nordenskiöld, L.; Laaksonen, A. Spermine: an “invisible” component in the crystals of B-DNA. A grand canonical Monte Carlo and molecular dynamics simulation study. J. Mol. Biol. 2001, 308, 907–917. [Google Scholar] [CrossRef]
- Nordenskiöld, L.; Lyubartsev, A.P.; Korolev, N. DNA-DNA interaction. In DNA Interactions with Polymers and Surfactants; Dias, R.S., Lindman, B., Eds.; John Wiley & Sons, Inc.: London, UK, 2008; pp. 209–237. [Google Scholar]
- Montoro, J.C.G.; Abascal, J.L.F. Ionic distribution around simple B-DNA models. II. Deviations from cylindrical symmetry. J. Chem. Phys. 1998, 109, 6200–6210. [Google Scholar] [CrossRef]
- Savelyev, A.; Materese, C.K.; Papoian, G.A. Is DNA’s rigidity dominated by electrostatic or nonelectrostatic interactions? J. Am. Chem. Soc. 2011, 133, 19290–19293. [Google Scholar] [CrossRef]
- Savelyev, A. Do monovalent mobile ions affect DNA’s flexibility at high salt content? Phys. Chem. Chem. Phys. 2012, 14, 2250–2254. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Khokhlov, A.R. Statistical Physics of Macromolecules; AIP Press: New York, NY, USA, 1994; p. 350. [Google Scholar]
- Åqvist, J. A simple way to calculate the axis of an α-helix. Comput. Chem. (Oxford) 1986, 10, 97–99. [Google Scholar] [CrossRef]
- Christopher, J.A.; Swanson, R.; Baldwin, T.O. Algorithms for finding the axis of a helix: Fast rotational and parametric least-squares methods. Comput. Chem. 1996, 20, 339–345. [Google Scholar] [CrossRef]
- Enkhbayar, P.; Damdinsuren, S.; Osaki, M.; Matsushima, N. HELFIT: Helix fitting by a total least squares method. Comput. Biol. Chem. 2008, 32, 307–310. [Google Scholar] [CrossRef]
- Hagerman, P.J. Investigation of the flexibility of DNA using transient electric birefringence. Biopolymers 1981, 20, 1503–1535. [Google Scholar] [CrossRef]
- Baumann, C.G.; Smith, S.B.; Bloomfield, V.A.; Bustamante, C. Ionic effects on the elasticity of single DNA molecules. Proc. Natl. Acad. Sci. USA 1997, 94, 6185–6190. [Google Scholar] [CrossRef]
- Rizzo, V.; Schellman, J. Flow dichroism of T7 DNA as a function of salt concentration. Biopolym. 1981, 20, 2143–2163. [Google Scholar] [CrossRef]
- Lu, Y.; Weers, B.; Stellwagen, N.C. DNA persistence length revisited. Biopolym. 2002, 61, 261–275. [Google Scholar] [CrossRef]
- Manning, G.S. The persistence length of DNA is reached from the persistence length of its null isomer through an internal electrostatic stretching force. Biophys. J. 2006, 91, 3607–3616. [Google Scholar]
- Odijk, T. Polyelectrolytes near the rod limit. J. Polym. Sci.: Polym. Phys. Ed. 1977, 15, 477–483. [Google Scholar] [CrossRef]
- Skolnick, J.; Fixman, M. Electrostatic persistence length of a wormlike polyelectrolyte. Macromol. 1977, 10, 944–948. [Google Scholar] [CrossRef]
- Lipfert, J.; Wiggin, M.; Kerssemakers, J.W.; Pedaci, F.; Dekker, N.H. Freely orbiting magnetic tweezers to directly monitor changes in the twist of nucleic acids. Nat. Commun. 2011, 2, 439. [Google Scholar] [CrossRef]
- Hagerman, P.J. Flexibility of DNA. Annu. Rev. Biophys. Biophys. Chem. 1988, 17, 265–286. [Google Scholar] [CrossRef]
Supplementary Files
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Korolev, N.; Luo, D.; Lyubartsev, A.P.; Nordenskiöld, L. A Coarse-Grained DNA Model Parameterized from Atomistic Simulations by Inverse Monte Carlo. Polymers 2014, 6, 1655-1675. https://doi.org/10.3390/polym6061655
Korolev N, Luo D, Lyubartsev AP, Nordenskiöld L. A Coarse-Grained DNA Model Parameterized from Atomistic Simulations by Inverse Monte Carlo. Polymers. 2014; 6(6):1655-1675. https://doi.org/10.3390/polym6061655
Chicago/Turabian StyleKorolev, Nikolay, Di Luo, Alexander P. Lyubartsev, and Lars Nordenskiöld. 2014. "A Coarse-Grained DNA Model Parameterized from Atomistic Simulations by Inverse Monte Carlo" Polymers 6, no. 6: 1655-1675. https://doi.org/10.3390/polym6061655





