2.1. Experimental Results
Any attempt to formulate accurate predictions by amending and overcoming CNT limitations should rest upon interpretation of some basic experimental observations. For instance, experimental data show that nuclei number density (
n) of a new phase (crystals, droplets) depends simultaneously on both time (
t) and supersaturation (Δ
μ), i.e.,
n =
n(
t, Δ
μ). S-shaped dependences of
n vs.
t at constant supersaturation have been known to cause electrochemical new-phase nucleation for a long time e.g., [
13,
14]. But they remained unelucidated [
15] until recently, when it was shown that they obey logistic functional dependence [
16]. The same function also governs insulin crystal nucleation—large amounts of data for which can be found in [
17]. Using custom-made quasi-two-dimensional all-glass cells with intentionally introduced air bubbles,
n vs.
t dependences were measured in this study simultaneously at four typical places: in solution bulk, at the glass support, at the air/solution interface, and at the three-phase boundary solution/glass/air. Stationary nucleation rates were determined from the linear parts of the corresponding plots, and energy barriers for nucleus formation and nucleus sizes were estimated. By simply focusing the microscope on the upper glass plate of the cell, heterogeneous on-glass crystal nucleation is differentiated from the one in the bulk solution. It is also argued that the latter proceeds heterogeneously, on some (unknown) foreign particles of biological origin. Seven different supersaturations have been studied with BioChemika-insulin, showing that crystal nucleation in bulk solution prevails greatly [
17].
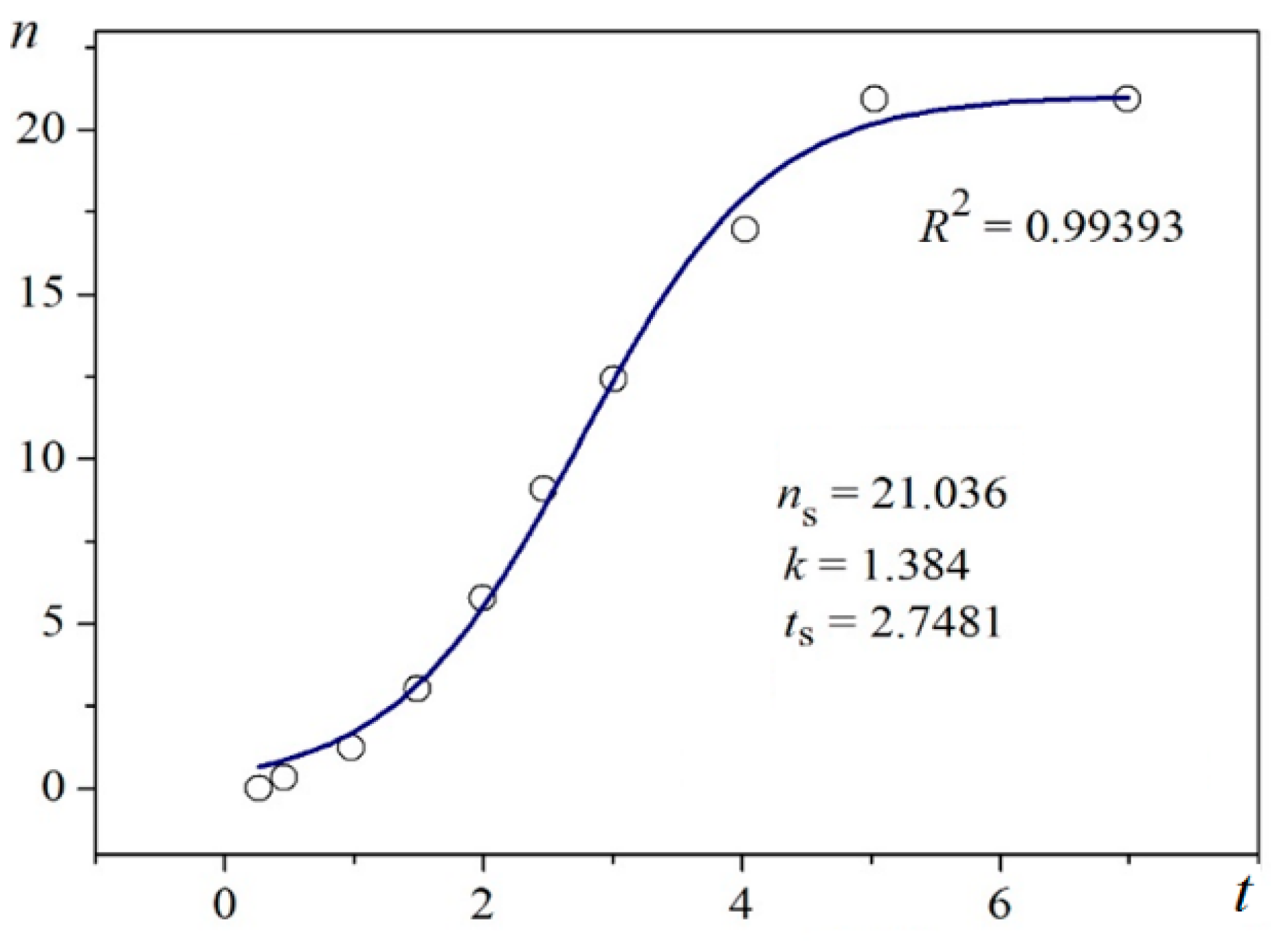
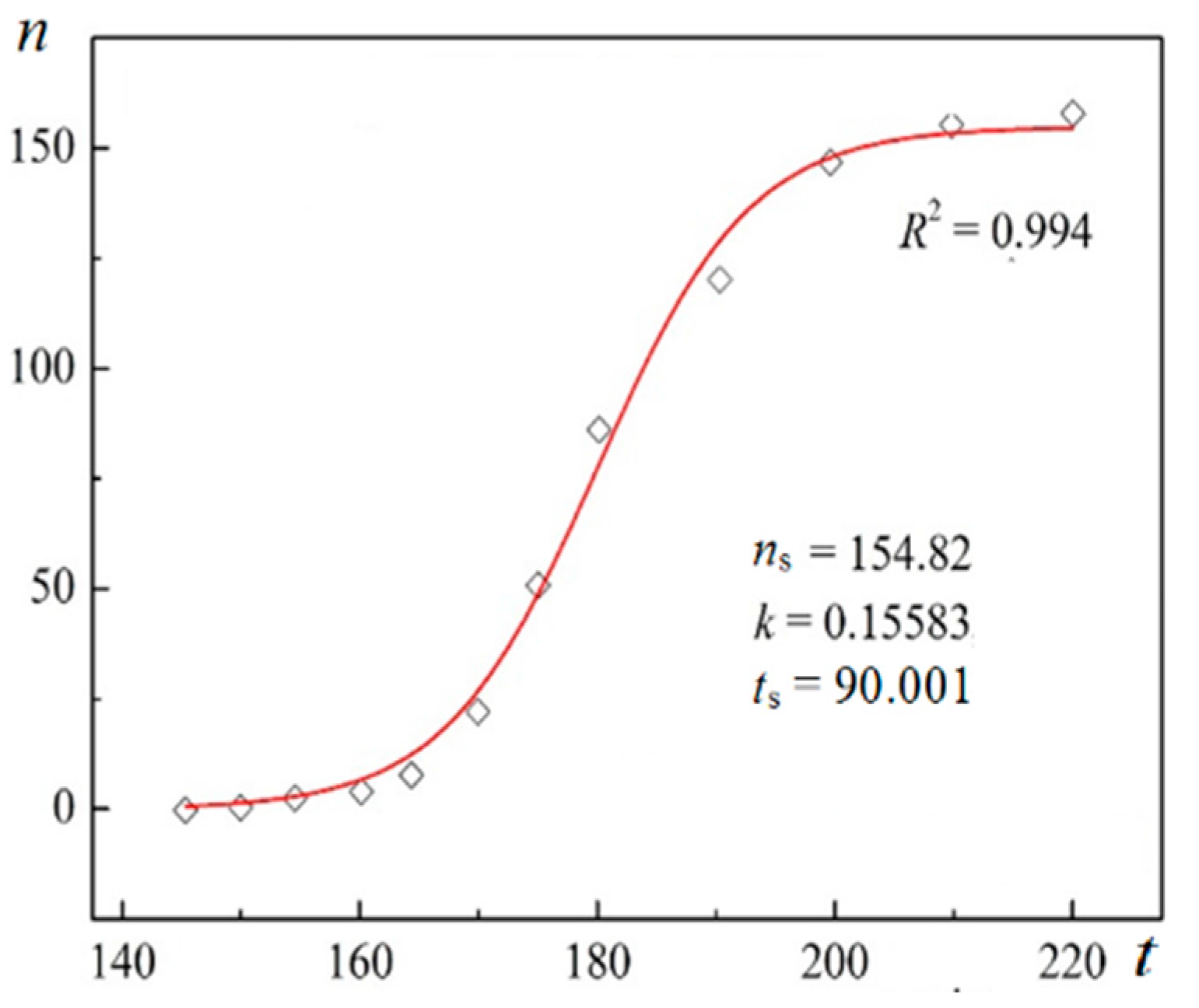
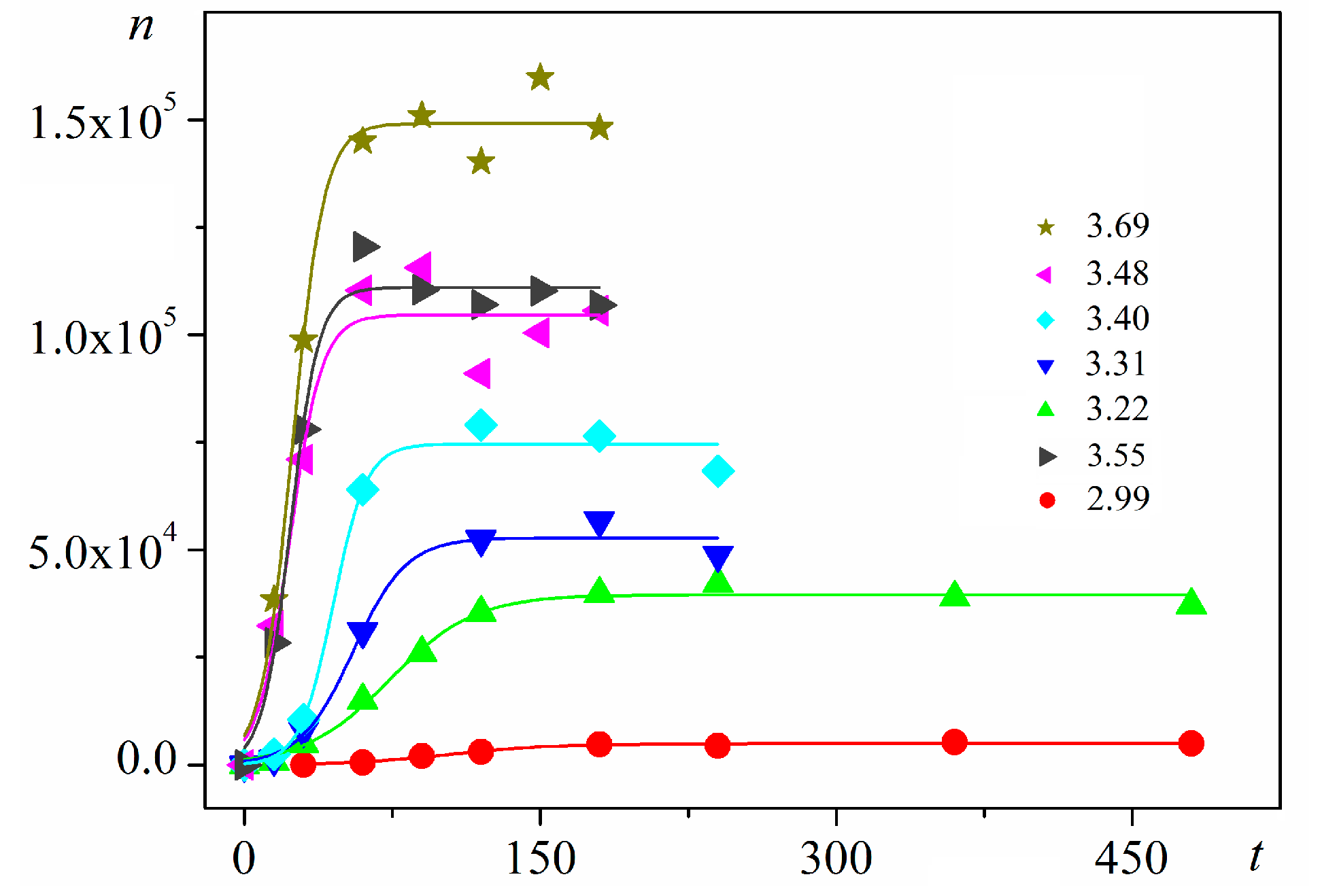
Using digitalized original experimental data from [
14,
18], logistic dependences (with very high goodness of fit,
R2) are presented in
Figure 1 and
Figure 2. Such time dependence has also been established for bovine β-lactoglobulin crystal nucleation which proceeds by a TSNM [
6]. Good logistic fits of insulin crystal nucleation data for seven different supersaturations are shown in
Figure 3, where appropriate (supersaturation dependent) parameters are used. The relations, showing the degrees to which saturated crystal-nuclei number densities (
ns) are neared, (
n/
ns), are plotted vs.
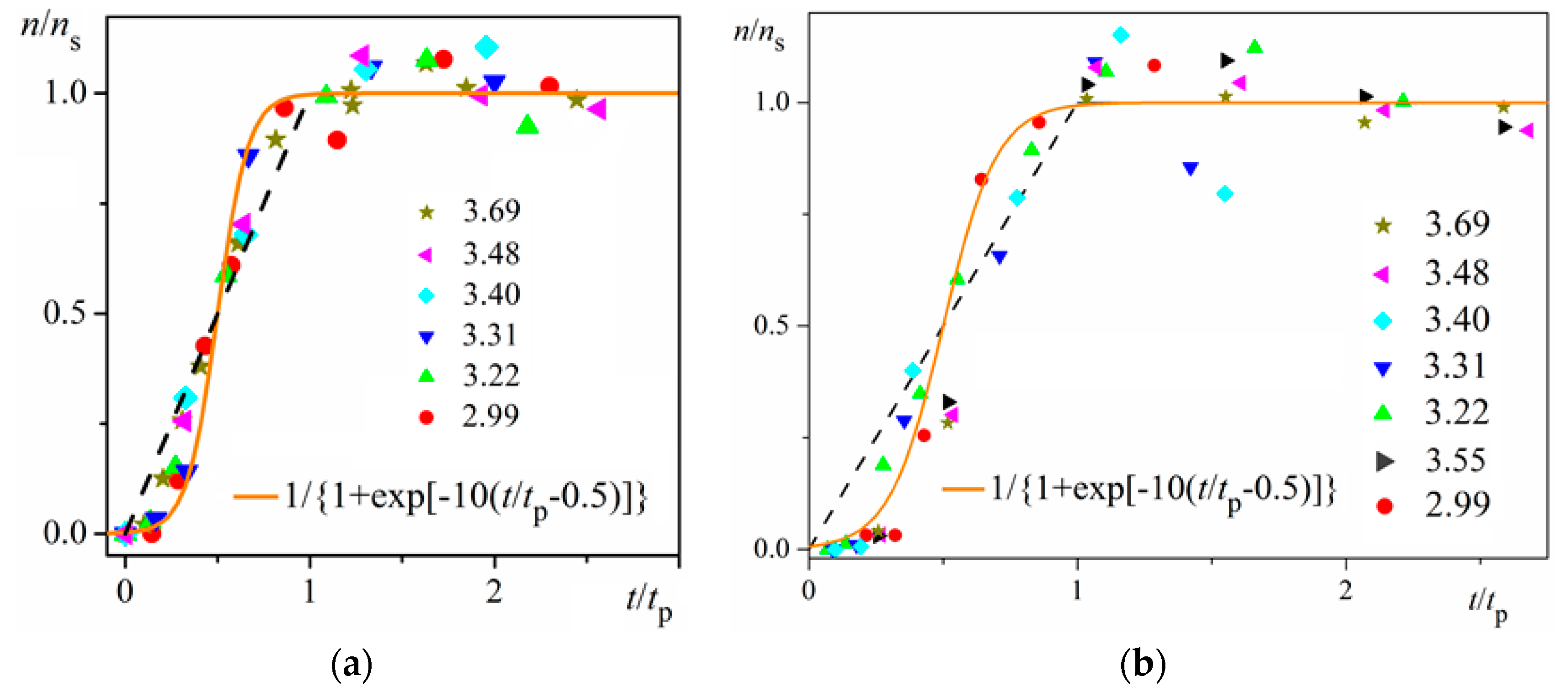
t/
tp (using Equation (2); here
tp is the time for reaching
ns;
tp = 2
tc, and
tc is the time when the half of
ns is reached (namely the mid-point of the corresponding sinusoid). Plots in
Figure 4a are for bulk insulin crystal nucleation, and in
Figure 4b—for on-glass crystal nucleation. This issue will be considered below.
In conclusion, being common for both small inorganic molecules and large bio-molecules, the S-shaped dependences of nuclei number densities on time underline a common physical aspect of the nucleation processes.
2.2. Logistic Time Dependence of Protein and Small Molecule Crystal Nucleation
The fluctuation-based concept of CNT supposes that a new distribution of larger clusters starts replacing the equilibrium one immediately after establishing supersaturation in the system. Since the larger the cluster is, the longer it takes for it to emerge, the critically sized cluster should appear the latest. Importantly, the nucleus is the cluster of maximum energy and minimum concentration. Therefore, many subcritical clusters, smaller than the critical nucleus by a single molecule only, are formed in the meantime. However, the rearrangement of cluster size distribution does not end with the emergence of the very first critical cluster. Accommodation of the supersaturated system state continues gradually, leading to an enhanced supply of nuclei. Thus, the nucleation rate increases throughout the initial non-steady-state nucleation period.
As per definition, the momentary nucleation rate (dn/dt) during the initial non-steady-state nucleation period, i.e., the rate at any point of the n vs. t graph, is given by the number (n) of nuclei formed in a unit volume (1 cm3) divided by the (infinitesimally short) nucleation time (t). Denoting the frequency of molecule attachments leading to formation of nuclei by k (s−1), gives dn/dt = kn. Here, the attachment frequency k is defined as the frequency of molecule attachments to clusters which are smaller than the critical nucleus by a single molecule, minus the frequency of molecule detachments.
The attachment frequency
k depends on supersaturation, which, however, remains constant during the whole nucleation process. The reason is that the extremely small nucleus volume (typically about 10
−19 cm
3) and nucleation per se does not change the overall supersaturation—even during the most intensive nucleation (e.g.,
n approaching 10
6 cm
−3). Thus, beginning with a single nucleus, the nucleation process advances in an exponential manner with time. Nonetheless, no unlimited nuclei augmentation is physically feasible. Experimental results show that after a rapid initial increase, the nucleation process gradually decelerates to an almost constant nucleation rate up to reaching saturated nuclei number densities (
ns) in the plateau regions of the
n vs.
t dependences (
Figure 3). Nucleation rate changes have been attributed [
16] to two retardation factors acting simultaneously for heterogeneous nucleation (different for homogeneous nucleation).
A basic assumption of CNT is the supposition of continuous cluster size changes, which is a good approximation to reality only for large critical clusters. The consideration presented here does not suffer from such a limitation—irrespective of the mechanism involved, either CNT or TSNM, it is capable of accounting for discrete cluster size changes as well.
2.2.1. Heterogeneous Nucleation
During solution crystallization, heterogeneous nucleation is the pervasive process. It is the energy barrier that makes it the preferred nucleation process—heterogeneous nucleation energy barrier is only a fraction of the energy barrier of homogenous nucleation. Two nucleation retardation factors acting simultaneously during heterogeneous nucleation have been anticipated in [
16]: (1) occupation of nucleation-active particles and/or centers (generally known as nucleants), associated with the nucleation process itself; and (2) appearance of nucleation exclusion zones (NEZ) formed around growing nuclei. NEZ gradually engulf some of the active nucleants, such that are situated close enough to the formed nuclei, lie in the arising NEZ and are deactivated. This process starts soon after nucleation onset. However, as seen, NEZ do not change the overall system supersaturation.
Accounting for the two retardation factors acting in parallel, and under constant supersaturation, the rate of new-phase heterogeneous nucleation (d
n/d
t) is expressed by the following single first-order non-linear ordinary differential equation [
16]:
Depending on the
k-values, nucleation processes can be categorized into the following groups: (1) fast kinetics, e.g., electrochemical nucleation, characterized by very large
k-values (of orders 10
3 to 10
4 (s
−1)); (2) slow kinetics, e.g., protein crystal nucleation (insulin, bovine β-lactoglobulin),
k-values of order 10
−3 to 10
−4 (s
−1); and (3) extremely slow kinetics, e.g., crystallization of cordierite glass,
k ≈ 10
−5 (s
−1); see in [
16].
Integration of Equation (1) gives [
16]:
In fact, Equation (1) is a special case of Bernoulli differential equation. Substituting the dimensionless functions
y(x) =
n/
ns and x =
k(
t −
tc) in it, and with
tc = const. we have:
The solution of Equation (3) is the standard logistic function:
With constant of integration C = 1 {\displaystyle C = 1} C = 1, this gives the logistic curve definition: y(x) = exp (x)/[exp (x) + 1] = 1/[1 + exp (−x)], which is Equation (2).
Equation (1) shows that the maximum nucleation rate is reached when nucleation acceleration and deceleration tendencies equilibrate, at time
tc, when
n =
ns/2:
which is the (quasi-)stationary nucleation rate, mentioned above.
Unambiguity of the Logistic Nucleation Time-Dependence
Figure 1 and
Figure 2 exemplify the high goodness (R
2 > 0.99) of logistic plots. Considered from a physical perspective (as presented above), the good fit of experimental
n/
ns vs.
t/
tc data for insulin crystal nucleation (
Figure 4a,b) shows more stringently the logistic nucleation time-dependence. Firstly, recalling that
n =
ns when
t = 2
tc, x =
k (
t −
tc) results in x
ns =
ktc = const., this explains the self-adjustment between
k and
tc occurring for all supersaturations. Secondly, the (orange) logistic curves in
Figure 4a,b result from the logistic equation with 2
ktc = 10 (see the inserts in the figures). Hence, these are standard logistic functional plots with ±
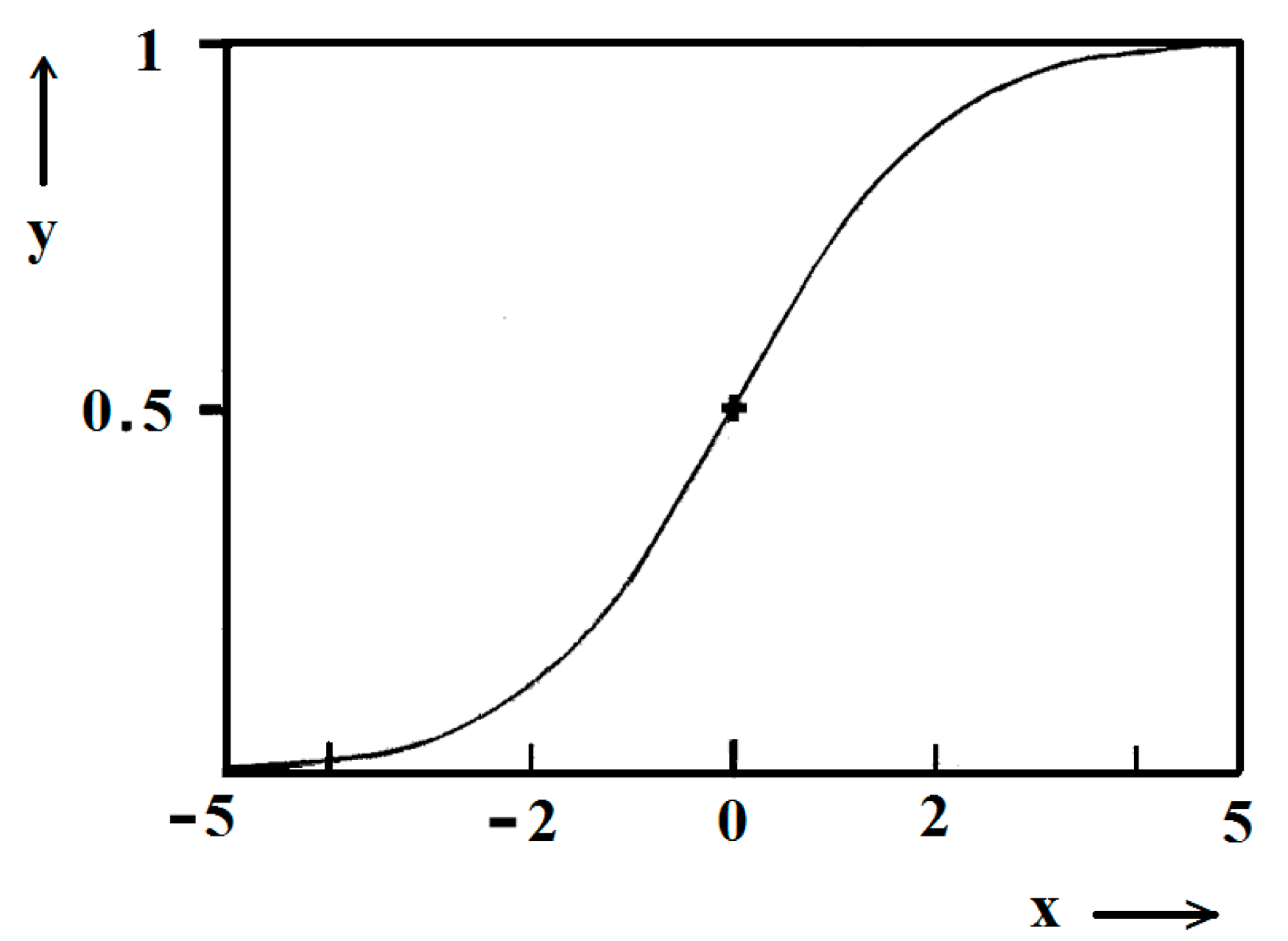
ktc = 5. Due to the function exponential nature, the standard logistic function obtains its real values in the range of x = ± 5 on both sides of its midpoint (
Figure 5); in the case under consideration, the latter being at
ns/2. It is logical to conclude that an x-value from −6 to −5 can be attributed to the so-called nucleation induction time.
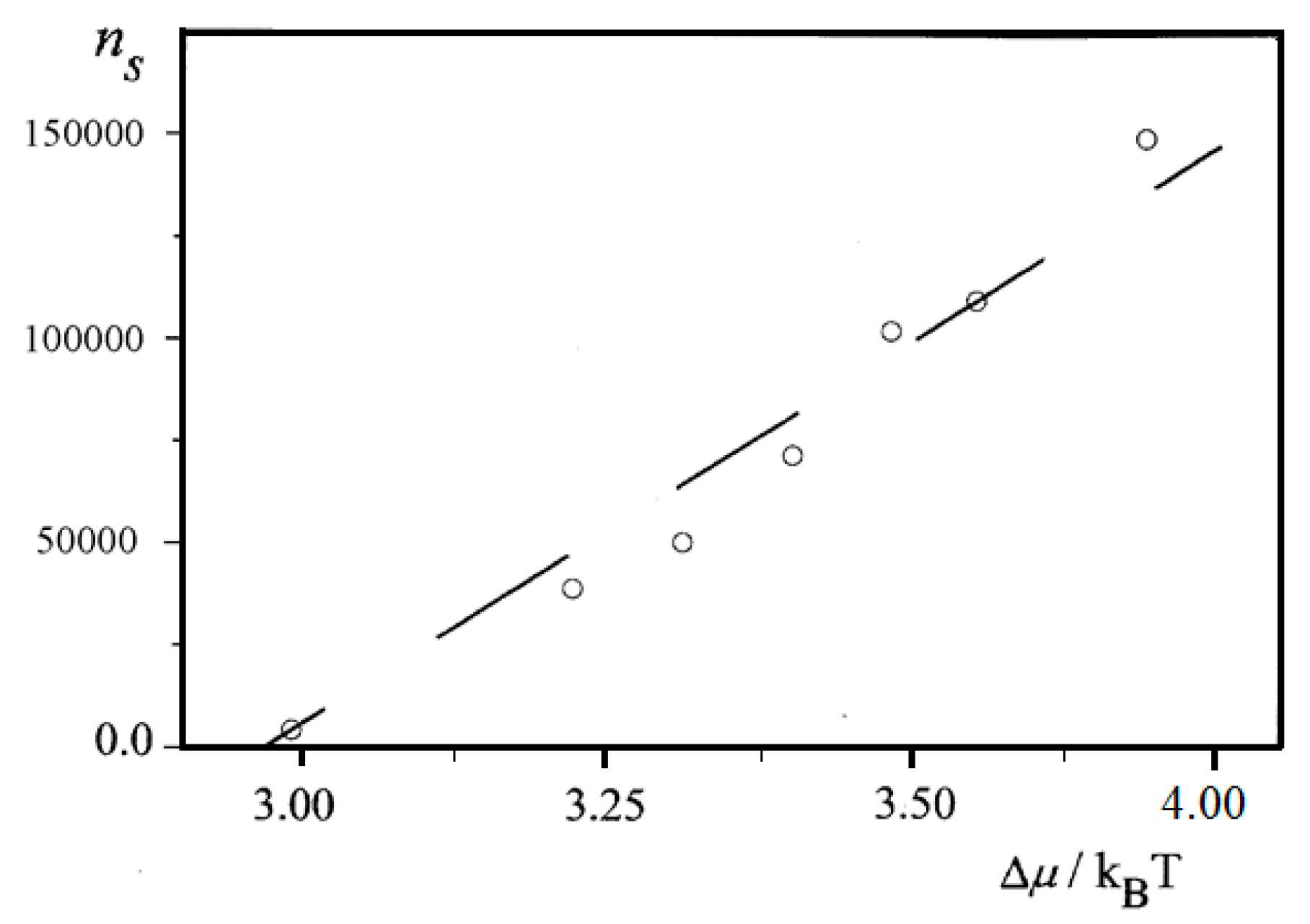
Further, an almost linear increase of
ns on Δ
μ is observed for insulin (BioChemika, ≥85% (GE), ~24 IU/mg) crystal nucleation in bulk solution,
Figure 6. However, it is highly improbable that sets of nucleants possessing nucleation-promoting abilities which correspond exactly to each supersaturation used are present. It is rather a situation where lesser nucleants are engulfed by NEZ (and thus, deactivated) at higher supersaturations.
2.2.2. Rate of Homogeneous Nucleation
Notwithstanding the substantially higher supersaturation required, homogeneous nucleation is indispensable in systems without nucleants. Removal of all nucleants from a protein solution is not an easy task, albeit achievable in the vapor phase. For instance, liquid droplets nucleate homogeneously by rapidly expanding and cooling exceptionally pure water vapors. An exponential increase in water droplet nucleation rate has been measured by means of different techniques [
19]. However, homogeneous nucleation could also pose an issue because no unlimited nuclei augmentation is physically feasible. An evident obstacle for observing nucleation rate limits may be the uncountable number of the nucleated droplets. Additional experimental work is needed to compare nucleation rate measurement data to theoretical considerations. Until then, a theoretical approach to the issue is worth attempting.
Like the heterogeneous case, homogeneous nucleation should be a self-limiting process. Again, there are two factors decelerating it. The first one is like the one in heterogeneous nucleation, namely, increase in the number of NEZ appearing around some nuclei and diminishing the volume where nucleation can still occur. The second decelerating factor, namely, a drop in system’s overall supersaturation, is different. It is enacted only during prolonged nuclei growth and consumption of a noticeable molecule amount. Furthermore, while the two retardation factors act in parallel in a heterogeneous nucleation, in a homogeneous process they act consecutively, being interrupted by an intermediate period. This constitutes the substantial difference between both processes.
Effect of NEZ
As already mentioned (see
Section 2.2), the overall supersaturation remains constant initially. Thus, the probability (
n/α) for NEZ appearance, where α (s) is the time needed for the formation of the very first NEZ, also remains constant. The initial nucleation rate (d
n/d
t)
init can be expressed as:
where
K (s
−1) ≠
k and
K’ =
K − 1/α are new coefficients.
Preserving the exponential character during the initial nucleation stage, the graphical n vs. t track of the homogeneous nucleation is indistinguishable from the corresponding part of the heterogeneous nucleation curve. However, knowing that merely one decelerating factor is acting, the homogeneous n vs. t dependence should be steeper and relatively longer.
Effect of Decreasing Supersaturation
Increasing in number, soon or latter, the NEZ start overlapping. This indicates that the first nucleation decelerating factor is of no importance on the account of the second one—decrease in system’s overall supersaturation. Intermediately, new nuclei appear in the remaining interstitials between NEZ, but there is a substantial deceleration in the exponential increase of
n. When Δ
μ decreases bellow the nucleation-limiting threshold,
n vs.
t dependence should reach a plateau, corresponding to a zero nucleation rate. Supersaturation dependence of nucleation rate is given by the well-known equation of Volmer. For the second homogeneous nucleation stage, it should be written as:
where A is a pre-exponential coefficient which denotes the number of nuclei that appear in a unit volume (1 cm
3) per unit time (1 s); Δ
G* is the thermodynamic energy barrier for nucleus formation; the constant B for homogeneously formed spherical nucleus is B = 16π
Ω2γ3/3 (because Δ
G* = 16π
Ω2γ3/3Δ
μ2); and
Ω is the volume of a crystal building block. Qualitatively, this behavior of the system gives a S-shaped dependence of
n on time elapsed,
t. However, despite the different scenarios involved in heterogeneous and homogeneous nucleation, the exponential functions make their S-shaped time dependent nuclei number densities indistinguishable.
Equation (7) shows that a symmetric S-shape (logistic) curve may describe the homogeneous nucleation, only provided Δ
μ depends linearly on
t, i.e., Δ
μ = −s
t, where −s is the line slope. Under constant temperature, however, supersaturation decrease results from nuclei growth itself, making the linear dependence physically infeasible. Since the new-phase particles nucleate at different time-points, they grow in different sizes and the size difference is amplified due to the Gibbs-Thomson effect [
20]—smaller crystals grow slower than larger crystals; the reason being that the larger the crystal, the lower the saturation with which it stands in equilibrium. That is why, along with an increase in number, nucleated crystals accelerate their growth with the time and increase the rate of supersaturation depletion. In view of the extremely high sensitivity of (d
n/d
t)
second on Δ
μ-value expressed by Equation (7), only the precise function of Δ
μ on
t (but not its linear substitute) is meaningful. Thus, in contrast to the symmetric S-shaped (logistic) curve describing heterogeneous nucleation, a non-symmetric S-shaped curve should describe the
n vs.
t dependence for homogeneous nucleation.
2.3. Biochemical Specificity of the Protein Crystal Nucleation
In proteins, it is only the molecule surface structure that dictates protein ability to bind to partners. This is attributed to the molecular interactions in protein bulk concealed under amino acid residues situated on the molecular surface. Because of millions of years of natural selection, physiological protein-protein bonds are highly specific. Proteins operate within the cellular context with typical concentrations of up to 300 mg/mL. Therefore, any non-specific inter-protein interaction may be fatal. It is known that physiological protein-protein bonds result from strong hydrophobic interactions via which contacting areas occupy relatively large portions on the protein molecule surface.
In contrast, the protein crystal lattice contacts are hydrophilic, polar and smaller in size [
21]. Yet again, it is only the molecular surface structure that dictates proteins’ ability to bind to partners in a crystallization setting. In such a setting, a limited number of discrete patches, that are the only attractive molecule portions, appear on the protein surface. If supersaturation is extremely high, amorphous precipitation will occur even under crystallization conditions; such a disordered aggregation is a result of very strong hydrophobic protein-protein interactions. Therefore, it is logical to assume that attraction strength between crystallizing protein molecules should be fine-tuned. Attraction should be large enough to promote crystallization, while not being too large to provoke amorphous precipitation. This means that also protein crystal lattice contacts are formed by a selection of the most appropriate patches on the protein molecule surface. Selection preferences have been revealed using X-ray diffraction data for protein crystal lattice contacts available in Protein Data Bank [
21,
22].
Strict selection of crystal lattice contacting patches is also evidenced by relatively simple experiments [
23]. Periodically alternated layer-by-layer crystal overgrowth has been observed with the unique protein couple apo- and holoferritin. Despite the dramatically different core, their surface structure is identical. Uniform in thickness overlaying crystal layers have been deposited using equimolar protein concentrations under the same solution conditions, рН-value, CdSO
4, and buffer concentrations. Since no reentrant corners have been observed (
Figure 7), those crystals should be single-crystals composed of alternating apo- and holoferritin layers, rather than poly-crystals. Crystals of each protein are used as substrates for a sequential in contiguity crystallization of the counterpart protein in a completely repeatable process. A monocrystalline overgrowth of three to four alternating layers apo- on holoferritin, and vice versa, was achieved [
23]. A clear distinction is allowed as the layers are of different color (apoferritin crystals are yellowish; holoferritin crystals—reddish-brown).
In contrast, no homoepitaxial monocrystalline overgrowth is possible with proteins possessing differing molecule surfaces. Apoferritin crystals have been purposefully introduced in solutions designed for lysozyme crystallization. No single-crystalline overgrowth, but merely formation of poly-crystalline lysozyme-apoferritin aggregates, has been observed [
23]. This shows that a molecule attachment to the protein crystal lattice does not occur at random. It requires selection of the binding partner. It is worth noting that no binding selection is needed for small-molecule crystallization, e.g., by electrodeposition of metal alloys.
Selection of protein-protein patchy interactions has been accounted for by the so-called bond selection mechanism (BSM) [
24]. It assumes that a successful collision between protein molecules, leading to formation of a crystalline connection, requires not only sufficiently close proximity of the protein molecules (respectively molecules to clusters), but also their proper spatial orientation. Because relatively small fractions of molecule surface are occupied by contacting patches, the arising steric restriction to protein-protein association postpones the nucleation process significantly. Thus, based on the biochemical specificity of proteins, BSM explains the slow protein crystal nucleation kinetics [
25]. Although requiring unusually high supersaturation, it is orders of magnitude slower in comparison to the process with small molecule substances, e.g., during electrochemical nucleation [
13,
14]. Recalling that crystal nucleation rate changes with process stages, one can only compare the (quasi)-stationary nucleation rates expressed by Equation (5). As seen in
Section 2.2.1,
k-values determining nucleation frequency are 6 to 8 orders of magnitude lower for protein crystallization than
k-values for small molecule new-phase nucleation, e.g., electrochemical nucleation (also proceeding in solutions). So, due to BSM, a much lower attachment frequency (
νR*) of molecules to the critical cluster must be in place in the pre-exponential coefficient of Volmer’s equation:
where
c1 is solute concentration, and
Z is known as Zeldovich factor.