Building Trust—One Gift at a Time
Abstract
: This paper reports an experiment evaluating the effect of gift giving on building trust. We have nested our explorations in the standard version of the investment game. Our gift treatment includes a dictator stage in which the trustee decides whether to give a gift to the trustor before both of them proceed to play the investment game. We observe that in such case the majority of trustees offer their endowment to trustors. Consequently, receiving a gift significantly increases the amounts sent by trustors when controlling for the differences in payoffs created by it. Trustees are, however, not better off by giving a gift as the increase in the amount sent by trustors is not large enough to offset the trustees' loss associated with the cost of giving a gift.1. Introduction
The majority, if not all, economic interactions rely on trust [1] and thus, engaging in trusting behavior provides a socially desirable outcome since it (often) improves economic efficiency [2–4] and well being [5–10]. However, there exist individuals without a preference for fair outcomes who betray this trust by appropriating the majority or the entire created surplus. If the proportion of such people in the population is high, trusting everyone might not be optimal. Given this, mechanisms to foster trust and trustworthiness may play a crucial role in establishing relationships and allowing transactions to occur. Negotiations literature suggests that one way to create trust is to make concessions (e.g., [11]) or gestures before the transaction takes place. This advice is also commonly presented in the popular press [12].
Previous experimental literature sheds some light on the reasons why concessions might be so crucial. In a nice experiment [13] find that cooperation is best achieved when the parties first cooperate in a small-stakes, low-temptation environment and then slowly evolve through a series of successful interactions into a large-stakes partnership. Based on [13] insight, concessions could be viewed as giving a gift prior to the transaction and thus creating goodwill or a reputation for being kind that influences the behavior of the other party [14–19].
A similar argument has been previously made in [20,21] with respect to generosity. Both anecdotal and scientific evidence shows that people care about the well-being of others and often are willing to sacrifice a significant amount of resources to promote fair outcomes, reward kind actions with kindness and punish deliberately hostile actions [22–31]. Therefore, it is likely that a trustee's gift might influence trustor's perception of the trustee and subsequently increase his trust. To explore this issue further we evaluate the effect of gift giving on trust in a stylized setting of the investment game [32]. We build on our previous research presented in [33] that compares the ability of monetary and non-monetary mechanisms to enhance trusting behavior. This earlier study provides evidence that a gift does have the potential to increase trust. While certain aspects of gift giving have previously been explored in the context of dictator and gift-exchange games (see [26,28,34] for excellent surveys), the novelty of our setup is that here the gift preceeds the actual transaction and acts as a catalyst.
The importance of gift exchange has been addressed in various areas of economics, such as labor relations (e.g., [35,36]), customer relations [24], bargaining [37], and price setting [38]. [34,39] provide a thorough account of the laboratory experiments on gift-exchange in labor markets. The relatively robust laboratory results that the higher the gift the stronger the reciprocal response have also been tested in the field [40–42]. While [43] and [44] provide additional evidence for the importance of gift exchange respectively in a charitable donation setting and a tree-planting firm, [45] find that positive reciprocity effects detected in lab experiments can wear off quickly in a door-to-door fundraising task or in library data entry. On the other hand, also in a library data entry task, [46] observe a strong effect of giving a physical gift (a thermos) to worker subjects on their productivity, but no effect of an equivalent value cash gift.
In our experiment a gift is a binary decision of a trustee who can send either nothing or all of his $10 endowment to the trustor in a dictator game stage prior to playing the investment game. If a gift is given, then in the case of zero return on investment, the trustor is at least as well off as if no transaction ever took place. Notice also that if a gift is given, the trustor's intermediate endowment increases by the amount of the gift. Since a prior gain has been shown to increase risk seeking [47], it is possible that subjects will respond to this change in their endowment as well, especially if they consider the return on investment as uncertain due to the unknown reaction of the other player. Therefore, if one observes more investment following a gift than in the baseline investment game, it could be because the trustor has more money (endowment effect) or because this behavior was directly triggered by the gift (gift effect). In this companion paper we make use of the Baseline and Gift treatment data that were previously presented in [33] and add a third treatment, called Endowment Control, which allows us to experimentally identify these two effects. We conclude that the increase in investment observed in [33] is caused by the gift effect and not the endowment effect.
A gift in our experiment is very stylized. However, historically gifts were also used to signal intent between two parties attempting to form a transaction [48,49] and thus served as building stones of relationships by strengthening trust [50–56]. This leads to an important question: What is trust? A somewhat general but intuitive definition can be found in [57] who states that trust is the expectation of the trustor that the decision process of the trustee will be guided by certain rules or norms in order to reach fair outcomes (see also [58] for a discussion of repeated interaction and partner selection). From this perspective, a gift increases the trustor's belief that the trustee will play by some rules or norms to allow for mutual, fair gains from the interaction. However, in order to operationalize gifts and observe their impact on trust, throughout this paper we adopt the view presented in [59] according to which:
[A trusting action is] an action that generates a monetary gain which could be shared with another agent and exposes the trustor to the risk of a loss of utility if the other agent defects and appropriates too much or all of the monetary gain.
A similar definition can also be found in [60]. [61–63] define trust in a similar spirit explaining that an individual is trusting if he is willing to be vulnerable based on an expectation of cooperation. As pointed out in a meta-analysis of experimental trust games by [64]:
[T]he social capital literature is concerned more broadly with aggregate societal resources linked to networks of relations [65]. These networks are generally associated with members' willingness to engage in activities that are not strictly self-interested, though the exact nature of this other-regarding behavior is left somewhat vague.
Although the gift mechanism, as implemented in our experiment, does not make the interaction between a trustor and a trustee repeated per se, it adds an extra stage to the game. This aspect relates our experiment to the recent experimental findings that relationships evolve gradually and cooperation grows with each previous success. The aforementioned [13] consider twice repeated prisoner's dilemma game in which they varied the distribution of payoffs between the two rounds. They find that total benefits from cooperation are highest when the payoffs are lower in the first than in the second round. A similar idea has also been studied by [66]. Their subjects play 10 rounds of the investment game with a fixed partner. The authors find that the rates of cooperation are higher in the repeated interaction condition than in the baseline one-shot condition [67].
Our study differs in the following respect. While the previous papers focus on repeated interactions and explore what kind of repeated interaction can lead to a trusting relationship, we are interested in a much different (and simpler) situation in which the trustee can make a gesture by sending a gift prior to a one-shot game. Notice that it is very difficult to make a similar gesture in the repeated interaction framework considered by [66] because the action of the trustee always follows that of the trustor. It is therefore hard to disentangle whether the amount returned by the trustee indicates intentions for the future or whether it is a response to the amount sent by the trustor. In other words, is it a “promise” to cooperate tomorrow and/or is it a “thank you” for being nice to me today. Our design disallows the latter and enables us to focus on the effect of the former due to the nature of one-shot interaction. In addition, the relative simplicity of our design allows us to pin down the motivation behind the trustor's behavior.
In another related experiment [68] examines satisfaction guaranteed, a potentially costly mechanism, that explicitly promises to refund the price to the buyer. In reality, not honoring satisfaction guarantee can have legal consequences for sellers, but suing over a small transaction can be too costly, and thus this trust building contract device can be seen as nonbinding for some sellers. In his experimental design, [68] combines the investment game with the ultimatum game [20], thus giving the trustor an option to annul the transaction if he is not satisfied with the outcome. If satisfaction guaranteed is voluntary and non-binding, the trust of buyers is greatly reduced compared to when it is binding. The decrease in trust is well justified as only 17% of sellers chose to honor the guarantees. The main difference between our study and [68] (other than a gift and satisfaction guaranteed not being strategically equivalent) is the fact that a gift is given before the transaction takes place, and hence there is no way to reverse the gift if the trustee defects whereas in satisfaction guaranteed sellers can renege if a refund is requested.
Transactions can often be supported using commitment devices [69,70]. [71] study a simple precommitment mechanism in the context of an investment game. Similarly to our experiment, they also add a pre-game stage during which the trustee has an opportunity to place some amount of money into an escrow account. The entire sum from the escrow account is returned to him if the trustor does not invest any money or if the trustor invests and the trustee splits the surplus. However, if the trustor invests and trustee appropriates the surplus, the entire escrow amount gets forfeited, but the trustor does not receive anything. [71] find that the efficiency of the mechanism depends on the amount that is deposited into an escrow account, but not so much on whether it is chosen voluntarily or imposed by the experimenter.
The common feature of satisfaction guaranteed and escrow account is that they both reduce the need for trust by enforcing a certain degree of cooperation. Thus, the punishment mechanism drives the behavior of trustors and trustees as the investment can be recouped and escrow forfeited. However, enforceable satisfaction guaranteed and escrow accounts are not always available to the transacting parties. Therefore, it is important to understand how much we can accomplish by widely available monetary mechanisms that do not rely on enforceability. Finally, this lack of enforceability connects our study to the previous research on costless mechanisms fostering trust and cooperation, such as communication (e.g., [72–77]) or the ability to observe past behavior [19,78].
2. The Experiment
2.1. Experimental Design
Our experiment consists of three treatments (Baseline, Gift, and Endowment Control) implemented in an across subjects design. Baseline is the standard investment game by [32]. There are two players, A and B, each endowed with $10 at the beginning of the game. The first mover, player A, decides on ‘an investment’—a whole dollar amount s∈ {0, 1, 2, …, 10} to be sent to his counterpart player B. The amount sent is tripled by the experimenter. The second mover, player B, then decides how much of the tripled amount, r∈ {0, …, 3s} to return to player A [79–90].
Gift involves the investment game as described in Baseline preceded by a dictator game stage during which player B has a binary decision of whether to transfer his entire $10 endowment to player A or not. In the investment game that follows, player A is still constrained to sending a maximum of $10 even if player B decided to transfer his endowment to player A.
Endowment Control treatment is analogous to Baseline and differs only in the endowment given to both players: Player A starts the game with $20 and player B with $0. This treatment is necessary to identify the endowment effect in subjects' behavior. In particular, giving a gift changes the players' payoffs from ($10, $10) to ($20, $0). It is therefore possible, that any changes in amounts sent by player As and returned by player Bs between Gift and Baseline treatments are due to changes in endowments rather than due to the pure effect of giving a gift [91,92].
2.2. Behavior
Our experiment was not designed to separate between behavioral theories. Instead, it focuses on studying the gift mechanism itself. However, it is certainly worthwhile to discuss the role of gift-giving in inducing trust in the context of some of the established behavioral models. Our discussion does not provide a comprehensive overview as we focus on a few select theories that we find most relevant. For the ease of exposition we keep the discussion informal.
The distributional models of inequity aversion, [80,81] predict a positive relationship between gift and trust in our design. By giving a gift to player A, player B ensures that the distribution of payoffs is (strongly) unequal, i.e., ($20, $0) instead of ($10, $10). Player B can therefore nudge an inequity-averse player A towards sending a positive amount to reduce this inequality of payoffs.
The gift may also signal intentions. Amongst intention-based theories two have received substantial attention in the literature: guilt aversion [88,89] and sequential reciprocity [84,85]. The theory of guilt aversion allows for (psychological) forward induction, which is particularly appealing in our context. In the framework of [89] a gift could be viewed as a costly signal of player B′s expectations [93]. In particular, according to psychological forward induction, a gift can signal, rather than reveal, a higher expectation of an investment after it was given. Whether this happens or not depends on the structure of the belief system between players. It could be that following a gift, a moderate initial belief is updated upward. If player As have a tendency to meet such expectations (e.g., they are motivated by guilt-aversion as in [88]), then a gift would have effectively increased player A′s trust towards player B.
The theory of sequential reciprocity can lead to various conclusions. It is well known that even in a simple gift-exchange type of environment it does not give clear-cut predictions. Depending on the belief structure, player A′s investment can be viewed as kind and will be reciprocated by player B; or it can be viewed as opportunistic in the sense that player A is trying to induce player B to reciprocate. Due to this property one might obtain either positive or negative reciprocity equilibrium. An inclusion of a pre-game stage where player B has an opportunity to transfer his endowment to player A does not remove the ambiguity of intentions. In fact, it is rather unlikely that a gift would reinforce trust in the reciprocity equilibrium (e.g., see the argument in [72]).
Finally, there are also some alternative Bayesian approaches such as the theory of conformism [94] and the theory of audience-effect [95,96]. Both these theories are based on a signaling argument. In our case, for the gift to enhance trust, it would have to signal that player B has preferences for fairness. Since the gift is costly for player B and increases player A′s balance, it could serve as a signal of pro-social disposition. In the theory of conformism, giving a gift could imply that player B believes that the fraction of fair-minded types in the population is high and thus a gift can convert conformist-types to the like. In the audience-effect theory, giving a gift exposes player B to a threat of losing money if player A happens to be self-regarding. Thus, by giving a gift, player B is asking for a fair division and deriving an extra utility from his action being publicly observable.
In summary, most of the reviewed behavioral theories imply a positive relationship between gift and trust. However, the prediction is not unanimous. The theory of sequential reciprocity may generate negative reciprocity equilibria. Similarly, Bayesian approaches, depending on parameterization, may result in pooling equilibria that would neutralize the relationship between gift and trust. In light of this, we do expect a positive impact of a gift on trust but at the same time keep a conservative approach to hypothesis testing by using two-tailed tests.
2.3. Procedures
The experiment consisted of 10 sessions conducted at the University of Canterbury in Christchurch, New Zealand with a total of 206 undergraduate students participating in the study. The subjects who participated in the experiment were selected randomly from a database using Exlab software. At the time of the experiment there were over 1000 undergraduate students in the database. Most of the experiment participants had previously been in economics experiments, but not in an investment-game-like scenario. Each subject only participated in a single session of the study. On average, a session lasted 50 minutes including initial instructional period and payment of subjects. Subjects earned on average 15.66 New Zealand Dollars (NZD) [97]. All sessions were hand run under a single-blind social distance protocol and the minimum number of participating subjects in a session was 12.
The subjects in each session were randomly assigned to be either player A or player B and randomly matched into pairs. The procedures for this allocation were as follows. The room used for the experiment was segmented in half such that the group of desks corresponding to a given type was located on the same half of the room. The desks for each type were arranged in rows facing opposite walls such that subjects of opposing types could not see each other while making decisions during the experiment. At the beginning of each session, subjects were free to choose any desk upon entering the room. The allocation of types to the two different groups of subjects was done by publicly flipping a coin. The experimenter then randomly assigned a member from each group to create individual and anonymous player A and B pairings.
All instructions were projected on an overhead screen and read aloud. Subjects were encouraged to privately ask any questions they may have throughout the experiment. In the Gift treatment, the investment game and general procedures were explained first. Only then did the experimenters announce that before the described game is played, player B has an opportunity to send their endowment to their counterpart player A. Upon completion of the instructional phase for this dictator game stage, players B made their decisions of whether to transfer their endowment or not to their counterpart on provided decision sheets, which were afterwards collected by the experimenters. The decision of player Bs' was written by the experimenter on their counterpart player As' investment game decision sheet in the following form:
Player B has transferred $____ to you before the start of the game. This amount is yours to keep and will be added to your earnings.
Given this information, player As were asked to answer a question of why they believed that their counterpart player B transferred or did not transfer their endowment to them [98]. It was made clear to subjects that their answer to this question would be private information and not shared with their counterparts. This completed the dictator game phase of the Gift treatment.
The following investment game procedures were the same for all three treatments. Player As wrote on their private decision sheet of how much money they wanted to transfer to their counterpart player B. Player As' decision sheets were collected, the amount transferred was tripled by the experimenter and written on their counterpart player B′s decision sheet, and then all decision sheets were returned to the subjects. Now knowing how much their counterpart transferred to them, player Bs decided how much of that tripled amount they wanted to transfer back to their counterpart player A and how much to keep for themselves. The experimenters then collected all decision sheets, copied player Bs' decisions on their counterpart player As' decision sheets, and returned the sheets to all players to reveal their earnings. Lastly, subjects were privately paid their experimental earnings.
3. Results
3.1. Behavior of Player As
Player As are obviously better off in monetary terms when they receive a gift [99]. As reported in [33], player As send more on average in Gift than in the Baseline. However, is the increase in amount sent under Gift due to the gift effect or due to the endowment effect?
The summary statistics from all three treatments, including the number of independent observations, is summarized in the first three columns of Table 1 [100]. Player As sent the lowest average amount of 4.73 in Endowment Control, slightly higher of 5.50 in Baseline, while in Gift the average amount was 6.50 (7.31 if the gift was actually given and 3.75 if not). This difference is even more pronounced when looking at medians. While in Baseline and Endowment Control the median amount sent was equal to 5, it was 9.50 in Gift (10 if the gift was given and 2 if not).
The Wilcoxon rank-sum (WRS) and a more conservative robust rank-order (RRO) two-sided tests presented in Table 2 break up the behavior of player As into an endowment effect and a gift effect. It might be somewhat surprising that player As sent on average less money when they were endowed with $20 than when they were endowed with only $10. This behavior does not support the conjecture presented in the previous literature that subjects are more likely to “gamble” with (more) house money, but rather suggests that player As realize that given the asymmetry in endowments it is rather unlikely that they will benefit financially from sending money to player Bs. The (negative) endowment effect, however, is not statistically significant.
Similarly, no statistically significant difference is detected for the amount sent in Gift versus Endowment Control or for the amount sent in Gift versus Baseline at the treatment level. So just having a chance to receive a gift or having a larger endowment does not change player A′s behavior. Hence we observe no significant changes in efficiency solely based on treatment participation.
Our main question is concerned with what happens if the gift is actually given. The twenty-six out of thirty-four player As who received a gift from player Bs sent on average 7.31 (with the median of 10), whereas the remaining eight who did not receive a gift sent on average only 3.75 (with the median of 2). To separate out the gift effect, the appropriate point of reference is the Endowment Control treatment data. When we control for the endowment differences, receiving a gift is responsible for an increase in the amount sent by player A as reported by WRS and RRO tests (p = 0.043 and 0.055, respectively) presented in row 4 of Table 2.
A combination of the gift effect and the endowment effect (i.e., the comparison of the data when a gift was given with Baseline) is also statistically significant at the 10% level as reported in row 3 of the same table (p = 0.087 and 0.102). Thus, we conclude that receiving a gift caused player As to send higher amounts in our experiment, thereby providing higher efficiency levels. The auxiliary analysis of non-salient responses, presented in [33], sheds some additional light on what is driving player As' behavior. In particular, the player As' interpretations of gifts have been coded into the following six categories: minimizing risk, indicating good will, inducing guilt, implying reciprocity, implying both players being better off and other. Content analysis revealed that most gifts were interpreted as an attempt to establish a reciprocal relationship between the players and that this interpretation had a significant impact on player As' behavior.
3.2. Behavior of Player Bs
In this subsection we analyze whether (i) player Bs are made better off in monetary terms by giving a gift and (ii) how does giving a gift affect the amounts player Bs return back to player As.
Giving a gift is costly to player B as he might be forgoing $10 if player A decides not to send anything. In order to determine whether player Bs are made better off in monetary terms by giving a gift, we compare the payoffs of player Bs who give a gift with those who do not (within treatment comparison) and also with those who participate in Baseline (across treatment comparison). Twenty-six players Bs who gave a gift earned on average $18.35 while those eight who did not made on average $18.50. This difference is not statistically significant according to WRS test (p = 0.525). On the other hand, thirty-three player Bs who participated in Baseline and thus did not have an option to give a gift made on average $21.76. Albeit higher, this amount is not statistically significantly different from payoffs of player Bs who gave a gift according to WRS test (p = 0.639). Nevertheless, when comparing means, the increase in the amounts sent by player As was too low to offset the reduction in player Bs' payoffs due to giving a gift [101].
Next we discuss the effect of gift giving on the amount returned by player B′s. Table 2 presents a summary of player B′s behavior in our experiment. Note that in the investment game the strategy space available to a player B′s depends on the decision of player A. In particular, if player A sends 0, player B has no other option than to return 0. Therefore, to make a better assessment of player B′s behavior we exclude such subject pairs from our analysis. This partly corrects for correlation of choices caused by the experimental design. We then compare the distributions of amount returned by player B′s using Epps-Singleton test (last column in Table 2).
We find that the highest average amount returned is in Baseline (6.44), followed by Gift (4.26) and Endowment Control (4.13). If a gift was given, the average amount returned is 4.23. The Epps-Singleton tests reveal that the differences between the amount returned in Baseline and Endowment Control as well as Endowment Control and Gift when a gift was given are statistically insignificant. However, the amount returned in Baseline is significantly higher than after a gift was given (p = 0.020), suggesting a presence of an entitlement effect [102] after player B′s paid to influence the outcome of the transaction.
4. Discussion
This paper reports an experiment that studies the effectiveness of gift giving in promoting trust (i.e., increasing amount sent and thus efficiency). We have nested our findings in the standard version of the investment game to clearly observe the directional changes. We observe that when controlling for the endowment differences, receiving a gift significantly increases the amount sent by player As in the investment game. However, player Bs are not better off monetarily by giving a gift as the increase in the amount sent is not large enough to offset the loss to player Bs. The data also show that player Bs decrease the amount returned after they have given a gift. Our design adds a step to making the investment game more realistic for a set of important applications and adds an additional facet of potential reciprocal behavior. Moreover, it provides another twist in the discussion of opportunistic and other-regarding behavior in fairness games.
Our findings suggest that giving a gift increases trust. However, an interesting follow up question arises: How does the size of the gift implemented in the experiment interact with the decisions of both players? Our primary goal in the current paper was not to provide an exact recommendation on how to use gifts in order to induce an optimal amount of trust, but rather to illustrate that a gift could be an important step in building a trusting relationship. On the other hand, our data also point out that the player Bs are not being sufficiently compensated to cover the size of the gift. This could be an artifact of our design, e.g., the gift choice being binary and relatively expensive. Previous experimental evidence on bargaining and dictator games [26] suggests that people usually do not give more than the equal split. For our design this implies that, if a gift was given and player A sends the maximum amount of $10, the most he might expect to get in return is $10, since this outcome equalizes monetary payoffs at $20 for each player. However, player A already has $20 and thus sending any positive amount means that he is risking receiving a payoff of less than $20. Under a different parameterization where the potential gains are significantly larger than the gift itself, player As might be more likely to send more which in turn could make player Bs who gave a gift better off [103]. From this perspective one advantage of the current setup is that it provides a conservative test of the gift giving effect. One can expect that it will be amplified under different constellation of parameters or possibly by adding context in which the interaction takes place. As argued above, we have shown that receiving a gift increases the amount sent by player As. There could be numerous possible explanations for this behavior. One of them, reciprocity [84–87], is notably consistent with our data. In particular, when player As receive a gift, they seem to regard it as a kind action and respond positively. On the other hand, when giving a gift is an option and player Bs do not give, the few instances suggest that player As respond negatively by sending a smaller amount. Although it was not the purpose of our experiment to properly test this particular explanation, we believe that it might be interesting to pursue this question in future research.
Finally, recall that in our experiment it was publicly announced that giving a gift was an option and because of that not giving a gift could have had some consequences as well. Therefore, we think that an interesting extension of our design would be to give player Bs an option to send a gift without letting player As know about it. Although there are no surprises in equilibrium, there exists ample evidence that subjects in experiments do not follow Nash equilibrium predictions in games with salient fairness considerations. Therefore, it is possible that receiving a gift in such situation might have different behavioral implications. As before, we leave this line of research for future explorations.
| PANEL A | |||||||
|---|---|---|---|---|---|---|---|
| Data | Mean Amount Sent | Median Amount Sent | Frequency of Sending $10 | Mean Amount Returned | Median Amount Returned | Mean Amount Returned if s > 0 | Median Amount Returned if s > 0 |
| Baseline | 5.50 | 4.88 | 6.44 | 5 | |||
| [4.07] | 5 | 36% | [6.35] | 2 | [6.59] | ||
| {33} | {33} | {25} | |||||
| Gift | 6.50 | 3.38 | 4.26 | 0 | |||
| [4.17] | 9.50 | 50% | [5.09] | 0 | [5.38] | ||
| {34} | {34} | {27} | |||||
| Gift: If Gift Given | 7.31 | 3.58 | 4.23 | 2.5 | |||
| [3.82] | 10 | 58% | [4.50] | 0 | [4.61] | ||
| {26} | {26} | {22} | |||||
| Gift: If Gift Not Given | 3.75 | 2.75 | 4.40 | 0 | |||
| [4.33] | 2 | 25% | [7.00] | 0 | [8.76] | ||
| {8} | {8} | {5} | |||||
| Endowment Control | 4.73 | 2.38 | 4.13 | 2 | |||
| [4.49] | 5 | 35% | [4.27] | 0 | [4.98] | ||
| {26} | {26} | {15} | |||||
| PANEL B | |||||||
| Data | Average Earnings Player As | Average Earnings Player Bs | |||||
| Baseline | $9.33 | $21.76 | |||||
| Gift | $14.56 | $18.38 | |||||
| Gift: If Gift Given | $16.27 | $18.35 | |||||
| Gift: If Gift Not Given | $9.00 | $18.50 | |||||
| Endowment Control | $17.65 | $11. 81 | |||||
Standard deviations in brackets. Number of subjects in braces.
| Data | Effects Tested | Wilcoxon Rank-Sum Test for Amount Sent | Robust Rank-Order Test for Amount Sent | Epps-Singleton Test for Amount Returned a |
|---|---|---|---|---|
| Gift vs. Baseline Gift vs. | - | 0.99 (0.323) | 0.93 (0.353) | 7.60 (0.107) |
| Endowment Control | - | 1.53 (0.127) | 1.42 (0.156) | 3.18 (0.528) |
| Gift Given vs. Baseline | gift effect endowment | 1.71 (0.087) | 1.39 (0.102) | 11.70 (0.020) |
| Gift Given vs. Endowment Control | gift effect | 2.03 (0.043) | 1.92 (0.055) | 2.79 (0.594) |
| Baseline vs. Endowment Control | endowment effect | 0.72 (0.519) | 0.60 (0.549) | 4.68 (0.321) |
The first category is always the one with the higher amount sent. p-values in parentheses. All tests are two-tailed.aTests exclude observations where player A sent 0 to player B.
Acknowledgments
We are grateful to the University of Canterbury, College of Business and Economics for financial support. We thank Bram Cadsby, Jim Cox, Andrea Menclová, Ron Oaxaca, the Guest Editor Dorothea Herreiner and three anonymous referees for helpful comments and suggestions. Radovan Vadovič would like to thank the Asociación Méxicana de Cultura for financial support.
Appendix I. Individual Subjects' Behavior Figures
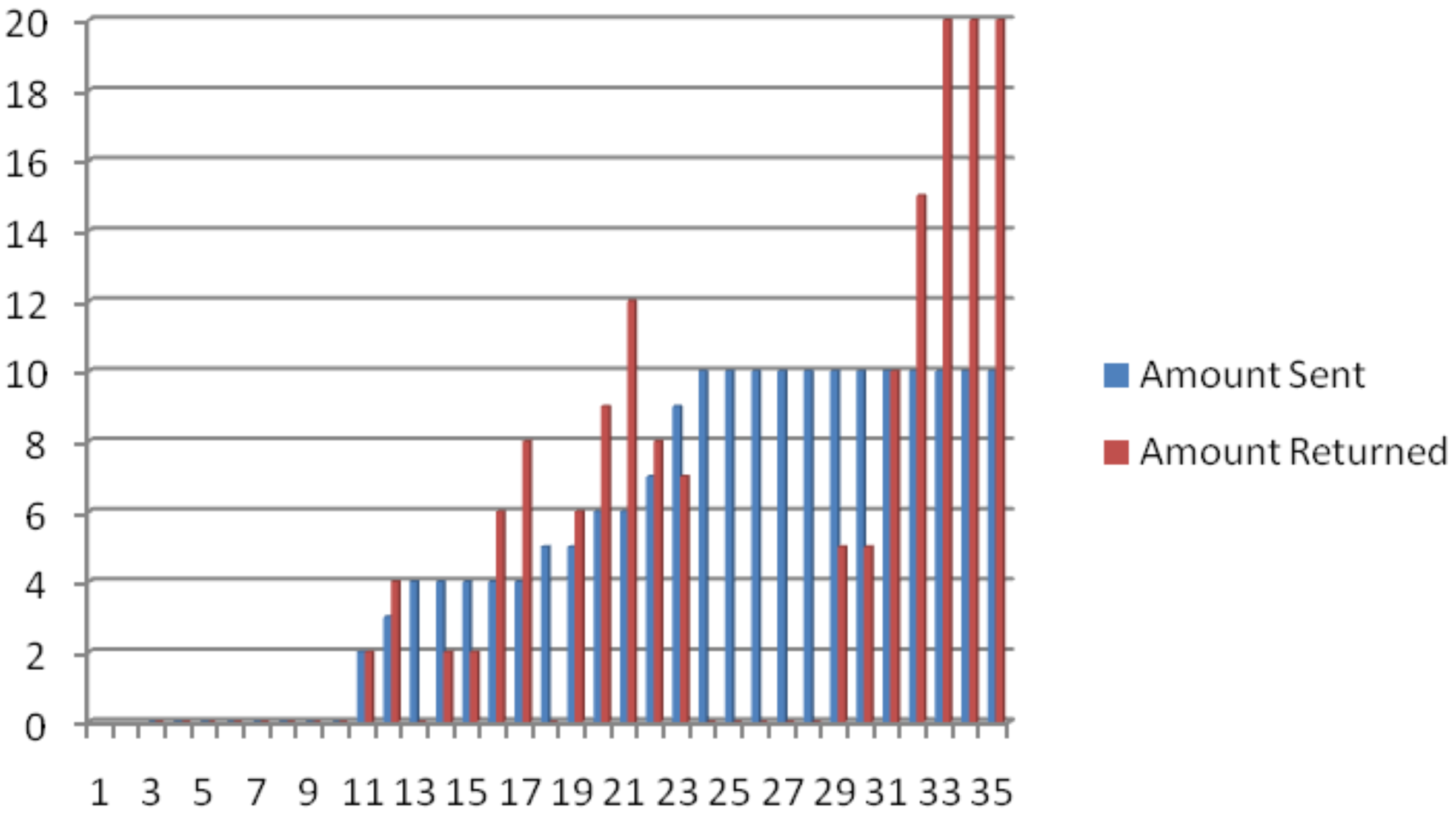

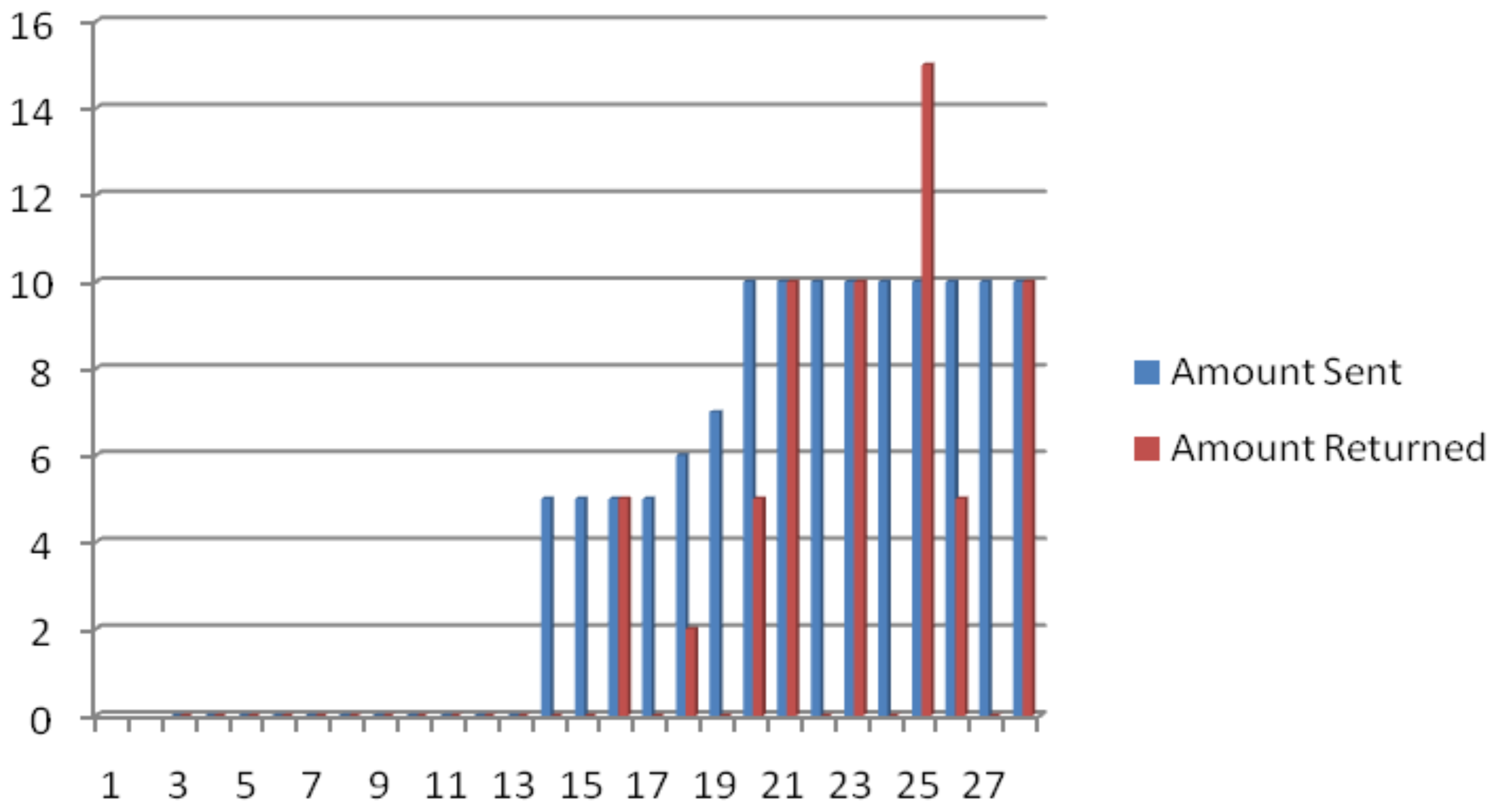
APPENDIX II. Subject Instructions and Decision Forms
| you are a player ____ | ID#:____ |
General Instructions
This is an experiment studying decision-making. The instructions are simple and if you follow them carefully and make good decisions, you might earn a considerable amount of money which will be paid to you in cash at the end of the experiment. It is therefore very important that you read these instructions with care.
No Talking Allowed
It is prohibited to communicate with other participants during the experiment. Should you have any questions please ask us. If you violate this rule, we shall have to exclude you from the experiment and from all payments.
Anonymity
Each person will be randomly matched with another person in the experiment. No one will learn the identity of the person she/he is matched with. You will be matched with the same person for the entire experiment.
Types
Each two person group will consist of two types of participants (Player A and Player B) that are assigned randomly. Your assigned type will be listed at the top of each task instruction sheet.
The Game
You are randomly paired with another individual. One member of your pair will be a player A and the other one will be player B. Find your type in the upper left corner of this sheet. You will never be able to find out the identity of the player you are paired with.
Each player's final dollar payout will be determined according to the process below. The game is divided into stages in which players take turns making decisions. Both player A and player B begin the game with $10. We will refer to this initial $10 as each player's endowment.
Stage 1:
At the beginning to stage 1, player A has the opportunity to transfer all, any portion, or none of his/her $10 endowment to player B. The amount that is not transferred is player A′s to keep. The amount that player A transfers triples when it reaches player B. For example, if A transfers $10 to B, B receives $30. If A transfers $5 to B, B receives $15. If A transfers $0 to B, B receives $0.
Stage 2:
Player B then has the opportunity to transfer all, any portion, or none of the tripled amount that was transferred to him/her from player A. The amount that is not transferred is player B′s to keep, and the amount transferred is added to player A′s final dollar payout.
| you are a player B | ID#:____ |
Pre-Game Decision Sheet
Player A is endowed with $10. Player B is endowed with $10.
The Game to be played NEXT:
Player A must decide how much, if any, of his/her $10 endowment he/she wants to transfer to player B.
Each dollar that is not transferred is player A′s to keep.
Each dollar that is transferred to Player B is multiplied by 3 by the experimenter.
Player B must then decide how much, if any, of this tripled amount they want to transfer back to player A and the remaining portion is theirs to keep.
Before we play this game, Player B has the opportunity to transfer his/her $10 endowment to player A.
If player B transfers the $10, then it is added to player A′s earnings.
If player B does not transfer the $10, then it is added to player B′s earnings.
Note: If the $10 endowment is transferred by player B,
it DOES NOT increase the amount that player A has available to transfer in Stage 1.
the $10 transferred IS NOT tripled.
Player A is guaranteed to be at least as well off as the initial starting position ($10 endowment) regardless of both players' transfer decisions during the game.
Please complete the statements below by circling one of the amounts:
I have decided to transfer the following to player A: $0 or $10
Why did you transfer or not transfer your $10 endowment to player A?
__________________________________________________________________________________
__________________________________________________________________________________
| you are a player A | ID#:____ |
The Game: Stage 1 Decision Sheet
Player B has transferred $____ to you before the start of the game.
This amount is yours to keep and will be added to your earnings.
Why do you believe Player B transferred or did not transfer their $10 endowment to you in the pre-game?
__________________________________________________________________________________
__________________________________________________________________________________
The Game decision:
You must decide how much, if any, of your $10 endowment you want to transfer to player B.
Each dollar that is not transferred is yours to keep.
Each dollar that is transferred to Player B is multiplied by 3 by the experimenter.
Please complete the statements below. Your decisions must be non-negative integers, e.g., 0, 1, 2,…, 10.
I have decided to transfer $ ____ to player B.
Therefore, I have decided to keep $ ____ for myself.
| you are a player B | ID#:____ |
The Game: Stage 2 Decision Sheet
Player A has transferred $ ____ to you in Stage 1.
The experimenter has tripled this amount, and you have received $ ____.
Why do you believe Player A transferred $____ to you in stage 1?
__________________________________________________________________________________
__________________________________________________________________________________
You must decide how much, if any, of the $ ____ you want to transfer to player A.
Each dollar that is not transferred is yours to keep.
Each dollar that is transferred is added to player A′s earnings.
Please complete the statements below. Your decisions must be non-negative integers.
I have decided to transfer $ ____ to player A.
Therefore, I have decided to keep $ ____ for myself.
References and Notes
- Arrow, K.J. The Limits of Organization; Norton: New York, NY, USA, 1974. [Google Scholar]
- Frank, R.H. Passion within Reason: The Strategic Role of the Emotions; W.W. Norton & Company Inc.: New York, NY, USA, 1988. [Google Scholar]
- Konovsky, M.; Pugh, D. Citizenship behavior and social exchange. Acad. Manag. J. 1994, 37, 656–669. [Google Scholar]
- Dirks, K.T.; Ferrin, D.L. Trust in leadership: Meta-analytic findings and implications for research and practice. J. Appl. Psychol. 2002, 87, 611–628. [Google Scholar]
- Putnam, R. Making Democracy Work: Civic Traditions in Modem Italy; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Fukuyama, F. Trust: The Social Virtues and the Creation of Prosperity; Free Press: New York, NY, USA, 1995. [Google Scholar]
- Knack, S.; Keefer, P. Does social capital have an economic payoff? A cross-country investigation. Q. J. Econ. 1997, 112, 1251–1288. [Google Scholar]
- La Porta, R.; Lopez-de-Salanes, F.; Shleifer, A.; Vishny, R. Trust in large organizations. Am. Econ. Rev. Pap. Proc. 1997, 87, 333–338. [Google Scholar]
- Dasgupta, P. Economic progress and the idea of social capital. In Social Capital: A Multifaceted Perspective; Dasgupta, P., Serageldin, I., Eds.; World Bank: Washington, DC, USA, 2000. [Google Scholar]
- Zak, P.J.; Knack, S. Trust and growth. Econ. J. 2001, 111, 295–321. [Google Scholar]
- Walton, R.; McKersie, R.B. A Behavioral Theory of Labor Negotiations: An Analysis of a Social Interaction System; ILR Press: Ithaca, NY, USA, 1991. [Google Scholar]
- Tips to Build Trust during Negotiation; The New York Times: New York, NY, USA; 6; January; 2009.
- Andreoni, J.; Samuelson, L. Building rational cooperation. J. Econ. Theory 2006, 127, 117–154. [Google Scholar]
- If there exists a possibility for reputation building due to repeated interaction [15,16] and/or if the contract between the transacting parties is verifiable and enforceable [17], the problem whether to trust or not is easily mitigated because the parties face severe punishments on the off-equilibrium path. A competition among trustees is observed to have even stronger effects than reputation building [18], although [19] show in a somewhat different setting that observing past behavior also has a powerful impact on relationships.
- Kreps, D.; Milgrom, P.; Roberts, J.; Wilson, R. Rational cooperation in the finitely repeated prisoners' dilemma. J. Econ. Theory 1982, 27, 245–252. [Google Scholar]
- Kreps, D.; Wilson, R. Reputation and imperfect information. J. Econ. Theory 1982, 27, 253–279. [Google Scholar]
- Charness, G.; Cobo-Reyes, R.; Jiménez, N. An investment game with third party intervention. J. Econ. Behav. Organ. 2008, 68, 18–28. [Google Scholar]
- Huck, S.; Ruchala, G.; Tyran, J.-R. Competition Fosters Trust; University of Copenhagen working paper; University of Copenhagen: Copenhagen, Denmark, 2006. [Google Scholar]
- Bracht, J.; Feltovich, N. Whatever you say, your reputation precedes you: Observation and cheap talk in the trust game. J. Pub. Econ. 2009, 93, 1036–1044. [Google Scholar]
- Servátka, M. Separating reputation, social influence, and identification effects in a dictator game. Eur. Econ. Rev. 2009, 53, 197–209. [Google Scholar]
- Servátka, M. Does generosity generate generosity? J. Socio. Econ. 2010, 39, 11–17. [Google Scholar]
- See the seminal papers on the importance of fairness in economic decision making by [23–25]. The experimental literature dealing with fairness and other-regarding behavior is surveyed in [26] and more recently in [27] and [28]. [29–31] provide a nice account of the literature on fairness ideals and distributive justice.
- Güth, W.; Schmittberger, R.; Schwarze, B. An experimental analysis of ultimatum bargaining. J. Econ. Behav. Organ. 1982, 3, 367–388. [Google Scholar]
- Kahneman, D.; Knetsch, J.L.; Thaler, R. Fairness as a constraint on profit seeking: Entitlements in the market. Am. Econ. Rev. 1986, 76, 728–741. [Google Scholar]
- Rabin, M. Incorporating fairness into game theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Camerer, C. Behavioral Game Theory: Experiments on Strategic Interaction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Fehr, E.; Schmidt, K. The Economics of fairness, reciprocity and altruism—Experimental evidence and new theories. In Handbook of the Economics of Giving, Altruism and Reciprocity; Kolm, S.-C., Ythier, J.M., Eds.; Elsevier: London, UK, 2006; Volume 1. [Google Scholar]
- Cooper, D.; Kagel, J. Other regarding preferences: A selective survey of experimental results. In The Handbook of Experimental Economics; Kagel, J.H., Roth, A., Eds.; Princeton University Press: Princeton, NJ, USA, 2009; Volume 2. [Google Scholar]
- Konow, J. A positive theory of economic fairness. J. Econ. Behav. Organ. 1996, 31, 13–35. [Google Scholar]
- Konow, J. Fair shares: Accountability and cognitive dissonance in allocation decisions. Am. Econ. Rev. 2000, 90, 1072–1091. [Google Scholar]
- Kaplow, L.; Shavell, S. Fairness versus Welfare; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Berg, J.; Dickhaut, J.; McCabe, K. Trust, reciprocity, and social history. Game. Econ. Behav. 1995, 10, 122–142. [Google Scholar]
- Servátka, M.; Tucker, S.; Vadovič, R. Words speak louder than money. J. Econ. Psychol. 2011, 32, 700–709. [Google Scholar]
- Charness, G.; Kuhn, P. Lab Labor: What can labor economists learn from the lab? Handbook of Labor Economics 4. in press.
- Akerlof, G.A. Labor contracts as partial gift exchange. Q. J. Econ. 1982, 97, 543–569. [Google Scholar]
- Bewley, T.F. Why Wages Don't Fall During a Recession; Harvard University Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Camerer, C.; Thaler, R. Ultimatums, dictators, and manners. J. Econ. Perspect. 1995, 9, 209–219. [Google Scholar]
- Huck, S.; Wallace, B. Reciprocal strategies and aspiration levels in a Cournot-Stackelberg experiment. Econ. Bull. 2002, 3, 1–7. [Google Scholar]
- Fehr, E.; Goette, L.; Zehnder, C. The behavioral economics of the labor market: Central findings and their policy implications. Annu. Rev. Econ. 2009, 1, 355–384. [Google Scholar]
- For interesting robustness studies that stand in contrast with this result see [41,42].
- Engelmann, D.; Ortmann, A. The robustness of laboratory gift exchange: A reconsideration; Working paper; CERGE-EI: Prague, Czech Republic, 2002. [Google Scholar]
- Charness, G.; Frechette, G.R.; Kagel, J.H. How robust is laboratory gift exchange? Exp. Econ. 2004, 7, 189–205. [Google Scholar]
- Falk, A. Gift-Exchange in the field. Econometrica 2007, 75, 1501–1511. [Google Scholar]
- Bellemare, C.; Shearer, B. Gift giving and worker productivity: Evidence from a firm-level experiment. Game. Econ. Behav. 2009, 67, 233–244. [Google Scholar]
- Gneezy, U.; List, J.A. Putting behavioral economics to work: Testing for gift exchange in labor markets using field experiments. Econometrica 2006, 74, 1365–1384. [Google Scholar]
- Kube, S.; Puppe, C.; Marechal, M.A. The currency of reciprocity—Gift-exchange in the workplace. Am. Econ. Rev. In press.
- Thaler, R.H.; Johnson, E.J. Gambling with the house money and trying to break even: The effects of prior outcomes on risky choice. Manag. Sci. 1990, 36, 643–660. [Google Scholar]
- Mauss, M. The Gift: Forms and Functions of Exchange in Archaic Societies; Cohen and West: London, UK, 1969. [Google Scholar]
- Posner, R. A theory of primitive society with special reference to law. J. Law Econ. 1980, 23, 1–53. [Google Scholar]
- A nice account of anthropology, sociology, and social psychology literature on gift giving can be found in [51] who also presents a psychological game-theoretic model of gift giving that incorporates emotions. See also the study of [52] on cost perception and the preference to give or receive a gift, [53] on the use of gifts for creating social ties, [54] on how worthless but costly gifts can facilitate courtship, [55] for a model explaining how gifts can enhance welfare, and [56] for a study analyzing the role of gifts in repeated interactions.
- Ruffle, B.J. Gift giving with emotions. J. Econ. Behav. Organ. 1999, 39, 399–420. [Google Scholar]
- Robben, H.S.J.; Verhallen, T.M.M. Behavioral costs as determinants of cost perception and preference formation for gifts to receive and gifts to give. J. Econ. Psychol. 1994, 15, 333–350. [Google Scholar]
- Zelizer, V.A. Payments and social ties. Sociol. Forum. 1996, 11, 481–495. [Google Scholar]
- Sozou, P.D.; Seymour, R.M. Costly but worthless gifts facilitate courtship. Proc. Biol. Sci. 2005, 272, 1877–1884. [Google Scholar]
- Kaplan, T.; Ruffle, B.J. In search of welfare-improving gifts. Eur. Econ. Rev. 2009, 53, 445–460. [Google Scholar]
- Bolle, F. Why to buy your darling flowers—On cooperation and exploitation. Theory Decis. 2001, 50, 1–28. [Google Scholar]
- Lahno, B. Trust and strategic rationality. Ration. Soc. 1995, 7, 442–464. [Google Scholar]
- Lahno, B. Trust, reputation, and exit in exchange relationships. J. Confl. Resolut. 1995, 39, 495–510. [Google Scholar]
- Cox, J.C. Implications of Game Triads for Observations of Trust and Reciprocity; University of Arizona discussion paper; University of Arizona: Tucson, AZ, USA, 2000. [Google Scholar]
- Fehr, E. On the economics and biology of trust. J. Eur. Econ. Assoc. 2009, 7, 235–266. [Google Scholar]
- Rousseau, D.; Sitkin, M.; Burt, R.; Camerer, C. Not so different after all: A cross-discipline view of trust. Acad. Manag. Rev. 1998, 23, 393–404. [Google Scholar]
- Mayer, R.C.; Davis, J.H.; Schoorman, F.D. An integrative model of organizational trust. Acad. Manag. Rev. 1995, 20, 709–734. [Google Scholar]
- Schoorman, F.D.; Mayer, R.C.; Davis, J.H. An integrative model of organizational trust: Past, present, and future. Acad. Manag. Rev. 2007, 32, 344–354. [Google Scholar]
- Johnson, N.D.; Mislin, A.A. Trust games: A meta-analysis. J. Econ. Psychol. in press.
- Bourdieu, P. Forms of capital. In Handbook of Theory and Research for the Sociology of Education; Richards, J.C., Ed.; Greenwood Press: New York, NY, USA, 1983. [Google Scholar]
- Kurzban, R.; Rigdon, M.; Wilson, B. Incremental approaches to establishing trust. Exp. Econ. 2008, 11, 370–389. [Google Scholar]
- [66] considered three repeated interaction conditions: incremental condition in which first movers had to increment their amount sent from round to round, decremental condition with the opposite restriction, and an unrestricted condition. Interestingly, they do not find significant differences in the amounts sent by the first movers across these three conditions.
- Andreoni, J. Trust, Reciprocity, and Contract Enforcement: Experiments on Satisfaction Guaranteed; University of California San Diego working paper; University of California: San Diego, CA, USA, 2005. [Google Scholar]
- Williamson, O.E. Credible commitments: Using hostages to support exchange. Am. Econ. Rev. 1983, 73, 519–540. [Google Scholar]
- Raub, W.; Keren, G. Hostages as a commitment device. A game-theoretic model and an empirical test of some scenarios. J. Econ. Behav. Organ. 1993, 21, 43–67. [Google Scholar]
- Bracht, J.; Feltovich, N. Efficiency in the trust game: An experimental study of precommitment. Int. J. Game Theory 2008, 37, 39–72. [Google Scholar]
- Charness, G.; Dufwenberg, M. Promises and partnership. Econometrica 2006, 74, 1579–1601. [Google Scholar]
- Charness, G.; Dufwenberg, M. Bare promises: An experiment. Econ. Lett. 2010, 107, 281–283. [Google Scholar]
- Ben-Ner, A.; Putterman, L. Trust, communication and contracts: An experiment. J. Econ. Behav. Organ. 2009, 70, 106–121. [Google Scholar]
- Ben-Ner, A.; Putterman, L.; Ren, T. Lavish returns on cheap talk: Non-binding communication in a trust experiment. J. Sociol. Econ. 2011, 40, 1–13. [Google Scholar]
- Deck, C. An experimental investigation of trust and sequential trade. South Econ. J. 2010, 76, 993–1004. [Google Scholar]
- Deck, C.; Servátka, M.; Tucker, S. Do People Keep Socially Unverifiable Promises? University of Canterbury working paper; University of Canterbury: Canterbury, New Zealand, 2011. [Google Scholar]
- Bolton, G.; Katok, E.; Ockenfels, A. How effective are electronic reputation mechanisms? An experimental investigation. Manag. Sci. 2004, 50, 1587–1602. [Google Scholar]
- In the existing literature, the behavior of player A and player B in an investment game is often interpreted as proxies for trusting and trustworthy behavior [17,32]. There are other possible motivations why players would send and return positive amounts, such as distributive other-regarding preferences [80–82], preferences for increasing social welfare [83], reciprocity [25,84–87] or various psychological motivations, such as guilt aversion [88,89]. One could, of course, also ask the follow up question: How does a gift affect other-regarding preferences? [90] presents an experiment that separates trust and reciprocity from other-regarding preferences in the investment game. Similarly, it is possible to design an experiment that would identify the effect of gift separately on trust and other-regarding preferences. In this paper we are primarily concerned with the size of the investment and efficiency as the measure of trust.
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar]
- Bolton, G.E.; Ockenfels, A. ERC: A theory of equity, reciprocity, and competition. Am. Econ. Rev. 2000, 90, 166–193. [Google Scholar]
- Cox, J.C.; Sadiraj, V. On modeling voluntary contributions to public goods. Pub. Fin. Rev. 2007, 35, 311–332. [Google Scholar]
- Charness, G.; Rabin, M. Understanding social preferences with simple tests. Q. J. Econ. 2002, 117, 817–869. [Google Scholar]
- Dufwenberg, M.; Kirchsteiger, G. A theory of sequential reciprocity. Game. Econ. Behav. 2004, 47, 268–298. [Google Scholar]
- Falk, A.; Fischbacher, U. A theory of reciprocity. Game. Econ. Behav. 2006, 54, 293–315. [Google Scholar]
- Cox, J.C.; Friedman, D.; Gjerstad, S. A tractable model of reciprocity and fairness. Game. Econ. Behav. 2007, 59, 17–45. [Google Scholar]
- Cox, J.C.; Friedman, D.; Sadiraj, V. Revealed altruism. Econometrica 2008, 76, 31–69. [Google Scholar]
- Battigalli, P.; Dufwenberg, M. Guilt in games. Am. Econ. Rev. 2007, 97, 170–176. [Google Scholar]
- Battigalli, P.; Dufwenberg, M. Dynamic psychological games. J. Econ. Theory 2009, 144, 1–35. [Google Scholar]
- Cox, J.C. How to identify trust and reciprocity. Game. Econ. Behav. 2004, 46, 260–281. [Google Scholar]
- An alternative design would be to include a “mandatory gift” treatment where both players begin with $10, but the experimenter imposes a “gift” of $10 on the trustee. While this alternative addresses the possibility of player A′s internalizing the $20 endowments, it is also likely to introduce experimenter demand effects and possibly even create confusion among subjects. One of the referees pointed out another control that also removes the intentions in the initial gift decision. In particular, one could implement a random device that determines whether player B′s endowment is transferred to player A.
- We implemented the dictator game stage decision of player B to be binary for two reasons: (i) it makes mimicking of trustworthy types simple and (ii) it makes it easy to design a treatment controlling for the amount of money possessed by the two players when making their respective decisions.
- Recall that gift is a monetary transfer by which player B can put himself at a loss, but does not preclude him from appropriating a large share of the surplus created by player A′s investment.
- Sliwka, D. Trust as a signal of a social norm and the hidden costs of incentive schemes. Am. Econ. Rev. 2007, 97, 999–1012. [Google Scholar]
- Ellingsen, T.; Johannesson, M. Pride and prejudice: The human side of incentive theory. Am. Econ. Rev. 2008, 98, 990–1008. [Google Scholar]
- Andreoni, J.; Bernheim, B.D. Social image and the 50–50 norm: A theoretical and experimental analysis of audience effects. Econometrica 2009, 77, 1607–1636. [Google Scholar]
- The adult minimum wage in New Zealand at the time of the experiment was 10.25 NZD per hour.
- As already mentioned, we make use of the Baseline and Gift treatment data that were presented in [33]. This other paper included a communication treatment where among other things we studied decision maker's interpretation of the message as an alternative for a 3rd party interpretation. The decision forms thus included a non-salient question of why player As thought they were sent a message and what did the message mean to them. In order to be consistent across treatments an analogous question was asked in the Gift treatment analyzed in the current study. By including the non-salient questions asking about motivations behind subjects' behavior our procedures differ from the standard way the investment game is run. We have checked our data against data in [90] for any effects of including these questions and found no significant differences in subjects' behavior in the respective baseline treatments.
- The average earnings of player As who received a gift were equal to $16.27 while those of who did not received a gift was equal to $9.00. For a comparison, the average earnings of a player A in Baseline were $9.33.
- Individual subjects' behavior is presented in Figures 1 through 3 in Appendix I.
- The difference between the average amounts sent by player As who received a gift and those in Baseline is equal to $1.81. So even if this amount is tripled and would be all retained by player Bs, they would be better off monetarily by not giving the $10 gift.
- Gächter, S.; Riedl, A. Moral property rights in bargaining with infeasible claims. Manag. Sci. 2005, 51, 249–263. [Google Scholar]
- We thank an anonymous referee for suggesting this explanation.
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Servátka, M.; Tucker, S.; Vadovič, R. Building Trust—One Gift at a Time. Games 2011, 2, 412-433. https://doi.org/10.3390/g2040412
Servátka M, Tucker S, Vadovič R. Building Trust—One Gift at a Time. Games. 2011; 2(4):412-433. https://doi.org/10.3390/g2040412
Chicago/Turabian StyleServátka, Maroš, Steven Tucker, and Radovan Vadovič. 2011. "Building Trust—One Gift at a Time" Games 2, no. 4: 412-433. https://doi.org/10.3390/g2040412




