Wide Acoustic Bandgap Solid Disk-Shaped Phononic Crystal Anchoring Boundaries for Enhancing Quality Factor in AlN-on-Si MEMS Resonators
Abstract
:1. Introduction
2. Design and Simulations of ABG
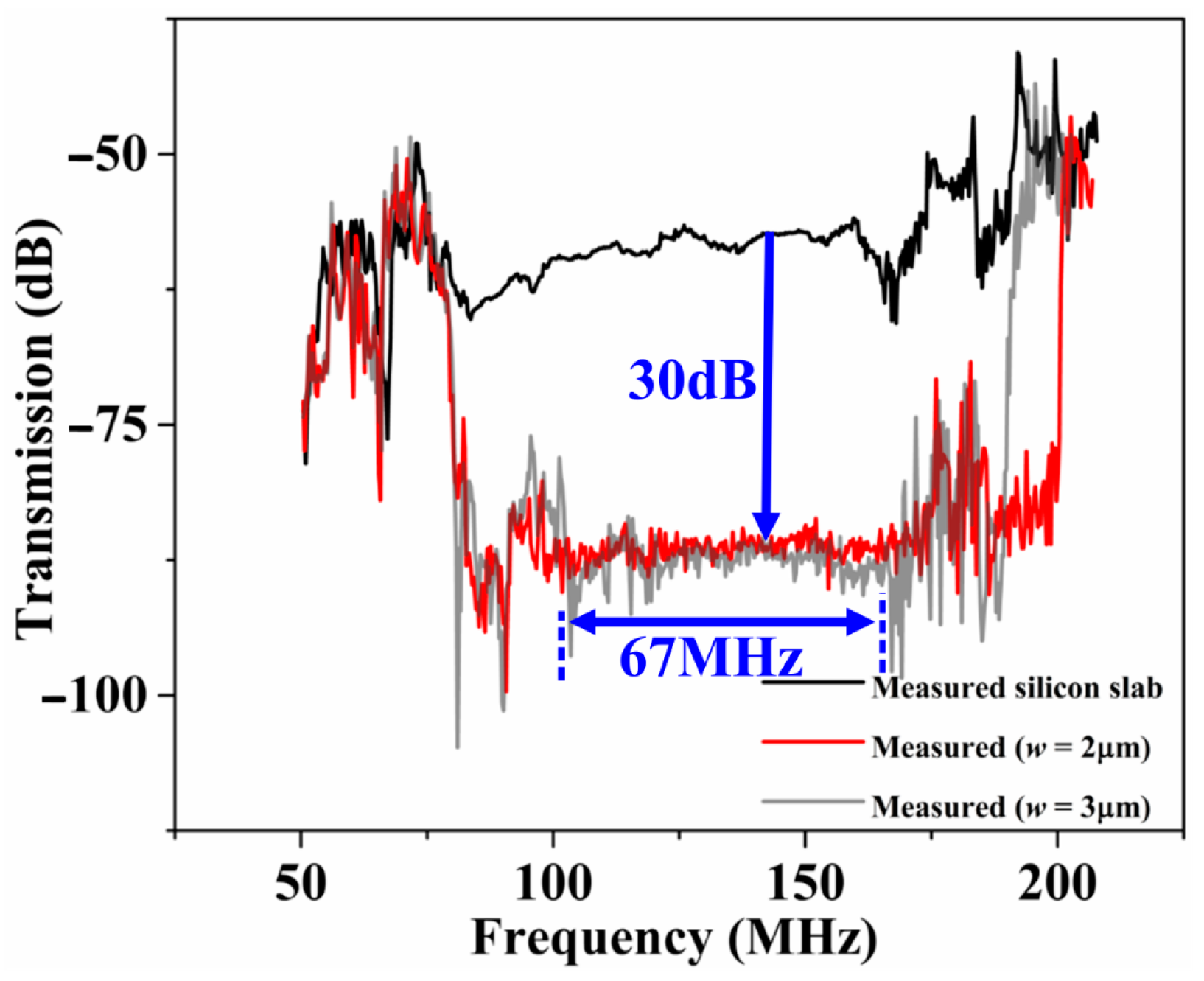
3. Experimental Validation of ABG
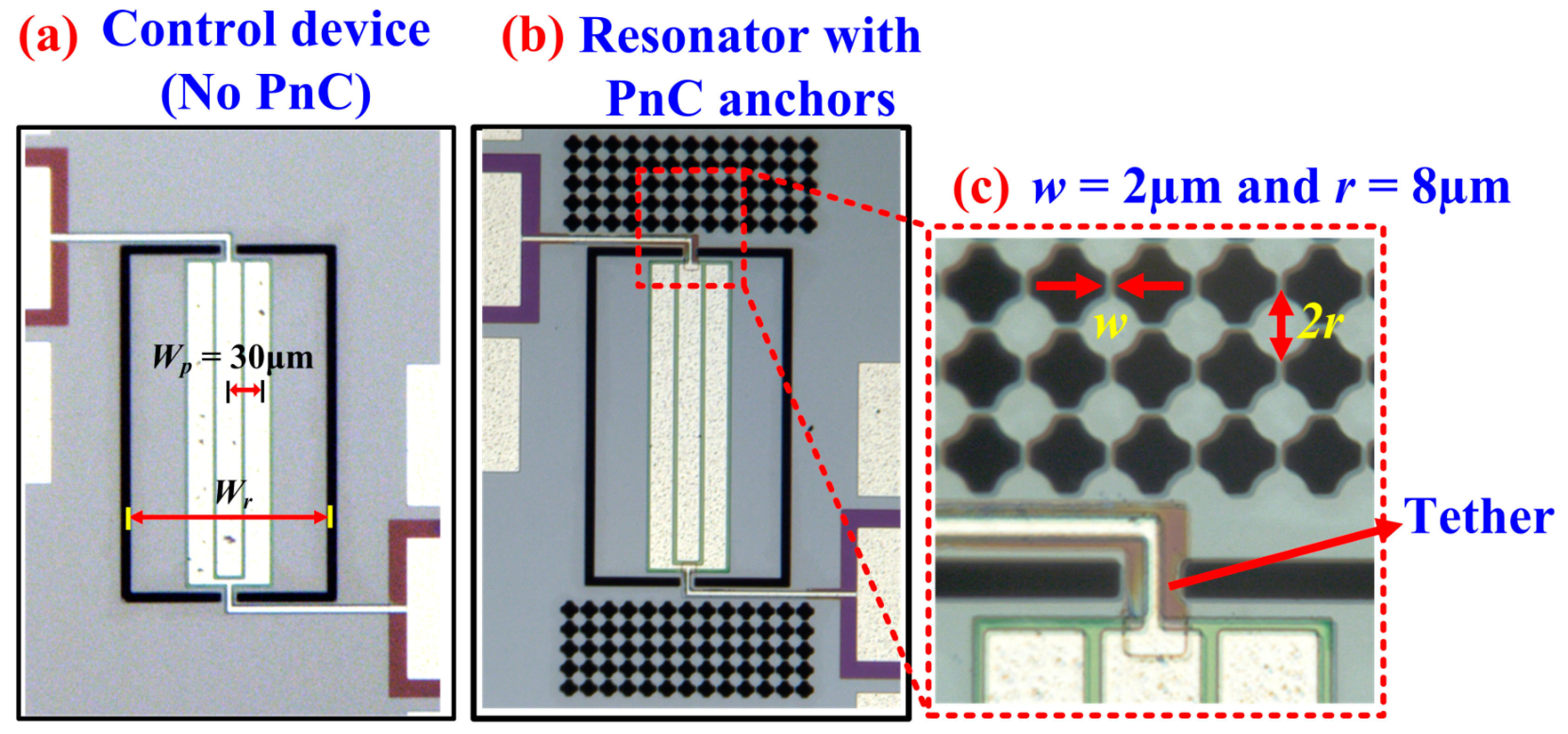
4. Experimental Validation of Q Enhancement with PnC Anchors
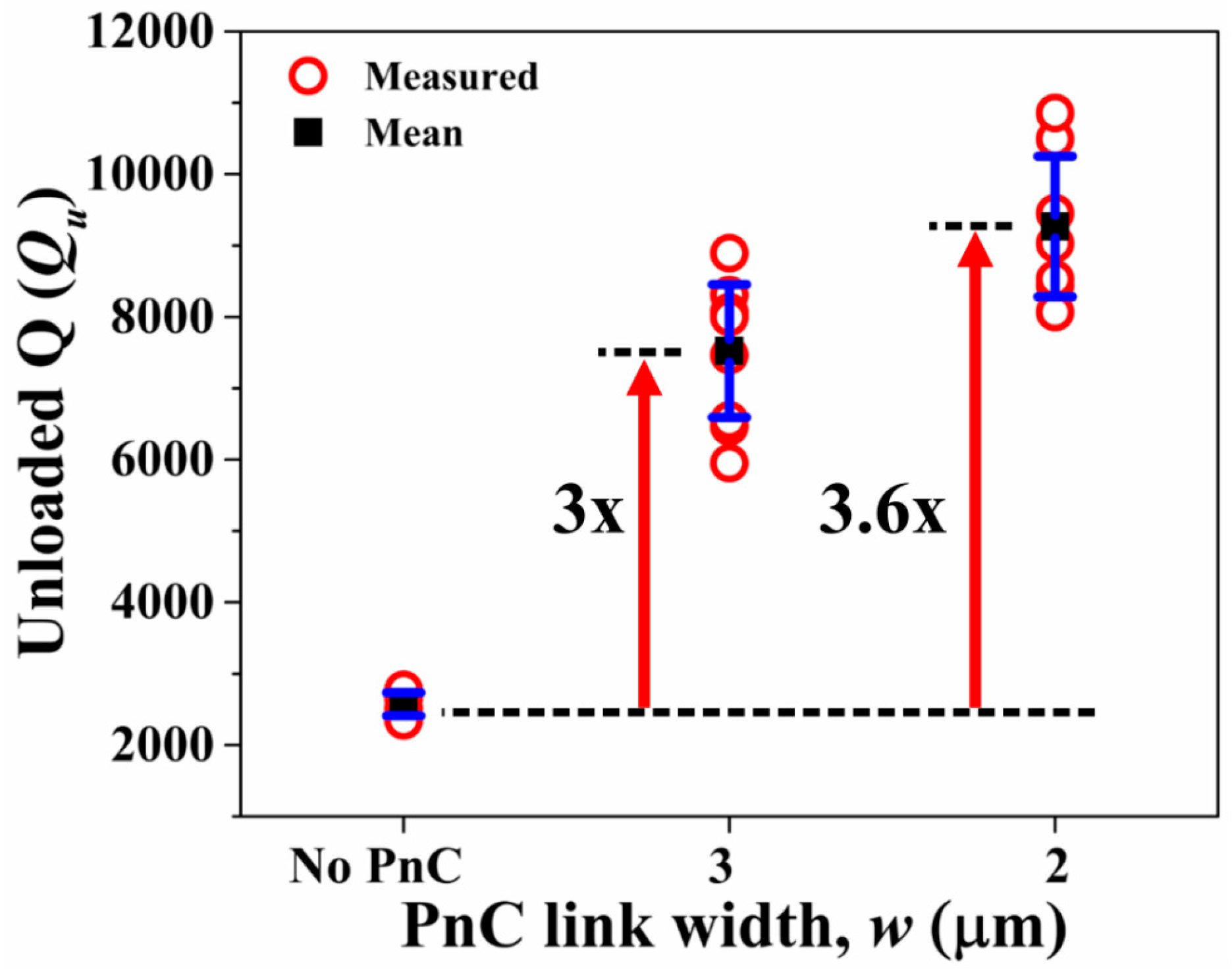
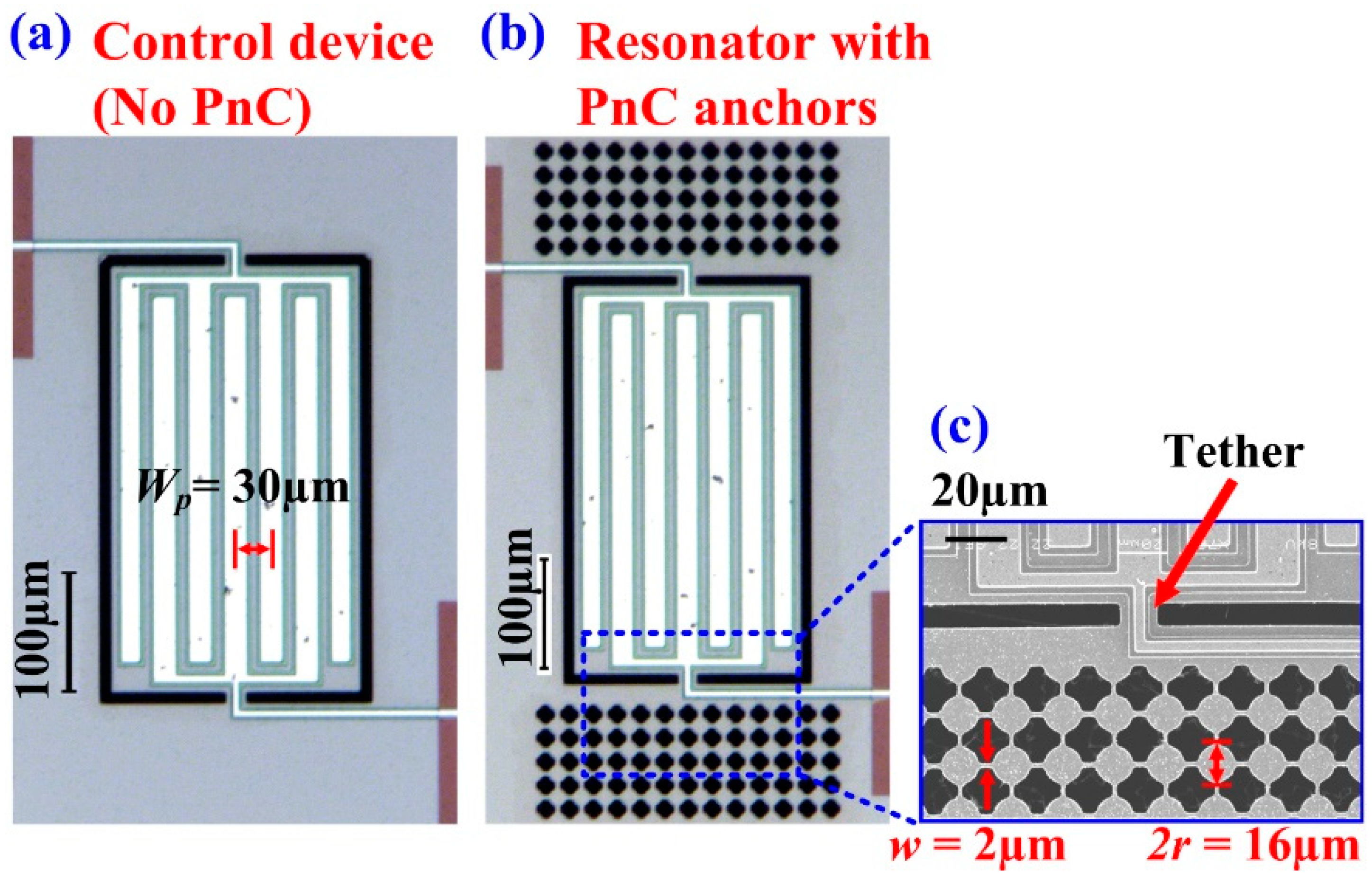
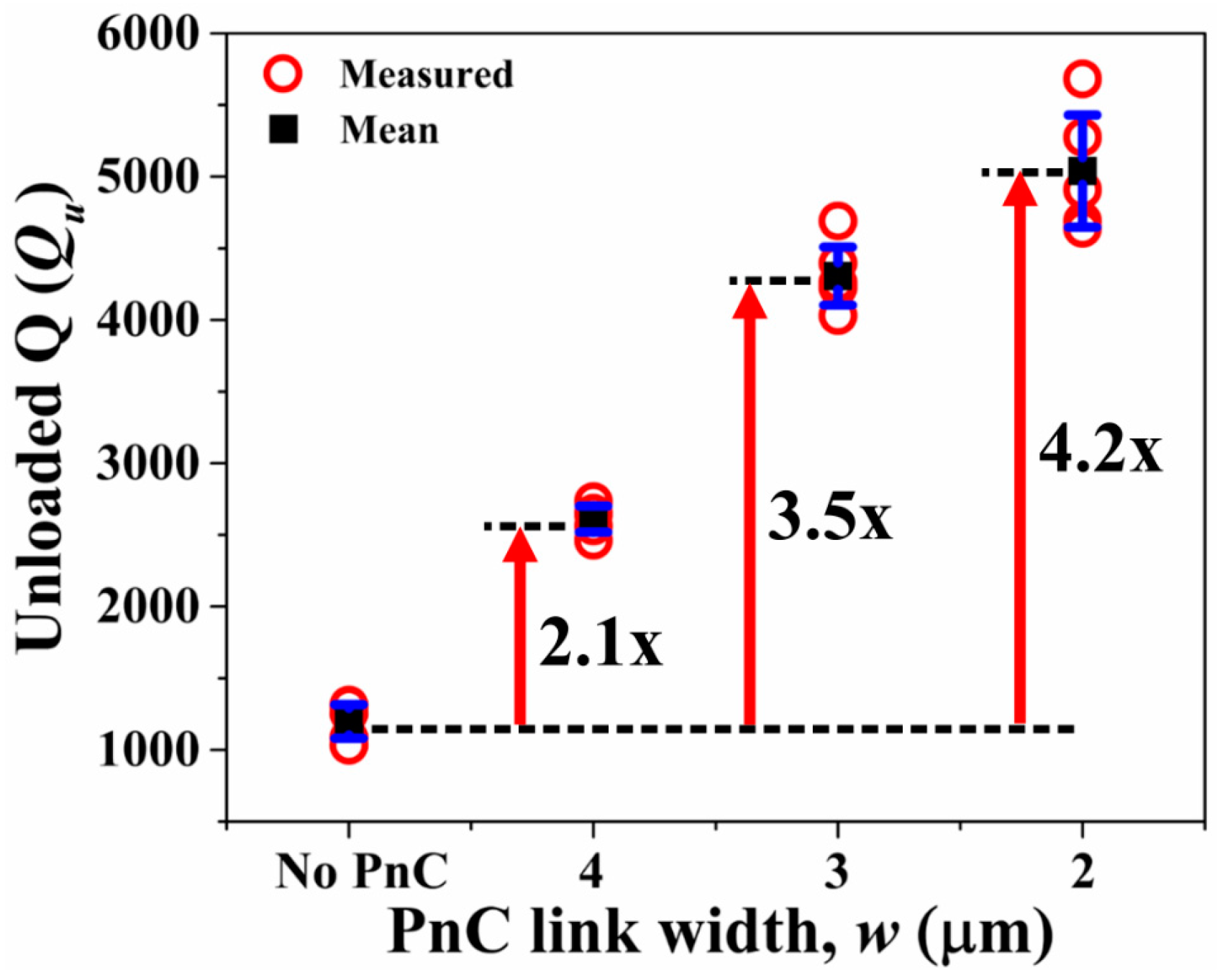
4.1. Resonators with Partial Coverage of Three IDT Fingers.
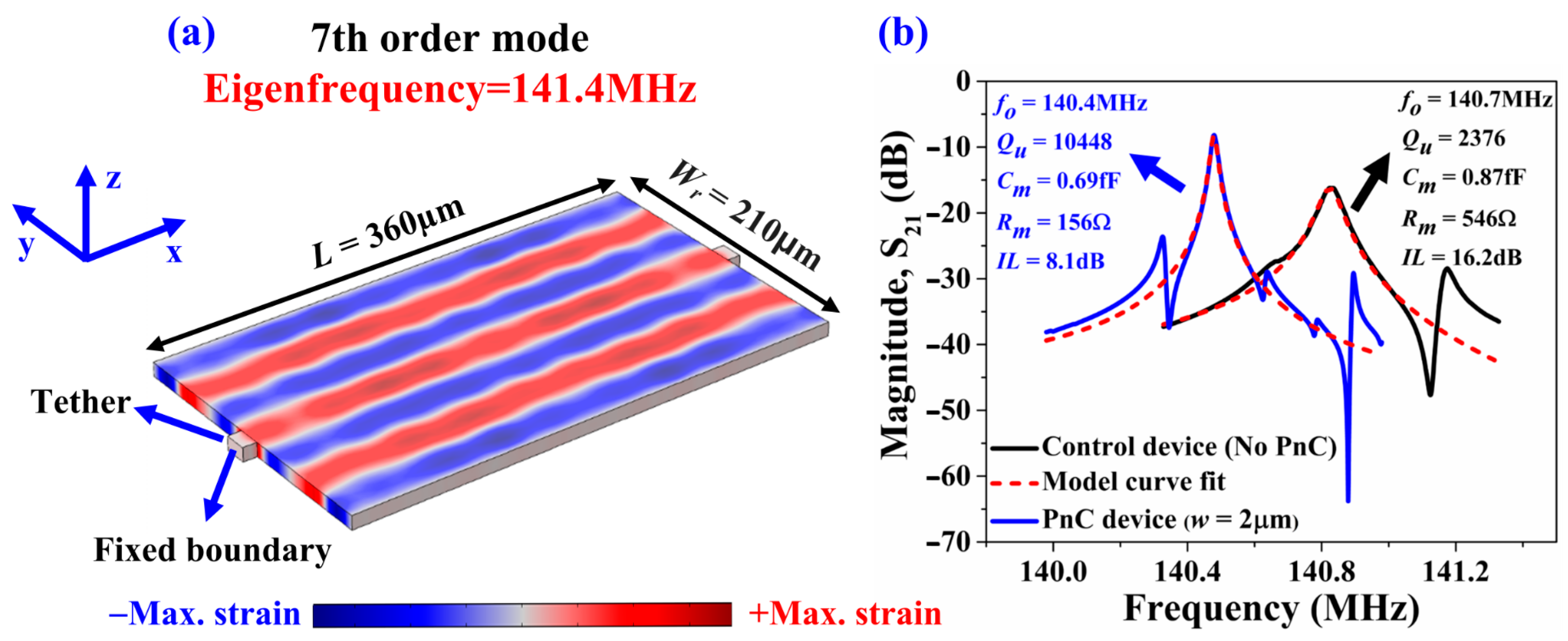
4.2. Resonators with Full Coverage of Seven IDT Fingers.
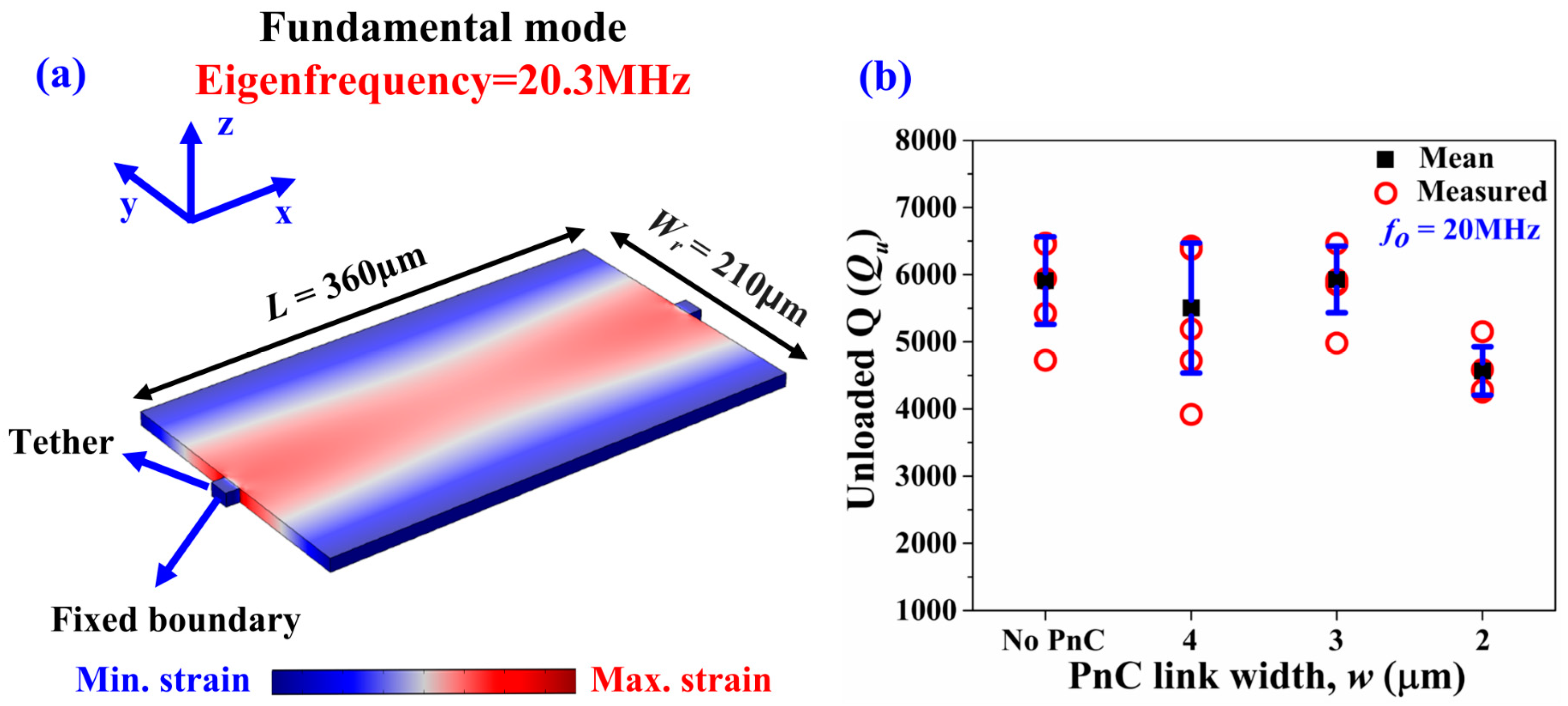
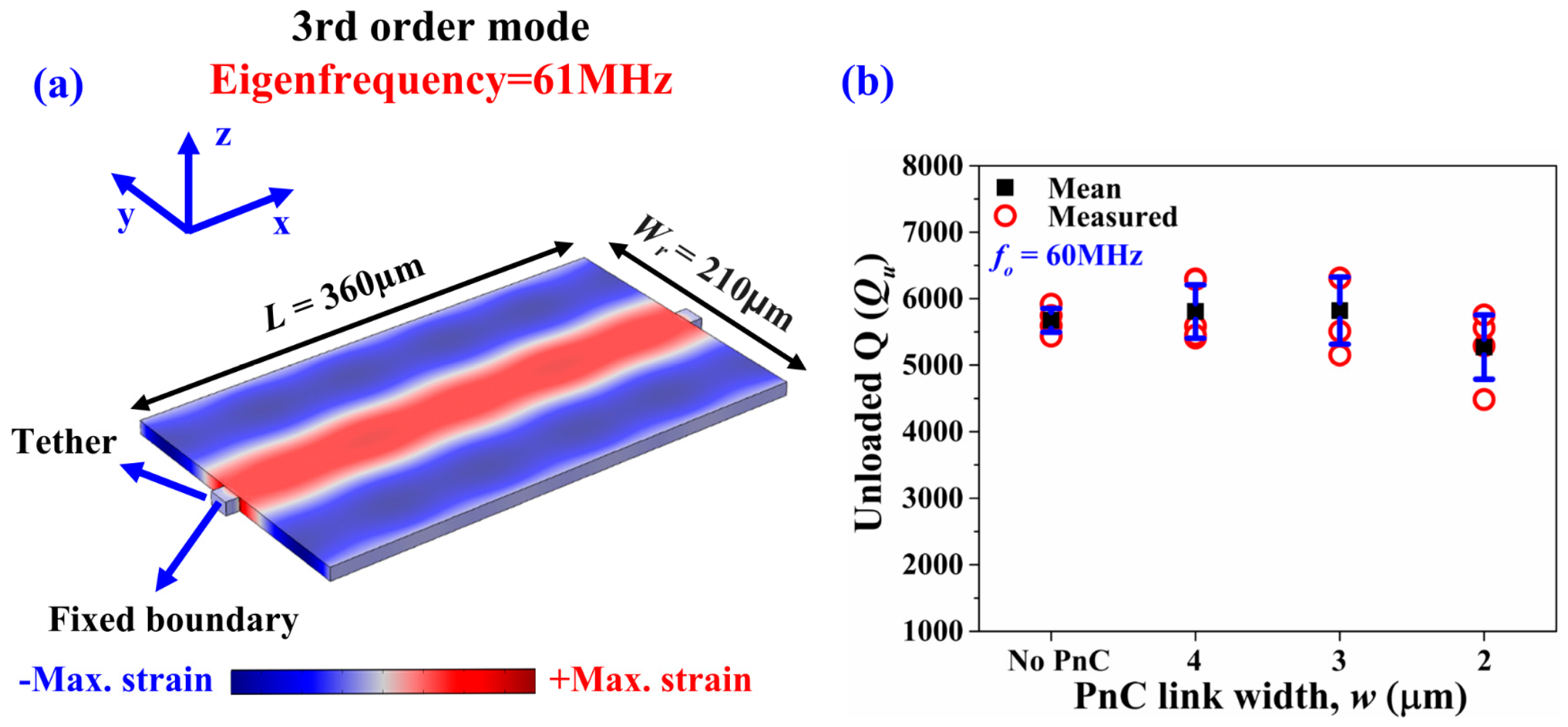
4.3. Frequency Selectivity of Q Enhancement.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ho, G.K.; Abdolvand, R.; Sivapurapu, A.; Humad, S.; Ayazi, F. Piezoelectric-on-silicon lateral bulk acoustic wave micromechanical resonators. J. Microelectromech. Syst. 2008, 17, 512–520. [Google Scholar] [CrossRef]
- Abdolvand, R.; Lavasani, H.M.; Ho, G.K.; Ayazi, F. Thin-film piezoelectric-on-silicon resonators for high frequency reference oscillator applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2596–2606. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.M.; Lai, Y.J.; Hsu, J.-C.; Seneskey, D.G.; Pisano, A.P. High-Q aluminum nitride Lamb wave resonators with biconvex edges. Appl. Phys. Lett. 2011, 99, 143501. [Google Scholar] [CrossRef]
- Zou, J.; Lin, C.-M.; Tang, G.; Pisano, A.P. High-Q Butterfly-shaped AlN Lamb wave resonators. IEEE Electron Device Lett. 2017, 38, 1739–1742. [Google Scholar] [CrossRef]
- Harrington, B.P.; Abdolvand, R. In-plane acoustic reflectors for reducing effective anchor loss in lateral-extensional MEMS resonators. J. Micromech. Microeng. 2011, 21, 085021. [Google Scholar] [CrossRef]
- Feng, D.; Xu, D.; Wu, G.; Xiong, B.; Wang, Y. Phononic crystal strip based anchors for reducing anchor loss of micromechanical resonators. J. Appl. Phys. 2014, 115, 024503. [Google Scholar] [CrossRef]
- Lin, C.-M.; Hsu, J.-C.; Senesky, D.G.; Pisano, A.P. Anchor loss reduction in AlN Lamb wave resonators using phononic crystal strip tethers. In Proceedings of the 2014 IEEE International Frequency Control Symposium (FCS), Taipei, Taiwan, 19–22 May 2014; pp. 371–375. [Google Scholar]
- Wu, G.; Zhu, Y.; Merugu, S.; Wang, N.; Sun, C.; Gu, Y. GHz spurious mode free AlN Lamb wave resonator with high figure of merit using one dimensional phononic crystal tethers. Appl. Phys. Lett. 2016, 109, 013506. [Google Scholar] [CrossRef]
- Zhu, H.; Lee, J.E.-Y. Design of phononic crystal tethers for frequency-selective quality factor enhancement in AlN piezoelectric-on-silicon resonators. Procedia Eng. 2015, 120, 516–519. [Google Scholar] [CrossRef]
- Sorenson, L.; Fu, J.L.; Ayazi, F. One-dimensional linear acoustic bandgap structures for performance enhancement of AlN-on-Silicon micromechanical resonators. In Proceedings of the 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 918–921. [Google Scholar]
- Zhu, H.; Lee, J.E.-Y. AlN piezoelectric on silicon MEMS resonator with boosted Q using planar patterned phononic crystals on anchors. In Proceedings of the 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 18–22 January 2015; pp. 797–800. [Google Scholar]
- Rawat, U.; Nair, D.R.; DasGupta, A. Piezoelectric-on-Silicon array resonators with asymmetric phononic crystal tethering. J. Microelectromech. Syst. 2017, 26, 773–781. [Google Scholar] [CrossRef]
- Wang, S.; popa, L.C.; Weinstein, D. GaN MEMS resonator using a folded phononic crystal structure. In Proceedings of the Hilton Head Workshop 2014: A Solid-State Sensors, Actuators and Microsystems, Sonesta Resort, Hilton Head Island, 8–12 June 2014; pp. 72–75. [Google Scholar]
- Wang, N.; Tsai, J.M.-L.; Hsiao, F.-L.; Soon, B.W.; Kwong, D.-L.; Palaniapan, M.; Lee, C. Micromechanical resonators based on silicon two-dimensional phononic crystals of square lattice. J. Microelectromech. Syst. 2012, 21, 801–810. [Google Scholar] [CrossRef]
- Li, F.; Liu, J.; Wu, Y.H. The investigation of point defect modes of phononic crystal for high Q resonance. In Proceedings of the 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 438–441. [Google Scholar]
- Mohammadi, S.; Eftekhar, A.A.; Hunt, W.D.; Adibi, A. High-Q micromechanical resonators in a two-dimensional phononic crystal slab. Appl. Phys. Lett. 2009, 94, 051906. [Google Scholar] [CrossRef]
- Mohammadi, S.; Eftekhar, A.A.; Khelif, A.; Adibi, A. A high-quality factor piezoelectric-on-substrate phononic crystal micromechanical resonator. In Proceedings of the 2009 IEEE International Ultrasonics Symposium, Rome, Italy, 20–23 September 2009; pp. 1158–1160. [Google Scholar]
- Huang, C.-Y.; Sun, J.-H.; Wu, T.-T. A two-port ZnO/silicon Lamb wave resonator using phononic crystals. Appl. Phys. Lett. 2010, 97, 031913. [Google Scholar] [CrossRef]
- Wang, N.; Tsai, J.M.; Soon, B.W.; Kwong, D.-L.; Hsiao, F.-L.; Palaniapan, M.; Lee, C. Experimental demonstration of microfabricated phononic crystal resonators based on two-dimensional silicon plate. In Proceedings of the 2011 Defense Science Research Conference and Expo (DSR), Singapore, 3–5 August 2011; pp. 1–4. [Google Scholar]
- Lu, R.; Manzaneque, T.; Yang, Y.; Gong, S. Lithium Niobate phononic crystals for tailoring performance of RF laterally vibrating devices. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Baboly, M.G.; Reinke, C.M.; Graiffin, B.A.; El-Kady, I.; Leseman, Z.C. Acoustic waveguiding in a silicon carbide phononic crystals at microwave frequencies. Appl. Phys. Lett. 2018, 112, 103504. [Google Scholar] [CrossRef]
- Kuo, N.-K.; Piazza, G. Ultra high frequency air/aluminum nitride fractal phononic crystals. In Proceedings of the 2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum (FCS), San Francisco, CA, USA, 2–5 May 2011; pp. 1–4. [Google Scholar]
- Benchabane, S.; Khelif, A.; Rauch, J.-Y.; Robert, L.; Laude, V. Evidence for complete surface wave band gap in a piezoelectric phononic crystal. Phys. Rev. E 2006, 73, 065601. [Google Scholar] [CrossRef] [PubMed]
- Ardito, R.; Cremonesi, M.; D’Alessandro, L.; Frangi, A. Application of optimally-shaped phononic crystals to reduce anchor losses of MEMS resonators. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; pp. 1–3. [Google Scholar]
- Siddiqi, M.W.U.; Lee, J.E.-Y. AlN-on-Si MEMS resonator bounded by wide acoustic bandgap two-dimensional phononic crystal anchors. In Proceedings of the 2018 IEEE International Conference on Micro Electro Mechanical Systems, Belfast, UK, 21–25 January 2018; pp. 727–730. [Google Scholar]
- Siddiqi, M.W.U.; Lee, J.E.-Y. Effect of mode order, resonator length, curvature, and electrode coverage on enhancing the performance of biconvex resonators. J. Micromech. Microeng. 2018, 28, 094002. [Google Scholar] [CrossRef] [Green Version]
- Binci, L.; Tu, C.; Zhu, H.; Lee, J.E.-Y. Planar ring-shaped phononic crystal anchoring boundaries for enhancing the quality factor of Lamb mode resonators. Appl. Phys. Lett. 2016, 109, 203501. [Google Scholar] [CrossRef]
- Cowen, A.; Hames, G.; Glukh, K.; Hardy, B. PiezoMUMPs Design Handbook; CMC Microsystems: Windsor, ON, Canada, 2014. [Google Scholar]
- Tu, C.; Lee, J.E.-Y. VHF-band biconvex AlN-on-silicon micromechanical resonators with enhanced quality factor and suppressed spurious modes. J. Micromech. Microeng. 2016, 26, 065012. [Google Scholar] [CrossRef]
- Zuo, C.; Sinha, N.; Spiegel, J.V.; Piazza, G. Multi-frequency pierce oscillator based on piezoelectric AlN contour-mode MEMS resonators. In Proceedings of the 2008 IEEE International Frequency Control Symposium, Honolulu, HI, USA, 19–21 May 2008; pp. 402–407. [Google Scholar]
- Wojciechowski, K.E.; Olsson, R.H.; Tuck, M.R.; Roherty-Osmun, E.; Hill, T.A. Single-chip precision oscillators based on multi-frequency, high-Q aluminum nitride MEMS resonators. In Proceedings of the 2009 International Solid-State Sensors, Actuators and Microsystems Conference, Denver, CO, USA, 21–25 June 2009; pp. 2126–2130. [Google Scholar]



| PnC Shape | Dimensions (μm) | ABG Range (MHz) | fc (MHz) | BG (%) |
|---|---|---|---|---|
| Air-Hole |  | 136–147 | 141.5 | 7.7 |
| Ring |  | 107–144 | 125.5 | 29.4 |
| Cross Inclusion |  | 89–147 | 118 | 49.1 |
| Square Hole |  | - | - | - |
| Fractal |  | 146–192 | 169 | 27.2 |
| Solid-Disk (this work) |  | 93–175 | 134 | 61.1 |
| Reference | Technology | Frequency (MHz) | Q | f∙Q (1011 Hz) |
|---|---|---|---|---|
| [30] | AlN | 175 | 1500 | 2.6 |
| [31] | AlN | 101.71 | 1257 | 1.27 |
| [2] | AlN-on-Si | 106 | 4000 | 4.24 |
| [27] | AlN-on-Si | 100 | 5369 | 5.36 |
| [10] | AlN-on-Si | 178 | 1400 | 2.49 |
| [9] | AlN-on-Si | 141.5 | 5730 | 8.10 |
| This work (w/o PnC) | AlN-on-Si | 140.9 | 2510 | 3.53 |
| This work (with PnC) | AlN-on-Si | 140.5 | 10,492 | 14.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddiqi, M.W.U.; Lee, J.E.-Y. Wide Acoustic Bandgap Solid Disk-Shaped Phononic Crystal Anchoring Boundaries for Enhancing Quality Factor in AlN-on-Si MEMS Resonators. Micromachines 2018, 9, 413. https://doi.org/10.3390/mi9080413
Siddiqi MWU, Lee JE-Y. Wide Acoustic Bandgap Solid Disk-Shaped Phononic Crystal Anchoring Boundaries for Enhancing Quality Factor in AlN-on-Si MEMS Resonators. Micromachines. 2018; 9(8):413. https://doi.org/10.3390/mi9080413
Chicago/Turabian StyleSiddiqi, Muhammad Wajih Ullah, and Joshua E.-Y. Lee. 2018. "Wide Acoustic Bandgap Solid Disk-Shaped Phononic Crystal Anchoring Boundaries for Enhancing Quality Factor in AlN-on-Si MEMS Resonators" Micromachines 9, no. 8: 413. https://doi.org/10.3390/mi9080413






