Transfer Function of Macro-Micro Manipulation on a PDMS Microfluidic Chip
Abstract
:1. Introduction
2. Related Works
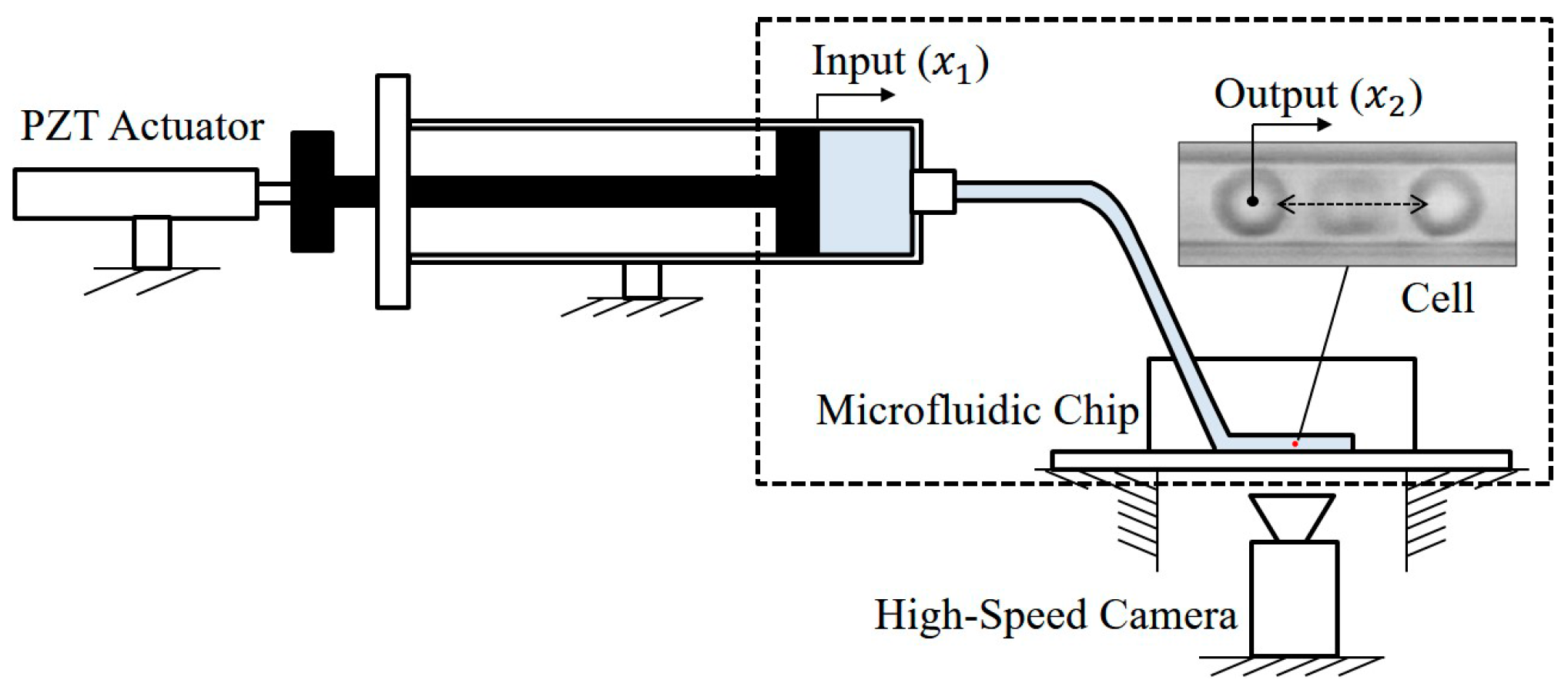
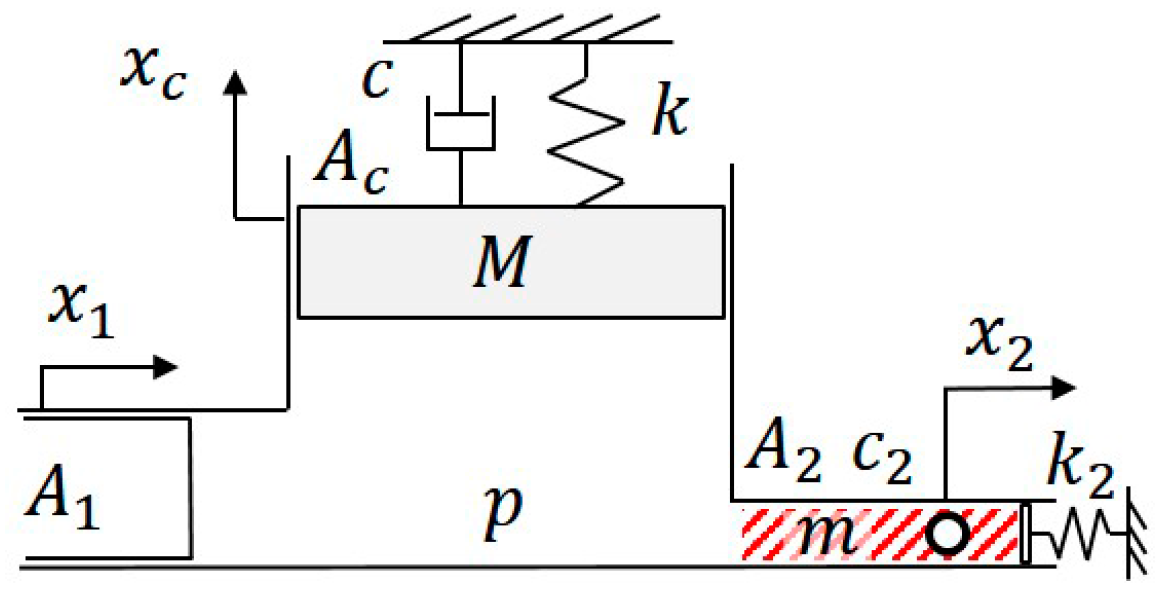
3. Modeling of Transfer Function with a PDMS Microfluidic Channel
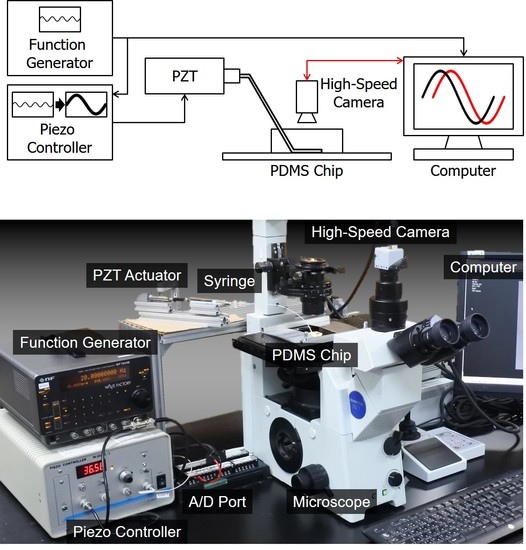
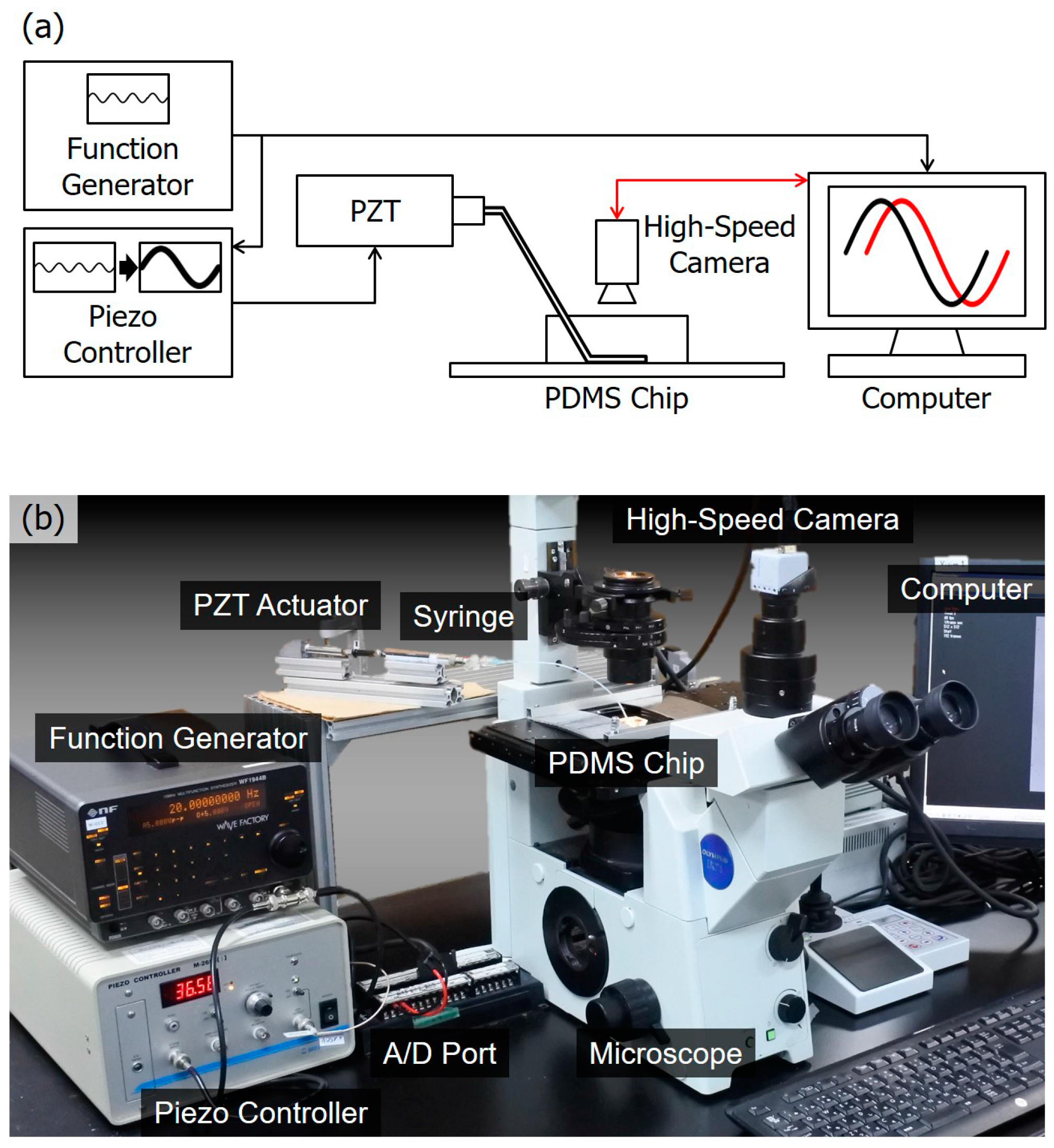
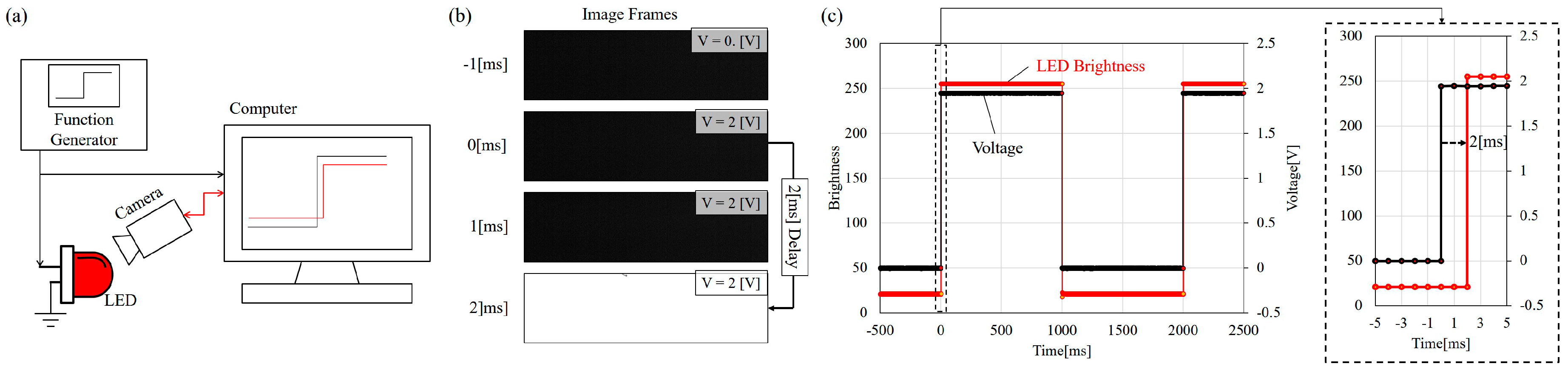
4. Experiments
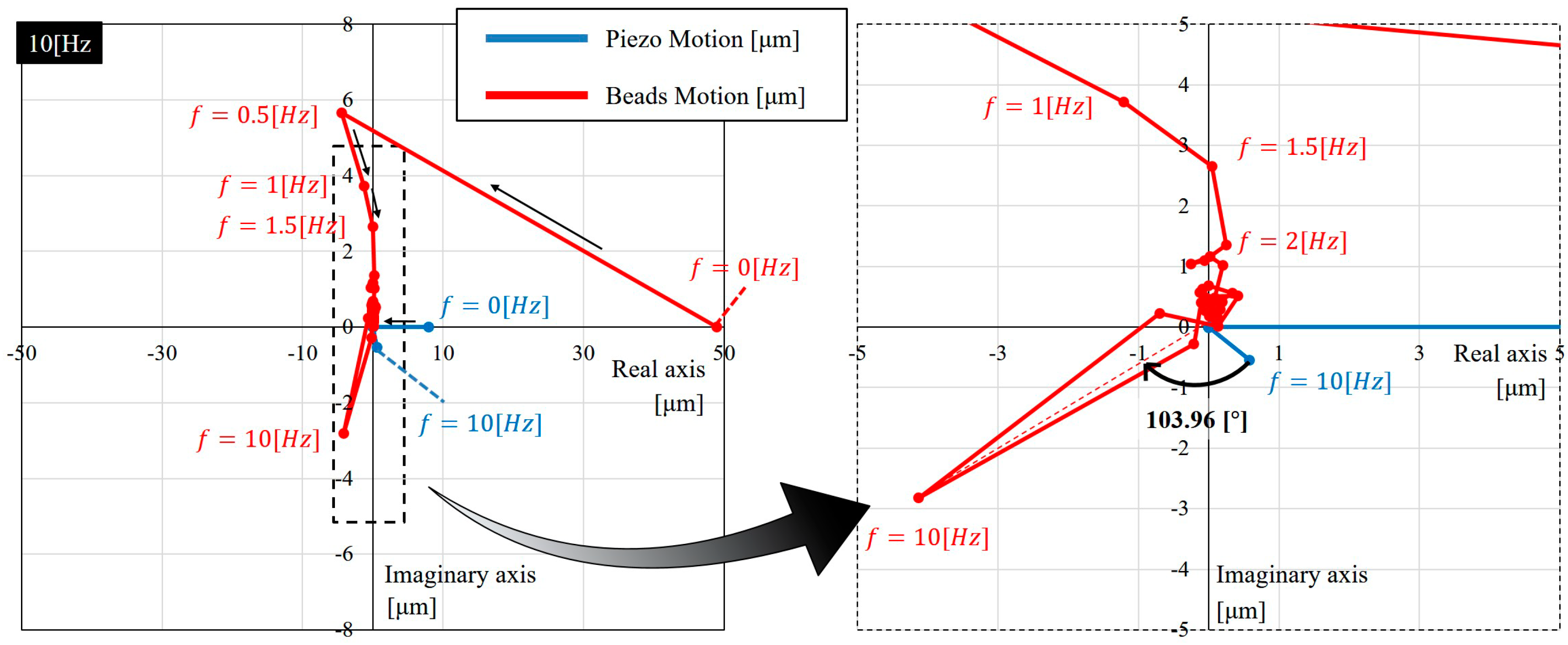
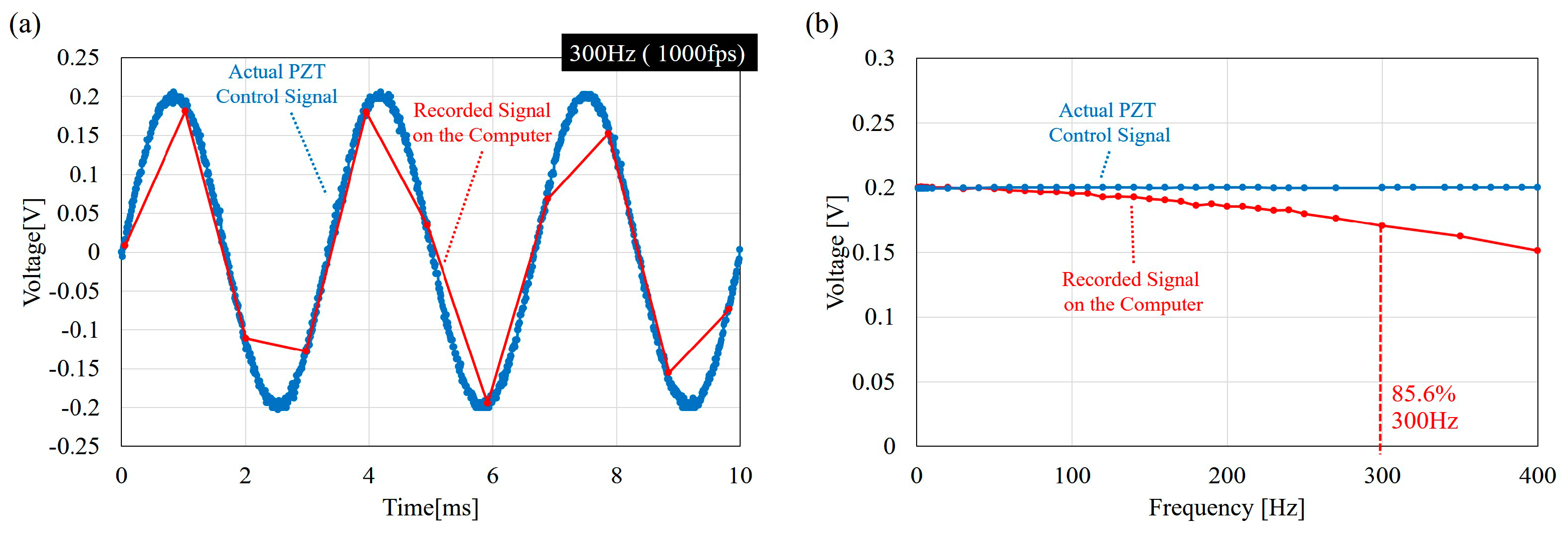
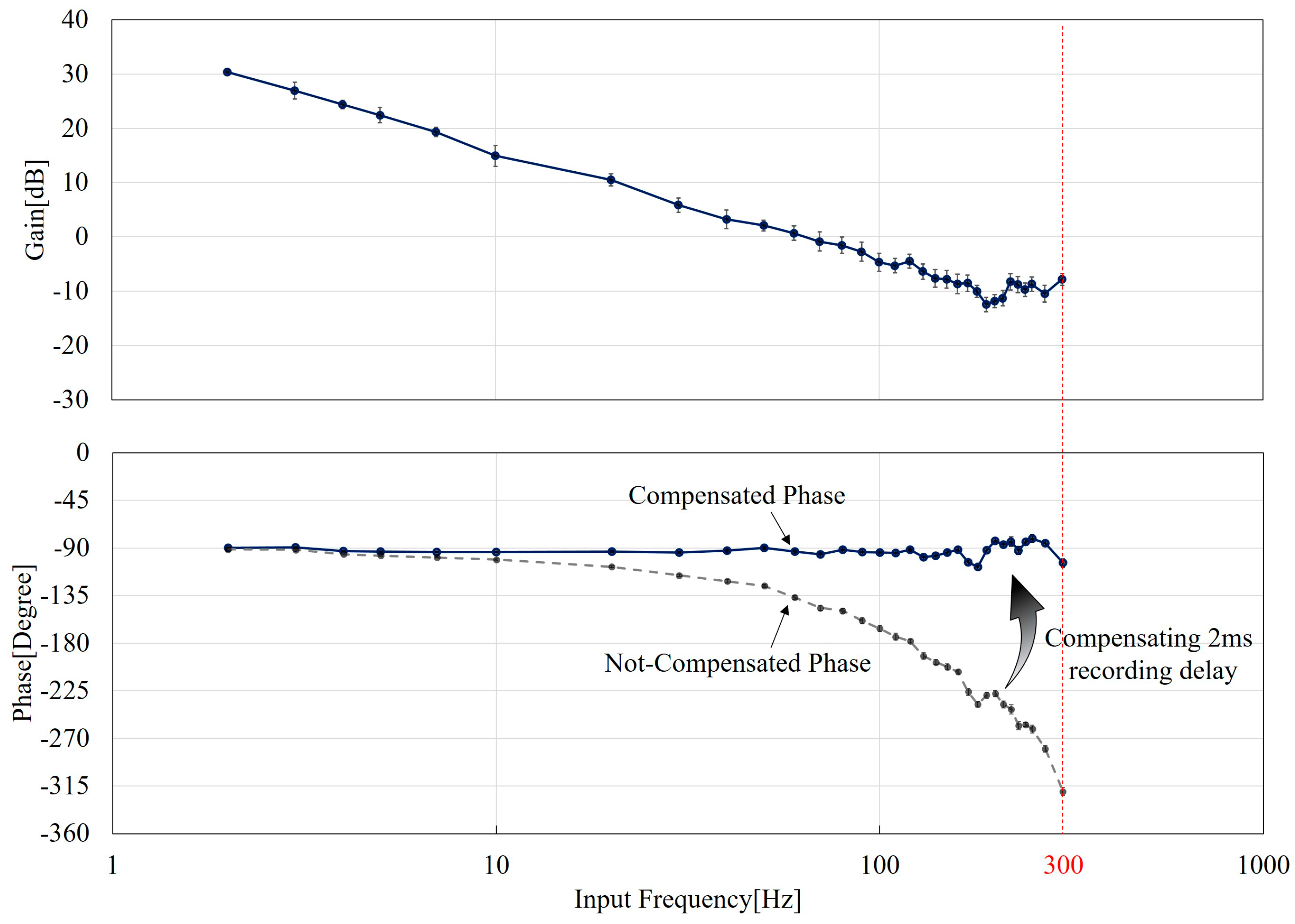
5. Results
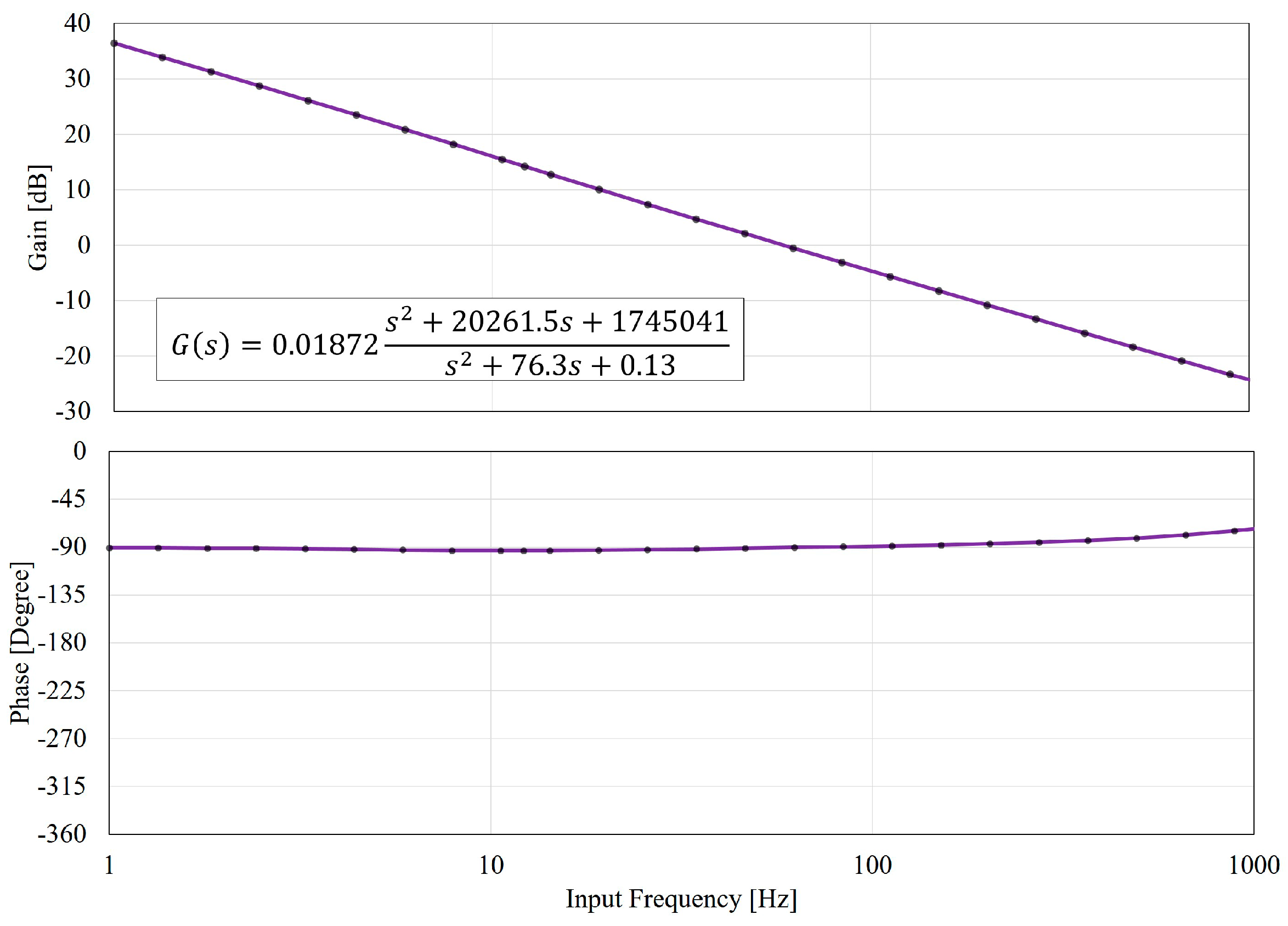
5.1. Input-Output Relation
5.2. The Gain and Phase Characteristics
6. Discussions
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
References
- Yun, H.; Kim, K.; Lee, W.G. Cell manipulation in microfluidics. Biofabrication 2013, 5, 22001. [Google Scholar] [CrossRef] [PubMed]
- Monzawa, T.; Kaneko, M.; Tsai, C.D.; Sakuma, S.; Arai, F. On-chip actuation transmitter for enhancing the dynamic response of cell manipulation using a macro-scale pump. Biomicrofluidics 2015, 9, 14114. [Google Scholar] [CrossRef] [PubMed]
- Bransky, A.; Korin, N.; Khoury, M.; Levenberg, S. A microfluidic droplet generator based on a piezoelectric actuator. Lab Chip 2009, 9, 516–520. [Google Scholar] [CrossRef] [PubMed]
- Anis, Y.; Houkal, J.; Holl, M.; Johnson, R.; Meldrum, D. Diaphragm pico-liter pump for single-cell manipulation. Biomed. Microdevices 2011, 13, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Kawahara, T.; Sugita, M.; Hagiwara, M.; Arai, F.; Kawano, H.; Shihira-Ishikawa, I.; Miyawaki, A. On-chip microrobot for investigating the response of aquatic microorganisms to mechanical stimulation. Lab Chip 2013, 13, 1070–1078. [Google Scholar] [CrossRef] [PubMed]
- Sakuma, S.; Kuroda, K.; Arai, F.; Taniguchi, T.; Ohtani, T.; Sakata, Y.; Kaneko, M. High Resolution Cell Positioning Based on a Flow Reduction Mechanism for Enhancing Deformability Mapping. Micromachines 2014, 5, 1188–1201. [Google Scholar] [CrossRef]
- Sakuma, S.; Kuroda, K. Realization of 240 nanometer resolution of cell positioning by a virtual flow reduction mechanism. In Proceedings of the 2014 IEEE 27th International Conference on Micro Electro Mechanical Systems (MEMS), San Francisco, CA, USA, 26–30 January 2014; pp. 1031–1034.
- Sakuma, S.; Kuroda, K.; Tsai, C.D.; Fukui, W.; Arai, F.; Kaneko, M. Red blood cell fatigue evaluation based on the close-encountering point between extensibility and recoverability. Lab Chip 2014, 14, 1135–1141. [Google Scholar] [CrossRef] [PubMed]
- Mizoue, K.; Phan, M.; Tsai, C.-H.; Kaneko, M.; Kang, J.; Chung, W. Gravity-based precise cell manipulation system enhanced by in-phase mechanism. Micromachines 2016, 7, 116. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.; Yamane, T. Optical trapping and manipulation of single cells using infrared laser beams. Nature 1987, 330, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Hellmich, W.; Pelargus, C.; Leffhalm, K.; Ros, A.; Anselmetti, D. Single cell manipulation, analytics, and label-free protein detection in microfluidic devices for systems nanobiology. Electrophoresis 2005, 26, 3689–3696. [Google Scholar] [CrossRef] [PubMed]
- Chronis, N.; Lee, L.P. Electrothermally activated SU-8 microgripper for single cell manipulation in solution. J. Microelectromechanical Syst. 2005, 14, 857–863. [Google Scholar] [CrossRef]
- Avci, E.; Ohara, K.; Nguyen, C.N.; Theeravithayangkura, C.; Kojima, M.; Tanikawa, T.; Mae, Y.; Arai, T. High-speed automated manipulation of microobjects using a two-fingered microhand. IEEE Trans. Ind. Electron. 2015, 62, 1070–1079. [Google Scholar] [CrossRef]
- Hagiwara, M.; Kawahara, T. High-speed magnetic microrobot actuation in a microfluidic chip by a fine V-groove surface. IEEE Trans. Robot. 2013, 29, 363–372. [Google Scholar] [CrossRef]
- McDaid, A.J.; Aw, K.C.; Haemmerle, E.; Shahinpoor, M.; Xie, S.Q. Adaptive tuning of a 2DOF controller for robust cell manipulation using IPMC actuators. J. Micromech. Microeng. 2011, 21, 125004. [Google Scholar] [CrossRef]
- Voldman, J. Electrical Forces for Microscale Cell Manipulation. Annu. Rev. Biomed. Eng. 2006, 8, 425–454. [Google Scholar] [CrossRef] [PubMed]
- Gedge, M.; Hill, M. Acoustofluidics 17: Theory and applications of surface acoustic wave devices for particle manipulation. Lab Chip 2012, 12, 2998. [Google Scholar] [CrossRef] [PubMed]
- Wood, C.D.; Evans, S.D.; Cunningham, J.E.; O’Rorke, R.; Wälti, C.; Davies, A.G. Alignment of particles in microfluidic systems using standing surface acoustic waves. Appl. Phys. Lett. 2008, 92, 10–13. [Google Scholar] [CrossRef]
- Bruus, H. Acoustofluidics 02: Perturbation theory and ultrasound resonance modes. Lab Chip 2012, 12, 20–28. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.H.; Chou, S.H.; Chiang, H.; Tsai, F.; Zhang, K.; Lo, Y. Specific sorting of single bacterial cells with microfabricated. Anal. Chem. 2011, 83, 7269–7275. [Google Scholar]
- Murakami, R.; Tsai, C.D.; Ito, H.; Tanaka, M.; Sakuma, S.; Arai, F.; Kaneko, M. Catch, Load and Launch toward On-Chip Active Cell Evaluation. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1713–1718.
- Armani, D.; Liu, C.; Aluru, N. Re-configurable fluid circuits by PDMS elastomer micromachining. In Proceedings of the 1999 IEEE 12th International Conference on Micro Electro Mechanical Systems (MEMS), Orlando, FL, USA, 17–21 January 1999; pp. 222–227.
- Schlichting, H. Boundary-Layer Theory; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Ahn, Y.-C.; Jung, W.; Chen, Z. Optical sectioning for microfluidics: Secondary flow and mixing in a meandering microchannel. Lab Chip 2008, 8, 125–133. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mizoue, K.; Teramura, K.; Tsai, C.-H.D.; Kaneko, M. Transfer Function of Macro-Micro Manipulation on a PDMS Microfluidic Chip. Micromachines 2017, 8, 80. https://doi.org/10.3390/mi8030080
Mizoue K, Teramura K, Tsai C-HD, Kaneko M. Transfer Function of Macro-Micro Manipulation on a PDMS Microfluidic Chip. Micromachines. 2017; 8(3):80. https://doi.org/10.3390/mi8030080
Chicago/Turabian StyleMizoue, Koji, Kaoru Teramura, Chia-Hung Dylan Tsai, and Makoto Kaneko. 2017. "Transfer Function of Macro-Micro Manipulation on a PDMS Microfluidic Chip" Micromachines 8, no. 3: 80. https://doi.org/10.3390/mi8030080