Mini and Micro Propulsion for Medical Swimmers
Abstract
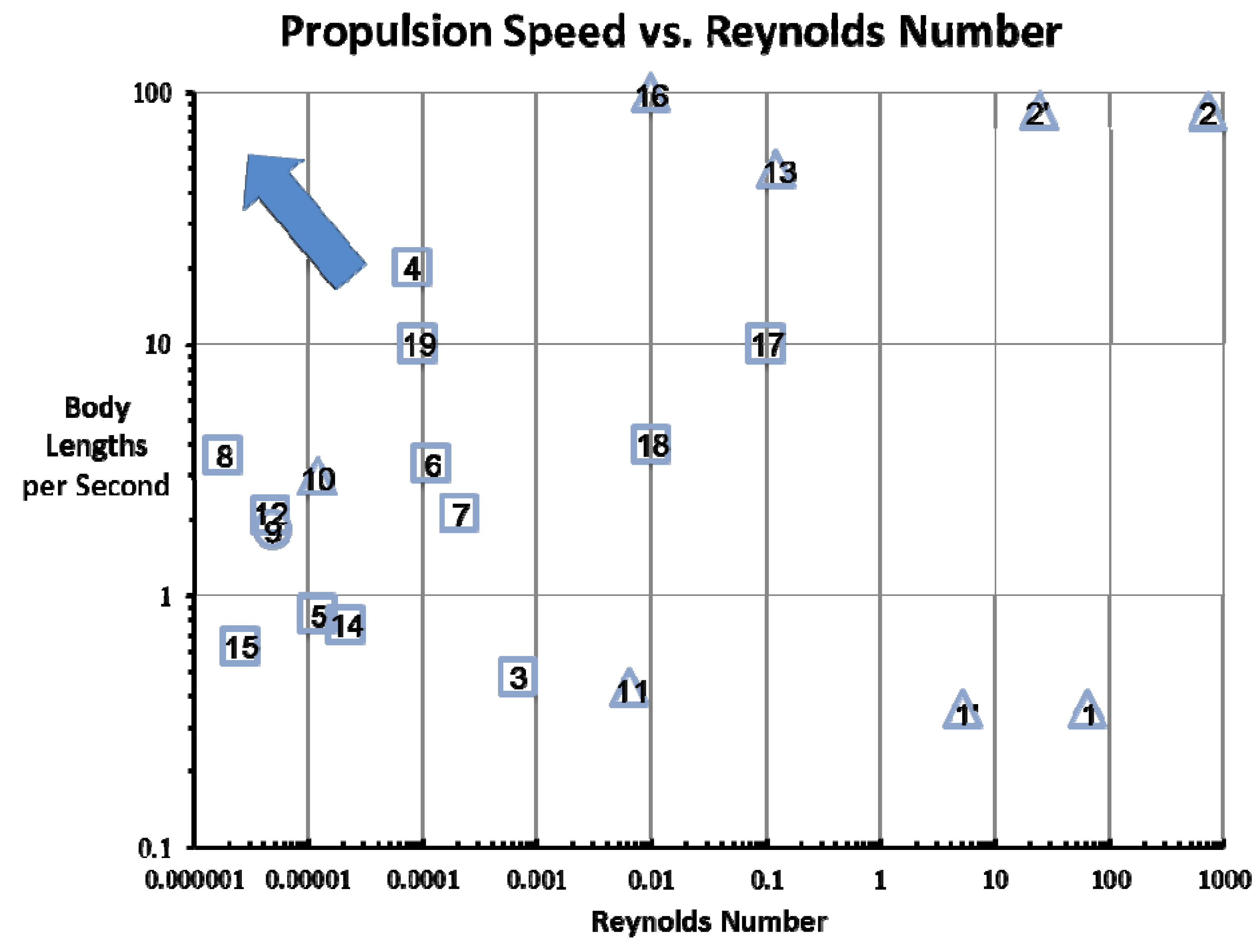
:1. Introduction

2. Propulsion in Millimeter Scale
3. Propulsion in Micron and Nano Scale
3.1. Propulsion by Irreversible Strokes
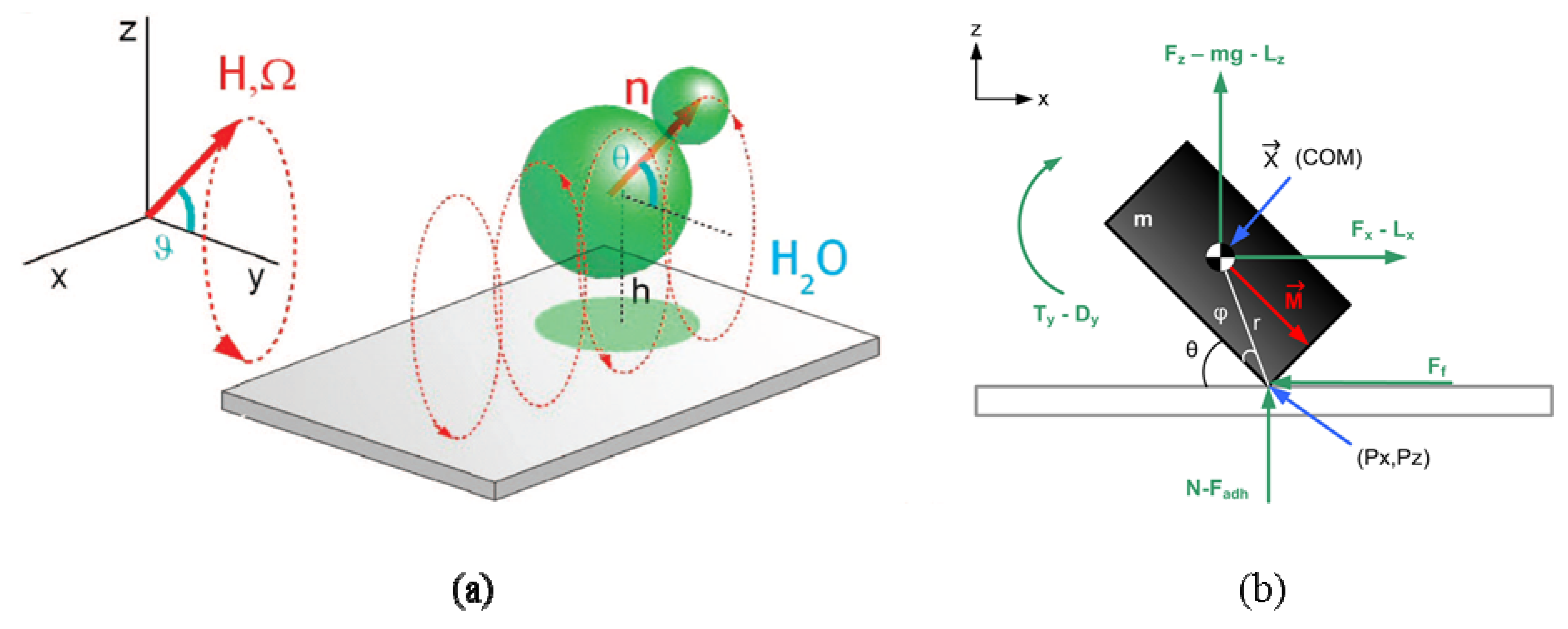
3.2. Propulsion by Bubbles

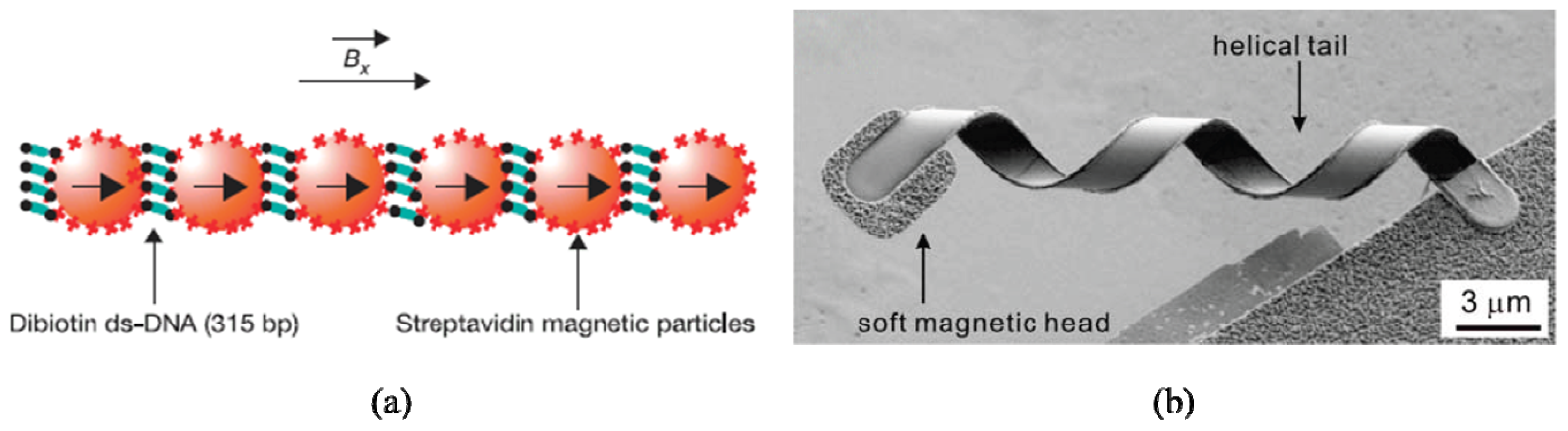
3.3. Propulsion by Magnetic Field
3.4. Propulsion by Biological Mechanism

3.5. Propulsion by Active Brownian Motion and Self Thermophoresis
3.6. Propulsion by Chemical Reaction

4. Concluding Remarks and Challenges
Acknowledgements
Conflicts of Interest
References
- Vince, G.; Wilson, C. The rise of the miniature medical robots. New Sci. 2009, 204, 50–53. [Google Scholar] [CrossRef]
- Sitti, M. Voyage of the microbots. Nature 2009, 458, 1121–1122. [Google Scholar] [CrossRef]
- Rubinstein, L. A Practical Nanorobot for Treatment of Various Medical Problems. In Proceedings of the 8th Foresight Conference on Molecular Nanotechnology, Bethesda, MD, USA, 2–5 November 2000.
- Fukuda, T.; Kawamoto, A.; Arai, F.; Matsuura, H. Mechanism and Swimming Experiment of Micro Mobile Robot in Water. In Proceedings of the 1994 IEEE International Conference on Micro Electro Mechanical Systems, Oiso, Japan, 25–28 January 1994; pp. 273–278.
- Wang, Z.; Wang, Y.; Li, J.; Hang, G. A Micro Biomimetic Manta Ray Robot Fish Actuated by SMA. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics, Guilin, China, 19–23 December 2009; pp. 1809–1813.
- Wang, Z.; Hang, G.; Li, J.; Wang, Y.; Xiao, K. A micro-robot fish with embedded SMA wire actuated flexible biomimetic fin. Sens. Actuators A 2008, 144, 354–360. [Google Scholar] [CrossRef]
- Shi, L.; Guo, S.; Asaka, K. A Novel Jellyfish-Like Biomimetic Microrobot. In Proceedings of the 2010 IEEEI/ICME International Conference on Complex Medical Engineering, Gold Coast, Australia, 13–15 July 2010; pp. 277–281.
- Guo, S.; Fukuda, T.; Asaka, K. A new type of fish-like underwater microrobot. IEEE/ASME Trans. Mechatron. 2003, 8, 136–141. [Google Scholar] [CrossRef]
- Guo, S.; Ge, Y. Underwater Swimming Micro Robot Using IPMC Actuator. In Proceedings of the 2006 IEEE International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 249–254.
- Kamamichi, N.; Yamakita, M.; Asaka, K.; Luo, Z.-W. A Snake-Like Swimming Robot Using IPMC Actuator/Sensor. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 1812–1817.
- Kim, B.; Kim, D.-H.; Jung, J.; Park, J.-O. A biomimetic undulatory tadpole robot using ionic polymer-metal composite actuators. Smart Mater. Struct. 2005, 14, 1579–1585. [Google Scholar] [CrossRef]
- Ming, A.; Park, S.; Nagata, Y.; Shimojo, M. Development of Underwater Robots Using Piezoelectric Fiber Composite. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May, 2009; pp. 3821–3826.
- Deng, X.; Avadhanula, S. Biomimetic Micro Underwater Vehicle with Oscillating Fin Propulsion: System Design and Force Measurement. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3312–3317.
- Liu, W.; Jia, X.; Wang, F.; Jia, Z. An in-pipe wireless swimming microrobot driven by giant magnetostrictive thin film. Sens. Actuators A 2010, 160, 101–108. [Google Scholar] [CrossRef]
- Toennies, J.L.; Tortora, G.; Simi, M.; Valdastri, P.; Webster, R.J. Swallowable medical devices for diagnosis and surgery: The state of the art. J. Mech. Eng. Sci. 2010, 224, 1397–1414. [Google Scholar] [CrossRef]
- Wang, J.; Manesh, K.M. Motion control at the nanoscale. Small 2009, 6, 338–345. [Google Scholar] [CrossRef]
- Lauga, E.; Powers, T.R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 2009, 72, 096601. [Google Scholar] [CrossRef]
- Brennen, C.; Winet, H. Fluid mechanics of propulsion by cilia and flagella. Ann. Rev. Fluid Mech. 1977, 9, 339–398. [Google Scholar] [CrossRef]
- Dijkink, R.J.; Dennen, van der Dennen, J.P.; Ohl, C.D.; Prosperetti, A. The “acoustic scallop”: A bubble-powered actuator. J. Micromech. Microeng. 2006, 16, 1653–1659. [Google Scholar] [CrossRef]
- Feng, J.; Cho, S.K. Micro Propulsion in Liquid by Oscillating Bubbles. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems, Taipei, Taiwan, 20–24 January 2013; pp. 63–66.
- Zhang, L.; Abbott, J.J.; Dong, L.; Peyer, K.E.; Kratochvil, B.E.; Zhang, H.; Bergeles, C.; Nelson, B.J. Characterizing the swimming properties of artificial bacterial flagella. Nano Lett. 2009, 9, 3663–3667. [Google Scholar] [CrossRef]
- Ghosh, A.; Fischer, P. Controlled propulsion of artificial magnetic nanostructured propellers. Nano Lett. 2009, 9, 2243–2245. [Google Scholar] [CrossRef]
- Tierno, P.; Golestanian, R.; Pagonabarraga, I.; Sagués, F. Magnetically actuated colloidal microswimmers. J. Phys. Chem. B 2008, 112, 16525–16528. [Google Scholar] [CrossRef]
- Martel, S.; Tremblay, C.C.; Ngakeng, S.; Langlois, G. Controlled manipulation and actuation of micro-objects with magnetotactic bacteria. Appl. Phys. Lett. 2006, 89, 233904. [Google Scholar] [CrossRef]
- Behkam, B.; Sitti, M. Bacterial flagella-based propulsion and on/off motion control of microscale objects. Appl. Phys. Lett. 2007, 90, 023902. [Google Scholar] [CrossRef]
- Williams, B.J.; Anand, S.V.; Rajagopalan, J.; Saif, M.T.A. A self-propelled biohybrid swimmer at low Reynolds number. Nat. Commun. 2014, 5, 3081. [Google Scholar] [CrossRef]
- Howse, J.R.; Jones, R.A.L.; Ryan, A.J.; Gough, T.; Vafabakhsh, R.; Golestanian, R. Self-motile colloidal particles: From directed propulsion to random walk. Phys. Rev. Lett. 2007, 99, 048102. [Google Scholar] [CrossRef]
- Gibbs, J.G.; Zhao, Y.-P. Autonomously motile catalytic nanomotors by bubble propulsion. Appl. Phys. Lett. 2009, 94, 1613104. [Google Scholar] [CrossRef]
- Vicario, J.; Eelkema, R.; Browne, W.R.; Meetsma, A.; Crois, R.M.L.; Feringa, B.L. Catalytic molecular motors: Fuelling autonomous movement by a surface bound synthetic manganese catalase. Chem. Commun. 2005, 3936–3938. [Google Scholar]
- Solovev, A.A.; Mei, Y.; Ureña, E.B.; Huang, G.; Schmidt, O.G. Catalytic microtubular jet engines self-propelled by accumulated gas bubbles. Small 2009, 5, 1688–1692. [Google Scholar] [CrossRef]
- Gao, W.; Uygun, A.; Wang, J. Hydrogen-bubble-propelled zinc-based microrockets in strongly acidic media. J. Am. Chem. Soc. 2012, 134, 897–900. [Google Scholar] [CrossRef]
- Kline, T.R.; Paxton, W.F.; Mallouk, T.E.; Sen, A. Catalytic nanomotors: Remote-controlled autonomous movement of striped metallic nanorods. Angew. Chem. Int. Ed. 2005, 44, 744–746. [Google Scholar] [CrossRef]
- Sundararajan, S.; Lammert, P.E.; Zudans, A.W.; Crespi, V.H.; Sen, A. Catalytic motors for transport of colloidal cargo. Nano Lett. 2008, 8, 1272–1276. [Google Scholar]
- Burdick, J.; Laocharoensuk, R.; Wheat, P.M.; Posner, J.D.; Wang, J. Synthetic nanomotors in microchannel networks: Directional microchip motion and controlled manipulation of cargo. J. Am. Chem. Soc. 2008, 130, 8164–8165. [Google Scholar]
- Buttinoni, I.; Volpe, G.; Kümmel, F.; Volpe, G.; Bechinger, C. Active Brownian motion tunable by light. J. Phys. Condens. Matter 2012, 24, 2841296. [Google Scholar] [CrossRef]
- Purcell, E.M. Life at low Reynolds number. Am. J. Phys. 1977, 45, 3–11. [Google Scholar] [CrossRef]
- Abbott, J.J.; Peyer, K.E.; Lagomarsino, M.C.; Zhang, L.; Dong, L.; Kaliakatsos, I.K.; Nelson, B.J. How should microrobots swim? Int. J. Robot. Res. 2009, 28, 1434–1447. [Google Scholar]
- Becker, L.E.; Koehler, S.A.; Stone, H.A. On self-propulsion of micro-machines at low Reynolds number: Purcell’s three-link swimmer. J. Fluid Mech. 2003, 490, 15–35. [Google Scholar] [CrossRef]
- Najafi, A.; Golestanian, R. A simplest swimmer at low Reynolds number: Three linked spheres. Phys. Rev. E 2004, 69, 063901. [Google Scholar] [CrossRef]
- Leoni, M.; Kotar, J.; Bassetti, B.; Cicuta, P.; Lagomarsino, M.C. A basic swimmer at low Reynolds number. Soft Matter 2009, 5, 472–476. [Google Scholar] [CrossRef]
- Plesset, M.S.; Prosperetti, A. Bubble dynamics and cavitation. Ann. Rev. Fluid Mech. 1977, 9, 145–185. [Google Scholar] [CrossRef]
- Ahmed, D.; Mao, X.; Shi, J.; Juluri, B.K.; Huang, T.J. A millisecond micromixer via single-bubble-based acoustic streaming. Lab Chip 2009, 9, 2738–2741. [Google Scholar]
- Tsai, J.-H.; Lin, L. Active microfluidic mixer and gas bubble filter driven by thermal bubble micropump. Sens. Actuators A 2002, 97–98, 665–671. [Google Scholar] [CrossRef]
- Chen, X.M.; Prosperetti, A. Thermal processes in the oscillations of gas bubbles in tubes. J. Acoust. Soc. Am. 1998, 104, 1389–1398. [Google Scholar] [CrossRef]
- Geng, X.; Yuan, H.; Og̃uz, H.N.; Prosperetti, A. The oscillation of gas bubbles in tubes: Experimental results. J. Acoust. Soc. Am. 1999, 106, 674–681. [Google Scholar] [CrossRef]
- Jenkins, A. An elementary treatment of the reverse sprinkler. Am. J. Phys. 2004, 72, 1276–1282. [Google Scholar] [CrossRef]
- Jenkins, A. Sprinkler head revisited: Momentum, forces, and flows in machian propulsion. Eur. J. Phys. 2011, 32, 1213–1226. [Google Scholar] [CrossRef]
- Feng, J.; Cho, S.K. Two-Dimensionally Steering Microswimmer Propelled by Oscillating Bubbles. In Proceedings of the 2014 IEEE 27th International Conference on Micro Electro Mechanical Systems, San Francisco, CA, USA, 26–30 January 2014.
- Ryu, K.; Zueger, J.; Chung, S.K.; Cho, S.K. Underwater Propulsion Using AC-Electrowetting-Actuated Oscillating Bubbles for Swimming Robots. In Proceedings of the 2010 IEEE 23rd International Conference on Micro Electro Mechanical Systems, Wanchai, Hong Kong, 24–28 January 2010; pp. 160–163.
- Zhao, Y.; Cho, S.K. Micro air bubble manipulation by electrowetting on dielectric (EWOD): Transporting, splitting, merging and eliminating of bubbles. Lab Chip. 2007, 7, 273–280. [Google Scholar] [CrossRef]
- Qiao, L.; Luo, C. Propulsion of a microsubmarine using a thermally oscillatory approach. J. Micromech. Microeng. 2013, 23, 105011. [Google Scholar] [CrossRef]
- Gillies, G.T.; Ritter, R.C.; Broaddus, W.C.; Grady, M.S.; Howard, M.A.I.; McNeil, R.G. Magnetic manipulation instrumentation for medical physics research. Rev. Sci. Instrum. 1994, 65, 533–562. [Google Scholar] [CrossRef]
- Ishiyama, K.; Arai, K.I.; Sendoh, M.; Yamazaki, A. Spiral-Type Micro-Machine for Medical Applications. In Proceedings of the 2000 International Symposium on Micromechatronics and Human Science, Nagoya, Japan, 22–25 October 2000; pp. 65–69.
- Dreyfus, R.; Baudry, J.; Roper, M.L.; Fermigier, M.; Stone, H.A.; Bibette, J. Microscopic artificial swimmers. Nature 2005, 437, 862–865. [Google Scholar] [CrossRef]
- Cox, R.G. Motion of long slender bodies in a viscous fluid. Part I. General theory. J. Fluid Mech. 1970, 44, 791–810. [Google Scholar] [CrossRef]
- Purcell, E.M. The efficiency of propulsion by a rotating flagellum. Proc. Natl. Acad. Sci. USA 1997, 94, 11307–11311. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Moldovan, R.; Yeung, C.; Wu, X.L. Swimming efficiency of bacterium Escherichia coli. Proc. Natl. Acad. Sci. USA 2006, 103, 13712–13717. [Google Scholar] [CrossRef]
- Zhang, L.; Abbott, J.J.; Dong, L.; Kratochvil, B.E.; Bell, D.; Nelson, B.J. Artificial bacterial flagella: Fabrication and magnetic control. Appl. Phys. Lett. 2009, 94, 064107. [Google Scholar] [CrossRef]
- Bell, D.J.; Leutenegger, S.; Hammar, K.M.; Dong, L.X.; Nelson, B.J. Flagella-Like Propulsion for Microrobots Using a Nanocoil and a Rotating Electromagnetic Field. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 1128–1133.
- Zhang, L.; Ruh, E.; Grützmacher, D. Anomalous coiling of SiGe/Si and SiGe/Si/Cr helical nanobelts. Nano Lett. 2006, 6, 1311–1317. [Google Scholar] [CrossRef]
- Temel, F.Z.; Yesilyurt, S. Magnetically Actuated Micro Swimming of Bio-Inspired Robots in Mini Channels. In Proceedings of the 2011 IEEE Intemational Conference on Mechatronics, Istanbul, Turkey, 13–15 April 2011; pp. 342–347.
- Gao, W.; Sattayasamitsathit, S.; Manesh, K.M.; Weihs, D.; Wang, J. Magnetically powered flexible metal nanowire motors. J. Am. Chem. Soc. 2010, 132, 14403–14405. [Google Scholar] [CrossRef]
- Floyd, S.; Pawashe, C.; Sitti, M. An Untethered Magnetically Actuated Micro-Robot Capable of Motion on Arbitrary Surfaces. In Proceedings of the 2008 IEEE International Conference on Robotics and AutomationPasadena, CA, USA, 19–23 May 2008; pp. 419–424.
- Lee, H.; Purdon, A.M.; Chu, V.; Westervelt, R.M. Controlled assembly of magnetic nanoparticles from magnetotactic bacteria using microelectromagnets arrays. Nano Lett. 2004, 4, 995–998. [Google Scholar] [CrossRef]
- Hiratsuka, Y.; Miyata, M.; Tada, T.; Uyeda, T.Q.P. A microrotary motor powered by bacteria. PNAS 2006, 103, 13618–13623. [Google Scholar] [CrossRef]
- Tarhan, M.C.; Yokokawa, R.; Bottier, C.; Collard, D.; Fujita, H. A nano-needle/microtubule composite gliding on a kinesin-coated surface for target molecule transport. Lab Chip. 2010, 10, 86–91. [Google Scholar] [CrossRef]
- Fujimoto, K.; Kitamura, M.; Yokokawa, M.; Kanno, I.; Kotera, H.; Yokokawa, R. Colocalization of quantum dots by reactive molecules carried by motor proteins on polarized microtubule arrays. ACS Nano 2013, 7, 447–455. [Google Scholar] [CrossRef]
- Vogel, V.; Hess, H. Nanoshuttles: Harnessing Motor Proteins to Transport Cargo in Synthetic Environments. In Controlled Nanoscale Motion; Linke, H., Månsson, A., Eds.; Månsson, A.,Eds.; Springer: Heidelberg, Germany, 2007; pp. 367–383. [Google Scholar]
- Hanggi, P.; Marchesoni, F. Artificial Brownian motors: Controlling transport on the nanoscale. Rev. Mod. Phys. 2009, 81, 387–442. [Google Scholar] [CrossRef]
- Volpe, G.; Buttinoni, I.; Vogt, D.; Kümmerer, H.-J.; Bechinger, C. Microswimmers in patterned environments. Soft Matter 2011, 7, 8810–8815. [Google Scholar] [CrossRef]
- Golestanian, R.; Liverpool, T.B.; Ajdari, A. Designing phoretic micro- and nano-swimmers. New J. Phys. 2009, 9, 126. [Google Scholar] [CrossRef]
- Jiang, H.-R.; Yoshinaga, N.; Sano, M. Active motion of a Janus particle by self-thermophoresis in a defocused laser beam. Phys. Rev. Lett. 2010, 105, 268302. [Google Scholar] [CrossRef]
- Córdova-Figueroa, U.M.; Brady, J.F. Osmotic propulsion: The osmotic motor. Phys. Rev. Lett. 2008, 100, 158303. [Google Scholar] [CrossRef]
- Paxton, W.F.; Baker, P.T.; Kline, T.R.; Wang, Y.; Mallouk, T.E.; Sen, A. Catalytically induced electrokinetics for motors and micropumps. J. Am. Chem. Soc. 2006, 14881–14888. [Google Scholar]
- Wang, Y.; Hernandez, R.M.; Bartlett, D.J., Jr.; Bingham, J.M.; Kline, T.R.; Sen, A.; Mallouk, T.E. Bipolar electrochemical mechanism for the propulsion of catalytic nanomotors in hydrogen peroxide solutions. Langmuir 2006, 22, 10451–10456. [Google Scholar] [CrossRef]
- Loget, G.; Kuhn, A. Propulsion of microobjects by dynamic bipolar self-regeneration. J. Am. Chem. Soc. 2010, 132, 15918–15919. [Google Scholar] [CrossRef]
- Sumino, Y.; Magome, N.; Hamada, T.; Yoshikawa, K. Self-running droplet: Emergence of regular motion from nonequilibrium noise. Phys. Rev. Lett. 2005, 94, 068301. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
JianFeng; Cho, S.K. Mini and Micro Propulsion for Medical Swimmers. Micromachines 2014, 5, 97-113. https://doi.org/10.3390/mi5010097
JianFeng, Cho SK. Mini and Micro Propulsion for Medical Swimmers. Micromachines. 2014; 5(1):97-113. https://doi.org/10.3390/mi5010097
Chicago/Turabian StyleJianFeng, and Sung Kwon Cho. 2014. "Mini and Micro Propulsion for Medical Swimmers" Micromachines 5, no. 1: 97-113. https://doi.org/10.3390/mi5010097
APA StyleJianFeng, & Cho, S. K. (2014). Mini and Micro Propulsion for Medical Swimmers. Micromachines, 5(1), 97-113. https://doi.org/10.3390/mi5010097