Approaches for a Fair Comparison and Benchmarking of Electromagnetic Vibration Energy Harvesters
Abstract
:1. Introduction
2. Benchmarking Parameters for Different Harvesting Mechanisms
3. Benchmarking of Resonant Electrodynamic Harvesters
- viscid drag
- lateral laminar flow Couette damping
- lateral laminar flow Stokes damping (Stokes damping here refers to the expression for small frequencies and air gaps)
- perpendicular laminar flow squeeze film damping
3.1. Viscid Damping
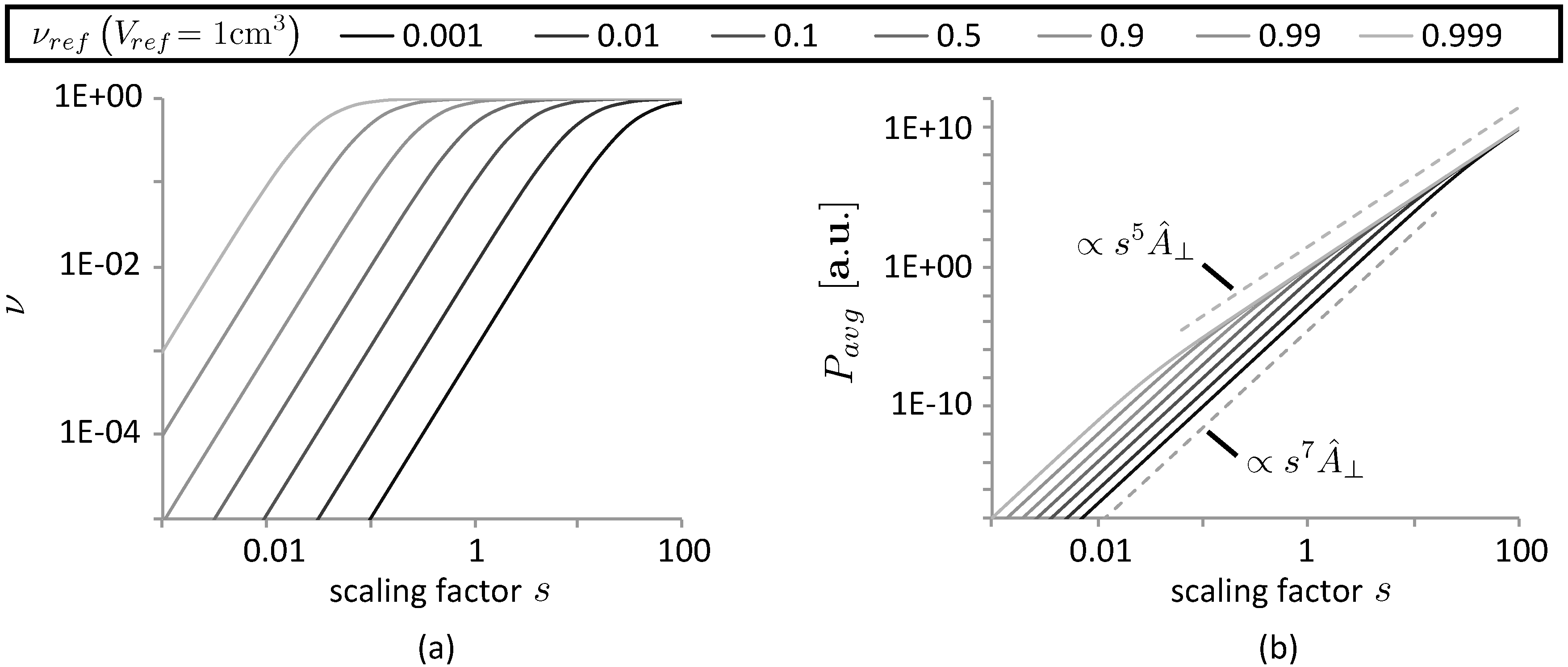
3.2. Material Damping
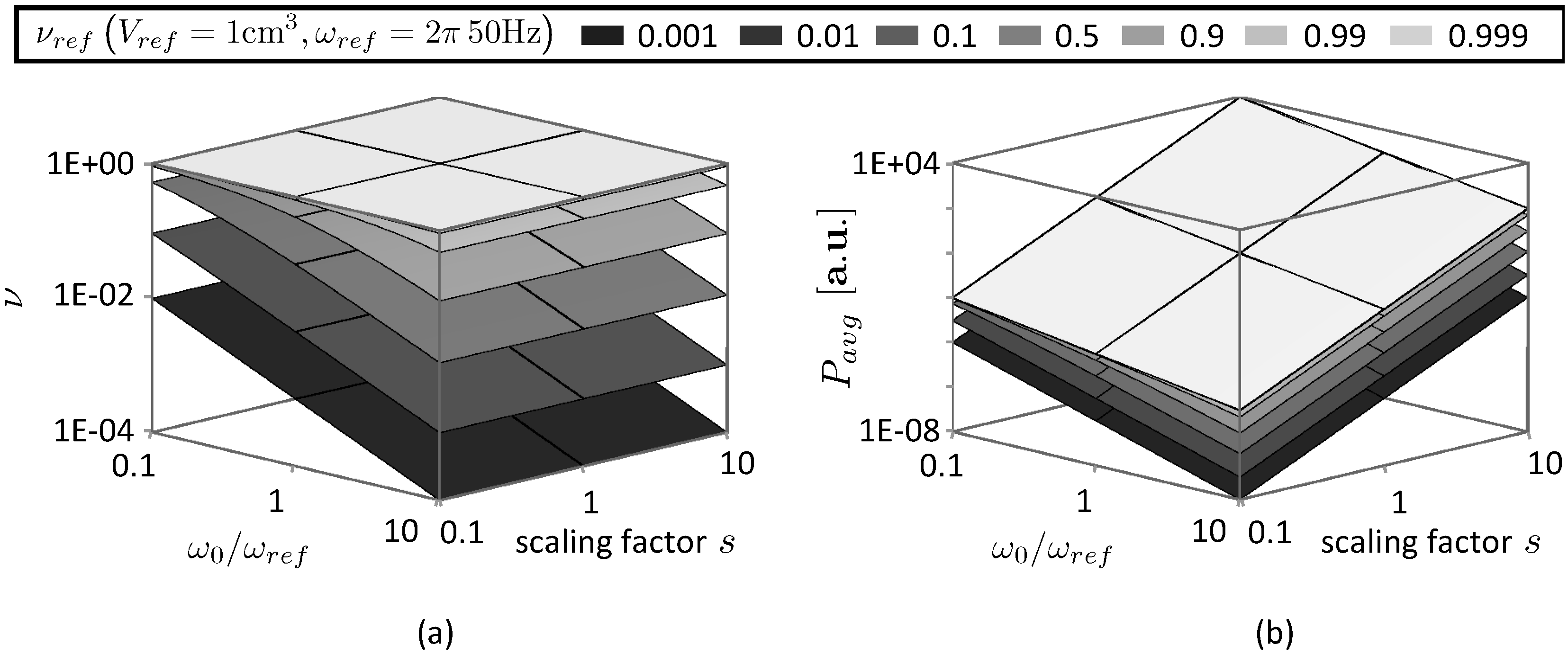
- inversely proportional to at a given acceleration
- proportional to the acceleration at a given and
- proportional to when and constant when
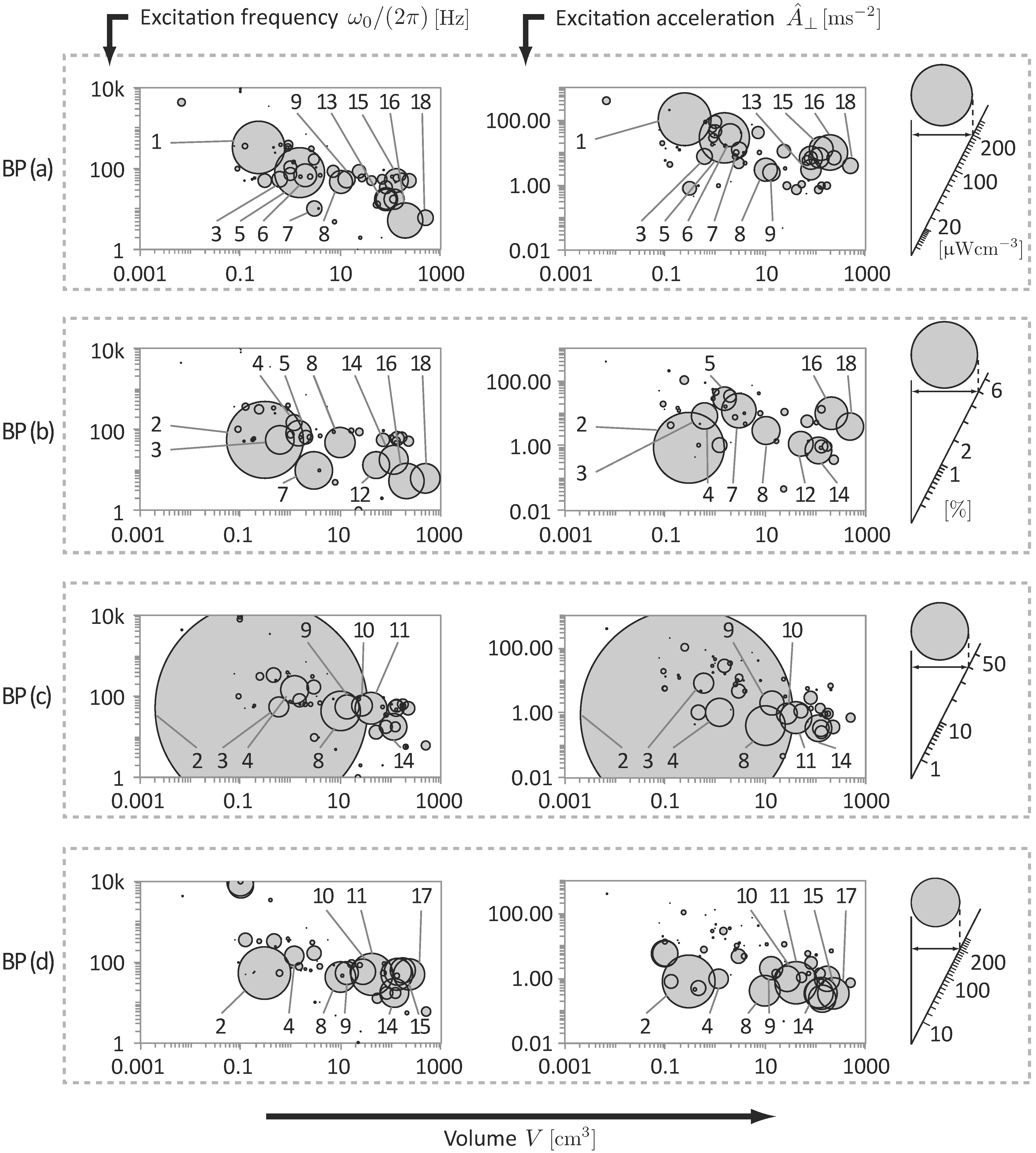
4. Benchmarking of Published Prototypes
- measurements taken only at excitations where the BPs result in low values
- an unfavorable aspect ratio, housing or included electronic circuit
- restricting boundary conditions
- a non-resonant harvester concept with different physics and, finally
- the fact, that the harvester was not effectively optimized
| # | Reference | |||||
|---|---|---|---|---|---|---|
| 1 | [15] MKI | 0.24 | 9 | 322 | 102 | 530 |
| 2 | [16] MKII | 0.3 | 6.2 | 51.6 | 0.83 | 45 |
| 3 | [17] | 0.6 | 6 | 54 | 7.9 | 115 |
| 4 | [18] | 1.2 | 3 | 143 | 1 | 12 |
| 5 | [19] | 1.50 | 15 | 80 | 28 | 3000 |
| 6 | [20] | 2.0 | 11 | 66 | 34.4 | 830 |
| 7 | [21] | 3.0 | 12 | 10 | 11.8 | 545 |
| 8 | [8 ] (updated) | 10.0 | 36.5 | 45.3 | 3 | 4200 |
| 44.6 | 0.4 | 138 | ||||
| 9 | [22] | 13.3 | 32 | 55.9 | 2.0 | 2050 |
| 2.5 | 3100 | |||||
| 10 | [23] | 27 | - | 57 | 0.98 | 1200 |
| 11 | [24] PMG7 | 41.3 | - | 50 | 0.71 | 3000 |
| 12 | [25] | 52 | 40 | 13.1 | 1.1 | 2000 |
| 13 | [26,27] | 80.0 | - | 17 | 7 | 33, 800 |
| 3 | 26, 000 | |||||
| 14 | [28] | 117 | 53 | 17.2 | 0.35 | 2850 |
| 15 | [29] | 130.7 | 55 | 50 | 13.9 | 58, 500 |
| 16 | [30] | 200 | 160 | 5.4 | 10 | 200, 000 |
| 17 | [31] | 229 | 63 | 50 | 0.35 | 2280 |
| 18 | [32] | 500 | 100 | 6 | 0.71 | 15, 000 |
| # | Design | Reference | ν | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | harvester (1) | [15] MKI | 0.15 | * | * | 2100 | ||||
| 2 | harvester (1) | [16] MKII1 | * | 0.23 | * | 0.00075* | 0.86* | 2000* | 18% | |
| 3 | harvester (27) | [17] | - | - | - | - | 0.0001 | - | 81 | - |
| 4 | harvester (30) | [18] | 7.7% | 1.00 | 0.33 | 8.4×10‒3 | 0.077 | 0.89 | 2900 | 0.8% |
| 5 | harvester (8) | [19] | - | - | - | - | - | - | 1000 | 37% |
| 6 | harvester (14) | [20] | - | - | - | - | - | - | - | - |
| 7 | harvester (10) | [21]2 | 0.5% | 0.13 | 0.02 | 3.7×10‒6 | - | 0.006 * | 1100 | - |
| 8 | harvester (28) | [8] | 4.5% | 0.38 | 0.67 | 7.7×10‒3 | 0.18 | 0.96 | 3500 | 1.5% |
| 9 | similar to (23) | [22] | 2.6% | 0.60 | 0.18 | 5.05×10‒4 | 0.85 | 0.82 | 1000 | 1.4% |
| 10 | [23] | - | - | - | - | - | - | - | - | |
| 11 | [24] PMG7 | - | - | - | - | - | - | 2050 | - | |
| 12 | harvester (1) | [25] | - | - | - | - | - | - | 820 | - |
| 13 | [26,27] | - | - | - | - | - | - | - | - | |
| 14 | [28] | - | - | - | - | - | - | - | - | |
| 15 | harvester (26) | [29] | - | - | - | - | - | - | - | - |
| 16 | harvester (5) | [30] | - | - | - | - | - | - | 177 | - |
| 17 | [31] | - | - | - | - | - | - | - | - | |
| 18 | NOT equal to (7) | [32] | - | - | - | - | - | - | - | - |
4.1. BP (c): Resonant Electrodynamic Harvesters with Viscid Damping
4.2. BP (d): Resonant Electrodynamic Harvesters with Material Damping
4.3. BP (a): Power Density
4.4. BP (b): Vibration Power Limit
5. Implications on Design
6. Conclusions
A. Derivation of Material Damping
Acknowledgments
Conflict of Interest
References
- Cepnik, C.; Lausecker, R.; Wallrabe, U. Review on electrodynamic energy harvesters-a classification approach. Micromachines, in press.
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy harvesting from human and machine motion for wireless electronic devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef] [Green Version]
- Arnold, D. Review of microscale magnetic power generation. Magn. IEEE Trans. 2007, 43, 3940–3951. [Google Scholar] [CrossRef]
- Stephen, N. On energy harvesting from ambient vibration. J. Sound Vib. 2006, 293, 409–425. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Green, T.C.; Yeatman, E.M.; Holmes, A.S. Architectures for vibration-driven micropower generators. J. Microelectromechan. Syst. 2004, 13, 429–440. [Google Scholar] [CrossRef]
- Mitcheson, P.; Reilly, E.; Toh, T.; Wright, P.; Yeatman, E. Performance limits of the three MEMS inertial energy generator transduction types. J. Micromech. Microeng. 2007, 17, 211–216. [Google Scholar] [CrossRef]
- Cepnik, C.; Wallrabe, U. On the Comparison, Scaling and Benchmarking of Electromagnetic Vibration Harvesters. In Proceedings of PowerMEMS 2011, Seoul, Korea, 15–18 November 2011; pp. 70–73.
- Cepnik, C.; Radler, O.; Rosenbaum, S.; Ströhla, T.; Wallrabe, U. Effective optimization of electromagnetic energy harvesters through direct computation of the electromagnetic coupling. Sens. Actuators A 2011, 167, 416–421. [Google Scholar] [CrossRef]
- Hang Bao, M. Micro Mechanical Transducers; Elsevier Science: Amsterdam, The Netherlands, 2000; Volume 8. [Google Scholar]
- Buser, R.; de Rooij, N. Very high Q-factor resonators in monocrystalline silicon. Sens. Actuators A 1990, 21, 323–327. [Google Scholar] [CrossRef]
- Johari, H.; Shah, J.; Ayazi, F. High Frequency XYZ-axis Single-Disk Silicon Gyroscope. In Proceedings of the IEEE 21st International Conference on Micro Electro Mechanical Systems, Tucson, AZ, USA, 13–17 January 2008; pp. 856–859.
- Kim, B.; Hopcroft, M.; Candler, R.; Jha, C.; Agarwal, M.; Melamud, R.; Chandorkar, S.; Yama, G.; Kenny, T. Temperature dependence of quality factor in MEMS resonators. J. Microelectromechan. Syst. 2008, 17, 755–766. [Google Scholar] [CrossRef]
- Lifshitz, R.; Roukes, M. Thermoelastic damping in micro-and nanomechanical systems. Phys. Rev. B 2000, 61, 5600–5609. [Google Scholar] [CrossRef]
- Prikhodko, I.; Zotov, S.; Trusov, A.; Shke, A. Sub-degree-per-hour Silicon MEMS Rate Sensor with 1 Million Q-Factor. In Proceedings of the Transducers’11, IEEE, Beijing, China, 5–9 June 2011; pp. 2809–2812.
- El-Hami, M.; Glynne-Jones, P.; White, N.; Hill, M.; Beeby, S.; James, E.; Brown, A.; Ross, J. Design and fabrication of a new vibration-based electromechanical power generator. Sens. Actuators A 2001, 92, 335–342. [Google Scholar] [CrossRef]
- Beeby, S.; Torah, R.; Tudor, M.; Glynne-Jones, P.; O’Donnell, T.; Saha, C.; Roy, S. A micro electromagnetic generator for vibration energy harvesting. J. Micromech. Microeng. 2007, 17, 1257–1265. [Google Scholar] [CrossRef]
- Park, J.; Bang, D.; Park, J. Micro-fabricated electromagnetic power generator to scavenge low ambient vibration. Magn. IEEE Trans. 2010, 46, 1937–1942. [Google Scholar] [CrossRef]
- Cepnik, C.; Wallrabe, U. A Flat High Performance Micro Energy Harvester Based on a Serpentine Coil with a Single Winding. In Proceedings of the Transducers’11, IEEE, Beijing, China, 5–9 June 2011; pp. 661–664.
- Spreemann, D.; Manoli, Y.; Folkmer, B.; Mintenbeck, D. Non-resonant vibration conversation. J. Micromech. Microeng. 2006, 16, 169–173. [Google Scholar] [CrossRef]
- Ching, N.N.H.; Wong, H.Y.; Li, W.J.; Leong, P.H.W.; Wen, Z. A laser-micromachined multi-modal resonating power transducer for wireless sensing systems. Sens. Actuators A 2002, 97–98, 685–690. [Google Scholar] [CrossRef]
- Zorlu, O.; Topal, E.; Kulah, H. A vibration-based electromagnetic energy harvester using mechanical frequency up-conversion method. Sens. J. IEEE 2011, 11, 481–488. [Google Scholar] [CrossRef]
- Spreemann, D.; Manoli, Y. Electromagnetic Vibration Energy Harvesting Devices: Architectures, Design, Modeling and Optimization. Ph.D. Thesis, University of Freiburg, Freiburg, Germany, 2012. [Google Scholar]
- Waters, R.; Chisum, B.; Jazo, H.; Fralick, M. Development of an Electro-Magnetic Transducer for Energy Harvesting of Kinetic Energy and Its’ Applicability to a MEMS-Scale Device. In Proceedings of the Nanopower Forum, Irvine, CA, USA, 2–4 June 2008.
- Beeby, S.; Tudor, M.; Torah, R.; Roberts, S.; O’Donnell, T.; Roy, S. Experimental comparison of macro and micro scale electromagnetic vibration powered generators. Microsyst. Technol. 2007, 13, 1647–1653. [Google Scholar] [CrossRef]
- Saha, C.; O’Donnell, T.; Loder, H.; Beeby, S.; Tudor, J. Optimization of an electromagnetic energy harvesting device. IEEE Trans. Magn. 2006, 42, 3509–3511. [Google Scholar] [CrossRef]
- Hadas, Z.; Zouhar, J.; Singule, V.; Ondrusek, C. Design of Energy Harvesting Generator Base on Rapid Prototyping Parts. In Proceedings of the 13th Power Electronics and Motion Control Conference (EPE/PEMC), IEEE, Poznan, Poland, 1–3 September 2008; pp. 1665–1669.
- Hadas, Z.; Singule, V.; Ondrusek, Č. Optimal design of vibration power generator for low frequency. Solid State Phenom. 2009, 147, 426–431. [Google Scholar]
- PMG27, Technical report; Perpetuum Ltd.: Southampton, UK, 2009.
- PMG17, Technical report; Perpetuum Ltd.: Southampton, UK, 2009.
- Mann, B.; Owens, B. Investigations of a nonlinear energy harvester with a bistable potential well. J. Sound d Vib. 2010, 329, 1215–1226. [Google Scholar] [CrossRef]
- PMG FSH, Technical report; Perpetuum Ltd.: Southampton, UK, 2009.
- Sasaki, K.; Osaki, Y.; Okazaki, J.; Hosaka, H.; Itao, K. Vibration-based automatic power-generation system. Microsyst. Technol. 2005, 11, 965–969. [Google Scholar] [CrossRef]
- Barton, D.; Burrow, S.; Clare, L. Energy harvesting from vibrations with a nonlinear oscillator. J. Vib. Acoust. 2010, 132. [Google Scholar] [CrossRef]
- Torah, R.; Beeby, S.; Tudor, M.; O’Donnell, T.; Roy, S. Development of a Cantilever Beam Generator Employing Vibration Energy Harvesting. In Proceedings of the PowerMEMS 2006, Berkeley, CA, USA, 29 November–1 December 2006; pp. 181–184.
- Roberts (Hampshire, GB), S.; Perpetuum Ltd. Electromechanical Generator for Converting Mechanical Vibrational Energy into Electrical Energy. Patent WO2007020383A1, 2007. [Google Scholar]
- Roberts (Hampshire, GB), S.; Perpetuum Ltd. Electromechanical Generator for Converting Mechanical Vibrational Energy into Electrical Energy. Patent WO2008132423A1, 2008. [Google Scholar]
- Roberts (Hampshire, GB), S.; Perpetuum Ltd. Electromechanical Generator for Converting Mechanical Vibrational Energy into Electrical Energy. Patent WO2009068856A3, 2009. [Google Scholar]
- Kulkarni, S.; Koukharenko, E.; Torah, R.; Tudor, J.; Beeby, S.; O’Donnell, T.; Roy, S. Design, fabrication and test of integrated micro-scale vibration-based electromagnetic generator. Sens. Actuators A 2008, 145, 336–342. [Google Scholar] [CrossRef]
- Koukharenko, E.; Tudor, M.; Beeby, S. Performance improvement of a vibration-powered electromagnetic generator by reduced silicon surface roughness. Mater. Lett. 2008, 62, 651–654. [Google Scholar] [CrossRef]
- Friedrich, K.; Wagner, N.; Bessler, W. Entwicklungsperspektiven von Li-Schwefel und Li-Luft-Batterien, Technical report; Institut für Technische Thermodynamik, Deutsches Zentrum für Luft- und Raumfahrt e.V., Energiespeichersymposium Stuttgart 2012: Stuttgart, Germany, 3 September 2013.
- Hadas, Z.; Ondrsek, C.; Singule, V. Power sensitivity of vibration energy harvester. Microsyst. Technol. 2010, 16, 691–702. [Google Scholar] [CrossRef]
- Stemme, G. Resonant silicon sensors. J. Micromech. Microeng. 1991, 1, 113–125. [Google Scholar] [CrossRef]
- Koyama, T.; Bindel, D.; He, W.; Quévy, E.; Govindjee, S.; Demmel, J.; Howe, R. Simulation Tools for Damping in High Frequency Resonators. In Proceedings of the IEEE Sensors, Irvine, CA, USA, 30 October–3 November 2005; pp. 1–4.
- Goodman, L. Material damping and slip damping. In Harris’ Shock and Vibration Handbook, 5th ed.; McGRAW-Hill: New York, NY, USA, 2002; pp. 36.1–36.30. [Google Scholar]
- Lazan, B. Effect of damping constants and stress distribution on the resonance response of members, Technical report, DTIC Document. 1952.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cepnik, C.; Wallrabe, U. Approaches for a Fair Comparison and Benchmarking of Electromagnetic Vibration Energy Harvesters. Micromachines 2013, 4, 286-305. https://doi.org/10.3390/mi4030286
Cepnik C, Wallrabe U. Approaches for a Fair Comparison and Benchmarking of Electromagnetic Vibration Energy Harvesters. Micromachines. 2013; 4(3):286-305. https://doi.org/10.3390/mi4030286
Chicago/Turabian StyleCepnik, Clemens, and Ulrike Wallrabe. 2013. "Approaches for a Fair Comparison and Benchmarking of Electromagnetic Vibration Energy Harvesters" Micromachines 4, no. 3: 286-305. https://doi.org/10.3390/mi4030286




