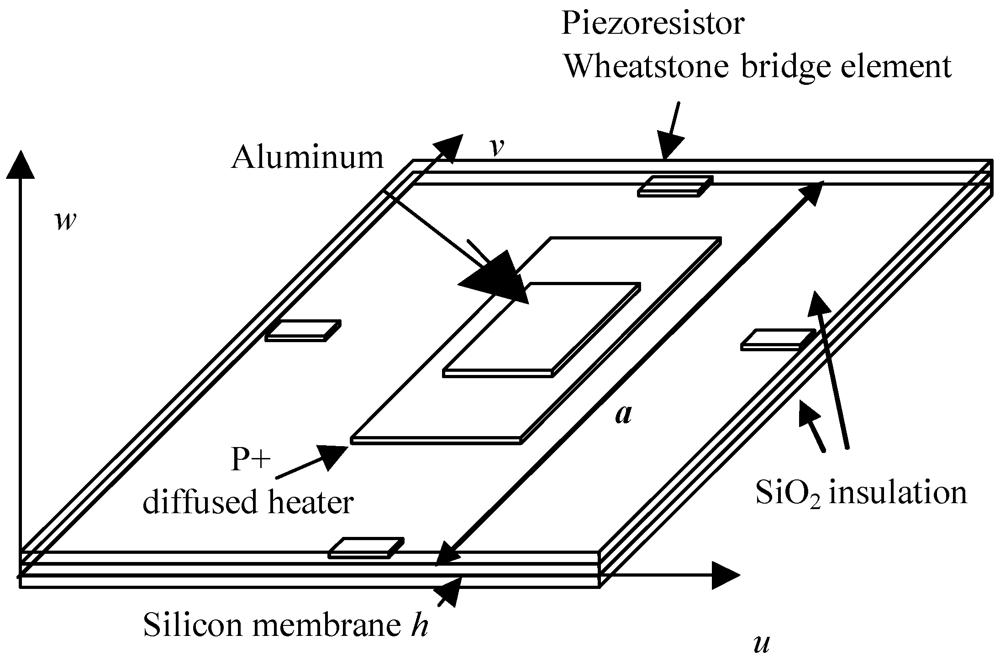
4.1. Finite Element Analysis
In order to investigate the time dependent vibration behavior of the membranes under sudden loads, a commercially available software package, COMSOL Multiphysics®, was used with its electrostatic-DC, heat conduction and stress-strain modules. The 3D domain consists of 2 subdomains: a silicon-membrane (2.5 mm × 2.5 mm × 15 µm) with a heating resistor (1.2 mm × 0.8 mm × 5 µm) embedded in the top 5 µm of the membrane. Stress-strain and heat equations are solved in both domains but the electrostatic equation is only solved in the resistor. For the electrostatic equation, a sheet resistance of 100 Ω/sq is used for the resistor. To obtain numerical convergence, rather than utilizing a step function, a 20 V bias is ramped at one end of the resistor in 5 µs and is left on for 20 µs before it is removed. For the stress-strain equation, simply supported boundary conditions were applied to all edges of the membrane.
The phase lag effect in the heat transfer analysis is not considered due to the fact that our analysis does not focus on what happens in the immediate vicinity of the thermal excitation but rather on the long-term oscillatory behavior that results from this thermal excitation. For this reason, the damping effect was not included in the stress-strain equation. However, it was expected that intrinsic thermal damping would lead to a quick decay of the oscillations [
16] and result in a change in the vibration frequency. This effect on the vibration frequency would be significant but small and fall within an acceptable difference if we take into account the other approximations that are assumed in this analysis.
The material properties of both domains for the stress-strain and the heat transfer equations, typical bulk properties of silicon, are listed in
Table 1. We took into account the anisotropy of the Young’s modulus of silicon reported in [
17] but realize that for small displacement, as is the case in these structures, the plane cross-section, which is initially perpendicular to the axis of the plate, is assumed to remain planar and perpendicular to the neutral axis during bending. As such, the stress-strain equation only needs to be solved for the x and y directions according to the orientation convention presented in
Figure 1. For (100) oriented silicon wafers, the Young’s modulus in the perpendicular directions of the axis of the membrane are equal according to [
17]. Thin oxide and aluminum layers are neglected in the simulations because their geometries with high aspect ratios would require much higher mesh requirements.
The resistor is meshed by 36 and 54 elements along its long edges while the long outer edges of the membrane are meshed by 37 elements each. Both domains have 1 element in thickness. Mesh points are interpolated by quadratic elements for temperature, electric potential and displacement field variables. The discretization leads to approximately 47,600 tetrahedral elements and 368,500 degrees of freedom. This time dependent problem was solved by the iterative Biconjugate Gradient Stabilized Method solver while the variables were fully coupled. Geometric Multigrid V-Cycle was utilized by lowering element orders to linear. A Successive Order Relaxation algorithm was used as the pre and post smoother in addition to a Parallel Direct Sparse Solver as the coarse solver. The solver took strictly half microsecond time steps with relative and absolute tolerances of 10−4 and 10−5 respectively.
The results match those predicted by the theory presented in the previous section indicating that the sudden thermal load sets the membrane in motion to vibrate at its natural frequency. The typical energy bias applied to the membrane shows only a slight increase in temperature of the membrane, matching the measurements shown in [
9]. The initial response is to move either up or down, depending on the layers of materials on the membrane, and oscillate around this static displacement location. This correlates with the theory developed by Boley [
10] as well as with our electrical measurements presented below. As the heat dissipates away from the center of the membrane the membrane will relax back to the starting position.
Joule heating results in a temperature increase at the center of the membrane. The temperature increase, due to the bias conditions of 20 V for 20 µs, is only 3.3 °C. This confirms the measurements taken with the in-situ diodes presented in [
9]. This peak temperature is reached in 35 µs, 10 µs after the heating bias has been removed. The temperature will then decay slowly down to room temperature.
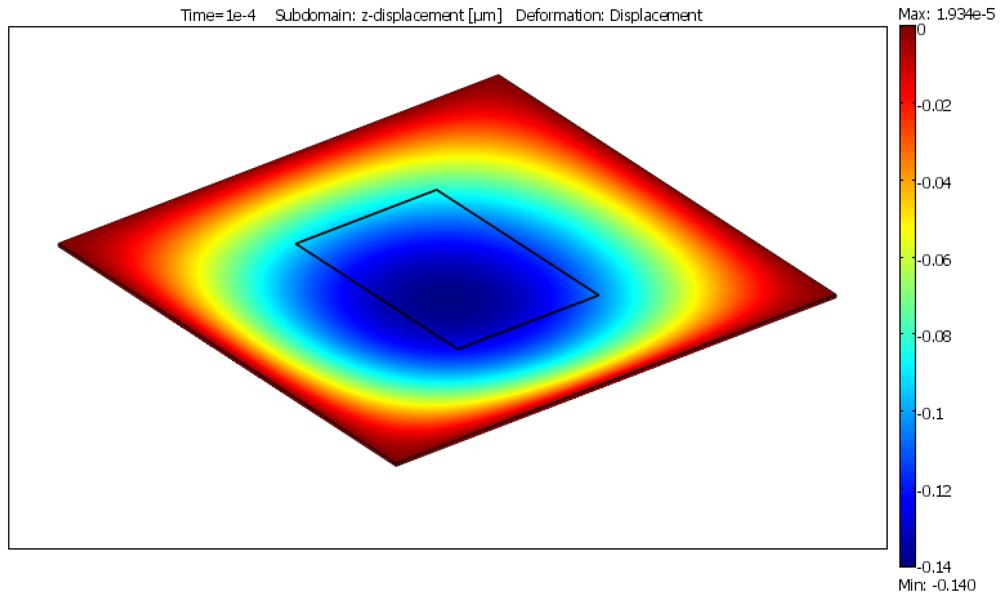
The temperature distribution of the membrane near its peak temperature is shown in
Figure 7. It can be observed that the temperature is highest at the center of the membrane and follows the same shape of the heating resistor and becomes more circular in shape as the heat leaves this region.
Figure 7.
Temperature distribution of the membrane after a 20 V–20 µs pulse.
Figure 7.
Temperature distribution of the membrane after a 20 V–20 µs pulse.
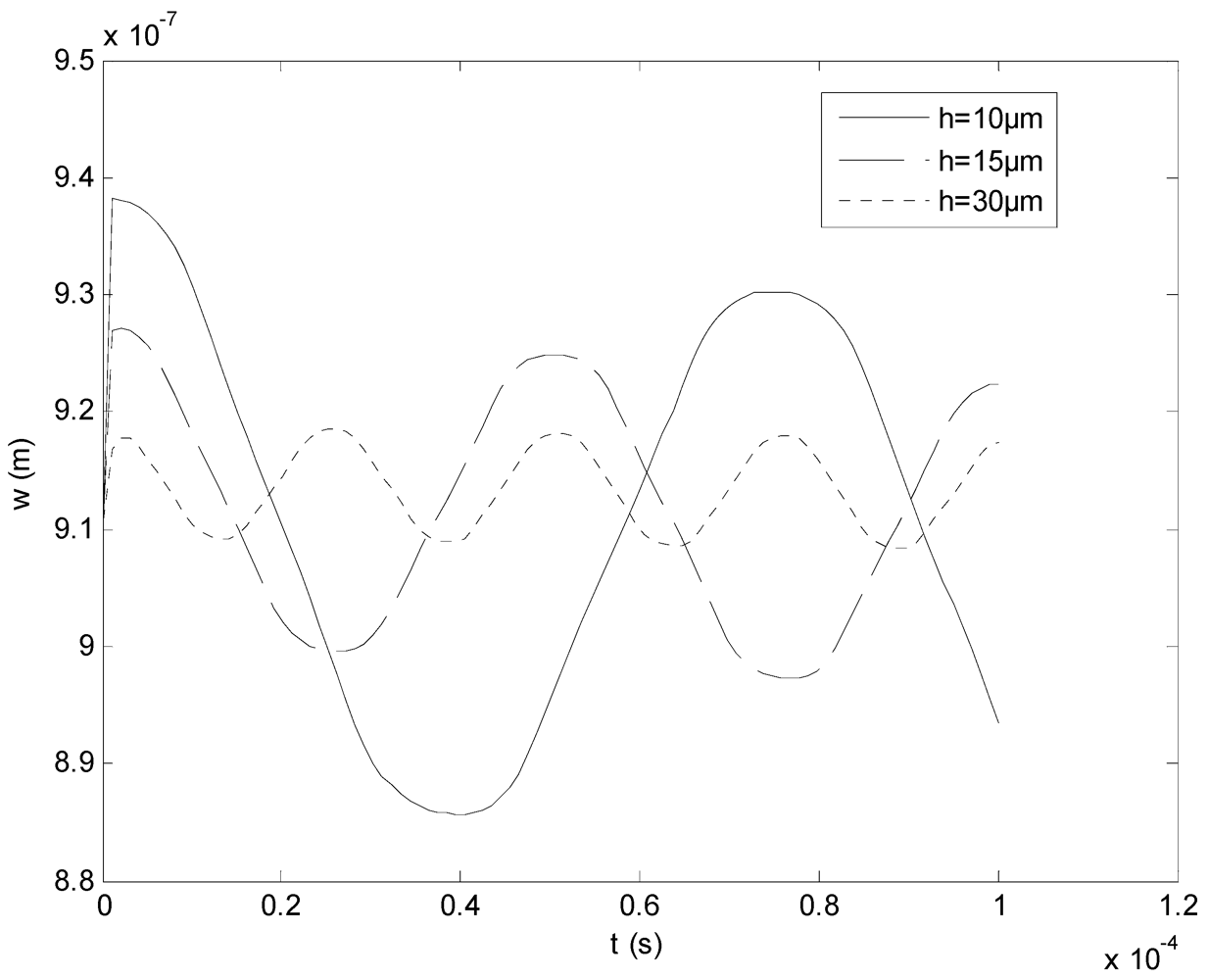
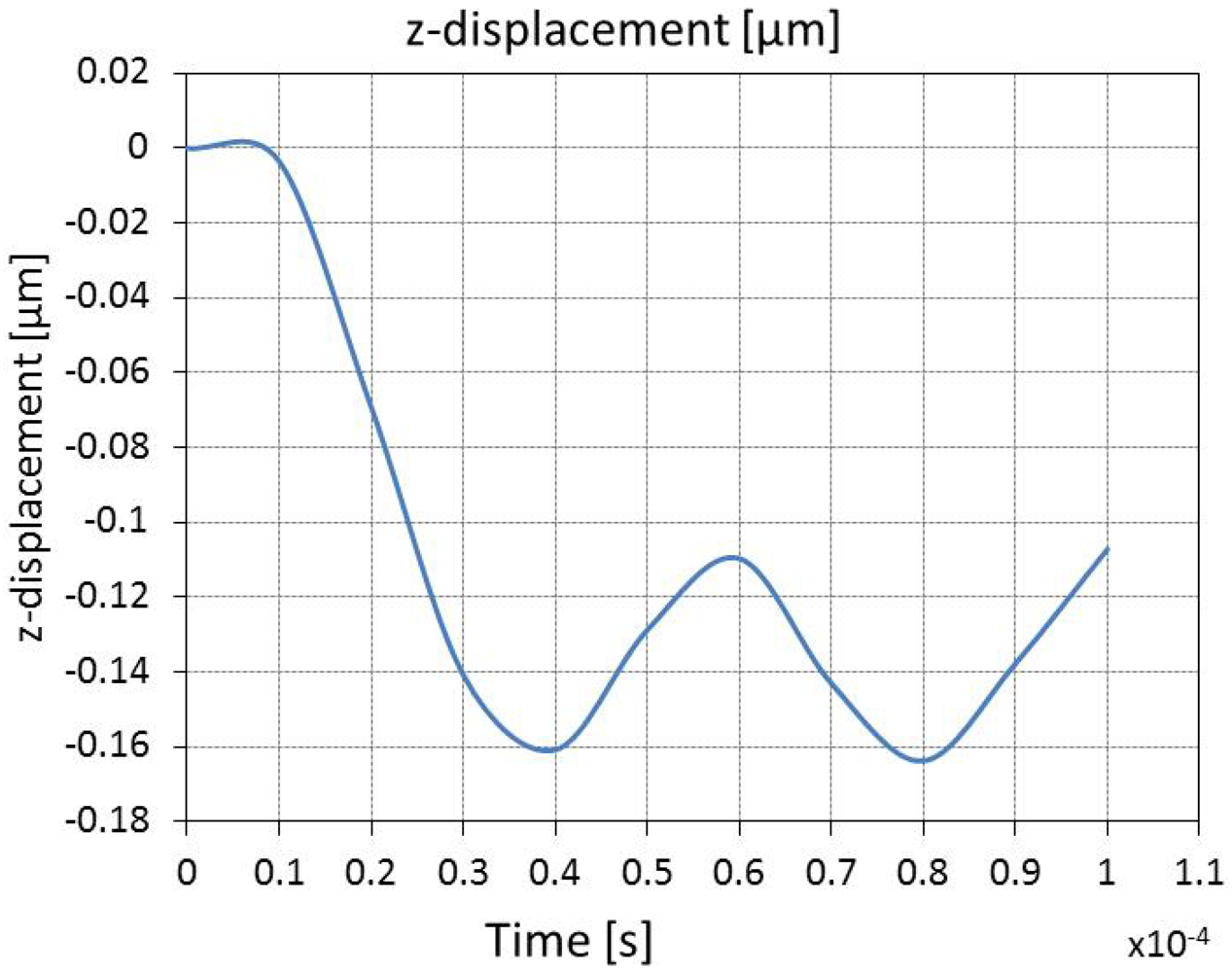
Figure 8 shows the time progression of the vertical displacement of the center of the membrane. As predicted by the theory and observed in the experimental data, the membrane will experience a static displacement and a dynamic displacement. The static displacement is lower than that predicted by the theory presented in the previous sections, but the simulation results match what is observed experimentally. This difference could be due to the choice of the parabolic heat transfer model instead of the more accurate hyperbolic model that is suggested by [
11]. We are not concerned about this initial displacement as our sensor application relies on the cyclical vibration that takes place after this initial displacement; the dynamic displacement.
Figure 8.
Membrane response to a 20 V–20 µs pulse of a 2.5 mm silicon membrane with a P+ diffused heater.
Figure 8.
Membrane response to a 20 V–20 µs pulse of a 2.5 mm silicon membrane with a P+ diffused heater.
The dynamic displacement value of ~60 nm around the static displacement matches both the theoretical and experimental results. The period of the oscillation is 41 µs, a frequency of 24,390 Hz, which is the natural frequency of vibration of this membrane structure [
12]. Thus, confirming that the inertia given to the membrane through the burst of heat will set the membrane to mechanically oscillate at its natural frequency.
Figure 9.
Membrane deformation in response to a 20 V–20 µs pulse of a 2.5 mm silicon membrane with a P+ diffused heater.
Figure 9.
Membrane deformation in response to a 20 V–20 µs pulse of a 2.5 mm silicon membrane with a P+ diffused heater.
The shape of the membrane during this oscillation is important in order to determine its interaction with the fluid being tested. As seen in
Figure 9, the deformation shape does not follow the shape of the heater. Instead, it takes a circular shape due to the boundary constraints of the simply supported square membrane. As such, it is important to conclude that the shape of the membrane during actuation will be assumed to be the same independent of the size and shape of the heater.
4.1. Mode of Vibration
In order to observe the mode of vibration of the membranes we analyzed the shape of the membrane using two different excitation schemes. First we used a piezoelectric actuator to find the resonant frequency of the membranes and observed the vibration mode shape. This allowed us to verify the frequency and mode of vibration. Secondly, we used a burst heat excitation through the in situ membrane heaters to set the membrane to vibrate freely and then we captured one full cycle of the vibration. Both of these measurements were performed using the Dynamic MEMS (DMEMS) option of Veeco’s Wyko NT-1100TM real-time dynamic optical surface profiler. The DMEMS option allows the user to synchronize the actuator signal with profilometer measurements to obtain accurate measurements of the surface of the sample.
A fabricated device was affixed with epoxy to a piezoelectric actuator as shown in
Figure 10. This piezoelectric actuator was biased with a high voltage by the DMEMS system and moved up and down. This movement also affected the devices, which were glued to its surface. The membrane of the device being tested was monitored by performing a surface profile measurement at a synchronized time interval. The frequency of the signal was increased until the surface profile indicated a resonant condition of the membrane. This happens when the deflection of the membrane dramatically increases with respect to the fixed frame of the structure. Once the frequency of resonance was determined, additional surface profiles were taken during one full cycle of resonance.
Figure 10.
Sensor glued to piezoelectric actuator to explore resonant frequency and mode of vibration of the membranes.
Figure 10.
Sensor glued to piezoelectric actuator to explore resonant frequency and mode of vibration of the membranes.
Figure 11 shows a composite of pictures illustrating a full oscillation cycle of a device with a P+ diffused heater in 40 degree increments. It can be observed that the membrane is originally down and it will oscillate up and down by a few nanometers. The data presented here shows that this displacement is not enough to break the original horizontal plane of the device. The measured resonant frequency of 14,500 Hz falls within the expected values for such a device. The mode of resonance is the fundamental mode, up and down in the center of the membrane, which is desired for the fluid measurements to be undertaken. The amplitude of the oscillation is relative to the amplitude of the actuator and is not relevant as it will be different, and much lower, when heat excitation is utilized.
Figure 11.
Full cycle of resonance of membrane actuated via a piezoelectric actuator.
Figure 11.
Full cycle of resonance of membrane actuated via a piezoelectric actuator.
This measurement is important because it confirms that the fabricated structures will vibrate in the (1,1) mode when excited at their natural frequency. The result confirms the validity of the boundary conditions assumed during both the analytical and simulation analysis. In the next section we analyze the vibration behavior of the membrane in response to heat excitation. If the shape and frequency of this vibration matches the results obtained here, it will indicate that the membrane is indeed vibrating at its natural frequency.
4.2. Free Vibration with Heat Excitation
The DMEMS measurement capabilities in the Wyko profilometer require that the movement of the structure to be measured is cyclical. The surface measurements are taken over several cycles at a determined time interval, which is synchronized with the actuation signal. As seen in the previous section, this is straightforward when the structure moves at the same frequency as the actuation signal. On the other hand, to measure the free vibration of a structure as a response to an impact load, as is the case in our devices, the measuring technique needs to be modified.
It is important to understand the nature of the excitation and the expected response of the structure in order to obtain accurate measurements. As such, an oscilloscope is used to electrically monitor the membrane movement. As can be seen in
Figure 12, the membrane will start to oscillate as soon as the excitation signal is removed. The heater is rapidly increased to −15 V for 20 µs at the end of the cycle in order to line up the sensor response at t = 0 of the next cycle. The frequency of oscillation of this particular device, D11, is 17,224 Hz and the oscillation decays to noise level after 20 cycles or ~1 ms.
Figure 12.
Heat excitation and membrane signal output during profilometer measurements.
Figure 12.
Heat excitation and membrane signal output during profilometer measurements.
The actuation signal was set to a frequency of 500 Hz, which corresponds to a period of 2 ms. The Wyko tool will perform measurements at a given time interval according to this actuation signal frequency. Dividing this time period by the 360 degrees, which the tool assumes as the full cycle of the oscillations, results in 5.556 µs/degree.
Figure 13.
Detail of membrane electrical signal output during profilometer measurements.
Figure 13.
Detail of membrane electrical signal output during profilometer measurements.
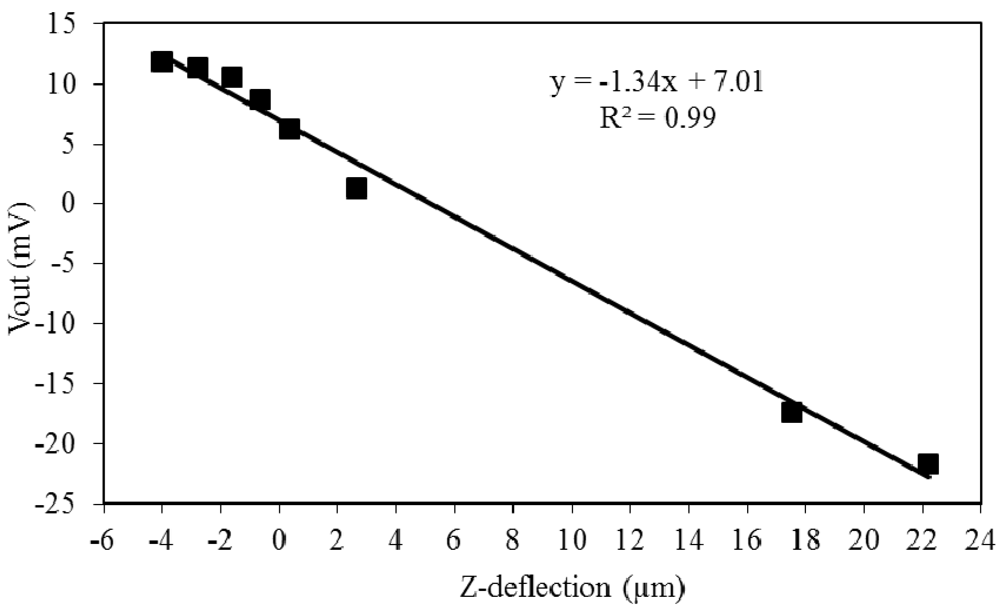
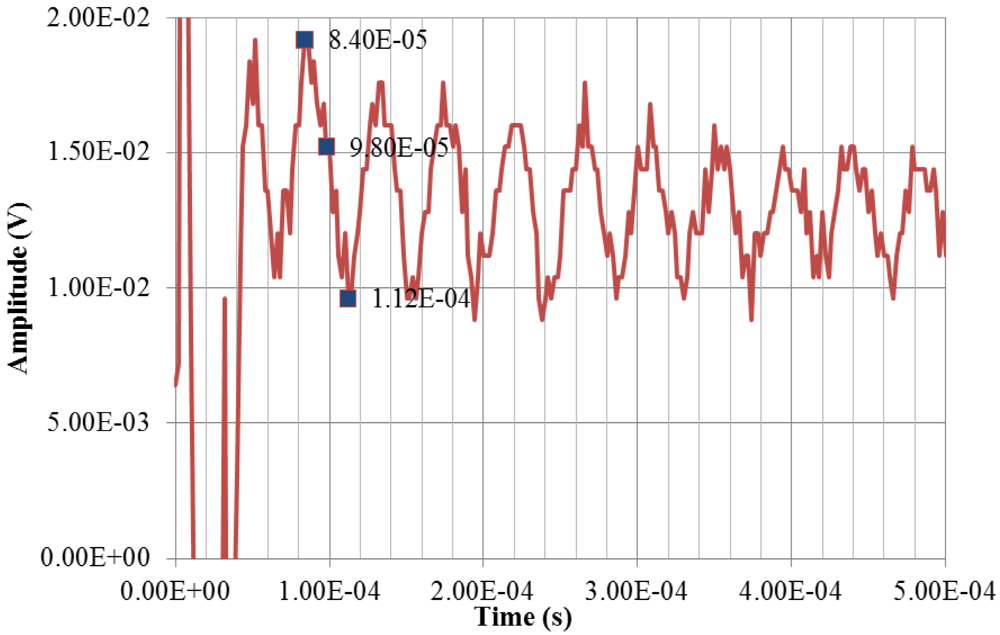
Figure 13 shows a close up view of the sensor signal. During the first few microseconds the signal is noisy. The measurements are taken during the second oscillation at t = 84 µs, 98 µs and 112 µs to obtain the maximum, middle and minimum position of the oscillation. These correspond to 15°, 17.5° and 20° of the actuator cycle respectively. The maximum value of this oscillation should be observed at 84 µs and the minimum at 112 µs. Knowing that the expected sensitivity is of 1.341 mV/µm, according to the calibration values obtained in the previous section, and keeping in mind that the output voltage has been amplified by a factor of 45 through an instrumentation amplifier, the oscillation level that we are trying to measure is of 290 nm.
Figure 14.
Surface profile results at top, middle and bottom of oscillation. These measurements were taken with a Wyko profilometer on a thermally actuated membrane vibrating at 17 KHz. The cycle amplitude is measured to be about 190 nm.
Figure 14.
Surface profile results at top, middle and bottom of oscillation. These measurements were taken with a Wyko profilometer on a thermally actuated membrane vibrating at 17 KHz. The cycle amplitude is measured to be about 190 nm.
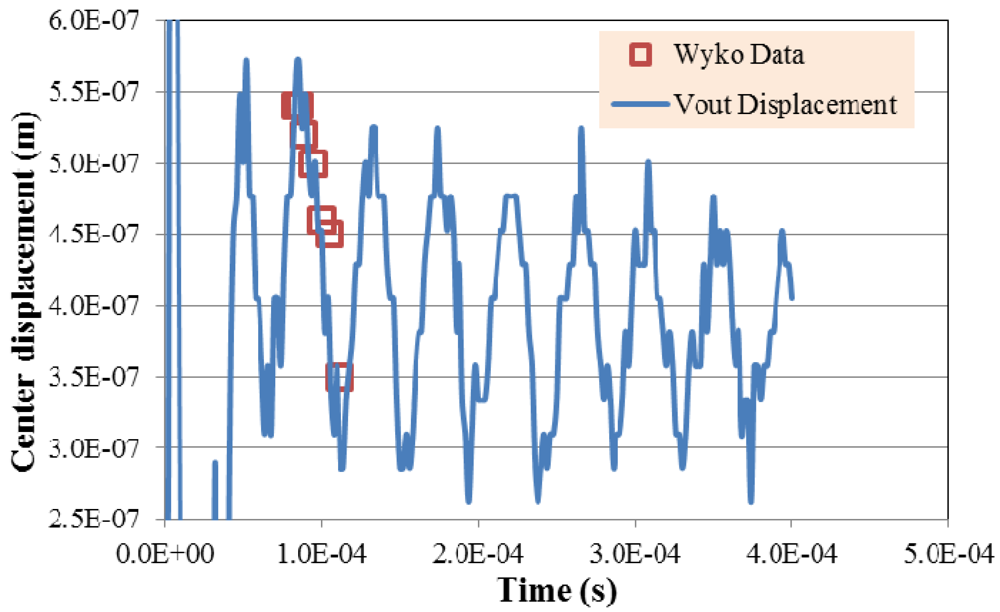
Figure 15.
Overlay of the electrical output and the center displacement measurements obtained with the Wyko profilometer for sensor D11 vibrating in air via heat excitation.
Figure 15.
Overlay of the electrical output and the center displacement measurements obtained with the Wyko profilometer for sensor D11 vibrating in air via heat excitation.
The resulting surface profiles are presented in
Figure 14 for the maximum, center and minimum displacement points. The total displacement measured with this method is 190 nm. This number is comparable to the 60 nm obtained through simulation and analytical analysis and lower than the 290 nm obtained with the electrical measurements.
Figure 14 shows a membrane with non-symmetrical deformation due to fabrication misalignment of the heater, such that the heater was not placed on the center of the membrane. Even with this non-ideal condition, the membrane displacement still resulted in a symmetrical deformation about the center of the membrane. This further confirms the simulation results, which indicated that the shape of the membrane during oscillation correspond to the (1,1) mode, irrespective of the shape or placement of the heating elements.
Figure 15 shows the data extracted from the Wyko measurements overlaid with the data obtained from the electrical measurements in units of displacement (m), after the calibration factor has been applied. The data for the open square symbols was obtained by capturing surface profiles of the membrane at the indicated times and measuring the relative center displacement of the membrane.
This is the first time that the actual shape of a thermally-actuated micromachined silicon-membrane has been experimentally observed during thermally-induced vibrations. These observations confirm that the membrane is vibrating when excited with a burst of heat as predicted by the theory and the simulation. It also confirms that this vibration is at its fundamental natural frequency as a (1,1) mode. More importantly, the vibration amplitude matches both the electrical measurements and the simulation’s values. Moreover, these results also confirm that the static calibration is valid for dynamic measurements.