1. Introduction
In microfluidic applications, mixing has been understood as one of the most fundamental and difficult-to-achieve issues. Thus far, many mixers have been developed and proposed for use in various areas of applications such as bio-, nano-, and environmental technologies. The users or designers of microfluidic mixers, however, must be careful in selecting mixers for use in their specific application because papers or patents describing the designs tend to stress the advantages, but rarely the disadvantages.
During the last five years, since two nice review papers [
1,
2] were published in 2005 on microfluidic mixing, several hundreds of papers have been published on this topic. We have found that among them about 50 papers proposed new or improved designs and demonstrated mixing performance equal to or better than the conventional designs. In this review paper we summarize the skeletons of the ideas behind the proposed designs and address the advantages as well as the disadvantages of each design for use in practical applications.
Since most microfludic applications deal with liquid, we confine ourselves to liquid mixing. Obviously miscible liquid is of our concern because we consider the diffusive action as the final stage of the whole mixing process. We also confine ourselves to low Reynolds-number flows, assuming that in most microfluidic applications, the Reynolds number is less than 1. Therefore, papers which proposed mixer designs showing fundamentally superior performance at higher Reynolds numbers, such as 10 or 100, are excluded in this review.
Jayaraj
et al. [
3] presented a review on the analysis and experiments of fluid flow and mixing in microchannels, but their review was based on the literature published mostly before 2005. Very recently, Falk and Commenge [
4] addressed use of the method of performance comparison or evaluation of micromixers by using the Villermaux/Dushman reaction. They combined the order-of-magnitude analysis and a phenomenological model to derive relation between the mixing time and other parameters such as the Reynolds number. Aubin
et al. [
5] presented experimental technique used in measuring the flow pattern and velocity as well as the mixing performance of micro mixers. However, no review paper has been found which addresses key features of various types of micro mixers and evaluates them in terms of their mixing performance, versatility of application and difficulty of fabrication,
etc. This review paper summarizes the fundamental ideas behind the mixer designs presented in the papers published in 2005 and thereafter, as well as the application range and the fabrication difficulty of these.
In the following section, basic principles and the related terminology of mixing will be presented. Then in
Section 3, we classify the mixer designs and review their features in terms of the mixing performance and the fabrication. Advantages and disadvantages of each design kind are summarized in
Section 4 as conclusions.
2. Principles and Terminology of Fluid Mixing
There are several words which can be used with the same meaning as
mixing without significant difficulty or confusion. These are
stirring,
blending,
agitation,
kneading,
etc. It is not our purpose here to differentiate one from the other in detail, but we need to stress the plausible definition made by Aref [
6] regarding the difference between mixing and stirring because the difference is related to the actual process occurring in mixing. That is, the term ‘mixing’ means a physical process where both the stirring and the diffusion occur simultaneously. Here, the word
stirring means the advection of material blobs subjected to mixing without diffusive action. In other words, we can say that good mixing of low-diffusivity materials occurs in two stages; stirring in the first stage and diffusion in the second stage.
Suppose we have two different kinds of liquids in contact with each other and our primary interest is in mixing the liquids; see
Figure 1. Although random motion of the liquid molecules occurs everywhere, it produces no apparent change in the bulk of each liquid far from the interface, because all the molecules in each separate liquid have the same properties. However in the region near the interface, molecules on both sides have different properties, and so random molecular motion results in permeation of molecules from one side to the other. Such apparent permeation is called
diffusion. Initially the interface is very sharp because no permeation has taken place, but the continuing diffusion causes gradual distribution of the liquid species across the interface. Such gradual distribution causes the diffusion process to occur more slowly. The flux of one species through the interface is proportional to the gradient of the concentration of the species, called Fick’s law, and the proportional constant is defined as molecular diffusivity.
Figure 1.
Cartoon illustrating the exchange of molecules across an interface between two different fluids activated by the molecules’ random motion; (a) before starting the exchange, (b) instantaneous state during the exchange.
Figure 1.
Cartoon illustrating the exchange of molecules across an interface between two different fluids activated by the molecules’ random motion; (a) before starting the exchange, (b) instantaneous state during the exchange.
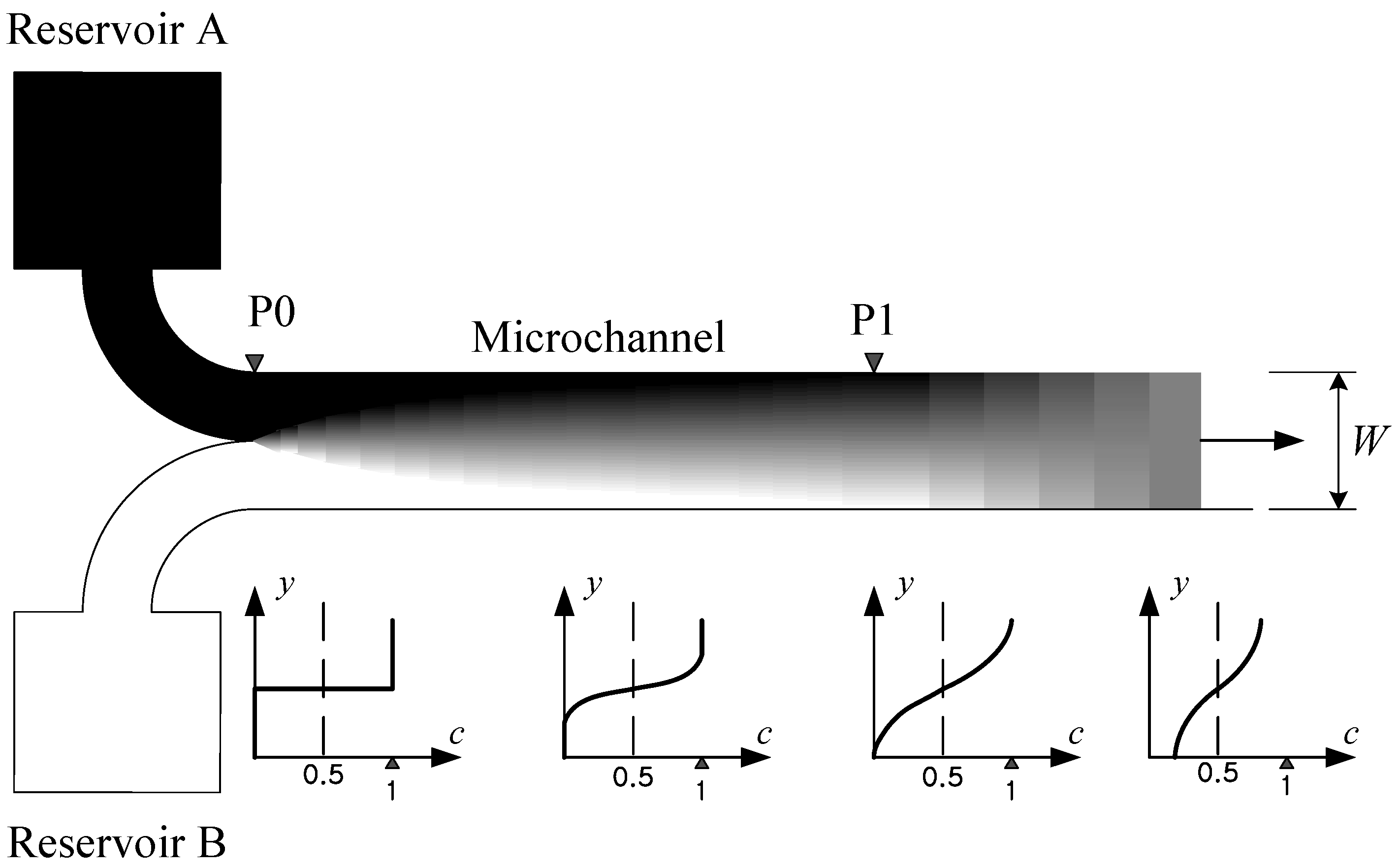
Figure 2 depicts a typical microchannel that has no specific mixing element or structure. Two different fluids from separate reservoirs flow parallel to each other, and therefore no stirring takes place and the mixing is totally diffusive. We designate
c as the fraction (or concentration) of the fluid A contained in an arbitrary, small space occupied by the mixture of fluids A and B. Then, at the entrance of the channel (
i.e., P0 in
Figure 2) where the two kinds of fluids begin to contact, the lower half region will be given
c = 0 while the upper half
c = 1. As shown in
Figure 2, the slope in the concentration distribution becomes more gradual further downstream from P0. However, the peak values of the concentration remain unchanged at
c = 1 and
c = 0 down to the point P1. Further downstream beyond this point, the maximum and minimum values of
c decreases and increases, respectively, finally approaching the ultimate value
c = 0.5.
Figure 2.
Schematic of a typical concentration distribution (grey level) within a microchannel without a specific mixing element. The graphs below show the concentration distribution as a function of the coordinate normal to the channel wall, y, at several channel sections.
Figure 2.
Schematic of a typical concentration distribution (grey level) within a microchannel without a specific mixing element. The graphs below show the concentration distribution as a function of the coordinate normal to the channel wall, y, at several channel sections.
Assuming that the concentration distribution is in a steady state and the flow fluid velocity is uniform over the channel,
u =
U,
v = 0, we can derive an approximate formula for the time needed for the diffusive mixing. The transport equation for
c reads
where diffusion along the main-stream direction is neglected. Introduce the Lagrangian coordinate
τ = x/U to obtain
The coordinates
y and
τ now measure, respectively, the space and time following the fluid material,
i.e., Lagrangian coordinates. Equation (2) is called the heat equation, and the exact solution is well known. However, it involves the error function, thus an additional calculation is needed for its evaluation. Therefore, in this study we employ an integral method to simplify the analysis. As the solution of the first-stage’s transient process (
i.e., between P0 and P1 in
Figure 2), we assume
where
η =
y −
W/2 and
δ(
τ) corresponds to the thickness of the interface between the high concentration in the upper region and the low concentration in the lower region. Substituting (3) into (2) and integrating the result over the full range of
η gives
As the solution for the second-stage’s diffusion process, the concentration profile can be approximated as
where
τ1 is the time needed for the first stage’s process, which can be given from the requirement
The time needed for the second stage,
τ2, depends on the requirement for the smallness of
ε ≡ 2|
c − 1/2|
max, e.g.,
ε = 0.01. Then we derive
The total time τ
tot ≡ τ
1 + τ
2 is then
As an example, for
D = 10
−11 m
2/s and
W = 200 µm, we calculate
τ1 = 66 s and
τ2 = 1,870 s, which are too large for the practical applications. This necessitates introduction of an additional mechanism to speed up mixing.
Figure 3 illustrates the concept of a typical configuration of the hydrodynamic focusing method contrived to speed up the mixing. The upper and lower fluids are guided into the channel in such a way that the contact area is increased significantly. Here again no stirring takes place, but the interfacial area is increased compared with the situation observed in
Figure 2. It can be shown that the time needed to finish the first and second stages of the concentration diffusion, respectively, are given from
and the total time is
τtot ≡
τ1 +
τ2, where
n denotes the number of fluid segments; for instance, in
Figure 3, we have
n = 6. As an example, for
D = 10
−11 m
2/s,
W = 200 µm and
n = 10, we get
τ1 = 0.66 s and
τ2 = 18.70 s, which is in an acceptable range. For a diffusivity 10-times smaller than this, however, we obtain
τtot = 194 s, which is again too large. In this case we may have to increase the number of split fluid segments or use another method to enhance the mixing, such as chaotic advection.
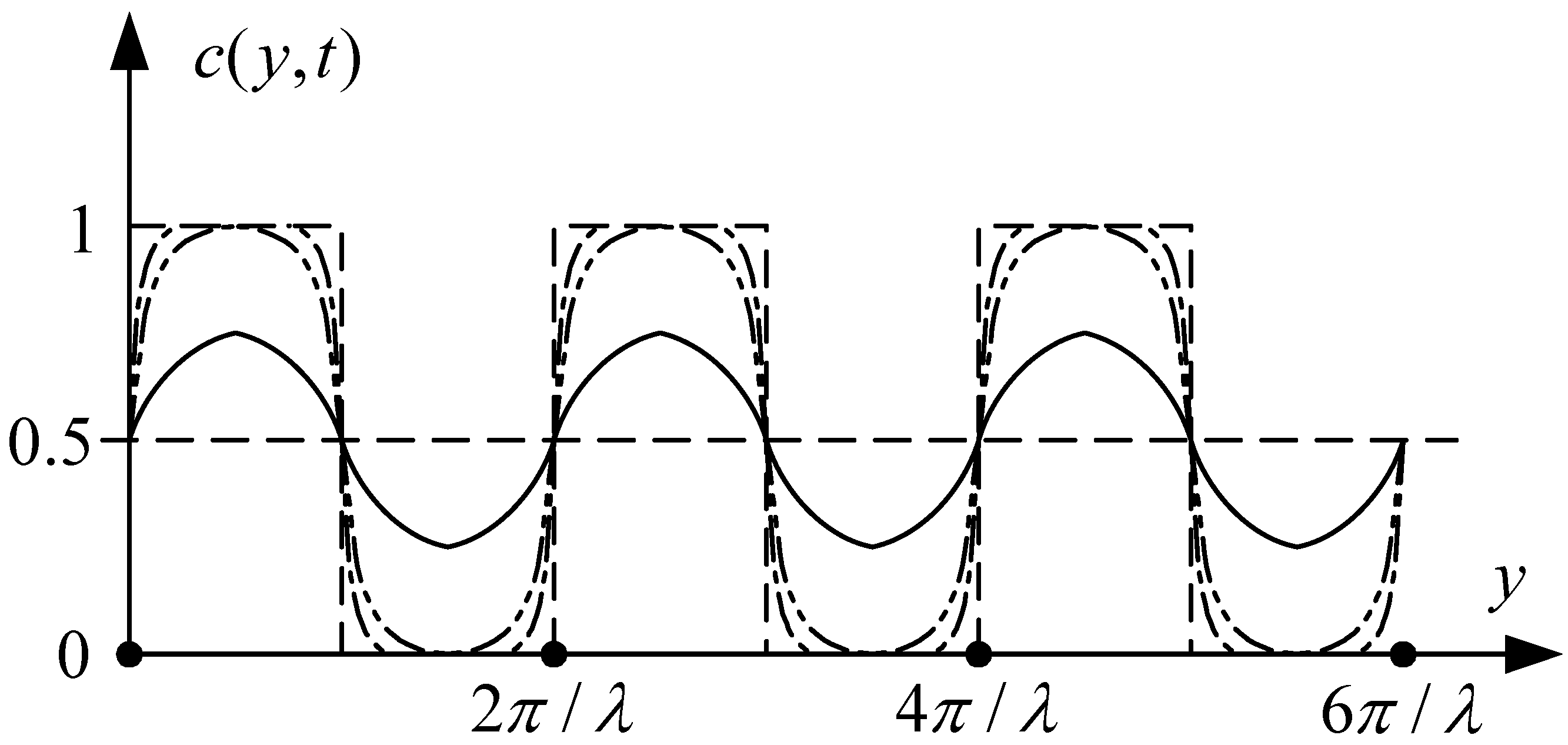
Figure 4 illustrates the typical concentration development along the cross-section of the channel in the hydrodynamic focusing method.
Figure 3.
Sketch illustrating the principle of hydrodynamic focusing. The graph shows a typical concentration distribution as a function of y.
Figure 3.
Sketch illustrating the principle of hydrodynamic focusing. The graph shows a typical concentration distribution as a function of y.
Figure 4.
Schematic of the two-stage development of concentration distribution along the cross-section of the channel in the one-dimensional diffusion model for the hydrodynamic focusing method; the dashed, dash-dot and dash-dot-dot lines depicts the first stage while the solid line is for the second stage.
Figure 4.
Schematic of the two-stage development of concentration distribution along the cross-section of the channel in the one-dimensional diffusion model for the hydrodynamic focusing method; the dashed, dash-dot and dash-dot-dot lines depicts the first stage while the solid line is for the second stage.
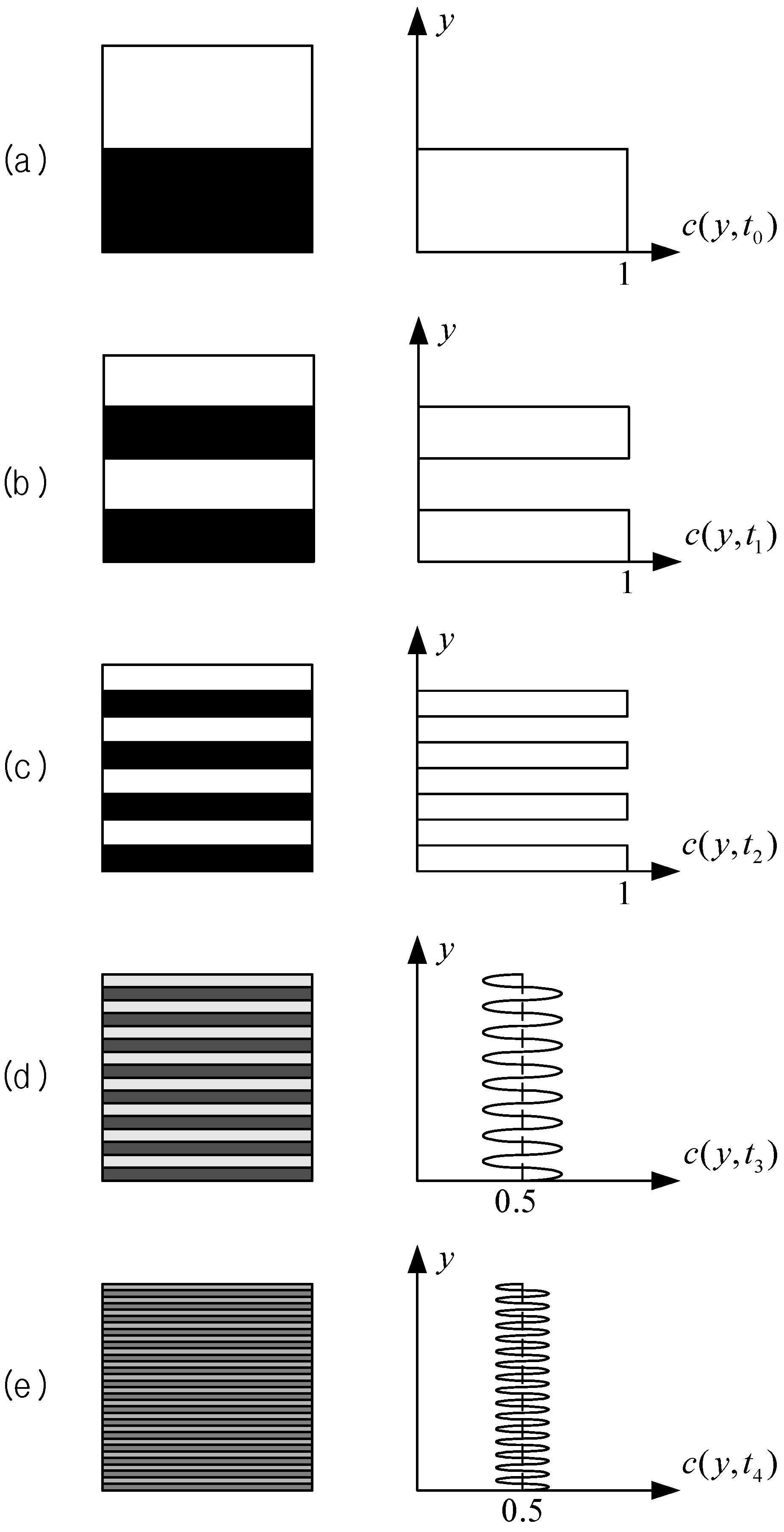
It is now accepted as a rule that the chaotic mixing mechanism is the best for mixing in micro scales.
Figure 5 illustrates the typical development of the striation pattern and the concentration distribution that is given by chaotic mixing to be realized from a one-dimensional model. In this cartoon, we identify two different mechanisms that occur simultaneously; the first one is the stretching and folding of fluid blobs resulting in the exponential decrease of the striation thickness, and the second one is the diffusion of the concentration across the striation. The former process is called
chaotic advection or
chaotic stirring, pioneered by Aref [
6]. The final process to reach a uniform distribution of the concentration, which is the symptom of the completion of mixing, is brought about by molecular diffusion,
i.e., the second mechanism. However, the fine structure in the striation pattern, which is a prerequisite for fast diffusion, is not possible without the help of the chaotic advection.
Figure 5.
Typical development of the striation pattern (left) and the concentration distribution (right) given by the chaotic advection and the molecular diffusion of the chaotic mixing mechanism. Profiles in (a) to (c) should also look smooth like in (d) and (e) but the chaotic advection has been exaggerated.
Figure 5.
Typical development of the striation pattern (left) and the concentration distribution (right) given by the chaotic advection and the molecular diffusion of the chaotic mixing mechanism. Profiles in (a) to (c) should also look smooth like in (d) and (e) but the chaotic advection has been exaggerated.
We try to estimate the mixing time for the case of chaotic mixing. For this, we assume that the stretching-folding process of
Figure 5 occurs periodically in time with the period
T; that is, the striation becomes half after every time period
T. Considering the stretching mechanism, we can write the one-dimensional governing equation for the concentration development as follows.
Notice that the second term on the left-hand-side of the above equation represents the material’s stretching effect and
ν is not the fluid velocity but the squeezing velocity of the striation; the fluid material is ‘stretched’ along the longitudinal direction of the striation but it can also be said to be ‘compressed’ across the striation pattern. Introducing the coordinate
η with its origin at the point where the concentration always remains at
c = 0.5, we can locally put
ν = −
αη. Further, we also assume the form (3) and employ the integral method. Then we get
where the relation
αT = ln2 has been used to eliminate
α. After a sufficiently long time,
δ reaches the limit value
. The number of periods
kc needed for the first stage is then given by equating
lk =
W/2
k and
δ∞;
The time needed for the first stage is then given by
τ1 =
kcT. Next, we introduce the Lyapunov exponent Λ (see e.g., [
7]) related to
T as Λ
T = ln2. Then we have
Finally, we derive
τ2, the time needed for the second stage of mixing. The analysis is the same as before, and we arrive at
τ2 = (
kd –
kc)
T where
kd is given from
The total time for the mixing is then obtained from
As an example, for
D = 10
−11 m
2/s,
W = 200 µm,
ε = 0.01 and
T = 3 s, we get
τ1 = 11.8 s,
τ2 = 4.76 s and
τtot = 16.6 s, which is again in the acceptable range. Even for diffusivity 10-times smaller than this, we get
τtot = 38.4 s, which is only one-sixth of the value obtained for the hydrodynamic focusing case.
The simple analysis provided so far may be enough to illustrate the important role of stirring in the whole mixing process. In many applications, the samples to be mixed, e.g., for a chemical reaction, have very low diffusivity owing to large molecular sizes of the materials. Therefore, the role of stirring should be dominant in the mixing process, and the chaotic advection or stirring is known to be the only mechanism that produces exponential stretching of material blobs required for the best mixing.
3. Review on Various Mixer Designs for Microfluidic Applications
Now we review the various ideas of the microfluidic mixers reported since 2005. Surveying the literature, we have found that many papers treat moderate or high Reynolds-number flows. However, we exclude these papers in this review because such moderate or high Reynolds-number flows are rarely found in microfluidic applications. Moreover, with such flows it may be easy to induce unsteady complex flows that naturally contribute significantly to the fluid mixing.
The microfluidic mixers can be classified in various ways. In this paper, we use the physical mechanism for classification; i.e., hydrodynamic focusing, alternate injection, geometry effect, electrokinetic method, droplet mixing and stirring by particles.
3.1. Hydrodynamic Focusing
The basic mechanism of the hydrodynamic focusing has already been presented in
Section 2. Floyd
et al. [
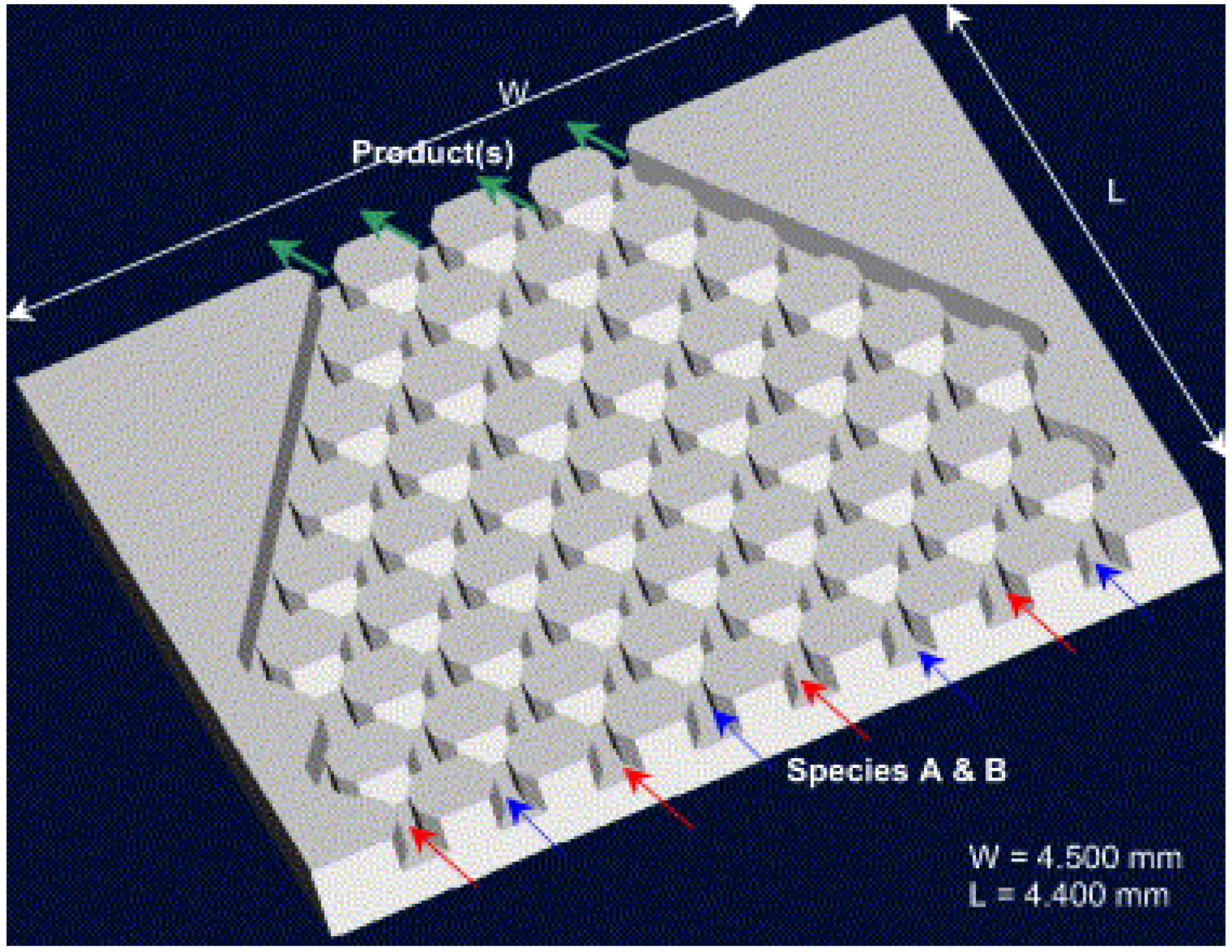
8] fabricated a silicon microchannel with 10 inlets for mixing acid and base solutions (
Figure 6). Their experimental measurement for the mixing performance was compared with computational fluid dynamics (CFD) results with good agreement in terms of the residence time. Nguyen and Huang [
9] presented a comparison between the analytical solution and the experimental measurement of the diffusion of samples in a hydrodynamic focusing means. They achieved the focusing by using a pair of inlet channels. Unique to their study is that they employed pulsed addition of solute to the channel to enhance the reaction. In this design, the valves at the inlets are actuated by two piezo discs. It is implied in this paper that the Taylor dispersion can further enhance the mixing. Adeosun and Lawal [
10,
11] introduced the so-called multilaminated/elongational micromixers to mix two fluid samples (
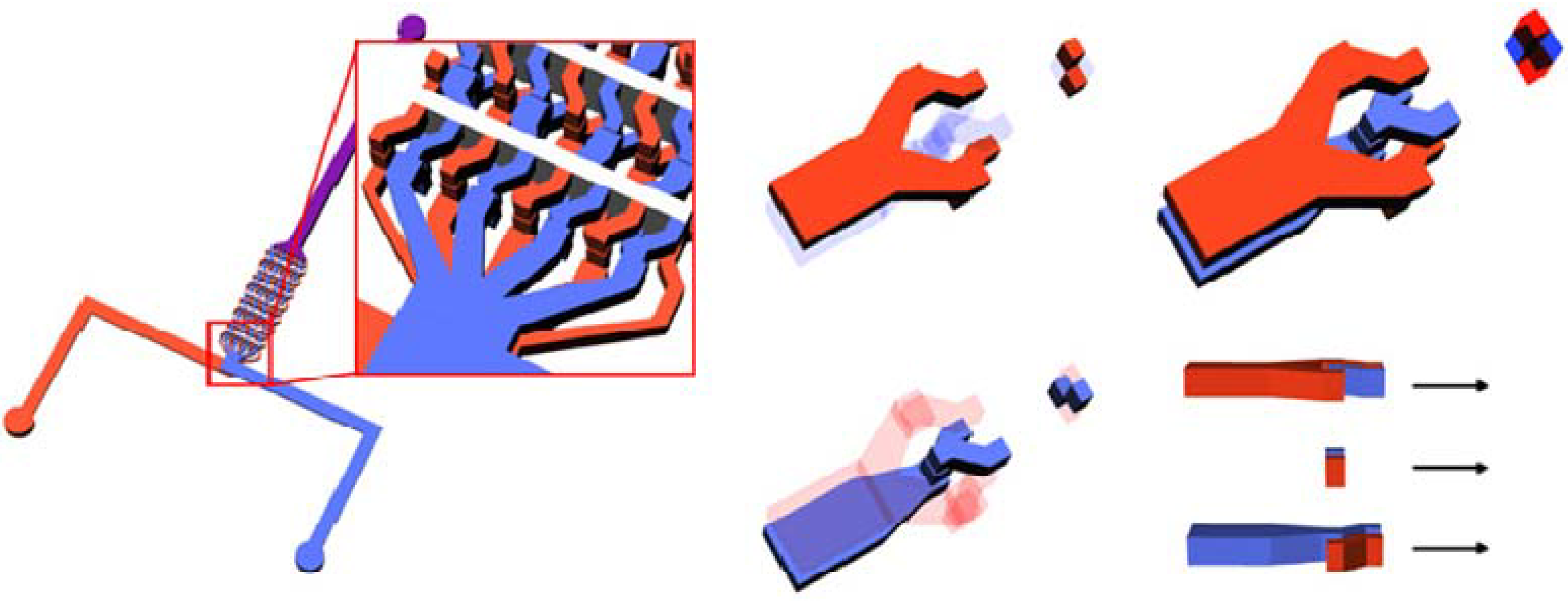
Figure 7). Their design is composed of many mixing structures strategically arranged on the channel floor of the mixing device and blocks arranged in a staggered way at the inlets. It was shown that their mechanism of fluid multilamination and elongation is highly effective in enhancing the mass transfer. Cha
et al. [
12] proposed a 3D micromixer combining the focusing and split-and-recombination (SAR) functions called the chessboard mixer (
Figure 8). For the flow rate of 12.7 µL/min, 90% of mixing occurs only within the length of 1.4 mm. Park
et al. [
13] demonstrated the use of sheath flows from the hydrodynamic focusing as an effective method in controlling the reaction of samples. They fabricated five inlet channels: the center for an analyte solution, the two sides for the solution B and the two diagonals for the solution A. In this way, they could prevent the undesired premixing of solutions before the focusing was completed. Mimicking the geometrical properties of a vascular system, Cieslicki and Piechna [
14] designed a branched channel and numerically investigated the mixing performance, particularly focusing on the effect of the number of branches.
Figure 6.
(a) Experimental and
(b) numerical visualizations of fluid mixing in hydrodynamic focusing channels (from Floyd
et al. [
8]).
Figure 6.
(a) Experimental and
(b) numerical visualizations of fluid mixing in hydrodynamic focusing channels (from Floyd
et al. [
8]).
Figure 7.
A multilaminated/elongational flow micromixer (from Adeosun and Lawal [
10]).
Figure 7.
A multilaminated/elongational flow micromixer (from Adeosun and Lawal [
10]).
Figure 8.
A schematic illustrating the structure of the chessboard mixer (from Cha
et al. [
12]).
Figure 8.
A schematic illustrating the structure of the chessboard mixer (from Cha
et al. [
12]).
All the papers investigating the hydrodynamic focusing principle indeed show its highly effective mixing performance, such as short mixing length or fast mixing time. The main problem in the hydrodynamic focusing, however, lies in how to distribute the fluids to the multiple inlet channels. Typically, for the mixing of two samples, each sample is stored in one of the two different reservoirs while multiple channels used for the focusing are usually arranged in a staggered way. Then the fabrication of the inlets must be of a two-layer structure, which adds to the complexity in the overall device design.
3.2. Alternate-Injection or Pulsed-Flow Mixing
Another popular method for enhancing the mixing performance is to inject samples of different species at the inlet in an alternating way; in view of each sample, the resulting flow is similar to a pulsed flow. Compared with the hydrodynamic focusing case, the alternate injection design does not require complex channel fabrication. MacInnes
et al. [
15] conducted a numerical and analytical study on the mixing performance for a case in which two different samples are introduced into the channel via a pulsating pressure. Such alternate injection increases the interfacial area, leading to a fast mixing. Goullet
et al. [
16] studied the effect of the geometry of the inlet channel (
i.e., “T” and “Y”,
etc.) as well as the phase difference between the two injected samples on the mixing performance of the pulsed-flow mixer. They also introduced ribs in the main channel and demonstrated significant improvement in the degree of mixing.
As the driving force for the sample injection, electroosmosis is sometimes more beneficial than pressure. The research group of Sinton [
17,
18] conducted an experimental study on the mixing effect in a channel design composed of a cross inlet channel and a larger mixing chamber (
Figure 9), where samples are sequentially injected via electroosmotic force. The decelerating flow in the expansion channel connected to the chamber makes the striation thinner and thinner, thus promoting the diffusion. It was shown that the optimum frequency for the best mixing in their specific parameter settings is in the range 1–2 Hz. Similar designs have also been proposed by Leong
et al. [
19] and Sun and Sie [
20].
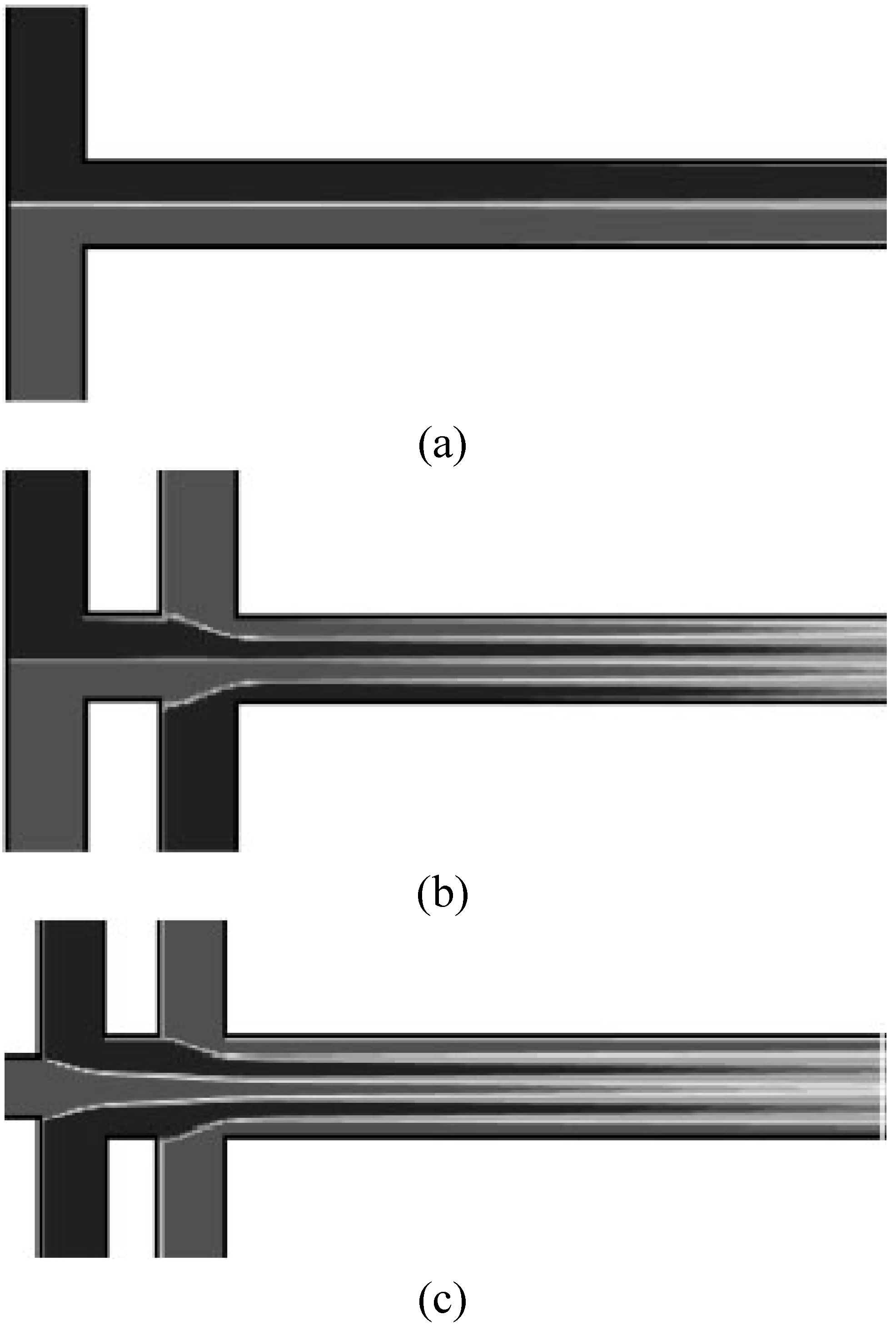
The concept of the simple alternate injection can be further improved or altered for better mixing. Fu and Tsai [
21] conducted a numerical simulation on the dispersion of concentration caused by alternately driven fluid through the simple “T” and double “T” channels. They showed that the double “T” channels provide a faster mixing effect compared with the single “T” design (
Figure 10). In the work of Lee
et al. [
22], a detailed analysis of the chaotic advection in an alternate-injection mixer was presented in terms of the non-linear dynamical terms, such as Lyapunov exponent and Poincare section. For the case with fluid injection through the side channels, they showed the existence of an optimum frequency of fluid injection for the best mixing. In the work of Chen and Cho [
23], in addition to the pulsating fluid injection through the inlet channels, the main channel walls are also designed in a wavy form so that each isolated slug of sample undergoes the stretching-folding process, which further enhances the mixing (
Figure 11).
Figure 9.
An alternate-injection mixer composed of an inlet cross channel and a larger chamber (from Coleman
et al. [
18]).
Figure 9.
An alternate-injection mixer composed of an inlet cross channel and a larger chamber (from Coleman
et al. [
18]).
Figure 10.
Three types of inlet channels; (
a) single “T”, (
b) double “T” and (
c) double cross channel (from Fu and Tsai [
21]).
Figure 10.
Three types of inlet channels; (
a) single “T”, (
b) double “T” and (
c) double cross channel (from Fu and Tsai [
21]).
Figure 11.
Distribution of species concentration in wavy-wall channels by
(a) continuous injection,
(b) pulsed injection with a certain period and
(c) pulsed injection with the period double that for (b) (from Chen and Cho [
23]).
Figure 11.
Distribution of species concentration in wavy-wall channels by
(a) continuous injection,
(b) pulsed injection with a certain period and
(c) pulsed injection with the period double that for (b) (from Chen and Cho [
23]).
Like the hydrodynamic focusing method, the alternate-injection method also suffers from a fundamental drawback; the stirring occurs only in the inlet region of the channel. Although the larger chamber attached to the inlet channel proposed by Sinton’s group [
17,
18], Leong
et al. [
19] and Sun and Sie [
20] promotes the mixing via the stretching of the slug, it is not like chaotic advection since the stretching occurs only linearly in time. Further, when elctroosmotic force is used for the fluid injection due to its feasibility in the injection control, bubble generation from the electrodes or the electrode degradation can cause another problem. For practical applications, therefore, those problems must be tackled.
3.3. Geometry Effect
Apparently, the simplest way to enhance mixing in a microchannel is to make the channel geometry complex, e.g., a serpentine structure [
24], or with grooves [
25] or blocks [
26] on the bottom wall. Kim
et al. [
27] proposed a two-layer microchannel composed of a series of F-shaped channel units (
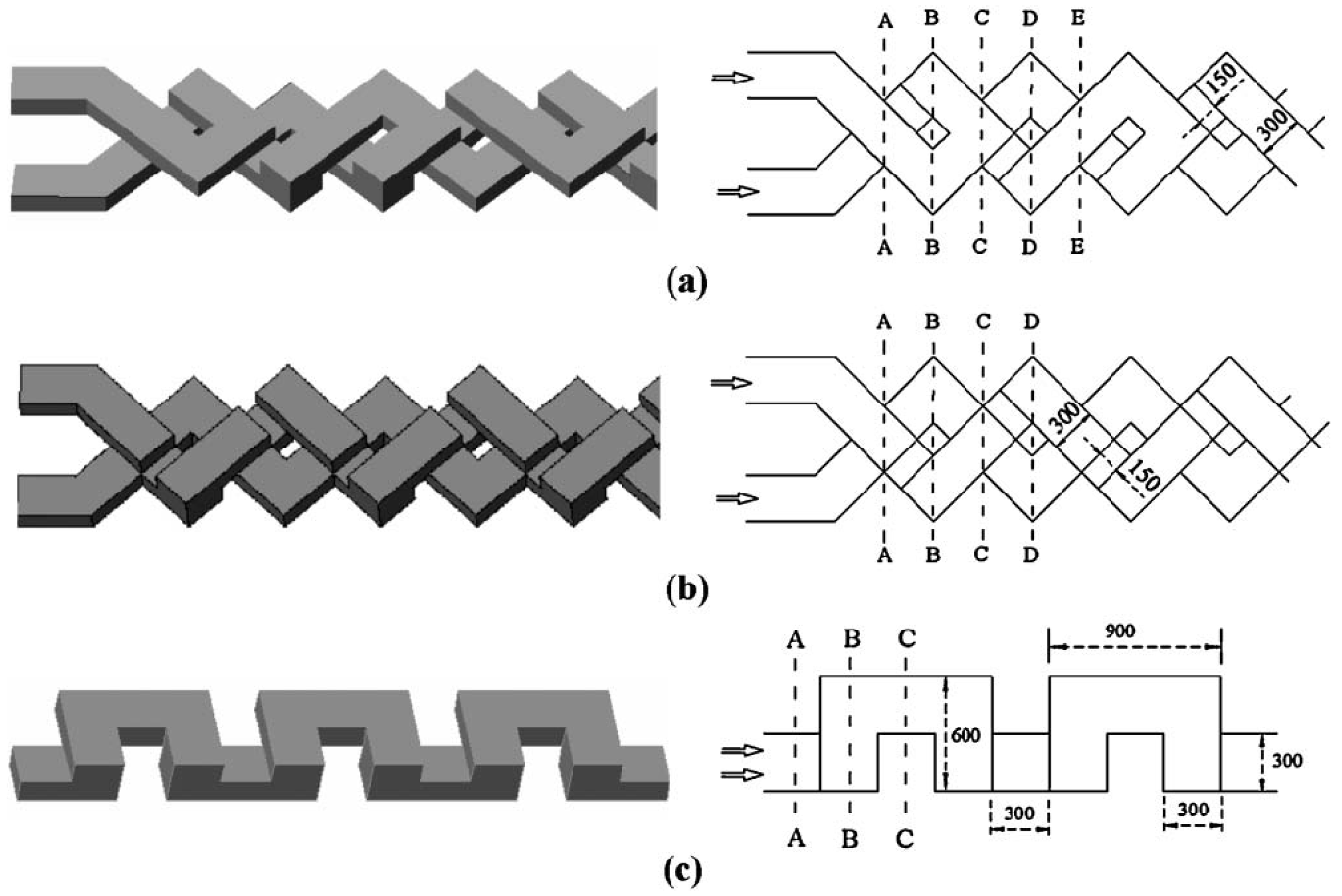
Figure 12), which was shown to bring chaotic advection via the stretching-folding mechanism. Xia
et al. [
28] compared three kinds of two-layer crossing channels in terms of the mixing effect including the basic serpentine mixer proposed by Liu
et al. [
24]; see
Figure 13. Their two types of design (
Figure 13a and
Figure 13b) revealed much better mixing performance than the basic serpentine structure (
Figure 13c) at low Reynolds numbers, implying that the basic serpentine microchannel is not suitable for low Reynolds-number flows. Further support for this argument was given by the numerical simulation of Ansari and Kim [
29]. The two-layer structures proposed by Kim
et al. [
27] and Xia
et al. [
28] are shown to provide chaotic advection, but again the main disadvantage of those structures is that the fabrication of the two layers separately should increase the device price. Howell
et al. [
30] also proposed a two-layer design, where not only the bottom but also the top walls carry grooves of stripes and chevrons. Their design brings faster mixing compared with the case with bottom grooves only [
25], but here again fabrication difficulty must be overcome to be useful for practical applications. Similarly, Yang
et al. [
31] proposed to build partitioning plates on the top wall in addition to the bottom grooves to stir the fluid in the region near the top wall, but the fabrication of such a channel may not be so simple.
Figure 12.
A serpentine laminating micromixer composed of a series of F-shaped channel units (from Kim
et al. [
27]).
Figure 12.
A serpentine laminating micromixer composed of a series of F-shaped channel units (from Kim
et al. [
27]).
As a single layer structure, the mixer proposed by Simonnet and Groisman [
32] deserves our attention. Their design is composed of a complex but single layer of PDMS (polydimethylsiloxane) attached to a top planar wall (
Figure 14). Visualization of a dye of very low diffusivity indeed demonstrated chaotic advection inside the channel, as shown in
Figure 15. The proposed design is shown to provide excellent mixing when two samples are introduced in the upper and lower domains of the channel section, but it is implied that no stirring occurs when they are introduced in the left and right domains, the latter corresponding to the most common situations. To shorten the mixing length, Camesasca
et al. [
33] proposed fractal patterning of grooves on the bottom of the channel (
Figure 16). The Weierstrass function was used in the design of the pattern with the fractal dimension
D as one of the key parameters. It was found that, depending on
D, the mixing can be enhanced compared with the original staggered herringbone mixer of Stroock
et al. [
25]. However, it is still questionable if the upper region of the channel may also show chaotic mixing because the flow in the region near the top wall is less disturbed by the bottom grooves. Various modifications of the grooved channel design have been tested. Yang
et al. [
34] designed side grooves in addition to the bottom grooves of Stroock
et al. [
25] so that secondary flows can be promoted (
Figure 17). It was found that the existence of side grooves brings a 10–50% increased mixing performance.
Figure 13.
Three kinds of two-layer microchannels (from Xia
et al. [
28]).
Figure 13.
Three kinds of two-layer microchannels (from Xia
et al. [
28]).
Figure 14.
(a, b) Sketch of the two kinds of channel mixer with a single-layer structure and
(c) the cross-sectional view of the plane cut by a dotted line in (b) (from Simonnet and Groisman [
32]).
Figure 14.
(a, b) Sketch of the two kinds of channel mixer with a single-layer structure and
(c) the cross-sectional view of the plane cut by a dotted line in (b) (from Simonnet and Groisman [
32]).
Figure 15.
Development of the striation pattern inside the channel (from a to f) showing chaotic advection (from Simonnet and Groisman [
32]).
Figure 15.
Development of the striation pattern inside the channel (from a to f) showing chaotic advection (from Simonnet and Groisman [
32]).
Figure 16.
Top view of the channel designs with different fractal patterning of bottom grooves and mSHM (modified staggered herringbone mixer) (from Camesasca
et al. [
33]).
Figure 16.
Top view of the channel designs with different fractal patterning of bottom grooves and mSHM (modified staggered herringbone mixer) (from Camesasca
et al. [
33]).
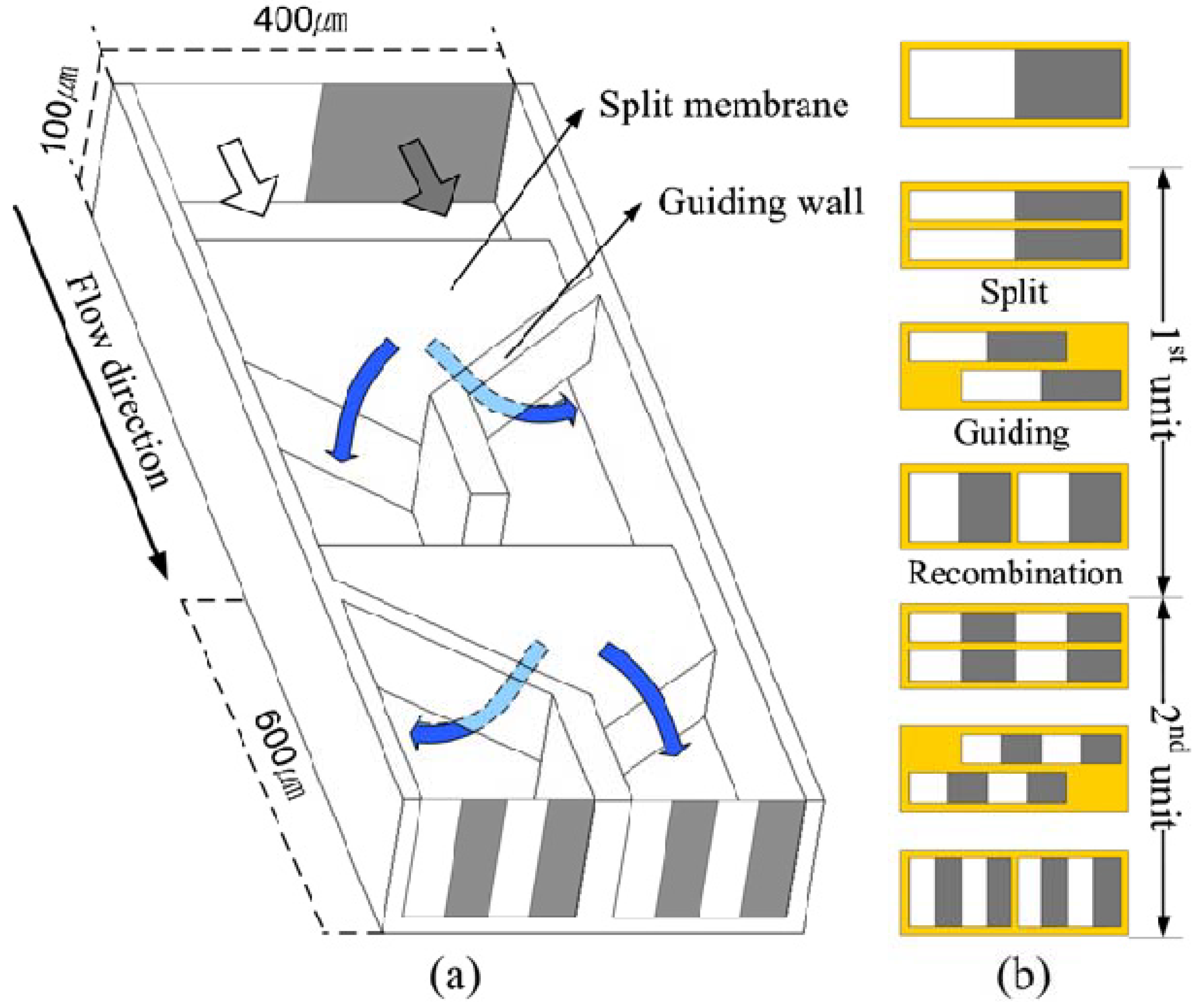
The design concept of SAR comes directly from the stretching-folding mechanism of chaotic advection. Hardt
et al. [
35] reported experimental and numerical results on the mixing performance with the SAR design mimicking the original concept of the stretching-folding scenario in the chaotic advection (
Figure 18). Compared with the design with grooves on the bottom wall, this design guarantees almost uniform mixing characteristics over the whole cross section of the channel. A problem, of course, lies in the difficulty of fabrication. Lee
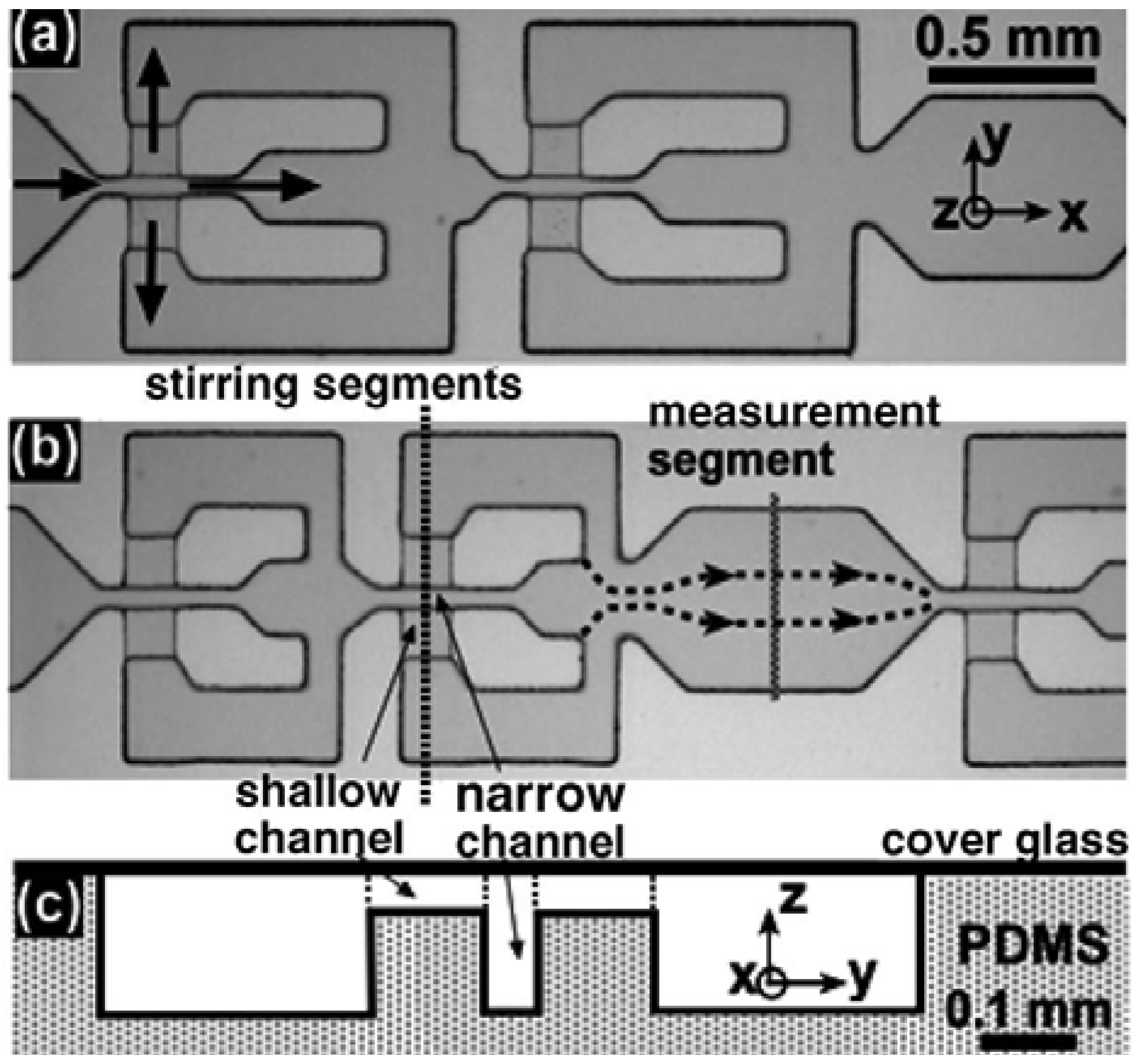
et al. [
36] proposed to use steps and partition blocks on the bottom wall of the channel (
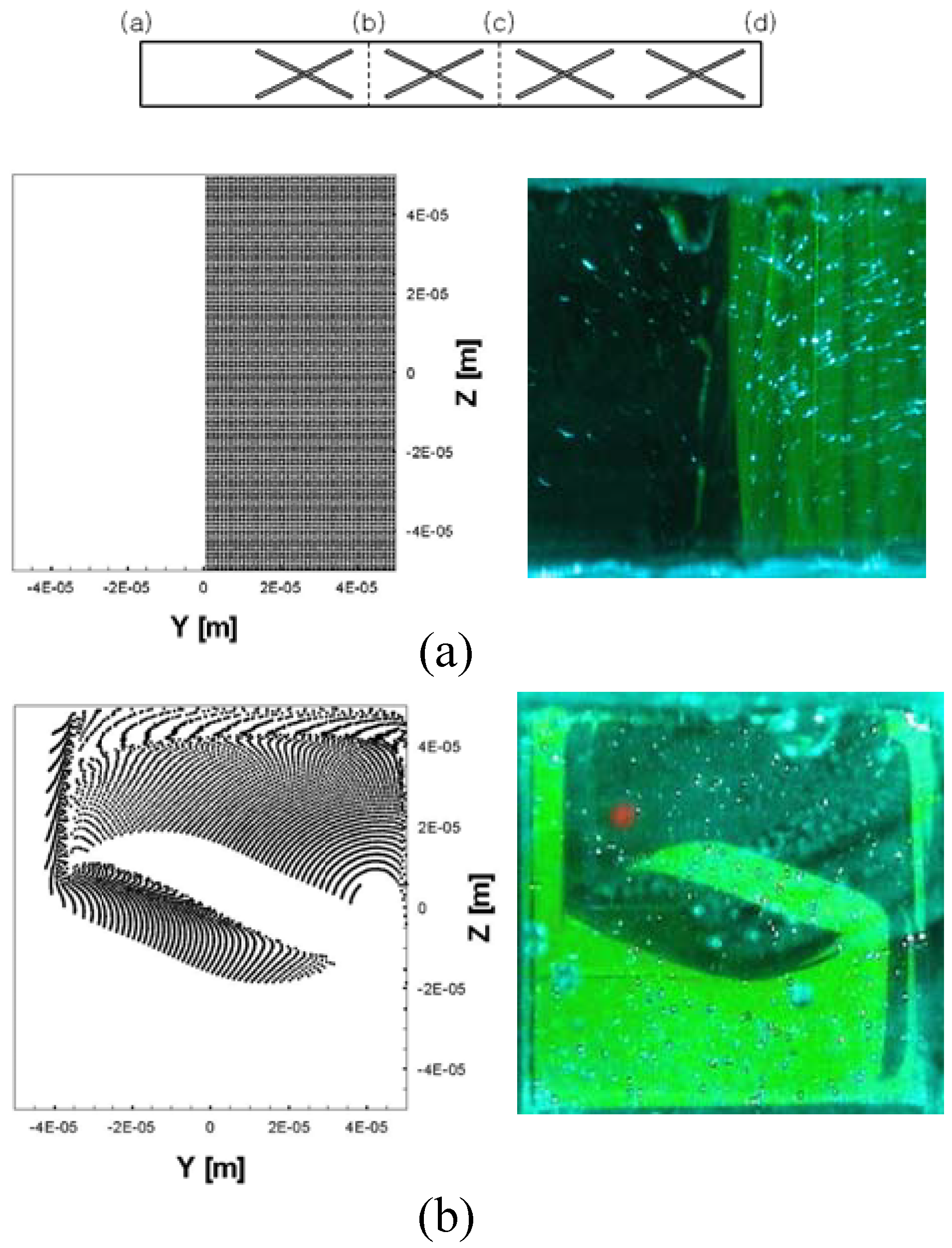
Figure 19) to establish the split-and-recombination function without fundamental difficulty in the fabrication process. Suh
et al. [
37] also presented a new channel design composed of a series of cross baffles. Clear evidence of stretching-folding action was revealed from both numerical and experimental visualizations (
Figure 20).
Figure 17.
Schematic of the two channel designs of CGM (connected-groove micromixer) with not only bottom but also side grooves:
(a) CGM-1 design;
(b) CGM-2 design (from Yang
et al. [
34]).
Figure 17.
Schematic of the two channel designs of CGM (connected-groove micromixer) with not only bottom but also side grooves:
(a) CGM-1 design;
(b) CGM-2 design (from Yang
et al. [
34]).
Figure 18.
Enlarged view of the SAR unit (left) composing the 8-unit mixer (from Hardt
et al. [
35]).
Figure 18.
Enlarged view of the SAR unit (left) composing the 8-unit mixer (from Hardt
et al. [
35]).
Figure 19.
(a) Perspective view of a SAR mixer with steps and partitioning blocks on the bottom wall and
(b) schematic illustration of mixing principle (from Lee
et al. [
36]).
Figure 19.
(a) Perspective view of a SAR mixer with steps and partitioning blocks on the bottom wall and
(b) schematic illustration of mixing principle (from Lee
et al. [
36]).
Figure 20.
Comparison of the mixing patterns from numerical (left) and experimental (right) results for each section of the channel (denoted as (a), (b), (c) and (d) shown on the top) of a cross-baffle mixer (from Suh
et al. [
37]).
Figure 20.
Comparison of the mixing patterns from numerical (left) and experimental (right) results for each section of the channel (denoted as (a), (b), (c) and (d) shown on the top) of a cross-baffle mixer (from Suh
et al. [
37]).
3.4. Electrokinetic Method
Electrokinetic forcing, in particular electroosmosis, serves as an effective means not only for liquid pumping but also for locally controlling fluid flow, which is essential for fluid mixing. In
Section 3.2, we have addressed several studies in which electroosmotic flow is used as a means for alternately injecting fluid through the inlet channels. In this section, we introduce studies on the local control of fluid flow and its effect on the mixing.
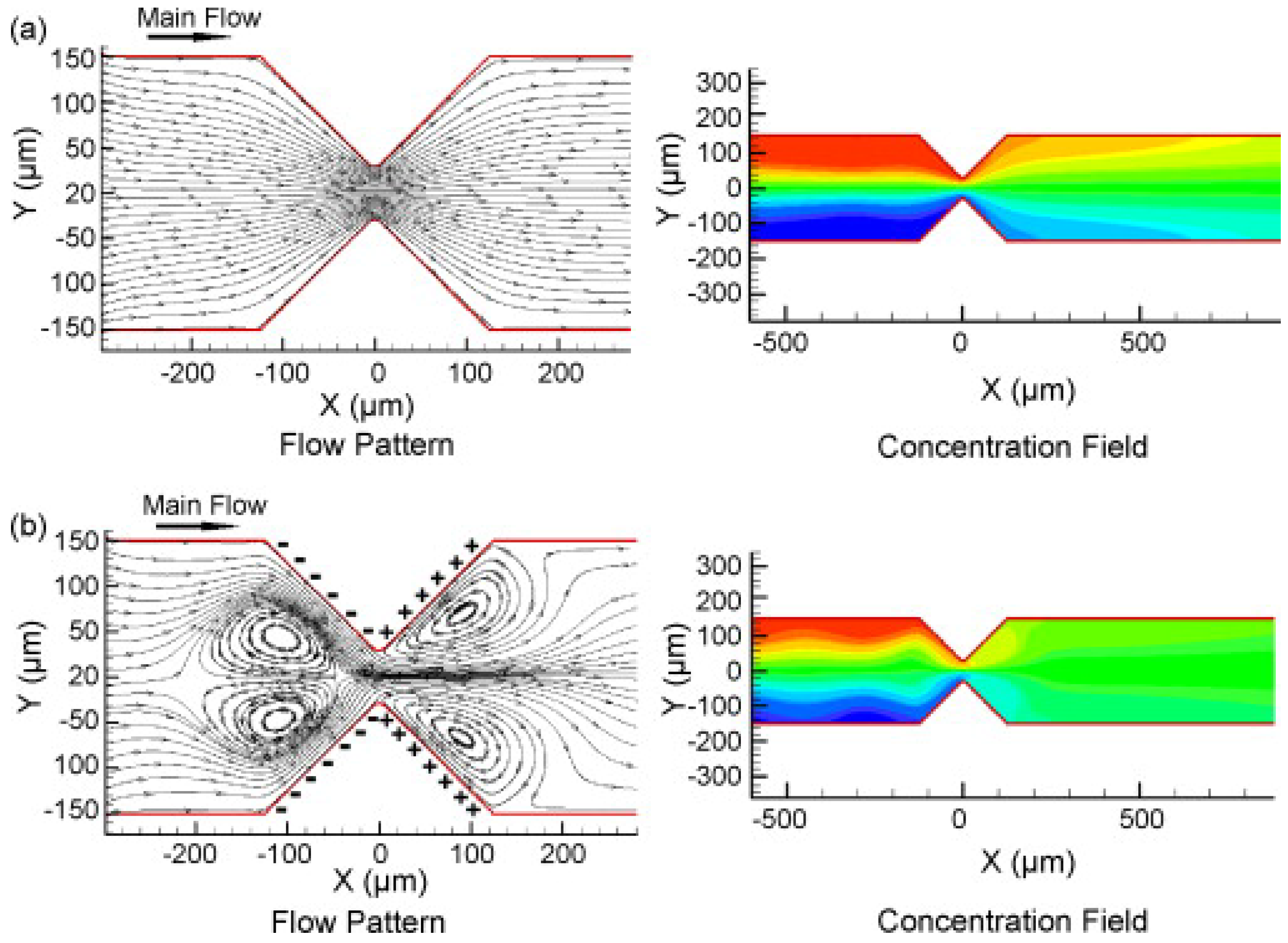
First, we survey studies on mixing with heterogeneous distribution of zeta potential on the channel walls. Zhang
et al. [
38] presented a numerical study on the fluid flow and mixing in a two-dimensional channel with side walls prescribed with spatially varying zeta potentials. It was shown that such heterogeneous zeta potential distribution can lead to a complex flow pattern which is responsible for the enhanced mixing. In the work of Chen and Cho [
39], the effect of additional wavy walls was also studied. Control of zeta potential on a part of the channel walls can be achieved by one of surface treatment technologies. On the other hand, simply putting conductors on the walls can also create locally vortical flows, as studied both experimentally and numerically by Wu and Li [
40]. Contrary to the dielectric wall, the conducting wall surface is maintained at a uniform electric potential so that the non-uniform distribution of the electric field near the conductor segment can lead to local vortices, which can be utilized in the mixing (
Figure 21). Kang
et al. [
41] conducted numerical simulation by using the lattice Boltzmann method for two- and three-dimensional microchannels with heterogeneous zeta potential distributions, which vary in time or remain constant. They validated their numerical codes by comparing their results with the ones given by a commercial code for a three-dimensional channel. For the time-varying zeta-potential case, there exists an optimum period of modulation for the best mixing.
Figure 21.
Flow and concentration fields around hurdles made of
(a) non-conducting and
(b) conducting materials (from Wu and Li [
40]).
Figure 21.
Flow and concentration fields around hurdles made of
(a) non-conducting and
(b) conducting materials (from Wu and Li [
40]).
Developments in the fabrication of microelectrodes in microchannels has intrigued ideas of controlling fluid flow and mixing by using electrodes embedded in walls or in direct contact with the liquid. Qian and Bau [
42] demonstrated chaotic advection within a rectangular cavity by employing time-dependent slip velocity on the top and bottom wall segments caused by electroosmosis. They performed a two-dimensional numerical simulation to obtain Poincare sections by using the semi-analytic solution for the Stokes flow within the cavity. The time-dependent zeta potential on the segments of walls could be achieved by adjusting electric potentials applied on the electrodes embedded beneath the wall segments. Zhao and Bau [
43] presented a two-dimensional numerical study on the mixing within an annulus. Chaotic advection could be achieved by temporally modulating the non-uniform distribution of electric potential on the surface of the inner wall. Wu and Liu [
44] considered a “T” channel carrying electrodes on the bottom wall of the channel embedded in a herringbone shape (
Figure 22). The mixing effect was found to be considerably enhanced by the use of zeta-potential control via the embedded electrodes. Sasaki
et al. [
45] demonstrated experimental evidence of enhanced mixing due to a meandering electrode pair on the bottom of the “Y” channel (
Figure 23), around which ac electroosmotic flow is created. More complex patterns of microelectrodes on the channel walls were also tried by Huang
et al. [
46] for further enhancement of mixing (
Figure 24).
Use of microelectrodes makes the local-flow control much easier than the other means, such as the pressure-driven flow. Needless to say, however, such additional equipment adds to the cost of the micro device. Furthermore, the application must be limited to conducting liquids.
Figure 22.
A “T” shape microchannel with aluminum electrodes embedded on the bottom wall to enhance mixing (from Wu and Liu [
44]).
Figure 22.
A “T” shape microchannel with aluminum electrodes embedded on the bottom wall to enhance mixing (from Wu and Liu [
44]).
Figure 23.
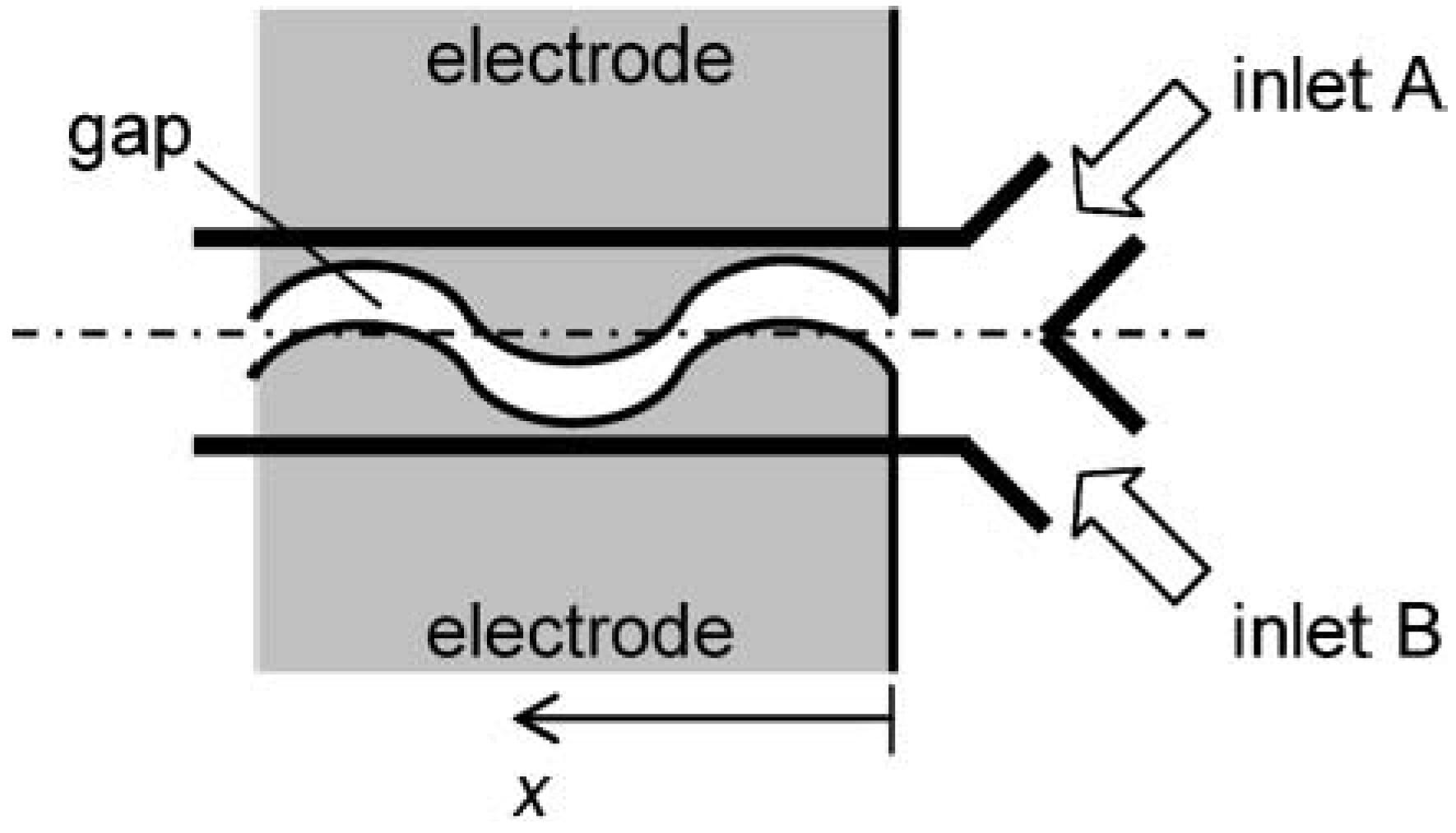
Schematic of “Y” shape microchannel with a pair of meandering electrodes for ac electroosmosis (from Sasaki
et al. [
45]).
Figure 23.
Schematic of “Y” shape microchannel with a pair of meandering electrodes for ac electroosmosis (from Sasaki
et al. [
45]).
Mixing enhancement can also be accomplished through electrokinetic and/or physicochemical instability. For instance, Shin
et al. [
47] conducted an experimental study on electrokinetic instability and its use in mixing. Input of two sodium-chloride solutions with different concentrations creates a conductivity gradient across the interface, which yields an electric charge. This charge distribution, coupled with the oscillating external electric field, promotes electrokinetic instability (
Figure 25), which is used as a driving mechanism to enhance mixing at the channel inlet. It was found that the optimum frequency for the best mixing is double the natural frequency of the electrokinetic instability. Chun
et al. [
48] presented an experimental study on a very fast mixer using the principle of space-charge creation due to ion depletion and enrichment near the polyelectrolytic gel electrodes with ac field. It was shown that the mixing effect is excellent and there exists an optimum frequency for the best mixing. They also successfully applied their design to the lysis of red blood cells. Mixing with such a mechanism, however, may be effective only when the interface between the two liquids subject to mixing shows an electrokinetic instability mainly caused by the concentration difference.
Figure 24.
(a) Various designs of electrode patterning for creating local vortices with ac electroosmosis.
(b) and
(c) show pictures of design types I and IV, respectively (from Huang
et al. [
46]).
Figure 24.
(a) Various designs of electrode patterning for creating local vortices with ac electroosmosis.
(b) and
(c) show pictures of design types I and IV, respectively (from Huang
et al. [
46]).
Figure 25.
Particle trajectories with static (left-hand-side photo) and time-varying (right-hand-side photo) electric fields at the inlet of the channel (from Shin
et al. [
47]).
Figure 25.
Particle trajectories with static (left-hand-side photo) and time-varying (right-hand-side photo) electric fields at the inlet of the channel (from Shin
et al. [
47]).
3.5. Mixing by Droplets
The pressure-driven flow employed in most continuous-flow mixers, such as hydrodynamic focusing, alternate injection or the geometry-modification technique, inevitably suffers from a broad distribution in the residence time due to the parabolic velocity profile. The method of droplet or slug mixing has been developed to overcome this problem. Due to a strong surface-tension effect at the interface between the sample (occupying the droplet) and the carrier fluid (usually oil), the droplet always takes an isolated form such as a sphere or finite cylinder, and thus every fluid particle within the droplet must experience almost the same residence time. Another advantage in the droplet mixing is that the internal flow required for the mixing can be relatively easily created by a meandering channel.
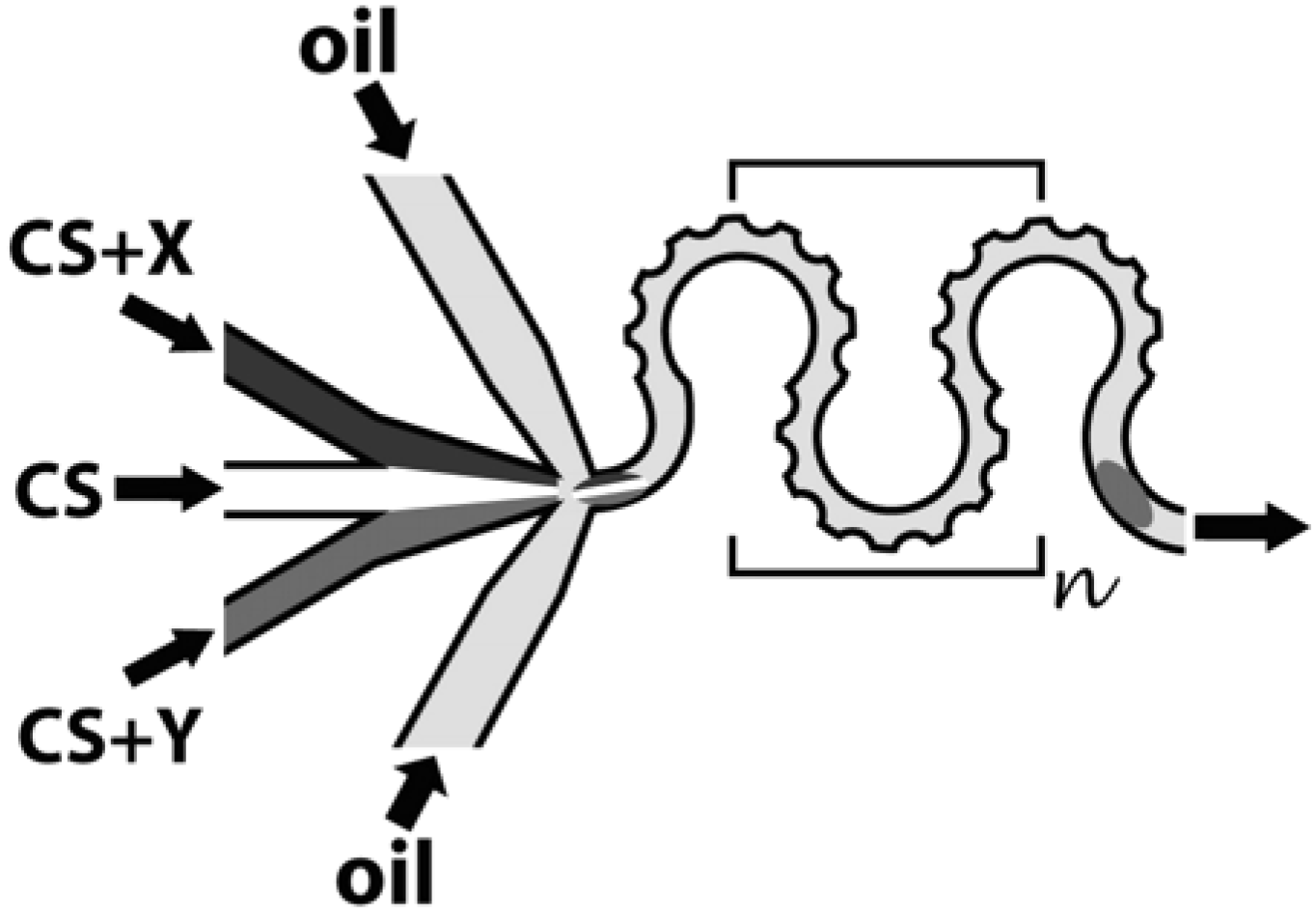
Liau
et al. [
49] designed a meandering channel whose curved part has bumps on the outer side (
Figure 26). This design makes the droplet’s internal flow more asymmetric than the case without bumps, because the oil film effectively becomes thinner on the bump side than the other smooth side resulting in higher shear stress acting on the fluid on the bump side. Muradoglu and Stone [
50] performed two-dimensional numerical simulations for the mixing inside a droplet flowing in a wavy channel. It was shown that the best mixing can be obtained when the drop size is comparable to the channel width. The effect of the capillary number is significant; the smaller the capillary number the better the mixing effect. The ratio of the viscosity of the drop to that of the ambient fluid must be as small as possible for better mixing. The effect of the channel geometry on the droplet mixing has been further studied by Tung
et al. [
51] for a serpentine microchannel with an oil as the carrier fluid, and by Dogan
et al. [
52] for a meandering channel with a gas as the carrier fluid. In the latter study, when the contact angle is less than 90 degrees the gas rather than the liquid takes a blunt-cylinder form. What these two studies and the other studies on this issue have in common is that they imply that there exists an optimum configuration of the channel for the fastest mixing rate in each design.
Figure 26.
A meandering channel with bumps on the outer side for use in mixing three kinds of liquids (from Liau
et al. [
49]).
Figure 26.
A meandering channel with bumps on the outer side for use in mixing three kinds of liquids (from Liau
et al. [
49]).
When estimating the mixing performance in terms of the distribution of species concentration, care must be given to the initial condition concentration distribution. Tanthapanichakoon
et al. [
53] numerically revealed that the initial concentrations is the most dominant parameter affecting the mixing rate, which was also addressed in the work of Wang
et al. [
54]. This means that the given flow field inside the droplet keeps a symmetric property. In order to investigate such a problem, Sarazin
et al. [
55] considered two kinds of methods in coalescing two droplets of different species subjected to mixing,
i.e., coalescing in a longitudinal arrangement and in a side-by-side arrangement. As shown in
Figure 27, coalescence of droplets in a longitudinal arrangement provides a much better mixing effect, which is in line with the studies of Tanthapanichakoon
et al. [
53] and Wang
et al. [
54]. As a carrier, fluid oil is most frequently used. On the other hand, Rhee and Burns [
56] used the air as the carrier fluid (
Figure 28). They managed to produce isolated droplets inside a microchannel and utilized the internal flow driven by the relative motion of the channel wall for better mixing. The droplets were reported to move through the channel without sticking to the side walls.
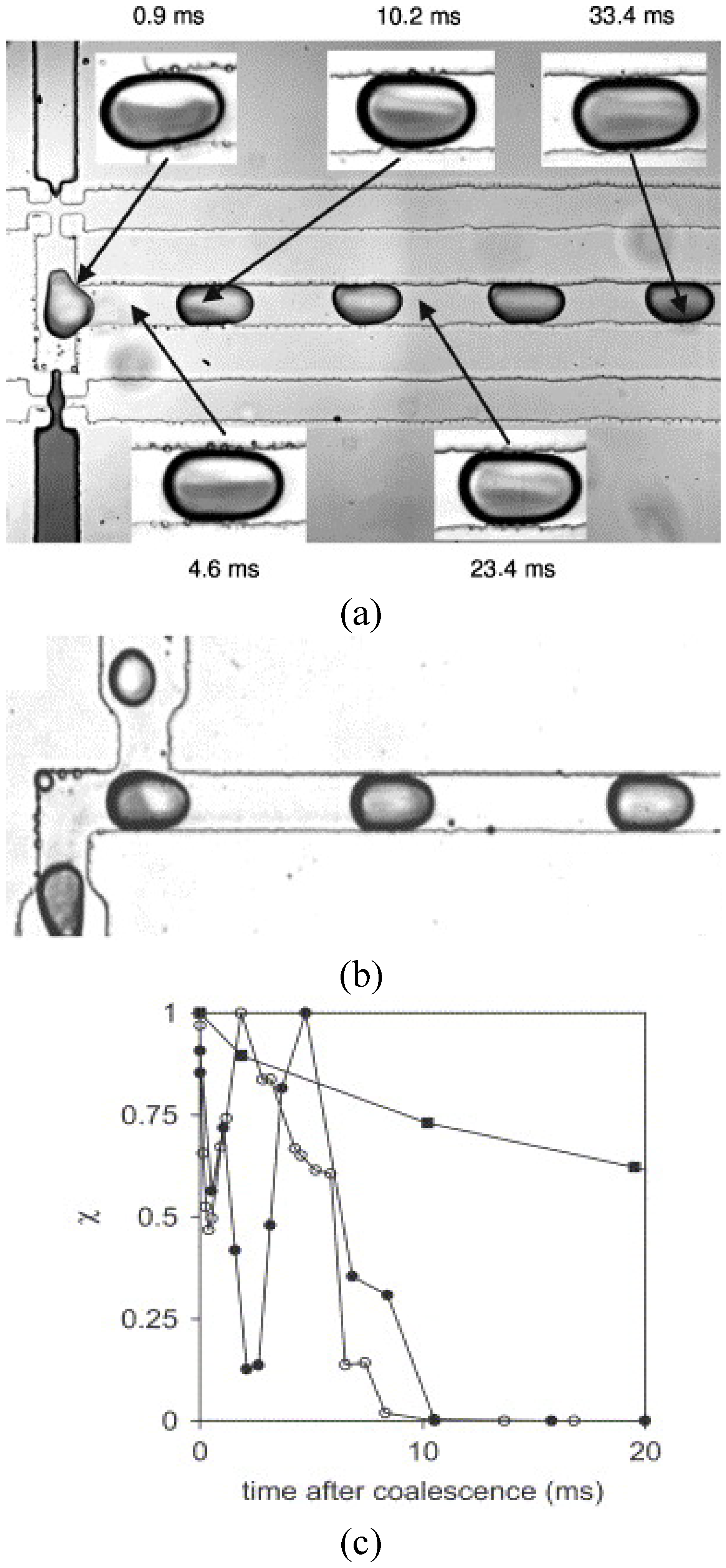
Figure 27.
Coalescing of two droplets in a
(a) side-by-side and
(b) longitudinal arrangement. Mixing performance is plotted in
(c): ■, mixing of dye and water in a side-by-side coalescence configuration; ●, mixing of dye and water in a longitudinal coalescence configuration; ○, bleaching reaction in a longitudinal coalescence configuration. Here a low level of
χ means a better mixing effect (from Sarrazin
et al. [
55]).
Figure 27.
Coalescing of two droplets in a
(a) side-by-side and
(b) longitudinal arrangement. Mixing performance is plotted in
(c): ■, mixing of dye and water in a side-by-side coalescence configuration; ●, mixing of dye and water in a longitudinal coalescence configuration; ○, bleaching reaction in a longitudinal coalescence configuration. Here a low level of
χ means a better mixing effect (from Sarrazin
et al. [
55]).
Figure 28.
A microchannel mixer with an air-inlet port to produce isolated droplets for better mixing (from Rhee and Burns [
56]).
Figure 28.
A microchannel mixer with an air-inlet port to produce isolated droplets for better mixing (from Rhee and Burns [
56]).
The requirement for the application of droplet mixing is that the carrier fluid and the target samples should be immiscible. Usually the samples are aqueous and thus we can easily find a carrier fluid, such as oil. The reaction results can also be easily observed without image deterioration if the droplet interface fully touches the channel wall so that the interface remains planar; in this case, the droplet is called “slug”. Momentarily, no serious disadvantage can be found in the method of droplet mixing.
3.6. Stirring by Particles
Stirring of fluid by use of magnetic particles is frequently applied for fluid mixing in micro devices. In the work of Grumann
et al. [
57], a mixing chamber of a diameter of approximately 6 mm included magnetic beads of the size of 68 μm and was subjected to spinning above a stationary disk on which permanent magnets are distributed in a radial in-and-out pattern, so that the magnetic particles experience a time-varying magnetic field and exhibit radially fluctuating motions inside the chamber. It was found that such a time-varying magnetic field enhances mixing, and switching the spinning direction further improves the mixing rate. It is well known that when a magnetic field is applied to a fluid containing scattered paramagnetic particles, they tend to align in a chain configuration (see e.g., [
58,
59,
60]). Obviously the linear structure of particles should be more effective than the isolated ones in fluid stirring for mixing. Calhoun
et al. [
61] focused on the enhanced fluid mixing due to a rotating chain of paramagnetic particles by performing two-dimensional lattice-Boltzmann simulations with the dipole model. It was shown that a suitable frequency of chain-breaking and -reforming is necessary for the best mixing. The feasibility of the method of fluid stirring with a rotating magnet and the magnetic chains was further verified experimentally by Franke
et al. [
62] and by Lee
et al. [
63]; superparamagnetic particles were used in the former study, whereas ferromagnetic particles in the latter. Roy
et al. [
64] demonstrated that even within a micron-sized droplet, the rotating magnetic field can be effectively used to stir the fluid for mixing by manipulating magnetic chains in the same manner as done in a large-size batch mixer. There is an optimum Mason number (ratio of the viscous and the magnetic forces) for the best mixing. Le
et al. [
65] performed numerical simulations of fluid flow and mixing in a microchannel caused by the motion of magnetic particles due to a temporally varying magnetic field. It was shown that an optimum period of magnetic-field modulation exists for the best mixing. Interestingly enough, the aggregated particles form discrete bluff bodies and propagate toward the region of a stronger magnetic field, which is thought to be responsible for the fluid mixing (
Figure 29).
As the mixing device becomes smaller, the particles for stirring must also be smaller too, and the magnetic force mobilizing the particles becomes accordingly weaker since it is a kind of body force. Therefore, the main problem with this method is how to concentrate the magnetic field for such small-scale applications.
Not only non-biological materials such as beads but also biological bodies can be used in the fluid mixing. Kim and Breuer [
66] employed Escherichia coli to control mixing in a “ψ” shape microchannel and exhibited fast spreading of species near the center of the channel caused by the motion of E. coli. They controlled the distribution of concentration by adding the E. coli to either one side of the buffer reservoirs. The possible application of the bacteria flagella motion in the stirring of fluid was also demonstrated.
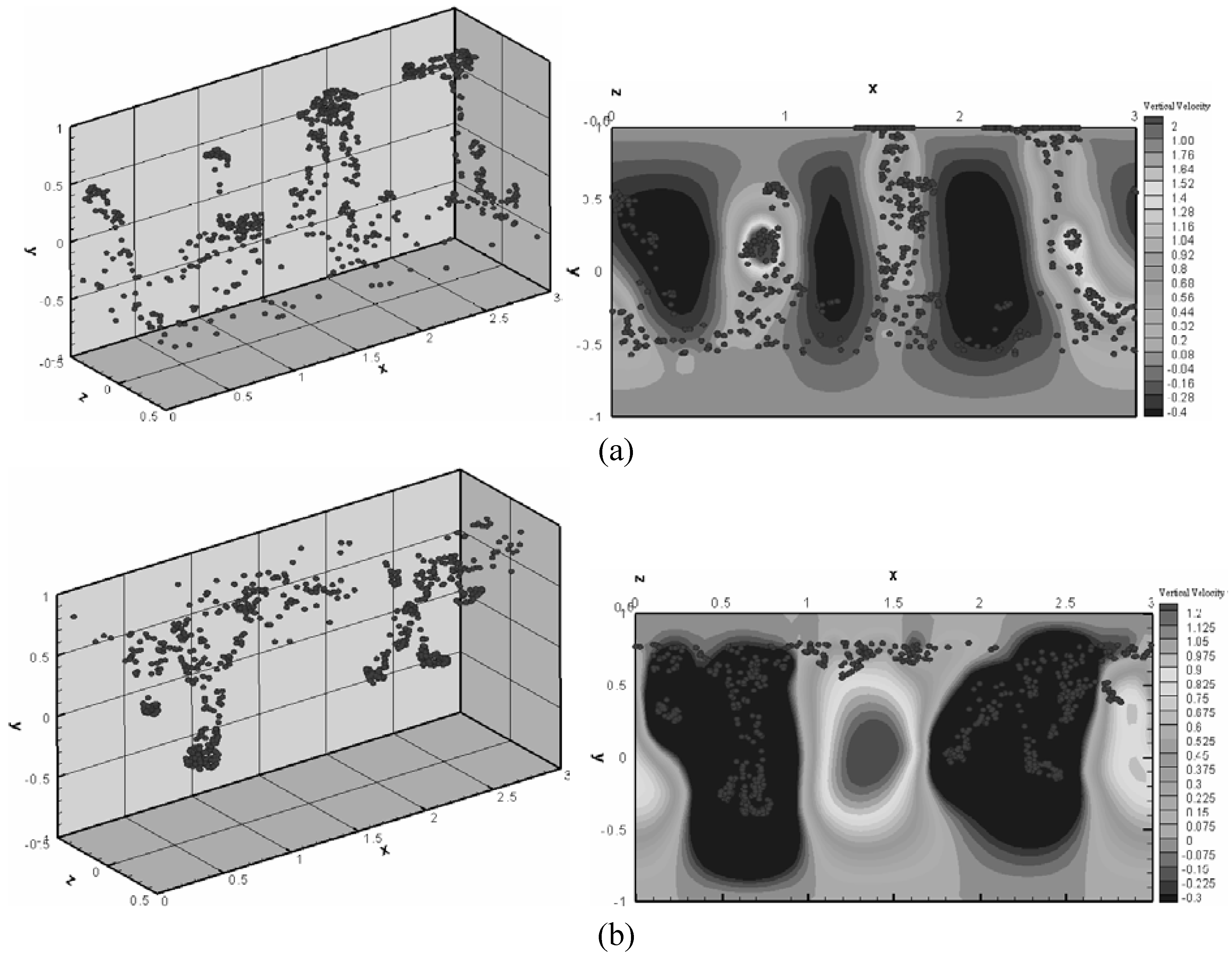
Figure 29.
Distribution of magnetic particles (left) and the contours of the vertical velocity component (right) in a microchannel subjected to a time-varying magnetic field applied along the vertical direction; typical patterns during the
(a) first half and
(b) second half period (from Le
et al. [
65]).
Figure 29.
Distribution of magnetic particles (left) and the contours of the vertical velocity component (right) in a microchannel subjected to a time-varying magnetic field applied along the vertical direction; typical patterns during the
(a) first half and
(b) second half period (from Le
et al. [
65]).