Mathematic Modeling for Optimum Conditions on Aflatoxin B1 Degradation by the Aerobic Bacterium Rhodococcus erythropolis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Microorgamism and Culture Medium
2.2. Degradation of AFB1 by R. erythropolis in Liquid Culture
2.3. Experimental Design
2.3.1. Plackett-Burman Design
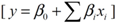
| Code | Variables (unit) | Levels a | ||
|---|---|---|---|---|
| −1 | 0 | +1 | ||
| X1 | Temperature (°C) | 15 | 25 | 35 |
| X2 | pH | 6.0 | 7.0 | 8.0 |
| X3 | Liquid volume (mL/100-mL) | 10 | 20 | 30 |
| X4 | Inoculum size (%) | 6 | 10 | 14 |
| X5 | Agitation speed (rpm) | 160 | 180 | 200 |
| X6 | Incubation time (h) | 48 | 72 | 96 |
2.3.2. Central Composite Design (CCD) and Response Surface Analysis (RSM)
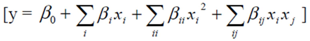
2.4. Inhibition of AFB1 by R. erythropolis in Peanuts
3. Results and Discussion
3.1. Plackett-Burman Design

| Run | x1 | x2 | x3 | x4 | x5 | x6 | y (%) |
|---|---|---|---|---|---|---|---|
| 1 | −1 | −1 | −1 | −1 | −1 | −1 | 18.1 |
| 2 | 1 | −1 | −1 | −1 | −1 | 1 | 10.6 |
| 3 | −1 | 1 | −1 | −1 | −1 | 1 | 80.9 |
| 4 | 1 | 1 | −1 | −1 | −1 | −1 | 12.6 |
| 5 | −1 | −1 | 1 | −1 | −1 | 1 | 75.0 |
| 6 | 1 | −1 | 1 | −1 | −1 | −1 | 13.4 |
| 7 | −1 | 1 | 1 | −1 | −1 | −1 | 26.2 |
| 8 | 1 | 1 | 1 | −1 | −1 | 1 | 11.8 |
| 9 | −1 | −1 | −1 | 1 | −1 | 1 | 51.4 |
| 10 | 1 | −1 | −1 | 1 | −1 | −1 | 10.9 |
| 11 | −1 | 1 | −1 | 1 | −1 | −1 | 27.2 |
| 12 | 1 | 1 | −1 | 1 | −1 | 1 | 11.3 |
| 13 | −1 | −1 | 1 | 1 | −1 | −1 | 49.0 |
| 14 | 1 | −1 | 1 | 1 | −1 | 1 | 9.2 |
| 15 | −1 | 1 | 1 | 1 | −1 | 1 | 90.6 |
| 16 | 1 | 1 | 1 | 1 | −1 | −1 | 34.9 |
| 17 | −1 | −1 | −1 | −1 | 1 | 1 | 26.6 |
| 18 | 1 | −1 | −1 | −1 | 1 | −1 | 15.8 |
| 19 | −1 | 1 | −1 | −1 | 1 | −1 | 14.5 |
| 20 | 1 | 1 | −1 | −1 | 1 | 1 | 12.5 |
| 21 | −1 | −1 | 1 | −1 | 1 | −1 | 22.9 |
| 22 | 1 | −1 | 1 | −1 | 1 | 1 | 22.8 |
| 23 | −1 | 1 | 1 | −1 | 1 | 1 | 85.7 |
| 24 | 1 | 1 | 1 | −1 | 1 | −1 | 21.2 |
| 25 | −1 | −1 | −1 | 1 | 1 | −1 | 12.2 |
| 26 | 1 | −1 | −1 | 1 | 1 | 1 | 8.7 |
| 27 | −1 | 1 | −1 | 1 | 1 | 1 | 62.8 |
| 28 | 1 | 1 | −1 | 1 | 1 | −1 | 26.7 |
| 29 | −1 | −1 | 1 | 1 | 1 | 1 | 40.3 |
| 30 | 1 | −1 | 1 | 1 | 1 | −1 | 19.8 |
| 31 | −1 | 1 | 1 | 1 | 1 | −1 | 32.3 |
| 32 | 1 | 1 | 1 | 1 | 1 | 1 | 45.2 |
| 33 | 0 | 0 | 0 | 0 | 0 | 0 | 79.4 |
| 34 | 0 | 0 | 0 | 0 | 0 | 0 | 81.4 |
| 35 | 0 | 0 | 0 | 0 | 0 | 0 | 79.8 |
| 36 | 0 | 0 | 0 | 0 | 0 | 0 | 80.9 |
| Variable | Coefficients | t Value | p-value |
|---|---|---|---|
| Intercept | 31.34688 | 10.52 | <0.0001 |
| x1 | −13.38438 | −4.49 | 0.0001 |
| x2 | 5.92813 | 1.99 | 0.0578 |
| x3 | 6.17188 | 2.07 | 0.0489 |
| x4 | 1.93438 | 0.65 | 0.5223 |
| x5 | −1.97187 | −0.66 | 0.5143 |
| x6 | 8.99063 | 3.02 | 0.0058 |
3.2. Central Composite Design and Response Surface Analysis
| Runs | x1 | x2 | x3 | x6 | y (%) |
|---|---|---|---|---|---|
| 1 | −1 | −1 | −1 | −1 | 57.6 |
| 2 | −1 | −1 | −1 | 1 | 47.8 |
| 3 | −1 | −1 | 1 | −1 | 74.9 |
| 4 | −1 | −1 | 1 | 1 | 80.4 |
| 5 | −1 | 1 | −1 | −1 | 64.2 |
| 6 | −1 | 1 | −1 | 1 | 72.4 |
| 7 | −1 | 1 | 1 | −1 | 65.3 |
| 8 | −1 | 1 | 1 | 1 | 90.4 |
| 9 | 1 | −1 | −1 | −1 | 47.0 |
| 10 | 1 | −1 | −1 | 1 | 46.3 |
| 11 | 1 | −1 | 1 | −1 | 64.8 |
| 12 | 1 | −1 | 1 | 1 | 62.0 |
| 13 | 1 | 1 | −1 | −1 | 54.6 |
| 14 | 1 | 1 | −1 | 1 | 59.7 |
| 15 | 1 | 1 | 1 | −1 | 60.5 |
| 16 | 1 | 1 | 1 | 1 | 65.1 |
| 17 | −2 | 0 | 0 | 0 | 68.1 |
| 18 | 2 | 0 | 0 | 0 | 53.7 |
| 19 | 0 | −2 | 0 | 0 | 69.1 |
| 20 | 0 | 2 | 0 | 0 | 92.2 |
| 21 | 0 | 0 | −2 | 0 | 68.5 |
| 22 | 0 | 0 | 2 | 0 | 95.5 |
| 23 | 0 | 0 | 0 | −2 | 60.7 |
| 24 | 0 | 0 | 0 | 2 | 95.8 |
| 25 | 0 | 0 | 0 | 0 | 82.6 |
| 26 | 0 | 0 | 0 | 0 | 84.4 |
| 27 | 0 | 0 | 0 | 0 | 83.7 |
| 28 | 0 | 0 | 0 | 0 | 83.9 |
| 29 | 0 | 0 | 0 | 0 | 83.4 |
| 30 | 0 | 0 | 0 | 0 | 82.2 |
| 31 | 0 | 0 | 0 | 0 | 84.0 |
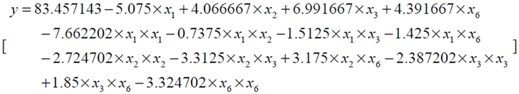
| Parameter | DF | Estimate | StandardError | t Value | Pr > |t| |
|---|---|---|---|---|---|
| Intercept | 1 | 83.457143 | 3.273286 | 25.50 | <0.0001 |
| x1 | 1 | −5.075000 | 1.767777 | −2.87 | 0.0111 |
| x2 | 1 | 4.066667 | 1.767777 | 2.30 | 0.0352 |
| x3 | 1 | 6.991667 | 1.767777 | 3.96 | 0.0011 |
| x6 | 1 | 4.391667 | 1.767777 | 2.48 | 0.0244 |
| x1 * x1 | 1 | −7.662202 | 1.619505 | −4.73 | 0.0002 |
| x2 * x1 | 1 | −0.737500 | 2.165075 | −0.34 | 0.7378 |
| x2 * x2 | 1 | −2.724702 | 1.619505 | −1.68 | 0.1119 |
| x3 * x1 | 1 | −1.512500 | 2.165075 | −0.70 | 0.4948 |
| x3 * x2 | 1 | −3.312500 | 2.165075 | −1.53 | 0.1456 |
| x3 * x3 | 1 | −2.387202 | 1.619505 | −1.47 | 0.1599 |
| x6 * x1 | 1 | −1.425000 | 2.165075 | −0.66 | 0.5198 |
| x6 * x2 | 1 | 3.175000 | 2.165075 | 1.47 | 0.1619 |
| x6 * x3 | 1 | 1.850000 | 2.165075 | 0.85 | 0.4055 |
| x6 * x6 | 1 | −3.324702 | 1.619505 | −2.05 | 0.0568 |
| Regression | DF | Type I Sum of Squares | R-Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Linear | 4 | 2651.125000 | 0.4205 | 8.84 | 0.0006 |
| Quadratic | 4 | 1983.513233 | 0.3146 | 6.61 | 0.0024 |
| Crossproduct | 6 | 469.407500 | 0.0745 | 1.04 | 0.4345 |
| Total Model | 14 | 5104.045733 | 0.8096 | 4.86 | 0.0017 |


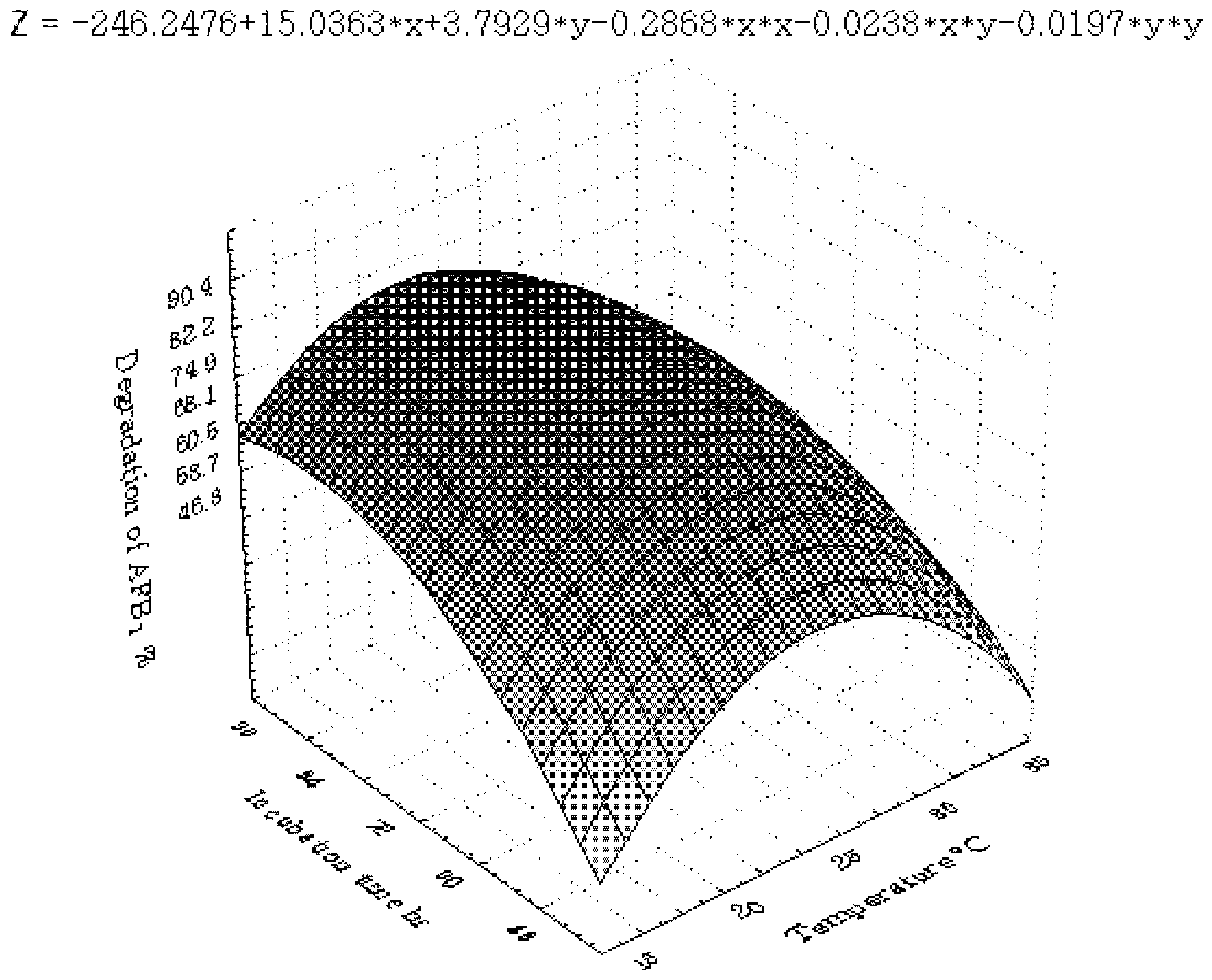
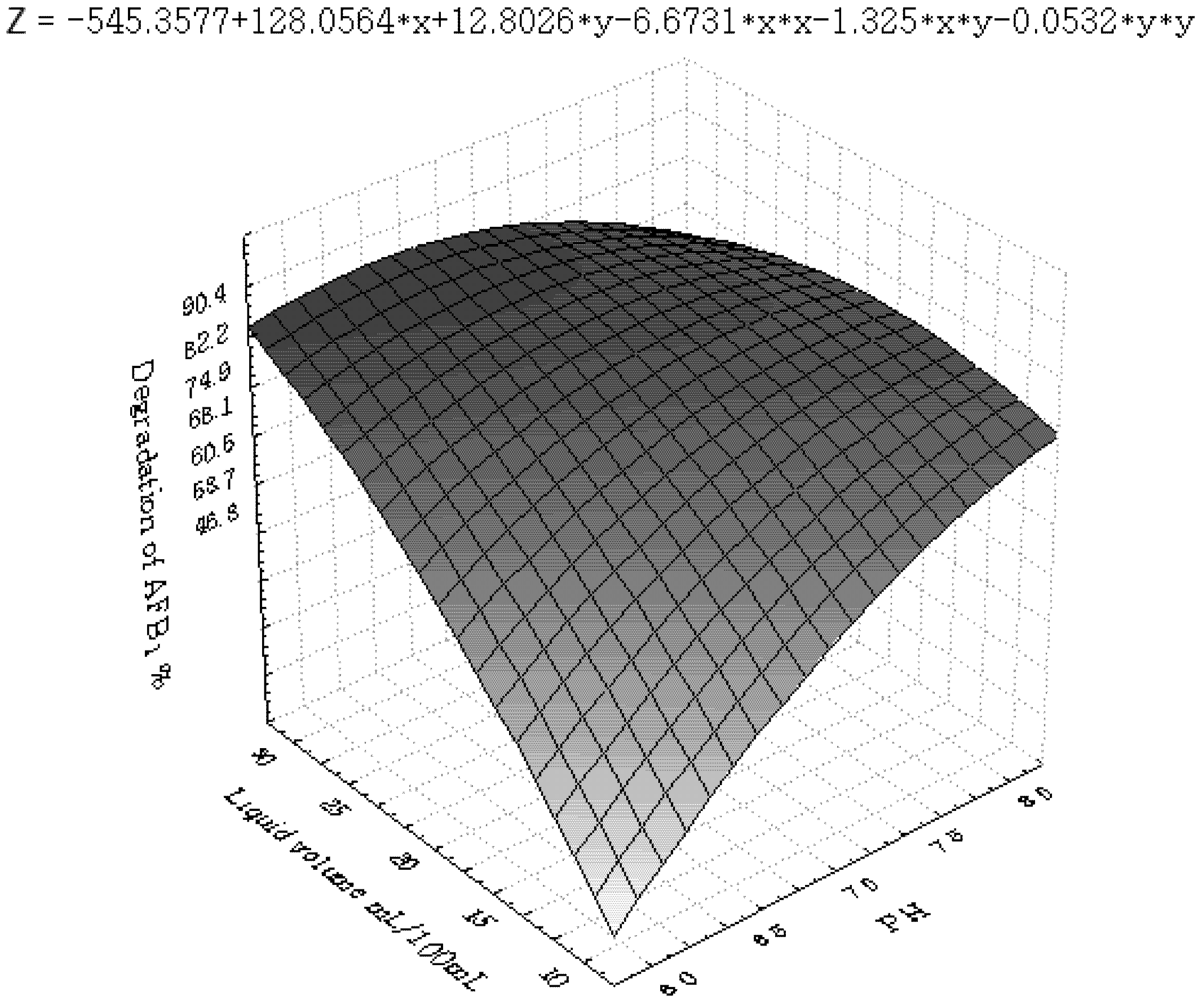

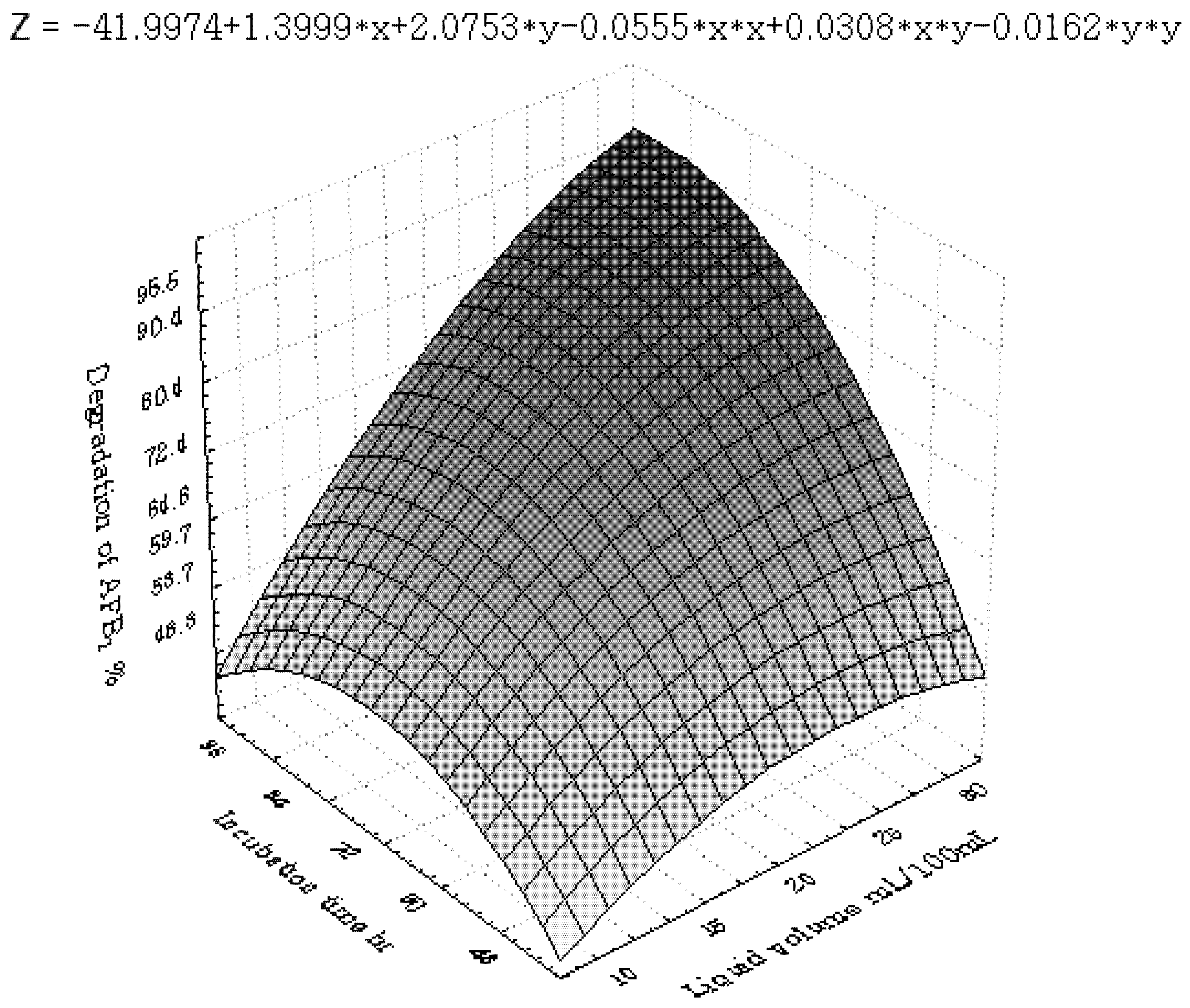
3.3. Inhibition of AFB1 by R. erythropolis in Peanuts
| Control | R. erythropolis | B. megaterium | R. erythropolis and B. megaterium | |
|---|---|---|---|---|
| Aflatoxin B1 (μg/kg) (mean ± SD) | 195.69 ± 1.92 | 178.38 ± 2.47 | 148.27 ± 3.87 | 140.80 ± 3.59 |
4. Conclusions
Acknowledgements
Conflict of Interest
References
- Nogueira, J.H.; Gonçalez, E.; Galleti, S.R.; Facanali, R.; Marques, M.O.; Felício, J.D. Ageratum conyzoides essential oil as aflatoxin suppressor of Aspergillus flavus. Int. J. Food Microbiol. 2010, 137, 55–60. [Google Scholar] [CrossRef]
- Jonsyn, F.E.; Lahai, G.P. Mycotoxic flora and mycotoxins in smoke-dried fish from Sierra Leone. Nahrung 1992, 5, 485–489. [Google Scholar] [CrossRef]
- Yu, J.; Fedorova, N.D.; Montalbano, B.G.; Bhatnagar, D.; Cleveland, T.E.; Bennett, J.W.; Nierman, W.C. Tight control of mycotoxin biosynthesis gene expression in Aspergillus flavus by temperature as revealed by RNA-Seq. FEMS Microbiol. Lett. 2011, 322, 145–149. [Google Scholar] [CrossRef]
- Amaike, S.; Keller, N.P. Aspergillus flavus. Annu. Rev. Phytopathol. 2011, 49, 107–133. [Google Scholar] [CrossRef]
- Williams, W.P.; Windham, G.L.; Buckley, P.M.; Perkins, J.M. Southwestern corn borer damage and aflatoxin accumulation in conventional and transgenic corn hybrids. Field Crops Res. 2005, 91, 329–336. [Google Scholar] [CrossRef]
- Commission Regulation (EU) No 165/2010. Amending Regulation (EC) No 1881/2006 setting maximum levels for certain contaminants in foodstuffs as regards aflatoxins. Off. J. Eur. Union 2010, 53, 8–12.
- Chang, P.K.; Horn, B.W.; Dorner, J.W. Sequence breakpoints in the aflatoxin biosynthesis gene cluster and flanking regions in nonaflatoxigenic Aspergillus flavus isolates. Fungal Genet. Biol. 2005, 42, 914–923. [Google Scholar] [CrossRef]
- Sindhu, S.; Chempakam, B.; Leela, N.K.; Suseela Bhai, R. Chemoprevention by essential oil of turmeric leaves (Curcuma longa L.) on the growth of Aspergillus flavus and aflatoxin production. Food Chem. Toxicol. 2011, 49, 1188–1192. [Google Scholar] [CrossRef]
- Reddy, K.R.N.; Reddy, C.S.; Muralidharan, K. Potential of botanicals and biocontrol agents on growth and aflatoxin production by Aspergillus flavus infecting rice grains. Food Control 2009, 20, 173–178. [Google Scholar] [CrossRef]
- Sánchez, E.; Heredia, N.; García, S. Inhibition of growth and mycotoxin production of Aspergillus flavus and Aspergillus parasiticus by extracts of Agave species. Int. J. Food Microbiol. 2005, 98, 271–279. [Google Scholar] [CrossRef]
- Tamil Selvi, A.; Joseph, S.; Jayaprakasha, G.K. Inhibition of growth and aflatoxin production in Aspergillus flavus by Garcinia indica extract and its antioxidant activity. Food Microbiol. 2003, 20, 455–460. [Google Scholar] [CrossRef]
- Razzaghi-Abyaneh, M.; Shams-Ghahfarokhi, M.; Yoshinari, T.; Rezaee, M.B.; Jaimand, K.; Nagasawa, H.; Sakuda, S. Inhibitory effects of Satureja hortensis L. essential oil on growth and aflatoxin production by Aspergillus parasiticus. Int. J. Food Microbiol. 2008, 123, 228–233. [Google Scholar] [CrossRef]
- Palumbo, J.D.; Baker, J.L.; Mahoney, N.E. Isolation of bacterial antagonists of Aspergillus flavus from almonds. Microb. Ecol. 2006, 52, 45–52. [Google Scholar] [CrossRef]
- Ciegler, A.; Lillehoj, E.B.; Peterson, R.E.; Hall, H.H. Microbial detoxification of aflatoxin. Appl. Microbiol. 1966, 14, 934–939. [Google Scholar]
- Hormisch, D.; Brost, I.; Kohring, G.W.; Giffhorn, F.; Kroppenstedt, R.M.; Stackebrandt, E.; Färber, P.; Holzapfel, W.H. Mycobacterium fluoranthenivorans sp. nov., a fluoranthene and aflatoxin B1 degrading bacterium from contaminated soil of a former coal gas plant. Syst. Appl. Microbiol. 2004, 27, 653–660. [Google Scholar] [CrossRef]
- Taylor, M.C.; Jackson, C.J.; Tattersall, D.B.; French, N.; Peat, T.S.; Newman, J.; Briggs, L.J.; Lapalikar, G.V.; Campbell, P.M.; Scott, C.; et al. Identification and characterization of two families of F420 H2-dependent reductases from Mycobacteria that catalyse aflatoxin degradation. Mol. Microbiol. 2010, 78, 561–575. [Google Scholar] [CrossRef]
- Kong, Q.; Shan, S.H.; Liu, Q.Z.; Wang, X.D.; Yu, F.T. Biocontrol of Aspergillus flavus on peanut kernels by use of a strain of marine Bacillus megaterium. Int. J. Food Microbiol. 2010, 139, 31–35. [Google Scholar] [CrossRef]
- Alberts, J.F.; Engelbrecht, Y.; Steyn, P.S.; Holzapfel, W.H.; van Zyl, W.H. Biological degradation of aflatoxin B1 by Rhodococcus erythropolis cultures. Int. J. Food Microbiol. 2006, 109, 121–126. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, W.G.; Hunter, J.S. Statistics for Experimenters; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Hibbert, D.B. Experimental design in chromatography: A tutorial review. J. Chromatogr. B 2012. [Google Scholar] [CrossRef]
- He, J.; Zhen, Q.; Qiu, N.; Liu, Z.; Wang, B.; Shao, Z.; Yu, Z. Medium optimization for the production of a novel bioflocculant from Halomonas sp. V3a′ using response surface methodology. Bioresour. Technol. 2009, 100, 5922–5927. [Google Scholar]
- Guo, W.Q.; Ren, N.Q.; Wang, X.J.; Xiang, W.S.; Ding, J.; You, Y.; Liu, B.F. Optimization of culture conditions for hydrogen production by Ethanoligenens harbinense B49 using response surface methodology. Bioresour. Technol. 2009, 100, 1192–1196. [Google Scholar]
- Reddy, L.V.; Wee, Y.J.; Yun, J.S.; Ryu, H.W. Optimization of alkaline protease production by batch culture of Bacillus sp. RKY3 through Plackett-Burman and response surface methodological approaches. Bioresour. Technol. 2008, 99, 2242–2249. [Google Scholar]
- Cavallarin, L.; Tabacco, E.; Antoniazzi, S.; Borreani, G. Aflatoxin accumulation in whole crop maize silage as a result of aerobic exposure. J. Sci. Food Agric. 2011, 91, 2419–2425. [Google Scholar]
- Sudarjanto, G.; Keller-Lehmann, B.; Keller, J. Optimization of integrated chemical-biological degradation of a reactive azo dye using response surface methodology. J. Hazard. Mater. 2006, 138, 160–168. [Google Scholar] [CrossRef]
- Tejada-Castañeda, Z.I.; Avila-Gonzalez, E.; Casaubon-Huguenin, M.T.; Cervantes-Olivares, R.A.; Vásquez-Peláez, C.; Hernández-Baumgarten, E.M.; Moreno-Martínez, E. Biodetoxification of aflatoxin-contaminated chick feed. Poult. Sci. 2008, 87, 1569–1576. [Google Scholar] [CrossRef]
- Lapalikar, G.V.; Taylor, M.C.; Warden, A.C.; Scott, C.; Russell, R.J.; Oakeshott, J.G. F420H2-dependent degradation of aflatoxin and other furanocoumarins is widespread throughout the Actinomycetales. PLoS One 2012, 7, e30114. [Google Scholar]
- Bashiri, G.; Rehan, A.M.; Greenwood, D.R.; Dickson, J.M.; Baker, E.N. Metabolicengineering of cofactor F420 production in Mycobacterium smegmatis. PLoS One 2010, 5, e15803. [Google Scholar]
- Isabelle, D.; Simpson, D.R.; Daniels, L. Large-scaleproduction of coenzyme F420-5,6 by using Mycobacterium smegmatis. Appl. Environ. Microbiol. 2002, 68, 5750–5755. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kong, Q.; Zhai, C.; Guan, B.; Li, C.; Shan, S.; Yu, J. Mathematic Modeling for Optimum Conditions on Aflatoxin B1 Degradation by the Aerobic Bacterium Rhodococcus erythropolis. Toxins 2012, 4, 1181-1195. https://doi.org/10.3390/toxins4111181
Kong Q, Zhai C, Guan B, Li C, Shan S, Yu J. Mathematic Modeling for Optimum Conditions on Aflatoxin B1 Degradation by the Aerobic Bacterium Rhodococcus erythropolis. Toxins. 2012; 4(11):1181-1195. https://doi.org/10.3390/toxins4111181
Chicago/Turabian StyleKong, Qing, Cuiping Zhai, Bin Guan, Chunjuan Li, Shihua Shan, and Jiujiang Yu. 2012. "Mathematic Modeling for Optimum Conditions on Aflatoxin B1 Degradation by the Aerobic Bacterium Rhodococcus erythropolis" Toxins 4, no. 11: 1181-1195. https://doi.org/10.3390/toxins4111181




