A Novel Iterative Thresholding Algorithm Based on Plug-and-Play Priors for Compressive Sampling
Abstract
:1. Introduction
2. Compressive Sampling and Fast Iterative Shrinkage-Thresholding Algorithm
| Algorithm 1. ISTA [26] |
| Input: the CS measurements y and the measurement matrix A |
| Initialization: x0 = 0, |
| for k = 1 to K do |
| (a) |
| (b) |
| end for |
| Algorithm 2. FISTA [21] |
| Input: the CS measurements y and the measurement matrix A |
| Initialization: x0 = r1 = 0, |
| for k = 1 to K do |
| (a) |
| (b) |
| (c) ; |
| end for |
3. CS via Composite Regularization and Adaptive Thresholding
3.1. The New Composite Model
3.2. Solving The Composite Model with Fast Composite Splitting Technique
| Algorithm 3. CS with Plug-and-play Priors |
| Input: the CS measurements y and the measurement matrix A |
| Initialization: x0 = r1 = 0, , , c |
| for k = 1 to K do |
| (a) |
| (b) |
| (c) |
| (d) |
| (e) |
| (f) ; |
| end for |
4. Experiments
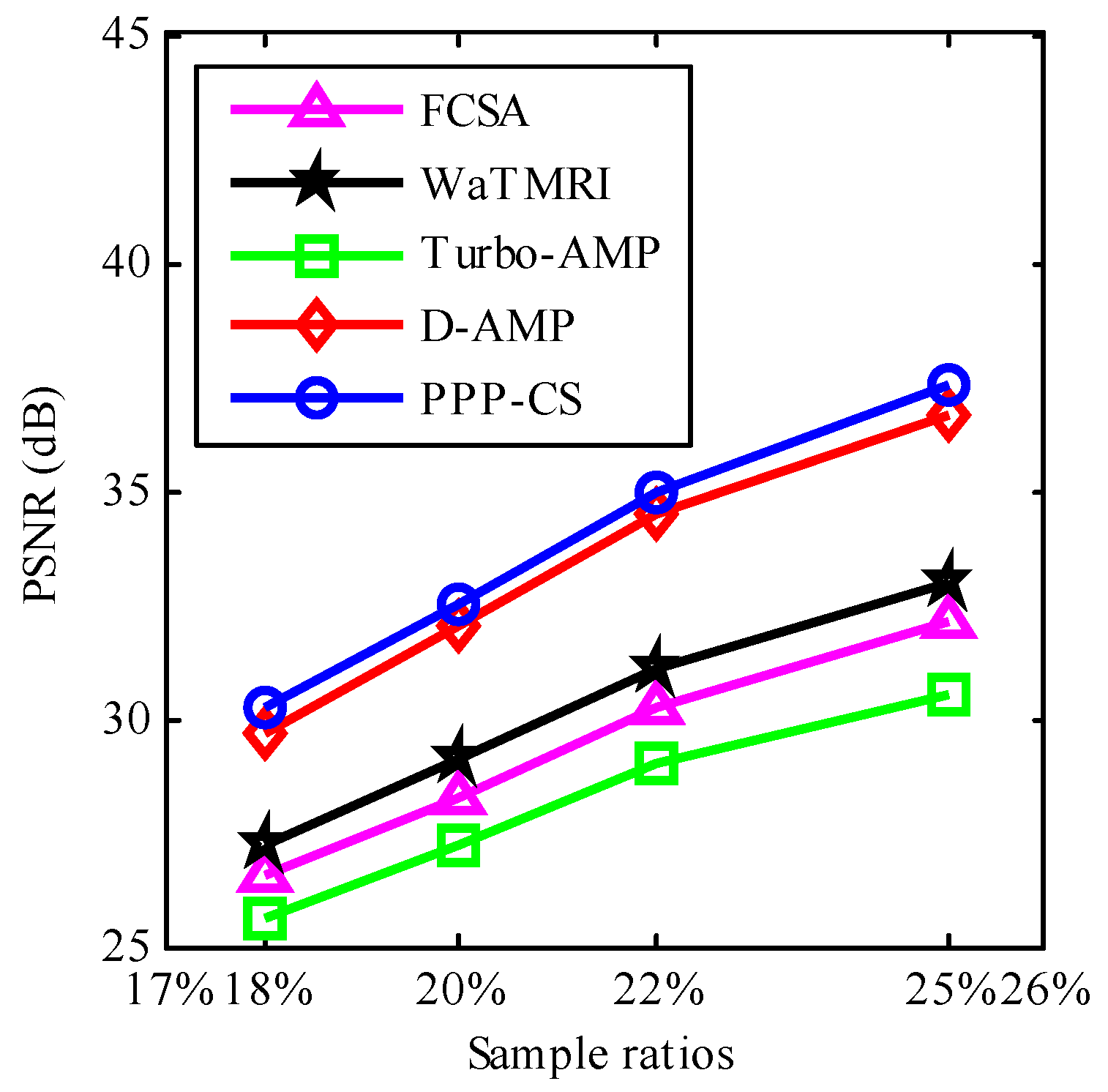
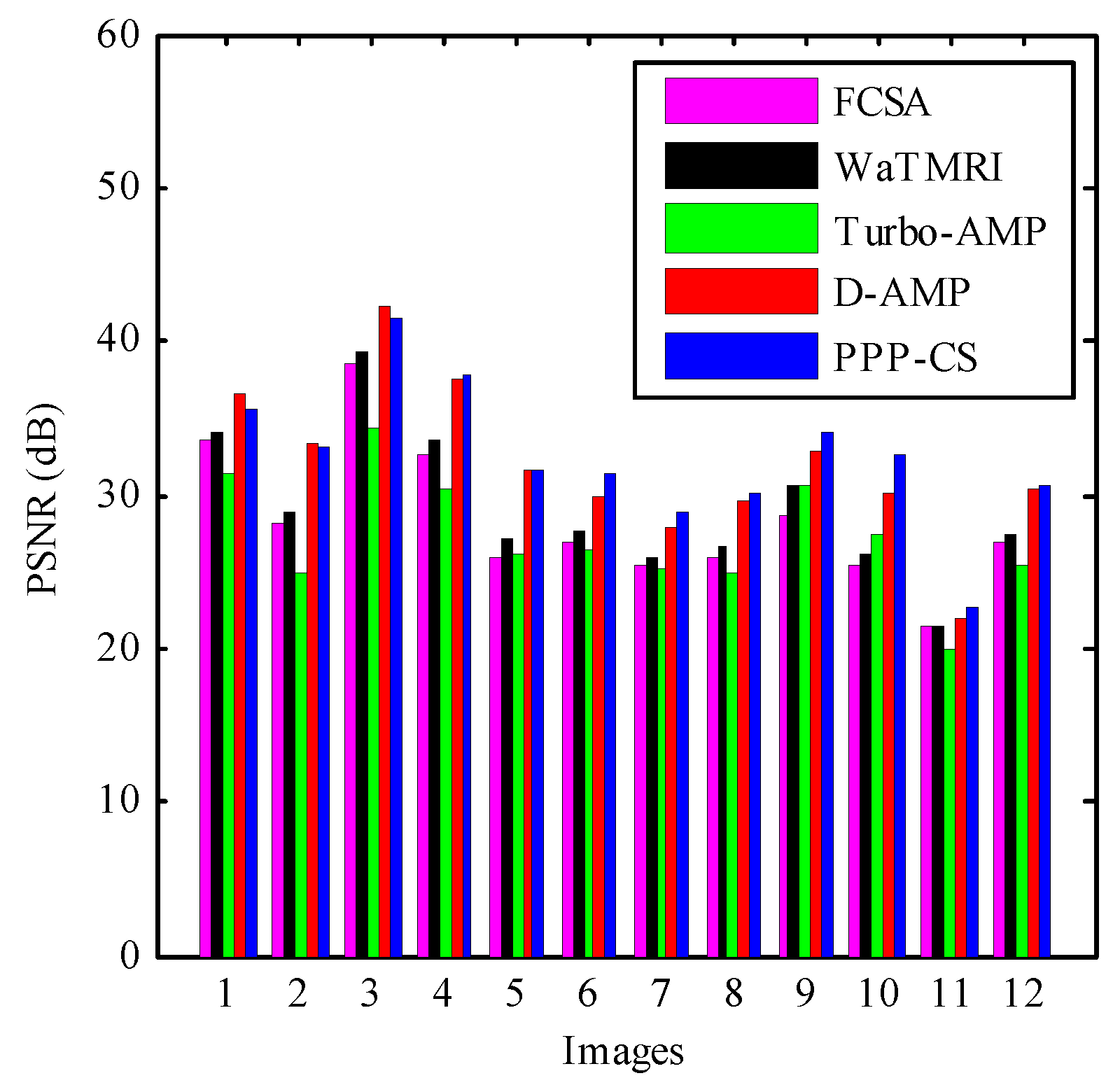
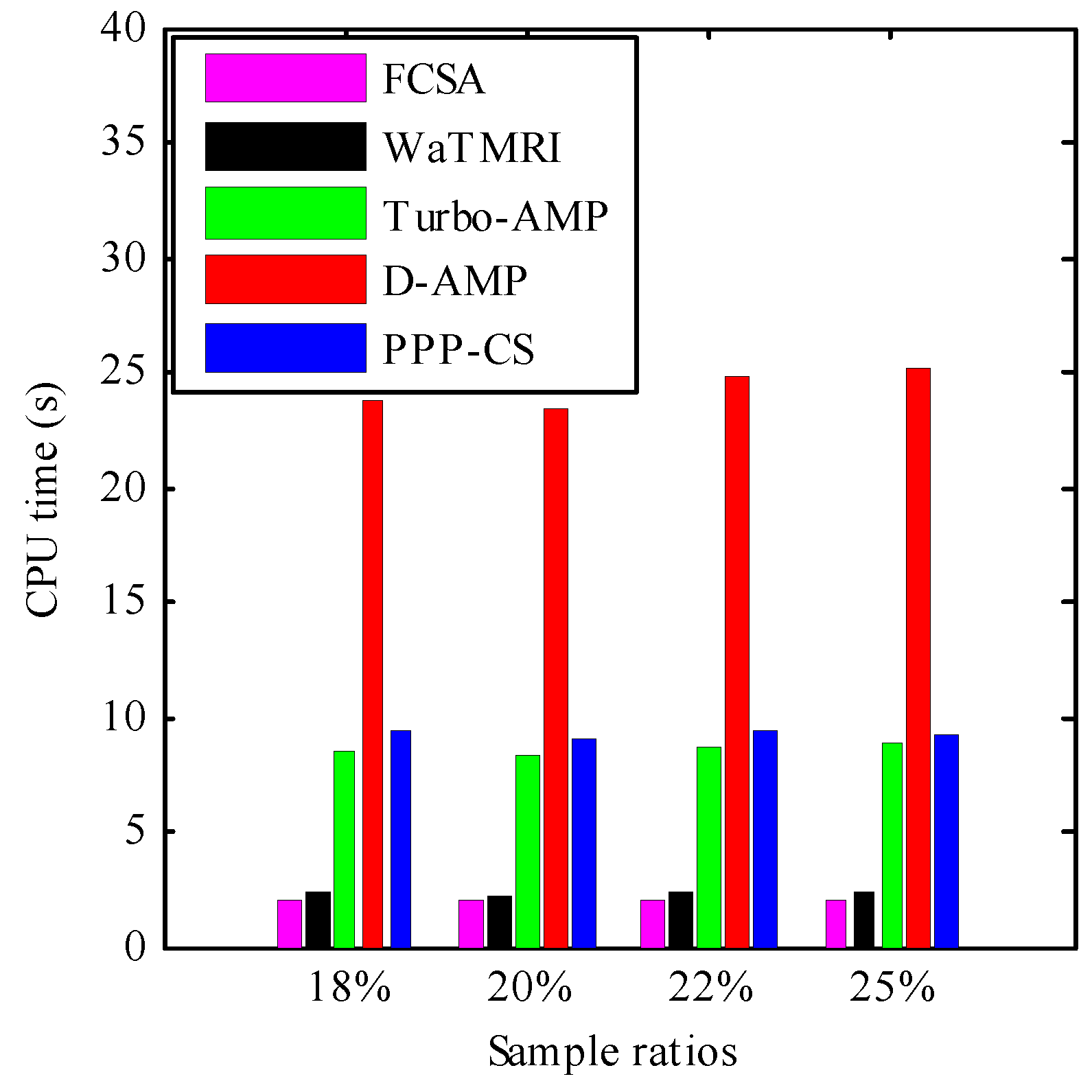
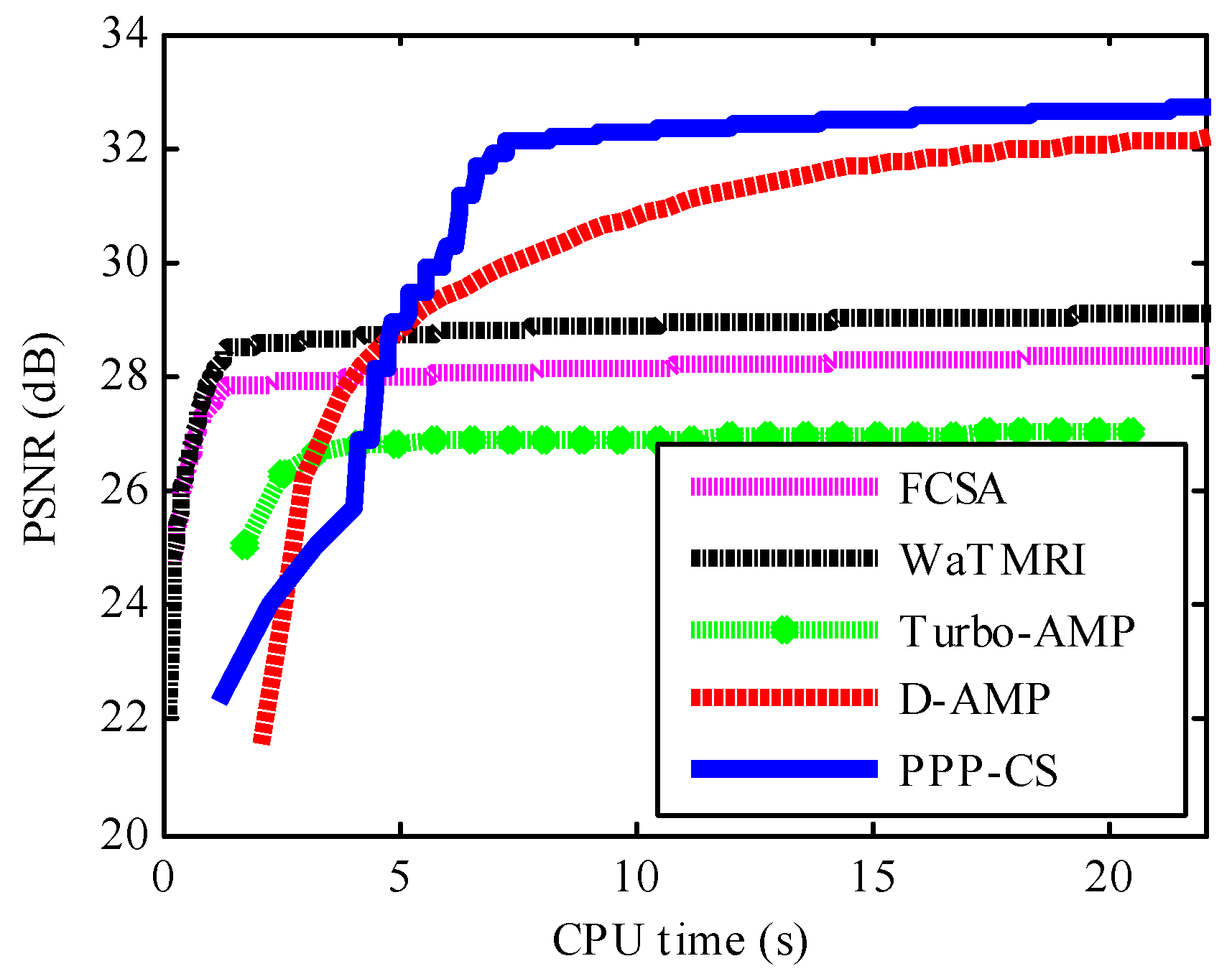
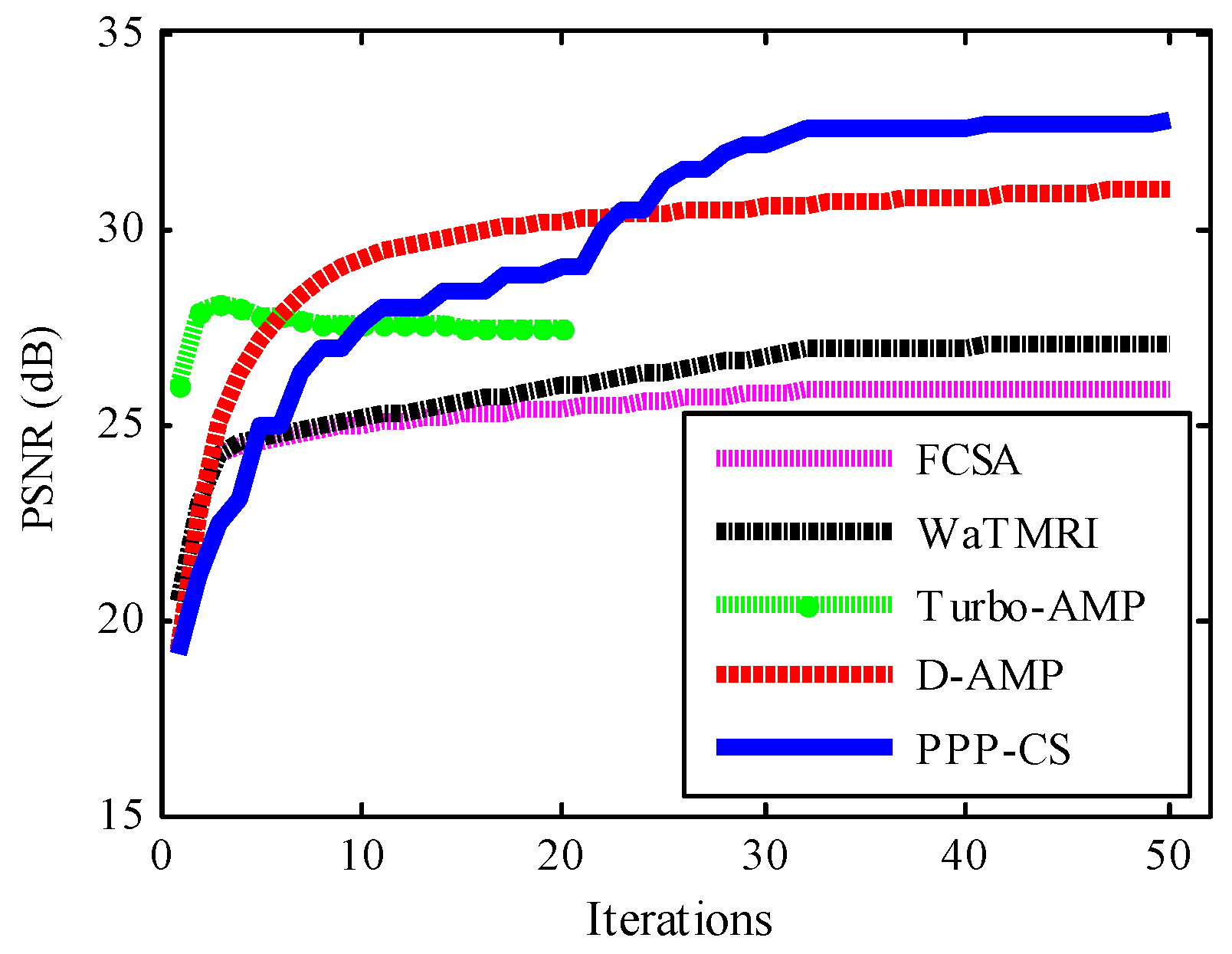
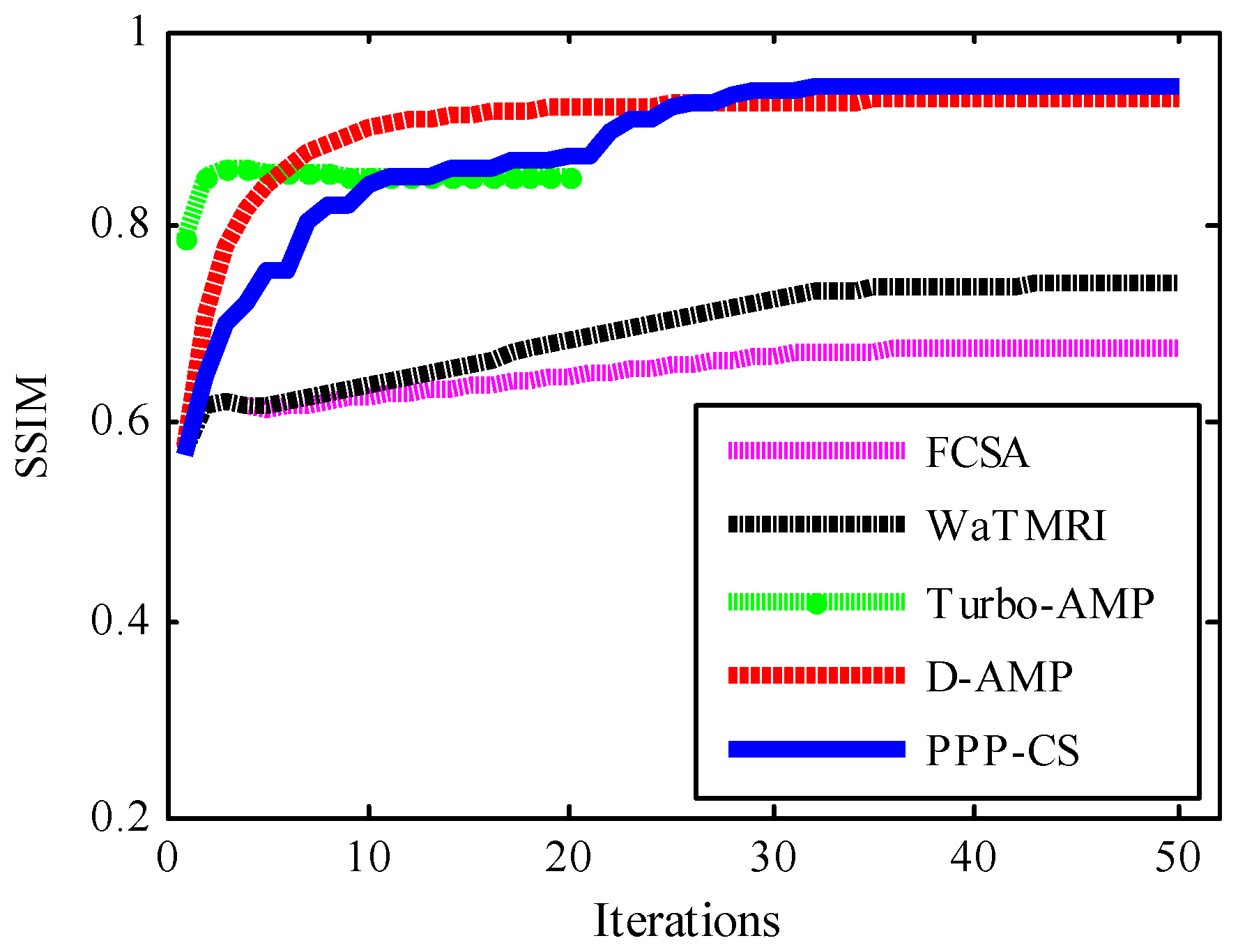
4.1. Quantative Evaluation
4.2. Visual Quality Evaluation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Tan, J.; Ma, Y.; Baron, D. Compressive Imaging via Approximate Message Passing with Image Denoising. IEEE Trans. Signal Process. 2015, 63, 424–428. [Google Scholar] [CrossRef]
- Zhu, Z.; Qi, G.; Chai, Y.; Chen, Y. A Novel Multi-Focus Image Fusion Method Based on Stochastic Coordinate Coding and Local Density Peaks Clustering. Future Internet 2016, 8, 53–70. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, S.; Metaxas, D. Efficient MR Image Reconstruction for Compressed MR Imaging. Med. Image Anal. 2011, 15, 670–679. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Huang, J. Exploiting the wavelet structure in compressed sensing MRI. Magn. Reson. Imaging 2014, 32, 1377–1389. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Wu, X.; Jing, W.; He, X. Reconstruction algorithm using exact tree projection for tree-structured compressive sensing. IET Signal Process. 2016, 10, 566–573. [Google Scholar] [CrossRef]
- Som, S.; Schniter, P. Compressive imaging using approxi- mate message passing and a markov-tree prior. IEEE Trans. Signal Process. 2012, 60, 3439–3448. [Google Scholar] [CrossRef]
- Zhang, X.; Bai, T.; Meng, H.; Chen, J. Compressive Sensing-Based ISAR Imaging via the Combination of the Sparsity and Nonlocal Total Variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 990–994. [Google Scholar] [CrossRef]
- Dong, W.; Shi, G.; Wu, X.; Zhang, L. A learning-based method for compressive image recovery. J. Vis. Commun. Image Represent. 2013, 24, 1055–1063. [Google Scholar] [CrossRef]
- Dong, W.; Shi, G.; Li, X.; Ma, Y.; Huang, F. Compressive sensing via nonlocal low-rank regularization. IEEE Trans. Image Process. 2014, 23, 3618–3632. [Google Scholar] [CrossRef] [PubMed]
- Metzler, C.A.; Maleki, A.; Baraniuk, R.G. From Denoising to Compressed Sensing. IEEE Trans. Inf. Theory 2016, 62, 5117–5144. [Google Scholar] [CrossRef]
- Metzler, C.A.; Maleki, A.; Baraniuk, R.G. BM3D-AMP: A New Image Recovery Algorithm Based on BM3D Denoising. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 3116–3120. [Google Scholar]
- Zhang, J.; Zhao, D.; Zhao, C.; Xiong, R.; Ma, S.; Gao, W. Image Compressive Sensing Recovery via Collaborative Sparsity. IEEE J. Emerg. Sel. Top. Circuits Syst. 2012, 2, 380–391. [Google Scholar] [CrossRef]
- Egiazarian, K.; Foi, A.; Katkovnik, V. Compressed Sensing Image Reconstruction via Recursive Spatially Adaptive Filtering. In Proceedings of the IEEE International Conference on Image Processing (ICIP), San Antonio, TX, USA, 16–19 September 2007; pp. I-549–I-552. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Knaus, C.; Zwicker, M. Dual-Domain Filtering. SIAM J. Imaging Sci. 2015, 8, 1396–1420. [Google Scholar] [CrossRef]
- Venkatakrishnan, S.; Bouman, C.A.; Wohlberg, B. Plug-and-Play Priors for Model Based Reconstruction. In Proceedings of the IEEE Global Conference on Signal and Information Processing (Global SIP), Austin, TX, USA, 3–5 December 2013; pp. 945–948. [Google Scholar]
- Brifman, A.; Romano, Y.; Elad, M. Turning a Denoiser into a Super-Resolver Using Plug and Play Priors. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 1404–1408. [Google Scholar]
- Liu, L.; Xie, Z.; Feng, J. Backtracking-Based Iterative Regularization Method for Image Compressive Sensing Recovery. Algorithms 2017, 10, 1–8. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Hosseini, M.S.; Plataniotis, K.N. High-accuracy total variation with application to compressed video sensing. IEEE Trans. Image Process. 2014, 23, 3869–3884. [Google Scholar] [CrossRef] [PubMed]
- Ling, Q.; Shi, W.; Wu, G.; Ribeiro, A. DLM: Decentralized Linearized Alternating Direction Method of Multipliers. IEEE Trans. Signal Process. 2015, 63, 4051–4064. [Google Scholar] [CrossRef]
- Yin, W.; Osher, S.; Goldfarb, D.; Darbon, J. Bregman iterative algorithms for l1-minimization with applications to compressed sensing. SIAM J. Imaging Sci. 2008, 1, 143–168. [Google Scholar] [CrossRef]
- Qiao, T.; Li, W.; Wu, B. A New Algorithm Based on Linearized Bregman Iteration with Generalized Inverse for Compressed Sensing. Circuits Syst. Signal Process. 2014, 33, 1527–1539. [Google Scholar] [CrossRef]
- Daubechies, I.; Defriese, M.; DeMol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar] [CrossRef] [PubMed]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Xie, Z.; Yang, C. A Novel Iterative Thresholding Algorithm Based on Plug-and-Play Priors for Compressive Sampling. Future Internet 2017, 9, 24. https://doi.org/10.3390/fi9030024
Liu L, Xie Z, Yang C. A Novel Iterative Thresholding Algorithm Based on Plug-and-Play Priors for Compressive Sampling. Future Internet. 2017; 9(3):24. https://doi.org/10.3390/fi9030024
Chicago/Turabian StyleLiu, Lingjun, Zhonghua Xie, and Cui Yang. 2017. "A Novel Iterative Thresholding Algorithm Based on Plug-and-Play Priors for Compressive Sampling" Future Internet 9, no. 3: 24. https://doi.org/10.3390/fi9030024





