Fast Cut Back Thermal Power Plant Load Rejection and Black Start Field Test Analysis
Abstract
: Fast and reliable black start plays a key role in improving the ability of the power system to resist the risk of large-scale blackouts. For a black start with high voltage and long-distance transmission lines, it is much easier to cause phenomena such as self-excitation and power frequency/operating overvoltage, which may lead to black start failure and impact the reliability of the system's restoration. Meanwhile, the long time needed to crank up the non-black start units will impact the speed of the restoration. This paper addresses the advantages of using a thermal power unit with a fast cut back (FCB) function as a black start unit, and studies the transient process of the FCB unit during the restoration. Firstly, key problems in the power system black start process are analyzed and a practical engineering criterion of self-excitation is proposed. Secondly, the dynamic model of the FCB unit is presented. Thirdly, the field test of the FCB unit load rejection and black start is introduced, which is the first successful field test of black start with 500 kV long-distance lines in China Southern Power Grid (CSG). Finally, the transient process of this test is simulated using the PSCAD/EMTDC software, and the simulation results accord well with the field test results, which verifies the correctness of the FCB model and the self-excitation engineering criterion proposed.1. Introduction
As the electricity demand in society continues to grow, the interconnected power grid is developing towards large-scale direction. However, new safety problems arise with the increase of the power grid profits. For example, local faults may induce cascading reactions and cause large-scale blackouts [1,2]. In recent years, there have been many large-scale power system blackouts worldwide, resulting in great economic losses and terrible political impacts [3,4]. Restoring the power supply after a large-scale blackout is a complicated and time-consuming process. A fast and reliable restoration can significantly reduce the economic losses and social impacts caused by blackouts.
In the power system restoration process, self-excitation and overvoltage caused by line charging, harmonics, and switch inrushes are the main problems that affect the success of black starts [5]. Research and practice show that the overvoltage problem becomes more serious under the conditions of high system voltage, long-distance transmission lines, and large charging transformer capacity [6]. Because of the typical high voltage levels and long transmission lines found in modern bulk power systems, self-excitation and power frequency/operating overvoltage are more likely to occur during the process of power system restoration, leading to the failure of the black start [7]. Meanwhile, as the main black start power sources in the traditional power system are hydropower units, diesel generating units, and gas turbines, it is hard for these small capacity units to crank up other non-black start units, which will result in a long duration restoration processes. Although thermal power units have the advantages of large capacity and wide distribution, and stand in the highest flight in the power system, in general they cannot be used as black start power sources [8,9]. Fortunately, through fast cut back (FCB) technical reform, the turbines and boilers of thermal power units can remain working after load rejection caused by the power grid failure [10]. After the elimination of the failure, the unit can parallel in the grid and start supplying power quickly, which will accelerate the power system restoration process. Hence, the FCB unit is an ideal kind of power source for a black start.
There are a lot of achievements in black start researches [5–7,11,12], but how to utilize FCB units to improve the black start capacity remains an open question. The existing literatures about FCB can be mainly classified into two categories. One mainly discussed the function of the FCB unit and introduced field tests about it [10]. The other mainly studied how to use the FCB unit to accelerate the black start process of power systems [13,14]. However, as far as the authors know, there is no paper that has studied the dynamic response of the FCB unit under load rejection and black start process conditions. Therefore, this paper studies the dynamic model of the FCB unit and introduces the FCB field test.
The remaining part of the paper is organized as follows: the key problems in power system restoration are introduced in Section 2, where an engineering criterion of self-excitation is also presented; the dynamic model of the FCB unit is proposed in Section 3; the FCB unit load rejection and the 500 kV transmission line black start field test are introduced in Section 4; the comparative analysis between the simulation results and the field test results is presented in Section 5; and the conclusions are drawn in Section 6.
2. Key Problems in the Black Start Process
The general black start process is as follows: generator units with self-starting ability (such as hydropower units) start themselves, charge the main transformers and the transmission lines, and finally start other remote generator units and loads. In this process, some electromagnetic transient problems may impact the reliability of the power system restoration, and the key ones are the self-excitation and overvoltage [12].
2.1. Self-Excitation and Its Engineering Criterion
Generator self-excitation is a phenomenon whereby the stator current and voltage will increase spontaneously because of the assisted effect of armature reactions. Its essence is the parameter resonance caused by the coordination between the generator stator inductance and the external circuit capacitance [15,16]. Research shows that the self-excitations of a synchronous generator can be divided into three categories: reaction synchronous self-excitations, repulsion synchronous self-excitations, and asynchronous self-excitations. There are manifest differences in terms of the occurrence conditions and the mechanisms among different types of self-excitations [17,18].
Reaction synchronous self-excitation is the type of self-excitation whose electric frequency is the same as its synchronous frequency, and the excitation is maintained by the reaction power generated from the alternations of direct axis reactance and quadrature axis reactance. Repulsion synchronous self-excitation is the type whose electric frequency is the same as the synchronous frequency, while the excitation is maintained by the reaction power generated from the alternations of direct axis and quadrature axis transient or sub-transient reactance. Asynchronous self-excitation is that the rotor maintains the synchronous speed, while the electric frequency is lower than the synchronous frequency and the self-excitation is maintained by asynchronous power generated by units. Table 1 shows the comparison of the three different self-excitation types [15–18].
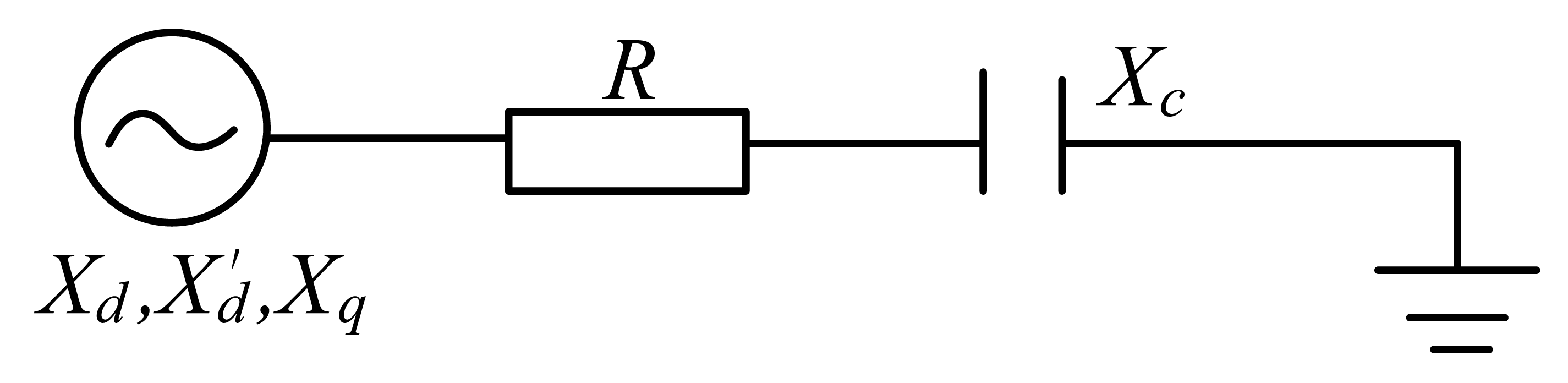
The system of Figure 1 is used to study the generator self-excitation. This system consists of a synchronous generator and its external equivalent circuit represented by impedance.
Xd denotes the direct-axis synchronous reactance of generator, Xd′ is the direct-axis transient reactance of generator, Xq is the quadrature axis synchronous reactance of generator, R and Xc are the equivalent resistance and equivalent capacitance of generator's external circuit, respectively.
If the parameters R and Xc reach critical values, the system will experience voltage and current spontaneous increase which is called self-excitation. The three different types of self-excitation are addressed as follows [18].
For the reaction synchronous self-excitation, the boundary condition is shown in Equation (1). The self-excitation area can be obtained by Equation (1) and is given in Figure 2a:
For the repulsion synchronous self-excitation, the boundary condition is shown in Equation (2) and its self-excitation area is given in Figure 2b:
For the asynchronous self-excitation, the boundary condition is shown in Equation (3):
For each specific slip frequency s, Equation (3) is an ellipse equation with the long axis paralleling to the R axis and the central point locating at the Xc axis. The central point moves downward to the origin point and the long axis decreases monotonously to 0 when s increases continuously from 0 to 1. All the areas covered by the ellipses are the asynchronous self-excitation areas shown in the Figure 2c.
The integrated area of self-excitation synthesized from Equations (1)–(3) can be obtained as shown in Figure 2d, the blue and green ones are the areas rid of self-excitation risk.
The quick calculation method and the impedance method are widely used in engineering to check the generator self-excitation [19]. The criterion of quick calculation method is shown in Table 2, where Q is the generator capacity (unit: 10 MVA) and L is the length of the line (unit: 100 km).
The criterion of impedance method is shown in Equation (4):
The quick calculation method criterion offers a rough estimation of the line capacitance, while the impedance method criterion can only be used to check the reaction synchronous self-excitation and does not consider the line equivalent resistances. For these reasons, a more comprehensive and practical engineering criterion for self-excitation is proposed as in Equations (5) and (6):
Equation (5) corresponds to the blue area and Equation (6) to the green one in Figure 2d. If the parameters of the generator and transmission lines satisfy one of Equations (5) and (6), any kind of self-excitations will not occur during the process of charging the transmission line from the generator.
If self-excitation occurs, the spontaneous increases of the generator current and voltage will damage the equipment and result in the failure of the black start. Hence, a comprehensive and practical engineering criterion is needed to assess the risk of the self-excitation. The black start scheme should be abandoned if a risk of self-excitation is detected by the criterion given in Equations (5) and (6).
2.2. Overvoltage
In the black start process, since the black start power sources are usually far away from the load center, generator units are required to pick up loads through long lines, which demands a lot of operations of switching on unloaded lines and may induce overvoltage problems such as the power frequency overvoltage and the operating overvoltage [12,15].
Power frequency overvoltage is mainly caused by the capacitance effect of the unloaded long lines, asymmetric grounding and the units' sudden load rejection. In the process of the black start, the main factor is the capacitance effect of the long unloaded lines. Power frequency overvoltage is a steady overvoltage, characterized by small amplitude and normally causes no harm to ordinary insulated electric equipment in a power system. However, the impact of the power frequency voltage is not ignorable in the black start process, because its increment will directly affect the amplitude of the operating overvoltage and the operating conditions of the protection equipment. Therefore, the power frequency overvoltage problem in the unloaded lines should receive special attention in the black start process. According to the basic theory of the power system, the voltage of line terminal can be easily deduced as shown in Equation (7) [20]:
Operating overvoltage is a transient overvoltage caused by abrupt operations of breakers and switchers. In the power system restoration, the line parameters are capacitive. Operating overvoltage is powered by the system itself, and the voltage amplitude is related to the line attenuation and the power frequency overvoltage level, i.e., the system parameters such as the system structure, line transmission characteristics, line length, lightning arrester characteristics, closing resistor, soil resistivity, paralleling compensation degree, etc. In general, the three most critical factors are: (1) the closing phase; (2) the asynchronous closing of three phases; and (3) the line residual voltage. The overvoltage is the largest under the closing phase α = ±90° and the theoretical value of closing overvoltage can reach 3.0 p.u. if there is residual voltage in the line.
3. The Dynamic Model of the FCB Unit
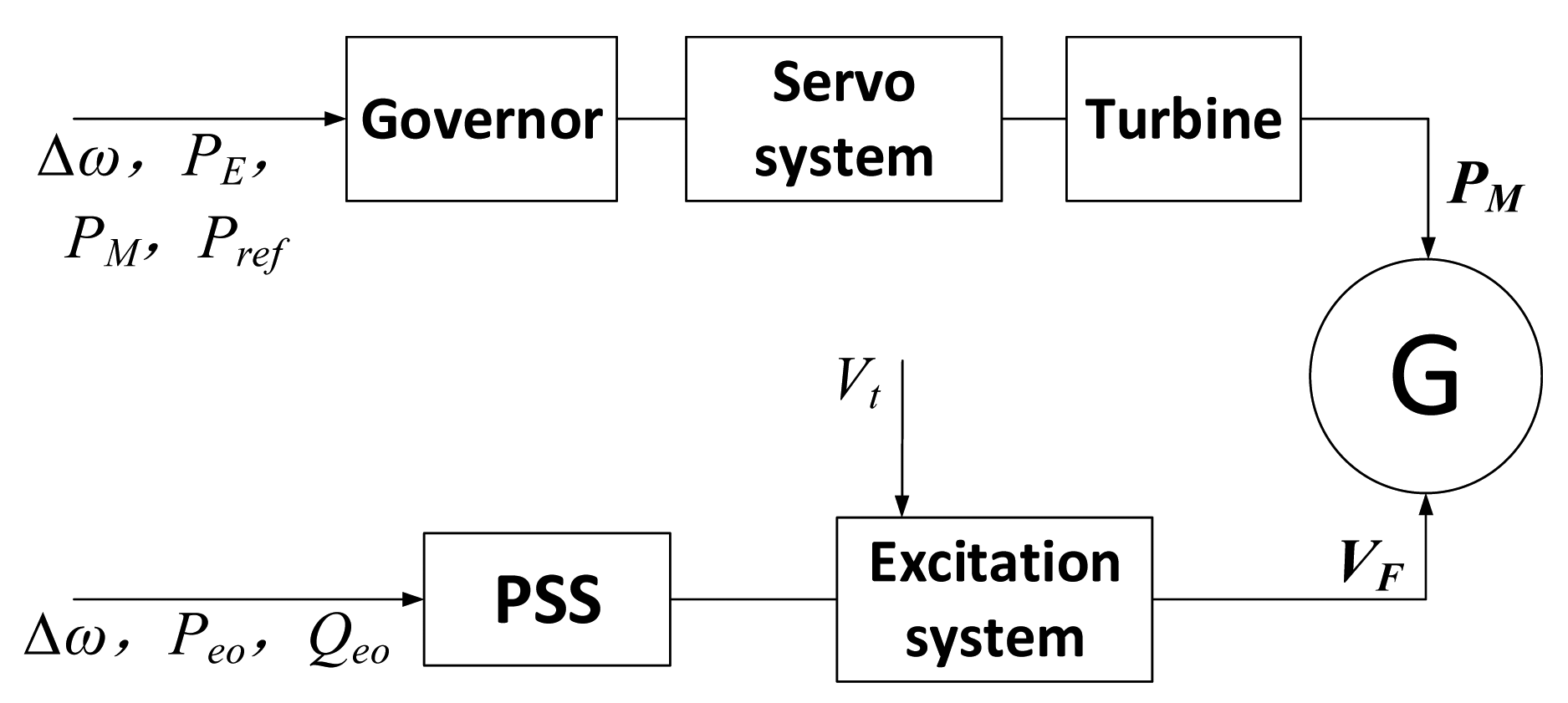
In the process of the power system failure and restoration, the unit parameters change dramatically [21]. The unit splitting from a power grid will cause a series of actions such as overspeed protection control (OPC) action, power system stabilizer (PSS) operation exit, governor primary frequency regulation exit, etc. These actions have a great impact on the stability of the unit in the FCB process and the process of the unit paralleling in the power grid again. However, the existing prime mover models have not considered the OPC part, the bypass system part and the switch of the governor control modes, which makes the models applicable only for small disturbance simulation but not for large disturbance cases such as FCB simulation. By using the No. 6 FCB unit in the Taishan power plant in China as a prototype, this section will study and establish a dynamic model for the FCB unit, which can be used to simulate the transient process of the FCB unit load rejection. The whole FCB dynamic mathematical model should contain the following basic modules: the governor model, the servo system model, the turbine model, and the generator model. The bypass system and extraction non-return valve should also be considered in the turbine model. Under the FCB working condition, the pressure of the boiler can be dredged through a bypass system, which ensures that the temperature and pressure vibration amplitudes of the boiler stream are small. Therefore, the boiler steam can be regarded as basically stable, and the influence of the boiler can be ignored in the FCB dynamic model. The whole structure of the dynamic model is shown in Figure 3.
The FCB unit dynamic model mainly adds the regulating valve fast shut down system, the bypass system that can affect the power output of the turbine, and the rotor speed control mode of the governor under FCB condition. Compared with traditional unit models, there is no significant difference in other parts such as the servo system and the generator.
3.1. Turbine Model of the FCB Unit
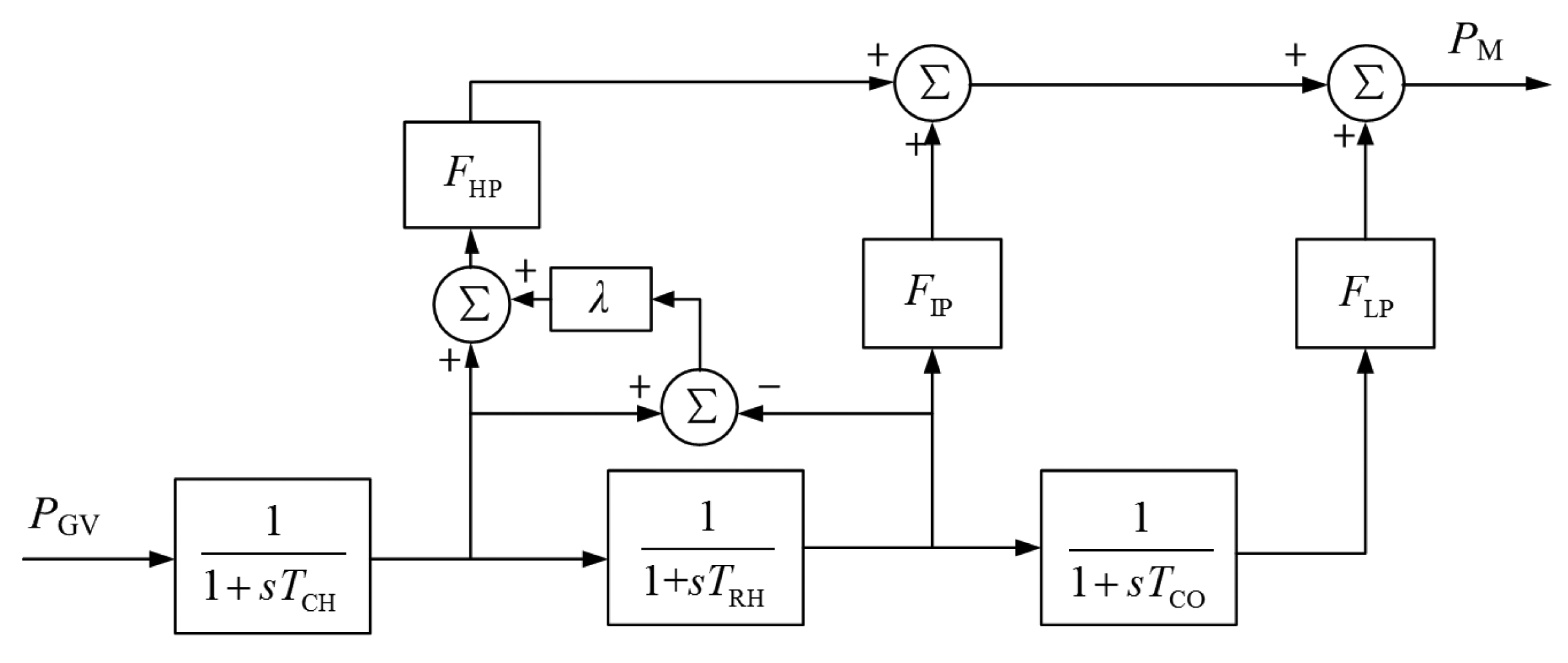
The structure diagram of the traditional reheat condensing stream turbine and its corresponding mathematical model given by the IEEE Committee are shown in Figures 4 and 5, respectively [22].
In Figure 5, TCH, TRH, and TCO are time constants which represent delays due to the steam chest and inlet piping, reheaters and crossover piping respectively. The fractions FHP, FIP and FLP represent portions of the total turbine power developed in the various cylinders. More details such as typical values can be found in literature [22]. This classical model is suitable for power system stability studies such as small signal simulation, but not for the FCB condition simulation whose parameters change dramatically. Hence, it is necessary to develop the dynamic model suited for FCB condition simulation.
The physical structure diagram of the FCB steam turbine is given in Figure 6 [10,23]. Compared with the diagram of the traditional reheat condensing stream turbine shown in Figure 4, it can be found that the FCB turbine has the high pressure (HP), the low pressure (LP) bypass systems (circled by the blue dashed box in Figure 6 and the regulating valve fast shut down system (circled by the red dashed box in Figure 6.
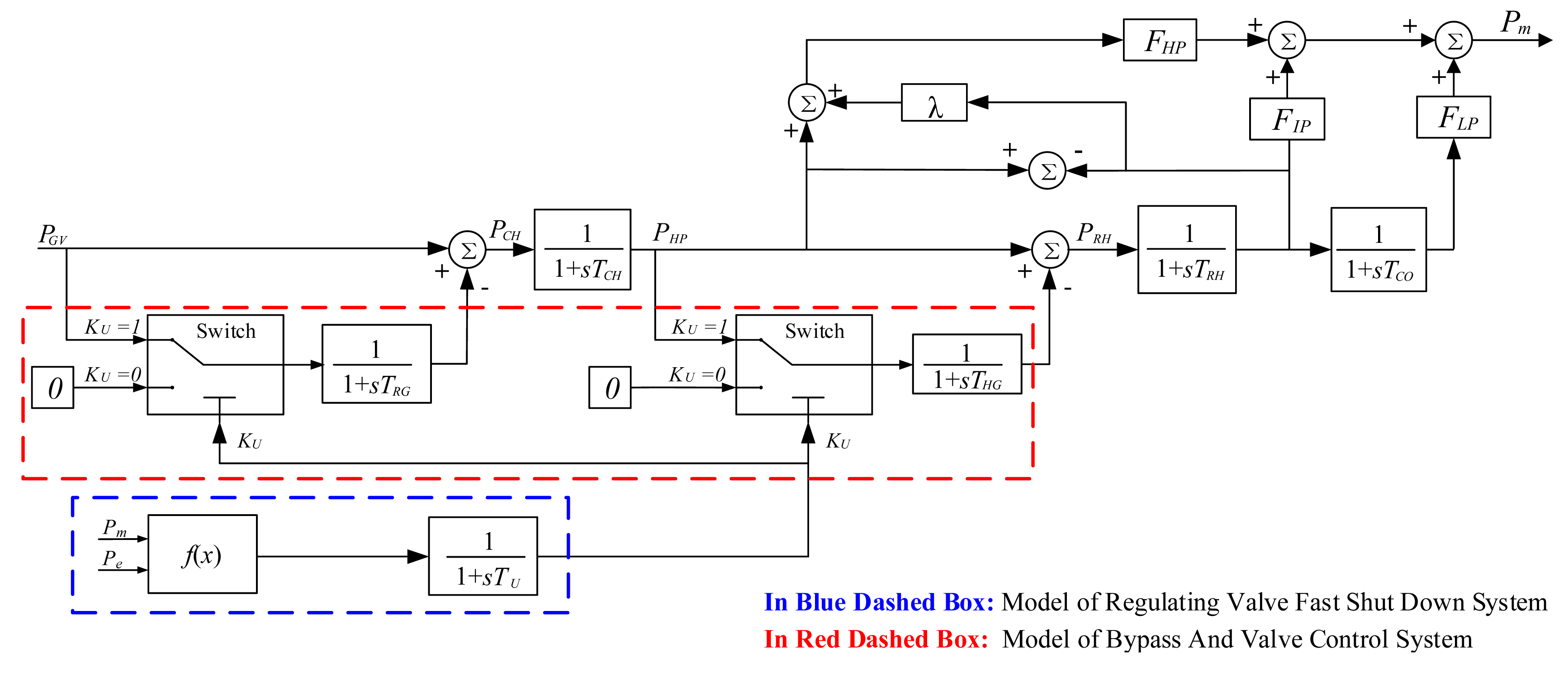
Its mathematical model is shown in Figure 7. Based on the classical reheat condensing stream turbine model, the new model adds the regulating valve fast shut down system and the bypass system. It enables the model to simulate the turbine dynamic characteristics under FCB condition.
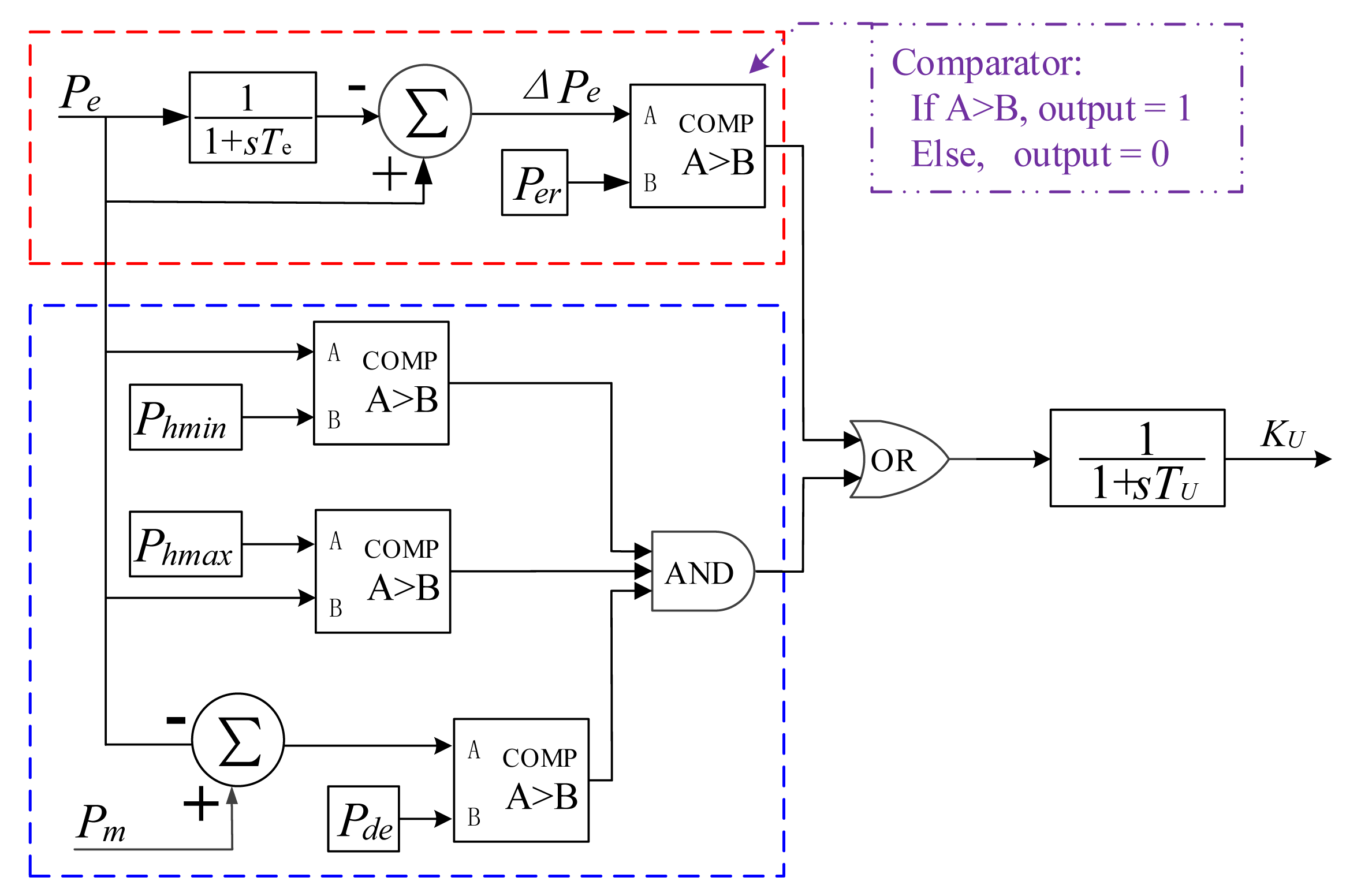
Parameters TCH, TRH, TCO, FHP, FIP, FLP and λ in Figure 7 are the same as those in Figure 5. PGV is the valve opening given by servo system. KU is a logic signal which indicates whether the unit has occurred load rejection, and it is generated by the regulating valve fast shut down system (circled by the blue dashed box in Figure 7. The function f(x) represents the load rejection controller which is detailed in Section 3.1.1. Pm and Pe are the mechanical power and the electromagnetic power of the unit, time constant TU represents the motion delay of the regulating valve fast shut down system. The model of bypass and valve control system (circled by the red dashed box in Figure 7) is addressed in Section 3.1.2. Definitions for model symbols are presented in Table A1 of the Appendix.
3.1.1. Regulating Valve Fast Shut down System
There will be a load rejection if the generator or the main transformer trips suddenly, which will cause a great increase of rotor speed. Once the load is cut off, the Digital Electro-Hydraulic Control System (DEH) will send out the load rejection signal KU, the bypass will open quickly and the governor will switch to the rotor speed control mode. After that, the stream flow in cylinder drop quickly and the power output of the turbine drop correspondingly, which finally ensures that the speed of the unit remains in a reasonable range. The main part of the regulating valve fast shut down system is the load rejection controller which is shown in Figure 8 in detail.
The load rejection judgments adopted by the controller consist of the following two conditions:
- (1)
The reduction of electromagnetic power Pe exceeds the threshold Per in Te seconds. As shown in Figure 8, the part which is circled by the red dashed box represents load sudden drop.
- (2)
The unit is operating under the islanded operation condition and the difference between the mechanical power Pm and electromagnetic power Pe exceeds the threshold Pde. As circled by the blue dashed box in Figure 8, constants Phmin and Phmax are the lower and upper limits of the power plant house load, respectively. And the inequality Phmin < Pe < Phmax represents that the unit keeps running only with house load.
No matter which condition above is satisfied, the controller will send out the load rejection signal KU to the governor, the servo system and the turbine to start FCB control.
3.1.2. Bypass and Valve Control System
Under the FCB working condition, to control the rotate speed in a reasonable range, the unit will reduce the mechanical power output of the turbine by opening the HP and LP bypasses rapidly, and closing the high and intermediate pressure regulating valves simultaneously. In this process, only the residual stream in the stream chest will continue to work in the HP cylinder, while most of the superheated stream from the boiler will flow into the HP bypass due to the restriction of the HP regulating valve. All of the stream in the bypass system and in the HP cylinder will enter the reheater, most of which will be expelled to the condenser through the LP bypass system after flowing out of the reheater. The residual stream in the crossover, intermediate pressure (IP) cylinder and LP cylinder will continue to work in the turbine. The mathematical model corresponding to this physical process is shown in Figure 9.
In Figure 9, PGV and PHP represent the power at the main valve outlet and that at the reheater outlet, respectively. When the load rejection logic signal is sent by the load rejection controller, the HP and LP bypasses will open quickly to reduce the stream inflow of the HP cylinder (PCH) and that of the IP cylinder (PRH), which will finally reduce the power output of the turbine and restrict the rotate speed.
3.2. Speed Governor Model of the FCB Unit
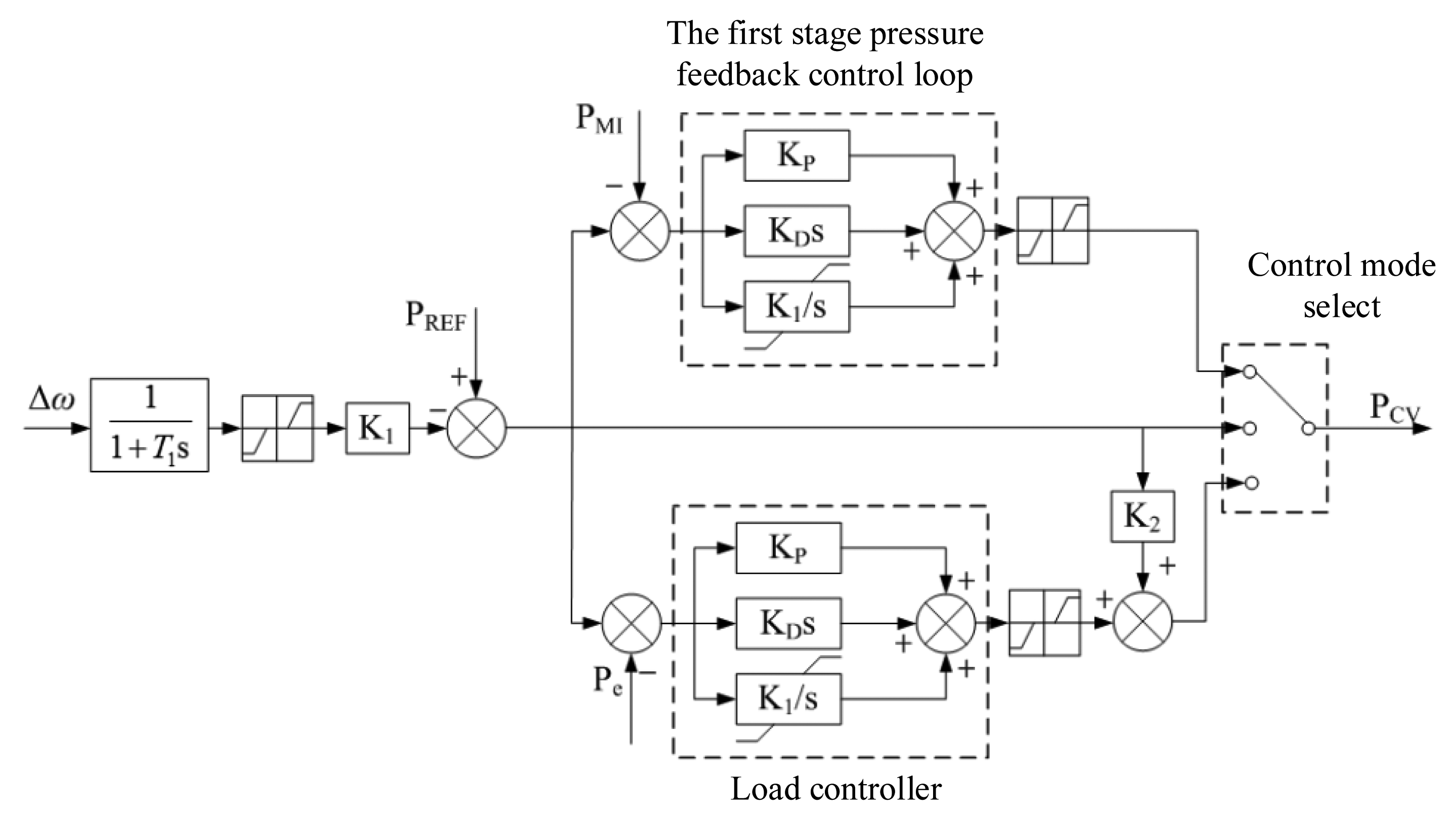
Under the normal condition, the governor has three control modes: (1) the governing stage feedback control; (2) the valve position control; and (3) the load feedback control. The corresponding mathematical model is shown in Figure 10.
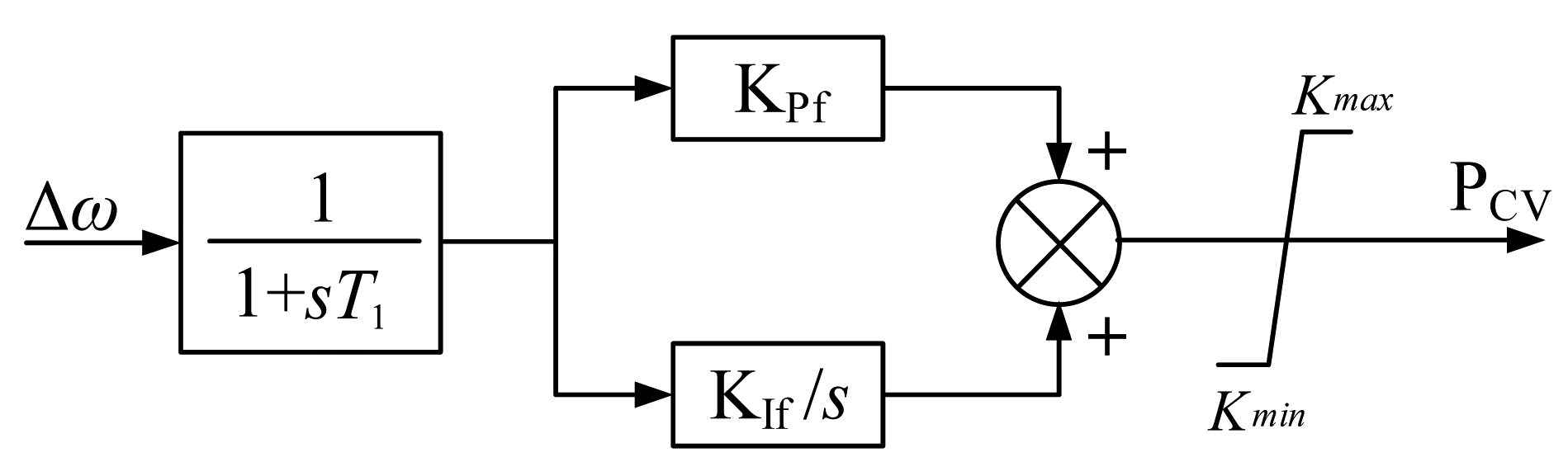
When the unit enters the FCB working condition, the governor will quit the above three control modes and switch to the rotor speed control mode. After the unit parallels in the grid again, the governor will quit the rotor speed control mode and reenter one of the three above control modes. The mathematical model of rotor speed control mode is given in Figure 11.
The input parameter of the speed controller is the rotor speed deviation Δω and the output is the gate position of the valve PCV. Time constant T1 represents the delay of the measurement. Constants KPf and KIf are the parameters of the proportional integral (PI) controller.
4. Introduction of the FCB Unit Load Rejection and Black Start Field Test
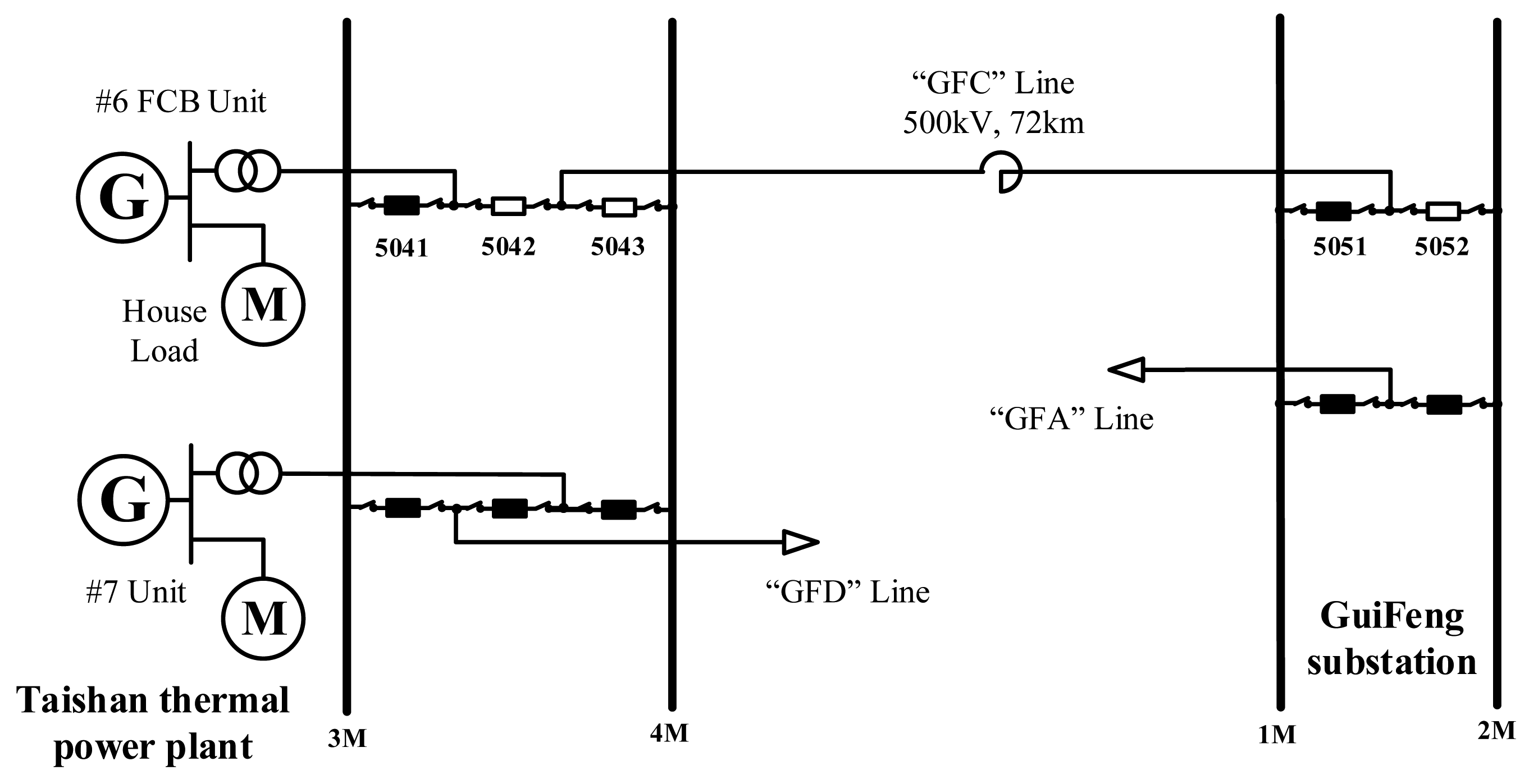
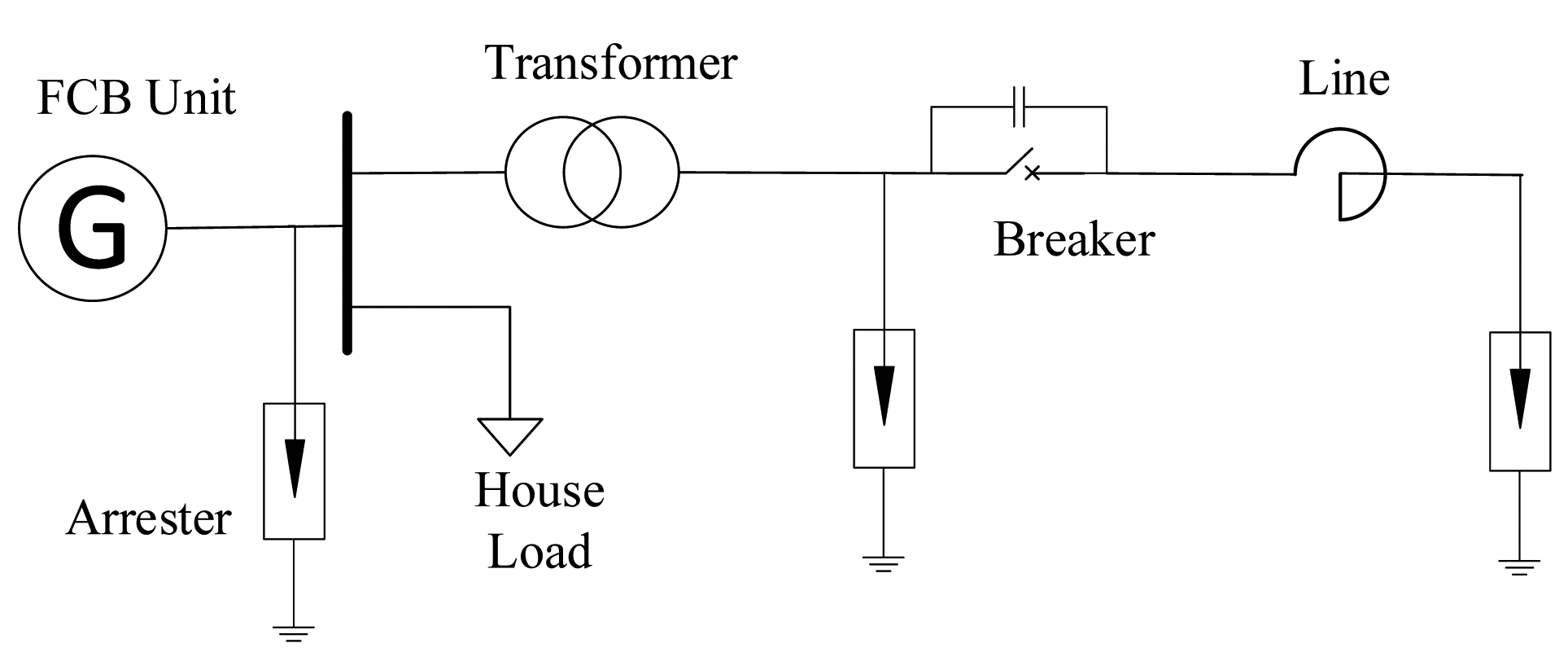
In July 2013, a FCB 50% load rejection and 500 kV transmission line black start field test was carried out in the Taishan thermal power plant of China Southern Power Grid (CSG). The purpose of the field test was to simulate the process of the FCB unit splitting from the power grid and switching to islanded operation after the blackout, then serving as the initial power source to restore the unpowered grid. The field test consisted of three parts: (1) the FCB unit load rejection test; (2) the rising voltage from zero test; and (3) the 90% voltage charging unloaded line test. The related test equipment concludes the No. 6 unit in Taishan thermal power plant, the boosting transformer of the unit, the “GFC” 500 kV transmission line and the corresponding switches. The No. 6 unit is a 1000 MW FCB unit with islanded operation function. After splitting from the power grid, it can continue islanded operation from 5 min to several hours under 3% rated load (house load). The generator voltage is 27 kV. The single line diagram of the field test is shown in Figure 12.
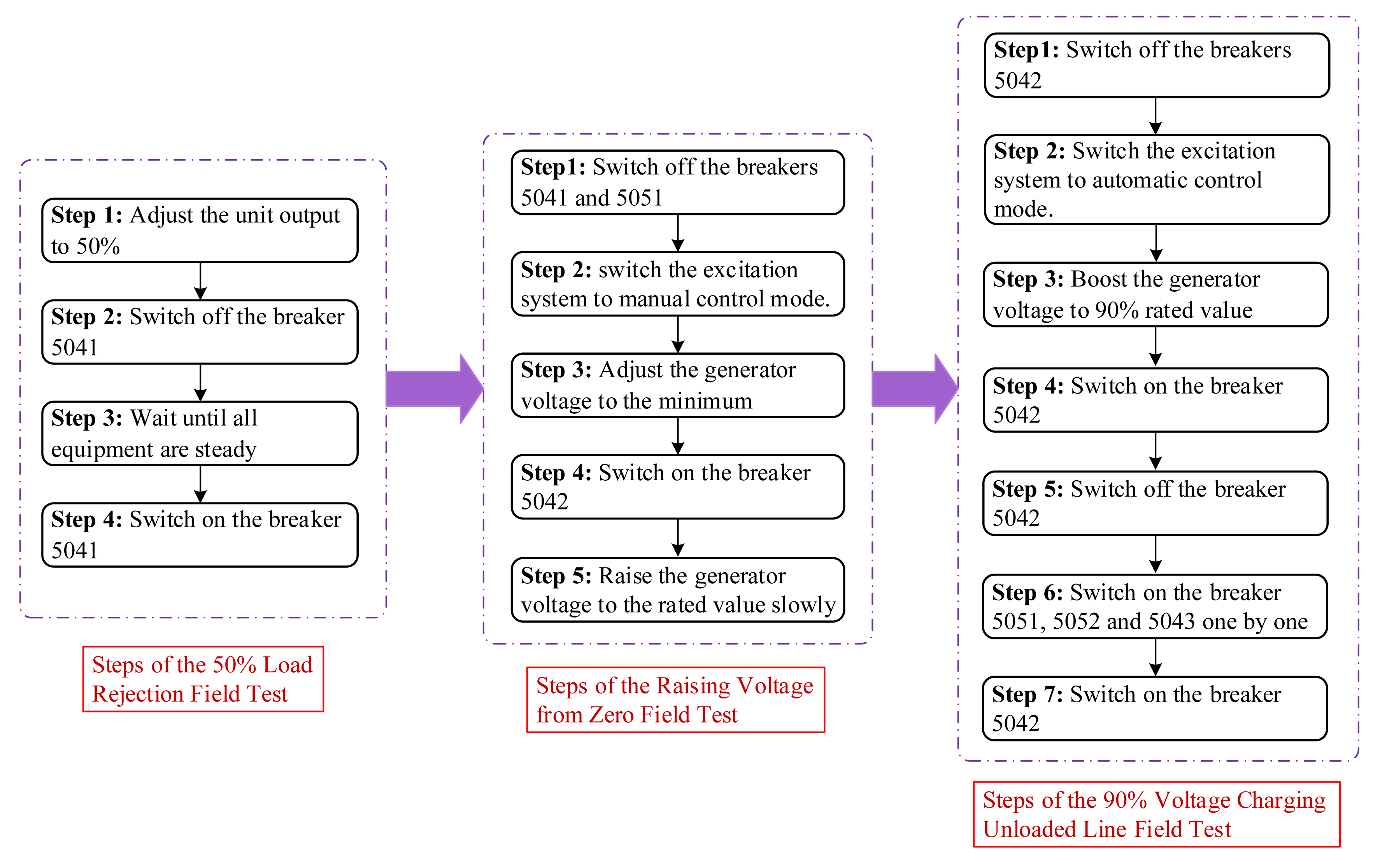
Before the field test, the Breakers 5041 and 5051 were closed and the Breakers 5042, 5043 and 5052 were in hot standby state. The steps of the field test are shown in detail in Figure 13.
4.1. The Field Test of 50% Load Rejection for the FCB Unit
This field test simulates the process of the FCB unit splitting from the power grid and switching to islanded operation after the blackout. Before the test, the regenerative system and the interlock protection of the unit have been put into operation. After the FCB function of the unit is triggered, the boiler reduces to 48% rated load and keeps running steadily, the HP bypass valve and LP bypass valve open quickly, the steam temperature and steam pressure keep in the normal range, and the rotor speed remain stable at the rated value after a peak. The test consists of four steps as follows:
- Step 1:
Adjust the unit output to 50% and wait until it runs steadily for 2 h. Since it is the first time to do the load rejection field test on the No. 6 unit, for safety reasons, this test is carried out under the 50% rated capacity of the unit.
- Step 2:
Switch off the breaker 5041 and trigger FCB logic of the unit. Before the field test, the Breaker 5042 is open and the No. 6 unit connects to the power grid by the Breaker 5041. Once the Breaker 5041 is opened, the FCB logic will be triggered and the No. 6 unit will enter to the FCB working condition.
- Step 3:
Wait until all equipment are steady. There will be a dramatic change in behaviors of the unit under the FCB condition and time is needed to stabilize the unit for the next step. For the No. 6 unit, the minimum time required is 5 min.
- Step 4:
Switch on the Breaker 5041. The FCB unit can reconnect to the power grid at any time once the unit is stable.
4.2. The Field Test of Rising Voltage from Zero
This field test is carried out after the 50% load rejection test. In the process of the black start, it is common that the unit picks up the load through a long transmission line which may induce generator self-excitation. This field test is designed to check the self-excitation of the No. 6 FCB unit and consists of five steps as follows:
- Step 1:
Switch off the Breakers 5041 and 5051 manually one by one. Before this test, the unit and the “GFC” line connects to the power grid by Breakers 5041 and 5051, respectively. After these two breakers are opened, the unit and “GFC” line are split from the grid.
- Step 2:
Switch the No. 6 excitation system to manual control mode.
- Step 3:
Adjust the generator voltage to the minimum.
- Step 4:
Switch on the Breaker 5042 and the No. 6 unit connects to the “GFC” line.
- Step 5:
Raise the generator voltage to the rated value slowly. In this step, once the phenomenon of the generator self-excitation is detected, emergency measures such as de-excitation should be taken and the test should be stopped.
4.3. The 90% Voltage Charging Unloaded Line Field Test
Inevitably, there will be a lot of operations of switching on unloaded lines in the process of the black start which may induce overvoltage problems and lead to failure of the black start. The purpose of this field test is to study the operating overvoltage problem in the process of the black start and the test consists of seven steps as follows:
- Step 1:
Switch off the Breaker 5042. The unit and the “GFC” line are disconnected.
- Step 2:
Switch the excitation system to automatic control mode and close the excitation switch.
- Step 3:
Boost the generator voltage to 90% rated value. In this step, the generator voltage should be monitored closely and be controlled within the normal range.
- Step 4:
Switch on the Breaker 5042 manually and charge the “GFC” line by the No. 6 unit.
- Step 5:
Switch off the Breaker 5042.
- Step 6:
Switch on the breaker 5051 and charge the “GFC” line by the Guifeng substation. Switch on the Breakers 5052 and 5043.
- Step 7:
Ensure that the No. 6 unit runs normally and then close the Breaker 5042. The No. 6 unit reconnects to the power grid and the field test is completed successfully.
5. Simulation and Test Result Analysis
5.1. Simulation Model
According to the field test, a simulation model based on PSCAD/EMTDC has been built and its structure diagram is shown in Figure 14. The parameters for the simulation model are presented in Table A1–A4 of the Appendix.
The FCB unit model is described in Section 3. The type of the excitation system is UNITROL 5000 produced by ABB company (Zurich, Switzerland) and its mathematical model is the FQ type exciter model. In a black start, the process of charging the unloaded lines is an electromagnetic transient process of a distributed parameter circuit. In other words, it is a wave process. The Bergeron model can be applied to simulate this wave process. Arresters are added in terminals of both transmission lines. The six order model is used for the generator model, the IEEE PSS2A type model for the PSS and the constant power load model for the house load.
5.2. Analysis for the Load Rejection Test
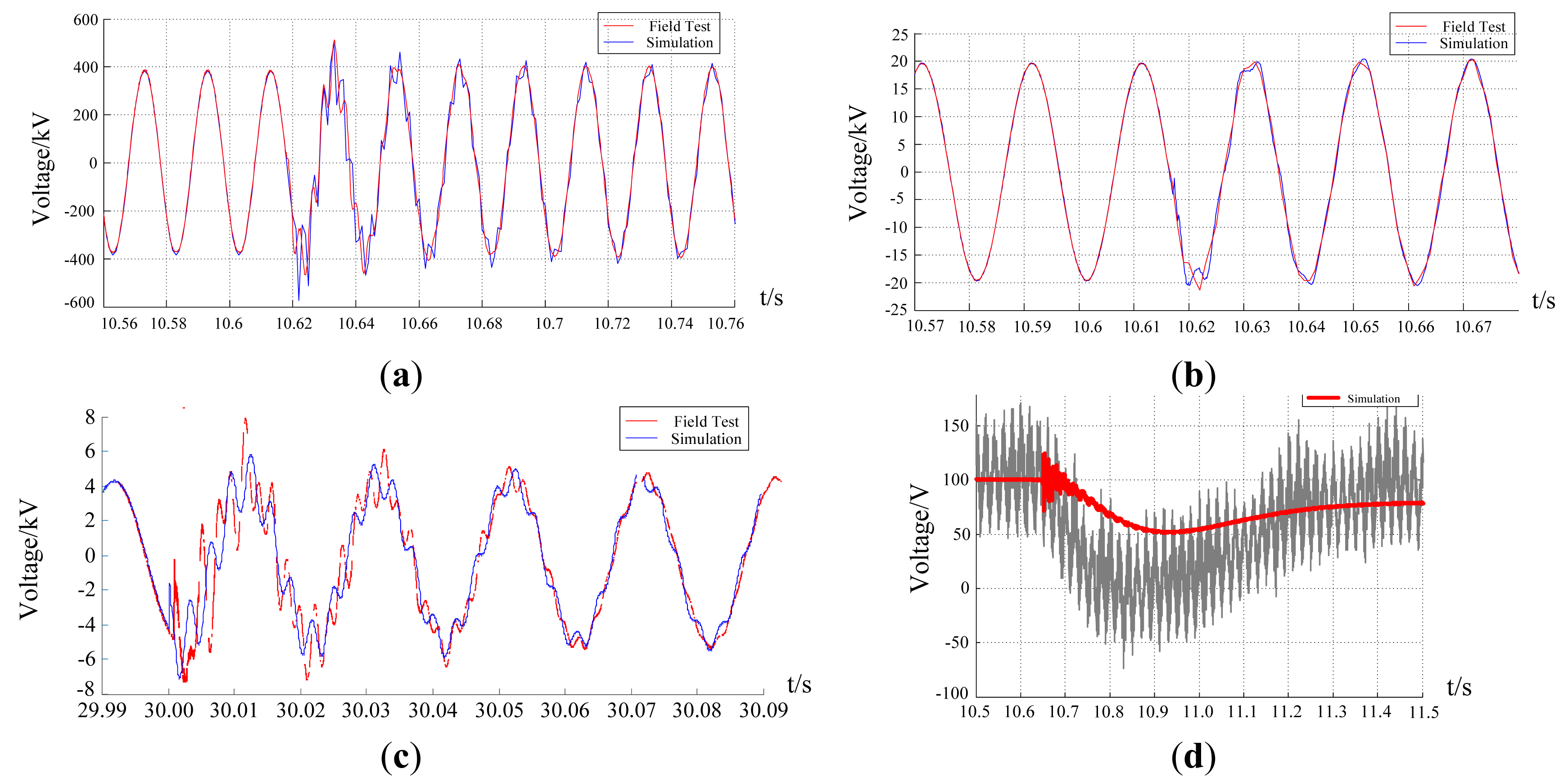
Before the load rejection test, the generator power output was 500 MW. After the breaker tripped, the unit entered the islanded operation condition to supply power for the house load (about 30 MW). The rotor speed was 3001 r/min before load rejection. After the breaker tripped, the speed increased drastically, and the unit closed the HP and IP regulating valves, opened the HP and the LP bypass system, and switched the governor to speed control mode. The rotor speed peaked at 3061 r/min in 1.1 s after load rejection. Then the HP and IP regulating valves reopened slowly and the speed tended to be steady after 22 s. Finally, the speed kept steady at 2995 r/min. The comparisons of waveforms between the field test and the simulation are shown in Figure 15.
The rotor speed of the unit didn't increase again after the first peak and decreased steadily without repeated jitter. The FCB unit ran steadily in the load rejection process, which satisfied the basic requirements as a black start power source in the system restoration. The simulation results coincided with the field test results well, which verified the correctness of the built FCB model.
5.3. Analysis for the Raising Voltage from Zero Test
Base on the parameters of the synchronous generator, the transformer and the “GFC” line which are presented in the Appendix, the generator external equivalent impedance Zin can be calculated by Equation (8):
The rising voltage from zero test was carried out to check whether the unit would occur self-excitation practically. The measured data are listed in the Table 3.
The measured data showed that the voltage, current, generator active and reactive power rose steadily. The field test result showed that the unit wouldn't undergo self-excitation, which verified the correctness of the proposed criterion for self-excitation in some extent.
5.4. Analysis for the Charging Unloaded Line Test
Utilize the model shown in the Figure 14 to simulate the transient process of charging the unloaded line with simulation time 80 s and simulation step 100 μs. The comparison between simulation results and the measured data is listed in Table 4.
In the process of charging the unloaded line, the voltage waveform comparisons between the field test and the simulation are shown in Figure 16.
During the process of the 500 kV transmission line black start, the transient voltages of each measurement point kept in normal range, and the transient process lasted for about four cycles. The field test and the simulation verified that the FCB unit had the ability to restore the high level voltage power grid and to accelerate the power system restoration process.
6. Conclusions
Since the thermal power unit with FCB function has many advantages such as large capacity and flexible distribution, it can be used as an ideal black start power source. The FCB unit can run steadily with house load when a failure in the power grid occurs. Meanwhile, once the failure is eliminated, the FCB unit can be integrated in the power grid quickly and provide high-capacity black start service for the power system. Doubtlessly, the above-mentioned features of the FCB unit are definitely crucial for the fast power system restoration.
In this paper, the key problems that influence the process of black start are studied, the dynamic model of the FCB unit is developed, a field test of black start in a 500 kV grid is introduced, and the transient process of the field test is reproduced by time domain simulation using the proposed model of the FCB unit. Conclusions are obtained as follows:
- (1)
The traditional models of the unit such as turbine and governor are just applicable for small disturbance simulation but not for large disturbance cases such as FCB simulation. To cope with this problem, this paper develops a dynamic model of the FCB unit which can be used to study the FCB working condition. The correctness of the proposed model is verified by comparing the results of the field test and the simulation of FCB load rejection.
- (2)
A self-excitation criterion is proposed through theoretical derivation, and the correctness of the criterion is verified by the field test of rising voltage from zero.
Acknowledgments
This work was supported by Special Fund of Key Science and Technology Projects of Gruangdong Power Grid Corporation, China (K-GD2011-553).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
Definitions and Values for Model Symbols
In addition to the special instructions, values in the following tables are based on a per unit system in which speed, valve or gate position, power and impedance are in per unit of rated values. Time constants are in seconds.
| Symbol | Description | Value |
|---|---|---|
| TCH | Steam chest time constant (control valves to HP exhaust) | 0.2456 |
| TRH | Reheat time constant (HP exhaust to IP exhaust) | 9.8957 |
| TCO | Crossover time constant (IP exhaust to LP exhaust) | 0.6855 |
| FHP | HP turbine power fraction | 0.2524 |
| FIP | IP turbine power fraction | 0.2560 |
| FLP | LP turbine power fraction | 0.4916 |
| λ | Natural power overshooting coefficient of HP cylinder | 0.6766 |
| TRG | HP bypass time constant | 0.02 |
| THG | LP bypass time constant | 0.02 |
| TU | Valve fast shut down time system constant | 0.08 |
| Te | Electromagnetic power delay time constant | 0.1 |
| Per | Decrement threshold of electromagnetic power | 0.875 |
| Pde. | Unbalance threshold of electromagnetic power and mechanical power | 0.12 |
| Phmin | Lower limit of the power plant house load | −0.01 |
| Phmax | Upper limit of the power plant house load | 0.12 |
| PGV | Power at gate or valve outlet | - |
| PCH | Power at steam chest | - |
| PHP | Power at reheater outlet | - |
| PRH | Power at intermediate valve outlet | - |
| Pm | Mechanical (shaft) power | - |
| Pe | Electromagnetic power | - |
| KU | Logic signal of load rejection | - |
| Symbol | Description | Value |
|---|---|---|
| T1 | Measurement delay time constant | 0.02 |
| KPf | Proportional gain constant of PI controller | 35 |
| KIf | Integral gain of PI controller | 1.0 |
| Kmin | Lower limit of gate position | 0 |
| Kmax | Upper limit of gate position | 1.0 |
| Δω | Speed deviation | - |
| PCV | Gate position | - |
| Symbol | Description | Value |
|---|---|---|
| PG | Rated real power (MW) | 1000 |
| UG | Rated voltage (kV) | 27 |
| cosφ | Rated power factor | 0.9 |
| N | Rated rotor speed (r/min) | 3000 |
| Ra | Armature resistance | 8.22 × 10−4 |
| Xd. | D-axis unsaturated reactance | 2.614 |
| Xd′ | D-axis unsaturated transient reactance | 0.264 |
| Xd″ | D-axis unsaturated sub-transient reactance | 0.225 |
| Xq. | Q-axis unsaturated reactance | 2.484 |
| Xq′ | Q-axis unsaturated transient reactance | 0.641 |
| Xq″ | Q-axis unsaturated sub-transient reactance | 0.248 |
| Tj. | Inertia constant (s) | 3.5 |
| Symbol | Description | Value |
|---|---|---|
| PHL | Equivalent load real power of house load (MW) | 30 |
| QHL | Equivalent load reactive power of house load (MVAr) | 27 |
| RT | Resistance of the main transformer | 5.59 × 10−4 |
| XT | Reactance of the main transformer | 0.163 |
| RL | Resistance of the “GFC” line | 6.9 × 10−3 |
| XL | Reactance of the “GFC” line | 0.089 |
| XB | Susceptance of the “GFC” line | 27.975 |
References
- Chen, Q.; Mili, L. Composite power system vulnerability evaluation to cascading failures using importance sampling and antithetic variates. IEEE Trans. Power Syst. 2013, 28, 2321–2330. [Google Scholar]
- Henneaux, P.; Labeau, P.E.; Maun, J.C. Blackout probabilistic risk assessment and thermal effects: Impacts of changes in generation. IEEE Trans. Power Syst. 2013, 28, 4722–4731. [Google Scholar]
- U.S.–Canada Power System Outage Task Force; Final Report on the August 14, 2003 Blackout in the United States and Canada: Causes and Recommendation; Minister of Natural Resources Canada: Ottawa, ON, Canada, 2004.
- Report of the Enquiry Committee on Grid Disturbance in Northern Region on 30th July 2012 and in Northern, Eastern & North-Eastern Regionon 31st July 2012; Enquiry Committee: New Delhi, India, 2012.
- Adibi, M.M.; Alexander, R.W.; Avramovic, B. Overvoltage control during restoration. IEEE Trans. Power Syst. 1992, 7, 1464–1470. [Google Scholar]
- Feltes, J.W.; Grande-Moran, C. Black Start Studies for System Restoration. Proceedings of the Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PS, USA, 20–24 July 2008.
- Datta, S.; Kolluri, S.; He, T.; Khodabakhchian, B. Development of an Alternative Black-Start Plan for System Restoration. Proceedings of the IEEE PES Power Systems Conference and Exposition, PSCE '06, Atlanta, GA, USA, 29 October–1 November 2006; pp. 1833–1839.
- Adibi, M.M.; Milanicz, D.P.; Volkmann, T.L. Remote cranking of steam electric stations. IEEE Trans. Power Syst. 1996, 11, 1613–1618. [Google Scholar]
- Lindstrom, R.R. Simulation and field tests of the black start of a large coal-fired generating station utilizing small remote hydro generation. IEEE Trans. Power Syst. 1990, 5, 162–168. [Google Scholar]
- Kitada, M.; Masuya, T.; Tanaka, H. Experimental house load operation at Tanagawa No. 2 oil-fired power station. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 2796–2803. [Google Scholar]
- Adibi, M.M.; Fink, L.H. Overcoming restoration challenges associated with major power system disturbances-Restoration from cascading failures. IEEE Power Energy Mag. 2006, 4, 68–77. [Google Scholar]
- Adibi, M.M.; Martins, N. Power System Restoration Dynamics Issues. Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PS, USA, 20–24 July 2008.
- Lu, E.; Qin, Z.; Liu, M.; Hou, Y.; Wang, N.; Wen, J. Increasing black start capacity by fast cut back function of thermal power plants. Int. J. Smart Grid Clean Energy 2013, 2, 60–66. [Google Scholar]
- Lu, E.; Wang, N.; Qin, Z.; Liu, H.; Hou, Y. Black-Start Strategy for Power Grids including Fast Cut Thermal Power Units. Proceedings of the 2013 IEEE Power and Energy Society General Meeting (PES), Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5.
- Wang, H.; Liu, Y. Generator Field Overvoltages due to Energizing Lines. Proceedings of the International Conference on Power System Technology, PowerCnon 2002, Kunming, Yunnan, China, 13–17 October 2002; Volume 4, pp. 2122–2125.
- Machowski, J.; Bialek, J.W.; Bumby, J.R. Power System Dynamic: Stability and Control, 2nd ed.; John Wiley & Sons: Chichester, UK, 2008; pp. 329–334. [Google Scholar]
- Xue, S.; He, J.; Xu, L.; Sun, J. Study of Self-Excitation Over-Voltage and Switching Over-Voltage and Their Suppression Measure in Ultra-High Long Distance Transmission Lines. Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference (APPEEC), Wuhan, Hubei, China, 25–28 March 2011; pp. 1–4.
- Fusheng, L.; Ronghan, J. Vector analysis of self-excitation of synchronous generators. Proc. CSEE 1987, 7, 67–73, In Chinese. [Google Scholar]
- Xu, Y. The Practical Criterion of Generator Self Excitation and Its Field Example Analysis. Proceedings of the IEEE Region 10 Conference on Computer, Communication, Control and Power Engineering (TENCON 1993), Beijing, China, 19–21 October 1993; Volume 5, pp. 1–4.
- Begamudre, R.D. Extra High Voltage A.C. Transmission Engineering, 3rd ed.; New Age International: New Delhi, India, 2006; pp. 318–323. [Google Scholar]
- De Mello, F.P.; Westcott, J.C. Steam plant startup and control in system restoration. IEEE Trans. Power Syst. 1994, 9, 93–101. [Google Scholar]
- IEEE Committee Report. Dynamic models for steam and hydro turbines in power system studies. IEEE Trans. Power Appar. Syst. 1973, PAS-92, 1904–1915. [Google Scholar]
- Wang, L.; Yang, Y.; Morosuk, T.; Tsatsaronis, G. Advanced thermodynamic analysis and evaluation of a supercritical power plant. Energies 2012, 5, 1850–1863. [Google Scholar]





| Self-excitation types | Electric frequency | Power source | Characteristic |
|---|---|---|---|
| Reaction synchronous self-excitation | Synchronous frequency | Reluctance power | Salient-pole machine peculiar |
| Repulsion synchronous self-excitation | Synchronous frequency | Sub-transient reluctance power | May occur in Salient-pole machine and non-salient pole machine |
| Asynchronous self-excitation | Sub-synchronous frequency | Asynchronous power | Diverging oscillations of voltage and current |
| Voltage of line | Criterion of hydro-turbine | Criterion of steam turbine |
|---|---|---|
| 220 kV | Q > 2 L | Q > 4 L |
| 500 kV | Q > 15 L | Q > 30 L |
| Measurement objects | 50% of UG | 100% of UG |
|---|---|---|
| High voltage side of main transformer/kV | 252.33 | 526.87 |
| Line voltage/kV | 253.54 | 529.4 |
| Generator voltage/kV | 12.76 | 26.76 |
| Generator current/A | 953.06 | 1920.5 |
| Generator active power/MW | 3.18 | 6.12 |
| Generator reactive power/MVar | −21.15 | −86.89 |
| Data type | Comparison object | High voltage side of main transformer | Generator | Excitation system |
|---|---|---|---|---|
| Measured data | Maximum of transient voltage/kV | 697.85 | 27.01 | 190.1 |
| Overvoltage multiple | 1.81 | 1.4 | 1.6 | |
| Duration time/ms | 86 | 31 | 52 | |
| Simulation data | Maximum of transient voltage/kV | 700.15 | 27.57 | 187.2 |
| Overvoltage multiple | 1.83 | 1.41 | 1.59 | |
| Duration time/ms | 82 | 40 | 58 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zeng, K.; Wen, J.; Ma, L.; Cheng, S.; Lu, E.; Wang, N. Fast Cut Back Thermal Power Plant Load Rejection and Black Start Field Test Analysis. Energies 2014, 7, 2740-2760. https://doi.org/10.3390/en7052740
Zeng K, Wen J, Ma L, Cheng S, Lu E, Wang N. Fast Cut Back Thermal Power Plant Load Rejection and Black Start Field Test Analysis. Energies. 2014; 7(5):2740-2760. https://doi.org/10.3390/en7052740
Chicago/Turabian StyleZeng, Kaiwen, Jinyu Wen, Longpeng Ma, Shijie Cheng, En Lu, and Ning Wang. 2014. "Fast Cut Back Thermal Power Plant Load Rejection and Black Start Field Test Analysis" Energies 7, no. 5: 2740-2760. https://doi.org/10.3390/en7052740




