Correcting the Actual Reproduction Number: A Simple Method to Estimate R0 from Early Epidemic Growth Data
Abstract
:1. Introduction
1.1. The Basic Reproduction Number
1.2. Statistical Estimation of R0
2. Methods
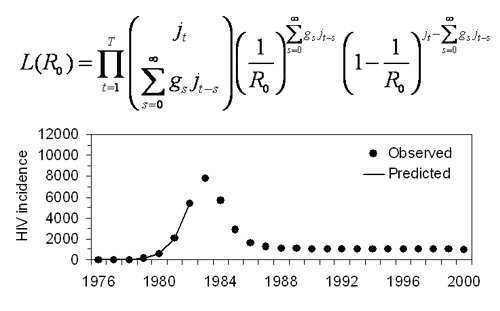
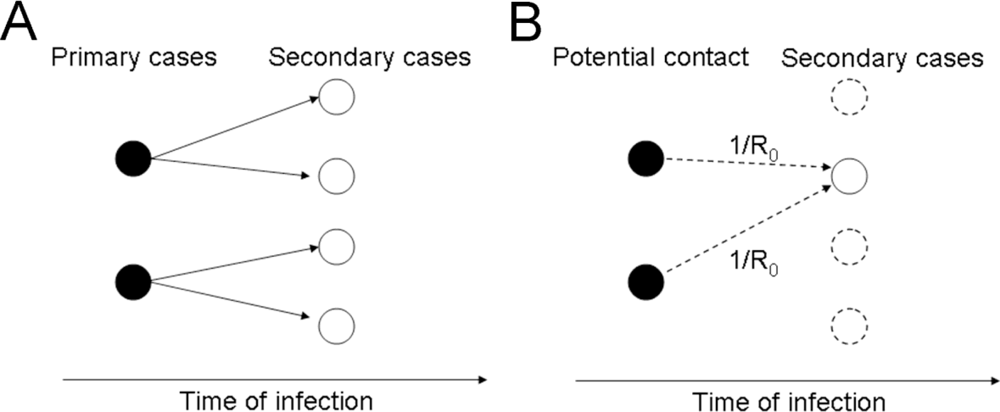
2.1. Actual Reproduction Number
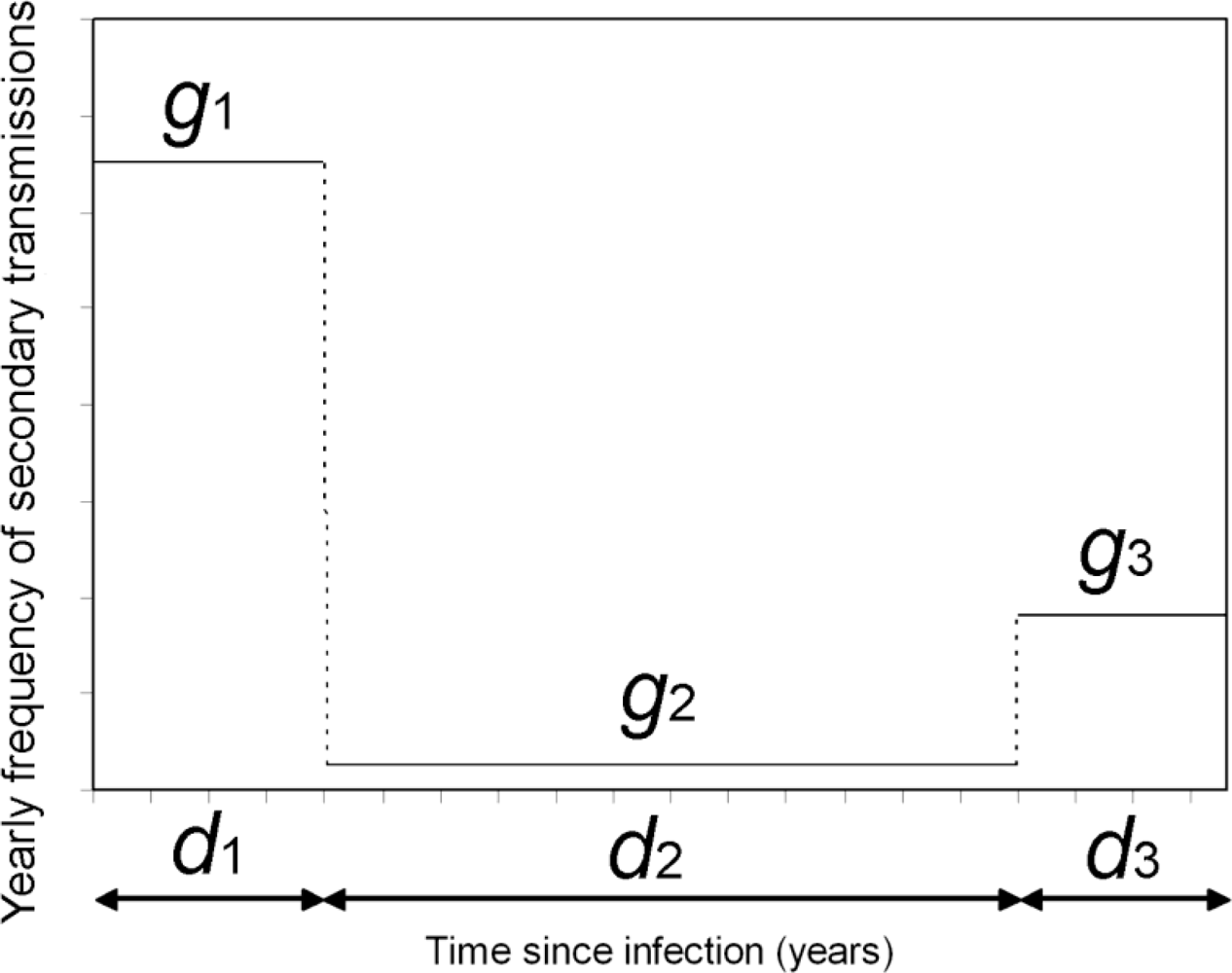
2.2. Correcting Ra
2.3. Data
2.4. Statistical Analysis
3. Results and Discussion
Acknowledgments
References
- Diekmann, O; Heesterbeek, JA; Metz, JA. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol 1990, 28, 365–381. [Google Scholar]
- Dietz, K. The estimation of the basic reproduction number for infectious diseases. Stat. Methods. Med. Res 1993, 2, 23–41. [Google Scholar]
- Becker, NG. Analysis of Infectious Disease Data; Chapman & Hall: Boca Raton, FL, USA, 1989. [Google Scholar]
- Smith, CE. Factors in the transmission of virus infections from animal to man. Sci Basis Med Ann Rev 1964, 125–150. [Google Scholar]
- Kendall, DG. Deterministic and stochastic epidemics in closed populations. In Proceedings of the 3rd Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1956; pp. 149–165. [Google Scholar]
- Ma, J; Earn, DJ. Generality of the final size formula for an epidemic of a newly invading infectious disease. Bull. Math. Biol 2006, 68, 679–702. [Google Scholar]
- Heffernan, JM; Wahl, LM. Improving estimates of the basic reproductive ratio: using both the mean and the dispersal of transition times. Theor. Pop. Biol 2006, 70, 135–145. [Google Scholar]
- Massad, E; Coutinho, FA; Burattini, MN; Amaku, M. Estimation of R0 from the initial phase of an outbreak of a vector-borne infection. Trop. Med. Int. Health 2009, 15, 120–126. [Google Scholar]
- Wallinga, J; Lipsitch, M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc. Roy. Soc. Lon. Ser. B 2007, 274, 599–604. [Google Scholar]
- Svensson, A. A note on generation times in epidemic models. Math. Biosci 2007, 208, 300–311. [Google Scholar]
- Diekmann, O; Heesterbeek, JAP. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation; John Wiley & Son: Chichester, UK, 2000. [Google Scholar]
- Garske, T; Clarke, P; Ghani, AC. The transmissibility of highly pathogenic avian influenza in commercial poultry in industrialised countries. PLoS ONE 2007, 2, e349. [Google Scholar]
- White, LF; Pagano, M. A likelihood-based method for real-time estimation of the serial interval and reproductive number of an epidemic. Stat. Med 2008, 27, 2999–3016. [Google Scholar]
- Amundsen, EJ; Stigum, H; Rottingen, JA; Aalen, OO. Definition and estimation of an actual reproduction number describing past infectious disease transmission: application to HIV epidemics among homosexual men in Denmark, Norway and Sweden. Epidemiol. Infect 2004, 132, 1139–1149. [Google Scholar]
- White, PJ; Ward, H; Garnett, GP. Is HIV out of control in the UK? An example of analysing patterns of HIV spreading using incidence-to-prevalence ratios. AIDS 2006, 20, 1898–1901. [Google Scholar]
- Chowell, G; Nishiura, H. Quantifying the transmission potential of pandemic influenza. Phys. Life. Rev 2008, 5, 50–77. [Google Scholar]
- Fraser, C. Estimating individual and household reproduction numbers in an emerging epidemic. PLoS ONE 2007, 2, e758. [Google Scholar]
- Nishiura, H; Chowell, G. The effective reproduction number as a prelude to statistical estimation of time-dependent epidemic trends. In Mathematical and Statistical Estimation Approaches in Epidemiology; Chowell, G, Hyman, JM, Bettencourt, LMA, Castillo-Chavez, C, Eds.; Springer: Dordrecht, Germany, 2009; pp. 103–121. [Google Scholar]
- Shiboski, SC; Jewell, NP. Statistical analysis of the time dependence of HIV infectivity based on partner study data. J. Amer. Statist. Assn 1991, 87, 360–372. [Google Scholar]
- Hollingsworth, TD; Anderson, RM; Fraser, C. HIV-1 transmission, by stage of infection. Int. J. Infect. Dis 2008, 198, 687–693. [Google Scholar]
- Wawer, MJ; Gray, RH; Sewankambo, NK; Serwadda, D; Li, X; Laeyendecker, O; Kiwanuka, N; Kigozi, G; Kiddugavu, M; Lutalo, T; Nalugoda, F; Wabwire-Mangen, F; Meehan, MP; Quinn, TC. Rates of HIV-1 transmission per coital act, by stage of HIV-1 infection, in Rakai, Uganda. Int. J. Infect. Dis 2005, 191, 1403–1409. [Google Scholar]
- Abu-Raddad, LJ; Longini, IM. No HIV stage is dominant in driving the HIV epidemic in sub-Saharan Africa. AIDS 2008, 22, 1055–1061. [Google Scholar]
- Artzrouni, M. Back-calculation and projection of the HIV/AIDS epidemic among homosexual/bisexual men in three European countries: Evaluation of past projections and updates allowing for treatment effects. Eur. J. Epidemiol 2004, 19, 171–179. [Google Scholar]
- Brookmeyer, R; Gail, MH. AIDS Epidemiology: A Quantitative Approach (Monographs in Epidemiology and Biostatistics); Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Jewell, NP; Dietz, K; Farewell, VT. AIDS Epidemiology: Methodological Issues; Birkhäuser: Berlin, Germany, 1992. [Google Scholar]
- Nishiura, H. Lessons from previous predictions of HIV/AIDS in the United States and Japan: epidemiologic models and policy formulation. Epidemiol. Perspect. Innov 2007, 4, 3. [Google Scholar]
- Bailey, NTJ. The Elements of Stochastic Processes with Applications to the Natural Sciences; Wiley: New York, NY, USA, 1964. [Google Scholar]
- Nishiura, H; Castillo-Chavez, C; Safan, M; Chowell, G. Transmission potential of the new influenza A(H1N1) virus and its age-specificity in Japan. Euro. Surveill 2009, 14, 19227. [Google Scholar]
- Wallinga, J; Teunis, P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Amer. J. Epidemiol 2004, 160, 509–516. [Google Scholar]
- Haydon, DT; Chase-Topping, M; Shaw, DJ; Matthews, L; Friar, JK; Wilesmith, J; Woolhouse, ME. The construction and analysis of epidemic trees with reference to the 2001 UK foot-and-mouth outbreak. Proc. Roy. Soc. Lon. Ser. B 2003, 270, 121–127. [Google Scholar]
- Nishiura, H; Schwehm, M; Kakehashi, M; Eichner, M. Transmission potential of primary pneumonic plague: time inhomogeneous evaluation based on historical documents of the transmission network. J. Epidemiol. Community Health 2006, 60, 640–645. [Google Scholar]
- Jacquez, JA; Simon, CP; Koopman, JS. The reproduction number in deterministic models of contagious diseases. Comments Theor. Biol 1991, 2, 159–209. [Google Scholar]
- Grassly, NC; Fraser, C. Mathematical models of infectious disease transmission. Nat. Rev. Microbiol 2008, 6, 477–487. [Google Scholar]
- Nishiura, H; Chowell, G; Heesterbeek, H; Wallinga, J. The ideal reporting interval for an epidemic to objectively interpret the epidemiological time course. J. R. Soc. Interface 2010, 7, 297–307. [Google Scholar]
- Nishiura, H; Chowell, G; Safan, M; Castillo-Chavez, C. Pros and cons of estimating the reproduction number from early epidemic growth rate of influenza A (H1N1) 2009. Theor. Biol. Med. Model 2010, 7, 1. [Google Scholar]
- Hethcote, HW; Yorke, JA. Gonorrhea Transmission Dynamics and Control (Lecture Notes in Biomathematics, 56); Springer-Verlag: Berlin, Germany, 1980. [Google Scholar]
- Muller, H; Bauch, C. When do sexual partnerships need to be accounted for in transmission models of human papilloma virus. Int J Environ Res Public Health 2010. [Google Scholar]

| Country | r (/year)1 | R0 (exponential growth) 2 | R0 (proposed likelihood) 3 |
|---|---|---|---|
| France | 1.15 (1.12, 1.17) | 3.65 (3.64, 3.66) | 3.59 (3.38, 3.81) |
| Western Germany | 2.15 (2.02, 2.29) | 4.08 (4.02, 4.14) | 3.74 (3.43, 4.08) |
| UK | 1.21 (1.18, 1.25) | 3.67 (3.66, 3.69) | 3.65 (3.38, 3.96) |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nishiura, H. Correcting the Actual Reproduction Number: A Simple Method to Estimate R0 from Early Epidemic Growth Data. Int. J. Environ. Res. Public Health 2010, 7, 291-302. https://doi.org/10.3390/ijerph7010291
Nishiura H. Correcting the Actual Reproduction Number: A Simple Method to Estimate R0 from Early Epidemic Growth Data. International Journal of Environmental Research and Public Health. 2010; 7(1):291-302. https://doi.org/10.3390/ijerph7010291
Chicago/Turabian StyleNishiura, Hiroshi. 2010. "Correcting the Actual Reproduction Number: A Simple Method to Estimate R0 from Early Epidemic Growth Data" International Journal of Environmental Research and Public Health 7, no. 1: 291-302. https://doi.org/10.3390/ijerph7010291