MCBT: Multi-Hop Cluster Based Stable Backbone Trees for Data Collection and Dissemination in WSNs
Abstract
:1. Introduction
2. Related Work
2.1. Traditional Energy Efficient Routing Protocols
2.2. Routing Protocols through a Backbone
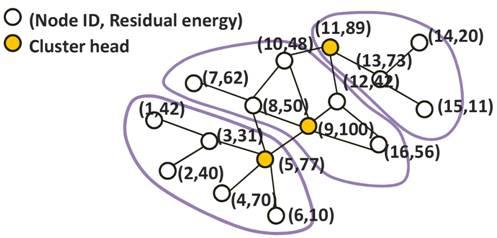
3. Multi-hop Cluster Based Stable Backbone Trees (MCBT)
3.1. Motivation and New Factor
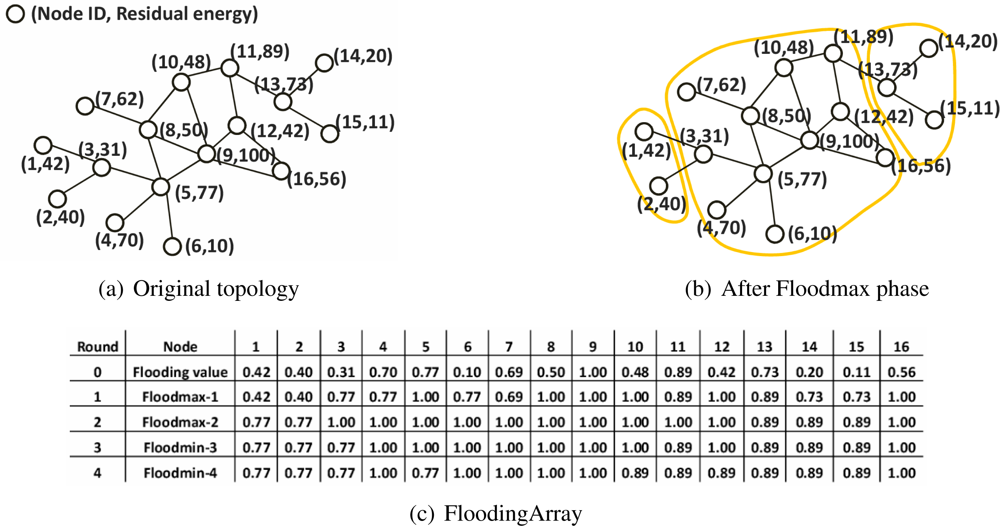
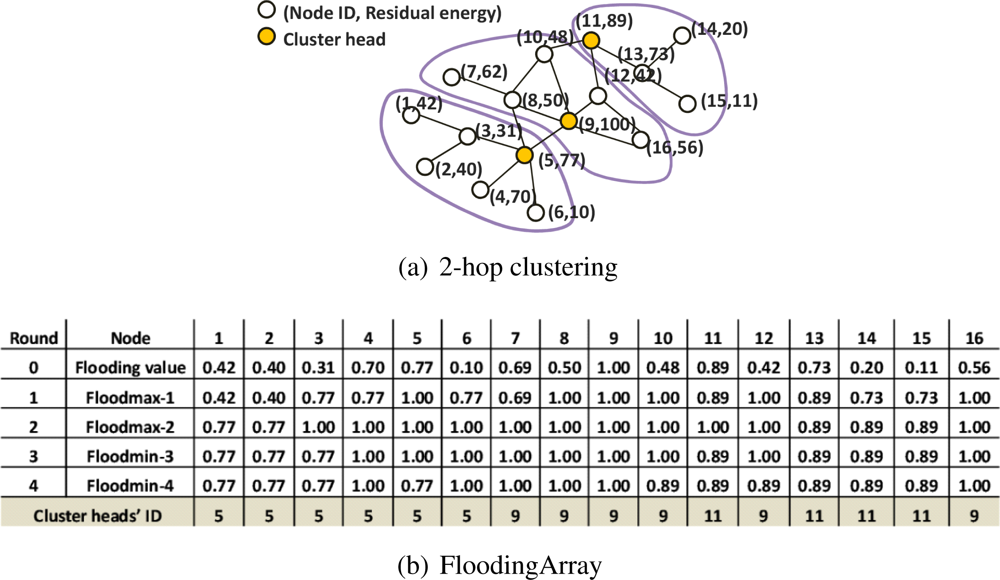
3.2. The Clustering Algorithm
- Rule 1: If a node x has the same value in Floodmin-2d of the 0th round value, node x declares itself a cluster head and skip the rest of the rules.
- Rule 2: If the first rule cannot be applied, node x compares d values of Floodmax with d values of Floodmin in its FloodingArray without order. If there is the value that appears in both Floodmax and Floodmin, node y that has this value is selected as the cluster head of node x. If node x has two or more of the same flooding values in its FloodingArray, it selects the node y that has a lower flooding value.
- Rule 3: If node y’ flooding value in 0th round is the same to the value of Floodmax-d of node x, node y becomes the cluster head of node x.
| // FloodingArrayi: FloodingArray of node i, CHi: Cluster head’ ID of node i | |
| MCBT(G, Eres, d) | |
| 01: | n ← The number of nodes |
| 02: | for i ← 1 to n |
| 03: | do, |
| where Si is a set of neighbors of node i including itself | |
| 04: | FloodingArrayi[0] ← f(i, ω) |
| // Floodmax Phase | |
| 05: | for k ← 1 to d |
| 06: | do for i ← 1 to n |
| 07: | do BROADCAST(FloodingArrayi[k − 1]) |
| // A node broadcasts its (k − 1)th flooding value to neighbors and receive | |
| // all neighbors’ (k − 1)th flooding value | |
| 08: | do for i ← 1 to n |
| 09: | do FloodingArrayi[k] ← maxj∈Si (FloodingArrayj[k − 1]) |
| // Floodmin Phase | |
| 10: | for k ← 1 to d |
| 11: | do for i ← 1 to n |
| 12: | do BROADCAST(FloodingArrayi[k − 1 + d]) |
| 13: | do for i ← 1 to n |
| 14: | do FloodingArrayi[k + d] ← minj∈Si (FloodingArrayj[k − 1 + d]) |
| // Cluster head Selection | |
| 15: | do for i ← 1 to n |
| 16: | do if (FloodingArrayi[2d]=FloodingArrayi[0]) |
| 17: | then CHi ← i |
| 18: | else if(Pair(i)) |
| 19: | then CHi ← CH_ID(Pair(i)) |
| 20: | else CHi ← CH_ID(FloodingArrayi[d]) |
| Pair(id) | |
| 01: | for i ← 1 to d |
| 02: | do for j ← (d + 1) to 2d |
| 03: | do if (FloodingArrayid[i] = FloodingArrayid[j]) |
| 04: | then return FloodingArrayid[i] |
| 05: | return 0 |
| CH_ID(floodingvalue) | |
| 01: | for i ← 1 to n |
| 02: | do if (FloodingArrayi[0] = floodingvalue) |
| 03: | then return i |
| 04: | return error |
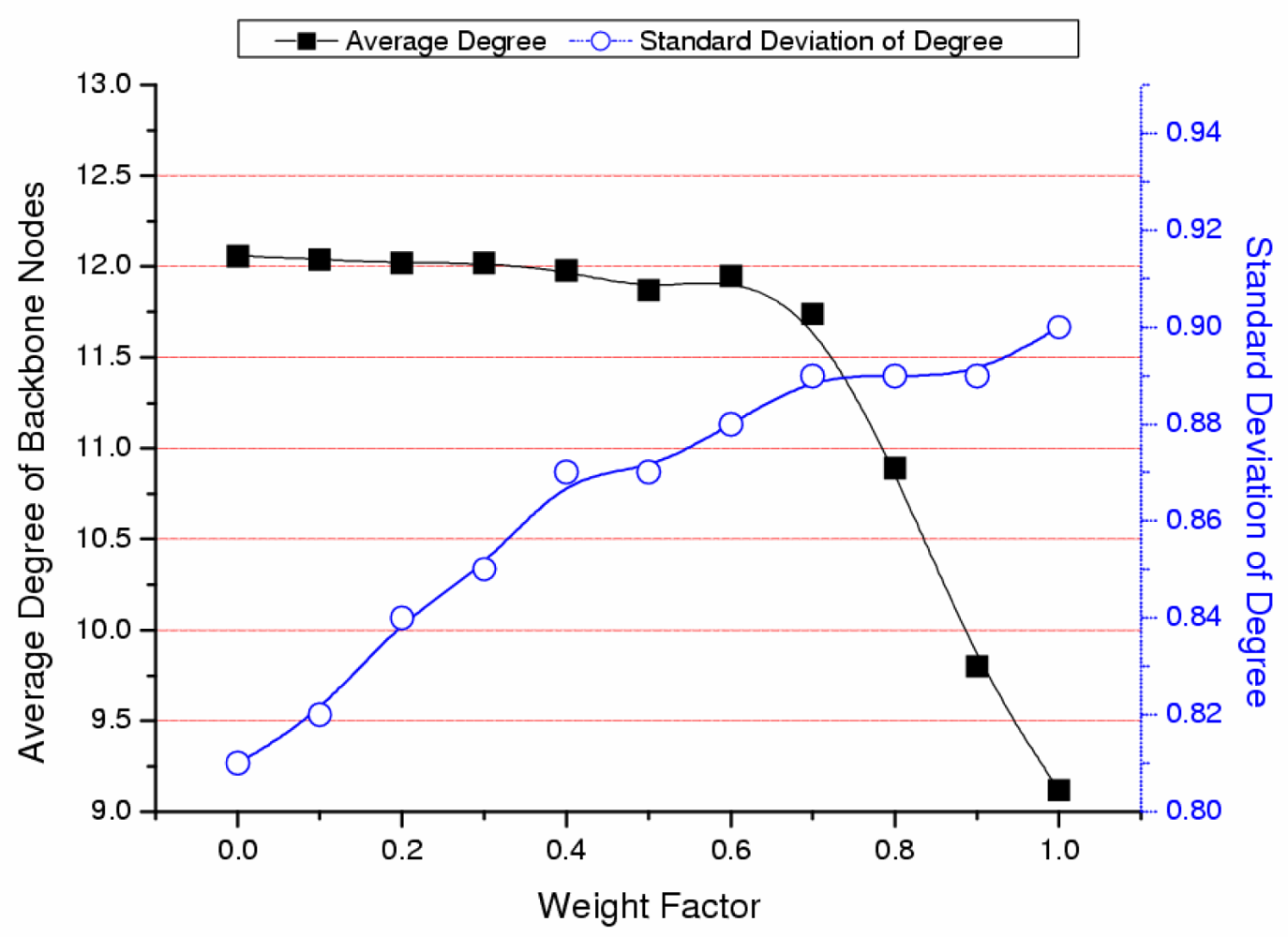
3.3. Validation of the Proposed Method and the Effect of Weight Factor (ω)
4. Performance Evaluation
4.1. Simulation Environment
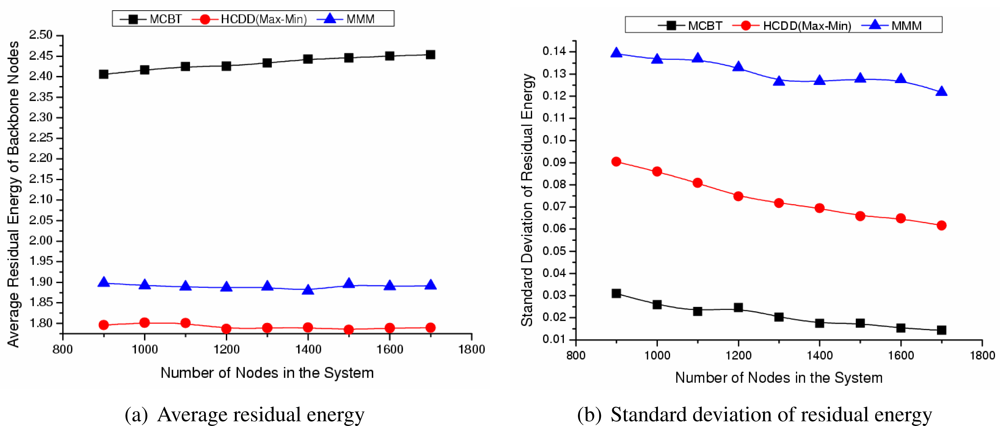
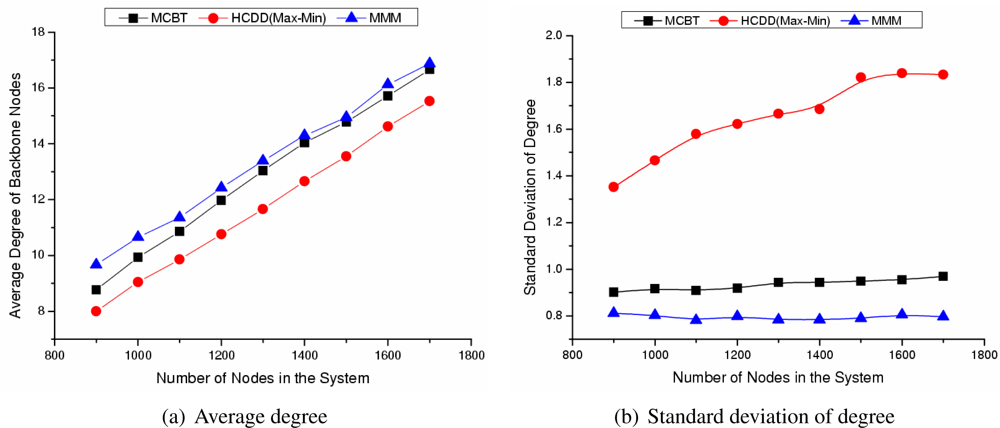
- Average residual energy or degree of backbone nodes:The residual energy or degree of the backbone nodes shows the stability of the backbone. The demands on the backbone nodes are larger than those of ordinary nodes and nodes around the cluster head consume more energy in order to forward packets. However, by selecting a node with higher energy or degree, the high energy consumption of specific nodes should be alleviated.
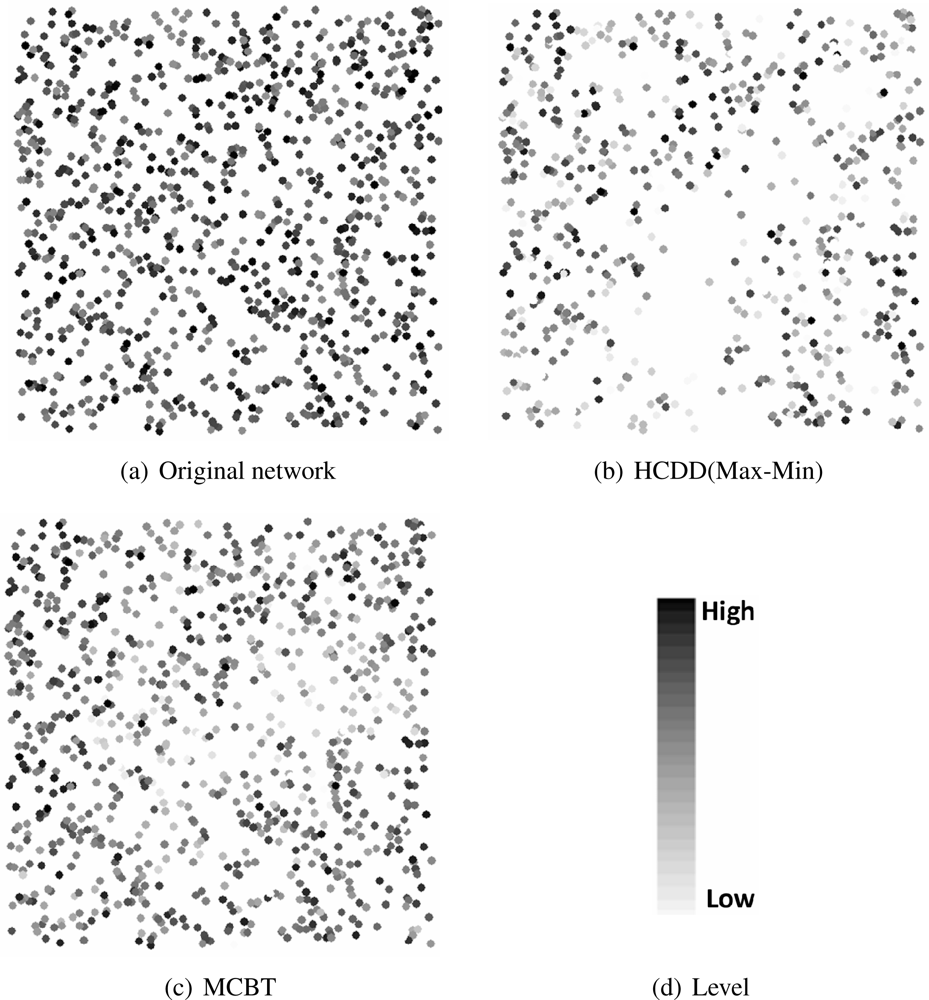
- The standard deviation of residual energy or degree of the backbone nodes:Assume that the number of backbone nodes in the network is m, the residual energy or degree of each backbone node is z, and the average residual energy or degree of backbone nodes is z̄, then the standard deviation is represented by . The standard deviation of the backbone nodes refers to the distribution rate of backbone nodes’ residual energy or degree. A small standard deviation means that the residual energy or degree of each backbone node is similar to the average value and the residual energy or degree of each backbone node is almost uniform. If the average residual energy or degree of backbone nodes is high and their standard deviation is low, then the node with higher residual energy or degree is selected as a backbone node in advance. Moreover, the backbone is composed of nodes with even characteristics. This may decrease the rapid disconnection of the network caused by a load imbalance.
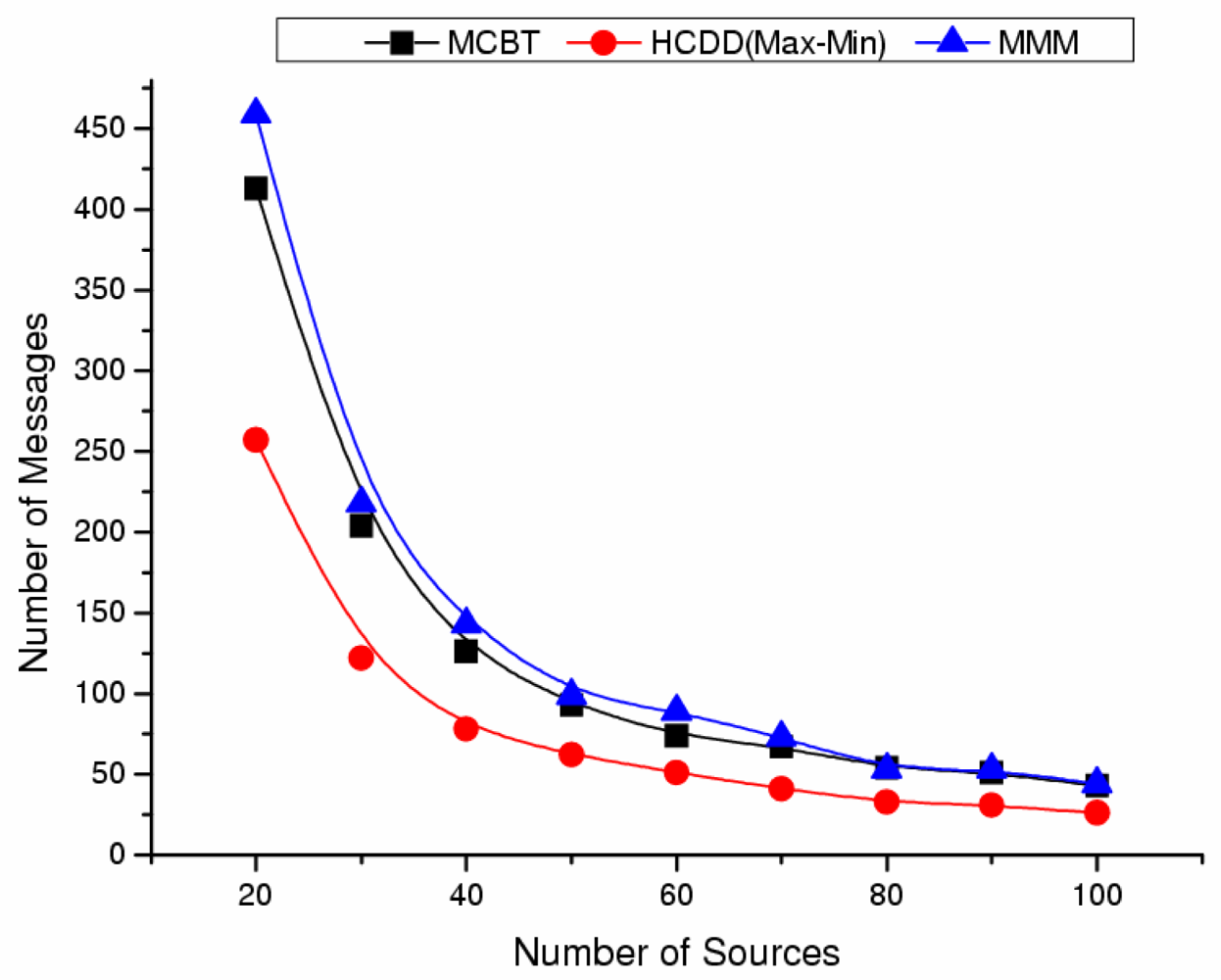
- The average residual energy of backbone nodes and the network lifetime after events occur:We can evaluate the network lifetime by measuring the operational time until the backbone is disconnected or by counting the maximum number of transmitted messages from source to sink. This indirectly indicates how long a backbone is maintained before its reconstruction. Reconstruction overhead places a heavy load on the network, and it is important to ensure the backbone is stable and maintained for a long time. The time can be affected by variable factors, such as routing paths and data transfer collisions. Thus, in this paper, we compare the network lifetime with other algorithms by evaluating the maximum number of transmitted messages.
4.2. Simulation Results
Influence of Number of Nodes
Influence of Number of Events
5. Conclusion
Acknowledgments
References and Notes
- Akyildiz, I.F.; Sankarasubramaniam, W.; Su, Y.; Cayirci, E. A Survey on Sensor Networks. IEEE Commun. Mag 2002, 40, 102–114. [Google Scholar]
- England, D.; Veeravalli, B.; Weissman, J.B. A Robust Spanning Tree Topology for Data Collection and Dissemination in Distributed Environments. IEEE T. Parall. Distr 2007, 18, 608–620. [Google Scholar]
- Ma, M.; Yang, Y. SenCar: an Energy Efficient Data Gathering Mechanism for Large Scale Multihop Sensor Networks. IEEE T. Parall. Distr 2007, 18, 1476–1488. [Google Scholar]
- Liu, C.; Wo, K.; Pei, J. An Energy-Efficient Data Collection Framework for Wireless Sensor Networks by Exploiting Spatiotemporal Correlation. IEEE T. Parall. Distr 2007, 18, 1010–1023. [Google Scholar]
- Liu, M.; Cao, J.; Chen, G.; Wang, X. An Energy-Aware Routing Protocol in Wireless Sensor Networks. MDPI Sensors 2009, 9, 445–462. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-Efficient Communication Protocol for Wireless Microsensor Networks. Proceedings of Hawaii International Conference on System Sciences, Island of Maui, Hawaii, USA, January 4–7, 2000; pp. 1–10.
- Chuang, S.-Y.; Chen, C. SmartBone: An Energy-Efficient Smart Backbone Construction in Wireless Sensor Networks. In proceedings of IEEE Wireless Communications and Networking Conference, Hong Kong, China, March 11–15, 2007; pp. 3394–3399.
- Manjeshwar, A.; Agrawal, D.P. TEEN: a routing protocol for enhanced efficiency in wireless sensor networks. Proceedings of IEEE International Parallel Distributed Processing Symposium, San Francisco, USA, April 23–27, 2001; pp. 2009–2015.
- Manjeshwar, A.; Agrawal, D.P. APTEEN: a hybrid protocol for efficient routing and comprehensive information retrieval in wireless sensor networks. Proceedings of IEEE International Parallel Distributed Processing Symposium, Fort Lauderdale, FL, USA, April 15–19, 2002; pp. 195–202.
- Intanagonwiwat, C.; Govindan, R.; Estrin, D.; Heidemann, J.; Silva, F. Directed Diffusion for Wireless Sensor Networking. IEEE/ACM T. Network 2003, 11, 2–16. [Google Scholar]
- Zalyubovskiy, V.; Erzin, A.; Astrakov, S.; Choo, H. Energy-efficient Area Coverage by Sensors with Adjustable Ranges. MDPI Sensors 2009, 9, 2446–2460. [Google Scholar]
- Park, S.; Shin, K.; Abraham, A.; Han, S. Optimized Self Organized Sensor Networks. MDPI Sensors 2007, 7, 5, 730–742. [Google Scholar]
- Lin, C.R.; Gerla, M. Adaptive Clustering for Mobile Wireless Networks. IEEE J. Sel. Area. Comm 1997, 15, 1265–1275. [Google Scholar]
- Akkaya, K.; Younis, M. A Survey on Routing Protocols for Wireless Sensor Networks. Ad Hoc Net 2005, 3, 325–349. [Google Scholar]
- Wang, Y.; Li, X.-Y. Efficient Distributed Low-Cost Backbone Formation for Wireless Networks. IEEE T. Parall. Distr 2006, 17, 681–693. [Google Scholar]
- Cheng, X.; Narahari, B.; Simha, R.; Cheng, M.X.; Liu, D. Strong Minimum Energy Topology in Wireless Sensor Networks: NP-Completeness and Heuristics. IEEE T. Mobile Comput 2003, 2, 248–256. [Google Scholar]
- Paruchuri, V.; Durresi, A.; Durresi, M.; Barolli, L. Routing through backbone structures in sensor networks. Proceedings of IEEE International Conference on Parallel and Distributed Systems, Las Vegas, Nevada, USA, September 12–14, 2005; pp. 397–401.
- Lin, C.J.; Chou, P.L.; Chou, C.F. HCDD: Hierarchical Cluster-based Data Dissemination in Wireless Sensor Networks with Mobile Sink. Proceedings of ACM International Conference on Wireless Communications and Mobile Computing, Vancouver, Canada, July 3–6, 2006; pp. 1189–1194.
- Amis, A.D.; Prakash, R.; Huynh, D.T.; Vuong, T.H.P. Max-Min D-Cluster Formation in Wireless Ad Hoc Networks. Proceedings of IEEE INFOCOM, Tel Aviv, Israel, March 26–30, 2000; 10, pp. 32–41.
- Heinzelman, W.R.; Kulik, J.; Balakrishnan, H. Adaptive Protocols for Information Dissemination in Wireless Sensor Networks. Proceedings of ACM/IEEE Mobile computing and networking, Seattle, Washington, USA, 1999; pp. 174–185.
- Jeon, H.; Park, K.; Hwang, D.-J.; Choo, H. Sink-oriented Dynamic Location Service Protocol for Mobile Sinks with an Energy Efficient Grid-Based Approach. MDPI Sensors 2009, 9, 1433–1453. [Google Scholar]
- Muthuramalingam, S.; Malarvizhi, R.; Veerayazhmi, R.; Rajaram, R. Reducing the Cluster Overhead by Selecting Optimal and Stable Cluster Head through Genetic Algorithm. Proceedings of IEEE Asia International Conference on Modeling & Simulation, Kuala Lumpur, Malaysia, May 13–15, 2008; pp. 540–545.
- Gerla, M.; Tsai, J.T.C. Multicluster, mobile, multimedia radio network. Wirel. Netw 1995, 1, 255–265. [Google Scholar]
- Bhardwaj, M.; Garnett, T.; Chandrakasan, A.P. Upper bounds on the lifetime of sensor networks. Proceedings of IEEE International Conference on Communications, St.-Petersburg, Russia, June 11–15, 2001; pp. 785–790.



| Schemes | Cluster head selection criteria | Time complexity |
|---|---|---|
| HCDD | ID | O (d) |
| MMM | Degree | O (n) |
| MCBT | Energy&Degree | O (d) |
| Network size | 500 m × 500 m |
| Transmission range | 28 m |
| Initial energy | 2.5 J |
| Data packet size | 500 bytes |
| Control packet size | 15 bytes |
| Energy consumption model Etx | α11 + α2rn |
| Energy consumption model Erx | α12 |
| α11, α12 | 80 nJ/bit |
| α2 | 1 pJ/bit/m2 |
| n | 2 |
© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shin, I.; Kim, M.; Mutka, M.W.; Choo, H.; Lee, T.-J. MCBT: Multi-Hop Cluster Based Stable Backbone Trees for Data Collection and Dissemination in WSNs. Sensors 2009, 9, 6028-6045. https://doi.org/10.3390/s90806028
Shin I, Kim M, Mutka MW, Choo H, Lee T-J. MCBT: Multi-Hop Cluster Based Stable Backbone Trees for Data Collection and Dissemination in WSNs. Sensors. 2009; 9(8):6028-6045. https://doi.org/10.3390/s90806028
Chicago/Turabian StyleShin, Inyoung, Moonseong Kim, Matt W. Mutka, Hyunseung Choo, and Tae-Jin Lee. 2009. "MCBT: Multi-Hop Cluster Based Stable Backbone Trees for Data Collection and Dissemination in WSNs" Sensors 9, no. 8: 6028-6045. https://doi.org/10.3390/s90806028