Extended Averaged Learning Subspace Method for Hyperspectral Data Classification
Abstract
:1. Introduction
2. Subspace Methods
2.1. CLAFIC and ALSM Subspace Methods
Theorem
2.2. Subspace Dimension
3. Preprocessing Methods and Data Sets
3.1. Normalization Methods
3.2. Eigenvalue Computation Methods
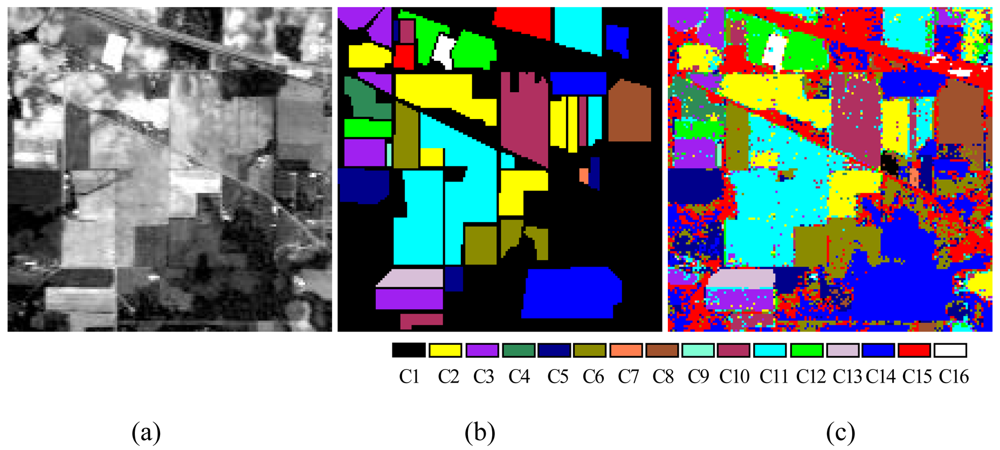
3.3. Data Sets and Experimental Settings
4. Experimental Results and Discussion
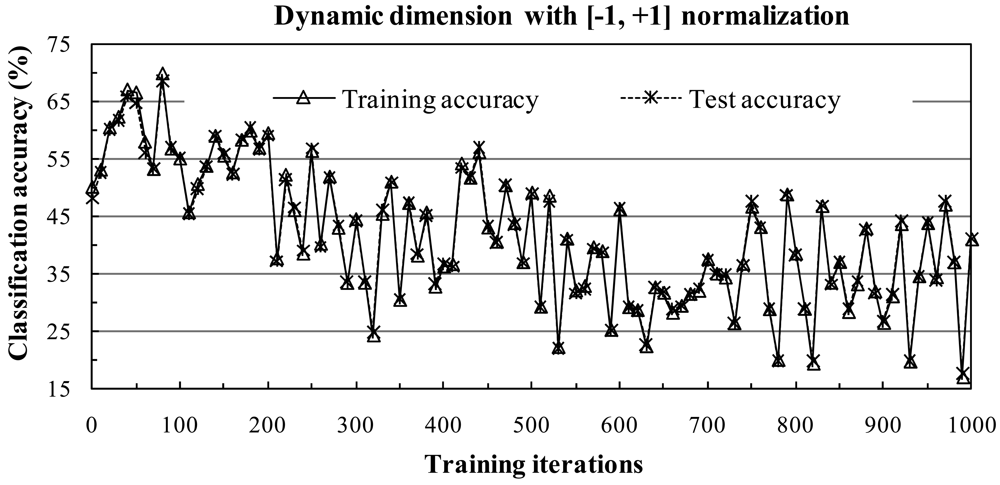
4.1. Subspace Method with [-1, +1] Normalization
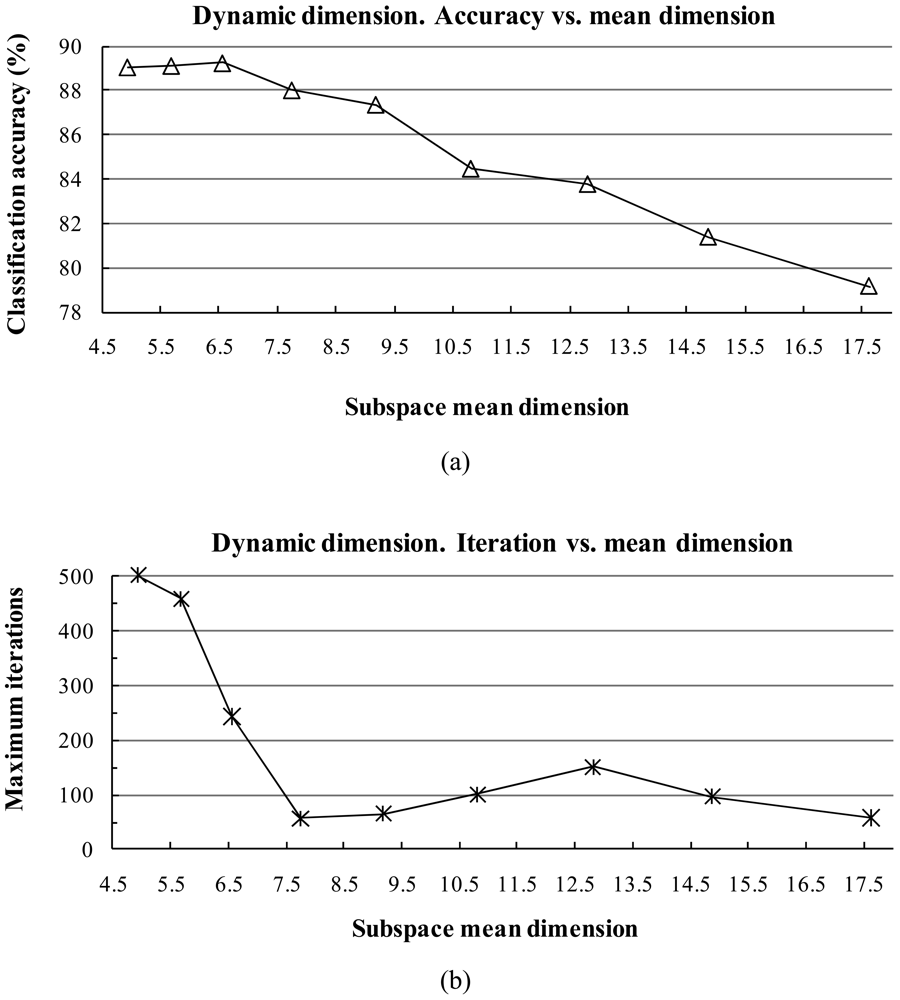
1) Influence of the Subspace Dimension
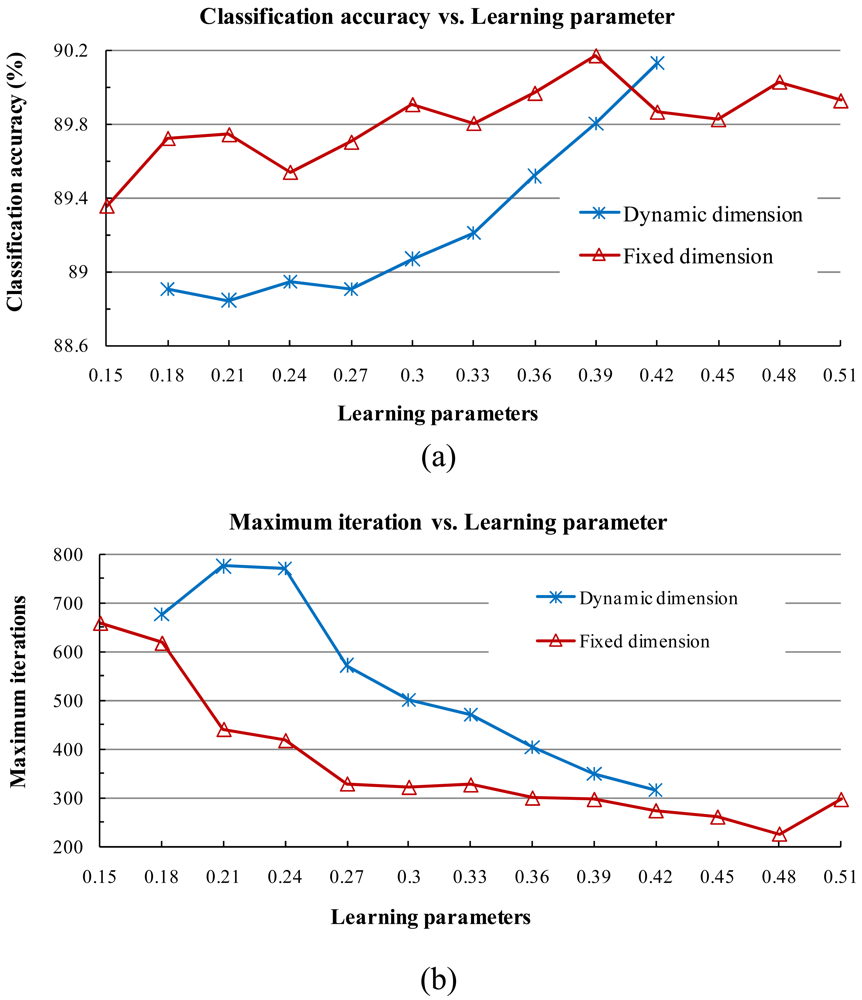
2) Stability of Learning Parameters
3) Influence of Parameters
4.2. Subspace Method with [0, 1] Normalization
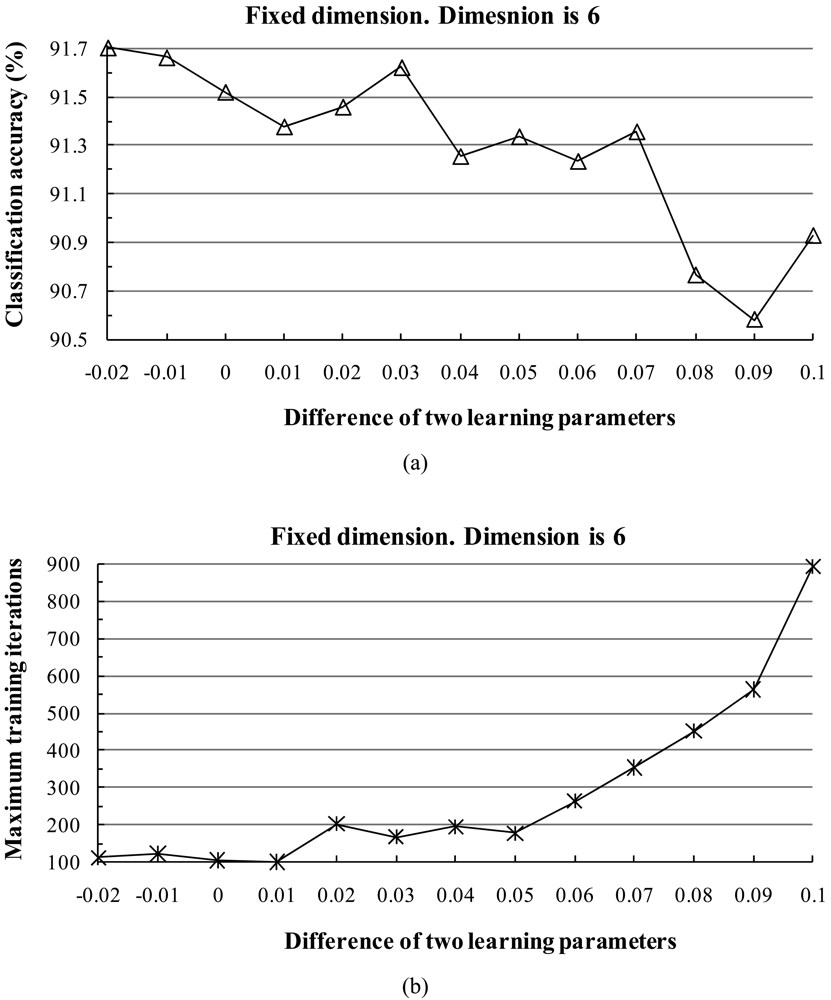
1) Behavior of the Two Learning Parameters
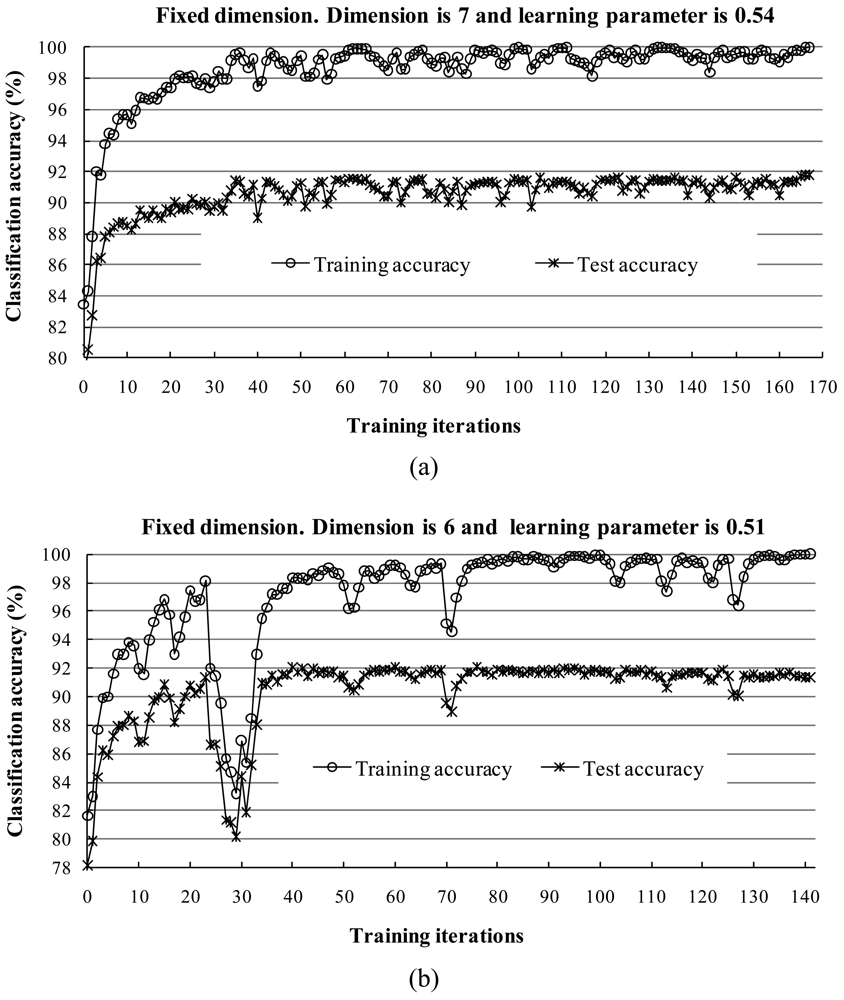
2) Behavior of Training and Test Sets in Learning Iterations
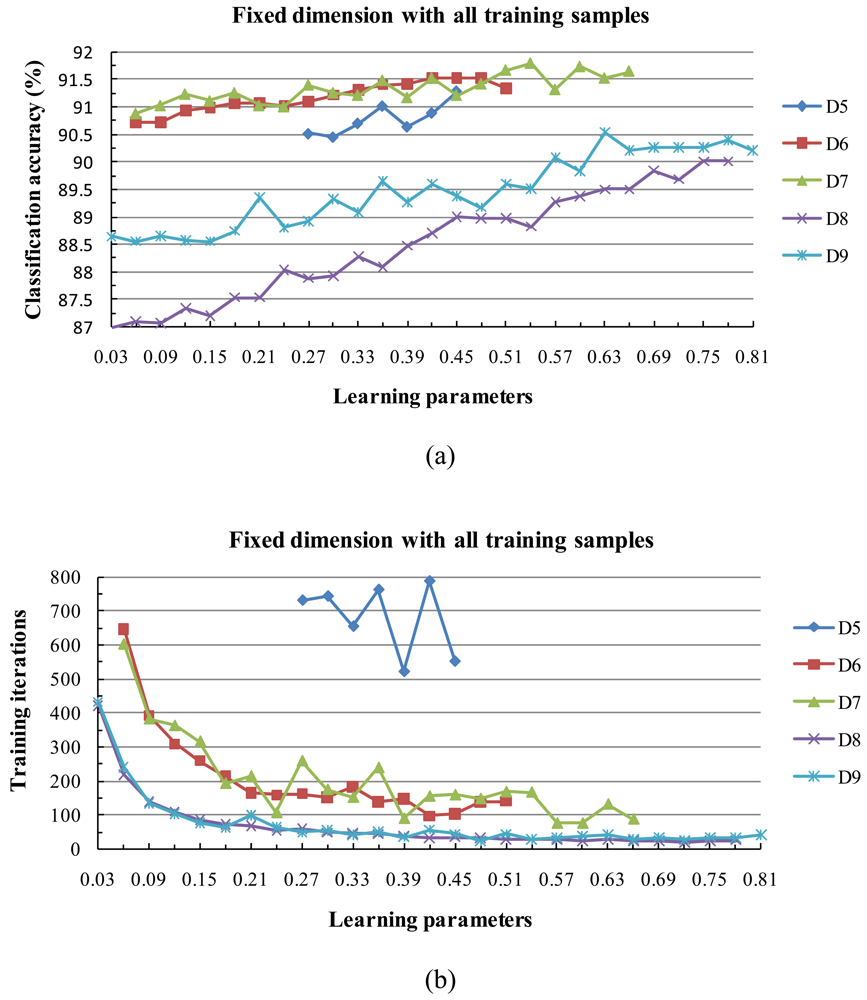
3) Behavior of Classification Accuracy and Training Time
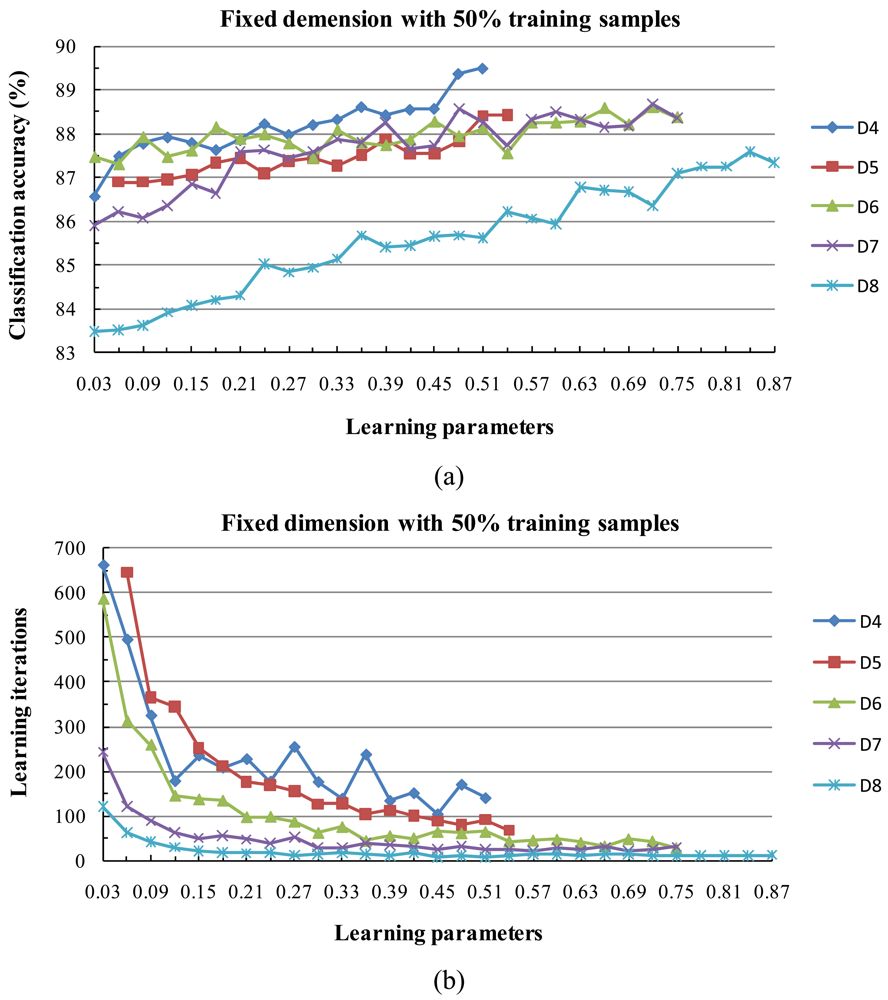
4) Behavior of the Algorithm for Low Sample Sizes
5. Conclusions
- The fixed subspace method in conjunction with the [0,1] normalization method is substantially more accurate than other approaches such as the dynamic subspace method.
- When the two learning parameters are equal or close to each other, the classification accuracy increases. When the value of the learning parameters is large, the classification accuracy tends to increase and the training time shortens.
- The classification accuracy is not sensitive to the dimension of the subspace when it is within at small interval, but a larger dimension tends to reduce the training time.
- Experimental results clearly showed the classification accuracy increased with the size of the training data set.
Acknowledgments
References
- Lee, C.; Landgrebe, D.A. Analyzing high-dimensional multispectral data. IEEE Trans. Geosci. Remote Sens. 1993, 31, 792–800. [Google Scholar]
- Jimenez, L.O.; Landgrebe, D.A. Supervised classification in high-dimensional space: Geometrical, statistical, and asymptotically properties of multivariate data. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 1998, 28, 39–54. [Google Scholar]
- Bajcsy, P.; Groves, P. Methodology for hyperspectral band selection. Photogramm. Eng. Remote Sens. 2004, 70, 793–802. [Google Scholar]
- Hughes, G.F. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, IT-14, 55–63. [Google Scholar]
- Plaza, A.; Martínez, P.; Plaza, J.; Pérez, R. Dimensionality reduction and classification of hyperspectral image data using sequences of extended morphological transformations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 466–479. [Google Scholar]
- Serpico, S.B.; Moser, G. Extraction of spectral channels from hyperspectral images for classification purposes. IEEE Trans. Geosci. Remote Sens. 2007, 45, 484–495. [Google Scholar]
- Miao, X.; Gong, P; Swope, S.; Pu, R.L.; Carruthers, R.; Anderson, G.L. Detection of yellow starthistle through band selection and feature extraction from hyperspectral imagery. Photogramm. Eng. Remote Sens. 2007, 73, 1005–1015. [Google Scholar]
- Jimenez-Rodriguez, L.O.; Arzuaga-Cruz, E.; Velez-Reyes, M. Unsupervised linear feature-extraction methods and their effects in the classification of high-dimensional data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 469–483. [Google Scholar]
- Bioucas-Dias, J.M.; Nascimento, J.M.P. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar]
- Gagnon, P.; Scheibling, R.E.; Jones, W.; Tully, D. The role of digital bathymetry in mapping shallow marine vegetation from hyperspectral image data. Int. J. Remote Sens. 2008, 29, 879–904. [Google Scholar]
- Harris, J.R.; Ponomarev, P.; Shang, J.; Rogge, D. Noise reduction and best band selection techniques for improving classification results using hyperspectral data: application to lithological mapping in Canada's Arctic. Can. J. Rem. Sens. 2006, 32, 341–354. [Google Scholar]
- Harsanyi, J.; Chang, C.-I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar]
- Bazi, Y.; Melgani, F. Toward an optimal SVM classification system for hyperspectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3374–3385. [Google Scholar]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and spatial classification of hyperspectral data using SVMs and morphological profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar]
- Zhao, K.G.; Popescu, S.; Zhang, X.S. Bayesian learning with Gaussian processes for supervised classification of hyperspectral data. Photogramm. Eng. Remote Sens. 2008, 74, 1223–1234. [Google Scholar]
- Guo, B.; Damper, R.I.; Gunn, S.R.; Nelson, J.D.B. A fast separability-based feature-selection method for high-dimensional remotely sensed image classification. Patt. Recog. 2008, 41, 1653–1662. [Google Scholar]
- Plaza, J.; Plaza, A.J.; Barra, C. Multi-channel morphological profiles for classification of hyperspectral images using support vector machines. Sensors 2009, 9, 196–218. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.B.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS) - interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar]
- Ball, J.E.; Bruce, L.M. Level set hyperspectral image classification using best band analysis. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3022–3027. [Google Scholar]
- Watanabe, S.; Lambert, P.F.; Kulikowski, C.A.; Buxton, J.L.; Walker, R. Evaluation and selection of variables in pattern recognition. In Computer and Information Sciences II; Tou, J.T., Ed.; Academic Press: New York, NY, USA, 1967; pp. 91–122. [Google Scholar]
- Sakano, H.; Mukawa, N.; Nakamura, T. Kernel mutual subspace method and its application for object recognition. Electron. Commun. Japan (Part II: Electron.) 2005, 88, 45–53. [Google Scholar]
- Omachi, S.; Omachi, M. Fast image retrieval by subspace method with polynomial approximation. IEICE Trans. Inf. Syst. 2008, J91-D, 1561–1568. [Google Scholar]
- Bagan, H.; Yasuoka, Y.; Endo, T.; Wang, X.; Feng, Z. Classification of airborne hyperspectral data based on the average learning subspace method. IEEE Geosci. Remote Sens. Lett. 2008, 5, 368–372. [Google Scholar]
- Elvidge, C.D.; Yuan, D.; Weerackoon, R.D.; Lunetta, R.S. Relative radiometric normalization of Landsat Multi-spectral Scanner (MSS) data using an automatic scattergram-controlled regression. Photogramm. Eng. Remote Sens. 1995, 61, 1255–1260. [Google Scholar]
- Olthof, I.; Pouliot, D.; Fernandes, R.; Latifovic, R. Landsat-7 ETM+ radiometric normalization comparison for northern mapping applications. Remote Sens. Environ. 2007, 95, 388–398. [Google Scholar]
- Parlett, B.N. The QR algorithm. Comput. Sci. Eng. 2000, 2, 38–42. [Google Scholar]
- Rutishauser, H. The Jacobi method for real symmetric matrices. Numer. Math. 1966, 9, 1–10. [Google Scholar]
- Landgrebe, D.A. Signal Theory Methods in Multispectral Remote Sensing; Wiley-Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Oja, E. Subspace Methods of Pattern Recognition; Research Studies Press and John Wiley & Sons: Letchworth, U.K., 1983. [Google Scholar]
- Tsuda, K. Subspace classifier in the Hilbert space. Patt. Recog. Lett. 1999, 20, 513–519. [Google Scholar]
- Laaksonen, J.; Oja, E. Subspace dimension selection and averaged learning subspace method in handwritten digit classification. Proceedings of the International Conference on Artificial Neural Networks, Bochum, Germany, 16–19 July, 1996; pp. 227–232.
- Chang, C.C.; Lin, C.J. LIBSVM: a library for support vector machines. 2001. [Online]. URL: http://www.csie.ntu.edu.tw/~cjlin/libsvm (last date accessed: 1 May 2009).
- Golub, G.H.; van der Vorst, H.A. Eigenvalue computation in the 20th century. J. Comput. Appl. Math. 2000, 123, 35–65. [Google Scholar]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remote Sensed Data: Principles and Practices, 1st Ed. ed; Lewis Publishers: Boca Raton, FL, USA, 1999; p. 137. [Google Scholar]
- Foody, G.M. Thematic map comparison evaluating the statistical significance of differences in classification accuracy. Photogramm. Eng. Remote Sens. 2004, 70, 627–633. [Google Scholar]
- Mathur, A.; Sanchez-Hernandez, C.; Boyd, D.S. Training set size requirements for the classification of a specific class. Remote Sens. Environ. 2006, 104, 1–14. [Google Scholar]
- Waske, B.; Benediktsson, J.A. Fusion of support vector machines for classification of multisensor data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3858–3866. [Google Scholar]
- Scholkopf, B.; Smola, A.; Muller, K.R. Nonlinear component analysis as a kernel eigenvalue problem. Neur. Comput. 1998, 10, 1299–1319. [Google Scholar]
- Washizawa, Y.; Yamashita, Y. Kernel projection classifiers with suppressing features of other classes. Neur. Comput. 2006, 18, 1932–1950. [Google Scholar]


| Class | Training Samples | Test Samples |
|---|---|---|
| C1. alfalfa | 26 | 26 |
| C2. corn-notill | 671 | 671 |
| C3. corn-min | 400 | 400 |
| C4. corn | 98 | 99 |
| C5. grass-pasture | 228 | 228 |
| C6. grass-trees | 357 | 357 |
| C7. grass-pasture | 13 | 13 |
| C8. hay-windrowed | 241 | 241 |
| C9. oats | 10 | 10 |
| C10. soybean-notill | 480 | 480 |
| C11. soybean-min | 1,137 | 1,137 |
| C12. soybean-cleantill | 282 | 283 |
| C13. wheat | 104 | 105 |
| C14. woods | 617 | 618 |
| C15. bldg-grass | 180 | 181 |
| C16. stone-steel | 44 | 45 |
| Total | 4,888 | 4,894 |
| C1 | C2 | C3 | C4 | C 5 | C 6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 6 | 7 | 6 | 4 | 7 | 2 | 5 | 2 | 8 | 8 | 8 | 6 | 5 | 8 | 5 |
| Fidelity value | 0.99985 | 0.99986 | 0.99987 | 0.99988 | 0.09989 | 0.9999 | 0.99991 | 0.99992 | 0.99993 |
| Mean dimension | 4.94 | 5.69 | 6.56 | 7.75 | 9.19 | 10.81 | 12.81 | 14.88 | 17.63 |
| Class | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | User acc. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 92 |
| 2 | 0 | 618 | 10 | 6 | 0 | 0 | 0 | 0 | 0 | 19 | 47 | 2 | 0 | 0 | 0 | 1 | 87.91 |
| 3 | 0 | 10 | 344 | 7 | 0 | 0 | 0 | 0 | 0 | 5 | 15 | 11 | 0 | 0 | 0 | 0 | 87.76 |
| 4 | 0 | 8 | 9 | 82 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 81.19 |
| 5 | 0 | 0 | 0 | 0 | 224 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 98.68 |
| 6 | 0 | 0 | 0 | 0 | 1 | 349 | 0 | 0 | 0 | 3 | 1 | 1 | 0 | 2 | 2 | 0 | 97.21 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| 8 | 3 | 0 | 0 | 0 | 0 | 0 | 3 | 236 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 97.52 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 90.91 |
| 10 | 0 | 7 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 416 | 24 | 2 | 0 | 0 | 0 | 1 | 92.04 |
| 11 | 0 | 27 | 27 | 2 | 2 | 1 | 0 | 0 | 0 | 32 | 1044 | 8 | 0 | 0 | 0 | 3 | 91.1 |
| 12 | 0 | 1 | 10 | 0 | 1 | 0 | 0 | 0 | 0 | 3 | 5 | 257 | 0 | 0 | 1 | 0 | 92.45 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 105 | 0 | 1 | 0 | 99.06 |
| 14 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 599 | 39 | 0 | 93.74 |
| 15 | 0 | 0 | 0 | 1 | 0 | 5 | 0 | 3 | 0 | 0 | 0 | 1 | 0 | 17 | 136 | 0 | 83.44 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 40 | 97.56 |
| Total | 26 | 671 | 400 | 99 | 228 | 357 | 13 | 241 | 10 | 480 | 1137 | 283 | 105 | 618 | 181 | 45 | |
| Prod. acc | 88.46 | 92.1 | 86 | 82.83 | 98.25 | 97.76 | 69.23 | 97.93 | 100 | 86.67 | 91.82 | 90.81 | 100 | 96.93 | 75.14 | 88.89 | (%) |
| Class | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training | 13 | 335 | 200 | 49 | 114 | 178 | 13 | 120 | 10 | 240 | 568 | 141 | 52 | 308 | 90 | 22 | 2453 |
| Test | 26 | 671 | 400 | 99 | 228 | 357 | 13 | 241 | 10 | 480 | 1137 | 283 | 105 | 618 | 181 | 45 | 4894 |
| 100% of training data | 50% of training data | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Dimension | D5 | D6 | D7 | D8 | D9 | D4 | D5 | D6 | D7 | D8 |
| Classification accuracy | 91.28% | 91.52% | 91.79% | 90.01% | 90.54% | 89.50% | 88.43% | 88.60% | 88.68% | 87.60% |
| Training iterations | 553 | 97 | 167 | 33 | 41 | 141 | 68 | 44 | 27 | 11 |
| Learning parameter | 0.45 | 0.42 | 0.54 | 0.75 | 0.63 | 0.51 | 0.54 | 0.72 | 0.72 | 0.84 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bagan, H.; Takeuchi, W.; Yamagata, Y.; Wang, X.; Yasuoka, Y. Extended Averaged Learning Subspace Method for Hyperspectral Data Classification. Sensors 2009, 9, 4247-4270. https://doi.org/10.3390/s90604247
Bagan H, Takeuchi W, Yamagata Y, Wang X, Yasuoka Y. Extended Averaged Learning Subspace Method for Hyperspectral Data Classification. Sensors. 2009; 9(6):4247-4270. https://doi.org/10.3390/s90604247
Chicago/Turabian StyleBagan, Hasi, Wataru Takeuchi, Yoshiki Yamagata, Xiaohui Wang, and Yoshifumi Yasuoka. 2009. "Extended Averaged Learning Subspace Method for Hyperspectral Data Classification" Sensors 9, no. 6: 4247-4270. https://doi.org/10.3390/s90604247
APA StyleBagan, H., Takeuchi, W., Yamagata, Y., Wang, X., & Yasuoka, Y. (2009). Extended Averaged Learning Subspace Method for Hyperspectral Data Classification. Sensors, 9(6), 4247-4270. https://doi.org/10.3390/s90604247





