2. Working Principle
As shown schematically in
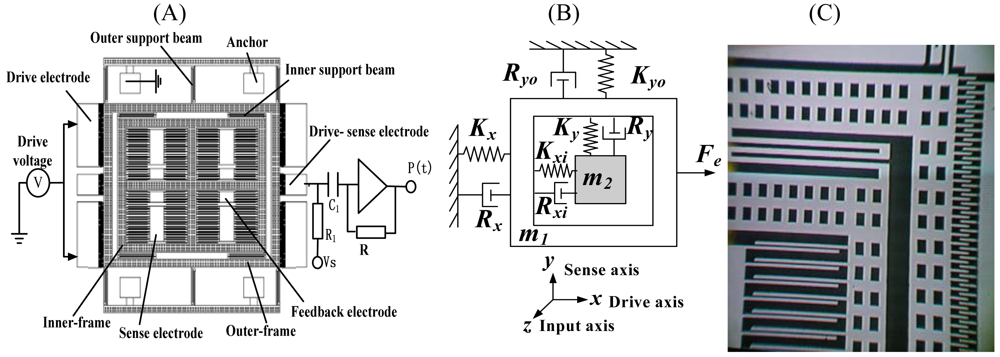
Figure 1(A), the micro-gyroscope consists of two silicon frames (outer-frame and inner-frame); the outer-frame is anchored on a glass substrate by six outer support beams and is connected with the inner-frame through four inner support beams. The outer-frame and the fixed interdigitated drive electrode on the glass substrate form the drive capacitors. The alternating drive force of the out-frame along the x-axis is generated through applying alternating current (AC) voltage with direct current (DC) bias voltage to the fixed drive electrode. Since the stiffness of the inner support beam along the x-axis (K
xi≫ K
x) is very large, the outer-frame and the inner-frame are driven together to vibrate along the x-axis by the alternating drive force, which causes the alternating capacitance between the outer-frame and fixed drive-sense electrode. We can capture the drive displacement by detecting the alternating capacitance. When the rotation rate along the z-axis is input, according to the Coriolis effect, the Coriolis force along the y-axis will be loaded on both the outer-frame and the inner-frame. Because the stiffness of the outer support beam along the y-axis (K
yo≫K
y) is very large, only the inner-frame is driven to vibrate along the y-axis by the Coriolis force, which induces the alternating capacitance between the inner-frame and fixed sense electrode. We can obtain the rotation rate along the z-axis by detecting the alternating capacitance.
The simplified motion equations of SMG are described by:
where x and y are separately the drive axis displacements and sense axis displacements in meters, Ω the rotation rate along the z-axis in radians/second, m
x (m
x=m
1+m
2) and m
y (m
y=m
2) the drive proof mass and the sense proof mass in kilograms, R
x and R
y the damping in Newtons/meter/second, K
x and K
y the stiffness in Newtons/meter, and −2
m xΩ
ẋ the denote of the Coriolis force. F
e (F
e=F
dsinω
dt) is the electrostatic force used to maintain the drive-mode vibration at a specified amplitude in terms of displacement, and at a resonant frequency of the drive-mode. Mechanical thermal noise on the drive axis is represented by the random force n(t), in units of force.
Ignoring the influence of the random force n(t), the drive axis displacements and sense axis displacements in the steady state are described by:
where
;
;
;
; ω
nx =(K
x/m
x)
(1/2); ω
ny =(K
y/m
y)
(1/2); Q
x=m
xω
nx/R
x, Q
y=m
yω
ny/R
y.
When ω
d=ω
nx=ω
ny, the maximum drive axis displacements and sense axis displacements are described by:
3. Mechanical Thermal Noise
Consider the damped harmonic oscillator:
The presence of damping in the system suggests that any oscillation would continue to decrease in amplitude forever. Inclusion of the fluctuating force n(t) prevents the system temperature from dropping below that of the system's surroundings. The damper provides a path for energy to leave the mass-spring system. This is the essence of the Fluctuation-Dissipation Theorem. According to Equipartition, if any collection of energy storage mode is in thermal equilibrium, then each mode will have an average energy equal to (1/2)kBT where kB is Boltzmann's constant(1.38×10-23J/K) and T is the absolute temperature in degrees Kelvin. A mode of energy storage is one in which the energy is proportional to the square of some coordinate; e.g., kinetic and spring potential.
When this system is in thermal equilibrium, the probability distribution of x and
ẋ is given by
equation (8):[
12]
For the oscillator, the energy is the sum of the kinetic and spring potential energy:
From here, the equipartition theorem can be derived, namely that the mean energy in any energy storage mode is equal to(1/2)k
BT. Thus:
where <·>denotes an ensemble average. The form of the distribution
p(
x, ẋ) indicates that
x and
ẋ are independent, Gaussian, and have zero mean. Since this holds for all values of m
x and K
x, the thermal noise n(t) must be a white Gaussian noise with two sided spectral density [
10]:
The spectral density of drive displacements due to thermal noise is:
So the noise power spectrum is:
The RMS noise displacements due to thermal noise is:
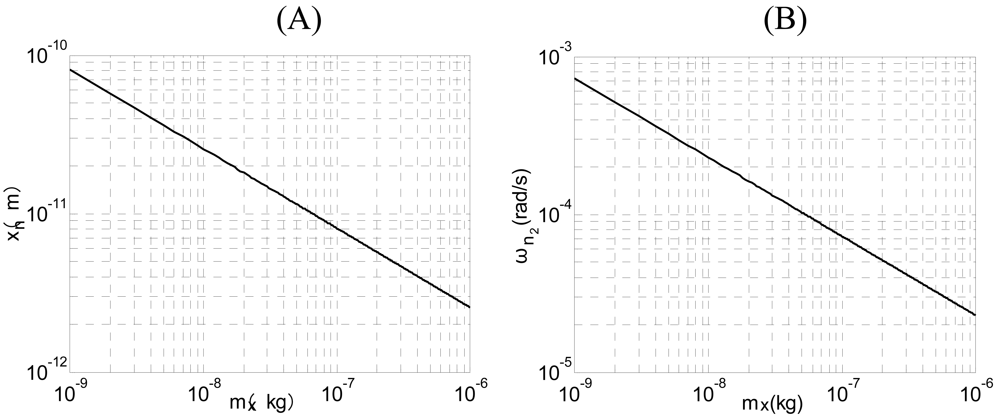
The above equation indicates that we can improve the signal-to-noise ratio by increasing the quality Qx and driving force amplitude Fd, or by reducing the stiffness and temperature.
4. Closed-loop Driving and System Model
As is known in the art of Coriolis force sensors, in order to achieve an acceptable response from the sensor, the proof mass vibration of the drive-mode should have a frequency at, or close to, the resonant frequency of the proof mass. At the same time, in order to improve the entire performance of the SMG, a high stability of the driving frequency and the amplitude of the drive-mode are needed. To satisfy those demands, the closed-loop driving of the drive-mode must be achieved. To this end, the drive signal has a frequency equal to the resonant frequency of the proof mass. However, parasitic capacitances between the drive electrode and the drive-sense electrode can cause significant errors. That is, when the drive signal capacitively couples into the drive-sense electrode, the accuracy of amplitude control by the feedback circuit is degraded and the harmonic frequency of the closed-loop system departs from the resonant frequency of the proof mass, resulting in less than optimum sensor performance, so we must eliminate the capacitive coupling. Various techniques are generally utilized in an effort to reduce capacitive coupling. In this paper, such a technique is utilized as follows: the drive electrode is arranged on the left, the drive-sense electrode is arranged on the right and the anchor of the SMG is connected with the ground or the virtual ground, which is shown in
Figure 1(A). By separating the drive-sense interface (drive-sense electrode) from the interference source (drive voltage), we can reduce these capacitive couplings. Besides, the SMG studied in this paper is executed in vacuum encapsulation, with a working pressure under 10
-1 Torr and the quality factor of the drive-mode above 2,500, which can also reduce these capacitive coupling by decreasing the drive voltage. The modulation-demodulation method through applying high-frequency carrier to the proof mass can also reduce these capacitive couplings.
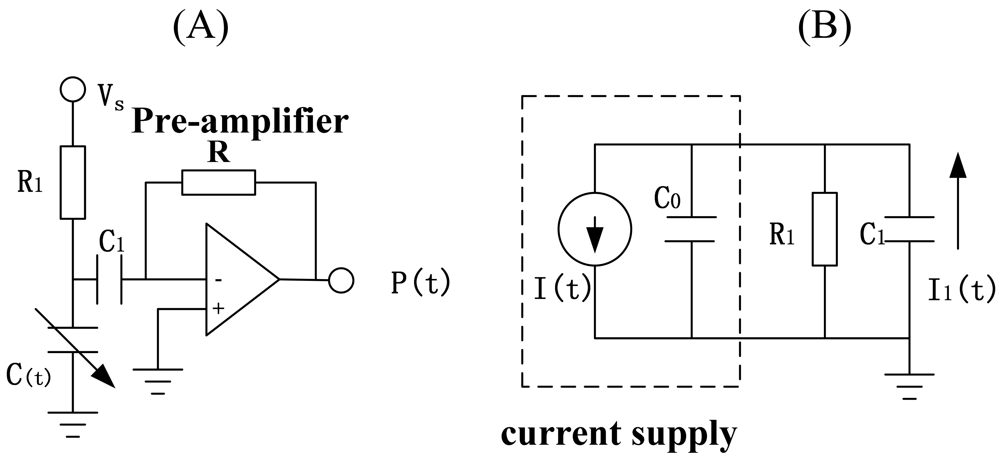
First, we need to extract the resonance signal of the drive-mode. The simplified interface circuitry is shown in
Figure 1.
Figure 2 show the details of the interface circuit and the equivalent circuit. Here in
Figure 2, C (t) is the alternating drive-sense capacitance, C(t)=C
0+ΔC, C
0 is constant capacitance. The part of signal sense can be equivalent to a current supply I(t) and a internal resistance C
0 [see
Figure 2(B)], where:
In
Equation (16), the differential of driving capacitance to displacement K
xc is a constant relating to the structure. The capacitance C
0 is very minute and generally has hundreds of fF, thus the impedance of C
0 is very large and we can ignore the influence of the impedance C
0. The resistance R
1 generally has a few MΩ, the capacitance C
1 hundreds of nF, ω/ 2ᴫ a few kHz (ω≈ω
nx), so R
1≫1/ωC
1, the output voltage P(t) is described by:
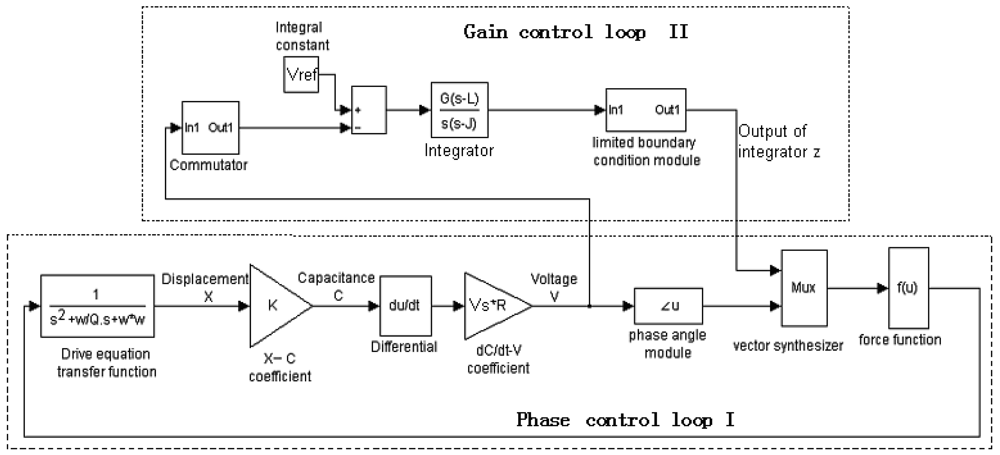
Figure 3 is the frame of the closed-loop driving. In this figure s is a complex variable. V
s, V
ref and V
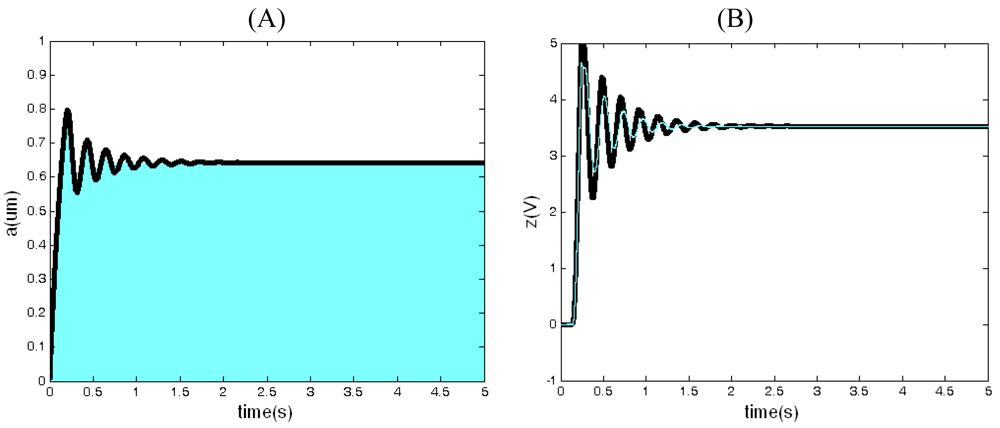
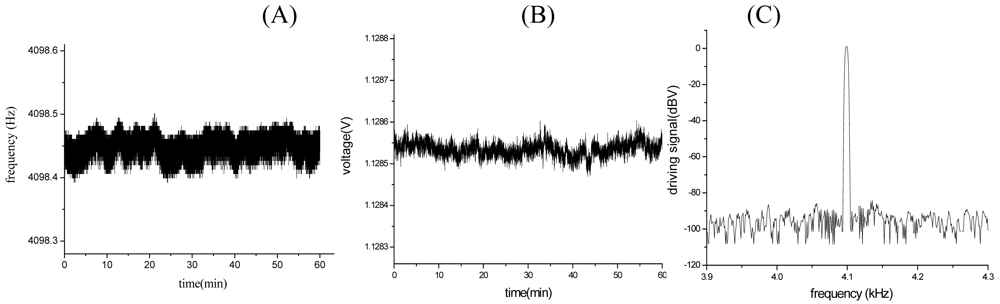
sup are the direct current biases. L and J are the zero and the pole of the integrator separately. G is the gain of the integrator. In order to improve the precision and the stability of the closed-loop driving, the Q-factor of the drive-mode should be increased (the SMG is executed in vacuum encapsulation), while the well closed-loop control should be achieved. The closed-loop control must meet such two conditions: 1. The phase of the whole loop θ=2nπ (n is an integer); 2. The gain of the whole loop A>1.
A new closed-loop drive scheme which decouples the phase and the gain of the closed-loop driving system is adopted in the SMG, so that the phase and the gain can be optimized, respectively. The gain of the whole closed-loop system is controlled by the branch circuit above, and the phase is controlled by the branch circuit below. These two branch circuits respectively fulfill the two conditions of closed-loop control, adjusting and optimizing the closed-loop parameter separately. The “voltage comparator” is the key component of the closed-loop driving. The output of the “voltage comparator”, with an invariable output amplitude, only reserves the phase information of the input signal, so the phase conditions of the closed-loop are isolated from the gain conditions. Except the drive mode of SMG and “voltage comparator”, with the suppose that the phase of the other parts is fixed, when the phase of the “voltage comparator” is changed, the vibrating frequency of the closed-loop system will depart from the resonant frequency of the proof mass, so the phase condition controls the frequency of the driving displacement. It is obvious that the gain branch controls the amplitude of the driving displacement. According to
Equations (34) and
(35) (See Section 5), ignoring the influence of the random processes n
1(t) and n
2(t), we can know that average amplitude
ā and average phase
φ̄ are decoupled, so the phase branch and the gain branch can be optimized respectively and the new closed-loop drive scheme is succeeded.
To make sure that the harmonic frequency of the closed-loop system equals, or gets close to the resonant frequency of the proof mass, that is to say, the phase of the whole loop θ = 2nπ(n is an integer). When ω
d=ω
nx, the phase-shift of the drive displacement x(t) comparing to the drive force F
e is -π/2(See
Equation (5)), the phase-shift of the output voltage of pre-amplifier P(t) comparing to drive displacement x(t) is -π/2 and the phase-shift of the output voltage of the “voltage comparator” V
cp(t) comparing to output voltage of preamplifier P(t) is −π. The other parts, which in fact all have tiny phase errors, have no phase-shifts, so the closed-loop control meets the phase conditions. In this way, it is hoped that the above closed-loop phase errors should be as tiny as possible. Various techniques are generally utilized in an effort to reduce closed-loop phase error, or drift, in servo circuits, such as amplifier circuits utilizing an operational amplifier. One such technique includes the addition of one or more zeros (i.e., a lead filter) in cascade with the open-loop gain of the operational amplifier in order to flatten the open-loop gain over a portion of the frequency band, generally resulting in only moderate closed-loop error reduction and also compromising stability. Another technique for reducing gain and phase errors is to increase the gain-bandwidth product associated with the operational amplifier. However, use of this technique is limited by the gain-bandwidth product of commercially available operational amplifiers as well as by the acceptable increased power dissipation associated with higher performance operational amplifiers. However, a Phase-Corrected Amplifier Circuit can be used to remove the closed-loop phase error [
13]. An amplifier circuit having a bandpass circuit in cascade with the forward loop gain is provided, with the bandpass circuit having a transfer function approximating one plus a bandpass characteristic, the passband of which corresponds to the information band. This arrangement increases the open-loop gain of the amplifier circuit around the information frequency without affecting the open-loop gain at DC and crossover so as to reduce phase and gain errors around the information frequency.
In
Figure 1, the drive capacitance and the electrical potential energy stored in the capacitance is described as:
where ε
0 is the permittivity, h the thickness of the comb fingers, x
0 the overlap length of the fingers, and d the width of the gap between fingers. According to
Figure 3, the electrostatic drive force is described by:
where
is the differential of driving capacitance to displacement, the z(t) is a DC and V
cp(t) is a AC with the frequency near the resonant frequency ω
nx. The first term of
Equation (20) is a constant and does not contribute to the oscillating driving force. Since the amplitude of the AC driving voltage is chosen to be much smaller than the bias voltage, the third term of
Equation (20) is much smaller than the second term and can be neglected. Therefore, under proper bias, the driving force is approximately proportional to the AC driving voltage.
According to
Figure 3, the drive-mode of the SMG is modeled as a second-order spring-mass-damper system with a dynamic behavior described by:
where F
n(u) is electrostatic drive force
, and suppose z(t)≥0.
Simplifying the integrator (See
Figure 3) into the basic integral function, so:
i.e.:
where |
ẋ| is modulus of the driving velocity and:
So the output of the “voltage comparator” is:
In summary, the entire closed-loop driving system, shown in
Figure 3, are described by
Equations (24)∼
(25):
where R
eq is equivalent damper.
Equations (24) and
(25) show the closed-loop system model. With the ignorance of the influence of the random process n(t),
Equation (24) shows a free spring-mass-damper oscillating system and
Equation (25) shows the control principle of the integrator. The closed-loop system reduces the system damper R
eq through adjusting the output of the integrator z(t). When the equivalent damper R
eq is bigger than the zero(e.g.R
eq>0), the gain control loop reduces the output of the integrator z(t) and then the equivalent damper R
eq will decrease near the zero (R
eq≈0,
is inverse-phase with K
xc). When the equivalent damper R
eq is smaller than the zero (e.g.R
eq<0), the gain control loop enhances the output of the integrator z(t) and thus, the equivalent damper will increase near the zero (R
eq≈0). So the closed-loop system shows approximately an undamped-free vibration with the invariable amplitude and frequency(e.g. the resonant frequency ω
nx). However, the random process n(t) will influence the stability of the driving amplitude and frequency.
5. Stochastic Averaging of the Gyroscope Dynamics
After the vacuum encapsulation, the quality factor of the drive-mode Q
x becomes very big. The drive-mode of the SMG can be equivalent to a band-pass filter. Only the displacement with the resonant frequency ω
nx can be magnified and the other harmonics are attenuated greatly. So the transient displacement can be simplified into a pure sin component. In order to analyze the transient behavior of the system, the driving displacement of the SMG is defined as [
14]:
where a(t) is the amplitude, and φ(t) is the phase of the driving displacement signal respectively.
Differentiating
Equation (26) with respect to time gives the velocity:
One of the equations used to determine
a and
φ is obtained by assuming that the sum of the last two terms can be set equal to zero:
Thus, the velocity equation becomes:
The acceleration is obtained by differentiating
Equation (28) with respect to time:
It should be noted that
Equations (31)∼
(33) are the exact differential equations describing the evolution of the amplitude and phase of the driving displacement, as well as that of the output states of the integrator. However, these equations are difficult to analyze because they are substantially non-autonomous. It is evident that instantaneous phase ω
nxt evolves much faster than the other variables, such as
a, φ, z and functions sin(ω
nxt+
φ) and cos(ω
nxt+
φ) are almost periodic. Within a period of these sinusoidal functions, variables other than ω
nxt change very little. Hence, it is possible to apply the averaging method to the non-autonomous system described by
Equations (31)∼
(33) and approximate it by an autonomous system [
14-
15].
As pointed out above, instantaneous phase ω
nxt is regarded as an independent variable and the differential equations
Equations (31)∼
(33) are averaged, with respect to ω
nxt, over the interval [-π, π]. The averaged autonomous equations are:
where the bars denote averaged variables. The random processes n
1(t) and n
2(t) are independent white noise with the same intensity as n (t) [
10].
Equations (34)∼
(36) describe approximately how the displacement amplitude and phase evolve with time. According to
Equations (34) and
(35), it is evident that average amplitude
ā and average phase
φ̄ are decoupled – when one of them is changed, the other does not change, so the phase branch and the gain branch can be optimized respectively.
Ignoring the influence of the random processes n
1(t) and n
2(t), the equilibrium of the averaged system described by
Equations (34)∼
(36) is:
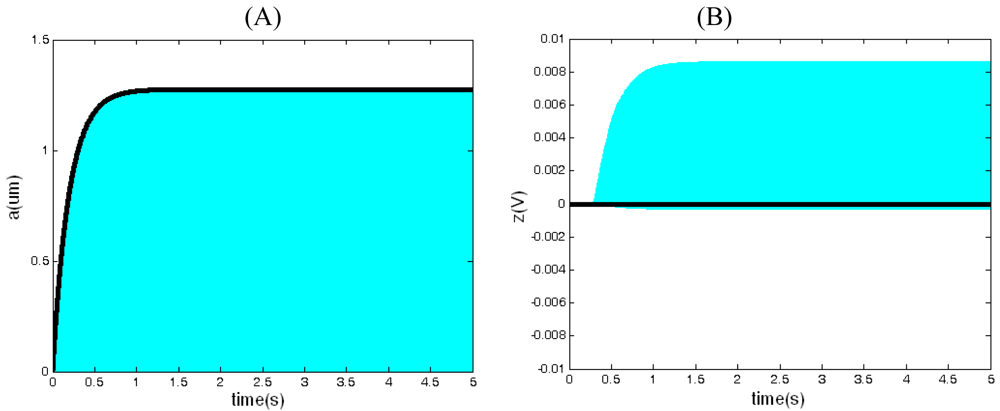
When the power is switched on, the system stabilizes finally in equilibrium. According to
Equation (37), it is evident that the equilibrium of the average amplitude
ā
o is independent from the quality factor Q
x, so the change of quality factor resulting from the variety of temperature and pressure does not impact on the equilibrium of the average amplitude
ā
o, which is very important in the practical application. The speciality of this system is obviously different from the literature [
16].
Ignoring the influence of the random processes n
1(t) and n
2(t), the Jacobian matrix of the nonlinear dynamic system of
Equations (34)∼
(36) at equilibrium is:
and its characteristic equation is:
where
γ is the variable of the characteristic equation. All the eigenvalues of the linearized averaged system are asymptotically stable, if and only if all coefficients is positive. It is evident
Equation (40) satisfies this condition because
is inverse-phase with K
xc. In order to make sure that the square root is in existence, the inequation hereinafter must be satisfied:
i.e.:
where the V
ref is the referring DC voltage used as a reference to the amplitude of the pre-amplifier output voltage. The V
refo is the criterion voltage. When V
ref < V
refo, the gain control branch works normally. When V
ref >V
refo, the gain control branch loses the control ability. Because the
Equations (34)∼
(36) are extremely complex, the averaged system is linearized in the equilibrium, i.e.:
where
ā
n =
ā −
ā
o, z̄
n =
z̄ −
z̄
o.
ā
n can be expressed in Laplace transform domain as:
where
,
Ā
n(
s) is Laplace transform of
ā
n, and
N1(
s) is Laplace transform of the
n1, so the steady-state spectral density for the noise component of the
ā
n is:
So the noise power spectrum is:
The RMS noise amplitude due to thermal noise is:
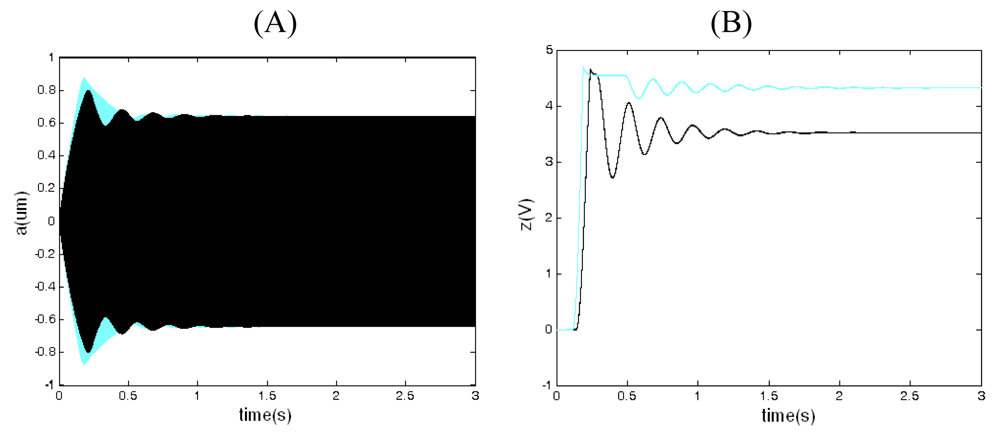
Comparing
Equation (14) with
Equation (47), we know the RMS noise amplitude due to thermal noise in the opened-loop driving is equal to that in the closed-loop driving, so the closed-loop driving does not reduce the RMS noise amplitude due to thermal noise. By the way, the RMS noise amplitude is independent from the quality factor Q
x.
According to
ā =
ā
o +
ā
n ≈
ā
o,
Equation (43) can be rewritten as:
where
ω̄
n is the noise frequency, so the power spectral density of the noise frequency
ω̄
n is
Suppose the work bandwidth is f
BHz, the noise power is:
The RMS noise frequency due to thermal noise is:
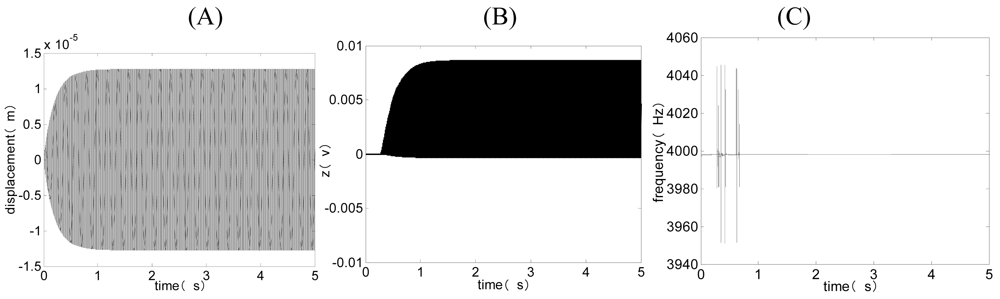
It is useful to reduce RMS noise frequency by increasing quality factor Qx and drive amplitude ā0.