Scale Issues in Remote Sensing: A Review on Analysis, Processing and Modeling
Abstract
:1. Introduction
2. The definition of scale and relevant terminologies
2.1. Notions of scales
- Observation scale can be called a “measurement scale”. It depends on the method or the characteristics of the instrument and can be thought of as measurement units (i.e., intervals or areas or volumes) at which data is measured or sampled. To remote sensing, the measurement scale refers to the description of resolution, time interval, spectral range, solid angle or polarization direction. As the limitation of data collection and storage capacity, the smaller measurement scale usually corresponds to the smaller geographic scale and vice versa.
- Modeling scale is the scale at which the model is built or derived in order to give reliable output. Both the measurement scale and the operational scale may influence the modeling scale. Observations sampled at a measurement scale are used as input for models, so the measurement scale must coincide with the modeling scale. If the measurement scale is smaller or larger than the modeling scale, it should be scaled. Again, a model needs to reveal the process; the modeling scale should also coincide with the operational scale. Similarly, it also needs to be scaled.
- Operational scale refers to the scale at which a certain process is supposed to operate. It can also be called the “scale of action”. For example, thunderstorms may happen in an area of dozens of square kilometers. The operational scale of thunderstorms may be dozens of kilometers. It can be defined either as spatial extent (the lifetime), period (cycle) or the correlation length (integral scale), depending on the nature of the process [5]. Here, if the operational scale is smaller than the modeling scale, the variability lower than the modeling scale may be lost and the process may not be observed or found.
- Geographic scale, which is also called “coverage”, refers to the spatial extent of research. It determines the biological organization level on which the surface property is observed, such as the leaves (a few centimeters), the canopy (10 to 100 m), the landscape (100 m to a few kilometers) or the region (about 100 km) [19]. A larger geographic scale study involves a larger spatial area, and a smaller geographic scale study only contains a smaller spatial area. The ratio between geographic scale and measurement scale often determines data volume and constrains storage and processing capacities.
- Policy scale is the scale at which the decisions are made or the policy is implemented [15]. For example, whether the crop yield of one specific village is reduced or not, may be judged on village level on the basis of one year. In order to infer a reliable conclusion, the policy scale should be larger than the operational scale.
- Cartographic scale is defined simply as the ratio between distance on the map and on the ground. It is often used to represent the spatial distribution of research results. Generally speaking, a smaller cartographic scale corresponds to a larger geographic scale and may show fewer instances of features or less detail when compared to a larger cartographic scale.
2.2. Characteristics of scales
2.3. Scale threshold and scale domain
2.4. Scaling and scale effects
3. Mechanism analyses of scale effects
3.1. Main causes of scale effects
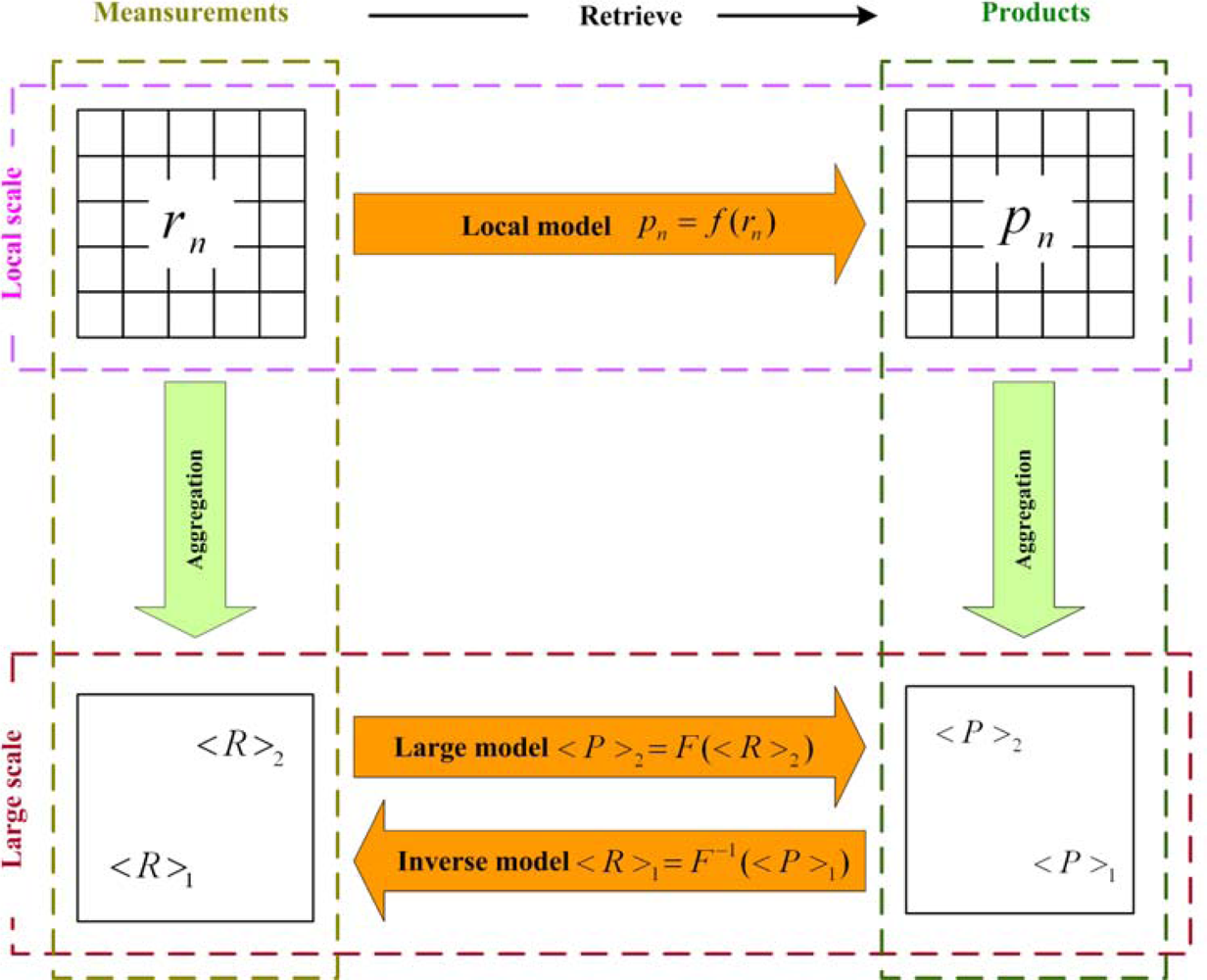
3.2. Effects of scale on the measurements, retrieval models and products
4. Quantitative descriptions of scale threshold and scale domain
4.1. Geographic variance method (GVM)
4.2. Wavelet transform method (WTM)
4.3. Local variance method (LVM)
4.4. Semivariogram based method (SVM)
4.5. Fractals method (FM)
5. Overview of general scaling methods
5.1. Scaling methods for measurements
5.2. The scaling methods for retrieval models
5.3. The scaling methods for products
6. Conclusions
Acknowledgments
References
- Goodchild, M.F.; Quattrochi, D.A. Introduction: Scale, Multiscaling, Remote Sensing, and GIS. In Scale in remote sensing and GIS; Quattrochi, D.A., Goodchild, M.F., Eds.; Lewis Publishers: Boca Raton, Fla, 1997; pp. 1–12. [Google Scholar]
- Marceau, D.J.; Hay, G.J. Remote sensing contributions to the scale issue. Can. J. Remote Sens 1999, 25, 357–366. [Google Scholar]
- Cao, C.Y.; Lam, N. Understanding the scale and resolution effects in remote sensing and GIS. In Scale in remote sensing and GIS; Quattrochi, D.A., Goodchild, M.F., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1997; pp. 57–72. [Google Scholar]
- Raffy, M. Change of Scale in Models of Remote Sensing : A General Method for Spatialisation of Models. Remote Sens. Environ 1992, 40, 101–112. [Google Scholar]
- Bloschl, G.; Sivapalan, M. Scale issues in hydrological modeling - A review. Hydrol. Processes 1995, 9, 251–290. [Google Scholar]
- Stewart, J.B.; Engman, E.T.; Feddes, R.A.; Kerr, Y.H. Scaling up in hydrology using remote sensing: Summary of a workshop. Int. J. Remote Sens 1998, 19, 181–194. [Google Scholar]
- Bloschl, G. Scaling issues in snow hydrology. Hydrol. Processes 1999, 13, 2149–2175. [Google Scholar]
- Raupach, M.R.; Finnigan, J.J. Scale issues in boundary - layer meteorology : surface energy balances in heterogeneous terrain. Hydrol. Processes 1995, 9, 589–612. [Google Scholar]
- Zhang, N.; Yu, Z.L.; Yu, G.R.; Wu, J.G. Scaling up ecosystem productivity from patch to landscape: a case study of Changbai Mountain Nature Reserve, China. Landsc. Ecol 2007, 22, 303–315. [Google Scholar]
- Xie, J.; Liu, T.; Wei, P.; Jia, Y.; Luo, C. Ecological application of wavelet analysis in the scaling of spatial distribution patterns of Ceratoides ewersmanniana. Acta Ecol. Sin 2007, 27, 2704–2714. [Google Scholar]
- Malenovsky, Z.; Bartholomeus, H.M.; Acerbi-Junior, F.W.; Schopfer, J.T.; Painter, T.H.; Epema, G.F.; Bregt, A.K. Scaling dimensions in spectroscopy of soil and vegetation. Int. J. Appl. Earth Obs. Geoinf 2007, 9, 137–164. [Google Scholar]
- Openshaw, S. The Modifiable Areal Unit Problem; Geo Books: Norwich, United Kingdom, 1984. [Google Scholar]
- Lam, N.S.-N.; Quattrochi, D.A. On the issues of scale, resolution, and fractal analysis in the mapping sciences. Prof. Geogr 1992, 44, 88–98. [Google Scholar]
- Bian, L. Multiscale nature of spatial data in scaling up environmental models. In Scale in remote sensing and GIS; Quattrochi, D.A., Goodchild, M.F., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1997; pp. 13–26. [Google Scholar]
- Bierkens, M.F.P.; Finke, P.A.; De Willigen, P. Upscaling and downscaling methods for environmental research; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Pelgrum, H. Spatial Aggregation of Land Surface Characteristics, PhD thesis,. Wageningen, University, Netherlands, 2000.
- Hufkens, K.; Bogaert, J.; Dong, Q.H.; Lu, L.; Huang, C.L.; Ma, M.G.; Che, T.; Li, X.; Veroustraete, F.; Ceulemans, R. Impacts and uncertainties of upscaling of remote-sensing data validation for a semi-arid woodland. J. Arid Environ 2008, 72, 1490–1505. [Google Scholar]
- Liang, S. Quantitative remote sensing of land surfaces; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Quantifying spatial heterogeneity at the landscape scale using variograrn models. Remote Sens. Environ 2006, 103, 81–96. [Google Scholar]
- Skoien, J.O.; Bloschl, G.; Western, A.W. Characteristic space scales and timescales in hydrology. Water Resour. Res. 2003, 39, SWC11.1–SWC11.19. [Google Scholar]
- Tian, Y.H.; Wang, Y.J.; Zhang, Y.; Knyazikhin, Y.; Bogaert, J.; Myneni, R.B. Radiative transfer based scaling of LAI retrievals from reflectance data of different resolutions. Remote Sens. Environ 2002, 84, 143–159. [Google Scholar]
- Liu, Y.B.; Hiyama, T.; Yamaguchi, Y. Scaling of land surface temperature using satellite data: A case examination on ASTER and MODIS products over a heterogeneous terrain area. Remote Sens. Environ 2006, 105, 115–128. [Google Scholar]
- Zhang, R.H.; Li, Z.L.; Tang, X.Z.; Sun, X.M.; Su, H.B.; Zhu, C.; Zhu, Z.L. Study of emissivity scaling and relativity of homogeneity of surface temperature. Int. J. Remote Sens 2004, 25, 245–259. [Google Scholar]
- Chehbouni, A.; Watts, C.; Kerr, Y.H.; Dedieu, G.; Rodriguez, J.C.; Santiago, F.; Cayrol, P.; Boulet, G.; Goodrich, D.C. Methods to aggregate turbulent fluxes over heterogeneous surfaces: application to SALSA data set in Mexico. Agric. For. Meteorol 2000, 105, 133–144. [Google Scholar]
- Li, X.; Strahler, A.H. Geometric-Optical modeling of a conifer forest canopy. IEEE Trans. Geosci. Remote Sens 1985, GE-23, 705–721. [Google Scholar]
- Albers, B.J.; Strahler, A.H.; Li, X.O.; Liang, S.L.; Clarke, K.C. Radiometric Measurements of Gap Probability in Conifer Tree Canopies. Remote Sens. Environ 1990, 34, 179–192. [Google Scholar]
- Li, X.W.; Wang, J.D.; Strahler, A.H. Apparent reciprocity failure in directional reflectance of structured surfaces. Prog. Nat. Sci 1999, 9, 747–752. [Google Scholar]
- Li, X.W.; Strahler, A.H.; Friedl, M.A. A conceptual model for effective directional emissivity from nonisothermal surfaces. IEEE Trans. Geosci. Remote Sens 1999, 37, 2508–2517. [Google Scholar]
- Su, L.; Li, X.; Liang, S.; Strahler, A.H. Simulation of scaling effects of thermal emission from non-isothermal pixels with the typical three-dimensional structure. Int. J. Remote Sens 2003, 24, 3743–3753. [Google Scholar]
- Wu, J.; Jelinski, D.E.; Luck, M.; Tueller, P.T. Multiscale Analysis of Landscape Heterogeneity: Scale Variance and Pattern Metrics. Geogr. Inf. Sci 2000, 6, 6–19. [Google Scholar]
- Chen, J.M. Spatial scaling of a remotely sensed surface parameter by contexture. Remote Sens. Environ 1999, 69, 30–42. [Google Scholar]
- Chen, J.M.; Pavlic, G.; Brown, L.; Cihlar, J.; Leblanc, S.G.; White, H.P.; Hall, R.J.; Peddle, D.R.; King, D.J.; Trofymow, J.A.; Swift, E.; Van der Sanden, J.; Pellikka, P.K.E. Derivation and validation of Canada-wide coarse-resolution leaf area index maps using high-resolution satellite imagery and ground measurements. Remote Sens. Environ 2002, 80, 165–184. [Google Scholar]
- Hu, Z.; Islam, S. A framework for analyzing and designing scale invariant remote sensing algorithms. IEEE Trans. Geosci. Remote Sens 1997, 35, 747–755. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Influence of landscape spatial heterogeneity on the non-linear estimation of leaf area index from moderate spatial resolution remote sensing data. Remote Sens. Environ 2006, 105, 286–298. [Google Scholar]
- Western, A.W.; Bloschl, G. On the spatial scaling of soil moisture. J. Hydrol 1999, 217, 203–224. [Google Scholar]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ 1990, 34, 75–91. [Google Scholar]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ 1984, 16, 125–141. [Google Scholar]
- Smolander, S.; Stenberg, P. A method to account for shoot scale clumping in coniferous canopy reflectance models. Remote Sens. Environ 2003, 88, 363–373. [Google Scholar]
- Hu, Z.L.; Islam, S. Effects of spatial variability on the scaling of land surface parameterizations. Boundary Layer Meteorol 1997, 83, 441–461. [Google Scholar]
- Liang, S.L.; Fang, H.L.; Chen, M.Z.; Shuey, C.J.; Walthall, C.; Daughtry, C.; Morisette, J.; Schaaf, C.; Strahler, A. Validating MODIS land surface reflectance and albedo products: methods and preliminary results. Remote Sens. Environ 2002, 83, 149–162. [Google Scholar]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ 2006, 105, 271–285. [Google Scholar]
- Brunsell, N.A.; Gillies, R.R. Scale issues in land-atmosphere interactions: implications for remote sensing of the surface energy balance. Agric. For. Meteorol 2003, 117, 203–221. [Google Scholar]
- Sridhar, V.; Elliott, R.L.; Chen, F. Scaling effects on modeled surface energy-balance components using the NOAH-OSU land surface model. J. Hydrol 2003, 280, 105–123. [Google Scholar]
- El Maayar, M.; Chen, J.M. Spatial scaling of evapotranspiration as affected by heterogeneities in vegetation, topography, and soil texture. Remote Sens. Environ 2006, 102, 33–51. [Google Scholar]
- Sasai, T.; Okamoto, K.; Hiyama, T.; Yamaguchi, Y. Comparing terrestrial carbon fluxes from the scale of a flux tower to the global scale. Ecol. Model 2007, 208, 135–144. [Google Scholar]
- Thorgeirsson, H.; Soegaard, H. Simulated carbon dioxide exchange of leaves of barley scaled to the canopy and compared to measured fluxes. Agric. For. Meteorol 1999, 98–99, 479–489. [Google Scholar]
- Hu, Z.L.; Islam, S.; Cheng, Y.Z. Statistical characterization of remotely sensed soil moisture images. Remote Sens. Environ 1997, 61, 310–318. [Google Scholar]
- Manfreda, S.; McCabe, M.F.; Fiorentino, M.; Rodriguez-Iturbe, I.; Wood, E.F. Scaling characteristics of spatial patterns of soil moisture from distributed modelling. Adv. Water Res 2007, 30, 2145–2150. [Google Scholar]
- Oldak, A.; Pachepsky, Y.; Jackson, T.J.; Rawls, W.J. Statistical properties of soil moisture images revisited. J. Hydrol 2002, 255, 12–24. [Google Scholar]
- Das, N.N.; Mohanty, B.P. Temporal dynamics of PSR-based soil moisture across spatial scales in an agricultural landscape during SMEX02: A wavelet approach. Remote Sens. Environ 2008, 112, 522–534. [Google Scholar]
- Jiang, Z.Y.; Huete, A.R.; Chen, J.; Chen, Y.H.; Li, J.; Yan, G.J.; Zhang, X.Y. Analysis of NDVI and scaled difference vegetation index retrievals of vegetation fraction. Remote Sens. Environ 2006, 101, 366–378. [Google Scholar]
- Tarnavsky, E.; Garrigues, S.; Brown, M.E. Multiscale geostatistical analysis of AVHRR, SPOT-VGT, and MODIS global NDVI products. Remote Sens. Environ 2008, 112, 535–549. [Google Scholar]
- Fernandes, R.A.; Miller, J.R.; Chen, J.M.; Rubinstein, I.G. Evaluating image-based estimates of leaf area index in boreal conifer stands over a range of scales using high-resolution CASI imagery. Remote Sens. Environ 2004, 89, 200–216. [Google Scholar]
- Jin, Z.; Tian, Q.; Chen, J.M.; Chen, M. Spatial scaling between leaf area index maps of different resolutions. J. Environ. Manage 2007, 85, 628–637. [Google Scholar]
- Simic, A.; Chen, J.M.; Liu, J.; Csillag, F. Spatial scaling of net primary productivity using subpixel information. Remote Sens. Environ 2004, 93, 246–258. [Google Scholar]
- Turner, D.P.; Ollinger, S.; Smith, M.L.; Krankina, O.; Gregory, M. Scaling net primary production to a MODIS footprint in support of Earth observing system product validation. Int. J. Remote Sens 2004, 25, 1961–1979. [Google Scholar]
- Chasmer, L.; Barr, A.; Hopkinson, C.; McCaughey, H.; Treitz, P.; Black, A.; Shashkov, A. Scaling and assessment of GPP from MODIS using a combination of airborne lidar and eddy covariance measurements over jack pine forests. Remote Sens. Environ 2009, 113, 82–93. [Google Scholar]
- Ma, Lingling; Li, Chuanrong; Tang, Bohui; Tang, Lingli; Bi, Yuyun; Zhao-Liang, L. Impact of Spatial LAI Heterogeneity on Estimate of Directional Gap Fraction from SPOT-Satellite Data. Sensors 2008, 8, 3767–3779. [Google Scholar]
- Moellering, H.; Tobler, W.R. Geographical variances. Geog. Anal 1972, 4, 34–64. [Google Scholar]
- Percival, D.P. On Estimation of the Wavelet Variance. Biometrika 1995, 82, 619–631. [Google Scholar]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ 1987, 21, 311–332. [Google Scholar]
- Artan, G.A.; Neale, C.M.U.; Tarboton, D.G. Characteristic length scale of input data in distributed models: implications for modeling grid size. J. Hydrol 2000, 227, 128–139. [Google Scholar]
- Wackernagel, H. Multivariate geostatistics : an introduction with applications; Springer: Berlin; New York, 2003. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F.; Morisette, J. Multivariate quantification of landscape spatial heterogeneity using variogram models. Remote Sens. Environ 2008, 112, 216–230. [Google Scholar]
- Mandelbrot, B.B. How long is the coast of Britain? Statistical self-similarity and fractal dimension. Sci 1967, 156, 636–638. [Google Scholar]
- Raffy, M. Autosimilarity, change of scale and remotely sensed parameters. In Remote Sensing from Space: Physical Aspects and Modelling; Cepadues-Editions: Centre national d’etudes spatiales, France, 1988; pp. 421–481. [Google Scholar]
- Xia, Z.G.; Clarke, K.C. Approaches to scaling of geo-spatial data. In Scale in remote sensing and GIS; Quattrochi, D.A., Goodchild, M.F., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1997; pp. 309–360. [Google Scholar]
- Raffy, M.; Gregoire, C. Semi-empirical models and scaling: a least square method for remote sensing experiments. Int. J. Remote Sens 1998, 19, 2527–2541. [Google Scholar]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model 1999, 124, 99–119. [Google Scholar]
- Hoedjes, J.C.B.; Chehbouni, A.; Jacob, F.; Ezzahar, J.; Boulet, G. Deriving daily evapotranspiration from remotely sensed instantaneous evaporative fraction over olive orchard in semi-arid Morocco. J. Hydrol 2008, 354, 53–64. [Google Scholar]
- Rastetter, E.B.; King, A.W.; Cosby, B.J.; Hornberger, G.M.; Oneill, R.V.; Hobbie, J.E. Aggregating Fine-Scale Ecological Knowledge to Model Coarser-Scale Attributes of Ecosystems. Ecol. Appl 1992, 2, 55–70. [Google Scholar]
- Friedl, M.A.; Michaelsen, J.; Davis, F.W.; Walker, H.; Schimel, D.S. Estimating Grassland Biomass and Leaf-Area Index Using Ground and Satellite Data. Int. J. Remote Sens 1994, 15, 1401–1420. [Google Scholar]
- Wylie, B.K.; Meyer, D.J.; Tieszen, L.L.; Mannel, S. Satellite mapping of surface biophysical parameters at the biome scale over the North American grasslands - A case study. Remote Sens. Environ 2002, 79, 266–278. [Google Scholar]
- Martinez, B.; Garcia-Haro, F.J.; Camacho-de Coca, F. Derivation of high-resolution leaf area index maps in support of validation activities: Application to the cropland Barrax site. Agric. For. Meteorol 2009, 149, 130–145. [Google Scholar]
- Hu, Z.L.; Islam, S. Effects of subgrid-scale heterogeneity of soil wetness and temperature on grid-scale evaporation and its parametrization. Int. J. Climatol 1998, 18, 49–63. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F. Modeling temporal changes in surface spatial heterogeneity over an agricultural site. Remote Sens. Environ 2008, 112, 588–602. [Google Scholar]
- Braswell, B.H.; Hagen, S.C.; Frolking, S.E.; Salas, W.A. A multivariable approach for mapping sub-pixel land cover distributions using MISR and MODIS: Application in the Brazilian Amazon region. Remote Sens. Environ 2003, 87, 243–256. [Google Scholar]
- Dubayah, R.; Wood, E.F.; Lavallee, D. Multiscaling Analysis in Distributed Modeling and Remote Sensing: An Application Using Soil Moisture. In Scale in remote sensing and GIS; Quattrochi, D.A., Goodchild, M.F., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1997; pp. 93–112. [Google Scholar]
- Hu, Z.L.; Chen, Y.Z.; Islam, S. Multiscaling properties of soil moisture images and decomposition of large- and small-scale features using wavelet transforms. Int. J. Remote Sens 1998, 19, 2451–2467. [Google Scholar]
- Brunsell, N.A.; Gillies, R.R. Determination of scaling characteristics of AVHRR data with wavelets: application to SGP97. Int. J. Remote Sens 2003, 24, 2945–2957. [Google Scholar]
- Viney, N.R.; Sivapalan, M. A framework for scaling of hydrologic conceptualizations based on a disaggregation-aggregation approach. Hydrol. Processes 2004, 18, 1395–1408. [Google Scholar]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ 2003, 85, 429–440. [Google Scholar]
| Meaning | Description | Remarks |
|---|---|---|
| Observation scale | The measurement units at which data is measured or sampled | Referring to the description of resolution, time interval, spectral range, solid angle or polarization direction. |
| Modeling scale | The scale at which the model is built or derived | In order to better reveal the process, the modeling scale should be coincided with both the observation scale and the operational scale. |
| Operational scale | The scale of action at which a certain process is supposed to operate. | Depending on the nature of the process. Variability lower than modeling scale may be lost if the operational scale is smaller than the modeling scale. |
| Geographic scale | The spatial extent of research | A larger geographic scale study involves a larger spatial area and a smaller geographic scale study only contains a smaller spatial area. |
| Policy scale | The scale at which the decisions are made or the policy is implemented | In order to infer a reliable conclusion, the policy scale should be larger than the operational scale. |
| Cartographic scale | The ratio between distance on the map and on the ground | A smaller cartographic scale corresponds to a larger geographic scale and may show fewer instances of features or less detail. |
| Methods | Advantages | Disadvantages | References |
|---|---|---|---|
| GVM |
| Its validity remains unclear and more analyses are needed. | [3] [30] [59] |
| WTM | It can investigate features of interest in the data set at an appropriate scale and find the length scale of the variability. |
| [16] [60] |
| LVM | The principle is easy to be understood. |
| [61] |
| SVM |
| The second order stationarity hypothesis should be satisfied. | [19] [63] |
| FM |
| No agreement has been reached on the definition of fractal dimension which can be used to determine the characteristic scale. | [13] [67] |
| Categories | Methods | Advantages | Disadvantages | Ref. |
|---|---|---|---|---|
| Scaling methods for measurements | AWM |
|
| [22] |
| FRPM |
|
| [15] | |
| Scaling methods for retrieval models | CGM |
|
| [4] [16] [68] |
| PSM |
|
| [11] [21] | |
| Scaling methods for products | ERM |
|
| [53] [74] |
| TSEM |
|
| [16] [33] [34] | |
| CPM |
|
| [31] [55] [44] [54] | |
| SFSM |
|
| [78] [47] [80] |
© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wu, H.; Li, Z.-L. Scale Issues in Remote Sensing: A Review on Analysis, Processing and Modeling. Sensors 2009, 9, 1768-1793. https://doi.org/10.3390/s90301768
Wu H, Li Z-L. Scale Issues in Remote Sensing: A Review on Analysis, Processing and Modeling. Sensors. 2009; 9(3):1768-1793. https://doi.org/10.3390/s90301768
Chicago/Turabian StyleWu, Hua, and Zhao-Liang Li. 2009. "Scale Issues in Remote Sensing: A Review on Analysis, Processing and Modeling" Sensors 9, no. 3: 1768-1793. https://doi.org/10.3390/s90301768




