A Tabu Search WSN Deployment Method for Monitoring Geographically Irregular Distributed Events
Abstract
:1. Introduction
2. Related Works
3. Problem Statement
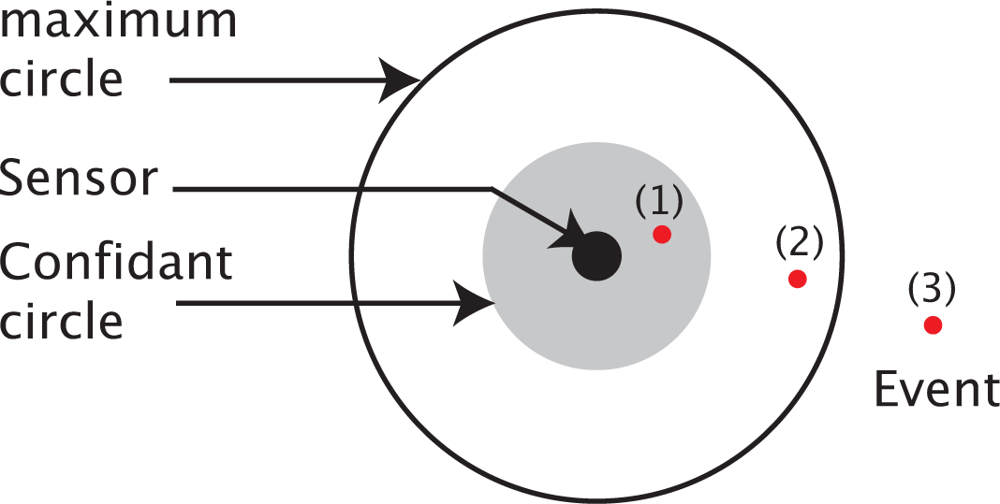
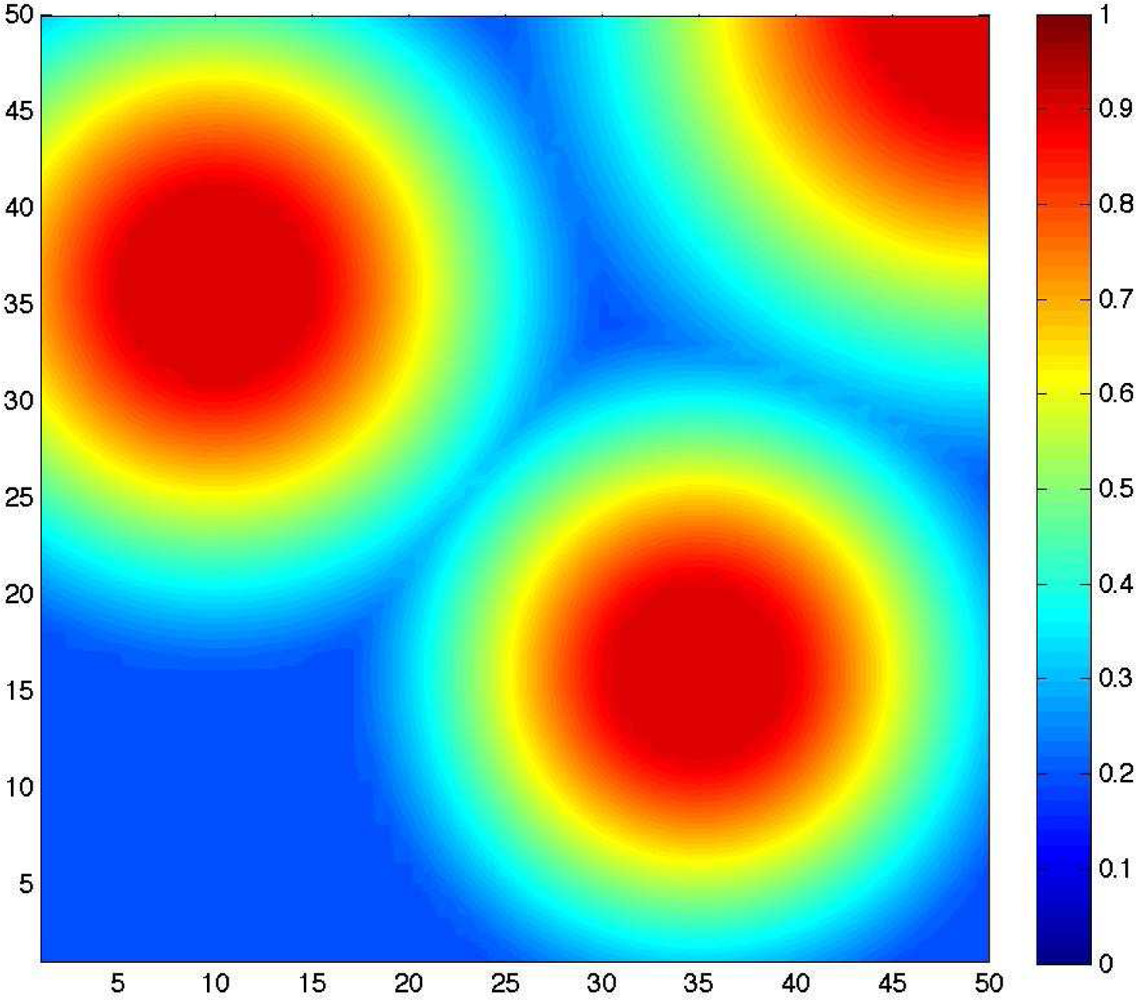
3.2. Problem Formalization
- Minimize the number of deployed sensors needed to satisfy the following two constraints (2 and 3).
- For each point p(i,j) ∈ 𝒜, minimize the difference between the required detection probability threshold r(i,j), and the after-deployment resulting detection probability (i,j).
- Ensure the wireless communication network connectivity.
4. Proposal: Tabu Search Approach
4.1. Resolution without communication connectivity constraint
- InitializationThe convergence of Tabu Search method depends on the judicious choice of the initial solution (s0). Ideally, the first solution has to be close to the optimal one, otherwise, since the maximum number of iterations is fixed, the algorithm may stop before reaching the best solution.We consider that the decision, D(x, y), of deploying a sensor in a point p(x,y) is a random variable, which follows a Bernoulli distribution with parameter α(x,y). The binary form of the decision rule motivates the choice of the Bernoulli law. Precisely, D(x, y) can assume a value of 1 with a probability of α(x,y) and the value of 0 with a probability of (1 − α(x,y)).The parameter α(x,y), associated to a point p(x,y), is chosen as the percentage of the points located in the vicinity of p(x,y) and not receiving the required probabilities of detection. The vicinity, denoted E(x,y), is defined as the set of neighbor points located inside the maximum monitoring circle of a sensor which would be placed in p(x,y). Formally,Here 1{cond} is the indicating function, which is equal to 1 if the condition cond is true and 0 otherwise. The initialization stage of our Tabu Search approach follows these steps:
- Step 1: The initial Tabu Search solution is started assuming zero deployed sensors. Thus, ∀p(x,y) ∈ 𝒜, Bernoulli parameters are computed using equation 3 with (x,y) = 0.
- Step 2: Generate a list, Linit, including all points of 𝒜. Linit is a decreasingly sorted list of points according to their Bernoulli parameters.
- Step 3: In Linit, select the point p(x,y) with the highest Bernoulli parameter, and remove it from the list. If the actual detection probability (x,y) associated to p(x,y) is lower than r(x,y), then a decision to deploy a sensor in p(x,y) is randomly generated through a Bernoulli decision rule with parameter α(x,y).
- Step 4: If the Bernoulli decision is to deploy a sensor (D(x, y) = 1), then (1) the probabilities of detection for all points in the vicinity of p(x,y) (the set E(x,y)) are recomputed. and (2) Linit is updated (sorted).
- Step 5: If Linit is not empty, go back to Step 3.
When the stop criterion of step 5 is satisfied, the resulting positions of deployed sensors are considered as the initial solution s0. The latter one is saved in the algorithm’s memory, called the Tabu List. In the remaining, we will refer to this list as T. The goal of the Tabu list is not to block the method on a local minimum of the cost function. - Neighborhood exploration functionAfter the initialization stage, a Tabu Search method executes N times the neighborhood exploration stage. Here, N is a chosen fixed parameter, which must be set in order to limit the number of Tabu Search iterations and to obtain a satisfactory (near to the optimal) solution.During the nth iteration of the neighborhood exploration stage, a given number V of possible neighbors of the solution selected in the previous iteration, noted sn−1, are generated and evaluated. Neighboring solutions are possible solutions which can be reached from sn−1 by a basic transformation. Solutions which are present in the Tabu List T are considered unreachable neighbors.We propose two neighboring generation methods, namely Suppression oriented stage (Hsupp) and Additional oriented stage (Hadd). These two methods alternate in the successive iterations of our Tabu Search approach in order to determine the set V. Both stages are detailed hereafter.
- Suppression oriented stage (Hsupp):The aim of this stage is to suppress some sensors among those deployed in over-covered areas. The method proceeds with the following steps:
- – Step 1’: Compute the Bernoulli parameters for all p(x,y) ∈ 𝒜 using the equation 4 and assuming the deployment obtained in the last Tabu Search iteration.
- – Step 2’: Generate a list, Lsupp, including all the points of 𝒜 where a sensor is deployed (D(x, y) = 1). The list is then decreasingly sorted according to the resulting Bernoulli parameters.
- – Step 3’: In Lsupp, select and remove the point p(x,y) with the highest Bernoulli parameter, and randomly generated the decision to suppress the sensor in p(x,y) through a Bernoulli decision rule with parameter β(x,y).
- – Step 4’: If the Bernoulli decision is to suppress the sensor (D(x, y) = 0), then the probabilities of detection for all points in the vicinity of p(x,y) are recomputed. In this case, the list Lsupp is updated (sorted) with the new values of the Bernoulli parameters associated to each point in Lsupp.
- – Step 5’: If Lsupp is not empty, go back to Step 3’.
Once the stop criteria on step 5’ is satisfied, the next Tabu Search iteration alternates toward an additional stage. - Additional oriented stage (Hadd):The aim of this stage is to add more sensors to the actual deployed ones in under-covered areas. The execution is very similar to the initialization stage, except Step 1 and Step 2 are replaced by the following steps:
- – Step 1”: Compute the Bernoulli parameters for all p(x,y) ∈ 𝒜 using the equation 3 and assuming the deployment obtained in the last Tabu Search iteration.
- – Step 2”: Generate a list Ladd including all the points of 𝒜 where a sensor is not deployed. The list one is then decreasingly sorted according to the resulting Bernoulli parameters.
Steps 3, 4 and 5, as detailed in initialization stage, are repeatedly executed until that the list Ladd is empty.
- Cost function and selection of new solutionAfter the neighborhood exploration (a suppression or an additional oriented stage) during the nth iteration, an elected solution sn must be chosen among the V explored candidates. This solution (which cannot be in the Tabu list T) is the one which provided by minimizing a given cost function F. The cost function reflects two objectives of the optimization problem described in section 3.2., minimize the number of deployed sensors and reduce the gap between the generated and requested event detection probabilities. The first objective could be quantified by counting the number of deployed sensors. Formally, as defined in section D(x, y) = 1, if a sensor is deployed in the point p(x,y). Otherwise, D(x, y) = 0. In order to minimize the cost function, F includes the following term:The second objective is integrated into the cost function through the following penalty function:Here [r(x,y) − (x,y)]+ denotes the projection of r(x,y) − (x,y) in IR +. Formally,According to the expression of penalty function, a successful deployment solution should lead to obtain detection probabilities higher than (or ideally equal to) the required detection thresholds. If it is not satisfied, the penalty function value translates how far is the solution to the required thresholds. This is exactly the second objective of the optimization problem.From the above objective expressions, the authors define two cost functions Fsupp and Fadd. The function Fsupp is used to choose the best next iteration solution in the case of a suppression oriented stage. The function Fsupp is formulated using only the equation 6. On the other hand, the cost function Fadd is used in the case of additional oriented stage. In this case, the two both terms associated to each objective of optimization problem are integrated into the cost function through the following additive expression:

4.2. Extension: Wireless Communication Network Connectivity
- Initialization stageCompared to the initialization stage described in section 4.1., the new version differs in the fact that once the Bernoulli decision to deploy the first sensor is made, the only points which will be tested (i.e. Bernoulli decision to deploy or not to deploy a sensor) are those which are located inside the communication range Rc of any deployed sensor. The connectivity is thus guaranteed by construction (gradually).Moreover, the selection order of the cell to be tested follows a decreasing order of the difference between the requested and the generated detection probabilities. That is, the next tested point is p(i,j) = maxp(x,y)∈ ((x,y) − r(x,y)), where denotes the set of points of 𝒜 which have not been tested yet at this stage.The positions of the resulting deployed sensors are considered as the initial solution s0. The latter one is saved in the algorithm’s memory (Tabu List).
- Selection of new solutionAfter the neighborhood exploration (a suppression or an addition oriented stage) during the nth iteration, an elected solution sn must be chosen among the V (size of the neighborhood) explored candidates. For each candidate, say C, we construct the graph of connectivity, denoted G(V, E). Here, V is the vertices set. The latter one is exclusively composed of points where, according to solution C, a sensor will be deployed. Moreover, E is the edges set. Formally,In the V solutions generated by the suppression stage, we eliminate the ones where the resulting communication graph G is not connected. Among the remaining candidates, the elected solution, sn, is the one which minimizes a given cost function F.
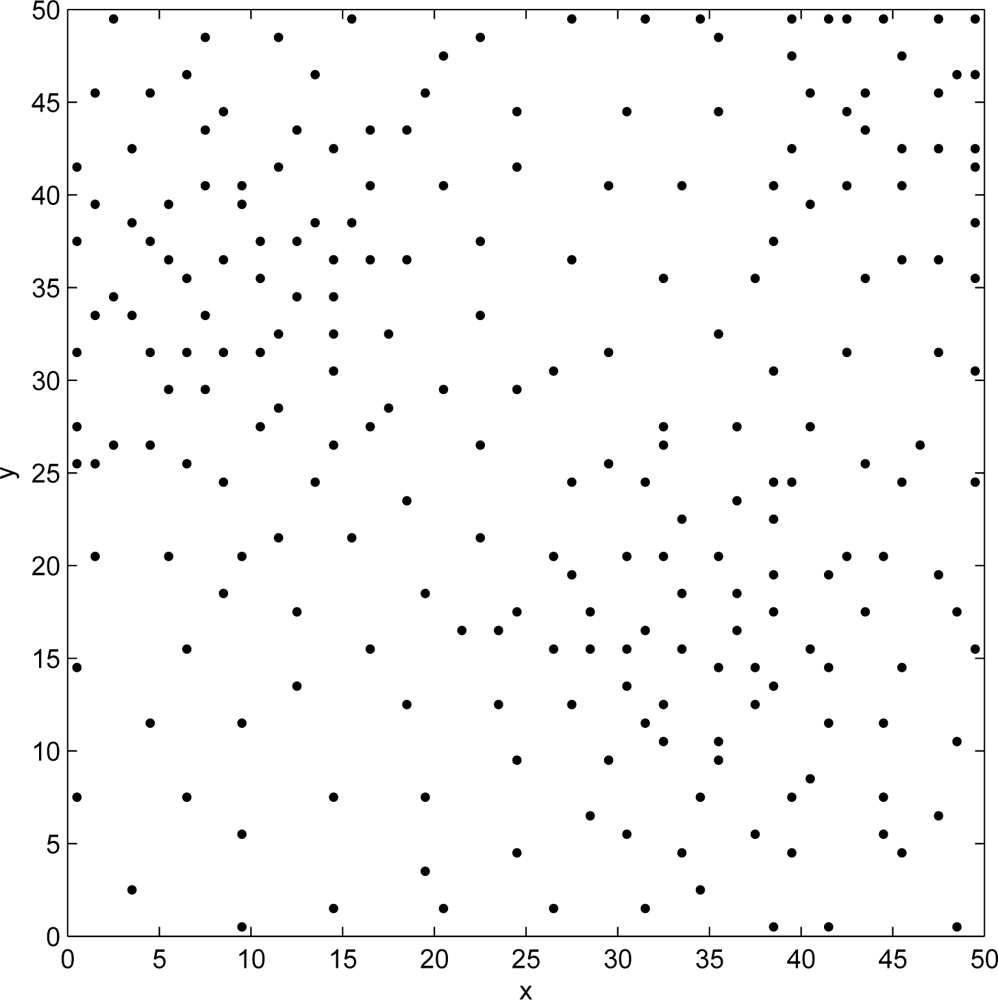
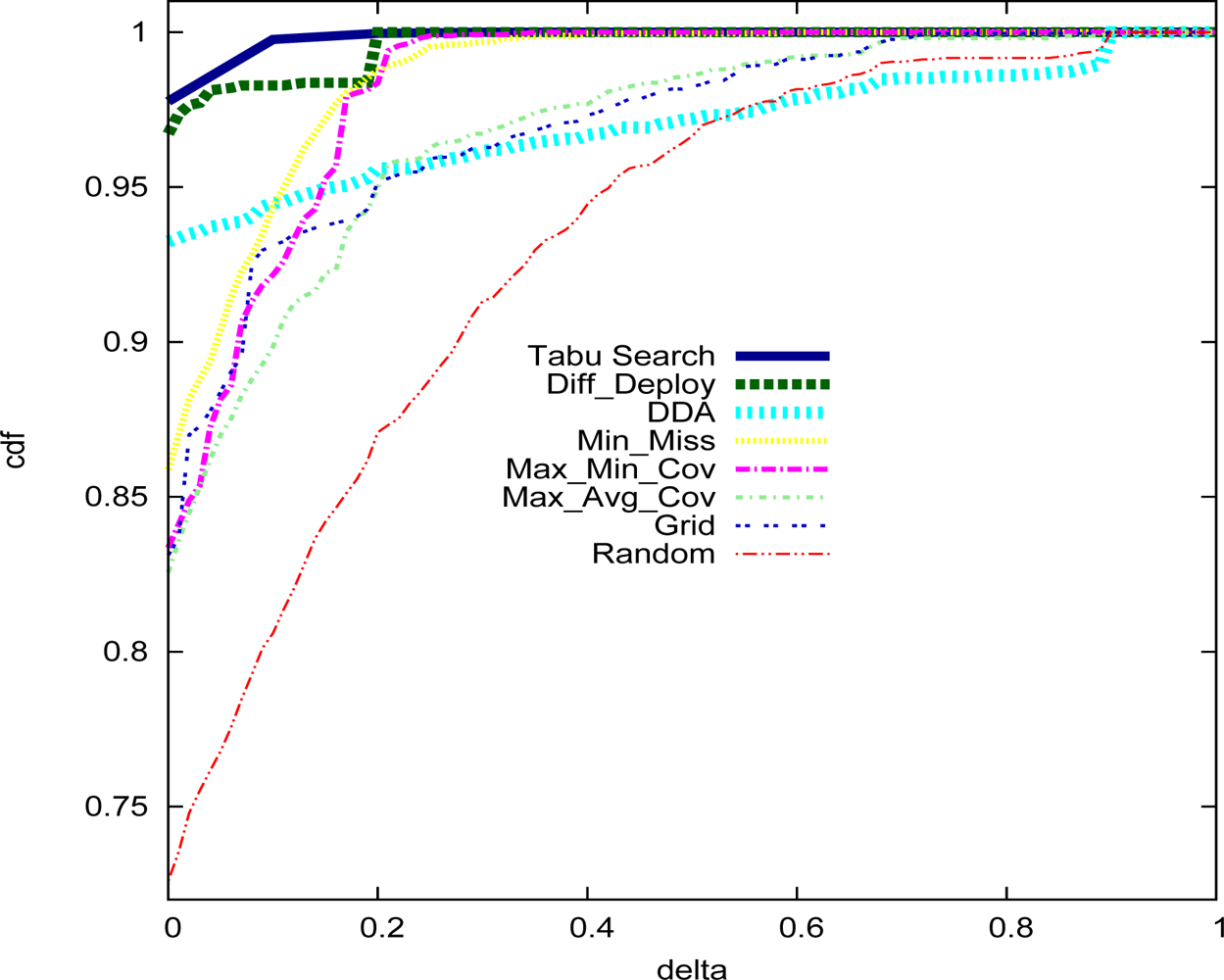
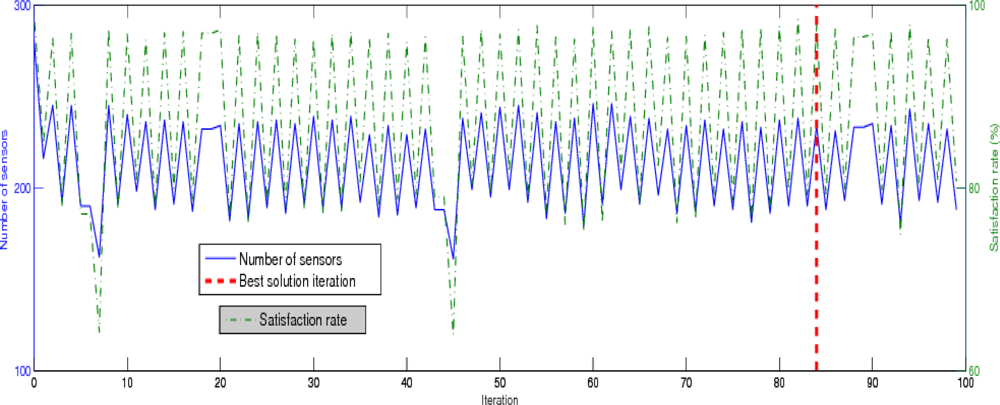
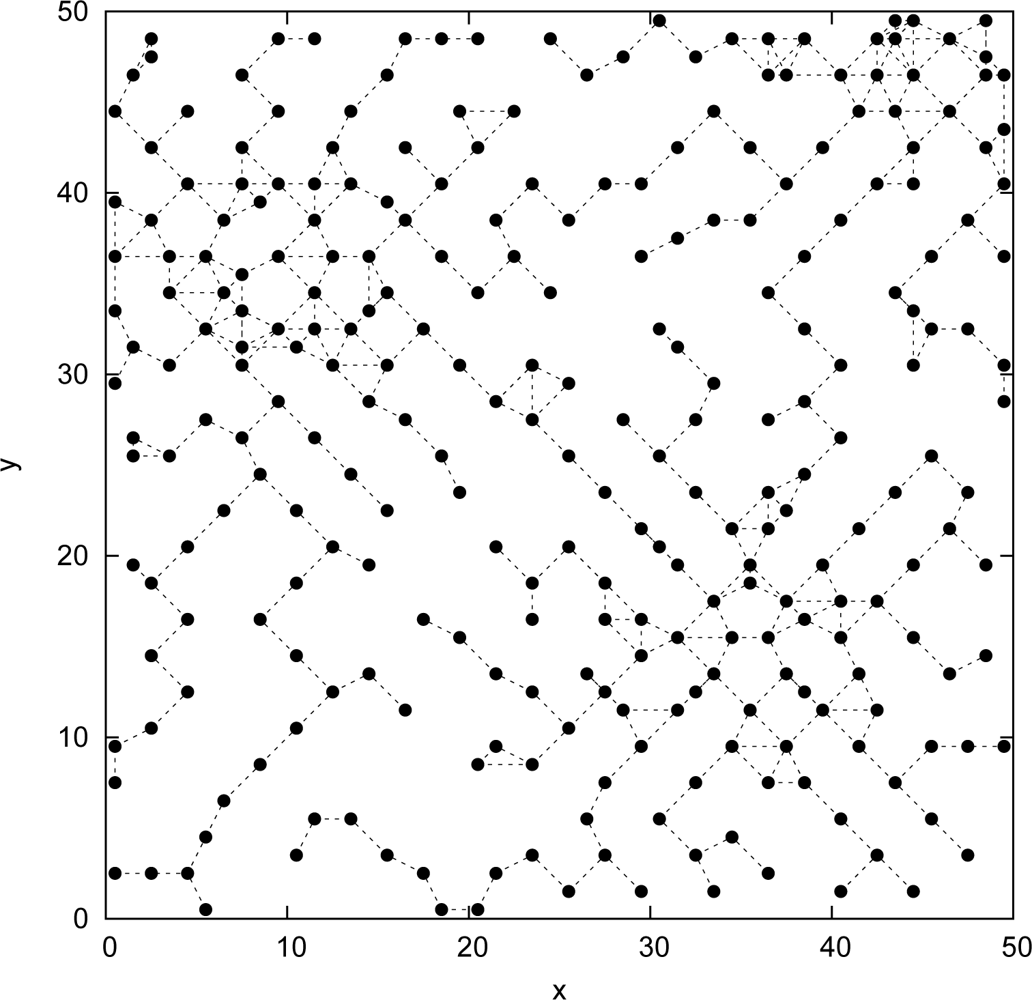
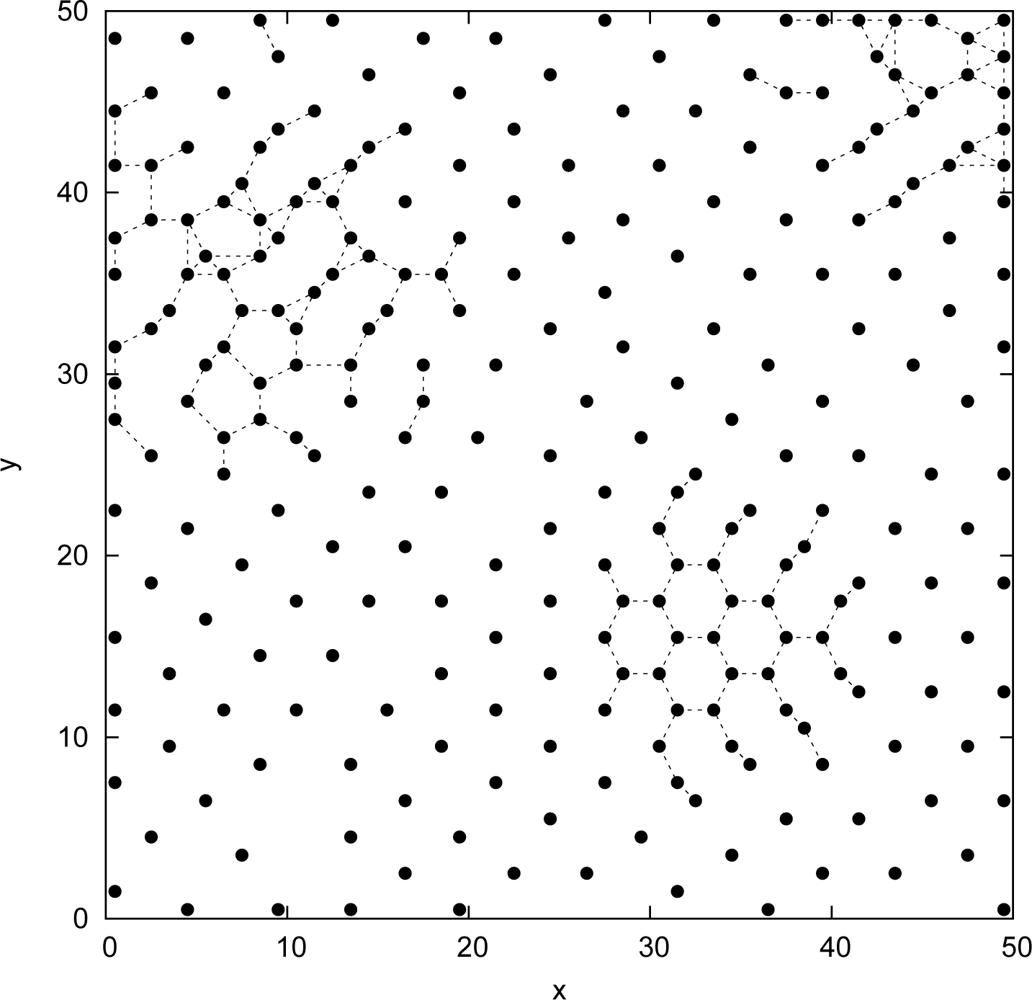
5. Performance Analysis
6. Conclusion and Future Work
References and Notes
- Akyildiz, I.F.; W. Su, Y. S.; Cayirci, E. Wireless Sensor Networks: a Survey. In Computer Networks: The International Journal of Computer and Telecommunications Networking; 2002; pp. 393–422. [Google Scholar]
- Huang, C.-F.; Tseng, Y.-C. The Coverage Problem in a Wireless Sensor Network. WSNA ’03: Proceedings of the 2nd ACM International Conference on Wireless Sensor Networks and Applications; 2003. [Google Scholar]
- Correia, L. H. A.; Macedo, D. F.; dos Santos, A.L.; Loureiro, A.A.F.; Nogueira, J.M.S. Transmission Power Control Techniques for Wireless Sensor Networks. Elsevier Computer Networks 2007. [Google Scholar]
- Maleki, M.; Pedram, M. Qom and Lifetime-constrained Random Deployment of Sensor Networks for Minimum Energy Consumption. IPSN ’05: Proceedings of the 4th International Symposium on Information Processing in Sensor Networks, Piscataway, NJ, USA; IEEE Press, 2005; p. 39. [Google Scholar]
- Chan, H.; Perrig, A.; Song, D. Random Key Predistribution Schemes for Sensor Networks. SP ’03: Proceedings of the 2003 IEEE Symposium on Security and Privacy, Washington, DC, USA; IEEE Computer Society, 2003; p. 197. [Google Scholar]
- Kar, K.; Banerjee, S. Node Placement for Connected Coverage in Sensor Networks. Proc. of WiOpt, Sophia Antipolis, France; 2003. [Google Scholar]
- Chakrabarty, K.; Iyengar, S.S.; Qi, H.; Cho, E. Grid Coverage for Surveillance and Target Location in Distributed Sensor Networks. IEEE Trans. Comput 2002, 51(12), 1448–1453. [Google Scholar]
- Dhillon, S.; Chakrabarty, K.; Iyengar, S. Sensor Placement for Grid Coverage under Imprecise Detections. Proceedings of International Conference on Information Fusion; 2002. [Google Scholar]
- Zou, Y.; Chakrabarty, K. Uncertainty-Aware and Coverage-Oriented Deployment for Sensor Networks. J. Parallel Distrib. Comput 2004, 64(7), 788–798. [Google Scholar]
- Zhang, J.; Tan, T.; S.H, S. Deployment Strategies for Differentiated Detection in Wireless Sensor Networks. SECON’06 2006. [Google Scholar]
- Aitsaadi, N.; Achir, N.; Boussetta, K.; Pujolle, G. Differentiated Underwater Sensor Network Deployment. IEEE/OES OCEANS’07 2007. [Google Scholar]
- Bai, X.; Kuma, S.; Xua, D.; Z., Y.; Lai, T. Deploying Wireless Sensors to Achieve Both Coverage and Connectivity. MobiHoc ’06: Proceedings of the 7th ACM International Symposium on Mobile Ad Hoc Networking and Computing; 2006; pp. 131–142. [Google Scholar]
- Y. Wang, C. H.; Tseng, Y. Efficient Deployment Algorithms for Ensuring Coverage and Connectivity of Wireless Sensor Networks. WICON ’05: Proceedings of the First International Conference on Wireless Internet; 2005; pp. 114–121. [Google Scholar]
- Elfes, A. Occupancy Grids: A Stochastic Spatial Representation for Active Robot Perception. Iyengar, S. S., Elfes, A., Eds.; In Autonomous Mobile Robots: Perception, Mapping, and Navigation (Vol. 1); pp. 60–70. IEEE Computer Society Press: Los Alamitos, CA, 1991. [Google Scholar]
- Kuo, S.-P.; Tseng, Y.-C.; Wu, F.-J.; Lin, C.-Y. A Probabilistic Signal-Strength-Based Evaluation Methodology for Sensor Network Deployment. AINA ’05: Proceedings of the 19th International Conference on Advanced Information Networking and Applications, Washington, DC, USA; IEEE Computer Society, 2005; pp. 319–324. [Google Scholar]
- Li, X.; Wan, P.; Wang, Y.; Frieder, O. Coverage in Wireless Ad-hoc Sensor Networks. ICC’02, IEEE International Conference on Communications; 2002. [Google Scholar]
- Brusco, M.; Stahl, S. all.; Branch-and-Bound Applications in Combinatorial Data Analysis; Springer, 2005. [Google Scholar]
- Glover, F. Tabu Search - Part I. ORSA journal on Computing 1989, 1(3), 190–206. [Google Scholar]
- Glover, F. Tabu Search - Part II. ORSA journal on Computing 1990, 2(1), 4–32. [Google Scholar]
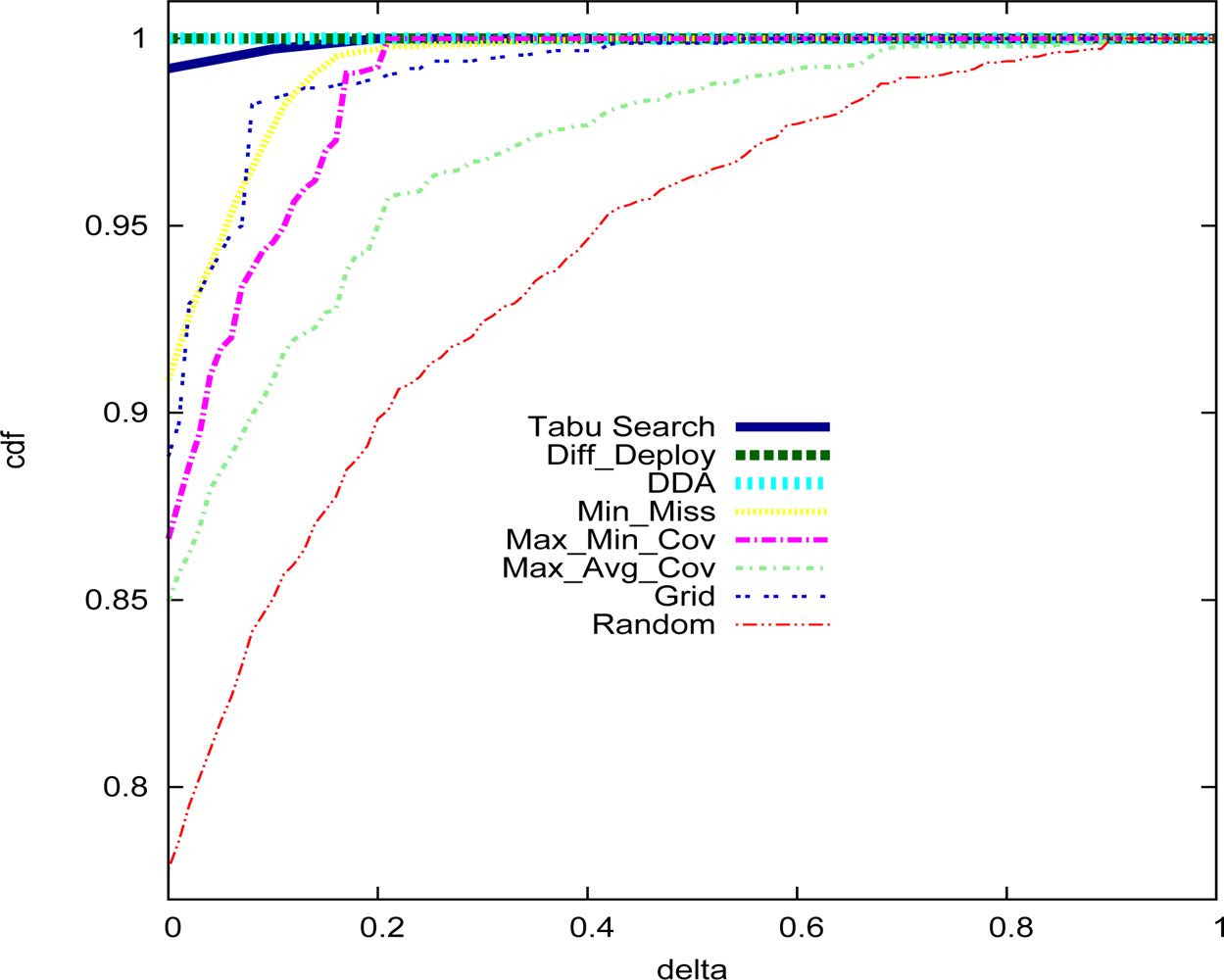
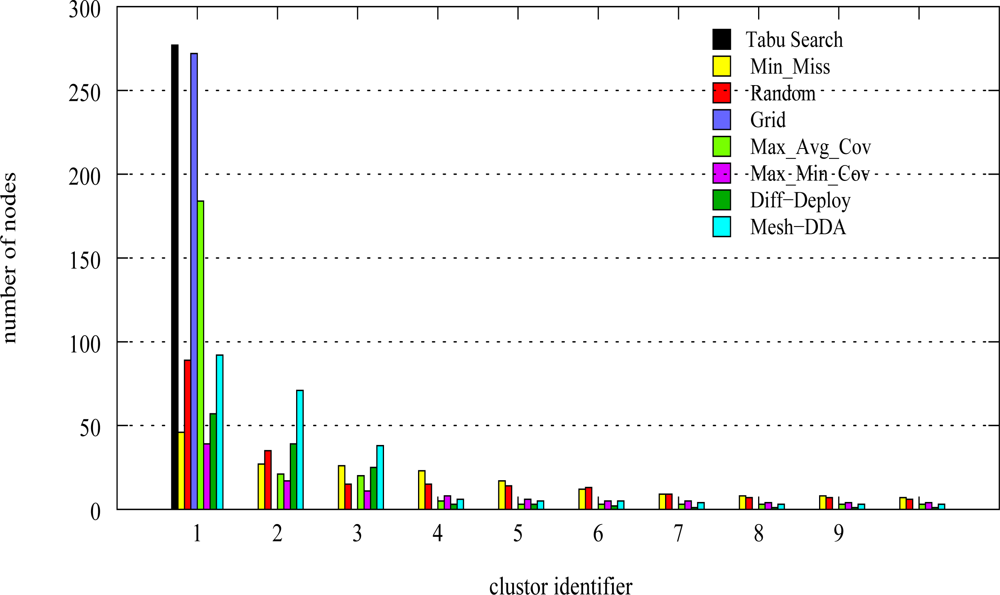
| Deployment strategy | Number of sensors |
|---|---|
| Random | 570 |
| Grid | 540 |
| Min_Miss | 351 |
| Max_Min_Cov | 385 |
| Max_Avg_Cov | 524 |
| Diff–Deploy | 235 |
| DDA | 251 |
| Tabu Search | 234 |
© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Aitsaadi, N.; Achir, N.; Boussetta, K.; Pujolle, G. A Tabu Search WSN Deployment Method for Monitoring Geographically Irregular Distributed Events. Sensors 2009, 9, 1625-1643. https://doi.org/10.3390/s90301625
Aitsaadi N, Achir N, Boussetta K, Pujolle G. A Tabu Search WSN Deployment Method for Monitoring Geographically Irregular Distributed Events. Sensors. 2009; 9(3):1625-1643. https://doi.org/10.3390/s90301625
Chicago/Turabian StyleAitsaadi, Nadjib, Nadjib Achir, Khaled Boussetta, and Guy Pujolle. 2009. "A Tabu Search WSN Deployment Method for Monitoring Geographically Irregular Distributed Events" Sensors 9, no. 3: 1625-1643. https://doi.org/10.3390/s90301625




