Comparison Between Fractional Vegetation Cover Retrievals from Vegetation Indices and Spectral Mixture Analysis: Case Study of PROBA/CHRIS Data Over an Agricultural Area
Abstract
:1. Introduction
2. Dataset
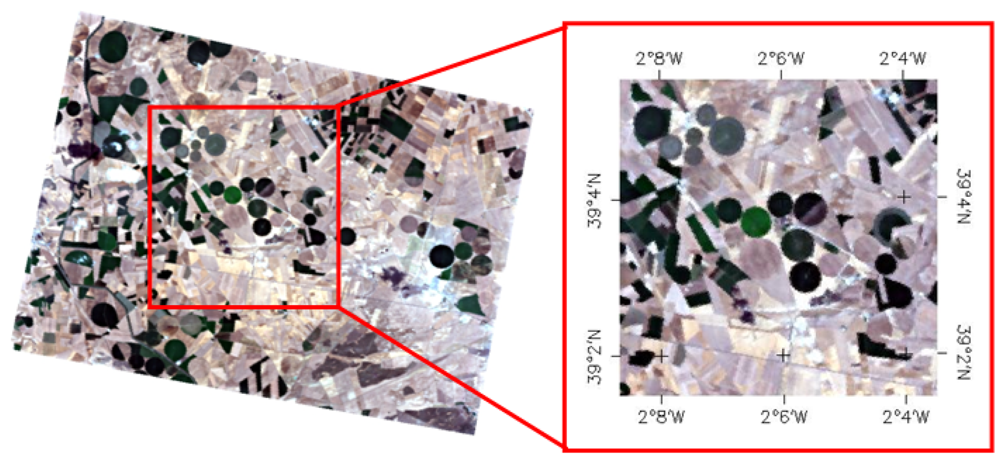
2.1. PROBA/CHRIS data, test site and the SPARC field campaigns
2.2. Atmospheric correction
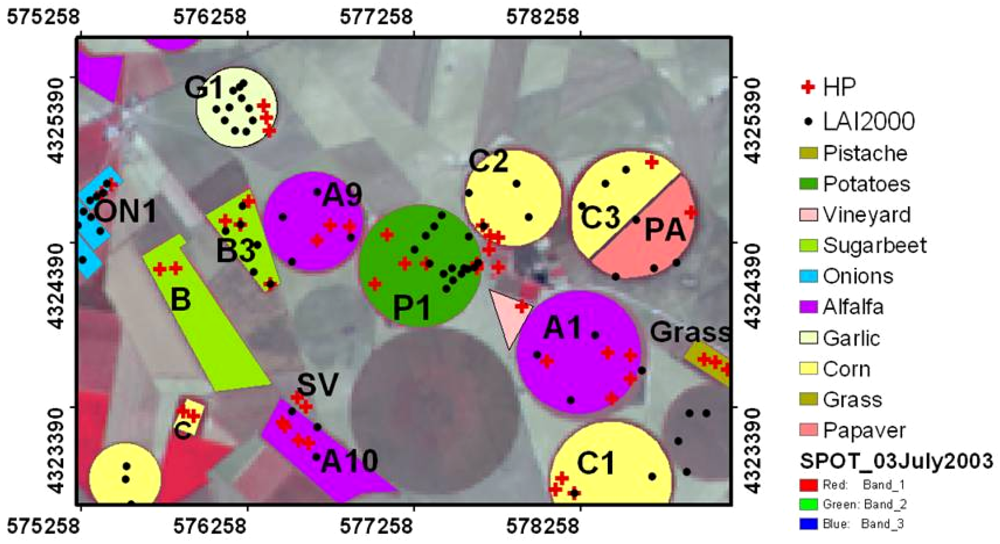
2.3. In-situ measurements
3. Derivation of FVC from Vegetation Indices
3.1. Normalized Difference Vegetation Index (NDVI)
3.2. Green Vegetation Index
3.3. Algorithms testing
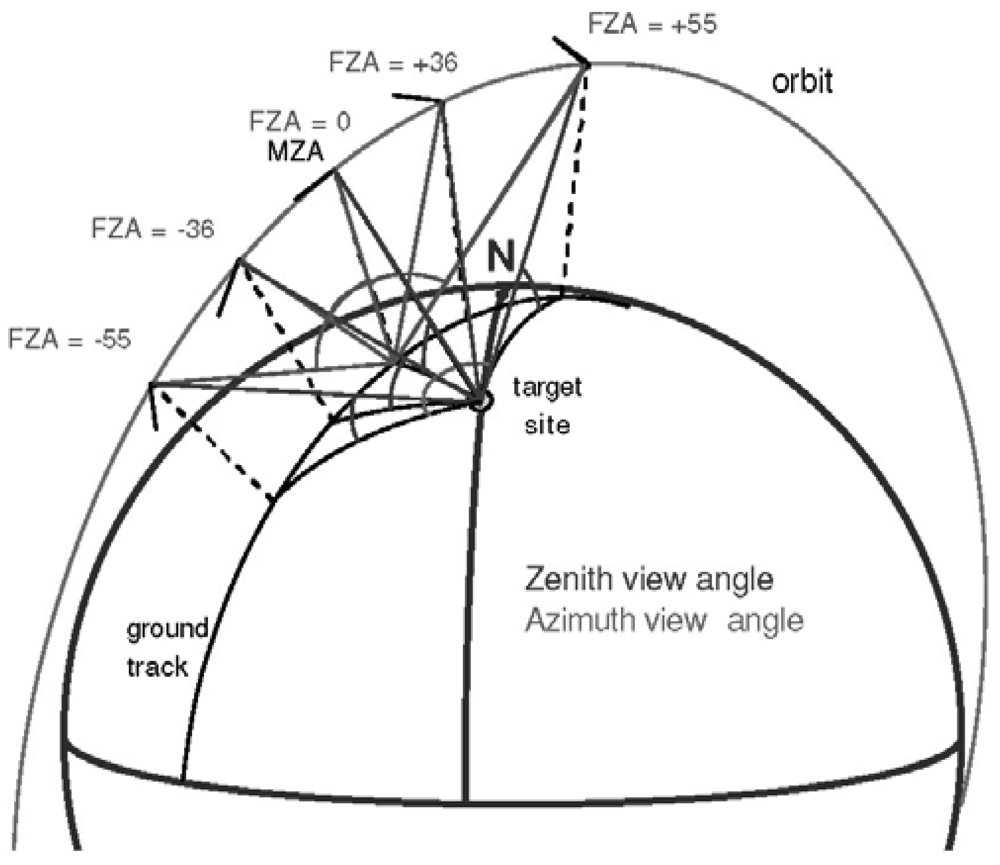
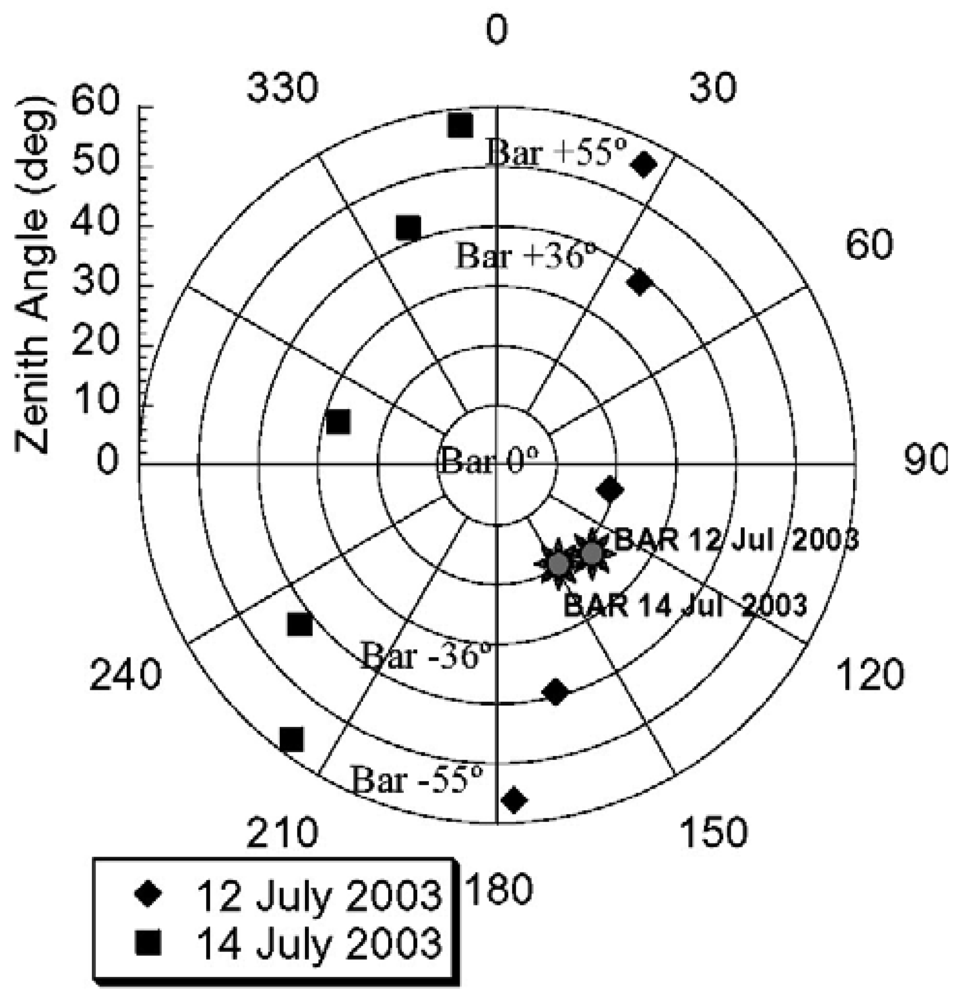
3.4. Angular sensitivity
4. Derivation of FVC from Spectral Mixture Analysis: case of Linear Spectral Unmixing
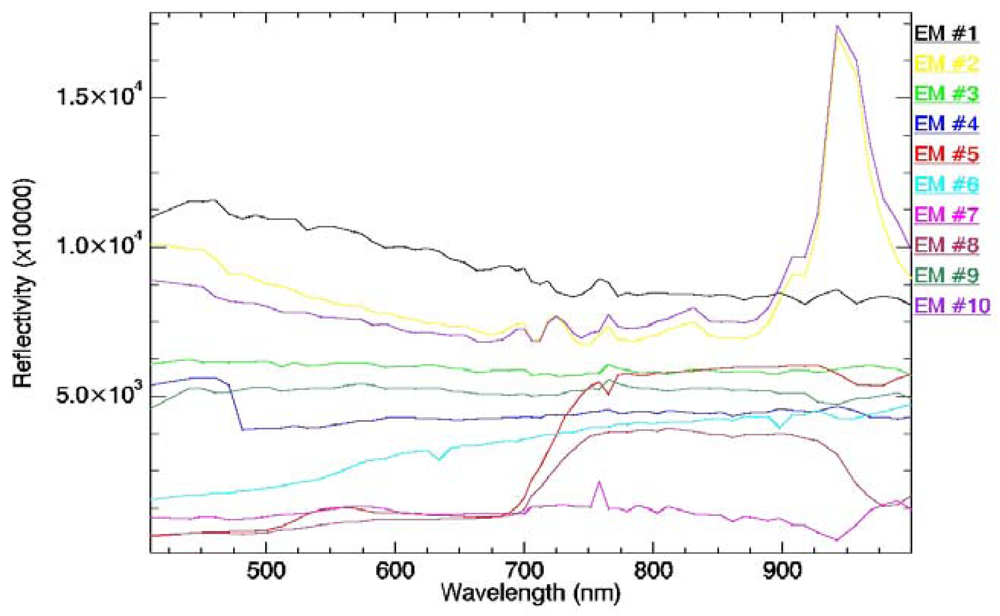
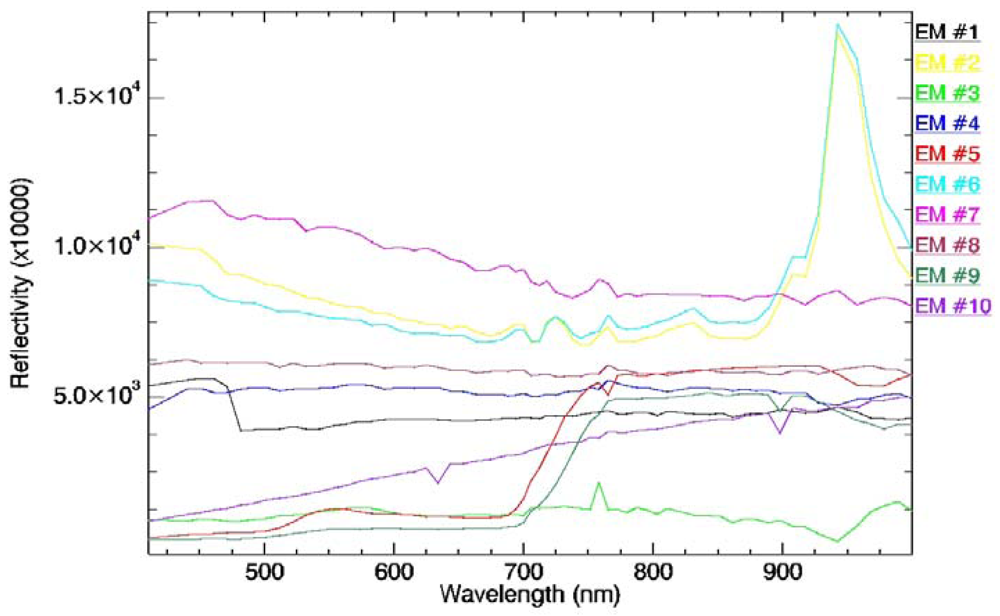
4.1. Endmember Extraction using a Land Use Map
4.2. Endmember Extraction using the Pixel Purity Index (PPI)
4.3. Automated Morphological Endmember Extraction (AMEE)
4.4. Algorithms testing
5. Summary and Conclusions
Acknowledgments
References
- Avissar, R; Pielke, R.A. A parameterization of heterogeneous land surfaces for atmospheric numerical models and its impact on regional meteorology. Monthly Weather Review 1989, 117, 2113–2136. [Google Scholar]
- Baret, F.; Clevers, J.G.P.W.; Steven, M.D. The Robustness of Canopy Gap Fraction Estimates from Red and Near-Infrared Reflectances: A Comparison of Approaches. Remote Sensing of Environment 1995, 54, 141–151. [Google Scholar]
- Barnsley, M.J.; Settle, J.J.; Cutter, M.; Lobb, D.; Teston, F. The PROBA/CHRIS mission: a low--cost smallsat for hyperspectral, multi-angle, observations of the Earth surface and atmosphere. IEEE Transactions on Geoscience and Remote Sensing 2004, 42, 1512–1520. [Google Scholar]
- Boardman, J.W.; Kruse, F.A.; Green, R.O. Mapping target signatures via partial unmixing of AVIRIS data. Proc. Summaries JPL Airborne Earth Sci. Workshop, Pasadena, CA; 1995; pp. 23–26. [Google Scholar]
- Camacho-De Coca, F.; García-Haro, F.J.; Gilabert, M.A.; Meliá, J. Vegetation cover seasonal changes assessment from TM imagery in a semi-arid landscape. International Journal of Remote Sensing 2004, 25(17), 3451–3476. [Google Scholar]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sensing of Environment 1997, 62, 241–252. [Google Scholar]
- Chang, C.-I.; Du, Q. Estimation of number of spectrally distinct signal sources in hyperspectral imagery. IEEE Transactions on Geoscience and Remote Sensing 2004, 42(3), 608–619. [Google Scholar]
- Cutter, M. Review of aspects associated with the CHRIS calibration. Proceedings of 2nd CHRIS/PROBA Workshop; ESA Publications Division: Frascati, Italy ESA-ESRIN. , 2004. [Google Scholar]
- Galvao, L.S.; Ponzoni, F.J.; Epiphanio, J.C.N.; Rudorff, B.F.T.; Formaggio, A.R. Sun and view angle effects on NDVI determination of land cover types in the Brazilian Amazon region with hyperspectral data. International Journal of Remote Sensing 25(10), 1861–1879.
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote sensing estimation of vegetation fraction. Remote Sensing of Environment 2002, 80, 76–87. [Google Scholar]
- Guanter, L.; Alonso, L.; Moreno, J. A Method for the Surface Reflectance Retrieval From PROBA/CHRIS Data Over Land: Application to ESA SPARC Campaigns. IEEE Transactions on Geoscience and Remote Sensing 2005, 43(12), 2908–2917. [Google Scholar]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. International Journal of Remote Sensing 1998, 19(8), 1533–1543. [Google Scholar]
- Jiménez-Munoz, J.C.; Sobrino, J.A.; Guaner, L.; Moreno, J.; Plaza, A.; Martínez, P. Fraccional Vegetation Cover Estimation from CHRIS/PROBA Data: Methods, Análisis of Angular Effects and Application to the Land Surface Emissivity Retrieval. Proceedings of the 3rd ESA CHRIS/Proba Workshop, March 2005; ESA Publications Division, ESTEC: Noordwijk, Holland.
- Kallel, A.; Le Hégarat-Mascle, S.; Ottlé, C.; Hubert-Moy, L. Determination of vegetation cover fraction by inversion of a four-parameter model based on isoline parametrization. Remote Sensing of Environment 2007, 111, 553–566. [Google Scholar]
- Kallel, A.; Le Hégarat-Mascle, S.; Hubert-Moy, L.; Ottlé, C. Fusion of Vegetation Indices Using Continuous Belief Functions and Cautious-Adaptive Combination Rule. IEEE Transactions on Geoscience and Remote Sensing 2008, 46(5), 1499–1513. [Google Scholar]
- Kaufman, Y.J.; Tanre, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. IEEE Transactions on Geoscience and Remote Sensing 1992, 30, 261–270. [Google Scholar]
- Malingreau, J.P. Global vegetation dynamics: satellite observations over Asia. International Journal of Remote Sensing 1986, 7, 1121–1146. [Google Scholar]
- Martínez, B.; Baret, F.; Camacho-de Coca, F.; García-Haro, F.J.; Verger, A.; Meliá, J. Validation of MSG vegetation products Part I. Field retrieval of LAI and FVC from hemispherical photographs. In Remote Sensing for Agriculture, Ecosystem and Hydrology; Owe, M., D'Urso, G., Gouweleeuw, B.T., Jochum, A.M., Eds.; SPIE: Bellingham, WA, 2004; Volume 5568, pp. 57–68. [Google Scholar]
- Moreno, J.; et al. The SPECTRA Barrax Campaign (SPARC): Overview and first results from CHRIS data. Proceedings of 2nd CHRIS/PROBA Workshop; ESA Publications Division: Frascati, Italy ESA-ESRIN. , 2004. [Google Scholar]
- Plaza, A.; Martínez, P.; Pérez, R.; Plaza, J. Spatial/spectral endmember extraction by multidimensional morphological operations. IEEE Transactions on Geoscience and Remote Sensing 2002, 40(9), 2025–2041. [Google Scholar]
- Plaza, A.; Martínez, P.; Pérez, R.; Plaza, J. A quantitative and comparative analysis of endmember extraction algorithms from hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing 2004, 42(3), 650–663. [Google Scholar]
- Plaza, A.; Chang, C.-I. Impact of initialization on design of endmember extraction algorithms. IEEE Transactions on Geoscience and Remote Sensing 2006, 44(11), 3397–3407. [Google Scholar]
- Research Systems, ENVI User's Guide; Research Systems, Inc.: Boulder, CO, 2006.
- Rouse, J.W.; Haas, R.H., Jr.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. Proc. ERTS-1 Symposium 3rd, Greenbelt, MD, 10–15 Dec. 1973; Vol. 1. NASA SP-351. NASA: Washington, DC, 1974. [Google Scholar]
- Sabol, D.E.; Gillespie, A.R.; Adams, J.B.; Smith, M.O.; Tucker, C.J. Structural stage in Pacific Northwest forests estimated using simple mixing models of multispectral images. Remote Sensing of Environment 2002, 80, 1–16. [Google Scholar]
- Smith, M.O.; Adams, J.B.; Sabol, D.E. Spectral mixture analysis: new strategies for the analysis of multispectral data. In Imaging Spectrometry – A Tool for Environmental Observations, Euro Courses, Remote Sensing; Hill, J., Megier, J., Eds.; Dordrecht; Kluwer Academic; Volume 4, 1994; pp. 125–143. [Google Scholar]
- Sobrino, J.A.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: application to Morocco. International Journal of Remote Sensing 2000, 21(2), 353–366. [Google Scholar]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martínez, P. Land Surface Emissivity Retrieval From Different VNIR and TIR Sensors. IEEE Transactions on Geoscience and Remote Sensing 2008, 46(2), 316–327. [Google Scholar]
- Trimble, S.W. Geomorphic effects of vegetation cover and management: some time and space considerations in prediction of erosion and sediment yield. In Vegetation and Erosion; Thornes, J.B., Ed.; London; John Wiley & Sons, 1990; pp. 55–66. [Google Scholar]
- Vercher, A.; Camacho de Coca, F.; Meliá, J. Influencia de la geometría de adquisición en el NDVI. Revista de Teledetección 2004, 21, 95–99, (in Spanish with English abstract). [Google Scholar]
- Verrelst, J.; Schaepman, M.E.; Koetz, B.; Kneubühler, M. Angular sensitivity analysis of vegetation indices derived from CHRIS/PROBA data. Remote Sensing of Environment 2008, 112, 2341–2353. [Google Scholar]
- Weiss, M.; Baret, F. Evaluation of canopy biophysical variable retrieval performances from the accumulation of large swath satellite data. Remote Sensing of Environment 1999, 70, 293–306. [Google Scholar]
- Wittich, K.P.; Hansinng, O. Area-averaged vegetative cover fraction estimated from satellite data. International Journal of Biometeorology 1995, 38, 209–215. [Google Scholar]
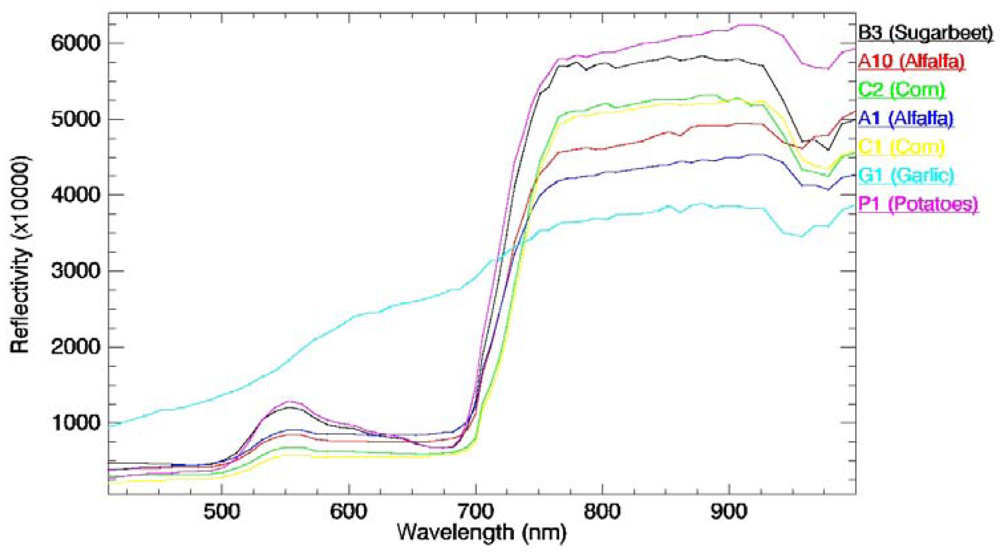
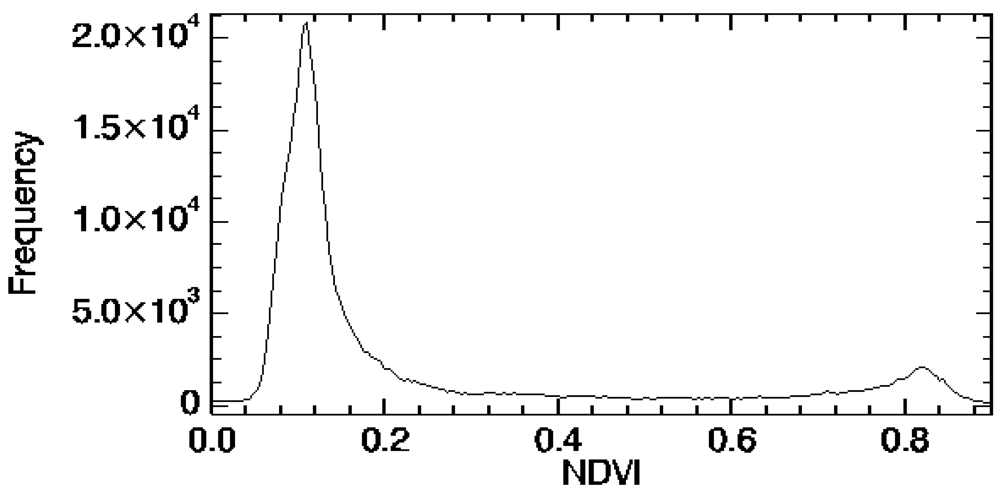
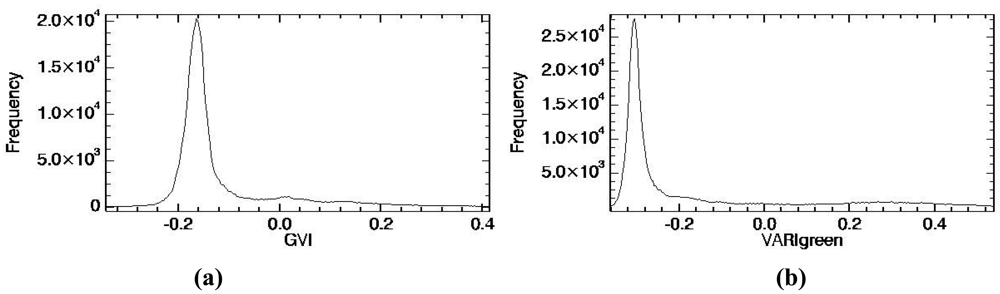
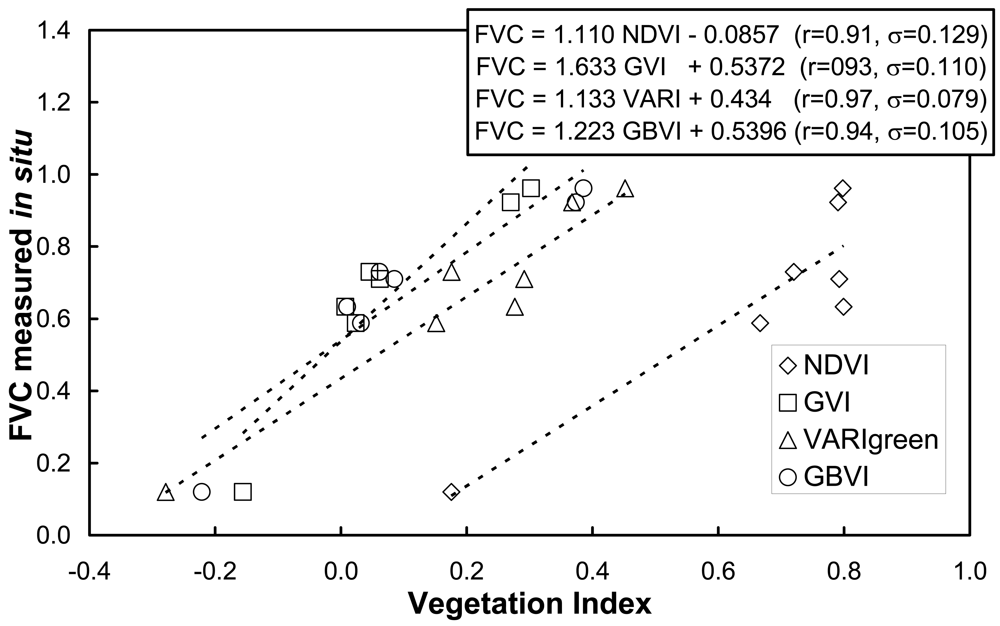
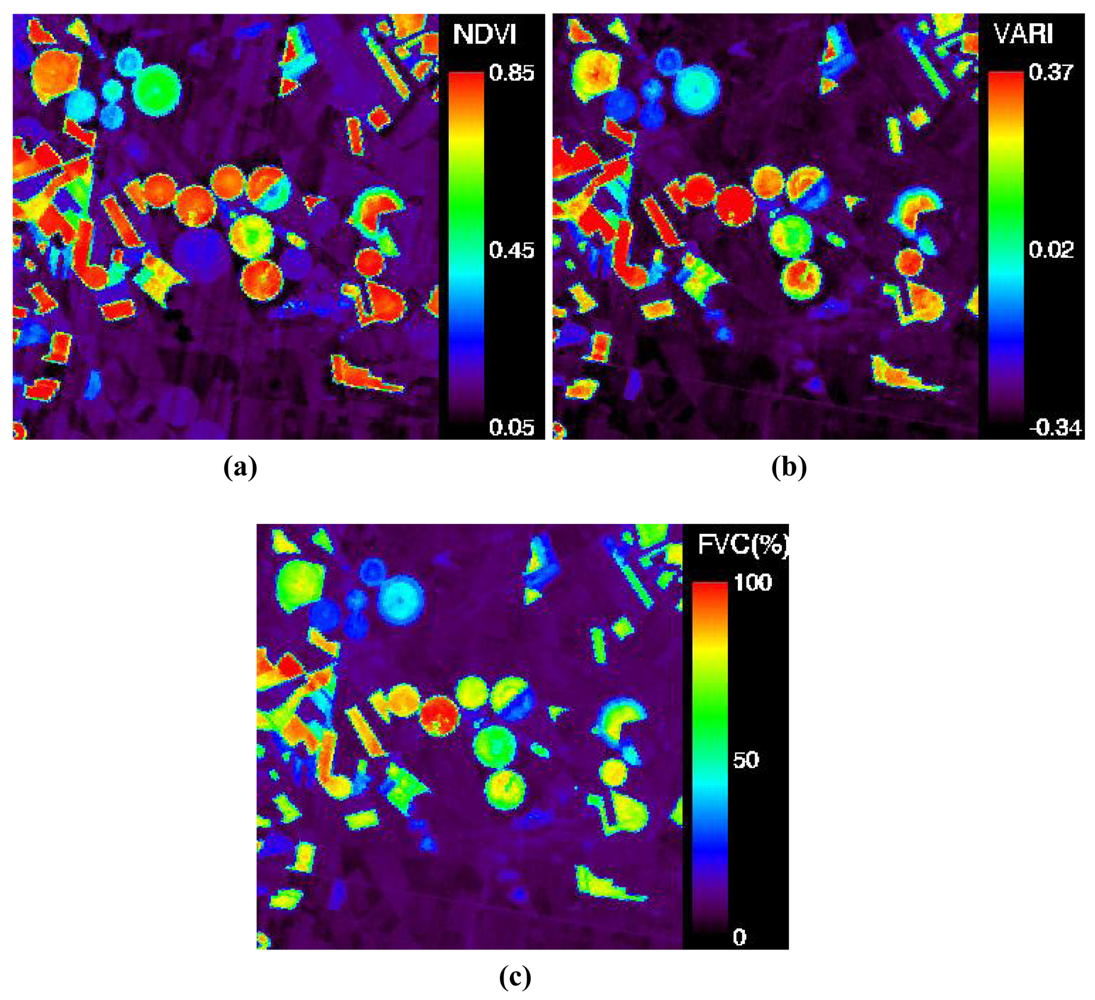
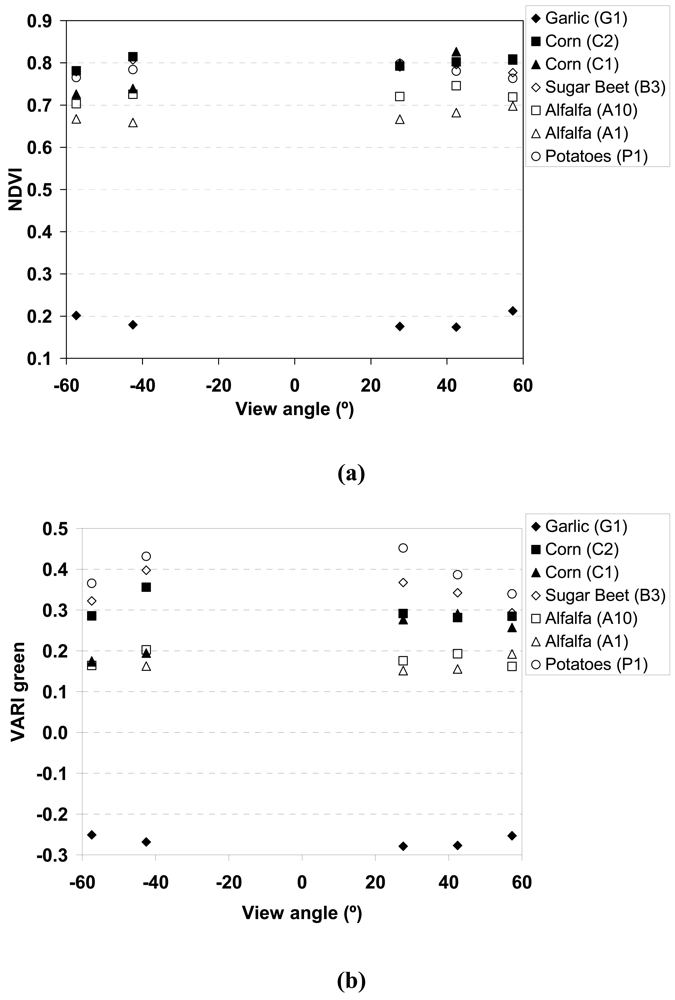
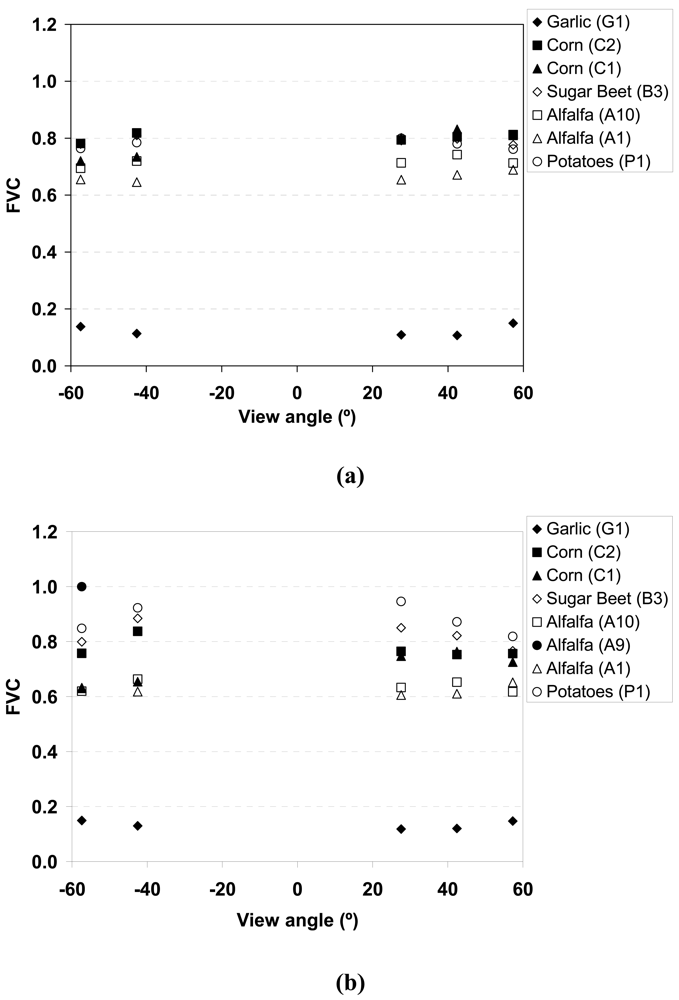


| Sample | Notation | FVCin situ | σ |
|---|---|---|---|
| Garlic | G1 | 0.12 | 0.09 |
| Corn | C2 | 0.71 | 0.12 |
| Corn | C1 | 0.63 | 0.08 |
| Sugarbeet | B3 | 0.923 | 0.013 |
| Alfalfa | A10 | 0.73 | 0.12 |
| Alfalfa | A1 | 0.59 | 0.12 |
| Potatoes | P1 | 0.96 | 0.04 |
| Sample | Notation | NDVI | σ |
|---|---|---|---|
| Garlic | G1 | 0.18 | 0.02 |
| Corn | C2 | 0.792 | 0.014 |
| Corn | C1 | 0.80 | 0.04 |
| Sugarbeet | B3 | 0.791 | 0.013 |
| Alfalfa | A10 | 0.72 | 0.05 |
| Alfalfa | A1 | 0.67 | 0.06 |
| Potatoes | P1 | 0.80 | 0.03 |
| Sample | Notation | GVI | σ | VARIgreen | σ | GBVI | σ |
|---|---|---|---|---|---|---|---|
| Garlic | G1 | -0.156 | 0.011 | -0.279 | 0.014 | -0.221 | 0.015 |
| Corn | C2 | 0.06 | 0.03 | 0.29 | 0.02 | 0.09 | 0.04 |
| Corn | C1 | 0.01 | 0.03 | 0.28 | 0.07 | 0.01 | 0.03 |
| Sugarbeet | B3 | 0.270 | 0.016 | 0.367 | 0.018 | 0.37 | 0.02 |
| Alfalfa | A10 | 0.05 | 0.04 | 0.18 | 0.06 | 0.06 | 0.06 |
| Alfalfa | A1 | 0.02 | 0.04 | 0.15 | 0.06 | 0.03 | 0.05 |
| Potatoes | P1 | 0.30 | 0.05 | 0.45 | 0.06 | 0.39 | 0.06 |
| VI | VIs | VIv | bias | stdev | RMSE |
|---|---|---|---|---|---|
| NDVI | 0.11 (histogram) | 0.82 (histogram) | 0.13 | 0.14 | 0.19 |
| NDVI | -0.14 (minimum) | 0.91 (maximum) | 0.11 | 0.12 | 0.17 |
| NDVI | 0.11 (histogram) | 0.91 (maximum) | 0.04 | 0.12 | 0.13 |
| NDVI | 0.15 (global) | 0.90 (global) | 0.04 | 0.13 | 0.13 |
| NDVI | 0.08 (in situ) | 0.98 (in situ) | 0.00 | 0.13 | 0.13 |
| GVI | -0.34 (minimum) | 0.41 (maximum) | -0.11 | 0.11 | 0.16 |
| GVI | -0.16 (histogram) | 0.41 (maximum) | -0.25 | 0.10 | 0.27 |
| GVI | -0.33 (in situ) | 0.28 (in situ) | 0.00 | 0.11 | 0.11 |
| VARIgreen | -0.36 (minimum) | 0.54 (maximum) | -0.04 | 0.07 | 0.08 |
| VARIgreen | -0.31 (histogram) | 0.54 (maximum) | -0.06 | 0.07 | 0.10 |
| VARIgreen | -0.38 (in situ) | 0.50 (in situ) | 0.00 | 0.08 | 0.08 |
| GBVI | -0.45 (minimum) | 0.49 (maximum) | -0.08 | 0.10 | 0.13 |
| GBVI | -0.24 (histogram) | 0.49 (maximum) | -0.20 | 0.10 | 0.22 |
| GBVI | -0.44 (in situ) | 0.38 (in situ) | 0.00 | 0.11 | 0.11 |
| FVC from NDVI | ||||||||
|---|---|---|---|---|---|---|---|---|
| FZA (°) | VZA (°) | G1 | C2 | C1 | B3 | A10 | A1 | P1 |
| -55 | -57.4 | 26.5 | -1.6 | -10.2 | -1.6 | -2.7 | 0.1 | -4.5 |
| -36 | -42.5 | 4.3 | 3.1 | -8.3 | 2.3 | 0.8 | -1.3 | -1.9 |
| 0 | 27.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 36 | 42.4 | -1.5 | 1.4 | 3.7 | 0.8 | 4.0 | 2.6 | -2.4 |
| 55 | 57.3 | 37.7 | 2.4 | 1.0 | -1.9 | -0.1 | 5.3 | -4.8 |
| mean | 13.4 | 1.1 | -2.8 | -0.1 | 0.4 | 1.3 | -2.7 | |
| std dev | 17.6 | 1.9 | 6.1 | 1.7 | 2.4 | 2.6 | 2.0 | |
| FVC from VARIgreen | ||||||||
| FZA (°) | VZA (°) | G1 | C2 | C1 | B3 | A10 | A1 | P1 |
| -55 | -57.40 | 26.5 | -0.9 | -15.7 | -6.0 | -2.1 | 4.5 | -10.4 |
| -36 | -42.53 | 10.1 | 9.5 | -12.4 | 4.0 | 4.8 | 2.1 | -2.4 |
| 0 | 27.60 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 36 | 42.44 | 1.7 | -1.5 | 2.2 | -3.3 | 3.1 | 0.8 | -7.9 |
| 55 | 57.29 | 24.5 | -1.1 | -2.9 | -9.9 | -2.5 | 7.6 | -13.5 |
| mean | 12.6 | 1.2 | -5.8 | -3.0 | 0.7 | 3.0 | -6.8 | |
| std dev | 12.4 | 4.7 | 7.9 | 5.3 | 3.2 | 3.1 | 5.6 | |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jiménez-Muñoz, J.C.; Sobrino, J.A.; Plaza, A.; Guanter, L.; Moreno, J.; Martinez, P. Comparison Between Fractional Vegetation Cover Retrievals from Vegetation Indices and Spectral Mixture Analysis: Case Study of PROBA/CHRIS Data Over an Agricultural Area. Sensors 2009, 9, 768-793. https://doi.org/10.3390/s90200768
Jiménez-Muñoz JC, Sobrino JA, Plaza A, Guanter L, Moreno J, Martinez P. Comparison Between Fractional Vegetation Cover Retrievals from Vegetation Indices and Spectral Mixture Analysis: Case Study of PROBA/CHRIS Data Over an Agricultural Area. Sensors. 2009; 9(2):768-793. https://doi.org/10.3390/s90200768
Chicago/Turabian StyleJiménez-Muñoz, Juan C., José A. Sobrino, Antonio Plaza, Luis Guanter, José Moreno, and Pablo Martinez. 2009. "Comparison Between Fractional Vegetation Cover Retrievals from Vegetation Indices and Spectral Mixture Analysis: Case Study of PROBA/CHRIS Data Over an Agricultural Area" Sensors 9, no. 2: 768-793. https://doi.org/10.3390/s90200768









